Experimental Evidence of Capillary Interruption of a Liquid Jet ()
Keywords:Mariotte Bottle, Modified Bernoulli Equation, Interfacial Energy Density Correction

1. Introduction
The simplest example of the use of Bernoulli’s equation in introductory physics course [1] is Torricelli’s law, which relates the velocity of efflux of a liquid issuing from the small orifice in a tank  to the hydrostatic head
to the hydrostatic head 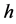 of the liquid:
of the liquid:
 (1)
(1)
where  is the acceleration due to gravity. This result was recently questioned [2] [3] in the light of experimental evidence that at any nonzero
is the acceleration due to gravity. This result was recently questioned [2] [3] in the light of experimental evidence that at any nonzero  the average discharge velocity is zero. The reason is that Bernoulli’s equation, which is a macroscopic mechanical balance of energy of an ideal, non-viscous liquid, cannot strictly be applied in the case of real flow due to the various dissipation effects [4] [5] , which Equation (1) does not include. Nevertheless, taking into account the energy losses, Bernoulli’s equation was used [3] to modified Equation (1) as follows:
the average discharge velocity is zero. The reason is that Bernoulli’s equation, which is a macroscopic mechanical balance of energy of an ideal, non-viscous liquid, cannot strictly be applied in the case of real flow due to the various dissipation effects [4] [5] , which Equation (1) does not include. Nevertheless, taking into account the energy losses, Bernoulli’s equation was used [3] to modified Equation (1) as follows:
 (2)
(2)
where 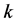 and
and  are empirical constants related, respectively, with the losses due to the losses proportional to the fluid velocity squared and the losses independent of the fluid velocity. While the presence of the constant
are empirical constants related, respectively, with the losses due to the losses proportional to the fluid velocity squared and the losses independent of the fluid velocity. While the presence of the constant  in Equation (2) is somehow justified, there is no physical explanation for the constant
in Equation (2) is somehow justified, there is no physical explanation for the constant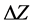 . The interpretation proposed in [6] associates
. The interpretation proposed in [6] associates  with capillary pressure, which hold up the liquid from coming out of the hole.
with capillary pressure, which hold up the liquid from coming out of the hole.
To give further understanding to this problem, we use the Bernoulli equation modified by the surface energy density and viscosity effect [5] to explain the physical meaning of the correction term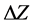 . The validity of this approach is demonstrated by measuring the discharge velocity of Newtonian liquids with different surface tension and viscosity using discharge tubes of different aspect ratio.
. The validity of this approach is demonstrated by measuring the discharge velocity of Newtonian liquids with different surface tension and viscosity using discharge tubes of different aspect ratio.
2. Theoretical Background
Consider a Newtonian liquid of density , viscosity
, viscosity  and surface tension
and surface tension  discharged under gravity through the short tube of radius
discharged under gravity through the short tube of radius  and length
and length  attached at the side of a large tank. A volume flux from the tube generates the axisymmetrical cylindrical jet of radius
attached at the side of a large tank. A volume flux from the tube generates the axisymmetrical cylindrical jet of radius . We apply the modified Bernoulli equation [5] with the interfacial energy density along the streamline as is schematically shown in Figure 1:
. We apply the modified Bernoulli equation [5] with the interfacial energy density along the streamline as is schematically shown in Figure 1:
 (3)
(3)
where  is the mechanical pressure,
is the mechanical pressure,  is the velocity at any point,
is the velocity at any point, 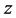 is the height of the liquid above a reference level, all measured at the same point inside the liquid. The term
is the height of the liquid above a reference level, all measured at the same point inside the liquid. The term  represents the interfacial energy density required to create a unit of free surface area of the jet, and
represents the interfacial energy density required to create a unit of free surface area of the jet, and  is the pressure head loss along the streamline due to various dissipative effects.
is the pressure head loss along the streamline due to various dissipative effects.
Let us apply Equation (3) for two points 1 and 2 of Figure 1, i.e. at the free liquid surface in the vessel and inside the jet. Since ,
,  ,
,  and
and , we get
, we get
 (4)
(4)
The derivative  in Equation (4) consists of two components, one being tangential and the other normal to the jet surface:
in Equation (4) consists of two components, one being tangential and the other normal to the jet surface:
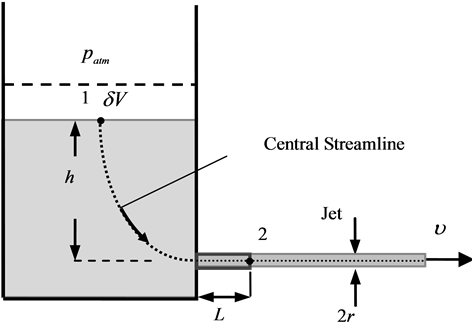
Figure 1. Schematic illustration of the discharge of Newtonian liquid from the tank.
 (5)
(5)
For an ideal cylindrical jet of length , volume
, volume  and surface area
and surface area , we have:
, we have: 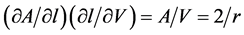 and
and , where
, where  is due to formation of a fluid-air interface and
is due to formation of a fluid-air interface and  due to its curvature. The physical meaning of these two effects can be clarified by considering the corresponding values of free energies. Whereas
due to its curvature. The physical meaning of these two effects can be clarified by considering the corresponding values of free energies. Whereas  is the interfacial surface energy, the value
is the interfacial surface energy, the value  gives
gives , the excess free energy due to the pressure jump across the interface. These two effects have to be considered together, therefore we have
, the excess free energy due to the pressure jump across the interface. These two effects have to be considered together, therefore we have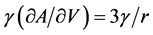 . However, since the shape of the jet is not a perfect cylinder, we introduce in this expression the shape factor
. However, since the shape of the jet is not a perfect cylinder, we introduce in this expression the shape factor  to get
to get
 (6)
(6)
Dissipation term 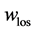 can be expressed [7] -[10] as the sum of the head loss at orifice entry of the tube and losses due to the skin friction within the tube orifice:
can be expressed [7] -[10] as the sum of the head loss at orifice entry of the tube and losses due to the skin friction within the tube orifice:
 (7)
(7)
Here,  is the coefficient of entry pressure loss, and
is the coefficient of entry pressure loss, and  is the skin friction coefficient, which depends on Reynolds number
is the skin friction coefficient, which depends on Reynolds number  as
as
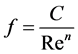 (8)
(8)
where  and
and  are constants.
are constants.
Combining Equation (4) with Equations (6) - (8), we obtain the sought equation for the average discharge velocity as a function of the pressure head:
 (9)
(9)
where constants  and
and  are typically,
are typically,  and
and 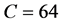 for laminar flow,
for laminar flow,  and
and  for turbulent flow [10] . For laminar flow, Equation (9) reduces to the quadratic equation for
for turbulent flow [10] . For laminar flow, Equation (9) reduces to the quadratic equation for  with the solution:
with the solution:
 (10)
(10)
which involves the effects of viscous resistance and surface tension showing that at  the discharge velocity approaches to zero. We refer to this phenomenon as capillary interruption of a liquid jet. When the viscosity term
the discharge velocity approaches to zero. We refer to this phenomenon as capillary interruption of a liquid jet. When the viscosity term  becomes negligible, Equation (10) reduces to Equation (2):
becomes negligible, Equation (10) reduces to Equation (2):
 (11)
(11)
with . Equations (10) and (11) for the discharge velocity
. Equations (10) and (11) for the discharge velocity  versus the pressure head
versus the pressure head  of real liquids are the main result of present paper.
of real liquids are the main result of present paper.
3. Experiment
To check the validity of the above theoretical approach we quantify the energy losses during the discharge of a real Newtonian fluid from the Mariotte bottle [11] -[13] (see Figure 2). We design a Mariotte bottle from the

Figure 2. Experimental set up for the measuring the discharge rate as a function of the pressure head υ(h).
plastic cylinder of diameter 78 mm and height 40 cm with the opening in the lower part of the wall. Plexiglas’s flange with O-ring at the top of the cylinder provides a seal.
An air intake tube of diameter 8 mm and length 50 cm was inserted through the flange using a compression fitting that seals with an o-ring. Glass capillary tubes with  and different lengths were separated inserted in the opening of the cylinder. As a liquid flows out of the bottle it is replaced by air, which enters through the air intake tube and bubbles up through the liquid level to provide a constant flow. The head, equal to the vertical distance from the bottom of the air-inlet tube to the outlet tube, was varied by raising or lowering the inserted tube. The discharge speed of liquid versus the pressure head was determined as follows. The force sensor, connected through a data logger to a computer, continuously recorded the fluid weight
and different lengths were separated inserted in the opening of the cylinder. As a liquid flows out of the bottle it is replaced by air, which enters through the air intake tube and bubbles up through the liquid level to provide a constant flow. The head, equal to the vertical distance from the bottom of the air-inlet tube to the outlet tube, was varied by raising or lowering the inserted tube. The discharge speed of liquid versus the pressure head was determined as follows. The force sensor, connected through a data logger to a computer, continuously recorded the fluid weight  escaped from the bottle as a function of time. The average discharge velocity was calculated from the slope
escaped from the bottle as a function of time. The average discharge velocity was calculated from the slope  as
as
 (12)
(12)
Then, using the nonlinear curve fitting procedure available in MATHEMATICA (see Ref. 24 in [5] ), Equation (10) was fitted to measured discharge rate versus the pressure head 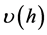 taking
taking 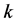 and
and 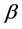 to be fitting parameters.
to be fitting parameters.
4. Results
To clarify the influence of surface tension and viscosity on the discharge rate of real liquids we used ordinary tap water with a density of , viscosity
, viscosity  and surface
and surface , and also 30% aqueous ethanol of density
, and also 30% aqueous ethanol of density , viscosity
, viscosity  and surface tension
and surface tension . Two tubes of diameter 2 mm and aspect ratio
. Two tubes of diameter 2 mm and aspect ratio 
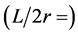 and 10 were separate inserts in the opening of Mariotte bottle. To determine the effusion velocity
and 10 were separate inserts in the opening of Mariotte bottle. To determine the effusion velocity  versus the pressure head,
versus the pressure head,  , the liquid of the bottle was poured out into a plastic capacity mounted on the force sensor with the precision of 0.005 N, so that the measurement error over three trial experiments didn’t exceed 1%. Typical results of the discharge rate
, the liquid of the bottle was poured out into a plastic capacity mounted on the force sensor with the precision of 0.005 N, so that the measurement error over three trial experiments didn’t exceed 1%. Typical results of the discharge rate  versus the pressure head
versus the pressure head 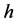 are shown in Figure 3 and Figure 4 for two test liquids discharged through
are shown in Figure 3 and Figure 4 for two test liquids discharged through
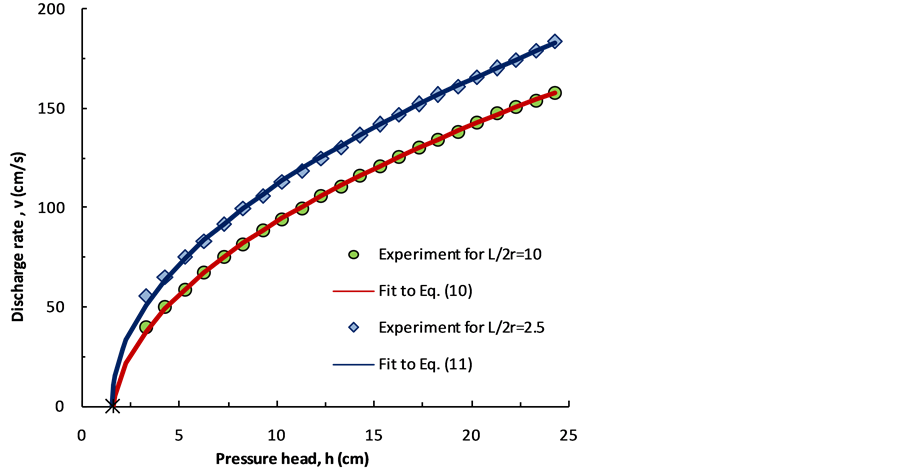
Figure 3. Discharge rate υ versus the pressure head h of tap water. Symbols denote experimental results. Solid lines are predicted by the present theory.
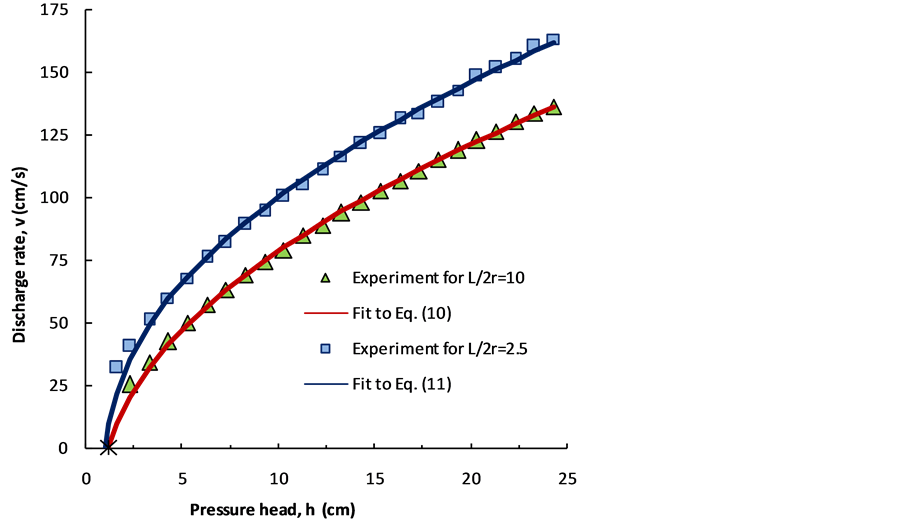
Figure 4. Discharge rate υ versus pressure head h of aqueous ethanol. Symbols denote experimental results. Solid lines are predicted by the present theory.
glass tubes with aspect ration  and 10 at temperature
and 10 at temperature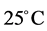 . It is seen that the discharge rate strongly depends on the fluid properties and the geometry of the outlet orifice. The range of the average discharge velocity,
. It is seen that the discharge rate strongly depends on the fluid properties and the geometry of the outlet orifice. The range of the average discharge velocity,  , Reynolds number, Re and fitting parameters k and b are presented in Table1
, Reynolds number, Re and fitting parameters k and b are presented in Table1
As expected, in the case of the discharge through the tube with 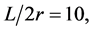 the viscous resistance plays a prominent role and the rate of discharge as function of the pressure head is better described by Equation (10), whereas Equation (11) provides the best fitting of experimental data
the viscous resistance plays a prominent role and the rate of discharge as function of the pressure head is better described by Equation (10), whereas Equation (11) provides the best fitting of experimental data  of the same liquids discharged
of the same liquids discharged
through the orifice with , despite the fact that initially, in the case of water, the Reynolds number was slightly higher than its limit value 3000 for the laminar flow.
, despite the fact that initially, in the case of water, the Reynolds number was slightly higher than its limit value 3000 for the laminar flow.
It can be seen also from Figure 3 and Figure 4, that over the range of the pressure head under operation, the rate of discharge of both liquids through the orifice with the aspect ratio  is considerably less than the rate discharge through the orifice with
is considerably less than the rate discharge through the orifice with , as attributed to the viscosity resistance. If the point
, as attributed to the viscosity resistance. If the point , at which the rate of the discharge
, at which the rate of the discharge 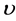 decays to zero, is added to Figure 3 and Figure 4, it can be seen that the fit is quite reasonable. That the plot of
decays to zero, is added to Figure 3 and Figure 4, it can be seen that the fit is quite reasonable. That the plot of  in Figure 3 and Figure 4, intersects the horizontal axis at the same point
in Figure 3 and Figure 4, intersects the horizontal axis at the same point  for each liquid independently of the tube aspect ratio,
for each liquid independently of the tube aspect ratio,  , is indeed related to the fact that fluid flow losses energy in creating the free surface area of the jet as predicted by the theoretical model.
, is indeed related to the fact that fluid flow losses energy in creating the free surface area of the jet as predicted by the theoretical model.
5. Summary
Subject of the discharge of Newtonian liquids from the container through the orifice of small diameter is an interesting topic in science education. One of the most important aspects that students can learn from these studies is the concepts of capillary pressure, interfacial energy and viscous. The use of the modified Bernoulli equation for the liquid jet, involving the interfacial energy density, is very useful for teaching the fundamentals of fluid flow. Students have the opportunity to study the effect of surface tension and viscosity on the fluid flow.
Acknowledgements
This work was partially supported by the Israel Ministry of Absorption and Immigration through the KAMEA Science Foundation.