1. Introduction
A real square matrix whose non-diagonal elements are non-positive is called a Z-matrix. The purpose of this paper is to show a necessary and sufficient condition for non-singularity of two types of Z-matrices.
The first is the Z-matrix whose row sums are all non-negative. In this paper, we denote this as a Non-negative Sums Z-matrix (NSZ-matrix).
The second is the Z-matrix A which satisfies 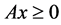 where
where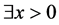 . In this paper, we denote this as a Non-negative Product Z-matrix (NPZ-matrix).
. In this paper, we denote this as a Non-negative Product Z-matrix (NPZ-matrix).
The following relation exists between these matrices.
Theorem 1.1 An NSZ-matrix is equivalent to an NPZ-matrix where all elements of 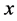 are the same number.
are the same number.
Proof. Let  be a set of numbers, and
be a set of numbers, and 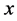 be a positive vector with all elements equal to the same number
be a positive vector with all elements equal to the same number .
.
If  is an NSZ-matrix, the ith element of
is an NSZ-matrix, the ith element of 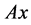 is
is .
. 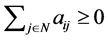 for
for  because
because 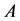 is an NSZ-matrix. Also,
is an NSZ-matrix. Also, 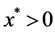 from the premise. Hence,
from the premise. Hence, 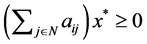 for
for 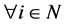 is satisfied.
is satisfied.
Therefore,  is an NPZ-matrix.
is an NPZ-matrix.
Conversely, consider that  is an NPZ-matrix which satisfies
is an NPZ-matrix which satisfies  for
for 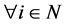 where
where . If we divide both sides of
. If we divide both sides of 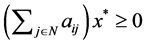 by
by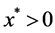 , we obtain
, we obtain 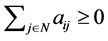 for
for . Thus,
. Thus,
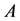 is an NSZ-matrix. [Q. E. D.]
is an NSZ-matrix. [Q. E. D.]
As Theorem 1.1 shows, the NSZ-matrix is a type of the NPZ-matrix. Therefore, if we can find a necessary and sufficient condition for non-singularity of the NPZ-matrix, we find the  necessary and sufficient condition for non-singularity of the NSZ-matrix automatically. However, we will prove the latter condition first, and then address the former condition.
necessary and sufficient condition for non-singularity of the NSZ-matrix automatically. However, we will prove the latter condition first, and then address the former condition.
We first state the basic propositions of linear algebra used in this paper.
The determinant of a square matrix 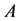 is denoted
is denoted 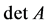 in this paper.
in this paper.
Theorem 1.2 Let  be a Z-matrix. Take a real number
be a Z-matrix. Take a real number  which is equal to or more than all diagonal elements and construct the matrix
which is equal to or more than all diagonal elements and construct the matrix  where
where  refers to the unit matrix.
refers to the unit matrix. 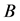 is a non-negative matrix.
is a non-negative matrix.
Proof. The non-diagonal elements of  are
are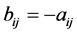 . As
. As  is a Z-matrix,
is a Z-matrix, 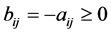 for
for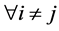 . On the other hand, the diagonal elements of B are
. On the other hand, the diagonal elements of B are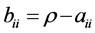 . Since
. Since 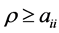 for
for 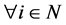 by the premise,
by the premise,  for
for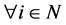 . Therefore,
. Therefore,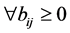 . [Q. E. D.]
. [Q. E. D.]
Theorem 1.3 A non-negative square matrix  always has a non-negative eigenvalue. Let
always has a non-negative eigenvalue. Let  be the maximum non-negative eigenvalue of
be the maximum non-negative eigenvalue of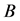 . Then there exists a non-negative eigenvector corresponding to
. Then there exists a non-negative eigenvector corresponding to .
.
If a Z-matrix  satisfies
satisfies ,
,  is called an M-matrix1.
is called an M-matrix1.
Theorem 1.4 An M-matrix  is non-singular if and only if
is non-singular if and only if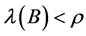 . In this case,
. In this case, 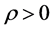 and all elements of the inverse of an M-matrix are non-negative. In particular, all diagonal elements of the inverse are equal to or more than
and all elements of the inverse of an M-matrix are non-negative. In particular, all diagonal elements of the inverse are equal to or more than  2.
2.
Proof. As Theorems 1.3 and 1.4 are well known, we entrust the proof to another work3. However, as it receives less attention that diagonal elements of  are
are 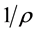 or more, we confirm this aspect.
or more, we confirm this aspect.
Regarding the inverse of an M-matrix ,
,  is satisfied4. Thus, if we set
is satisfied4. Thus, if we set  and
and ,
, 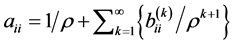 is satisfied. As
is satisfied. As 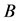 is a non-negative matrix and
is a non-negative matrix and ,
,  for
for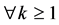 . Therefore, we can obtain
. Therefore, we can obtain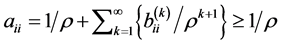 . [Q. E. D.]
. [Q. E. D.]
Theorem 1.5 If the row sums of a square matrix 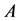 are all zeroes,
are all zeroes, .
.
Proof. Let 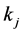 be the jth column vector of
be the jth column vector of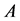 . We construct the linear combination
. We construct the linear combination . If the row sums of
. If the row sums of  are all zeroes,
are all zeroes, 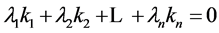 when
when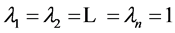 . Therefore,
. Therefore, 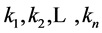 are linearly dependent. The determinant of a matrix whose column vectors are linearly dependent is zero5. [Q. E. D.]
are linearly dependent. The determinant of a matrix whose column vectors are linearly dependent is zero5. [Q. E. D.]
If 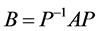 holds for the square matrices
holds for the square matrices  and
and  and a non-singular matrix
and a non-singular matrix ,
, 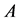 and
and 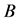 are called similar to each other.
are called similar to each other.
Theorem 1.6 When two matrices are similar, if one matrix is non-singular, the other is also non-singular.
Theorem 1.7 Similar matrices have the same eigenvalue6.
Here, we define the notation for submatrices in this paper.
Let 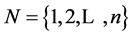 be a set of number of rows and columns of a square matrix
be a set of number of rows and columns of a square matrix  and let
and let  be a subset of
be a subset of  which is not empty.
which is not empty.  refers to a submatrix of
refers to a submatrix of  whose row and column elements belong to
whose row and column elements belong to . When
. When 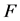 is a proper subset, we define
is a proper subset, we define 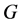 as the complement of
as the complement of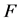 .
.  refers to a submatrix of
refers to a submatrix of  whose row elements belong to
whose row elements belong to  and column elements belong to
and column elements belong to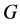 . Similarly,
. Similarly,  refers to a submatrix of
refers to a submatrix of 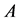 whose row elements belong to
whose row elements belong to 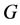 and column elements belong to
and column elements belong to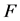 , and
, and  refers to a submatrix of
refers to a submatrix of  whose row and column elements belong to
whose row and column elements belong to . Clearly,
. Clearly, 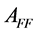 and
and 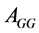 are principal submatrices.
are principal submatrices.  is
is  itself.
itself.
Based on the above, we confirm the following basic proposition.
Theorem 1.8 If 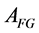 is a zero matrix,
is a zero matrix, 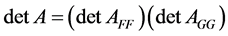 7.
7.
2. A Necessary and Sufficient Condition for Non-Singularity of the Z-Matrix Whose Row Sums Are All Non-Negative
In this section, we discuss the non-singularity of the NSZ-matrix. We reconfirm that the NSZ-matrix is defined as the Z-matrix whose row sums are all non-negative. 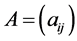 denotes an NSZ-matrix in this section.
denotes an NSZ-matrix in this section.
Theorem 2.1 An NSZ-matrix is an M-matrix8.
Proof. Take an NSZ-matrix 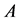 and a real number
and a real number 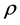 which is equal to or more than all diagonal element, and construct the matrix
which is equal to or more than all diagonal element, and construct the matrix .
. 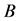 is a non-negative matrix from Theorem 1.2. Let
is a non-negative matrix from Theorem 1.2. Let 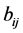 be the i th row and the jth column element of
be the i th row and the jth column element of  and let
and let  be the jth element of a non-negative eigenvector of
be the jth element of a non-negative eigenvector of 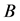 corresponding to
corresponding to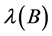 . Moreover, let
. Moreover, let 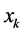 be a maximum of
be a maximum of . Incidentally, multiple candidates of
. Incidentally, multiple candidates of 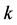 may exist. In that case, one can choose any
may exist. In that case, one can choose any 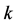 of these. From the definition of eigenvalue and eigenvector,
of these. From the definition of eigenvalue and eigenvector,
 is satisfied. On the other hand,
is satisfied. On the other hand,  for
for  because
because  is a maximum of
is a maximum of .
. 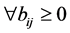 because
because 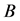 is a non-negative matrix. From these conditions,
is a non-negative matrix. From these conditions,  is satisfied generally. Thus,
is satisfied generally. Thus, .
.
Here, we confirm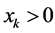 . Note that
. Note that  because it is an element of non-negative eigenvector. Therefore, if
because it is an element of non-negative eigenvector. Therefore, if  is zero,
is zero,  because
because  is the maximum of
is the maximum of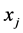 . However, the eigenvector is not a zero vector from its definition. Hence,
. However, the eigenvector is not a zero vector from its definition. Hence,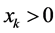 .
.
Based on the above, we divide both sides of the formula 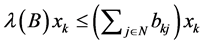 by
by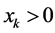 . Then, we can derive
. Then, we can derive . Note that
. Note that 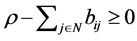 for
for 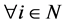 because
because 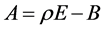 is an NSZ-matrix. Then,
is an NSZ-matrix. Then, . It is obvious that
. It is obvious that 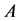 satisfies the definition of an M-matrix. [Q. E. D.]
satisfies the definition of an M-matrix. [Q. E. D.]
Theorem 2.2 An NSZ-matrix is non-singular if and only if it is a non-singular M-matrix.
Proof. It is obvious that an NSZ-matrix is non-singular if it is a non-singular M-matrix. Conversely, if an NSZ-matrix is non-singular, it is a non-singular M-matrix by Theorem 2.1. [Q. E. D.]
Considering Theorem 2.2, we see that finding a necessary and sufficient condition for non-singularity of the NSZ-matrix equates to finding a condition that it is a non-singular M-matrix. We will show this.
Theorem 2.3 All row sums of any principal submatrix of an NSZ-matrix are non-negative.
Proof. Regarding  itself, this is obvious because of the definition of the NSZ-matrix. In the following, we show a proof for principal submatrices which are not
itself, this is obvious because of the definition of the NSZ-matrix. In the following, we show a proof for principal submatrices which are not 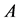 itself.
itself.
Let  be a proper subset of
be a proper subset of 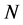 and
and  be the complement of
be the complement of . As all row sums of
. As all row sums of 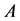 are non-negative,
are non-negative,  holds for
holds for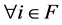 . Hence,
. Hence, . Because
. Because  is the complement of
is the complement of , it is clear that
, it is clear that  for
for  are non-diagonal elements of the Z-matrix A. Therefore, all of these are non-positive. Then,
are non-diagonal elements of the Z-matrix A. Therefore, all of these are non-positive. Then, 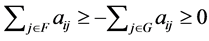 for
for 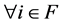 is true. [Q. E. D.]
is true. [Q. E. D.]
Theorem 2.4 If there exists at least one principal submatrix of an NSZ-matrix whose row sums are all zeroes, the matrix is singular.
Proof. If all row sums of 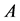 itself, which is one of the principal submatrices of an NSZ-matrix, are zeroes, the proposition is derived from Theorem 1.5 immediately. In the following, we show a proof for principal submatrices which are not
itself, which is one of the principal submatrices of an NSZ-matrix, are zeroes, the proposition is derived from Theorem 1.5 immediately. In the following, we show a proof for principal submatrices which are not 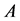 itself.
itself.
Choose  which is a proper subset of
which is a proper subset of , where the row sums of
, where the row sums of  are all zeroes.
are all zeroes. , which is the complement of
, which is the complement of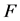 , is also not empty.
, is also not empty.
Based on this, we will confirm that  is a zero matrix. From the definition of an NSZ-matrix,
is a zero matrix. From the definition of an NSZ-matrix,
 holds for
holds for . Then,
. Then,  for
for  are obtained because
are obtained because  for
for 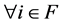 as defined. However,
as defined. However,  for
for 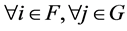 because
because 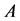 is a Z-matrix. For these two propositions to be compatible,
is a Z-matrix. For these two propositions to be compatible, 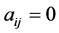 must hold for
must hold for . Therefore,
. Therefore,  is a zero matrix.
is a zero matrix.
Then, 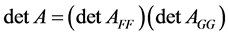 ||holds by Theorem1.8. Because all row sums of
||holds by Theorem1.8. Because all row sums of 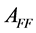 are zeroes,
are zeroes, 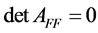 | |by Theorem 1.5. Thus,
| |by Theorem 1.5. Thus, 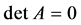 |. [Q. E. D.]
|. [Q. E. D.]
Theorem 2.5 If an NSZ-matrix is non-singular, at least one positive row sum exists in any principal submatrix of the matrix.
Proof. Due to the contraposition of Theorem 2.4, if an NSZ-matrix is non-singular, there does not exist a principal submatrix whose row sums are all zeroes. Then, by Theorem 2.3, at least one positive row sum exists in any principal submatrix of the matrix. [Q. E. D.]
As a result of Theorem 2.5, a necessary condition for non-singularity of the NSZ-matrix is shown. We now prove this is also a sufficient condition.
Theorem 2.6 If at least one positive row sum exists in any principal submatrix of an NSZ-matrix, the matrix is a non-singular M-matrix.
For the proof of Theorem 2.6, we have to use inference. In the following section, we will set 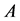 as an NSZ-matrix which has at least one positive row sum in any principal submatrix. Moreover, we take a real number
as an NSZ-matrix which has at least one positive row sum in any principal submatrix. Moreover, we take a real number 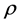 which is equal to or more than all diagonal elements and construct the matrix
which is equal to or more than all diagonal elements and construct the matrix . Note that, from Theorem 1.2,
. Note that, from Theorem 1.2, 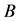 is a non-negative matrix. We now prove the following Lemmas.
is a non-negative matrix. We now prove the following Lemmas.
Lemma 2.7 Any row sum of all principal submatrices of 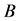 is equal to or less than
is equal to or less than .
.
Proof. It is obvious that  for
for  from the definition of
from the definition of .
. 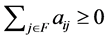 for
for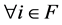 by Theorem 2.3. Thus,
by Theorem 2.3. Thus,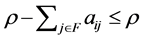 . Therefore,
. Therefore, 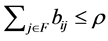 for
for . [Q. E. D.]
. [Q. E. D.]
Lemma 2.8 Any principal submatrix of 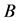 has at least one row sum which is less than
has at least one row sum which is less than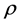 .
.
Proof. If we take ,
,  such that
such that 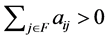 from the premise. Hence,
from the premise. Hence,  such that
such that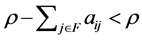 . Note that
. Note that  is true from the definition of
is true from the definition of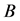 . Thus,
. Thus,  such that
such that 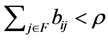 for
for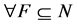 . [Q. E. D.]
. [Q. E. D.]
Then, we classify elements belonging to the number set .
.
According to Lemma 2.8, 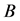 itself, which is one of the principal submatrices of
itself, which is one of the principal submatrices of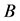 , has at least one row sum which is less than
, has at least one row sum which is less than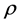 . We choose
. We choose 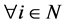 which satisfy
which satisfy 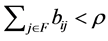 to belong to the set
to belong to the set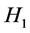 .
.  from the premise.
from the premise.
If  belong to
belong to , the classification is complete. In the following, we consider the case where
, the classification is complete. In the following, we consider the case where 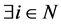 which does not belong to
which does not belong to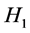 . First, we prove the following Lemma.
. First, we prove the following Lemma.
Lemma 2.9 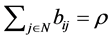 for
for .
.
Proof. By Lemma 2.7, 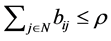 for
for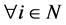 . Since
. Since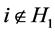 ,
, 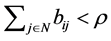 is not true from the definition of
is not true from the definition of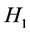 . Thus,
. Thus, 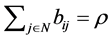 for
for . [Q. E. D.]
. [Q. E. D.]
We now consider the classification where  that does not belong to
that does not belong to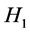 . We define
. We define 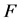 as the complement of
as the complement of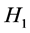 . By Lemma 2.8,
. By Lemma 2.8,  such that
such that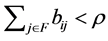 . We classify such i as belonging to the set
. We classify such i as belonging to the set .
.
If  belong to
belong to  or
or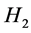 , the classification is complete. If
, the classification is complete. If 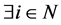 which belongs to neither set, we execute the third classification.
which belongs to neither set, we execute the third classification.
Generally,  classification steps are executed when
classification steps are executed when  which does not belong to any of
which does not belong to any of .
.
In such a case, we define  as the complement of
as the complement of . Then,
. Then,  such that
such that 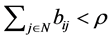 by Lemma 2.8. We classify such
by Lemma 2.8. We classify such 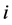 as belonging to the set
as belonging to the set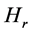 . The next Lemma is obvious from the past consideration.
. The next Lemma is obvious from the past consideration.
Lemma 2.10 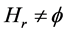 if
if 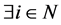 that belongs to the complement of
that belongs to the complement of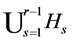 .
.
Then, the following Lemmas are derived.
Lemma 2.11 If  for
for , then
, then  for
for .
.
Proof. It is obvious by the method to construct  and mathematical induction. [Q. E. D.]
and mathematical induction. [Q. E. D.]
Lemma 2.12 If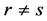 , then
, then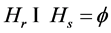 .
.
Proof. Without loss of generality, we suppose  and prove the Lemma under this supposition. If
and prove the Lemma under this supposition. If
 ,
,  belongs to the complement of
belongs to the complement of 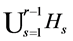 by the definition of
by the definition of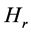 . Hence,
. Hence, 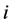 does not belong to
does not belong to
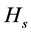 where
where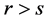 . That is,
. That is, . [Q. E. D.]
. [Q. E. D.]
From Lemmas 2.11 and 2.12, 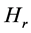 can be defined at most by
can be defined at most by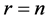 . In short, the classification is finished in limited time. If it is finished within
. In short, the classification is finished in limited time. If it is finished within 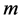 times, we derive the next Lemmas.
times, we derive the next Lemmas.
Lemma 2.13 .
.
Proof. It is obvious that . Hence, we prove
. Hence, we prove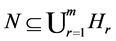 . We suppose that
. We suppose that 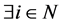 that belongs to the complement of
that belongs to the complement of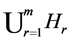 . Then,
. Then, 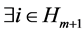 from Lemma 2.10, but this contradicts the definition of
from Lemma 2.10, but this contradicts the definition of . By reductio ad absurdum,
. By reductio ad absurdum, 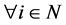 belong to
belong to . [Q. E. D.]
. [Q. E. D.]
Lemma 2.14 We define . If
. If  where
where 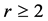 is not empty,
is not empty, 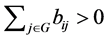 for
for .
.
Proof. Let 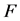 be the complement of
be the complement of  and
and  be any element of
be any element of  where
where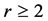 . By Lemma 2.9,
. By Lemma 2.9, 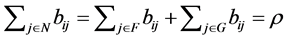 holds. Then,
holds. Then, 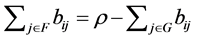 is satisfied.
is satisfied. 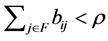 holds by the definition of
holds by the definition of . Therefore,
. Therefore,  holds. Thus, we obtain
holds. Thus, we obtain . [Q. E. D.]
. [Q. E. D.]
Note that because  is a non-negative matrix, a non-negative eigenvector corresponding to
is a non-negative matrix, a non-negative eigenvector corresponding to 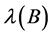 exists by Theorem 1.3. However,
exists by Theorem 1.3. However,  refers to a maximum non-negative eigenvalue of
refers to a maximum non-negative eigenvalue of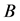 . Let
. Let 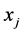 be the jth element of the non-negative eigenvector and
be the jth element of the non-negative eigenvector and 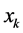 be a maximum of
be a maximum of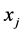 .
.
Lemma 2.15 If ,
, .
.
Proof.  for
for  from the definition of
from the definition of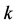 . Further,
. Further, 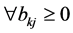 because
because 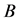 is a non-negative matrix. From these two conditions,
is a non-negative matrix. From these two conditions,  for
for .
.
On the other hand, 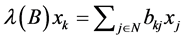 is true from the definition of eigenvalue and eigenvector. From these,
is true from the definition of eigenvalue and eigenvector. From these, 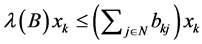 is derived.
is derived.
Note that if , which is a maximum of the non-negative eigenvector, is zero, the eigenvector must be a zero vector. However, this contradicts the definition of eigenvector. Thus,
, which is a maximum of the non-negative eigenvector, is zero, the eigenvector must be a zero vector. However, this contradicts the definition of eigenvector. Thus, . Then if we divide both sides of the former formula by
. Then if we divide both sides of the former formula by , we derive
, we derive . Note that
. Note that  from the premise
from the premise .
.
From these two formulas,  is derived. [Q. E. D.]
is derived. [Q. E. D.]
Lemma 2.16 Let  be a natural number equal to or more than 2. If
be a natural number equal to or more than 2. If 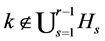 and
and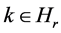 , then
, then
 .
.
Proof. We define  and
and  as the complement of
as the complement of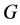 .
. 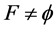 since
since , and
, and
 by Lemma 2.11. Let
by Lemma 2.11. Let 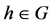 such that
such that 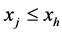 for
for . As
. As  is an element of the eigenvector corresponding to eigenvalue
is an element of the eigenvector corresponding to eigenvalue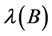 ,
,  holds.
holds.  for
for 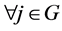 from the definition of
from the definition of  and
and 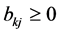 because
because  is a non-negative matrix. Hence,
is a non-negative matrix. Hence, 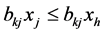 for
for  holds. Therefore,
holds. Therefore, 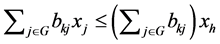 is satisfied. Further,
is satisfied. Further,  by the definition of
by the definition of  and
and . Accordingly,
. Accordingly,  for
for  holds. Hence,
holds. Hence, 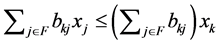 is satisfied. From the above results, we see that
is satisfied. From the above results, we see that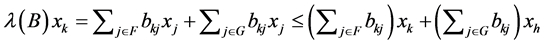 .
.
We divide the leftmost and rightmost sides of this formula by ,
, 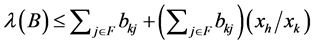
is derived. Note that  is defined as the maximum of the elements in the non-negative eigenvector corresponding to
is defined as the maximum of the elements in the non-negative eigenvector corresponding to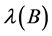 . Moreover,
. Moreover,  does not belong to
does not belong to 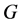 and
and  belongs to
belongs to . Hence,
. Hence, . Therefore,
. Therefore,
 . From the premise
. From the premise  where
where 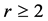 and Lemma 2.14,
and Lemma 2.14,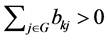 . Accordingly,
. Accordingly,
 holds. Hence,
holds. Hence, 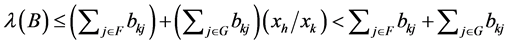 holds. As
holds. As , we derive
, we derive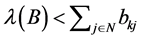 . Note that as
. Note that as  by the premise, it does not belong to
by the premise, it does not belong to 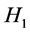 either. Therefore,
either. Therefore, 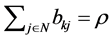 by Lemma 2.9.
by Lemma 2.9. 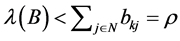 is derived. [Q. E. D.]
is derived. [Q. E. D.]
Proof of Theorem 2.6. By Lemma 2.13,  belong to any
belong to any . By Lemmas 2.15 and 2.16,
. By Lemmas 2.15 and 2.16,  is true when
is true when  belongs to any
belongs to any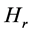 . From Theorem 1.4,
. From Theorem 1.4,  is a non-singular M-matrix. [Q. E. D.]
is a non-singular M-matrix. [Q. E. D.]
Now, we can show a necessary and sufficient condition for non-singularity of the NSZ-matrix. We will also show a necessary and sufficient condition for singularity of the matrix.
Theorem 2.17 A necessary and sufficient condition for non-singularity of the Z-matrix whose row sums are all non-negative is that at least one positive row sum exists in any principal submatrix of the matrix.
Proof. Necessity is shown in Theorem 2.5. Sufficiency is derived from Theorem 2.6. [Q. E. D.]
Theorem 2.18 A necessary and sufficient condition for singularity of the Z-matrix whose row sums are all non-negative is that there exists at least one principal submatrix of the matrix whose row sums are all zeroes.
Proof. By the contraposition of Theorem 2.17, a necessary and sufficient condition for singularity of the NSZ-matrix is that at least one principal submatrix of the NSZ-matrix whose row sums are all non-positive exists. From Theorem 2.3, this means that there exists at least one principal submatrix of the NSZ-matrix whose row sums are all zeroes. [Q. E. D.]
3. A Necessary and Sufficient Condition for Non-Singularity of the Z-Matrix Which Has a Non-Negative Product with a Positive Vector
In this section, we discuss the non-singularity of the NPZ-matrix. We reconfirm that the NPZ-matrix is defined as the Z-matrix 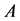 which satisfies
which satisfies 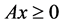 where
where .
. 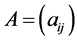 denotes an NPZ-matrix in this section.
denotes an NPZ-matrix in this section.
We construct the diagonal matrix  whose i th diagonal element is the ith element of
whose i th diagonal element is the ith element of . As the diagonal elements of
. As the diagonal elements of  are all positive, its inverse
are all positive, its inverse  exists. Note that
exists. Note that 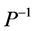 is a diagonal matrix whose ith diagonal element is
is a diagonal matrix whose ith diagonal element is .
.
We subsequently construct a matrix  which satisfies
which satisfies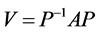 . A and V are similar to each other by the definition of matrix similarity.
. A and V are similar to each other by the definition of matrix similarity.
Theorem 3.1 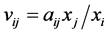 for
for .
.
Proof. As the ith row vector of  is
is  and the jth column vector of
and the jth column vector of  is
is
 , the
, the 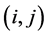 th element of
th element of  is
is . Thus, the ith row vector of
. Thus, the ith row vector of 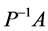 is
is . Further, the jth column vector of
. Further, the jth column vector of 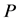 is
is . Thus, the
. Thus, the  th element of
th element of 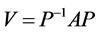 is
is . [Q. E. D.]
. [Q. E. D.]
Theorem 3.2 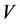 is an NSZ-matrix.
is an NSZ-matrix.
Proof.  for
for  because
because  is a Z-matrix, and
is a Z-matrix, and  because
because . Therefore,
. Therefore, for
for . Then,
. Then, 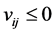 for
for  by Theorem 3.1. That is,
by Theorem 3.1. That is,  is a Z-matrix.
is a Z-matrix.
Moreover, 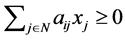 for
for  because
because  is an NPZ-matrix. If we divide both sides of this formula by
is an NPZ-matrix. If we divide both sides of this formula by , we obtain
, we obtain  for
for . From Theorem 3.1,
. From Theorem 3.1,  for
for 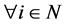 is derived.
is derived.
We have shown that  is a Z-matrix and all row sums of
is a Z-matrix and all row sums of  are non-negative. Thus,
are non-negative. Thus,  satisfies the definition of an NSZ-matrix. [Q. E. D.]
satisfies the definition of an NSZ-matrix. [Q. E. D.]
Theorem 3.3 An NPZ-matrix 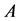 is non-singular if and only if at least one positive row sum exists in any principal submatrix of
is non-singular if and only if at least one positive row sum exists in any principal submatrix of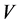 .
.
Proof.  is an NSZ-matrix from Theorem 3.2. Then, by Theorem 2.17,
is an NSZ-matrix from Theorem 3.2. Then, by Theorem 2.17,  is non-singular if and only if at least one positive row sum exists in any principal submatrix of
is non-singular if and only if at least one positive row sum exists in any principal submatrix of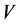 . Since
. Since  and
and 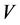 are similar to each other, this is also a necessary and sufficient condition for the non-singularity of
are similar to each other, this is also a necessary and sufficient condition for the non-singularity of 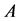 by Theorem 1.6. [Q. E. D.]
by Theorem 1.6. [Q. E. D.]
Further, we will prove that this is also an equivalent condition that 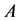 is a non-singular M-matrix.
is a non-singular M-matrix.
Theorem 3.4 Take a real number  which is equal to or more than all diagonal elements of
which is equal to or more than all diagonal elements of  and construct the matrix
and construct the matrix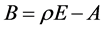 . Moreover, we construct
. Moreover, we construct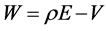 . Then,
. Then, 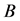 and
and 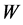 are similar to each other.
are similar to each other.
Proof. . [Q. E. D.]
. [Q. E. D.]
Theorem 3.5  is a non-negative matrix.
is a non-negative matrix.
Proof.  by the definition of
by the definition of 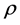 and
and  from Theorem 3.1. Then,
from Theorem 3.1. Then,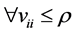 . Therefore,
. Therefore,  , which are diagonal elements of
, which are diagonal elements of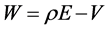 , are non-negative for
, are non-negative for . Then,
. Then,  , which are non-diagonal elements of
, which are non-diagonal elements of , are non-negative for
, are non-negative for 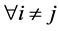 because
because 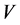 is a Z-matrix by Theorem 3.2. Thus,
is a Z-matrix by Theorem 3.2. Thus, 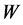 is a non-negative matrix. [Q. E. D.]
is a non-negative matrix. [Q. E. D.]
Theorem 3.6 An NPZ-matrix is an M-matrix9.
Proof. 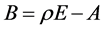 and
and  are both non-negative matrices due to Theorems 1.2 and 3.5. Thus, they have maximums of non-negative eigenvalues both by Theorem 1.3. Let
are both non-negative matrices due to Theorems 1.2 and 3.5. Thus, they have maximums of non-negative eigenvalues both by Theorem 1.3. Let  and
and 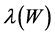 each be a maximum of a non-negative eigenvalue. Because
each be a maximum of a non-negative eigenvalue. Because 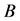 and
and  are similar by Theorem 3.4,
are similar by Theorem 3.4, 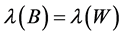 by Theorem 1.7. Note that
by Theorem 1.7. Note that 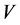 is an NSZ-matrix from Theorem 3.2. Then,
is an NSZ-matrix from Theorem 3.2. Then, 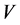 is an M-matrix from Theorem 2.1. Therefore,
is an M-matrix from Theorem 2.1. Therefore, 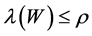 from the definition of an M-matrix. Then,
from the definition of an M-matrix. Then,  because
because . We can confirm that A satisfies the definition of an M-matrix. [Q. E. D.]
. We can confirm that A satisfies the definition of an M-matrix. [Q. E. D.]
Theorem 3.7 An NPZ-matrix is non-singular if and only if it is a non-singular M-matrix.
Proof. It is obvious that an NPZ-matrix is non-singular if it is a non-singular M-matrix. Conversely, if an NPZ-matrix is non-singular, it is a non-singular M-matrix by Theorem 3.6. [Q. E. D.]
By Theorem 3.3, we can find a necessary and sufficient condition for non-singularity of an NPZ-matrix. However, this condition is described with parts of  which is similar to
which is similar to . It is not described with parts of
. It is not described with parts of  and
and 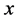 that are used in the definition of the NPZ-matrix. We will look for a condition described with such parts.
that are used in the definition of the NPZ-matrix. We will look for a condition described with such parts.
In the following, let  be a subset of
be a subset of  that is not empty, and
that is not empty, and  be the complement of
be the complement of 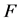 if
if  is a proper subset. Then, the next Theorems hold.
is a proper subset. Then, the next Theorems hold.
Theorem 3.8 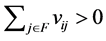 if and only if
if and only if 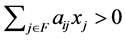 for
for  where
where .
.
Proof. This is true because 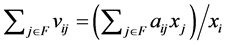 from Theorem 3.1 and
from Theorem 3.1 and  because
because 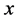 is a positive vector. [Q. E. D.]
is a positive vector. [Q. E. D.]
Theorem 3.9 If 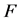 is a proper subset,
is a proper subset,  for
for .
.
Proof. Since 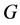 is the complement of
is the complement of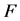 ,
, 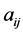 for
for 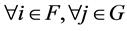 are non-diagonal elements of
are non-diagonal elements of . Then, they are non-positive because
. Then, they are non-positive because  is a Z-matrix. Moreover,
is a Z-matrix. Moreover,  because
because 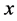 is a positive vector. Thus,
is a positive vector. Thus,  for
for . [Q. E. D.]
. [Q. E. D.]
Theorem 3.10 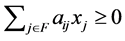 for
for 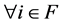 where
where .
.
Proof. If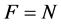 , this is obvious because of the definition of the NPZ-matrix. In the following, we show a proof for
, this is obvious because of the definition of the NPZ-matrix. In the following, we show a proof for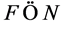 .
.
By the definition of an NPZ-matrix, 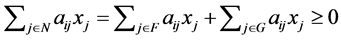 is satisfied. Hence, we obtain
is satisfied. Hence, we obtain . Note that
. Note that 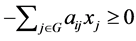 for
for 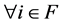 holds from Theorem 3.9. Accordingly,
holds from Theorem 3.9. Accordingly,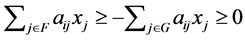 . [Q. E. D.]
. [Q. E. D.]
Theorem 3.11 Let 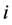 be any element of
be any element of . Then,
. Then,  or
or  such that
such that 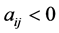 is a necessary and sufficient condition for
is a necessary and sufficient condition for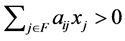 .
.
Proof.
[Sufficiency] We prove this Theorem by dividing it into two cases.
(1) The case .
.
If , this is obvious. In the following, we show a proof for
, this is obvious. In the following, we show a proof for .
.
By the supposition, 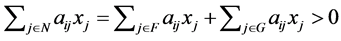 is satisfied. Therefore, we obtain
is satisfied. Therefore, we obtain . Note that if
. Note that if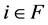 ,
, from Theorem 3.9. Hence,
from Theorem 3.9. Hence,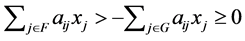 .
.
(2) The case  such that
such that .
.
If ,
,  cannot be defined. Thus, this case is applied only when
cannot be defined. Thus, this case is applied only when .
.
Let 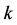 be one of
be one of  which satisfies aij<0 , and H be a set which removes k from G. By the define tion of an NPZ-matrix,
which satisfies aij<0 , and H be a set which removes k from G. By the define tion of an NPZ-matrix, 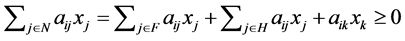 is satisfied. Then we obtain
is satisfied. Then we obtain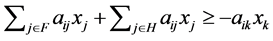 . Since we consider the case
. Since we consider the case , and
, and 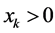 is true from the definition of an NPZ-matrix, we obtain
is true from the definition of an NPZ-matrix, we obtain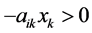 . Then
. Then ; in other words
; in other words  is true. Further, considering
is true. Further, considering  and
and ,
, 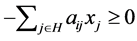 is satisfied by Theorem 3.9. Therefore, we obtain
is satisfied by Theorem 3.9. Therefore, we obtain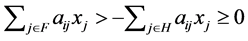 . [Q. E. D.]
. [Q. E. D.]
[Necessity] By the definition of an NPZ-matrix,  for
for 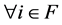 and
and 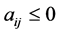 for
for 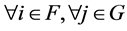 holds. Thus, the negative proposition of “
holds. Thus, the negative proposition of “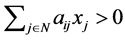 or
or  such that
such that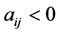 ” is “
” is “ and
and 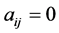 for
for ”. Further, as
”. Further, as , the negative proposition of “
, the negative proposition of “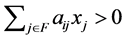 ” is “
” is “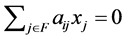 ” from Theorem 3.10. Therefore, the contraposition of this Theorem is as follows. Let
” from Theorem 3.10. Therefore, the contraposition of this Theorem is as follows. Let  be any element of
be any element of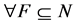 . If
. If 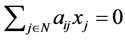 and
and  for
for ,
, .
.
When , this is obvious. When
, this is obvious. When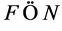 , if the supposition of the contraposition is satisfied,
, if the supposition of the contraposition is satisfied,
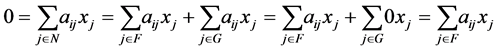
is true for  where
where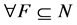 . That is, the contraposition is true. [Q. E. D.]
. That is, the contraposition is true. [Q. E. D.]
Now, we can show a necessary and sufficient condition for non-singularity of the NPZ-matrix described with parts of A and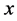 . We reconfirm that the NPZ-matrix is defined as a Z-matrix which satisfies
. We reconfirm that the NPZ-matrix is defined as a Z-matrix which satisfies  where
where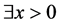 . Let
. Let 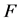 be a subset of the number set
be a subset of the number set 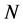 which is not empty, and
which is not empty, and  be the complement of
be the complement of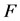 .
.
Theorem 3.12 Let the Z-matrix 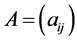 satisfy
satisfy  where
where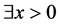 . A necessary and sufficient condition for the non-singularity of
. A necessary and sufficient condition for the non-singularity of 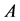 is
is 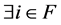 such that
such that 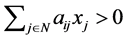 or
or 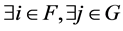 such that
such that 
for  10.
10.
Proof. By Theorem 3.3, an NPZ-matrix is non-singular if and only if 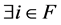 such that
such that  for
for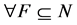 . By referring to Theorems 3.8 and 3.11, this condition can be rewritten as
. By referring to Theorems 3.8 and 3.11, this condition can be rewritten as  such that
such that or
or  such that
such that 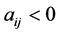 for
for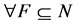 . [Q. E. D.]
. [Q. E. D.]
Theorem 3.13 Let the Z-matrix  satisfy
satisfy  where
where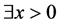 . A necessary and sufficient condition for the singularity of
. A necessary and sufficient condition for the singularity of  is
is 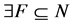 such that
such that 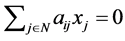 for
for 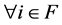 and
and  for
for
 11.
11.
Proof. By the contraposition of Theorem 3.12, an NPZ-matrix is singular if and only if  such that
such that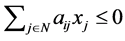 for
for 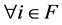 and
and  for
for . However,
. However,  for
for 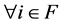 and
and
 for
for 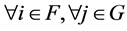 are satisfied by the definition of an NPZ-matrix. Therefore, this singularity condition means
are satisfied by the definition of an NPZ-matrix. Therefore, this singularity condition means 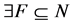 such that
such that  for
for  and
and  for
for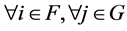 . [Q. E. D.]
. [Q. E. D.]
4. Derivation from the Conditions by Robert Beauwens and Michael Neumann
In fact, Robert Beauwens has already shown a condition which resembles what is shown in Theorem 2.17 as a necessary and sufficient condition for non-singularity of the NSZ-matrix. It is as follows.
First, we define the necessary concept.
If an  -dimensional square matrix
-dimensional square matrix  satisfies
satisfies  for
for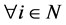 ,
,  is called diagonally dominant.
is called diagonally dominant.
Then, if a diagonally dominant matrix 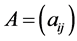 satisfies
satisfies 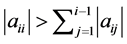 for
for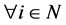 ,
,  is called lower semi-strictly diagonally dominant.
is called lower semi-strictly diagonally dominant.
In the following, a permutation of  denotes
denotes  by a permutation matrix
by a permutation matrix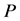 . Then, if
. Then, if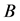 , a permutation of
, a permutation of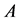 , is lower semi-strictly diagonally dominant,
, is lower semi-strictly diagonally dominant,  is called semi-strictly diagonally dominant.
is called semi-strictly diagonally dominant.
Beauwens showed the following Theorem.
Theorem 4.1 Let the Z-matrix  be diagonally dominant and have diagonal elements that are all non-negative.
be diagonally dominant and have diagonal elements that are all non-negative.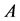 is a non-singular M-matrix if and only if it is semi-strictly diagonally dominant12.
is a non-singular M-matrix if and only if it is semi-strictly diagonally dominant12.
If  is a Z-matrix,
is a Z-matrix,  holds for all non-diagonal elements. If diagonal elements of
holds for all non-diagonal elements. If diagonal elements of 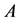 are nonnegative,
are nonnegative, 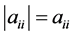 holds for all diagonal elements.
holds for all diagonal elements.
Thus, if 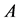 is diagonally dominant and has diagonal elements that are all non-negative, all row sums of
is diagonally dominant and has diagonal elements that are all non-negative, all row sums of  are non-negative. Conversely, if all row sums of the Z-matrix
are non-negative. Conversely, if all row sums of the Z-matrix  are non-negative, diagonal elements of it are all non-negative by Theorem 2.3, and it is obviously diagonally dominant.
are non-negative, diagonal elements of it are all non-negative by Theorem 2.3, and it is obviously diagonally dominant.
Therefore, the matrix which Theorem 4.1 addresses is nothing but the NSZ-matrix defined in this paper. Further, if 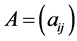 satisfies the premise of Theorem 4.1,
satisfies the premise of Theorem 4.1, 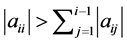 can be rewritten as
can be rewritten as . Hence, Theorem 4.1 can be rewritten as follows.
. Hence, Theorem 4.1 can be rewritten as follows.
Theorem 4.2 The NSZ-matrix  is a non-singular M-matrix if and only if
is a non-singular M-matrix if and only if  satisfies
satisfies  for
for 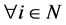 or
or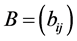 , a permutation of
, a permutation of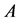 , satisfies
, satisfies  for
for .
.
Considering Theorem 2.2, Theorem 4.2 can be also rewritten as follows.
Theorem 4.3 The NSZ-matrix 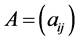 is non-singular if and only if
is non-singular if and only if  satisfies
satisfies  for
for  or
or , a permutation of
, a permutation of , satisfies
, satisfies 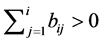 for
for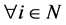 .
.
The Beauwens condition shown in Theorem 4.3 is equivalent to the condition shown in Theorem 2.17. However, before we prove this, we introduce another Theorem of Beauwens.
Theorem 4.4 The Z-matrix  is a non-singular M-matrix if and only if there exists a vector
is a non-singular M-matrix if and only if there exists a vector 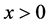
such that 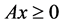 and
and 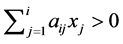 for
for  13.
13.
Furthermore, Michael Neumann showed the next Theorem.
Theorem 4.5 Let  be a Z-matrix and
be a Z-matrix and 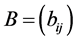 be a permutation of
be a permutation of .
.  is a non-singular Mmatrix if and only if there exists a vector
is a non-singular Mmatrix if and only if there exists a vector  such that
such that  and
and  for
for  14.
14.
The matrix which Theorems 4.4 and 4.5 address is nothing but the NPZ-matrix defined in this paper. Considering also Theorem 3.7, the following Theorem can be derived.
Theorem 4.6 The NPZ-matrix  is non-singular if and only if
is non-singular if and only if  satisfies
satisfies 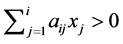 for
for 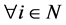 or
or , a permutation of
, a permutation of , satisfies
, satisfies  for
for .
.
The condition for non-singularity of the NPZ-matrix shown in Theorem 3.12 is equivalent to the Beauwens-Neumann condition shown in Theorem 4.6. We now prove this.
Theorem 4.7 Let  be an NPZ-matrix, and
be an NPZ-matrix, and 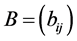 be a permutation of
be a permutation of .
. 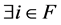 such that
such that
 for
for  is a necessary and sufficient condition that
is a necessary and sufficient condition that 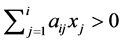 for
for 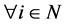 or
or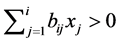 for
for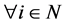 .
.
Proof.
[Sufficiency] Based on the premise,  such that
such that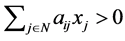 . If we permute this
. If we permute this 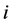 with
with ,
,
 is satisfied. Next, let
is satisfied. Next, let 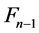 be a set which removes
be a set which removes 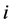 from
from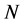 . Based on the premise,
. Based on the premise,
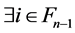 such that
such that . If we permute this
. If we permute this  with
with ,
,  is satisfied. After this, in the range of
is satisfied. After this, in the range of , let
, let  be a set which removes
be a set which removes  from
from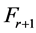 . Based on the premise,
. Based on the premise,  such that
such that . If we permute this
. If we permute this  with
with ,
,  is satisfied. If these steps are executed to
is satisfied. If these steps are executed to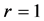 ,
, 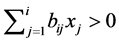 holds for
holds for . [Q. E. D.]
. [Q. E. D.]
[Necessity] 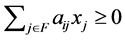 is guaranteed by Theorem 3.10. Then, the contraposition of the proposition is as follows. If
is guaranteed by Theorem 3.10. Then, the contraposition of the proposition is as follows. If 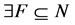 such that
such that 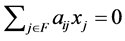 for
for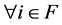 , then
, then  such that
such that 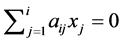 and
and 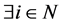 such that
such that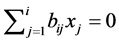 . We prove this contraposition.
. We prove this contraposition.
Let  be the maximum number of elements of F such that
be the maximum number of elements of F such that 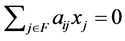 for
for . Naturally,
. Naturally, holds. Then, we prove
holds. Then, we prove .
.
If the number of elements of  is more than
is more than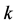 ,
,  cannot be the maximum number of elements of
cannot be the maximum number of elements of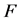 . Hence, there is no such possibility. Thus, if we define
. Hence, there is no such possibility. Thus, if we define ,
,  holds.
holds.
Then, we prove 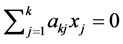 by dividing it into two cases.
by dividing it into two cases.
(1) The case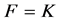 .
.
In this case,  is true. Moreover,
is true. Moreover, 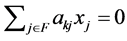 is true from the premise. Thus,
is true from the premise. Thus, .
.
(2) The case .
.
Let 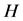 be the relative complement of
be the relative complement of 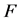 in
in .
.  is true. Since
is true. Since 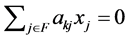 from the premise,
from the premise, .
.  because of Theorem 3.10. Therefore,
because of Theorem 3.10. Therefore,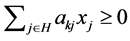 . On the other hand,
. On the other hand,  for
for 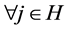 because
because ,
,  and
and 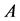 is a Z-matrix. Further,
is a Z-matrix. Further,  by the definition of the NPZ-matrix. Thus,
by the definition of the NPZ-matrix. Thus, . In order for these conditions to be compatible, we must have
. In order for these conditions to be compatible, we must have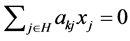 . Therefore,
. Therefore, .
.
Then, 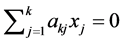 is proved in any case. Thus, we obtain
is proved in any case. Thus, we obtain 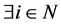 such that
such that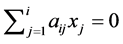 .
.
Next, we consider , a permutation of
, a permutation of . Let
. Let 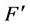 be a permutated set of
be a permutated set of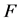 . Since
. Since 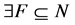 such that
such that  for
for 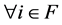 is premised on the contraposition, then
is premised on the contraposition, then 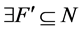 such that
such that  for
for .
.
Let 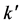 be the maximum number of elements of
be the maximum number of elements of . Then, we can also prove
. Then, we can also prove 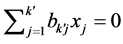 similarly to the proof for
similarly to the proof for . Thus, we also obtain
. Thus, we also obtain  such that
such that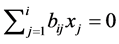 . [Q. E. D.]
. [Q. E. D.]
Theorem 4.8 Let 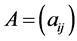 be an NPZ-matrix, and
be an NPZ-matrix, and  be a permutation of
be a permutation of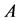 .
.  such that
such that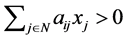 or
or 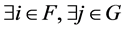 such that
such that  for
for 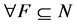 if and only if
if and only if 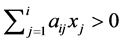 for
for 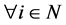 or
or 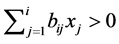 for
for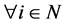 .
.
Proof. This is derived from Theorems 3.11 and 4.7 immediately. [Q. E. D.]
Theorem 4.8 shows the equivalence between the two non-singularity conditions of the NPZ-matrix, the condition in Theorem 3.12 and the Beauwens-Neumann condition in Theorem 4.6. Theorem 3.12 is also derived from Theorems 4.6 and 4.8.
The equivalence between the two non-singularity conditions of the NSZ-matrix, the condition in Theorem 2.17 and the Beauwens condition in Theorem 4.3, can be also proved.
Theorem 4.9 Let  be an NSZ-matrix, and
be an NSZ-matrix, and  be a permutation of
be a permutation of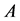 .
.  such that
such that
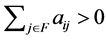 for
for 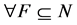 if and only if
if and only if 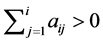 for
for  or
or  for
for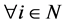 .
.
Proof. By Theorem 1.1,  is equivalent to an NPZ-matrix where all elements of
is equivalent to an NPZ-matrix where all elements of 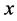 are the same number
are the same number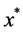 . Therefore, considering Theorem 4.7 in the case all
. Therefore, considering Theorem 4.7 in the case all  are equal to
are equal to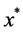 ,
, 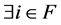 such that
such that
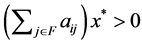 for
for 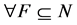 if and only if
if and only if 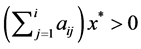 for
for  or
or 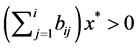 for
for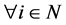 . If we divide
. If we divide 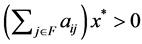 and
and 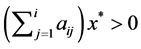 and
and  by
by , we obtain this Theorem. [Q. E. D.]
, we obtain this Theorem. [Q. E. D.]
If ,
, 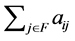 means a row sum of a principal submatrix of
means a row sum of a principal submatrix of . Thus,
. Thus,  such that
such that 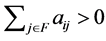
for  means that at least one positive row sum exists in any principal submatrix of
means that at least one positive row sum exists in any principal submatrix of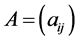 . Hence, Theorem 2.17 can be also derived from Theorems 4.3 and 4.9.
. Hence, Theorem 2.17 can be also derived from Theorems 4.3 and 4.9.
NOTES
1This definition is that given by Berman & Plemmons p. 133. Alexander Ostrowski, who used the concept M-matrix first, gave a different definition for M-matrix. Cf. Ostrowski p. 69, Berman & Plemmons p. 161. The definition of M-matrix given in Varga is also different. Cf. Varga p. 91.
2Theorems 1.3 and 1.4 are often called Frobenius theorem after their discoverer, Georg Frobenius.
3Cf. Berman & Plemmons pp. 6-7, p. 26, Nikaido pp. 101-102, Varga p. 51, p. 89.
4Cf. Nikaido p. 96, Varga p. 89.
5Cf. DeFranza & Gabliardi pp. 118-119.

6Cf. Anton & Rorres pp. 305-306 for Theorems 1.6 and 1.7.
7Cf. Bretscher p. 258.
8This theorem is stated in Plemmons p. 248.

9This theorem is stated in Berman & Plemmons p. 155.

10In the case , this condition is merely
, this condition is merely 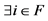 such that
such that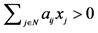 .
.
11In the case , this condition is merely
, this condition is merely 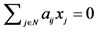 for
for .
.

12Cf. Beauwens pp. 110-111.
13It is written in Plemmons p. 181, p. 183 and Berman & Plemmons p. 136, p. 162 that this theorem was first shown in Beauwens .
14It is written in Berman & Plemmons p. 136, p. 162 that this theorem was first shown in Neumann .