Partial Integrability Conditions and an Integrating Algorithm for Fully Rheonomous Affine Constraints ()
1. Introduction
A lot of researches on nonholonomic systems have been actively done in the research fields of nonlinear control theory and robotics so far [1] -[5] . Moreover, sub-Riemannian geometry has been also studied in the research fields of differential geometry and control theory [6] [7] . In these two research fields, the common key is the existence of constraints, which is represented as differential equations. The concepts “integrability” and “nonintegrability” of such constraints are quite important since they determine various characteristics of systems. Hence, investigation of integrability and nonintegrability is an essential task in the first stage.
There are some classes in constraints, and the simplest class of constraints is called linear constraints: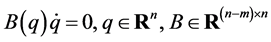 , which has been mainly studied so far. The class of the linear constraints covers wide-ranging mechanical systems such as mobile caars, acrobatic robots, and biomimetic robots. As a wider class of constraints than the linear constraints, the author has focused and researched scleronomous affine constraints:
, which has been mainly studied so far. The class of the linear constraints covers wide-ranging mechanical systems such as mobile caars, acrobatic robots, and biomimetic robots. As a wider class of constraints than the linear constraints, the author has focused and researched scleronomous affine constraints: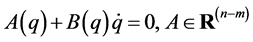 , and A-rheonomous affine constraints:
, and A-rheonomous affine constraints: 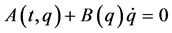 from the viewpoints of mathematics and control theory [8] -[12] . It must be noted that in the field of analytical mechanics, the terminology “rheonomous” means “time-varying,” and the opposite word of it is “scleronomous.” The affine constraints can be found in physical and mechanical systems: space robots with initial angular momenta, a ball on a rotating table, a ship on a running river, and so on. These work have made it possible to treat such constraints systematically, however, we are still interested in fully rheonomous affine constraints:
from the viewpoints of mathematics and control theory [8] -[12] . It must be noted that in the field of analytical mechanics, the terminology “rheonomous” means “time-varying,” and the opposite word of it is “scleronomous.” The affine constraints can be found in physical and mechanical systems: space robots with initial angular momenta, a ball on a rotating table, a ship on a running river, and so on. These work have made it possible to treat such constraints systematically, however, we are still interested in fully rheonomous affine constraints: 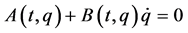 as a much wider class of constraints than the scleronomous affine constraints. In [13] , the author has derived a complete integrability condition for the fully rheonomous affine constraints. Moreover, in [14] , an integrating algorithm to calculate first integrals of the completely integrable fully rheonomous affine constraints is developed. The word “complete integrability” means all the constraints are integrable. However, there is another case called “partial integrability”, which means the situation where integrable constraints and nonintegrable ones are mixed. Researches on partially integrable fully rheonomous affine constraints have not been done.
as a much wider class of constraints than the scleronomous affine constraints. In [13] , the author has derived a complete integrability condition for the fully rheonomous affine constraints. Moreover, in [14] , an integrating algorithm to calculate first integrals of the completely integrable fully rheonomous affine constraints is developed. The word “complete integrability” means all the constraints are integrable. However, there is another case called “partial integrability”, which means the situation where integrable constraints and nonintegrable ones are mixed. Researches on partially integrable fully rheonomous affine constraints have not been done.
Hence, the aim of this paper is to develop partial integrability conditions and an integrating algorithm for the fully rheonomous affine constraints. This paper is organized as follows. First, in Section 2, some preliminaries on the fully rheonomous affine constraints are shown. Next, in Section 3, necessary and sufficient conditions on partial integrability for the fully rheonomous affine constraints are derived. Then, an integrating algorithm to calculate independent first integrals for partially integrable rheonomous affine constraints is developed in Section 4. After that, Section 5 illustrates in order to verify the effectiveness and the availability of the new results.
2. Preliminaries
2.1. Fully Rheonomous Affine Constraints (FRACs)
This section presents some preliminaries on fully rheonomous affine constraints are presented. See [13] for more details. First, this subsection gives the definition of fully rheonomous affine constraints and explains their geometric representation. Denote the time variable by 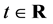 and a time interval by
and a time interval by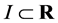 . Let
. Let 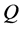 be an n-dimensional configuration manifold and
be an n-dimensional configuration manifold and 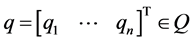 be a local coordinate of
be a local coordinate of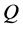 . Associated with
. Associated with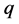 , we refer
, we refer 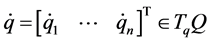 as a tangent vector field. A set of
as a tangent vector field. A set of 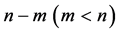 of differential equations in the form:
of differential equations in the form:
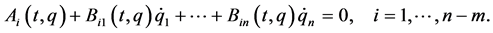 (1)
(1)
is called fully rheonomous affine constraints (FRACs). Note that all the coefficients 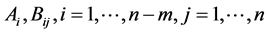 explicitly depend on the time variable
explicitly depend on the time variable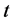 . We now rewrite (1) as
. We now rewrite (1) as
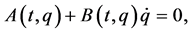 (2)
(2)
where a rheonomous affine term 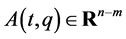 is a vector-valued function whose i-th entry is
is a vector-valued function whose i-th entry is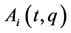 , and a rheonomous velocity coefficient matrix
, and a rheonomous velocity coefficient matrix 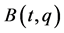 is a matrix-valued function whose ij-th entry is
is a matrix-valued function whose ij-th entry is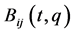 . In this paper, we assume the following sufficient condition on independency of the FRACs (2):
. In this paper, we assume the following sufficient condition on independency of the FRACs (2):
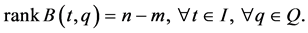 (3)
(3)
Next, a geometric representation method of the FRACs (2) is explained. From (3), we see that the 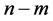 row vectors of
row vectors of 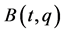 in (2) are independent of each other. Hence, we consider
in (2) are independent of each other. Hence, we consider 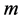 vector fields which are independent of each other and annihilators of the
vector fields which are independent of each other and annihilators of the 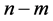 row vectors of
row vectors of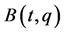 , and denote them by
, and denote them by 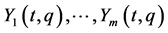 as time-varying vector fields on
as time-varying vector fields on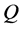 . Furthermore, we also denote a space spanned by
. Furthermore, we also denote a space spanned by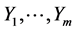 , that is, a time-varying distribution on
, that is, a time-varying distribution on 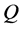 by
by
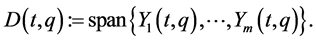 (4)
(4)
Since the basial vectors of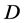 :
: 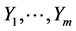 are independent of each other,
are independent of each other, 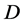 is a nonsingular distribution, that is,
is a nonsingular distribution, that is,
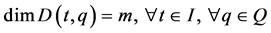 (5)
(5)
holds. A curve on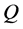 :
: 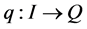 is said to satisfy the FRACs (2) if for a time-varying vector field on
is said to satisfy the FRACs (2) if for a time-varying vector field on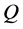 :
: 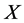 and the generalized velocity of
and the generalized velocity of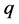 :
: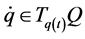 ,
,
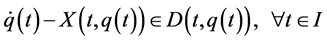 (6)
(6)
holds. We call 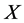 a rheonomous affine vector field and it satisfies the equation:
a rheonomous affine vector field and it satisfies the equation:
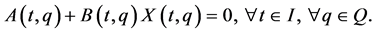 (7)
(7)
This definition is a natural extension of the one for the scleronomous affine constraints that do not contain the time variable explicitly [8] . Geometric representation of the FRACs is defined as follows and can allow us to analyze them geometrically and derive geometric properties.
2.2. Rheonomous Bracket
Next, this subsection explains a new operator for the fully rheonomous affine constraints (2), called the rheonomous bracket. The rheonomous bracket is originally introduced in order to analyze the A-rheonomous affine constraints in [10] -[12] , and plays important roles in derivation of a complete integrability condition and an integrating algorithm. The rheonomous bracket is fundamentally defined based on the normal Lie bracket 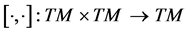 which is an operator for two vector fields
which is an operator for two vector fields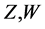 :
:
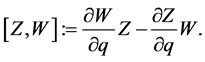 (8)
(8)
The definition of the rheonomous bracket for the FRACs (2) is as follows [10] -[12] .
| Definition 2 [10] -[12] : For the vector fields defined on  on the geometric representation of the FRACs (2): on the geometric representation of the FRACs (2):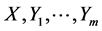 , the rheonomous bracket is an operator: , the rheonomous bracket is an operator: 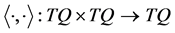 that satisfies the following three properties: that satisfies the following three properties: (a) For a rheonomous affine vector field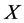 , , 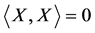 (9) (9)
holds. (b) 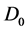 is defined as a set of vector fields that consists of is defined as a set of vector fields that consists of 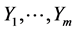 and iterated rheonomous brackets of and iterated rheonomous brackets of 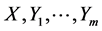 and does not contain and does not contain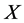 . For a rheonomous affine vector field . For a rheonomous affine vector field 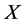 and a vector field and a vector field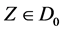 , , 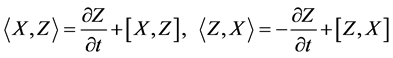 (10) (10)
holds. (c) For two vector fields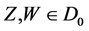 , , 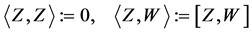 (11) (11)
holds. □ |
For the rheonomous bracket, it is noted that the rheonomous affine vector field 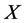 is perceived as special, and this yields an additional term of a time differential of a vector field as the property (b). It must be also noted that from Definition 2 the rheonomous bracket is equivalent to the normal Lie bracket for scleronomous affine constraints, that is, constraints that do not contain the time variable explicitly. The following proposition shows that the rheonomous bracket has some important characteristics in common with the normal Lie bracket [10] -[12] .
is perceived as special, and this yields an additional term of a time differential of a vector field as the property (b). It must be also noted that from Definition 2 the rheonomous bracket is equivalent to the normal Lie bracket for scleronomous affine constraints, that is, constraints that do not contain the time variable explicitly. The following proposition shows that the rheonomous bracket has some important characteristics in common with the normal Lie bracket [10] -[12] .
| Proposition 1: For the vector fields on the geometric representation of the FRACs (2): 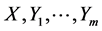 and the set of iterated vector fields of them: and the set of iterated vector fields of them: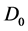 , the following properties (a), (b), and (c) hold. , the following properties (a), (b), and (c) hold. (a) Bilinearlity: 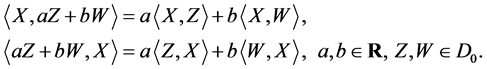 (12) (12)
(b) Skew-symmetry: 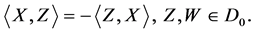 (13) (13)
(c) Jacobi’s identity: 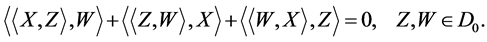 (14) (14)
□ |
From Proposition 1, it can be confirmed that we only have to consider the iterated rheonomous brackets in the form:
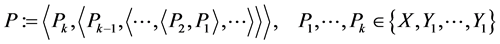 (15)
(15)
in checking a complete integrability condition for the FRACs, which will be shown in the next subsection. Furthermore, the Philip Hall basis [2] , which is a systematic method to generate iterated Lie brackets with an order efficiently, can be also constructed for the rheonomous bracket as follows [10] -[12] .
3. Partial Integtability Conditions for FRACs
In this section, a partial integrability condition for the FRACs (2) is derived. In the simplest terms, the partially integrable case means that some constraints are integrable and the others are nonintegrable. If the 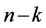 FRACs in (2) are integrable, that is, there exist
FRACs in (2) are integrable, that is, there exist 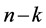 independent first integrals of (2), then they are said to be k-th order partially integrable. Now, we define a smallest and involutive time-varying distribution
independent first integrals of (2), then they are said to be k-th order partially integrable. Now, we define a smallest and involutive time-varying distribution 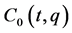 which contains
which contains 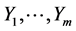 and iterated rheonomous brackets of them, and satisfies
and iterated rheonomous brackets of them, and satisfies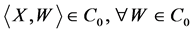 , that is,
, that is, 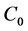 is spanned by all the rheonomous brackets of
is spanned by all the rheonomous brackets of 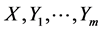 with the exception of
with the exception of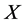 . Then, necessary and sufficient conditions on partilly integrability for the FRACs (2) are given as the next theorem.
. Then, necessary and sufficient conditions on partilly integrability for the FRACs (2) are given as the next theorem.
| Theorem 1: For the fully rheonomous affine constraints defined on an n-dimensional manifold 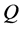 (2) and a time interval (2) and a time interval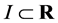 , the following statements (a) and (b) are equivalent to each other. If they hold, the fully rheonomous affine constraints (2) are said to be k-th order partially integrable , the following statements (a) and (b) are equivalent to each other. If they hold, the fully rheonomous affine constraints (2) are said to be k-th order partially integrable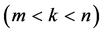 . . (a) There exist 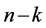 independent first integrals of the fully rheonomous affine constraints (2). independent first integrals of the fully rheonomous affine constraints (2). (b) For a smallest and involutive time-varying distribution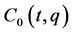 , , 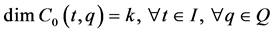 (16) (16)
holds. |
(Proof) Let us consider the 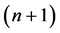 -dimensional product space
-dimensional product space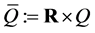 , where
, where 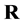 is the space of the time variable
is the space of the time variable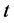 , and the local coordinate of
, and the local coordinate of 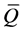 is given by
is given by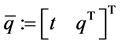 . On
. On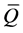 , the FRACs (2) can be represented by Pfaffian equations of
, the FRACs (2) can be represented by Pfaffian equations of 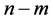 differential forms:
differential forms:
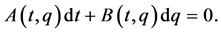 (17)
(17)
Since the rheonomous affine vector field 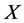 of geometric representation satisfies (7),
of geometric representation satisfies (7), 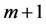 vector fields on
vector fields on 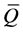 which annihilate (17) are given by
which annihilate (17) are given by
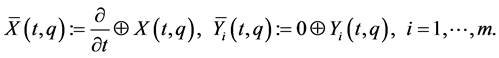 (18)
(18)
We now define an involutive distribution 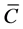 defined on
defined on 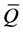 which contains
which contains 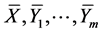 and iterated Lie brackets for
and iterated Lie brackets for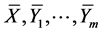 . Therefore, by Frobenius’ theorem [1] [2] [15] [16] and the results [13] [14] , It can be confirmed that a necessary and sufficient condition on k-th order partial integrability for (17) is given by
. Therefore, by Frobenius’ theorem [1] [2] [15] [16] and the results [13] [14] , It can be confirmed that a necessary and sufficient condition on k-th order partial integrability for (17) is given by
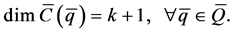 (19)
(19)
Calculating the iterated Lie brackets for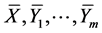 , then we obtain
, then we obtain
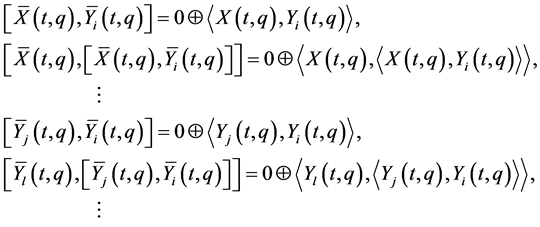 (20)
(20)
We can easily see that 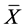 is independent of
is independent of 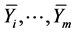 and the iterated Lie brackets (20). Hence, we can change the necessary and sufficient condition (19) into the condition such that
and the iterated Lie brackets (20). Hence, we can change the necessary and sufficient condition (19) into the condition such that 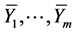 and the iterated Lie brackets which consist of
and the iterated Lie brackets which consist of 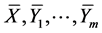 span an k-dimensional space. From the calculations (18) and (20), we only have to consider
span an k-dimensional space. From the calculations (18) and (20), we only have to consider 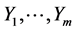 on
on 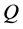 instead of
instead of 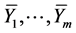 on
on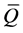 , and iterated rheonomous brackets for
, and iterated rheonomous brackets for 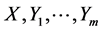 on
on 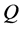 instead of Lie brackets for
instead of Lie brackets for 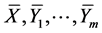 on
on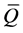 . Consequently, a necessary and sufficient condition on k-th order partially integrability for the FRACs (2) is that
. Consequently, a necessary and sufficient condition on k-th order partially integrability for the FRACs (2) is that 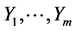 and the iterated rheonomous brackets for
and the iterated rheonomous brackets for 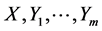 span an k-dimensional space, that is, (16) holds.
span an k-dimensional space, that is, (16) holds.
From Theorem 1, it turns out that the partial integrability condition for the FRACs (2) is quite simple and is a natural extension of the case of the complete integrability case [13] [14] . Moreover, we can see that the rheonomous bracket plays a significant role in the condition (16).
4. Integrating Algorithm for Partially Integrable FRACs
4.1. Integrating Algorithm
The result in Section 3 shows that if the FRACs (2) are k-th order partially integrable, there exist 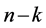 independent first integrals of them. For reduction of the dimension of a given configuration manifold subject to partially integrable FRACs, we need the explicit forms of independent first integrals of them. The author has developed algorithms to calculate independent first integrals of them in the case of complete integrability [14] . However, the algorithm cannot be utilized for the case of partial integrability. Hence, in this subsection, an integrating algorithm for partially integrable FRACs (2) is constructed.
independent first integrals of them. For reduction of the dimension of a given configuration manifold subject to partially integrable FRACs, we need the explicit forms of independent first integrals of them. The author has developed algorithms to calculate independent first integrals of them in the case of complete integrability [14] . However, the algorithm cannot be utilized for the case of partial integrability. Hence, in this subsection, an integrating algorithm for partially integrable FRACs (2) is constructed.
Assume that the FRACs (2) satisfy Theorem 1, that is, they are k-th order partially integrable. Then, we can find 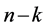 vector fields
vector fields 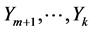 that satisfy
that satisfy
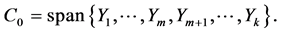 (21)
(21)
In addition, set linearly independent vector fields 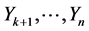 for
for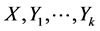 , that is
, that is
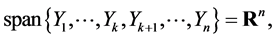 (22)
(22)
holds. Then, let us denote flows (1-parameter local transformation groups) of 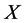 and
and 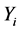 by
by 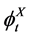 and
and 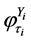 with parameters
with parameters 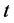 and
and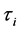 , respectively. We set an initial point at the initial time
, respectively. We set an initial point at the initial time 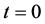 as
as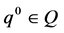 . We also consider
. We also consider 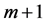 vector fields defined on the expanded configuration manifold
vector fields defined on the expanded configuration manifold 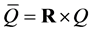 (18), and then their flows on
(18), and then their flows on 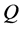 are obtained as
are obtained as
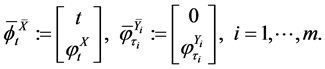 (23)
(23)
Calculating the composite mapping of 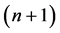 flows (23) yields
flows (23) yields
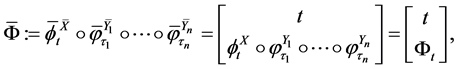 (24)
(24)
where
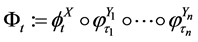 (25)
(25)
is the composite mapping of 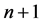 flows
flows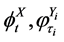 . From (24), we can see that the projection of
. From (24), we can see that the projection of 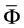 onto
onto 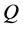 is equivalent to
is equivalent to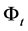 . Hence, by applying the idea of the integrating algorithm for scleronomous linear constraints defined on
. Hence, by applying the idea of the integrating algorithm for scleronomous linear constraints defined on 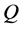 [1] [2] to
[1] [2] to 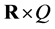 and considering projection of it onto
and considering projection of it onto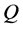 , Consequently, we have the following algorithm to calculate
, Consequently, we have the following algorithm to calculate 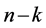 independent first integrals of partially integrable FRACs.
independent first integrals of partially integrable FRACs.
4.2. Theoretical Analysis of Integrating Algorithm
Next, this subsection gives theoretical analysis on the integrating algorithm for partially integrable FRACs (Algorithm 2). In Algorithm 2, we have to derive the inverse function of the combined mapping: 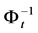 in order to calculate independent first integrals. However, the existence of the inverse function is not guaranteed. In general, it is quite difficult to calculate an inverse function of a given function. For Algorithm 2, the next proposition guarantees the existence of the inverse mapping
in order to calculate independent first integrals. However, the existence of the inverse function is not guaranteed. In general, it is quite difficult to calculate an inverse function of a given function. For Algorithm 2, the next proposition guarantees the existence of the inverse mapping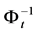 .
.
(Proof) Set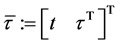 . Calculating the partial differential of (24) with the chain rule of differential calculation, we have
. Calculating the partial differential of (24) with the chain rule of differential calculation, we have
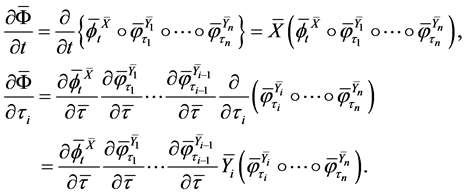 (29)
(29)
Substituting 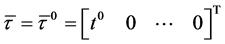 into (29), we obtain
into (29), we obtain
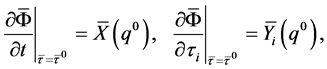 (30)
(30)
that is to say,
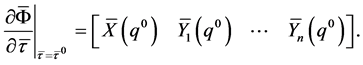 (31)
(31)
Since 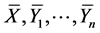 are linearly independent of each other,
are linearly independent of each other,
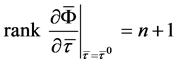 (32)
(32)
holds. Therefore, it turns out that 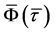 is a diffeomorphism by the implicit function theorem [15] [16] . Since the projection of
is a diffeomorphism by the implicit function theorem [15] [16] . Since the projection of 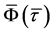 onto
onto 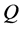 is equivalent to
is equivalent to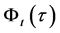 ,
, 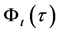 is also a diffeomorphism. Consequently, the proposition is proven.
is also a diffeomorphism. Consequently, the proposition is proven.
From Proposition 2, we can see that similar to the case of complete integrability [14] , the existence of the inverse mapping 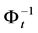 is also guaranteed. For an example of calculation of independent first integrals for the partially integrable FRACs, see the next section.
is also guaranteed. For an example of calculation of independent first integrals for the partially integrable FRACs, see the next section.
5. Example
Finally, this section deals with an example to evaluate the new results. Let us consider a 3-dimensional configuration manifold:
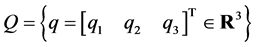 (33)
(33)
with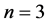 , and a fully rheonomous affine constraints on
, and a fully rheonomous affine constraints on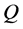 :
:
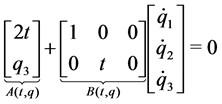 (34)
(34)
with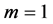 . We here consider a time interval
. We here consider a time interval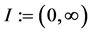 . Then, it turns out that Assumption 1 holds for (34). One geometric representation for (34) can be obtained as follows:
. Then, it turns out that Assumption 1 holds for (34). One geometric representation for (34) can be obtained as follows:
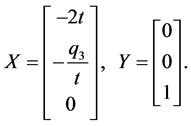 (35)
(35)
Calculating an iterated rheonomous bracket for 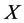 and
and 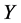 above, we obtain
above, we obtain
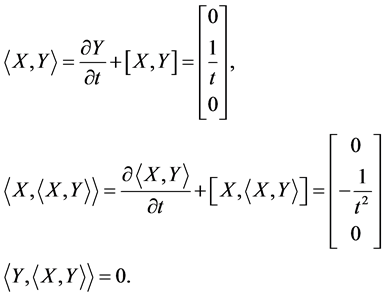 (36)
(36)
Since 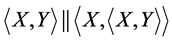 holds, we have
holds, we have
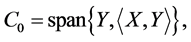 (37)
(37)
and then it can be confirmed that
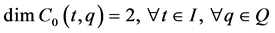 (38)
(38)
holds. From Theorem 1, it turns out that the FRACs (34) are 2nd order partially integrable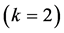 , that is, there exists one independent first integrals of (34).
, that is, there exists one independent first integrals of (34).
Next, we shall calculate the first integrals of (34) according to Algorithm 1. Set 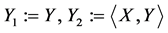 and a new vector field that satisfy (26) as
and a new vector field that satisfy (26) as
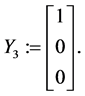 (39)
(39)
For the vector fields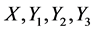 , we calculate their flows as
, we calculate their flows as
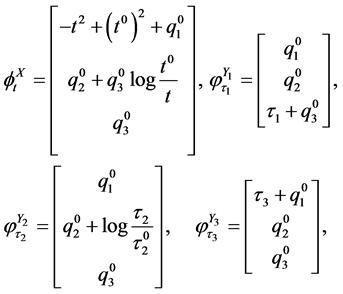 (40)
(40)
where 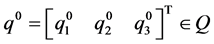 is the initial point at the initial time
is the initial point at the initial time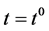 . Combining the flows (40) like (28), we have
. Combining the flows (40) like (28), we have
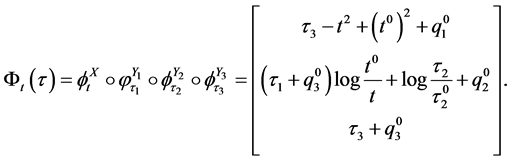 (41)
(41)
By solving the equation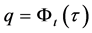 , we calculate the inverse mapping of (41) as
, we calculate the inverse mapping of (41) as
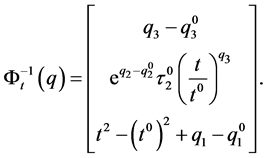 (42)
(42)
Consequently, we can obtain one independent first integrals of (34) as the last component of (43):
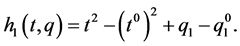 (43)
(43)
6. Conclusions
This paper has studied necessary and sufficient conditions for the fully rheonomous affine constraints (FRACs) in the case of partial integrability, and develops an integrating algorithm in order to calculate independent first integrals. It turns out that the new proposed integrating algorithm is expected to be a powerful mathematical tool and can be utilized in various research fields.
Future work includes applications of the new results to various systems, extensions of sub-Riemannian geometry, and analysis of more general classes of constraints.