A Series Solution for Three-Dimensional Navier-Stokes Equations of Flow near an Infinite Rotating Disk ()
1. Introduction
Von Karman swirling viscous flow [1] is a well-known classical problem in fluid mechanics. The original problem raised by Von Karman is about the viscous flow induced by an infinite rotating disk where the fluid, far from the disk, is at rest. Then the problem is generalized in considering the case where the fluid itself is rotating as a solid body far from the disk with suction or injection at the disk surface [2] . This generates a parameter, i.e. the ratio of the angular velocity of the fluid at infinity to the angular velocity of the disk. Another generalization is to consider the viscous flow between two infinite coaxial rotating disks with suction or injection at both disks and this reveals another parameter, i.e. the Reynolds number determined by the distance of the two disks.
Nonlinear phenomena play a crucial role in applied mathematics and physics. It is known that most of engineering problems are nonlinear and solving them analytically is very difficult. Various powerful mathematical methods such as inverse scattering method [3] , tanh method [4] , sine-cosine method [5] , homogeneous balance method [6] , Exp-function method [7] and variational methods [8] -[12] have been proposed for obtaining exact and approximate analytic solutions. Recently, two analytical techniques have drawn specific attention, namely homotopy analysis method (HAM) and homotopy perturbation method (HPM). The essential idea in these methods is introducing a homotopy parameter, like , which takes the value from 0 to 1. For
, which takes the value from 0 to 1. For , the system of equations takes a simplified form, which readily admits a particularly simple solution. When
, the system of equations takes a simplified form, which readily admits a particularly simple solution. When  is gradually being increased to 1, the system goes through a sequence of “deformations”, the solution of each of which is “close” to that at the previous stage of “deformation”. Eventually at
is gradually being increased to 1, the system goes through a sequence of “deformations”, the solution of each of which is “close” to that at the previous stage of “deformation”. Eventually at  the system takes the original form of equation and the final stage of “deformation” gives the desired solution. In 1992, Liao [13] [14] has been the leading exponent of homotopy analysis method (HAM). In HAM, Liao keeps sufficient room for experimenting the convergence of approximations by introducing auxiliary parameter and also, an auxiliary non-zero function. Another way of viewing homotopy approach is to think of
the system takes the original form of equation and the final stage of “deformation” gives the desired solution. In 1992, Liao [13] [14] has been the leading exponent of homotopy analysis method (HAM). In HAM, Liao keeps sufficient room for experimenting the convergence of approximations by introducing auxiliary parameter and also, an auxiliary non-zero function. Another way of viewing homotopy approach is to think of  as a perturbation parameter. In 1998, He [15] has transformed this idea into homotopy perturbation method (HPM). The approximate solution given by HAM is the same as the approximate solution given by HPM, when auxiliary parameter and auxiliary non-zero function are taken −1 and 1, respectively [16] -[19] . So, the approximate analytical solution obtained by HAM contains the solution obtained by HPM. However, the implementation of these methods shows that HAM is more effective than HPM. The convergence of HAM solution series depends on four factors, i.e. initial guess, auxiliary linear operator, auxiliary non-zero function and auxiliary parameter
as a perturbation parameter. In 1998, He [15] has transformed this idea into homotopy perturbation method (HPM). The approximate solution given by HAM is the same as the approximate solution given by HPM, when auxiliary parameter and auxiliary non-zero function are taken −1 and 1, respectively [16] -[19] . So, the approximate analytical solution obtained by HAM contains the solution obtained by HPM. However, the implementation of these methods shows that HAM is more effective than HPM. The convergence of HAM solution series depends on four factors, i.e. initial guess, auxiliary linear operator, auxiliary non-zero function and auxiliary parameter  However, as a special case of homotopy analysis method by having
However, as a special case of homotopy analysis method by having , the convergence of HPM solution series only depends on two factors: the auxiliary linear operator and the initial guess. Therefore, having the initial guess and the auxiliary linear operator, HPM cannot provide other ways to ensure that the solution is convergent. Note that the HAM has already been applied to the analytical solution of several other problems [20] -[22] .
, the convergence of HPM solution series only depends on two factors: the auxiliary linear operator and the initial guess. Therefore, having the initial guess and the auxiliary linear operator, HPM cannot provide other ways to ensure that the solution is convergent. Note that the HAM has already been applied to the analytical solution of several other problems [20] -[22] .
Ismail and Rabboh [23] presented a restrictive Padé approximation for the generalized Fisher and Burger-Fisher equations. The Padé approximants that often show superior performance over series approximations provide a successful tool and promising scheme for identical applications.
The purpose of this paper is to extend homotopy analysis method and Padé approximant to solve three-dimensional Navier-Stokes equations for the viscous flow near an infinite rotating disk.
2. Flow Analysis and Mathematical Formulation
The Navier-Stokes equations for cylindrical coordinate are as follows:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
where ,
, 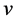 and
and  are velocities in the
are velocities in the ,
,  and
and  directions; respectively.
directions; respectively. ,
,  and
and  are density, pressure and viscosity. Consider the steady flow which results if the infinite plane
are density, pressure and viscosity. Consider the steady flow which results if the infinite plane  rotates at constant angular velocity
rotates at constant angular velocity  about the axis
about the axis 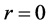 beneath a Newtonian viscous fluid which otherwise be at rest. The viscous drag of the rotating surface would set up a swirling flow toward the disk. All three velocity components
beneath a Newtonian viscous fluid which otherwise be at rest. The viscous drag of the rotating surface would set up a swirling flow toward the disk. All three velocity components ,
, 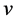 and
and  would be involved in a genuine three-dimensional motion, but because of radial symmetry they will be independent of
would be involved in a genuine three-dimensional motion, but because of radial symmetry they will be independent of  as would the pressure
as would the pressure , so it is required to solve the equation for these four variables as functions of
, so it is required to solve the equation for these four variables as functions of  and
and  from the continuity equation and the momentum equations in the
from the continuity equation and the momentum equations in the ,
,  and
and  directions we obtain
directions we obtain
 (5)
(5)
 (6)
(6)
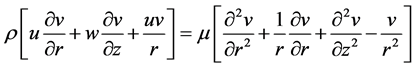 (7)
(7)
 (8)
(8)
The boundary conditions are no-slip at the disk wall and inviscid flow far from the disk (except an axial inflow):
 (9)
(9)
 (10)
(10)
Note that we refrain from imposing any conditions on  as
as , because we expect (by hindsight, to be sure) that the disk will have a centrifugal pumping action which must be balanced by a uniform axial inflow
, because we expect (by hindsight, to be sure) that the disk will have a centrifugal pumping action which must be balanced by a uniform axial inflow far from the disk. Also the condition
far from the disk. Also the condition  (a convenient constant) at the wall is by hindsight. It has been deduced that
(a convenient constant) at the wall is by hindsight. It has been deduced that 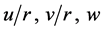 and
and  are all functions of
are all functions of . Since the only two parameters in the problem are
. Since the only two parameters in the problem are  and
and , it is easy to see that the proper dimensionless variable must be
, it is easy to see that the proper dimensionless variable must be  Regarding Karman (1921), we propose the new dimensionless variables
Regarding Karman (1921), we propose the new dimensionless variables ,
,  ,
,  and
and  as
as
 (11)
(11)
These variables are substituted into Equations (5)-(8) and the following set of nonlinear ordinary coupled differential equations is obtained:
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
3. Basic Concepts of HAM
Consider the following differential equation
 (16)
(16)
where  is a nonlinear operator,
is a nonlinear operator,  denotes an independent variable,
denotes an independent variable,  is an unknown function which is the solution for the equation. The function is defined as
is an unknown function which is the solution for the equation. The function is defined as
 (17)
(17)
and
 (18)
(18)
where,  and
and  are the initial guesses which satisfy the initial or boundary condition.
are the initial guesses which satisfy the initial or boundary condition.
By means of generalizing the traditional homotopy method, Liao [13] forms the so-called zero-order deformation equation as follows
 (19)
(19)
where 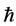 is the auxiliary parameter which increases the convergence of result ,
is the auxiliary parameter which increases the convergence of result ,  is an auxiliary function and
is an auxiliary function and 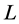 is an auxiliary linear operator,
is an auxiliary linear operator,  increases from 0 to 1, the solution
increases from 0 to 1, the solution  changes between the initial guess
changes between the initial guess  and solution
and solution . Expanding
. Expanding  in Taylor series with respect to
in Taylor series with respect to , we obtain
, we obtain
 (20)
(20)
where
 (21)
(21)
if the auxiliary linear operator, the initial guess, the auxiliary parameter  and the auxiliary function are so properly chosen, the series (20) converges at
and the auxiliary function are so properly chosen, the series (20) converges at , so we have
, so we have
 (22)
(22)
which must be one of the solutions of the original nonlinear equation, as proved by Liao [13] . It is clear that if the auxiliary parameter is , and auxiliary function is determined to be
, and auxiliary function is determined to be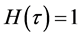 , Equation (19) would be
, Equation (19) would be
 (23)
(23)
This statement is commonly used in HPM procedure. Indeed, in HPM, the nonlinear differential equation is solved by separating every Taylor expansion term. Now, the vector of  is defined as
is defined as
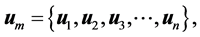 (24)
(24)
according to the definition Equation (21), the governing equation and the corresponding initial condition of  can be deduced from zero-order deformation Equation (19). Differentiating Equation (19), m times with respect to the embedding parameter
can be deduced from zero-order deformation Equation (19). Differentiating Equation (19), m times with respect to the embedding parameter  and setting
and setting  and finally dividing by
and finally dividing by , we will have the socalled mth order deformation equation in the following from
, we will have the socalled mth order deformation equation in the following from
 (25)
(25)
where
 (26)
(26)
and
 (27)
(27)
Therefore by applying inverse linear operator to both sides of the linear equation, Equation (25), we can easily solve the equation and compute the generation constant by applying the initial or boundary conditions.
4. HAM-Padé Solution
In this section the HAM is used to find approximate solutions of the Equations (12)-(15). We choose the initial approximation as
 (28)
(28)
and the linear operator for Equations (12) to (15)
 (29)
(29)
 (30)
(30)
 (31)
(31)
 (32)
(32)
We convert Equations (12) through (15) to nonlinear form:
 (33)
(33)
 (34)
(34)
 (35)
(35)
 (36)
(36)
Assuming  we use the above definitions to form the zero-order deformation equations
we use the above definitions to form the zero-order deformation equations
 (37)
(37)
 (38)
(38)
 (39)
(39)
 (40)
(40)
Obviously, when  and
and ,
,
 (41)
(41)
 (42)
(42)
 (43)
(43)
 (44)
(44)
Differentiating the zero-order deformation Equations (37)-(40) m times respecting  and finally dividing by
and finally dividing by , we have the mth-order deformation equations as follows
, we have the mth-order deformation equations as follows
 (45)
(45)
 (46)
(46)
 (47)
(47)
 (48)
(48)
where
 (49)
(49)
 (50)
(50)
 (51)
(51)
 (52)
(52)
Using 10 terms in evaluating the approximate solution, and applying the padé approximation, we obtain
 (53)
(53)
 (54)
(54)
 (55)
(55)
 (56)
(56)
Noting that, the different from all other analytical techniques such as the perturbation method, Adomian decomposition method, expansion method, and etc., the solutions given by the HAM contain auxiliary parameters which could be used to control and adjust the convergence region and rate of the HAM series.
which could be used to control and adjust the convergence region and rate of the HAM series.
5. Convergence of HAM
It has been proven that, as long as a series solution given by the homotopy analysis method is converging, it is certainly one of the exact solutions. The solution series contains the auxiliary parameters  and which provides us with a simple way to adjust and control the convergence of the solution series. In general, by means of the so-called
and which provides us with a simple way to adjust and control the convergence of the solution series. In general, by means of the so-called  -curve, i.e., a curve of versus
-curve, i.e., a curve of versus . As pointed by Liao [13] , the valid region of
. As pointed by Liao [13] , the valid region of  is a horizontal line segment. To see the range of admissible values of these parameters, the curves of
is a horizontal line segment. To see the range of admissible values of these parameters, the curves of  are plotted in Figure 1 for
are plotted in Figure 1 for  and
and  given by 10th-order approximation. For better presentation, these valid regions are listed in Table 1. A wide valid zone is evident in these figures ensuring convergence of the series. To choose optimal value of auxiliary parameter, the averaged residual errors [24] are defined as
given by 10th-order approximation. For better presentation, these valid regions are listed in Table 1. A wide valid zone is evident in these figures ensuring convergence of the series. To choose optimal value of auxiliary parameter, the averaged residual errors [24] are defined as
 (57)
(57)
 (58)
(58)

Table 1. The admissible values of  for each
for each .
.
 (59)
(59)
 (60)
(60)
where ∆x = 10/λ and λ = 20. For a given order of approximation m, the optimal values of  is given by the minimum of Em, corresponding to nonlinear algebraic equations
is given by the minimum of Em, corresponding to nonlinear algebraic equations
 (61)
(61)
It is noticed that the optimal value of  is replaced into the equations. Table 1 shows optimal values obtained for the auxiliary parameters
is replaced into the equations. Table 1 shows optimal values obtained for the auxiliary parameters  . To see the accuracy of the solutions, the residual errors for the system are defined as
. To see the accuracy of the solutions, the residual errors for the system are defined as
 (62)
(62)
 (63)
(63)
 (64)
(64)
 (65)
(65)
where Fn(t), Gn(t), Hn(t) and Kn(t) are the HAM solutions for f (t), g(t), h(t) and k(t).
6. Results and Discussion
HAM-Padé, in this paper was used to find approximate solutions for nonlinear equations obtained by the steady, laminar, axially symmetric viscous flow near an infinite rotating disk. The accuracy of the method is appropriate and obtained results are close to the numerical solution. It is proper mentioning that the numerical results have been obtained using the fourth-order Runge-Kutta method along shooting method for satisfying boundary conditions at infinity. Figures 2-4 show the velocities in the ,
,  and
and  directions respectively. Figure 5 demonstrates distribution of pressure in the
directions respectively. Figure 5 demonstrates distribution of pressure in the  direction. In Table 1
direction. In Table 1  is not a good approximation in every case. The results show that the HPM-Padé isonly valid for small values of independent variable.
is not a good approximation in every case. The results show that the HPM-Padé isonly valid for small values of independent variable.
7. Conclusions
In this paper, homotopy analysis method (HAM) and Padé approximant were considered for finding analytical solution of three-dimensional viscous flow near an infinite rotating disk which is a well-known classical problem in fluid mechanics. A comparison of HAM-Padé and HPM-Padé is made. Unlike perturbation method, the HAM does not depend on any small physical parameters. Thus, it is valid for both weak and strong nonlinear problems. Besides, the HAM provides us with a convenient way of controlling the convergence of approximation series, by means of auxiliary parameter, which is a fundamental qualitative difference in analysis between the HAM and other methods. Also the figures show that the HAM-Padé is a powerful mathematical tool for solving the system of non-linear partial differential equations having wide applications in engineering.
Finally, the recent appearance of nonlinear differential equations as models in some fields of applied mathematics makes it necessary to investigate innovative methods of solution for such equations.
NOTES
*Corresponding author.