Variations of Enclosing Problem Using Axis Parallel Square(s): A General Approach ()
1. Introduction
Given a set  points in a plane, enclosing problem in computational geometry is concerned with finding the smallest geometrical object of a given type that encloses all the points of
points in a plane, enclosing problem in computational geometry is concerned with finding the smallest geometrical object of a given type that encloses all the points of . Some well known instances of the enclosing problem are finding minimum enclosing circle [1] , minimum area triangle [2] , minimum area rectangle [3] , minimum bounding box [4] , and smallest width annulus [5] .
. Some well known instances of the enclosing problem are finding minimum enclosing circle [1] , minimum area triangle [2] , minimum area rectangle [3] , minimum bounding box [4] , and smallest width annulus [5] .
The  -enclosing problem is an important variant of enclosing problem. Here the objective is to compute a smallest region of given type that encloses at least
-enclosing problem is an important variant of enclosing problem. Here the objective is to compute a smallest region of given type that encloses at least  points of
points of .
.  -enclosing problems using rectangles and squares are studied [6] -[11] are also studied extensively.
-enclosing problems using rectangles and squares are studied [6] -[11] are also studied extensively.
A closely related problem locates one or more copies of a given region to maximize the size of the subset enclosed. In other words, instead of fixing 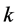 and computing an optimal enclosing region, the problem is to maximize the number of points enclosed by the given region(s) of fixed size and shape. This type of problem has similar applications as the problems mentioned above. These so called problems of maximal enclosing using single object, each of fixed size and orientation, have also received attention of many researchers. The objects used are circle [12] and convex polygon [13] [14] . Younies et al. [15] introduced a zero-one mixed integer formulation for the maximum enclosing problem where points are enclosed by parallelograms in a plane. Directional antennas is one of the applications where parallelogram shapes would be useful. In the context of bichromatic planar point set, Díaz-Báñez et al. [16] proposed algorithms for maximal enclosing by two disjoint axis-parallel unit squares and circles in
and computing an optimal enclosing region, the problem is to maximize the number of points enclosed by the given region(s) of fixed size and shape. This type of problem has similar applications as the problems mentioned above. These so called problems of maximal enclosing using single object, each of fixed size and orientation, have also received attention of many researchers. The objects used are circle [12] and convex polygon [13] [14] . Younies et al. [15] introduced a zero-one mixed integer formulation for the maximum enclosing problem where points are enclosed by parallelograms in a plane. Directional antennas is one of the applications where parallelogram shapes would be useful. In the context of bichromatic planar point set, Díaz-Báñez et al. [16] proposed algorithms for maximal enclosing by two disjoint axis-parallel unit squares and circles in  and
and  time respectively. Later, they improved the complexities to
time respectively. Later, they improved the complexities to  and
and  time respectively [17] .
time respectively [17] .
Problems Studied
An axis-parallel unit square is a square of unit size whose sides are parallel to one of the coordinate axes. An axis-parallel unit square  encloses a set of points those lie on the boundaries of
encloses a set of points those lie on the boundaries of  or in the interior of
or in the interior of . For a given set
. For a given set  of
of  points in two dimensional plane, in this paper we consider the following variation of the maximal covering problem.
points in two dimensional plane, in this paper we consider the following variation of the maximal covering problem.
• For each point , locate an axis-parallel unit square whose one side is constrained to pass through
, locate an axis-parallel unit square whose one side is constrained to pass through  and encloses the maximum number of points from
and encloses the maximum number of points from .
.
We propose an  time and
time and  space algorithm to solve the problem P1. It is shown that this algorithm can be used to compute a placement of one or more axis-parallel squares enclosing the maximum number of points from
space algorithm to solve the problem P1. It is shown that this algorithm can be used to compute a placement of one or more axis-parallel squares enclosing the maximum number of points from  if such a placement exists. We also use this result to construct an efficient algorithm for finding the smallest axis-parallel square enclosing at least
if such a placement exists. We also use this result to construct an efficient algorithm for finding the smallest axis-parallel square enclosing at least 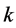 points of
points of  for large values of
for large values of 
 .
.
2 Maximal Enclosing Problem
This section considers the following problem P1: For each point , we locate an axis-parallel unit square whose one particular side is passing through
, we locate an axis-parallel unit square whose one particular side is passing through  and enclosing the maximum number of points from
and enclosing the maximum number of points from . Note that such axis-parallel unit square may not be unique. In that case, choose one among them and call that axis-parallel unit square as candidate square. Therefore, at most
. Note that such axis-parallel unit square may not be unique. In that case, choose one among them and call that axis-parallel unit square as candidate square. Therefore, at most  number of candidate squares can be obtained by considering alignments of four different sides for all points in
number of candidate squares can be obtained by considering alignments of four different sides for all points in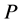 . Below we describe the pass for computing candidate squares whose bottom sides are passing through a point from
. Below we describe the pass for computing candidate squares whose bottom sides are passing through a point from  (See Figure 1).
(See Figure 1).
Without loss of generality, assume that no two points have the same  - or
- or 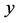 -coordinate. Consider two arrays
-coordinate. Consider two arrays  and
and  containing the points of
containing the points of 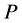 in ascending order of
in ascending order of  and
and 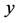 -coordinates respectively. Let us denote the
-coordinates respectively. Let us denote the  -coordinate of the i-th entry of
-coordinate of the i-th entry of  by
by  and similarly the
and similarly the  -coordinate of the i-th entry of
-coordinate of the i-th entry of  by
by ,
,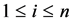 . Coordinates of a generic point
. Coordinates of a generic point  is denoted by
is denoted by . For a point
. For a point , let
, let  denote the minimum entry in
denote the minimum entry in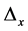 , say
, say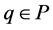 , such that
, such that .
.
Observation 1 Given the array , all intervals
, all intervals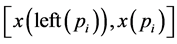 ,
,  can be computed in linear time.
can be computed in linear time.
In a similar way, for a point , let
, let 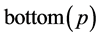 denote the minimum entry in
denote the minimum entry in , say
, say , such that
, such that . Likewise, we define
. Likewise, we define , and
, and  on the arrays
on the arrays  and
and  respectively.
respectively.
Algorithm for Reporting Candidate Squares
In this section we present sweep line algorithm combined with balanced search tree as data structure for computing candidate squares. Using the points in array , construct a balanced search tree
, construct a balanced search tree  with search key as the
with search key as the 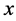 -coordinate values of the points in
-coordinate values of the points in . The leaves of
. The leaves of 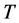 correspond to the ordered points of
correspond to the ordered points of . We attach two positive integral variables
. We attach two positive integral variables 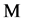 and
and  with each node of
with each node of . Before describing the algorithm in details, we first explain the role of
. Before describing the algorithm in details, we first explain the role of  and
and . The span
. The span 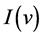 corresponding to an internal node
corresponding to an internal node  is an interval, generated by the
is an interval, generated by the  -coordinates of the left most and right most points at the leaves in the subtree rooted at
-coordinates of the left most and right most points at the leaves in the subtree rooted at . Moreover, span
. Moreover, span  of the leaf node
of the leaf node 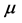 stores the
stores the  -coordinate of the point at the leaf node
-coordinate of the point at the leaf node 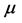 of
of . Our sweep line algorithm considers two horizontal sweep lines namely bottom sweep line
. Our sweep line algorithm considers two horizontal sweep lines namely bottom sweep line 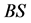 and top sweep line
and top sweep line . Let the current positions of
. Let the current positions of  and
and  be at heights
be at heights 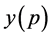 and
and  respectively such that
respectively such that  and
and  be the unit horizontal slab determined by
be the unit horizontal slab determined by  and
and . In case that the vertical distance between
. In case that the vertical distance between  and
and  is less than unity, shift
is less than unity, shift 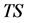 upwards to create a gap between
upwards to create a gap between  and
and 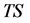 as unity. Note that, no additional points are included for such shifting of
as unity. Note that, no additional points are included for such shifting of  in upward direction.
in upward direction.
At the end of processing all points within , we get the following information by
, we get the following information by  and
and . The variable
. The variable  attached with an internal node
attached with an internal node  indicates that there exists a subset
indicates that there exists a subset  of size
of size  (i.e.,
(i.e., 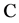 stores the count of the set
stores the count of the set ) such that each unit square whose bottom, top sides coincide with
) such that each unit square whose bottom, top sides coincide with ,
,  respectively and left boundary within span
respectively and left boundary within span  encloses the subset
encloses the subset . Observe that these spans
. Observe that these spans  are all different for all nodes
are all different for all nodes . The subsets
. The subsets 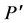 for nodes along the path from root to a leaf node are all disjoint. Here each node
for nodes along the path from root to a leaf node are all disjoint. Here each node 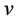 does not keep
does not keep  explicitly but only its count
explicitly but only its count . The variable
. The variable  attached with an internal node
attached with an internal node 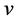 indicates that there exists a unit square
indicates that there exists a unit square 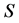 whose cardinality is the sum of
whose cardinality is the sum of 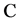 values of the ancestor nodes of
values of the ancestor nodes of  plus the
plus the  value at node
value at node ; bottom and top sides of
; bottom and top sides of 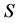 are constrained to coincide with
are constrained to coincide with ,
,  respectively, the left boundary of
respectively, the left boundary of 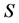 lies within the span
lies within the span . Moreover, the cardinality of
. Moreover, the cardinality of  is maximum among all unit squares within the slab
is maximum among all unit squares within the slab  and the left boundary of each such unit square lies within the span of
and the left boundary of each such unit square lies within the span of . We now recursively define
. We now recursively define  value for an internal node as the sum of its
value for an internal node as the sum of its  value and the maximum of
value and the maximum of  values of its two children-nodes. This recursive definition of
values of its two children-nodes. This recursive definition of  implies that variable
implies that variable 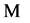 at the root of tree
at the root of tree  stores the cardinality of a candidate square whose bottom side is constrained to pass through the point
stores the cardinality of a candidate square whose bottom side is constrained to pass through the point . This type of integral variables attached to the nodes of segment tree are also used to handle stabbing counting queries [18] . The space requirement for this type of segment tree is linear [18] .
. This type of integral variables attached to the nodes of segment tree are also used to handle stabbing counting queries [18] . The space requirement for this type of segment tree is linear [18] .
In initial step, the variables 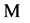 and
and  corresponding to all nodes are initialized with zero and both the sweep lines
corresponding to all nodes are initialized with zero and both the sweep lines  and
and  pass through the bottom most point
pass through the bottom most point . Assume that
. Assume that 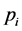 is the point corresponding to the i-th entry in
is the point corresponding to the i-th entry in ,
, . The algorithm processes all points
. The algorithm processes all points 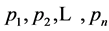 in
in  one at a time. We also explain the way of capturing information by the variables
one at a time. We also explain the way of capturing information by the variables  and
and  at the time of processing a point in
at the time of processing a point in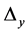 , encountered by sweep lines.
, encountered by sweep lines.
The sweep line  is moved up one point at a time, considering
is moved up one point at a time, considering  as the first encountered point. For each point
as the first encountered point. For each point  encountered by the sweep line
encountered by the sweep line , if the vertical distance of
, if the vertical distance of  from the current position of the sweep line
from the current position of the sweep line  is less than or equal to unity,
is less than or equal to unity,  is updated by Increment operation which is described below.
is updated by Increment operation which is described below.
For the interval , find the split node [18]
, find the split node [18] 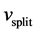 in
in , that is the least common ancestor of
, that is the least common ancestor of  and
and  in the balanced search tree
in the balanced search tree . Search for the leaf node containing
. Search for the leaf node containing  on the left subtree rooted at
on the left subtree rooted at 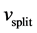 and, while traversing, if we turn left from node
and, while traversing, if we turn left from node , increment
, increment  of the right child of
of the right child of  by one. In case the right child of
by one. In case the right child of  is a leaf, increment its
is a leaf, increment its  instead of
instead of . Similarly, while traversing the right subtree of the split node for searching the leaf node containing
. Similarly, while traversing the right subtree of the split node for searching the leaf node containing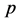 , if we turn right from node
, if we turn right from node , increment
, increment  of the left child of
of the left child of . Again, in case the left child is a leaf, increment its
. Again, in case the left child is a leaf, increment its  instead of
instead of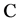 . Finally, increase the
. Finally, increase the  values of the leaf nodes containing
values of the leaf nodes containing 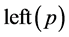 and
and  by one. We now recursively update the
by one. We now recursively update the  value of each internal node in the path from the leaf node containing
value of each internal node in the path from the leaf node containing  to the left child of the split node
to the left child of the split node , as the sum of its
, as the sum of its  value and the maximum of
value and the maximum of  values of its two children-nodes. Then update the
values of its two children-nodes. Then update the  value of each internal node in the path from the leaf containing
value of each internal node in the path from the leaf containing  to the root of
to the root of 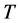 in similar way. In case
in similar way. In case , we find the leaf node
, we find the leaf node  of
of  that contains the point
that contains the point  and increment the
and increment the 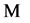 value of leaf node
value of leaf node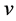 . The subsequent updation of
. The subsequent updation of  values associated with the internal nodes of
values associated with the internal nodes of  is same as described earlier.
is same as described earlier.
Again if the vertical distance of the encountered point  by
by  from the current position of
from the current position of  becomes greater than unity,
becomes greater than unity, 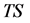 stops advancing to
stops advancing to  (i.e.,
(i.e., 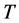 is not updated by Increment operation for the point
is not updated by Increment operation for the point ). For the point
). For the point  on the current position of
on the current position of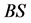 , update
, update  for the point
for the point  and report a candidate square with bottom boundary passing though
and report a candidate square with bottom boundary passing though 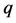 by the Decrement and Report operations which are explained below. The sweep line
by the Decrement and Report operations which are explained below. The sweep line 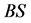 is then moved up one point at a time. For each point
is then moved up one point at a time. For each point  encountered by the sweep line
encountered by the sweep line , if the vertical distance between
, if the vertical distance between  and
and  is greater than unity,
is greater than unity, 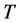 is updated by Decrement operation and a candidate square with bottom boundary passing though
is updated by Decrement operation and a candidate square with bottom boundary passing though  is reported by Report operation.
is reported by Report operation.
In case that the vertical distance of  from
from 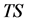 becomes smaller than unity, the sweep line
becomes smaller than unity, the sweep line  stops advancing and sweep line
stops advancing and sweep line  starts sweeping from its current position. The above process is continued till Report and Decrement operations are done for all the points.
starts sweeping from its current position. The above process is continued till Report and Decrement operations are done for all the points.
We now describe the Report operation. Let  be the candidate square with bottom boundary passing through the point
be the candidate square with bottom boundary passing through the point . Observe that the number of points enclosed by
. Observe that the number of points enclosed by 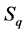 is equal to the
is equal to the  value at the root of the tree
value at the root of the tree . To find a placement of the left boundary of
. To find a placement of the left boundary of , move from the root of the tree
, move from the root of the tree  towards the leaf, each time picking the child with larger
towards the leaf, each time picking the child with larger  value. The leaf node thus reached stores the point through which the left boundary of
value. The leaf node thus reached stores the point through which the left boundary of  passes. Report
passes. Report  along with the number of points inside it.
along with the number of points inside it.
The Decrement operation is same as Increment operation with the following exception. For the interval  associated with point
associated with point , locate the split node in
, locate the split node in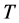 . During searching from the split node for the nodes containing
. During searching from the split node for the nodes containing  and
and , instead of incrementing, we decrement
, instead of incrementing, we decrement ’s and
’s and ’s by one as appropriate. The subsequent updation of
’s by one as appropriate. The subsequent updation of 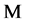 values associated with the internal nodes of
values associated with the internal nodes of  is similar to that in the Increment operation.
is similar to that in the Increment operation.
Theorem 1 Let 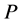 be a set of
be a set of  points in a two dimensional plane. Then all candidate squares for
points in a two dimensional plane. Then all candidate squares for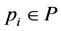 ,
,  , can be computed in
, can be computed in  time using
time using  space.
space.
Proof: For a point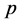 , each of Increment, Decrement and Report operation takes
, each of Increment, Decrement and Report operation takes  time. Since for each point in
time. Since for each point in , these operations are executed only once, they together take
, these operations are executed only once, they together take  time. Corollary 1 A placement of an axis-parallel unit square enclosing the maximum number of points from
time. Corollary 1 A placement of an axis-parallel unit square enclosing the maximum number of points from  can be computed in
can be computed in  time using
time using 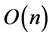 space.
space.
Proof: Let  be an axis-parallel unit square enclosing the maximum number of points from
be an axis-parallel unit square enclosing the maximum number of points from  and
and  be the set of points enclosed by
be the set of points enclosed by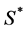 . Note that
. Note that  can always be repositioned, without altering the points enclosed by it, so that the extended lines of two adjacent sides of
can always be repositioned, without altering the points enclosed by it, so that the extended lines of two adjacent sides of  pass through two points of
pass through two points of  and these two points may not belong to
and these two points may not belong to . Sometimes the adjacent sides of
. Sometimes the adjacent sides of  may be passed through same point of
may be passed through same point of  and, in that case, the point is at one corner of
and, in that case, the point is at one corner of . Therefore, the maximum cardinality among the set of all possible candidate squares is equal to the cardinality of
. Therefore, the maximum cardinality among the set of all possible candidate squares is equal to the cardinality of . Corollary 2 An axis-parallel rectangle of fixed height and width that encloses the maximum number of points from
. Corollary 2 An axis-parallel rectangle of fixed height and width that encloses the maximum number of points from , can be placed in
, can be placed in  time using
time using 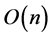 space.
space.
Proof: Follows directly from Corollary 1. Corollary 3 A placement of two disjoint axis-parallel unit squares together enclosing the maximum number of points from , can be computed in
, can be computed in  time using
time using 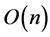 space.
space.
Proof: For each point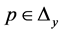 , we can compute the cardinality of candidate square whose top boundary is passing through
, we can compute the cardinality of candidate square whose top boundary is passing through  in
in  time. Now, we sweep from bottom to top to generate a subset of
time. Now, we sweep from bottom to top to generate a subset of 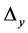 that reports the maximum cardinality candidate square whose top boundary lies below any point
that reports the maximum cardinality candidate square whose top boundary lies below any point . This sweeping process requires
. This sweeping process requires  time. It is interesting to generalize the maximal enclosing problem using
time. It is interesting to generalize the maximal enclosing problem using  disjoint axis-parallel unit squares,
disjoint axis-parallel unit squares,  and the problem is known to be NP-hard [19] . A set of
and the problem is known to be NP-hard [19] . A set of  rectangles (squares) on the plane is called
rectangles (squares) on the plane is called  -sliceable if they can be recursively partitioned by
-sliceable if they can be recursively partitioned by  horizontal or vertical lines [20] . We now assume there exists
horizontal or vertical lines [20] . We now assume there exists  -sliceable axis-parallel squares and propose an algorithm to locate three axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from
-sliceable axis-parallel squares and propose an algorithm to locate three axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from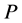 .
.
Let 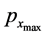 and
and 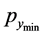 be the points with maximum
be the points with maximum  -coordinates and minimum
-coordinates and minimum  -coordinates among the points in
-coordinates among the points in  respectively. Similarly,
respectively. Similarly,  and
and  be the points with maximum
be the points with maximum  -coordinates and minimum
-coordinates and minimum  -coordinates among the points in
-coordinates among the points in  respectively.
respectively.
Observe that among these three squares, one square is separated from other two squares by a horizontal or a vertical line. Without loss of generality, assume that the line separating one square from other two squares is vertical (first pass). The other pass where the line separation is horizontal, can be handled in similar manner. Now we are describing the first pass of our proposed algorithm.
Let the vertical line passing through the i-th point in array  divides the point set
divides the point set 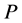 into two sub-set
into two sub-set  and
and  respectively; the subset
respectively; the subset  and
and  lie on the left and right side of this vertical line. For the position of the vertical line that passes through the i-point of
lie on the left and right side of this vertical line. For the position of the vertical line that passes through the i-point of , the result in Corollary 3 is used to place a pair of disjoint squares enclosing the maximum number of points from
, the result in Corollary 3 is used to place a pair of disjoint squares enclosing the maximum number of points from  and the result in Corollary 1 to place a square that encloses the maximum number of points from
and the result in Corollary 1 to place a square that encloses the maximum number of points from . This triplate of squares is a potential candidate for position of the vertical line that passes through the
. This triplate of squares is a potential candidate for position of the vertical line that passes through the  -th entry of
-th entry of . Observe that the time required to place these triplet of squares is
. Observe that the time required to place these triplet of squares is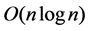 . Similarly use the result in Corollary 1 to place a square that encloses the maximum number of points from
. Similarly use the result in Corollary 1 to place a square that encloses the maximum number of points from  and the result in Corollary 3 to place a pair of disjoint squares enclosing the maximum number of points from
and the result in Corollary 3 to place a pair of disjoint squares enclosing the maximum number of points from . This triplate of squares is also a potential candidate for position of the vertical line that passes through the i-th entry of
. This triplate of squares is also a potential candidate for position of the vertical line that passes through the i-th entry of . Finally, a triplate of squares that together enclose greater number of points of
. Finally, a triplate of squares that together enclose greater number of points of  among the two sets of triplet of squares is kept. Now this process is repeated for each position of the vertical line that passes though a point
among the two sets of triplet of squares is kept. Now this process is repeated for each position of the vertical line that passes though a point . We thus have the following result.
. We thus have the following result.
Corollary 4 Given a set  of
of 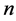 points in the plane, three axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from
points in the plane, three axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from  can be placed in
can be placed in  time and
time and  space.
space.
To solve the maximal enclosing problem using  axis-parallel unit squares, if we naively extend this approach then it is interesting to note that the solution would not have a polynomial time complexity in both
axis-parallel unit squares, if we naively extend this approach then it is interesting to note that the solution would not have a polynomial time complexity in both 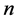 and
and . Now to solve this problem, we propose an
. Now to solve this problem, we propose an  time and
time and  space algorithm that uses (i) similar dynamic programming approach as proposed by Mukherjee et al. [21] , and (ii) the result in Corollary 1 as a subroutine.
space algorithm that uses (i) similar dynamic programming approach as proposed by Mukherjee et al. [21] , and (ii) the result in Corollary 1 as a subroutine.
Observe that placing horizontal and vertical partitioning lines among the points of  can generate
can generate  subsets of
subsets of . Let
. Let  be the subset of points enclosed by the minimum enclosing rectangle (MER) defined by the points
be the subset of points enclosed by the minimum enclosing rectangle (MER) defined by the points 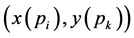 and
and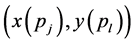 ,
,  and
and  as bottom-left and top-right corners respectively. Given a subset
as bottom-left and top-right corners respectively. Given a subset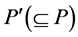 , let
, let 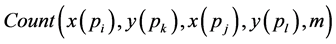 denote the maximum number of points from
denote the maximum number of points from 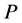 jointly enclosed by
jointly enclosed by  disjoint axis-parallel unit squares placed over the subset
disjoint axis-parallel unit squares placed over the subset .
.
In the first step, we compute  for all possible subsets of
for all possible subsets of  using the result in Corollary 1. Subsequently, it computes
using the result in Corollary 1. Subsequently, it computes  for all possible subsets of
for all possible subsets of  using the results of the previous steps in similar dynamic programming approach as proposed by Mukherjee et al. [21] . Finally, it reports
using the results of the previous steps in similar dynamic programming approach as proposed by Mukherjee et al. [21] . Finally, it reports .
.
In view of the Corollary 1, computation of the first step requires . Complexity of subsequent steps, and hence, the over all time complexity of the algorithm is
. Complexity of subsequent steps, and hence, the over all time complexity of the algorithm is . Corresponding space complexity can also be shown to be
. Corresponding space complexity can also be shown to be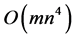 . Further details can be found in [21] . We thus have the following result.
. Further details can be found in [21] . We thus have the following result.
Theorem 2 A placement of 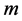 sliceable axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from
sliceable axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from  can be computed in
can be computed in  time using
time using  space.
space.
3. k-Enclosing Problem
Initially researchers considered the  -enclosing problem for computing a smallest area (perimeter) axis-parallel square or rectangle. Most of the algorithms proposed for
-enclosing problem for computing a smallest area (perimeter) axis-parallel square or rectangle. Most of the algorithms proposed for  -enclosing problems are efficient when
-enclosing problems are efficient when  is small and become inefficient for large values of
is small and become inefficient for large values of . Segal and Kedem [9] presented an
. Segal and Kedem [9] presented an  time algorithm for finding a smallest area
time algorithm for finding a smallest area  -enclosing axis-parallel rectangle for large values of
-enclosing axis-parallel rectangle for large values of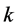 ,
, .
.
Matoušek [22] developed ,
, 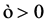 , time algorithm to find a smallest
, time algorithm to find a smallest  -enclosing circle that is especially efficient when
-enclosing circle that is especially efficient when  is close to
is close to . Given a set
. Given a set  of
of 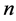 points in the plane and an integer
points in the plane and an integer 
 , we consider the problem of computing the minimum area axis-parallel square that encloses at least
, we consider the problem of computing the minimum area axis-parallel square that encloses at least  points of
points of 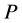 for large values of
for large values of . A
. A 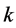 point enclosing square (rectangle)
point enclosing square (rectangle) 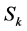 is said to be a
is said to be a  -square (
-square ( - rectangle) if there does not exist another square (rectangle) having area less than that of
- rectangle) if there does not exist another square (rectangle) having area less than that of  and enclosing
and enclosing  points from
points from  [10] .
[10] .
We use the idea of prune and search technique to solve the optimization problem for finding 
 .
.
Each pruning step uses the solution of the corresponding decision problem that guides the search process. The decision version of this problem asks whether there exists a square of side length 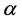 that encloses at least
that encloses at least  points where
points where  and
and  are the input parameters. In Section 4, we present some preliminary observations and it is shown that the Result in Corollary 1 can be used to solve a decision version of the optimization problem.
are the input parameters. In Section 4, we present some preliminary observations and it is shown that the Result in Corollary 1 can be used to solve a decision version of the optimization problem.
4. Preliminaries
Let  be the set of
be the set of  points in the plane. Our objective is to compute
points in the plane. Our objective is to compute  -square
-square . Without loss of generality, assume that no two points of
. Without loss of generality, assume that no two points of  have the same
have the same  or
or  coordinates. Let
coordinates. Let  and
and 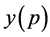 denote the
denote the  -coordinate and the
-coordinate and the  -coordinate of any point
-coordinate of any point  respectively. The size of a square is represented by the length of it's side. We have the following observation.
respectively. The size of a square is represented by the length of it's side. We have the following observation.
Observation 2 At least one pair of opposite sides of 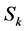 must contain points from
must contain points from .
.
The decision version of this problem can be stated as “given a length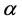 , does there exist a square of size
, does there exist a square of size  that encloses at least
that encloses at least 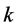 points of
points of ?”.
?”.
Let ,
,  ,
, 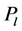 ,
,  and
and  be five subsets of
be five subsets of 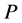 such that
such that  and all the subsets are not necessarily mutually disjoint. We define
and all the subsets are not necessarily mutually disjoint. We define  and
and  as the set of
as the set of  bottom most and
bottom most and  top most points of
top most points of  respectively;
respectively;  and
and  are the set of
are the set of  left most points and
left most points and  right most points of
right most points of 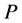 respectively; and
respectively; and  where
where .
.
Note that if 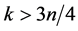 then
then  must contain at least one point of
must contain at least one point of . The following observation follows from the above definitions.
. The following observation follows from the above definitions.
Observation 3 For ,
, 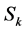 must enclose all the points of
must enclose all the points of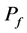 .
.
Proof: Let  be any point of the set
be any point of the set . At least
. At least 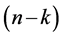 elements are on the right side of
elements are on the right side of . The position of
. The position of  in the left to right ordering of
in the left to right ordering of 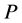 are at most
are at most . Therefore there are
. Therefore there are  number of points of
number of points of  on the left of
on the left of  for
for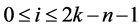 . Consequently at most
. Consequently at most  points are on left of
points are on left of . Hence right boundary of
. Hence right boundary of  is on right side of
is on right side of . Similarly left, top and bottom boundaries of
. Similarly left, top and bottom boundaries of  are on left, top and bottom sides of
are on left, top and bottom sides of  respectively. Hence the observation follows.
respectively. Hence the observation follows.
Let 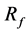 be the minimum area axis-parallel rectangle enclosing the point set
be the minimum area axis-parallel rectangle enclosing the point set . Suppose the length of the longest side of
. Suppose the length of the longest side of 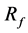 is
is  and the left, right, top and bottom boundaries of the rectangle
and the left, right, top and bottom boundaries of the rectangle  contain the points
contain the points ,
,  ,
, 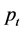 and
and  respectively (See Figure 2). We define
respectively (See Figure 2). We define ,
,  as an axis-parallel square of size
as an axis-parallel square of size  that includes the point set
that includes the point set  and the total number of points enclosed from
and the total number of points enclosed from  is maximized. It is easy to see that the bottom, top, left and right boundaries of
is maximized. It is easy to see that the bottom, top, left and right boundaries of  must lie within the ranges
must lie within the ranges ,
,  ,
, 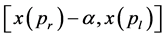 and
and  respectively.
respectively.
To locate 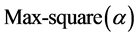 among the set
among the set , we use sweep line paradigm combined with binary search tree as data structure in similar way as described in Section 2.1. As earlier, our algorithm makes horizontal and vertical sweeps. Below we briefly describe the algorithm for horizontal sweep to locate
, we use sweep line paradigm combined with binary search tree as data structure in similar way as described in Section 2.1. As earlier, our algorithm makes horizontal and vertical sweeps. Below we briefly describe the algorithm for horizontal sweep to locate whose bottom side is aligned with a point from
whose bottom side is aligned with a point from . Look for all squares of size
. Look for all squares of size  whose bottom and left boundaries are within the range
whose bottom and left boundaries are within the range 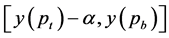 and
and  respectively.
respectively.
Now consider possible positions of the left boundary of  within the above mentioned range such that the left boundary or the right boundary passes through a point of
within the above mentioned range such that the left boundary or the right boundary passes through a point of . Notice that all squares with these restrictions include the point set
. Notice that all squares with these restrictions include the point set . Therefore the points in the set
. Therefore the points in the set  are the only points required to be processed to locate
are the only points required to be processed to locate  and the number of such points is at most
and the number of such points is at most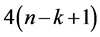 . This observation leads to the following theorem.
. This observation leads to the following theorem.
Corollary 5 For given , the axis-parallel square
, the axis-parallel square  containing the maximum number of points from
containing the maximum number of points from  and enclosing point set
and enclosing point set 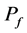 can be located in
can be located in  time using
time using  space.
space.
5. An Efficient Algorithm to Find k-Square for Large Values of k
In this section, we explain an efficient algorithm to find  for large values of
for large values of . The result in Corollary 5 to locate
. The result in Corollary 5 to locate  is used as a subroutine to find
is used as a subroutine to find  for
for . From Observation 2, we can conclude that either top and bottom sides of
. From Observation 2, we can conclude that either top and bottom sides of  contain points of
contain points of  or left and right sides of
or left and right sides of  contain points of
contain points of . Without loss of generality, assume that top and bottom sides of
. Without loss of generality, assume that top and bottom sides of 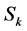 contain points from
contain points from . The other case where left and right sides of
. The other case where left and right sides of 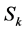 contain points of
contain points of , can be handled in similar manner. Let
, can be handled in similar manner. Let  be an ordering of points of the set
be an ordering of points of the set  in increasing order of their
in increasing order of their  -coordinate values. Consider
-coordinate values. Consider  to be the list of
to be the list of 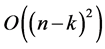 vertical distances
vertical distances ,
,  for each pair of points
for each pair of points  and
and .
.
Our objective is to find  for a given value
for a given value  such that
such that  encloses
encloses  points of
points of  and the value
and the value  is minimized. We iteratively reduce the size of
is minimized. We iteratively reduce the size of  by prune and search technique without explicitly computing
by prune and search technique without explicitly computing  elements of
elements of . Let
. Let  represent the list of vertical distances at
represent the list of vertical distances at 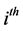 iteration. At
iteration. At  iteration we reduce the size of
iteration we reduce the size of  by
by . Initially
. Initially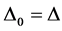 . Observe that for any
. Observe that for any ,
, 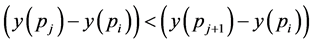 for
for . Without loss of generality, let the indices of the points
. Without loss of generality, let the indices of the points  and
and  remain same in
remain same in  also. Let us denote the set of vertical distances generating
also. Let us denote the set of vertical distances generating 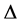 by the sequences
by the sequences  defined as follows.
defined as follows.

Note that the elements in each sequence  are in nondecreasing order. At
are in nondecreasing order. At  iterative step of the algorithm the current search space
iterative step of the algorithm the current search space  is reduced by pruning the
is reduced by pruning the ’s. Here, either upper or lower portion of
’s. Here, either upper or lower portion of  is pruned. Therefore, each
is pruned. Therefore, each  sequence can be represented by lower and upper indices of the original sequence. For any point
sequence can be represented by lower and upper indices of the original sequence. For any point , median element of the corresponding sequence
, median element of the corresponding sequence  is
is 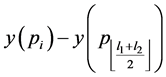
where  and
and  are the lower and upper indices of the sequence
are the lower and upper indices of the sequence . We denote the median element of
. We denote the median element of  as
as . So computing the median of the sequence of vertical distances corresponding to any point
. So computing the median of the sequence of vertical distances corresponding to any point  requires only a constant time arithmetic operation on the array indices.
requires only a constant time arithmetic operation on the array indices.
We represent each  as a vertical strip parallel to the
as a vertical strip parallel to the  -axis. All the vertical strips (
-axis. All the vertical strips ( ’s) are arranged along the
’s) are arranged along the  -axis such that
-axis such that 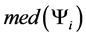 's fall on the
's fall on the  -axis and the median values are in nonincreasing order along the
-axis and the median values are in nonincreasing order along the 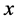 -axis (See Figure 3). Again the elements of each
-axis (See Figure 3). Again the elements of each  are arranged in nondecreasing order parallel to the
are arranged in nondecreasing order parallel to the  -axis. At initial step of iteration, all medians
-axis. At initial step of iteration, all medians 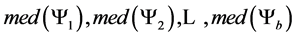 are in nonincreasing order. This ordering may change in subsequent iterations due to pruning of
are in nonincreasing order. This ordering may change in subsequent iterations due to pruning of  's. Therefore at each iteration, we need to rearrange
's. Therefore at each iteration, we need to rearrange ’s such that
’s such that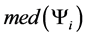 ’s are in nonincreasing order. Let
’s are in nonincreasing order. Let 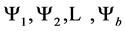 be an arrangement of the sequences in
be an arrangement of the sequences in  such that
such that . At
. At  iteration we
iteration we
find an index  such that
such that  is half of the size of
is half of the size of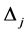 . Observe that the size of
. Observe that the size of  is at most
is at most  of the size of
of the size of . Consider
. Consider  as
as  and compute Max-
and compute Max- . If
. If 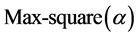 encloses at least
encloses at least  points of
points of , then size of
, then size of  is less than or equal to
is less than or equal to  and we can ignore the elements in
and we can ignore the elements in  greater than
greater than . Note that all the
. Note that all the  values corresponding to
values corresponding to 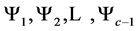 are greater than
are greater than . Therefore for each
. Therefore for each 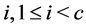 we can delete upper half of
we can delete upper half of . In case,
. In case, 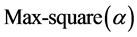 encloses less than
encloses less than  points, we similarly delete lower half of each
points, we similarly delete lower half of each  for
for . Now continue with the subsequent iterations until we end up at an iteration, say maxit, such that size of
. Now continue with the subsequent iterations until we end up at an iteration, say maxit, such that size of 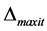 is constant.
is constant.
Lemma 1 At every iterative step the size of the current solution space is reduced by a factor of .
.
Proof: At  iteration, either we discard upper half of
iteration, either we discard upper half of  or lower half of
or lower half of . As the total number of elements in the sequences
. As the total number of elements in the sequences  is
is  of size of
of size of , we can discard at least
, we can discard at least 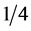 elements of
elements of . Similar amount of elements is discarded for pruning of lower half. Now we have the following theorem.
. Similar amount of elements is discarded for pruning of lower half. Now we have the following theorem.
Theorem 3 Given a set  of
of  points in the plane and an integer
points in the plane and an integer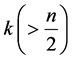 , the smallest area square enclosing at least
, the smallest area square enclosing at least 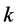 points of
points of  can be computed in
can be computed in 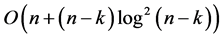 time using linear space.
time using linear space.
Proof: Partitioning the set  to generate subsets
to generate subsets  and
and  requires
requires 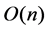 time. Sorting the points of the sets
time. Sorting the points of the sets  and
and  with respect to their
with respect to their  -coordinates requires
-coordinates requires 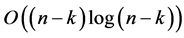 time. We do not store the
time. We do not store the  's explicitly. Instead, for all
's explicitly. Instead, for all 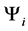 's, we maintain an array
's, we maintain an array  whose each element
whose each element 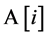 contains the index information
contains the index information  and
and 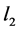 for
for  at each iteration. So for each
at each iteration. So for each 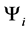 we need only an additional constant amount of space. Altogether in linear amount of space we can execute our algorithm. Time complexity can be established from the following algorithmic steps at iteration
we need only an additional constant amount of space. Altogether in linear amount of space we can execute our algorithm. Time complexity can be established from the following algorithmic steps at iteration .
.
• Computation of  for each
for each  requires constant amount of time.
requires constant amount of time.
• Sorting the set of all medians  takes
takes  time.
time.
• Determining  such that
such that  is half of the size of
is half of the size of , needs
, needs 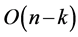 time.
time.
• Computation of  takes
takes  time (see Theorem 5).
time (see Theorem 5).
• We maintain the index structure of the arrays . This involves updating of
. This involves updating of  and
and  for each
for each  when half of it's elements are discarded. This step requires constant amount of time for each
when half of it's elements are discarded. This step requires constant amount of time for each .
.
From Lemma 1, we get that at  iterative step at least
iterative step at least  elements are discarded where
elements are discarded where  denotes the size of
denotes the size of . This leads to the following recurrence relation.
. This leads to the following recurrence relation.
 (1)
(1)
Hence the theorem. The technique used to derive the result in Theorem 3 can also compute  for all values of
for all values of . Hence we have the following theorem.
. Hence we have the following theorem.
Theorem 4 Given a set  of
of  points in the plane and an integer
points in the plane and an integer , the smallest area square enclosing at least
, the smallest area square enclosing at least  points of
points of  can be computed in
can be computed in  time using linear amount of space.
time using linear amount of space.
Acknowledgments
This research was partially supported by the DST PURSE scheme at University of Kalayni, India.