1. Introduction
The two-dimensional (2d) Navier-Stokes system of partial differential equations (PDEs) for a Newtonian fluid with a constant density  and a constant kinematic viscosity
and a constant kinematic viscosity 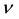 in a gravity field
in a gravity field 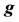 is
is
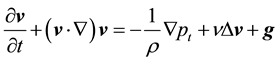 , (1-2)
, (1-2)
where 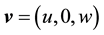 is a vector field of the flow velocity,
is a vector field of the flow velocity,  is a vector field of the gravitational acceleration,
is a vector field of the gravitational acceleration, 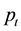 is a scalar field of the total pressure,
is a scalar field of the total pressure,  and
and 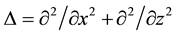 are the gradient and the Laplacian in the 2d Cartesian coordinate system
are the gradient and the Laplacian in the 2d Cartesian coordinate system 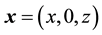 of the three-dimensional (3d) space with unit vectors
of the three-dimensional (3d) space with unit vectors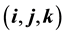 , respectively, and
, respectively, and 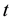 is time.
is time.
By a flow vorticity 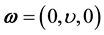 of the velocity field
of the velocity field
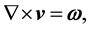 (3)
(3)
Equation (1) may be written into the Lamb-Pozrikidis form [1] [2]
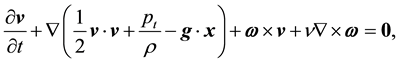 (4)
(4)
which sets a dynamic balance of inertial, potential, vortical, and viscous forces, respectively.
Using a dynamic pressure per unit mass [3]
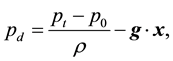 (5)
(5)
where ![]() is a reference pressure, a kinetic energy per unit mass
is a reference pressure, a kinetic energy per unit mass ![]() the 2d Helmholtz decomposition [4] of the velocity field
the 2d Helmholtz decomposition [4] of the velocity field
![]() (6)
(6)
and the vortex force
![]() (7)
(7)
Equation (4) is reduced to the Lamb-Helmholtz PDE
![]() (8)
(8)
for a scalar Bernoulli potential
![]() (9)
(9)
and a vector Helmholtz potential
![]() (10)
(10)
where ![]() and
and ![]() are scalar potentials,
are scalar potentials, ![]() and
and ![]() are vector potentials,
are vector potentials, ![]() and
and ![]() are pseudovector potentials of
are pseudovector potentials of ![]() and
and ![]() respectively. The Lamb-Helmholtz PDE (8) means a dynamic balance between potential and vortical forces of the Navier-Stokes PDE (1), which are separated completely.
respectively. The Lamb-Helmholtz PDE (8) means a dynamic balance between potential and vortical forces of the Navier-Stokes PDE (1), which are separated completely.
A linear part of the kinematic problem for free-surface waves of the theory of the ideal fluid with ![]() implies the exponential Fourier eigenfunctions [5] , which are obtained by the classical method of separation of variables of the 2d Laplace Equation in [4] and [1] . This analytical method was recently developed into the computational method of solving PDEs by decomposition into invariant structures. In [3] , the Boussinesq-Rayleigh- Taylor structures were developed for topological flows away from boundaries. The trigonometric Taylor structures and the trigonometric-hyperbolic structures [6] were used to describe spatiotemporal cascades of exposed and hidden perturbations of the Couette flow, respectively. In [7] , the theory of the invariant trigonometric, hyperbolic, and elliptic structures was constructed and applied for modeling dual perturbations of the Poiseuille-Hagen flow.
implies the exponential Fourier eigenfunctions [5] , which are obtained by the classical method of separation of variables of the 2d Laplace Equation in [4] and [1] . This analytical method was recently developed into the computational method of solving PDEs by decomposition into invariant structures. In [3] , the Boussinesq-Rayleigh- Taylor structures were developed for topological flows away from boundaries. The trigonometric Taylor structures and the trigonometric-hyperbolic structures [6] were used to describe spatiotemporal cascades of exposed and hidden perturbations of the Couette flow, respectively. In [7] , the theory of the invariant trigonometric, hyperbolic, and elliptic structures was constructed and applied for modeling dual perturbations of the Poiseuille-Hagen flow.
To treat linear and nonlinear parts of kinematic and dynamic problems for 2d internal waves in the theory of Newtonian flows with harmonic velocity, kinematic Fourier (KF) structures, exponential kinematic Fourier (KEF) structures, dynamic exponential Fourier (DEF) structures, and KEF-DEF structures with constant structural coefficients are developed in the current paper. The structure of this paper is as follows. In section 2, the kinematic problems for velocity components and dual potentials of the velocity field are formulated in upper and lower domains and treated in the KF and KEF structures. To compute and explore Jacobian determinants (JDs) of the velocity field, the DEF structure is also constructed in this section. In section 3, the dynamic problems for the Bernoulli potential and the total pressure are formulated and computed in the KF, KEF, and KEF-DEF structures. The Navier-Stokes system of PDEs is employed for verification of experimental and theoretical solutions for cumulative upper and lower flows in this section, as well. Visualization and discussion of the developed structures and fluid-dynamic variables is given in section 4, which is followed by a summary of main results in Section 5.
2. Kinematic Problems for Conservative Flows
The following solutions and admissible boundary conditions for the kinematic problems of section 2 in the KF and DEF structures were primarily computed experimentally in Maple™ by programming with lists of equations and expressions in the virtual environment of a global variable Eqs with 29 procedures of 670 code lines.
2.1. Formulation of Theoretical Kinematic Problems for Velocity Components
Theoretical kinematic problems for harmonic velocity components ![]() and
and ![]() of a cumulative flow
of a cumulative flow ![]() of a Newtonian fluid are given by vanishing the
of a Newtonian fluid are given by vanishing the![]() component of the vorticity Equation (3) and the continuity Equation (2), respectively,
component of the vorticity Equation (3) and the continuity Equation (2), respectively,
![]() (11-12)
(11-12)
To consider nonlinear interaction of ![]() internal, conservative waves with a harmonic velocity field, the cumulative flow is decomposed into a superposition of local flows
internal, conservative waves with a harmonic velocity field, the cumulative flow is decomposed into a superposition of local flows
![]() (13)
(13)
such that the local vorticity and continuity equations are
![]() (14-15)
(14-15)
where ![]() If Equations (14)-(15) for the local flows are fulfilled, then substitution of superpositions (13) into (11)-(12) and changing order of summation and differentiation yield that Equations (11)-(12) for the cumulative flow are also satisfied.
If Equations (14)-(15) for the local flows are fulfilled, then substitution of superpositions (13) into (11)-(12) and changing order of summation and differentiation yield that Equations (11)-(12) for the cumulative flow are also satisfied.
Upper flows are specified by the Dirichlet condition in the KF structure on a lower boundary ![]() of an upper domain
of an upper domain ![]() and
and ![]() (see Figure 1)
(see Figure 1)
![]() (16)
(16)
and a vanishing condition as ![]()
![]() (17)
(17)
Lower flows are identified by the Dirichlet condition on a lower boundary ![]() of a lower domain
of a lower domain ![]() and
and ![]() (see Figure 1)
(see Figure 1)
![]() (18)
(18)
and a vanishing condition as ![]()
![]() (19)
(19)
Thus, an effect of surface waves on the internal waves is described by the Dirichlet conditions (16) and (18). Here, a structural notation
![]() (20)
(20)
is used for kinematic structural functions ![]() and
and ![]() where
where ![]() and
and ![]() are boundary coefficients,
are boundary coefficients, ![]() is an argument of the kinematic and dynamic structural functions,
is an argument of the kinematic and dynamic structural functions, ![]() is a propa-
is a propa-
![]()
Figure 1. Configuration of upper and lower domains for internal, conservative waves.
gation coordinate, ![]() is a wavenumber,
is a wavenumber, ![]() is a celerity, and
is a celerity, and ![]() is an initial coordinate for all
is an initial coordinate for all ![]()
As we will see later, boundary conditions for ![]() are then redundant since boundary parameters of
are then redundant since boundary parameters of ![]()
![]() (21-22)
(21-22)
for the upper and lower flows, respectively, depend on boundary parameters of![]() . Similarly to
. Similarly to ![]()
![]() vanishes as
vanishes as ![]()
![]() (23-24)
(23-24)
for the upper and lower flows, respectively.
Thus, the![]() and
and![]() components of the velocity field of the cumulative flows are expanded in the KF structures with constant structural coefficients
components of the velocity field of the cumulative flows are expanded in the KF structures with constant structural coefficients
![]() (25)
(25)
![]() (26)
(26)
and the velocity components vanish as ![]()
![]() (27)
(27)
![]() (28)
(28)
for the upper and lower cumulative flows, respectively.
2.2. Theoretical Solutions for the Velocity Field
Theoretical solutions of kinematic problems (11)-(28) are constructed in the KF structure ![]() of two spatial variables
of two spatial variables ![]() and time
and time ![]() with a general term
with a general term ![]() which in the structural notation may be written as
which in the structural notation may be written as
![]() (29)
(29)
where first letters ![]() and
and ![]() of structural coefficients
of structural coefficients ![]() and
and ![]() refer to the kinematic structural functions
refer to the kinematic structural functions ![]() and a second letter to the expanded variable
and a second letter to the expanded variable ![]() Thus, general terms of the velocity components of the local flows in the structural notation become
Thus, general terms of the velocity components of the local flows in the structural notation become
![]() (30-31)
(30-31)
It may be shown that spatial derivatives of ![]() are
are
![]() (32-33)
(32-33)
Application of (32)-(33) to (30)-(31), substitution in (14)-(15), and collection of the structural functions reduce the vorticity and continuity PDEs to the following system of two vorticity and continuity ordinary differential equations (ODEs) in the KF structures:
![]() (34-35)
(34-35)
For Equations (34)-(35) to be satisfied exactly for all variables, parameters, and functions of the local flows: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]() all coefficients of two kinematic structural functions must vanish. Thus, two ODEs (34)-(35) are reduced to two systems of ODEs for
all coefficients of two kinematic structural functions must vanish. Thus, two ODEs (34)-(35) are reduced to two systems of ODEs for ![]()
![]() and
and ![]()
![]() respectively:
respectively:
![]() (36-37)
(36-37)
![]() (38-39)
(38-39)
Since boundary conditions (25)-(26) are expanded in the KF structure exactly, remainders of structural approximations (34)-(35) vanish, and exact solutions of ODEs (36)-(39) produce exact solutions of vorticity and continuity PDEs (14)-(15). If (25)-(26) are replaced with series approximations, then their remainders constitute errors of the series approximations.
Solutions of ODEs for structural coefficients (36)-(39) are constructed in an exponential structure
![]() (40)
(40)
where ![]() and
and ![]() are structural coefficients. Substitution of exponential structure (40) in Equations (36) and (38) reduces these ODEs to algebraic equations (AEs) for structural parameters:
are structural coefficients. Substitution of exponential structure (40) in Equations (36) and (38) reduces these ODEs to algebraic equations (AEs) for structural parameters:
![]() (41)
(41)
Substitution of (40) and (41) in (37) and (39) reduces these ODEs to AEs for admissible values of the structural coefficient ![]() with the following solutions for the upper and lower flows, respectively:
with the following solutions for the upper and lower flows, respectively:
![]() (42)
(42)
Since the admissible values of ![]() coincide for Equations (37) and (39), ODEs for structural coefficients (36)-(39) are compatible both for the upper and lower flows.
coincide for Equations (37) and (39), ODEs for structural coefficients (36)-(39) are compatible both for the upper and lower flows.
Finally, substitutions of (40)-(42) in (30)-(31) and (13) yield the velocity components in the KEF structures for the upper cumulative flow
![]() (43-44)
(43-44)
and the lower cumulative flow
![]() (45-46)
(45-46)
while boundary conditions (16)-(19) and (21)-(28) are obviously satisfied.
2.3. The DEF structure and Theoretical Jacobian Determinants of the Velocity Components
Define two KEF structures ![]() and
and ![]() with general terms
with general terms ![]() and
and ![]() by using a generalized Einstein notation for summation, which is extended for exponents,
by using a generalized Einstein notation for summation, which is extended for exponents,
![]() (47)
(47)
Computation of a general term![]() by summation of diagonal terms yields
by summation of diagonal terms yields
![]() (48)
(48)
Trigonometric structural functions ![]()
![]()
![]() and
and ![]() of the DEF structure are defined by the following expressions:
of the DEF structure are defined by the following expressions:
![]() (49)
(49)
where capital letters ![]() and
and ![]() stand for dynamic structural functions cosine and sine, letter
stand for dynamic structural functions cosine and sine, letter ![]() for arguments
for arguments ![]() and letters
and letters ![]() and
and ![]() for sum and difference of arguments
for sum and difference of arguments ![]() and
and ![]()
A general term ![]() computed by rectangular summation of non-diagonal terms becomes
computed by rectangular summation of non-diagonal terms becomes
![]() (50)
(50)
By triangular summation, ![]() is reduced to
is reduced to
![]() (51)
(51)
Using general terms (48) and (51), summation formula for the product of the KEF structures is written as the DEF structure
![]() (52)
(52)
with the following structural coefficients:
![]() (53)
(53)
where first two letters ![]()
![]()
![]() and
and ![]() of structural coefficients
of structural coefficients ![]()
![]()
![]() and
and![]() stand for dynamic structural functions
stand for dynamic structural functions ![]()
![]()
![]() and
and![]() , respectively, and a third letter for variable
, respectively, and a third letter for variable ![]()
Computation of local JDs for the velocity components of the upper and lower flow, respectively, yields
![]() (54)
(54)
Thus, velocity components ![]() and
and ![]() are independent for non-trivial structural coefficients
are independent for non-trivial structural coefficients ![]() and
and ![]() since the local JDs vanish when
since the local JDs vanish when ![]()
Computation of a global JD by using (52)-(53) for velocity components of the upper and lower cumulative flows (43)-(46) with slant internal waves gives
![]() (55)
(55)
So, ![]() is a superposition of a propagation JD with general term
is a superposition of a propagation JD with general term ![]() proportional to
proportional to ![]() an interaction JD with
an interaction JD with ![]() proportional to
proportional to ![]() and an interaction JD with
and an interaction JD with ![]() proportional to
proportional to ![]() which describe interaction between parallel and orthogonal internal waves, respectively.
which describe interaction between parallel and orthogonal internal waves, respectively.
![]() coincides with (54). They describe propagation of internal waves and vanish only for internal waves with
coincides with (54). They describe propagation of internal waves and vanish only for internal waves with ![]()
![]() vanishes for parallel waves with
vanishes for parallel waves with
![]() (56)
(56)
Global JD (55) then becomes
![]() (57)
(57)
Thus, the global JD does not vanish for parallel waves with non-vanishing ![]()
![]() vanishes for orthogonal waves with
vanishes for orthogonal waves with
![]() (58)
(58)
In this case, global JD (55) is reduced to
![]() (59)
(59)
Thus, the global JD does not vanish also for orthogonal waves with non-vanishing ![]() In the general case (55) of slant internal waves, both
In the general case (55) of slant internal waves, both ![]() and
and ![]() are non-vanishing. So, both propagating and interacting waves are independent for structural coefficients with
are non-vanishing. So, both propagating and interacting waves are independent for structural coefficients with ![]() for all
for all ![]()
2.4. Theoretical Solutions for the Pseudovector and Scalar Potentials in the KEF Structures
Theoretical kinematic problems for cumulative pseudo-vector potential ![]() and cumulative scalar potential
and cumulative scalar potential ![]() of
of ![]() are set by the global Helmholtz PDEs (6)
are set by the global Helmholtz PDEs (6)
![]() (60)
(60)
![]() (61)
(61)
since the potential-vortical duality the velocity field admits two presentations: ![]() for
for ![]() and
and![]() for
for ![]() The cumulative kinematic potentials are decomposed into a superposition of local kinematic potentials
The cumulative kinematic potentials are decomposed into a superposition of local kinematic potentials
![]() (62)
(62)
such that the local Helmholtz PDEs are
![]() (63)
(63)
![]() (64)
(64)
where ![]() The boundary conditions for
The boundary conditions for ![]() and
and ![]() and redundant when the problem is formulated in the KF structures.
and redundant when the problem is formulated in the KF structures.
Construct general terms of the kinematic potentials of the local flows in the KF structure with space-depen- dent coefficients
![]() (65-66)
(65-66)
Application of (32)-(33) to (65)-(66), substitution in (63)-(64), and collection of the structural functions reduce four Helmholtz PDEs to the following system of two Helmholtz ODEs and two Helmholtz AEs for the upper flows
![]() (67-68)
(67-68)
![]() (69-70)
(69-70)
and the lower flows
![]() (71-72)
(71-72)
![]() (73-74)
(73-74)
For Equations (67)-(74) to be satisfied exactly for all variables, parameters, and functions of the upper and lower flows: ![]() and
and ![]() all coefficients of structural functions
all coefficients of structural functions ![]() and
and![]() must vanish. Thus, two Helmholtz ODEs and two Helmholtz AEs are reduced to the following four AEs and four ODEs with respect to
must vanish. Thus, two Helmholtz ODEs and two Helmholtz AEs are reduced to the following four AEs and four ODEs with respect to ![]()
![]()
![]() and
and ![]() for the upper flows
for the upper flows
![]() (75)
(75)
![]() (76)
(76)
and the lower flows
![]() (77)
(77)
![]() (78)
(78)
Since general terms of remainders of structural approximations (67)-(74) vanish, exact solutions of AEs and ODEs (75)-(78) produce exact solutions of the Helmholtz PDEs (63)-(64).
Solving AEs (75) and (77) with respect to ![]()
![]()
![]() and
and ![]() gives for the upper flows
gives for the upper flows
![]() (79)
(79)
and the lower flows
![]() (80)
(80)
Substitution of solutions (79)-(80) in ODEs (76) and (78) reduces them to identities.
Substitution of structural coefficients (79)-(80) in the KF structures (65)-(66) and super positions (62) returns the cumulative pseudo vector and scalar potentials in the KEF structures for the upper cumulative flow
![]() (81-82)
(81-82)
and the lower cumulative flow
![]() (83-84)
(83-84)
2.5. Harmonic Relationships for the Velocity Components and the Kinematic Potentials
Comparison of solutions for ![]() and
and ![]() with spatial derivatives in
with spatial derivatives in ![]() of
of ![]() and
and ![]() shows that they are directly proportional to each other, respectively, for the upper flows
shows that they are directly proportional to each other, respectively, for the upper flows
![]() (85)
(85)
and the lower flows
![]() (86)
(86)
In fluid dynamics, these connections mean that a non-uniform vertical flow generates a horizontal flow and a non-uniform horizontal flow produces a vertical flow.
Similarly, comparison of solutions for ![]() and
and ![]() with solutions for
with solutions for ![]() and
and ![]() shows that they are also directly proportional, respectively, for the upper flows
shows that they are also directly proportional, respectively, for the upper flows
![]() (87)
(87)
and the lower flows
![]() (88)
(88)
Finally, comparison of solutions for ![]() and
and ![]() with spatial derivatives in
with spatial derivatives in ![]() of
of ![]() and
and ![]() shows that they are proportional to each other, respectively, for the upper flows
shows that they are proportional to each other, respectively, for the upper flows
![]() (89)
(89)
and the lower flows
![]() (90)
(90)
Connections (85)-(90) between solutions in the KEF structures are available since there are only two independent combinations of trigonometric structural functions ![]() and
and ![]()
Computation of ![]() by using (81)-(84) both for the upper and lower flows gives
by using (81)-(84) both for the upper and lower flows gives
![]() (91)
(91)
Thus, local isocurves of ![]() and
and ![]() remain orthogonal for all times in agreement with the Helmholtz Equations (63)-(64). Similarly, local isocurves of
remain orthogonal for all times in agreement with the Helmholtz Equations (63)-(64). Similarly, local isocurves of![]() and
and![]() remain orthogonal since both for the upper and lower flows
remain orthogonal since both for the upper and lower flows
![]() (92)
(92)
in agreement with the local vorticity and continuity Equations (14)-(15).
Computation of ![]() by (52)-53) and (81)-(84) both for the upper and lower cumulative flows gives
by (52)-53) and (81)-(84) both for the upper and lower cumulative flows gives
![]() (93)
(93)
Thus, global isocurves of ![]() and
and ![]() also remain orthogonal for all times in agreement with the cumulative Helmholtz Equations (60)-(61). Finally, global isocurves of
also remain orthogonal for all times in agreement with the cumulative Helmholtz Equations (60)-(61). Finally, global isocurves of ![]() and
and ![]() remain orthogonal since both for the upper and lower cumulative flows
remain orthogonal since both for the upper and lower cumulative flows
![]() (94)
(94)
in agreement with the cumulative vorticity and continuity Equations (11)-(12).
It is a straightforward matter to show that for the KEF structure ![]() with a general term
with a general term ![]()
![]() (95)
(95)
spatial derivatives of second order in the ![]() and
and ![]() directions are
directions are
![]() (96-97)
(96-97)
and the Laplacian of ![]() vanishes. Thus, the KEF structure is an invariant, harmonic structure both for the upper and lower flows.
vanishes. Thus, the KEF structure is an invariant, harmonic structure both for the upper and lower flows.
Application of (96)-(97) to (43)-(46) shows that ![]() and
and ![]() are conjugate harmonic functions since
are conjugate harmonic functions since
![]() (98)
(98)
both for the upper and lower flows, in agreement with vector identity ![]() By Equations (13),
By Equations (13), ![]() and
and ![]() are also conjugate harmonic functions
are also conjugate harmonic functions
![]() (99)
(99)
both for the upper and lower cumulative flows, in agreement with vector identity ![]()
Similarly, applying (96)-(97) to (81)-(84) shows that ![]() and
and ![]() are conjugate harmonic functions as
are conjugate harmonic functions as
![]() (100)
(100)
both for the upper and lower flows, in agreement with ![]() and
and ![]() By Equation (62),
By Equation (62), ![]() and
and ![]() are also conjugate harmonic functions
are also conjugate harmonic functions
![]() (101)
(101)
both for the upper and lower cumulative flows, in agreement with vector identities ![]() and
and
![]()
The theoretical solutions in the KEF and DEF structures for the kinematic problems of section 2 were computed theoretically in Maple™ by programming with symbolic general terms in the virtual environment of a global variable Equation with 26 procedures of 591 code lines. The theoretical solutions for velocity components (43)-(46), the products of the KEF structures (52)-(53), and the kinematic potentials (81)-(84) of the upper and lower cumulative flows were justified by the correspondent experimental solutions for ![]()
3. Dynamic Problems for Conservative Flows
The following solutions for the dynamic problems of section 3 in the KF, DEF, and KEF-DEF structures were primarily computed experimentally by programming with lists of equations and expressions in the virtual environment of the global variable Equations with 19 procedures of 472 code lines.
3.1. Theoretical Solutions for the Helmholtz and Bernoulli Potentials in the KEF Structures
Theoretical dynamic problems in the KF structures for the Helmholtz and Bernoulli potentials of the cumulative flows are set by the Lamb-Helmholtz PDEs (8)
![]() (102-103)
(102-103)
while (10) for the vortical presentation with ![]() is reduced to
is reduced to
![]() (104)
(104)
Equations (102-104) are complemented by the local Lamb-Helmholtz PDEs
![]() (105-106)
(105-106)
where
![]() (107)
(107)
since the cumulative dynamic potentials are again decomposed into the local dynamic potentials as follows:
![]() (108)
(108)
Boundary conditions are again redundant because the problem is formulated in the KF structures.
Construct a general term of the Bernoulli potential of the local flows in the KF structure with space-dependent coefficients
![]() (109)
(109)
Computation of the temporal derivative of ![]() application of (32)-(33), substitution in (105)-(106), and collection of the structural functions reduce two Lamb-Helmholtz PDEs to the following system of the Lamb-Helmholtz AE and ODE for the upper flows
application of (32)-(33), substitution in (105)-(106), and collection of the structural functions reduce two Lamb-Helmholtz PDEs to the following system of the Lamb-Helmholtz AE and ODE for the upper flows
![]() (110)
(110)
and the lower flows
![]() (111)
(111)
For Equations (110)-(111) to be satisfied exactly for all ![]() and
and ![]() all coefficients of structural functions
all coefficients of structural functions ![]() and
and ![]() must vanish. Thus, the Lamb-Helmholtz AE and ODE are reduced to the following two AEs and two ODEs for space-dependent structural coefficients
must vanish. Thus, the Lamb-Helmholtz AE and ODE are reduced to the following two AEs and two ODEs for space-dependent structural coefficients ![]() and
and ![]() for the upper flows
for the upper flows
![]() (112-113)
(112-113)
and the lower flows
![]() (114-115)
(114-115)
Since general terms of remainders of structural approximations (110)-(111) vanish, exact solutions of (112)-(115) produce exact solutions of (105)-(106).
Solving AEs (112) and (114) for structural coefficients ![]() and
and ![]() yields for the upper flows
yields for the upper flows
![]() (116)
(116)
and the lower flows
![]() (117)
(117)
Substitution of solutions (116)-(117) in ODEs (113) and (115) reduced them to identities.
Substitution of structural coefficients (116)-(117) in super positions (108) and the KF structure (109) gives the cumulative Helmholtz and Bernoulli potentials in the KEF structures for the upper cumulative flow
![]() (118-119)
(118-119)
and the lower cumulative flow
![]() (120-121)
(120-121)
Similar to the kinematic potentials (87)-(88), the dynamic potentials and the velocity components are directly proportional both for the upper and lower flows
![]() (122)
(122)
Like in (89)-(90), the Helmholtz and Bernoulli potentials and derivatives of the Bernoulli and Helmholtz potentials in![]() are directly proportional to each other both for the upper flows
are directly proportional to each other both for the upper flows
![]() (123)
(123)
and the lower flows
![]() (124)
(124)
Analogous to (91)-(94), isocurves of ![]() and global isocurves of
and global isocurves of ![]() are orthogonal for all times
are orthogonal for all times
![]() (125-126)
(125-126)
in agreement with the Lamb-Helmholtz Equations (105)-(106) and (102)-(103). For the same reason, ![]() and
and ![]() are local and global conjugate harmonic functions as
are local and global conjugate harmonic functions as
![]() (127-128)
(127-128)
3.2. Theoretical Solutions for the Total Pressure in the KEF-DEF Structures
Theoretical dynamic problems in the KEF-DEF structures for the kinetic energy per unit mass ![]() the dynamic pressure per unit mass
the dynamic pressure per unit mass ![]() and the total pressure
and the total pressure ![]() of the cumulative flows are formulated by definition
of the cumulative flows are formulated by definition
![]() (129)
(129)
the Bernoulli Equation (9) with ![]()
![]() (130)
(130)
and the hydrostatic Equation (5)
![]() (131)
(131)
where ![]() is the reference pressure at
is the reference pressure at ![]()
Computation of ![]() by (52)-(53) and (43)-(46) returns
by (52)-(53) and (43)-(46) returns
![]() (132)
(132)
for the upper and lower cumulative flows, respectively. Substitution of (119), (121), and (132) in (131) yields
![]() (133)
(133)
for the upper and lower cumulative flows, respectively.
3.3. Theoretical Verification by the System of Navier-Stokes PDEs
The system of the Navier-Stokes PDEs (1)-(2) in the scalar notation becomes
![]() (134-135)
(134-135)
![]() (136)
(136)
Computation of spatial derivatives of (43)-(46) by (32)-(33) immediately reduces (136) to identity. Temporal derivatives of ![]() in the KEF structures for the upper and lower cumulative flows, respectively, are
in the KEF structures for the upper and lower cumulative flows, respectively, are
![]() (137-138)
(137-138)
The directional derivatives of (134)-(135) computed by (52)-(53) in the DEF structures for the upper and lower cumulative flows, respectively, become
![]() (139)
(139)
![]() (140)
(140)
By using (32) and (33), components of the gradient of (133) may be written in the KEF-DEF structures for the upper and lower cumulative flows, respectively, as
![]() (141)
(141)
![]() (142)
(142)
Substitution of Equations (137)-(142) and (99) in (134)-(135) reduces then to identities. Thus, Equations (43)-(46) and (133) constitute exact solutions in the KEF, DEF, and KEF-DEF structures for interaction of ![]() internal waves both in the upper and lower domains.
internal waves both in the upper and lower domains.
The theoretical solutions in the KEF, DEF, and KEF-DEF structures for the dynamic problems of section 3 were computed theoretically by programming with symbolic general terms in the virtual environment of the global variable Equation with 15 procedures of 405 code lines. The theoretical solutions for the Helmholtz and Bernoulli potentials (118)-(121), the total pressure (133), the temporal derivatives (137)-(138), the directional derivatives (139)-(140), and the pressure gradient (141)-(142) of the upper and lower cumulative flows were justified by the correspondent experimental solutions for ![]()
4. Visualization and Discussion
The Fourier series with eigenfunctions ![]() and
and ![]() where
where ![]() is an integer, model a periodic function with a constant period
is an integer, model a periodic function with a constant period ![]() and a wavenumber
and a wavenumber ![]() [4] . The trigonometric structural functions
[4] . The trigonometric structural functions ![]() and
and ![]() of the KF, KEF, DEF, and KEF-DEF structures coincide with the Fourier eigenfunctions if
of the KF, KEF, DEF, and KEF-DEF structures coincide with the Fourier eigenfunctions if ![]() When
When ![]() where
where ![]() is a prime number,
is a prime number, ![]() and
and ![]() model a function with a period approaching infinity as
model a function with a period approaching infinity as ![]() [6] . For instance, if a sequence of
[6] . For instance, if a sequence of ![]() is
is
![]() (143)
(143)
local periods of the structural functions grow as ![]()
![]() (144)
(144)
and a global period of the interaction solution (43)-(46) increases as ![]()
![]() (145)
(145)
The KEF structures of conjugate harmonic solutions are visualized in Figure 2 by instantaneous 3d surface plots with isocurves for ![]() and
and![]() , for
, for ![]()
![]()
![]()
![]()
![]() and
and ![]() at
at![]() . In two dimensions, the pseudovector potential coincides with the stream function and isocurves of
. In two dimensions, the pseudovector potential coincides with the stream function and isocurves of ![]() coincides with streamlines [2] .
coincides with streamlines [2] .
The DEF and KEF-DEF structures are visualized in Figure 3 by instantaneous 3d surface plots with isocurves
![]()
![]()
Figure 3. Kinetic energy (left) and dynamic pressure (right) of the lower cumulative flow.
for ![]() and
and ![]() where
where ![]() is given by (133), for
is given by (133), for![]()
![]()
![]()
![]()
![]() and
and ![]() at
at![]() . In agreement with the Bernoulli Equation [1] , local maximums of the DEF structure for
. In agreement with the Bernoulli Equation [1] , local maximums of the DEF structure for ![]() correspond to local minimums of the KEF-DEF structure for
correspond to local minimums of the KEF-DEF structure for ![]()
The rate of vanishing of the DEF structure is larger than that of the KEF structure. Animations of ![]() and
and![]() show a transitional behavior of these variables that approach a deterministic chaos, which is determined by
show a transitional behavior of these variables that approach a deterministic chaos, which is determined by ![]() parameters:
parameters: ![]() and
and ![]() as
as![]() .
.
5. Conclusions
The analytical methods of undetermined coefficients and separation of variables are extended by the computational method of solving 2d PDEs by decomposition in invariant structures. The method is developed by the experimental computing with lists of equations and expressions and the theoretical computing with symbolic general terms. The experimental computing of the kinematic and dynamic problems is implemented by 48 procedures of 1142 code lines and the theoretical computing by 41 procedures of 996 code lines.
To compute the upper and cumulative flows for nonlinear interaction of ![]() internal waves in the KF structures, the KEF, DEF, and KEF-DEF structures were treated both experimentally and theoretically. These structures with constant and space-dependent structural coefficients are invariant with respect to various differential and algebraic operations. The structures continue the Fourier series for linear and nonlinear problems with solutions vanishing at infinity and model flows of a deterministic wave chaos with the period that approaches infinity.
internal waves in the KF structures, the KEF, DEF, and KEF-DEF structures were treated both experimentally and theoretically. These structures with constant and space-dependent structural coefficients are invariant with respect to various differential and algebraic operations. The structures continue the Fourier series for linear and nonlinear problems with solutions vanishing at infinity and model flows of a deterministic wave chaos with the period that approaches infinity.
The exact solutions of the Navier-Stokes PDEs for the nonlinear interaction of ![]() conservative waves are computed in the upper and lower domains by formulating and solving the Dirichlet problem for the vorticity, continuity, Helmholtz, Lamb-Helmholtz, and Bernoulli equations. The conservative waves are not affected by dissipation since they are derived in the class of flows with the harmonic velocity field. The harmonic relationships between fluid-dynamic variables and their spatial derivatives with respect to
conservative waves are computed in the upper and lower domains by formulating and solving the Dirichlet problem for the vorticity, continuity, Helmholtz, Lamb-Helmholtz, and Bernoulli equations. The conservative waves are not affected by dissipation since they are derived in the class of flows with the harmonic velocity field. The harmonic relationships between fluid-dynamic variables and their spatial derivatives with respect to ![]() both for upper and lower flows are obtained.
both for upper and lower flows are obtained.
Acknowledgements
The author thanks S. P. Bhavaraju for the stimulating discussion at the 2013 SIAM Annual Meeting. Support of the College of Mount Saint Vincent and CAAM is gratefully acknowledged.