A Comparison of Sufficiency Condtions for the Goldbach and the Twin Primes Conjectures ()
1. Introduction
Let  and
and 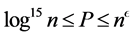 for
for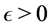 . Let
. Let 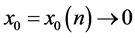 rapidly. When
rapidly. When  and
and 
let 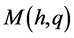 denote the closed interval
denote the closed interval , a so-called major arc.
, a so-called major arc.
It is easily shown, for any choice of , that all the
, that all the  are disjoint and contained in the closed interval
are disjoint and contained in the closed interval .
.
For each  let
let  be those points in
be those points in 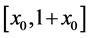 which are not in any closed neighborhood (major arc)
which are not in any closed neighborhood (major arc)
of radius  about any rational number
about any rational number , where
, where 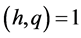 and
and .
.
For each  let
let 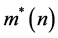 be those points in
be those points in 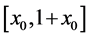 which are not in any closed neighborhood (major arc)
which are not in any closed neighborhood (major arc)
of radius  about any rational number
about any rational number , where
, where  and
and .
.
Let  denote the number of ways
denote the number of ways 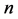 (even) can be represented as a sum of two primes.
(even) can be represented as a sum of two primes.
Let  denote the number of twin primes less than or equal to
denote the number of twin primes less than or equal to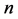 .
.
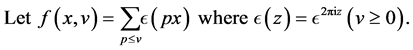
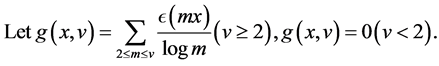

In [1] the following two theorems are established:
Theorem 1.1 Under the generalized Riemann hypothesis with  and
and  if
if
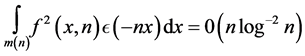 , then
, then  for all even
for all even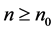 .
.
Theorem 1.2 Let  and
and 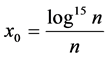 if
if
 , then
, then 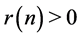 for all even
for all even .
.
In [2] the following two theorems are established:
Theorem 1.3 Under the assumption that Siegel zeros do not exist with  and
and  if
if
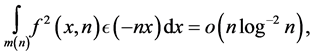 then
then 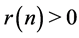 for all even
for all even .
.
Theorem 1.4 Let  and
and . If
. If
 , then
, then  for all even
for all even .
.
The proof of Theorem 1.3 and, in particular, the proof of Theorem 1.4 is very complicated.
In Section 6 of [2] it is shown, by a very complicated argument, that a particularly natural approach for eliminating the condition 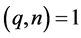 in Theorem 1.2 does not work.
in Theorem 1.2 does not work.
As we will now see, the situation with regard to the twin prime conjecture is significantly, very less complicated. The reason is primarily because we only need to consider the Ramanujan sums  rather than the sums
rather than the sums , which appear in all of the theorems above, related to the Goldbach conjecture.
, which appear in all of the theorems above, related to the Goldbach conjecture.
In Section 2 we will establish Theorem 1.5 Let 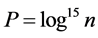 and
and .
.  if
if 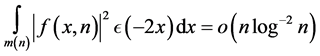 as
as  goes to infinity in some suitable sequence.
goes to infinity in some suitable sequence.
2. A Proof of Theorem 1.5
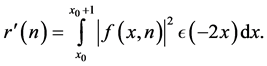
We decompose the above integral

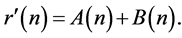
It is immediate by the prime numbers theorem that

By definition
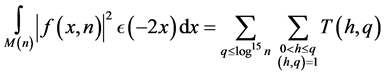
where
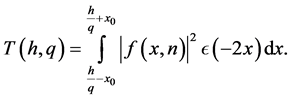
Lemma 2.1 Let 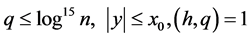 and
and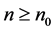 . Then
. Then

This is Theorem 58 in [3] .
Lemma 2.2 Under the hypothesis of Lemma 2.1 we have
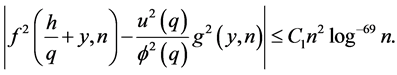
Proof. This follows immediately from Lemma 2.1 and the trivial inequalities  and
and 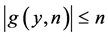 and the fact that if
and the fact that if  and
and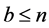 , then
, then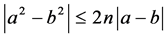 .
.
Hence it is immediate that

By the change of variable  we have
we have

However, by (2.1) we have
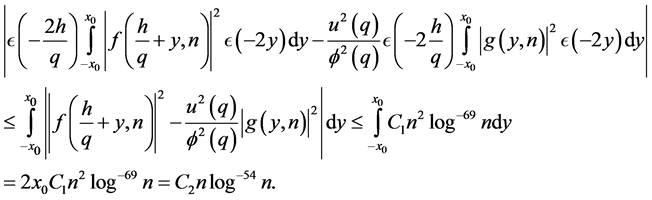
Let 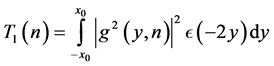 so that if
so that if  then
then
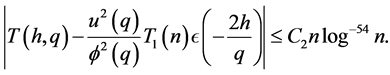
Let 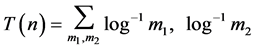 with the condition of summation
with the condition of summation  and
and .
.
It is easy to see that

For 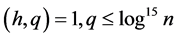 we have
we have
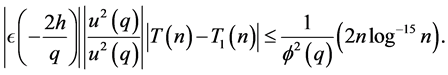
Hence for 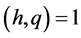 and
and 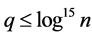

so that for some fixed  we have:
we have:

But  and by definition
and by definition

so that it follows immediately that
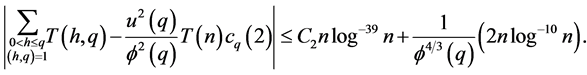
Now summing over all 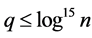 we have
we have
since by Theorem 327 page 267 in [3]

Hence

where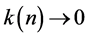 . Now let
. Now let
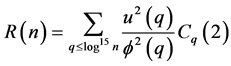
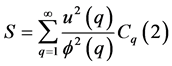
Lemma 2.3
Proof. [4] page 211.
It is immediate by Lemma 2.3 that

What remains to be done is to show  is bounded away from 0.
is bounded away from 0.
Let

Since 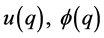 and
and 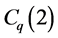 are all multiplicative functions of
are all multiplicative functions of ,
, 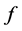 is a multiplicative function of
is a multiplicative function of . Also, by means of the trivial estimate on
. Also, by means of the trivial estimate on , namely 2, and a direct application of Theorem 327 page 267 in [5] we have
, namely 2, and a direct application of Theorem 327 page 267 in [5] we have
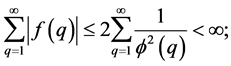
so that by Theorem 2 [3] page 3 we have


Hence

3. A Primitive Formulation of the Circle Method
1) Part I
We assume 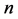 (even)
(even)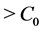 .
. 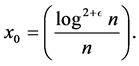
For each  let
let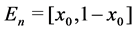 .
.
Let  be the number of representations of
be the number of representations of 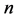 as the sum of two primes, each of which is less than
as the sum of two primes, each of which is less than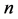 .
.
Clearly,
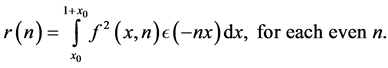
We decompose this integral
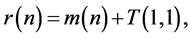
where

Clearly, by Theorem 55 in [3] and the last paragraph on page 63 in [3] we have

By direct application of the easily established Equation (151) in [3]
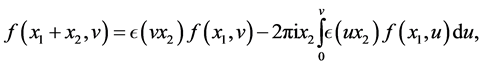 (3.0)
(3.0)
and the Equation (204) in [3]
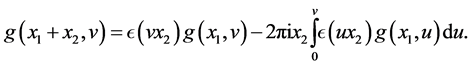 (3.1)
(3.1)
We have for 
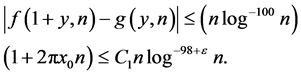 (3.2)
(3.2)
By the trivial inequalities 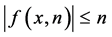 and
and 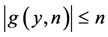 and the fact that if
and the fact that if 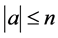 and
and , then
, then 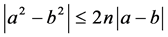 with
with 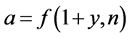 and
and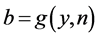 , we have for
, we have for 
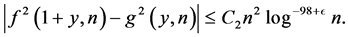 (3.3)
(3.3)
By the change of variable , we have
, we have

so that


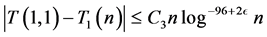
 (3.4)
(3.4)
Clearly

Also, the number of terms on the right hand side of (3.4) is  and each term is greater than
and each term is greater than  and less than 1 so that
and less than 1 so that
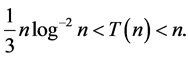
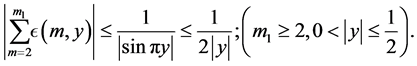
Hence by definition of  and Abel's lemma we have
and Abel's lemma we have


so that
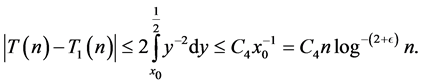 (3.5)
(3.5)
Hence,
 (3.6)
(3.6)
Let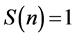 . Then
. Then 
so that
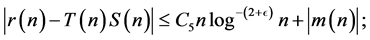
so that we have

Remark. Unfortunately, the integral  cannot be
cannot be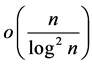 ; since for almost all
; since for almost all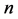 , the integral is asymptotically
, the integral is asymptotically  where
where  is the usual singular series.
is the usual singular series.
We assume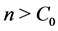 . For each
. For each 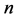 let
let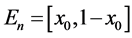 .
.
Let  be the number of twin primes, each of which is less than
be the number of twin primes, each of which is less than .
.
Clearly,
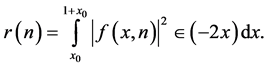
We decompose this integral

where
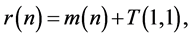
where

Immediately, from (3.3) we have

By the change of variable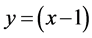 , we have
, we have
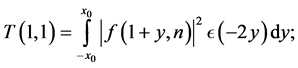
so that
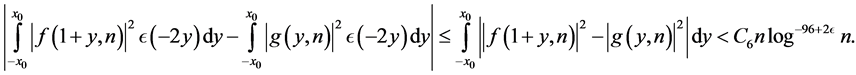
Let


Let
 (3.7)
(3.7)
Clearly,

Also, the number of terms on the right hand side of (3.7) is  and each term is greater than
and each term is greater than 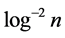 and less than 1 so that
and less than 1 so that
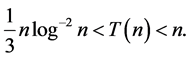
Hence by definition of  and Abel’s lemma we have
and Abel’s lemma we have
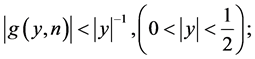
so that
 (3.8)
(3.8)
Hence
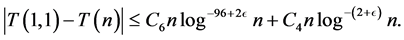 (3.9)
(3.9)
Let  Then
Then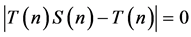 ;
;
so that

so that we have 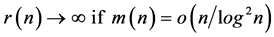 as
as 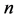 goes to infinity in some suitable sequence.
goes to infinity in some suitable sequence.
2) Part II
For each (even)  let
let  be a prime in
be a prime in  Let
Let  be those points in
be those points in
 which are not in
which are not in  and not in any closed interval of radius
and not in any closed interval of radius 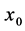 about any rational number
about any rational number 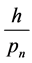 where
where
 .
.
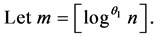
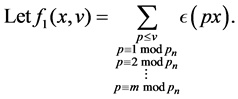
Let  be the number of representations of
be the number of representations of 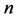 as the sum of two primes, which are limited to those primes in the
as the sum of two primes, which are limited to those primes in the  arithmetic progressions mod
arithmetic progressions mod .
.
Clearly,

We decompose this integral
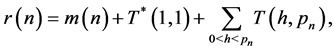
where


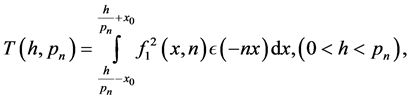
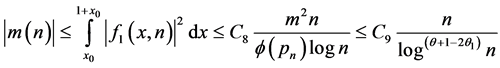

Conjecture 1.
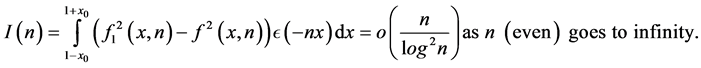
We now estimate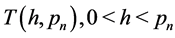 .
.
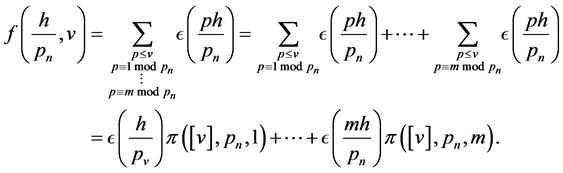
But consider



so that uniformly 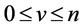



Hence for  uniformly
uniformly 
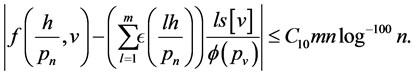
So by (100) and (101) for 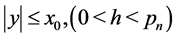

But since  and since
and since , we have by the inequalities immediately below (3.2) for
, we have by the inequalities immediately below (3.2) for 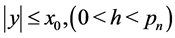
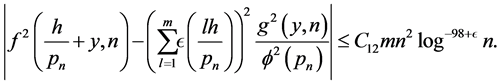
But

Hence for 
 (3.10)
(3.10)
By a change of variable  we have
we have

However,

Let

Hence, if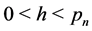 ,
,
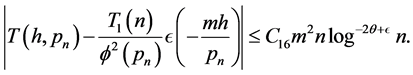
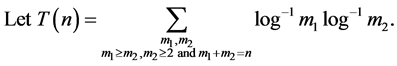
By (3.5) we have

and

But
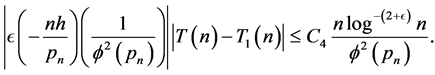
Hence, if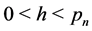 ,
,

so that
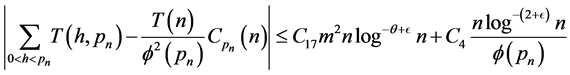
where

But by (3.6) we have
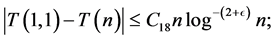
so that

so that

Let

By Theorem 272 in [5]
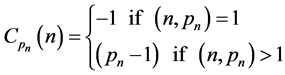
so that , since we assume
, since we assume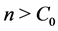 .
.
Hence
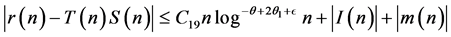
so that 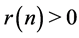 if Conjecture 1 is true.
if Conjecture 1 is true.
Let  be the number of twin primes, each of which is in one of the arithmetic progressions mod
be the number of twin primes, each of which is in one of the arithmetic progressions mod  defined above.
defined above.
Clearly,
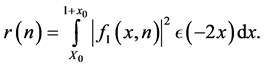
We decompose the integral

Conjecture 2.

infinity in some suitable sequence.
From (3.10) we have for 

By change of variable 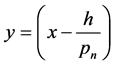 we have
we have
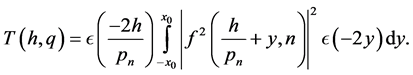
However,
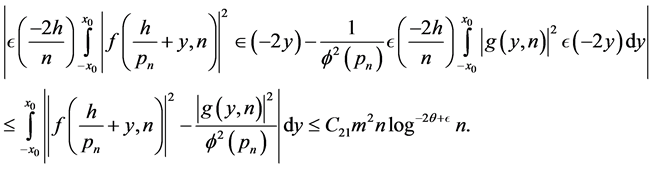
Let

Hence, if 
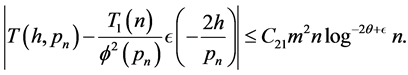

Clearly,
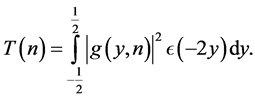
So that by (3.8)
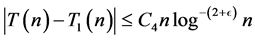
and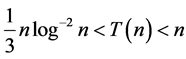 .
.
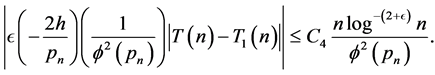
Hence, if ,
,

so that

where

But by (3.6)

so that
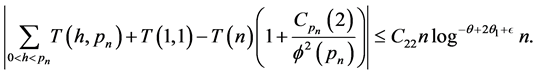
Hence

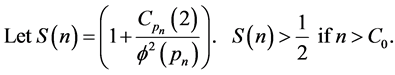
Hence

so that 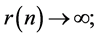 if Conjecture 2 is true, as
if Conjecture 2 is true, as  goes to infinity in a sequence that satisfies the conjecture.
goes to infinity in a sequence that satisfies the conjecture.
4. Some Heuristics
Theorem 4.1 If

then every sufficiently large even integer is the sum of two primes, where 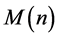 is an exceptional set, whose measure goes to 0 with
is an exceptional set, whose measure goes to 0 with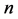 .
.
Proof. This is established in [1] .
Theorem 4.2 Let 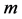 be an arbitrary fixed integer. Then
be an arbitrary fixed integer. Then

uniformly for almost all .
.
Proof. This deep result is immediate by (5-2) in [6] .
There is no compelling reason to assume Theorem 4.2 is not true for .
.
It is worthwile to investigate if Carleson’s proof can be modified to establish Theorem 4.2 with 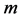 replaced with
replaced with 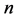 and
and 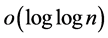 replaced with
replaced with .
.
In [7] Tao presents a heuristic argument to establish that the major arc contribution in the circle method is
 . He states that his argument can be made rigorous.
. He states that his argument can be made rigorous.
However, it follows from the proof of Theorem 1.5 that the major arc contribution is not  in any sequence of
in any sequence of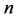 .
.
But it is well known that 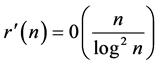 so that the contribution of the minor arc in the circle method approach to the twin primes conjecture (Theorem 1.5) is
so that the contribution of the minor arc in the circle method approach to the twin primes conjecture (Theorem 1.5) is , which makes plausible that the required estimate of
, which makes plausible that the required estimate of  might be true.
might be true.
It is plausible that in Theorem 1.3

where the latter integral is that of Theorem 1.5, which makes plausible that the required estimate of  might be true.
might be true.
Those, who seriously attempt Conjecture 2 have the advantage that there is some degree of freedom in the choice of 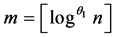 and in the choice of
and in the choice of  for each
for each ; and the
; and the  estimate is required only as
estimate is required only as  goes to infinity in some suitable sequence.
goes to infinity in some suitable sequence.
Acknowledgements
I thank R. C. Vaughan for the Remark in Part I, Section 3.