Electrodynamics of Inhomogeneous (Laminated, Angular) Structures ()
1. Introduction
Let us consider the interface S between two media having different electrophysical properties. On each of its side the magnetic-field and magnetic-inductance vectors as well as the electric-field and electric-displacement vectors are finite and continuous; however, at the surface S they can experience a discontinuity of the first kind. Furtermore, at the interface there arise induced surface charges σ and surface currents i (whose vectors lie in the plane tangential to the surface S) under the action of an external electric field.
There are no closing relations for induced charge and the surface current, which makes it necessary to intro- duce the surface-impedance matrix; one determines this matrix experimentally or in some cases theoretically from quantum representation:
Where n is the normal to the surface, which is directed to the field region and i and k are the subscripts char- actering the orthogonal coordinate directions on the surface.
In radio-physics, one often uses, for the problem of propagation of electromagnetic waves in the presence of “perfectly conducting” bodies, a surface impedance of the form as the boundary condition in determining out- side the conductor (M. A. Leontovich, 1948);
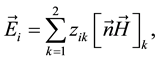
the fulfillment of the condition of continuity of the tangential components of the electric and magnetic field strength, i.e., the absence of a surface current, is assumed.
Not only do the induced surface charge and current character the properties of the surface, but they are also functions of the process; therefore, surface impedances hold for conditions under which they have been deter- mined. Under other experimental conditions, one cannot use surface impedances, since surface impedances de- pend on the structure of the determined field and are not boundary conditions in the ordinary sense. When the notion “surface impedance” is used there are a number of constraints and assumptions: the depth of penetration of an electromagnetic wave into a medium and the wavelength in it must be small compared to the wavelength in the ambient space, compared to the distances from the field’s sources, and compared to the radii of curvature of the body’s surface; the changes in the relative permittivity along the body’s length and in the magnetic per- meability at distance of the order of the wavelength (or on a length equal to the penetration depth) are small.
Furthermore, we have no ware absorption or it is minor, it is difficult to use the existing impedance conditions, since in the body, there can be waves traveling not only from the surface but from the body as well.
By virtue of the aforesaid, the scattering of electromagnetic waves by a group of closely spaced bodies assumes the use of exact boundary conditions with introduction of a surface charge and a surface current.
Numerical codes under the general name “Finite Difference Time Domain (FDTD)” are currently available, which allow calculation, within the framework of initial and boundary-value problems, of wave fields in a three- dimensional and nonstationary situation in inhomogeneous dissipative media possessing time dispersion alike. It should be noted that these numerical schemes are efficient also for calculating fields not only in liner media but in nonlinear ones. There is an ample amount of literature on FDTD codes, but practical implementation of the indicated method is hindered by the necessity of prescribing a surface-impedance matrix at the boundary of ad- jacent media. Nonstationary thermal and diffusion processes, and also dispersion affect the surface-impedance matrix, which makes the problem of simulation of wave propagation in a heterogeneous ion conductor or a con- ductor with mixed conduction fundamentally more complicated. When the surface-impedance matrix is used at the boundaries of adjacent media it is also difficult to obtain expressions for the energy density and the heat re- leased in the absorbing medium.
In dielectrics, when conduction currents are negligible, the induced surface charge and the surface current are also insignificant; therefore, the well-known geometric laws of reflection and rarefaction in propagation of light through the boundary of two media and Frenel formulas hold; here, the amplitude of the incident wave is as- sumed to be equal to the sum of the amplitudes of the transmitted and reflected waves. This condition is widely used in optics and radio-physics, since for a monochromatic wave, solution of the problem is reduced to the Helmholtz control, e.g., light propagation in a photon crystal. We emphasize that a plane monochromatic wave is infinitesimal. However, while considering the electromagnetic properties of structures from composite mate- rials representing homogeneous matrices with a large number of distributed small material in homogeneities, we must take into account, in mathematical models of chiral, bi isotropic, bi anisotropic, Faraday, and gyrotropic media and metamaterials, the induced surface charge and the surface current whose prescription involves fun- damental difficulties.
Invariably topical are radiolocation and radio communication problems. Successful solution of any radioloca- tion problem requires that the space-time characteristics of diffraction fields of electromagnetic waves scattered by the object of location into the ambient space be known. Irradiated object have a very intricate architecture and geometric shale of the surface consisting of smooth portions, surface fractures, sharp edges, and edges with corner radii much smaller than the wavelength of a probing signal; therefore, we cannot use regular Leontovich impedance conditions. The object has larger geometric dimensions compared to the length of the incident elec- tromagnetic wave and numerous coatings with different radiophysical properties. Therefore, solution of radio- location problems calls for the methods of calculation of the diffraction fields of electromagnetic waves excited and scattered by different surface portions of the objects, in particular, their wedge-shaped formations, since the latter are some of the principal sources of scattered waves.
The issues of diffraction of electromagnetic waves in wedge-shaped regions have been the focus of numerous investigations. Representation of the diffraction field in a corner (wedge-shaped) region in the form of A. Som- merfeld’s integral is the most promising technique of solution of the problem for a perfectly conducting and im- pedance wedge in the quasioptical wavelength range.
G. D. Malynzhinets has obtained, from A. Sommerfeld’s method, an asymptotic solution for the scalar problem on excitation of an impedance wedge with semiinfinite sides and an arbitrary opening angle by a plane acoustic wave; the same author substantiated the method subsequently called the “Sommerfeld-Malynzhinets method”. It is noteworthy that finding exact solutions of a generalized wave equation on impedance and dielectric structures by the Sommerfeld-Malynzhinets method presents exceptional mathematical difficulties; these solutions have only been performed for monochromatic waves for a semi-infinite wedge; the corresponding magnetic or electric vectors are oriented in parallel to the wedge edge.
It is difficult to use this method in the presence of the normal components of the electromagnetic vector and for nonmonochromatic waves. In this case it is possible, in principle, to use the surface-impedance matrix in simulating, as has been noted above. As we believe, the calculation method, the physicomathematical model of scattering of a signal e.g. a ballistic object, may not depend on the object’s geometry and on empirical coefficients which are dependent on the structure of the electromagnetic field.
The existence of a surface charge at the interface S between the two media having different electrophysical properties is clearly demonstrated by the following example. We will consider the traverse of a direct current through a flat capacitor filled with two dielectric materials having relative permittivities ε1 and ε2 and electrical conductivities λ1 and λ2. A direct-current voltage U is applied to the capacitor plates; the total resistance of the capacitor is R (Figure 1). It is necessary to calculate the surface electric charge induced by the electric current.
From the electric-charge conservation law follows the constancy of flow in a circuit; therefore, the following equation is fulfilled:
 (1)
(1)
where 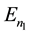 and
and 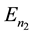 are the normal components of the electric-field vector.
are the normal components of the electric-field vector.
At the interface between the dielectrics, the normal components of the electric-inductance vector change spasmodically under the action of the electric field by a value equal to the value of the induced surface charge σ:
 (2)
(2)
Solving the system of equations (see Equations (1) and (2)), we obtain the expression for σ
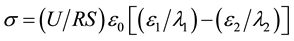 (3)
(3)
It follows from (see Equation (3)) that the charge σ is determined by the current and the multiplier accounting
![]()
Figure 1. Dielectric media inside a flat capacitor.
for the properties of the medium. If
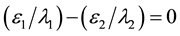 (4)
(4)
a surface charge σ is not formed. What is more, recent trends are toward increased use of micromachines and engines made from plastic materials, where the appearance of a surface charge is undesirable. For oiling of elements of such machines, it is best to use an oil with a permittivity 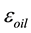 satisfying the relation
satisfying the relation
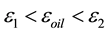 (5)
(5)
This oil makes it possible to decrease the electrization of the moving machine parts made from dielectric materials. In addition to the charge σ, a contact potential difference arises always independently of the current.
An electric field interacting with a material is investigated with the use of the Maxwell equation (1857). For convenience and correctness of further presentation we denote the axial vector of magnetic field strength, induction as 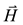 and
and 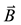
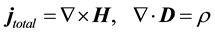 (6)
(6)
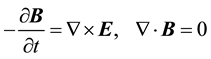 (7)
(7)
where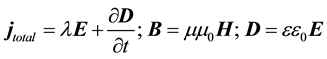 . In this case, at the interface S the above system of equations is
. In this case, at the interface S the above system of equations is
supplemented with the boundary conditions [1] [2] (Monzon, I.; Yonte,T.; Sanchez-Soto, L., 2003; Eremin,Y. & Wriedt, T., 2002)
 (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
The indices (subscripts) n and τ denote the normal and tangential components of the vectors to the surface S, and the indices 1 and 2 denote the adjacent media with different electrophysical properties. The index τ denotes any direction tangential to the discontinuity surface. At the same time, a closing relation is absent for the induced surface charge σ, which generates a need for the introduction of an impedance matrix [3] -[7] (Wei Hu & Hong Guo, 2002; Danae, D., et al., 2002; Larruquert, J. I., 2001; Koludzija, B. M., 1999; Ehlers, R. A. & Meta- xas, A. C., 2003) that is determined experimentally or, in some cases, theoretically from quantum representations [8] -[12] (Barta, O.; Pistora, I.; Vesec, I. et al., 2001; Broe, I. & Keller, O., 2002; Keller, 1995; Keller, O., 1995; Keller, O., 1997). We note that the Maxwell equation of electromagnetic field does not coincide comple- tely with the modern form of them (6), (7) which was first given by Hertz (1884) and independently of him by Heaviside (1885). One should bear in mind that electric field strength E is a polar vector. Gradients of concen- tration and temperature are also polar vectors. On the contrary, magnetic field strength![]() , as well as
, as well as![]() , are axial vectors, or pseudovectors. This is well seen from the formula for the Lorentz force
, are axial vectors, or pseudovectors. This is well seen from the formula for the Lorentz force![]() . The Biot-Savart-Laplace law establishes the value and direction of the axial vector
. The Biot-Savart-Laplace law establishes the value and direction of the axial vector ![]() at an arbitrary point of a magnetic field produced by a semiconductor element de (the vector is a coincident with the direction of the current i).
at an arbitrary point of a magnetic field produced by a semiconductor element de (the vector is a coincident with the direction of the current i).
![]()
Indeed, the behavior of ![]() on reflection at the origin of coordinates and substitution r ® (?r) is determined by the behavior of the polar vectors F and V and the properties of their vector product. On substitution r ® (?r) the directions of the vectors F and V change to the opposite; the sign of the vector product also reverses. Conse- quently, on substitution r ® (?r) the vector
on reflection at the origin of coordinates and substitution r ® (?r) is determined by the behavior of the polar vectors F and V and the properties of their vector product. On substitution r ® (?r) the directions of the vectors F and V change to the opposite; the sign of the vector product also reverses. Conse- quently, on substitution r ® (?r) the vector ![]() must remain constant. This property is assumed to be an attrib- ute of the axial vector.
must remain constant. This property is assumed to be an attrib- ute of the axial vector.
The induced surface charge σ not only characterizes the properties of a surface, but also represents a function of the process, i.e.,![]() ; therefore, the surface impedances [3] -[7] (Wei Hu & Hong Guo, 2002; Danae, D., et al., 2002; Larruquert, J. I., 2001; Koludzija, B. M., 1999; Ehlers, R. A. & Metaxas, A. C., 2003) are true for the conditions under which they are determined. These impedances cannot be used in experiments conducted under other experimental conditions.
; therefore, the surface impedances [3] -[7] (Wei Hu & Hong Guo, 2002; Danae, D., et al., 2002; Larruquert, J. I., 2001; Koludzija, B. M., 1999; Ehlers, R. A. & Metaxas, A. C., 2003) are true for the conditions under which they are determined. These impedances cannot be used in experiments conducted under other experimental conditions.
The problem of determination of surface charge and surface current on metal-electrolyte boundaries becomes even more complicated in investigating and modeling nonstationary electrochemical processes, e.g., pulse elec- trolysis, when lumped parameters L, C, and R cannot be used in principle.
We will show that σ can be calculated using the Maxwell phenomenological macroscopic electromagnetic equations and the electric-charge conservation law accounting for the special features of the interface between the adjacent media.
Separate consideration will be given to ion conductors. In constructing a physicomathematical model, we take into account that ![]() and
and ![]() are not independent functions; therefore, the wave equation for
are not independent functions; therefore, the wave equation for ![]() or
or ![]() is more preferable than the system of equations (see Equations (6) and (7)). It will be shown that in consideration of propagation, interference of waves in the heterogeneous medium it is preferable to use the wave equation for a polar vector of electric field strength.
is more preferable than the system of equations (see Equations (6) and (7)). It will be shown that in consideration of propagation, interference of waves in the heterogeneous medium it is preferable to use the wave equation for a polar vector of electric field strength.
2. Electron Conductors. New Closing Relations on the Boundaries of Adjacent Media
2.1. Generalized Wave Equation for ![]() and Conditions on the Boundaries in the Presence of Strong Discontinuities of the Electromagnetic Field
and Conditions on the Boundaries in the Presence of Strong Discontinuities of the Electromagnetic Field
2.1.1. Physicomathematical Model
We will formulate a physicomathematical model of propagation of an electromagnetic field in a heterogeneous medium. Let us multiply the left and right sides of the equation for the total current (see Equation (6)) by μμ0 and differentiate it with respect to time. Acting by the operator rot on the left and right sides of the first equation of equation (see Equation (7)) on condition that μ = const we obtain
![]() (12)
(12)
In Cartesian coordinates, equation (see Equation (12)) will take the form
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
At the interface, the following relation [2] (Eremin,Y. & Wriedt,T., 2002) is also true:
![]() (16)
(16)
Let us write conditions (see Equations (8)-(11)) in the Cartesian coordinate system:
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
where iτ = iyj + izk is the surface-current density, and the coordinate x is directed along the normal to the inter- face. The densities iy and iz of the surface currents represent the electric charge carried in unit time by a segment of unit length positioned on the surface drawing the current perpendicularly to its direction.
The order of the system of differential equations (see Equations (13)-(15)) is equal to 18. Therefore, at the in- terface S, it is necessary to set, by and large, nine boundary conditions. Moreover, the three additional condi- tions (see Equations (17) (21), and (22)) containing (prior to the solution) unknown quantities should be fulfilled at this interface. Consequently, the total number of conjugation conditions at the boundary S should be equal to 12 for a correct solution of the problem.
As an example we consider a one-dimensional case of heat propagation in the layered material. As is known, to solve the problem we must specify two conditions at the interface: the equality of heat fluxes and the equality of temperatures, since in the heat conduction equation we have the second derivative with respect to the coordi- nate.
Differentiating expression (see Equation (17)) with respect to time and using relation (see Equation (16)), we obtain the following condition for the normal components of the total current at the medium-medium interface:
![]() (23)
(23)
that allows one to disregard the surface charge σ. Let us introduce the arbitrary function f:
![]() . In this case, expression (see Equation (23)) will take the form
. In this case, expression (see Equation (23)) will take the form
![]() (24)
(24)
It is assumed that, at the medium-medium interface, Ex is a continuous function of y and z. Then, differentiat- ing equation (see Equation (23)) with respect to y and z, we obtain
![]() (25)
(25)
![]() (26)
(26)
Let us differentiate conditions (see Equations (20)-(22)) for the magnetic induction and the magnetic-field strength with respect to time. On condition that B = μμ0H.
![]() (27)
(27)
Using equation (see Equation (7)) and expressing (see Equation (27)) in terms of projections of the electric- field rotor, we obtain
![]() and
and ![]() (28)
(28)
![]() or
or ![]() (29)
(29)
![]() or
or ![]() (30)
(30)
Here, equation (see Equation (28)) is the normal projection of the electric-field rotor, equation (see Equation (29)) is the tangential projection of the rotor on y, and equation (see Equation (30)) is the rotor projection on z.
Assuming that Ey and Ez are continuous differentiable functions of the coordinates y and z, from conditions (see Equations (18) and (19)) we find
![]() (31)
(31)
![]()
In accordance with the condition that the tangential projections of the electric field on z and y are equal and in accordance with conditions (see Equations (18) and (19)), the expressions for the densities of the surface cur- rents iz and iy take the form
![]() (32)
(32)
where
![]() (33)
(33)
is the average value of the electrical conductivity at the interface between the adjacent media in accordance with the Dirichlet theorem for a piecewise-smooth, piecewise-differentiable function.
Consequently, formulas (see Equations (31)-(33)) yield
![]() (34a)
(34a)
Relation (see Equation (34)) and hence the equality of the normal components of the total current were ob- tained (in a different manner) by G. A. Grinberg and V. A. Fok [13] (Grinberg, G. A. & Fok, V. A., 1948). In this work, it has been shown that condition (34a) leads to the equality of the derivatives of the electric field strength along the normal to the surface
![]() (34b)
(34b)
With allowance for the foregoing we have twelve conditions at the interface between the adjacent media that are necessary for solving the complete system of equations (see Equations (13)-(15)):
1) the functions Ey and Ez are determined from equations (see Equations (18) and (19));
2) Ex is determined from condition (see Equation (24));
3) the values of ∂Ex/∂y, ∂Ex/∂z, and ∂Ex/∂x are determined from relations (see Equations (25) and (26)) with the use of the condition of continuity of the total-current normal component at the interface (see Equation (24)) and the continuity of the derivative of the total current with respect to the coordinate x;
4) the values of ∂Ey/∂y, ∂Ey/∂z, and ∂Ez/∂z are determined from conditions (see Equations (31) and (32)) in consequence of the continuity of the tangential components of the electric field along y and z;
5) the derivatives ∂Ey/∂x and ∂Ez/∂x are determined from conditions (see Equations (29) and (30)) as a conse- quence of the equality of the tangential components of the electric-field rotor along y and z.
Note that condition (see Equation (23)) was used by us in [14] (Grinchik, N. N. & Dostanko, A. P., 2005) in the numerical simulation of the pulsed electrochemical processes in the one-dimensional case. Condition (see Equation (28)) for the normal component of the electric-field rotor represents a linear combination of conditions (see Equations (31) and (32)); therefore, rotxE = 0 and there is no need to use it in the subsequent discussion. The specificity of the expression for the general law of electric-charge conservation at the interface is that the components ∂Ey/∂y and ∂Ez/∂z are determined from conditions (see Equations (31) and (32)) that follow from the equality and continuity of the tangential components Ey and Ez at the boundary S.
Thus, at the interface between the adjacent media the following conditions are fulfilled: the equality of the to- tal-current normal components; the equality of the tangential projections of the electric-field rotor; the elec- tric-charge conservation law; the equality of the electric-field tangential components and their derivatives in the tangential direction; the equality of the derivatives of the total-current normal components in the direction tan- gential to the interface between the adjacent media, determined with account for the surface currents and without explicit introduction of a surface charge. They are true at each cross section of the sample being investigated.
2.1.2. Features of Calculation of the Propagation of Electromagnetic Waves in Layered Media
The electromagnetic effects arising at the interface between different media under the action of plane electro- magnetic waves have a profound impact on the equipment because all real devices are bounded by the surfaces and are inhomogeneous in space. At the same time, the study of the propagation of waves in layered conducting media and, according to [15] (Born, 1970), in thin films is reduced to the calculation of the reflection and trans- mission coefficients; the function E(x) is not determined in the thickness of a film, i.e., the geometrical-optics approximation is used.
The physicomathematical model proposed allows one to investigate the propagation of an electromagnetic wave in a layered medium without recourse to the assumptions used in [3] -[5] [7] (Wei Hu & Hong Guo, 2002; Danae, D. et al., 2002; Larruquert, J. I., 2001; Ehlers, R. A. & Metaxas, A. C., 2003).
Since conditions (see Equations (23)-(32)) are true at each cross section of a layered medium, we will use schemes of through counting without an explicit definition of the interface between the media. In this case, it is proposed to calculate Ex at the interface in the following way.
In accordance with equation (see Equation (17)), Ex1 ≠ Ex2, i.e., Ex(x) experiences a discontinuity of the first kind. Let us determine the strength of the electric field at the discontinuity point x = ξ on condition that Ex(x) is a piecewise-smooth, piecewise-differentiable function having finite one-sided derivatives ![]() and
and![]() . At the discontinuity points xi,
. At the discontinuity points xi,
![]() (35)
(35)
![]() (36)
(36)
In this case, in accordance with the Dirichlet theorem [16] (Kudryavtsev, 1970), the Fourier series of the function E(x) at each point x, including the discontinuity point ξ, converges and its sum is equal to
![]() (37)
(37)
The Dirichlet condition (see Equation (37)) also has a physical meaning. In the case of contact of two solid conductors, e.g., dielectrics or electrolytes in different combinations (metal-electrolyte, dielectric-electrolyte, metal-vacuum, and so on), at the interface between the adjacent media there always arises an electric double layer (EDL) with an unknown (as a rule) structure that, however, substantially influences the electrokinetic effects, the rate of the electrochemical processes, and so on. It is significant that, in reality, the electrophysical characteristics λ, ε, and E(x) change uninterruptedly in the electric double layer; therefore, (see Equation (37)) it is true for the case where the thickness of the electric double layer, i.e., the thickness of the interphase boundary, is much smaller than the characteristic size of a homogeneous medium. In a composite, e.g., in a metal with embedments of dielectric balls, where the concentration of both components is fairly large and their characteristic sizes are small, the interphase boundaries can overlap and condition (see Equation (37)) can break down.
If the thickness of the electric double layer is much smaller than the characteristic size L of an object, (see Equation (37)) also follows from the condition that E(x) changes linearly in the EDL region. In reality, the thickness of the electric double layer depends on the kind of contacting materials and can comprise several tens of angstroms [17] (Frumkin, 1987). In accordance with the modern views, the outer coat of the electric double layer consists of two parts, the first of which is formed by the ions immediately attracted to the surface of the metal (a “dense” or a “Helmholtz” layer of thickness h), and the second is formed by the ions separated by dis- tances larger than the ion radius from the surface of the layer, and the number of these ions decreases as the dis- tance between them and the interface (the “diffusion layer”) increases. The distribution of the potential in the dense and diffusion parts of the electric double layer is exponential in actual practice (Frumkin, 1987), i.e., the condition that E(x) changes linearly breaks down; in this case, the sum of the charges of the dense and diffusion parts of the outer coat of the electric double layer is equal to the charge of its inner coat (the metal surface). However, if the thickness of the electric double layer h is much smaller than the characteristic size of an object, the expansion of E(x) into a power series is valid and one can restrict oneself to the consideration of a linear ap- proximation. In accordance with the more general Dirichlet theorem (1829), a knowledge of this function in the EDL region is not necessary to substantiate equation (see Equation (37)). Nonetheless, the above-indicated physical features of the electric double layer lend support to the validity of condition (see Equation (37)).
The condition at interfaces, analogous to equation (see Equation (370), has been obtain earlier [18] (Tikhonov, A. N. & Samarskii, A. A., 1977) for the potential field (where rot E = 0) on the basis of introduction of the sur- face potential, the use of the Green formula, and the consideration of the discontinuity of the potential of the double layer. In [18] (Tikhonov, A. N. & Samarskii, A. A., 1977), it is also noted that the consideration of the thickness of the double layer and the change in its potential at h/L = 1 makes no sense in general; therefore, it is advantageous to consider, instead of the volume potential, the surface potential of any density. Condition (see Equation (37)) can be obtained, as was shown in [16] (Kudryavtsev, 1970), from the more general Dirichlet theorem for a nonpotential vorticity field [18] (Tikhonov, A. N. & Samarskii, A. A., 1977).
Thus, the foregoing and the validity of conditions (see Equations (17)-(19) and (25)-(32)) at each cross sec- tion of a layered medium show that, for numerical solution of the problem being considered it is advantageous to use schemes of through counting and make the discretization of the medium in such a way that the boundaries of the layers have common points.
The medium was divided into finite elements so that the nodes of a finite-element grid, lying on the separation surface between the media with different electrophysical properties, were shared by these media at a time. In this case, the total currents or the current flows at the interface should be equal if the Dirichlet condition (see Equa- tion (37)) is fulfilled.
2.1.3. Results of Numerical Simulation of the Propagation of Electromagnetic Waves in Layered Media
Let us analyze the propagation of an electromagnetic wave through a layered medium that consists of several layers with different electrophysical properties in the case where an electromagnetic-radiation source is posi- tioned on the upper plane of the medium. It is assumed that the normal component of the electric-field vector Ex = 0 and its tangential component Ey = asin(ωt), where a is the electromagnetic-wave amplitude (Figure 2).
In this example, for the purpose of correct specification of the conditions at the lower boundary of the medium, an additional layer is introduced downstream of layer 6; this layer has a larger conductivity and, therefore, the electromagnetic wave is damped out rapidly in it. In this case, the condition Ey = Ez = 0 can be set at the lower boundary of the medium. The above manipulations were made to limit the size of the medium being con- sidered because, in the general case, the electromagnetic wave is attenuated completely at an infinite distance from the electromagnetic-radiation source.
Numerical calculations of the propagation of an electromagnetic wave in the layered medium with electro- physical parameters ε1 = ε2 = 1, λ1 = 100, λ2 = 1000, and μ1 = μ2 = 1 were carried out. Two values of the cyclic
![]()
Figure 2. Scheme of a layered medium: layers 1, 3, and 5 are characterized by the electrophysical parameters ε1, λ1, and μ1, and layers 2, 4, and 6―by ε2, λ2, μ2.
frequency ω = 2π/T were used: in the first case, the electromagnetic-wave frequency was assumed to be equal to ω = 1014 Hz (infrared radiation), and, in the second case, the cyclic frequency was taken to be ω = 109 Hz (ra- diofrequency radiation).
As a result of the numerical solution of the system of equations (see Equations (13)-(15)) with the use of con- ditions S (see Equations (24)-(34)) at the interfaces, we obtained the time dependences of the electric-field strength at different distances from the surface of the layered medium (Figure 3).
The results of our simulation (Figure 4) have shown that a high-frequency electromagnetic wave propagating in a layered medium is damped out rapidly, whereas a low-frequency electromagnetic wave penetrates into such a medium to a greater depth. The model developed was also used for calculating the propagation of a modulated signal of frequency 20 kHz in a layered medium. As a result of our simulation (Figure 5), we obtained changes in the electric-field strength at different depths of the layered medium, which points to the fact that the model proposed can be used to advantage for calculating the propagation of polyharmonic waves in layered media; such a calculation cannot be performed on the basis of the Helmholtz equation.
The physicomathematical model developed can also be used to advantage for simulation of the propagation of
![]()
Figure 3. Time change in the tangential component of the electric-field strength at a distance of 1 μm (1), 5 μm (2), and 10 μm (3) from the surface of the medium at λ1 = 100, λ2 = 1000, ε1 = ε2 = 1, μ1 = μ2 = 1, and ω = 1014 Hz. t, sec.
![]()
Figure 4. Distribution of the amplitude of the electric-field- strength at the cross section of the layered medium: ω = 1014 (1) and 109 Hz (2). y, μm.
electromagnetic waves in media with complex geometric parameters and large discontinuities of the electro- magnetic field (Figure 6).
Figure 6(a) shows the cross-sectional view of a cellular structure representing a set of parallelepipeds with different cross sections in the form of squares. The parameters of the materials in the large parallelepiped are
denoted by index 1, and the parameters of the materials in the small parallelepipeds (the squares in the Figure) are denoted by index 2.
An electromagnetic wave propagates in the parallelepipeds (channels) in the transverse direction. It is seen from Figure 6(b) that, in the cellular structure there are “silence regions,” where the amplitude of the electromagnetic-wave strength is close to zero, as well as inner regions where the signal has a marked value downstream of the “silence” zone formed as a result of the interference.
2.1.4. Results of Numerical Simulation of the Scattering of Electromagnetic Waves in Angular Structures
It is radiolocation and radio-communication problems that are among the main challenges in the set of problems solved using radio-engineering devices.
![]()
Figure 5. Time change in the electric-field strength at a distance of 1 (1), 5 (2), and 10 μm (3) from the surface of the medium. t, sec.
![]() (a) (b)
(a) (b)
Figure 6. Distribution of the amplitude of the electric-field strength in the two-dimensional medium and in depth at ε1= 15, ε2 = 20, λ1 = 10−6, λ2 = 10, μ1 = μ2 = 1, and ω = 109 Hz (the dark background denotes medium 1, and the light background?medium 2). x, y, mm; E, V/m. (a) Distribution of the amplitude of the electric-field strength in the two-dimensional medium; (b) Distribution of the amplitude of the electric-field strength in depth.
Knowledge of the space-time characteristics of diffraction fields of electromagnetic waves scattered by an object of location into the environment is necessary for solving successfully any radiolocation problem. Irradiated object have a very intricate architecture and geometric shape of the surface consisting of smooth portions and numerous wedge-shaped for formations of different type-angular joints of smooth portions, surface fractures, sharp edges, etc.―with rounded radii much smaller than the probing-signal wavelength. Therefore, solution of radiolocation problems requires that the methods of calculation of the diffraction fields of electromagnetic waves excited and scattered by different surface portions of the objects, in particular, by wedge-shaped formations, be known, since the latter are among the main sources of scattered waves.
For another topical problem, i.e., radio communication effected between objects, the most difficult are the issues of designing of antennas arranged on an object, since their operating efficiency is closely related to the geometric and radiophysical properties of its surface.
The issues of diffraction of an electromagnetic wave in wedge-shaped regions are the focus of numerous of the problems for a perfectly conducting and impedance wedge for monochromatic waves is representation of the diffraction field in an angular region in the form of a Sommerfeld integral [19] (Kryachko, A. F. et al., 2009).
Substitution of Sommerfeld integrals into the system of boundary conditions gives a system of recurrence functional equations for unknown analytical integrands. The system’s coefficients are Fresnel coefficients defining the reflection of plane media or their refraction into the opposite medium. From the system of functional equations, one determines, in a recurrence manner, sequences of integrand poles and residues in these poles.
The edge diffraction field in both media is determined using a pair of Fredholm-type singular integral equations of the second kind which are obtained from the above-indicated systems of functional equations with subsequent computation of Sommerfeld integrals by the saddle-point approximation. The branching points of the integrands condition the presence of creeping waves excited by the edge of the dielectric wedge.
The proposed method is only true of monochromatic waves and of the approximate Leontovich boundary conditions, when the field of the electromagnetic wave slowly varies from point to point on a wavelength scale (Leontovich, 1948).
We note that the existing approximate Leontovich conditions have a number of other constants and should be used with caution [20] (Leontovich, 1948).
In actual fact, the proposed calculation method does not work in the presence of, e.g., two wedges, when the sharp angles are pointed at each other, i.e., an optical knife, or in diffraction of the electromagnetic wave on a system of parallel lobes, when the gap between the lobes is in the region of microns, and the electromagnetic field is strongly “cut” throughout the space with a step much than the wavelength.
A) Optical Knife
Figure 7 shows the field of an electromagnetic wave in its diffraction on the optical knife. The parameters of the wave at entry and at exit are Ex = 104 sin(1010t), Ey = 104cos(1010t).
The electrophysical characteristics are as follows: the wedge is manufactured from aluminum: ε = 1; μ = 1; σ = 3.774 ´ 107 S/m; the ambient medium is air.
The dimensions of the computational domain are 0.1 × 0.05 m. The calculation time 10‒9 sec, and the time step is 10‒11 sec.
Numerical solution of the system of Equations (13)-(15) yields the dependences of the distribution Ex(x,y) и Ey(x,y) on the optical knife. The calculations results are in good agreement with the existing experimental data and experiments specially conducted at the Department of the Physics and Chemistry of Nonequilibrium Media of the A.V. Luikov Heat and Mass Transfer Institute of the National Academy of Sciences by A. I. Bereznyak.
The experiments were carried out with an optical-range laser and were tentative in character but the obtained experimental photographs of diffraction fields and the calculated results turned out to be in good qualitative agreement. The authors express their thanks to A. I. Bereznyak for the conducting of the experiments.
Known works of L. D. Landau and E. M. Lifshits also give the solution of the problem on the diffraction of light from the edge of a perfectly conducting wedge bounded by two intersecting half-planes (A. Sommerfeld). Complete presentation of this complicated mathematical theory involving special mathematical techniques is beyond the score of the present book. Theoretical foundations of solution of the problems of scattering of electromagnetic waves on dielectric and impedance wedge-shaped formations for monochromatic waves are given in the work [19] (A. F. Kryachko, I. et al., 2009). Using the Summerfeld-Malyuzhinets method, the authors were able to obtain exact and asymptotic solutions of the diffraction of a plane wave oblique with respect to the edge
of an impedance wedge. The results of analytical calculations were compared to experimental data. The results of numerical calculations in Figure 7 are in qualitative agreement with the data of work [19] (A. F. Kryachko, 2009); in both cases the intensity of electromagnetic radiation is maximum at the point of the wedge. In the pre- sent work, we do not give the specific electrophysical properties of the wedge and the value of the surface im- pedance of the dielectric wedge; therefore, it is impossible, in practice, to correctly compare different computa- tional methods. The concentration of electromagnetic energy on an angular structure is a well-known fact.
B) Diffraction Grating
The parameters of the wave and the interfacial conditions are the same, as those for the case “optical knife”. The electrophysical characteristics are as follows: 2D lobes, ε = 12; and σ = 100 S/m; the ambient medium is air; the characteristics of the prism and the square are identical to those of the lobes.
Figure 8 corresponds to a calculation time of 10‒10 sec; the time step is 10‒12 sec. Figure 9 corresponds to a calculation time of 10‒9 sec; the time step is 10‒11 sec.
It is seen from the modeling results that the proposed “comb” cab be used as a filter of a high-frequency signal. Furthermore, we carried out numerical calculations of a modulated signal at a frequency of 20 kHz. The results of the modulated-signal calculations are not given. To analyze the difference scheme for stability was analyzed by the initial data. When the time and space steps are large there appear oscillations of the grid solution and of its “derivatives” (“ripple”) which strongly decrease the accuracy of the scheme. Undoubtedly, this issue calls for separate consideration. The proposed algorithm of solution of Maxwell equations allows circuitry-engineering modeling of high-frequency radio-engineering devices and investigation of the propagation
![]()
![]() (a) (b)
(a) (b)
Figure 8. Amplitude Ex, amplitude Ey of the electromagnetic field strength.
![]()
![]() (a) (b)
(a) (b)
Figure 9. Amplitude Ex, amplitude Ey of the electromagnetic field strength.
of electromagnetic waves in media of intricate geometry in the presence of strong discontinuities of electro- magnetic field.
The result of Para 2.1 were published in part [21] (Grinchik, N. N. et al., 2009).
2.1.5. Conclusions
We were the first to construct a consistent physicomathematical model of propagation of electromagnetic waves in layered media without recourse to the matrices of the induced-surface-charge impedances. This model is
based on the Maxwell equations, the electric-charge conservation law, the total-current continuity, and the Dirichlet theorem. Our numerical investigations have shown that the physical and mathematical model proposed can be used to advantage for simulation of the propagation of a high-frequency electromagnetic wave in a medium consisting of layers having different electrophysical properties.
2.2 Wave Equation for ![]() and Conditions on the Boundaries in the Presence of Strong Discontinuities of the Electromagnetic Field. Numerical Modeling of Electrodynamic Processes in the Surface Layer
and Conditions on the Boundaries in the Presence of Strong Discontinuities of the Electromagnetic Field. Numerical Modeling of Electrodynamic Processes in the Surface Layer
2.2.1. Introduction
During the interaction of an external magnetic field and magnetic abrasive particles, the particles are magnetized, and magnetic dipoles with the moment oriented predominantly along the field are formed. “Chains” along the force lines of the field [22] [23] appear that periodically act on the processable surface with a frequency ω = l/v. A fixed elemental area of the material periodically experiences the effect of the magnetic field of one direction. Actually, the frequency and duration of the pulse will be still higher because of the rotation of the magnetic abrasive particle due to the presence of the moment of forces on contact and of the friction of the particle against the processable part. In what follows, we will not take into account the effect of rotation.
We assume that the particle velocity on the polisher is v. If the particle radius is r, then the angular frequency is ω = 2πv/r, and precisely this frequency determines the frequency of the effect of the variable magnetic field component due to the fact that for a ferromagnetic μ > 1. The magnetic permeability μ of ferromagnetics, which are usually used in magnetoabrasive polishing, is measured by thousands of units in weak fields. However, in polishing, the constant external magnetic field is strong and amounts to 105 - 106 A/m, and in this case the value of μ for compounds of iron and nickel and for Heusler alloy decreases substantially.
Because of the presence of a strong external magnetic field H0 the “small” absolute value of μ of an abrasive particle leads to a periodic “increase” and “decrease” in the normal component of the magnetic induction near the processable surface. In the present work we used neodymium magnets (neodymium-iron-boron) with H0 > 485,000 A/m. The magnetic permeability of a magnetic abrasive particle based on carbonyl iron was assumed in this case to be equal to μ1 = 100.
Due to the continuity of the normal magnetic induction component Bn1 = Bn2, where Bn1 = μ1μ0H1; Bn2=μ2μ0H2. For example, in glasses (μ2 = 1; therefore at the boundary of contact of the glass with the magnetic abrasive particle an additional variable magnetic field of strength H1 > H0 appears.
In [24] -[27] (Levin, M. N. et al., 2003; Orlov, A. M. et al., 2001; Makara, V. A. et al., 2001; Rakomsin, 2000), magnetic field-induced effects in silicon are considered: a nonmonotonic change in the crystal lattice parameters in the surface layer of silicon, the gettering of defects on the surface, the change in the sorption properties of the silicon surface, and the change in the mobility of the edge dislocations and in the microhardness of silicon.
In [28] -[30] (Golovin, Yu. I. et al.; Makara ,V. A. et al., 2008; Orlov, A. M. et al., 2003), the influence of an electromagnetic field on the domain boundaries, plasticity, strengthening, and on the reduction of metals and alloys was established.
In view of the foregoing, it is of interest to find the relationship between the discrete-impulse actions of a magnetic field of one direction on the surface layer of the processable material that contains domains. According to [22] (Shul’man, Z. P. & Kordonskii, V. I., 1982), the size of domains is as follows: 0.05 μm in iron, 1.5 μm in barium ferrite; 8 μm in the MnBi compound, and 0.5 - 1 μm in the acicular gamma ferric oxide. According to [31] (Akulov, 1961), the size of a domain may reach 10−6 cm3 (obtained by the method of magnetic metallogra- phy).
As a rule, an abrasive exhibits a distinct shape anisotropy, whereas the frequency of the effect is determined by the concentration of abrasive particles in a hydrophobic solution and by the velocity of its motion. We as- sume that on the surface of a processable crystal the magnetic field strength H(t) = H1sin4(ωt) + H0.
It is required to find the value of the magnetic field strength in the surface layer that has the characteristics λ1, ε1, and μ1 and contains domains with electrophysical properties λ2, ε2, and μ2. The domains may have the form of a triangular prism, a bar, a cylinder, etc.
2.2.2. Physicomathematical Model. Wave Equation for ![]()
We consider interaction of a nonstationary magnetic field with substance on an example of a specific technology of magneto-abrasive polishing based on use of magneto-rheological suspension. We will formulate a physico- mathematical model of propagation of electromagnetic waves in a heterogeneous medium. The media in contact are considered homogeneous. We operate with the operator rot on the left- and right-hand sides of the first equa- tion for the total current (see Equation (6)) and multiply by μ0μ; then we differentiate the second equation in equation (see Equation (7)) with respect to time. Taking into consideration the solenoidality of the magnetic field (see Equation (7)) and the rule of repeated application of the operator ∇ to the vector H, we obtain
![]() (38)
(38)
In the Cartesian coordinates equation (see Equation (38)) will have the form
![]() (39)
(39)
![]()
![]()
One fundamental electromagnetic field equation is the equation![]() . The use of the Dirichlet theorem for approximation of the value of the magnetic field strength on the boundaries between adjacent media analogously to that of the electric field strength does not necessarily guarantees the observance of the condition of sole modality of the magnetic field; furthermore, the magnetic properties of heterogeneous media were assumed constant in deriving generalized wave equations. The experience of numerical calculations has shown that when it is necessary to model non stationary magnetic phenomena it is better in many cases to use a generalized wave equation for
. The use of the Dirichlet theorem for approximation of the value of the magnetic field strength on the boundaries between adjacent media analogously to that of the electric field strength does not necessarily guarantees the observance of the condition of sole modality of the magnetic field; furthermore, the magnetic properties of heterogeneous media were assumed constant in deriving generalized wave equations. The experience of numerical calculations has shown that when it is necessary to model non stationary magnetic phenomena it is better in many cases to use a generalized wave equation for![]() , accordingly expressing
, accordingly expressing ![]() by
by ![]() and, if need be, to perform backward recalculation to
and, if need be, to perform backward recalculation to![]() . This approach is difficult to apply to modeling of heterogeneous media with different magnetic properties, when the magnetic permeability µ is dependent on coordinates.
. This approach is difficult to apply to modeling of heterogeneous media with different magnetic properties, when the magnetic permeability µ is dependent on coordinates.
In media with a weak heterogeneity where μ(x, y, z) is a piecewise continuous quantity, the application of the proposed method of through counting is quite justified. Indeed, the system of equations (see Equations (13)-(15), (39)) yields that the function’s discontinuity on the boundaries between adjacent media is determined by the complexes which will be called the generalized permeability ![]() and the generalized conductivity
and the generalized conductivity![]() . Using the Direchlet theorem for
. Using the Direchlet theorem for ![]() and
and![]() , we obtain their values on the boundaries between adjacent media and the values for the electric field strength at the discontinuity point (see Equation (37)); here, we note that the value of the electric field strength is obtained without solving Maxwell equations. In fact, at the discontinuity point, we use linear interpolation of the function to obtain the values of
, we obtain their values on the boundaries between adjacent media and the values for the electric field strength at the discontinuity point (see Equation (37)); here, we note that the value of the electric field strength is obtained without solving Maxwell equations. In fact, at the discontinuity point, we use linear interpolation of the function to obtain the values of![]() ,
, ![]() , and
, and
![]() . Consequently, for piecewise continuous quantity μ(x, y, z), the application of
. Consequently, for piecewise continuous quantity μ(x, y, z), the application of
the proposed method of through counting is justified. We note that the equality of the derivatives of the electric field strength along the normal to the surface at the discontinuity point according to equation (see Equation (34b)) holds. When the wave equation for ![]() is used for media with different magnetic permeabilities the condition of equality of the derivatives fails, i.e.,
is used for media with different magnetic permeabilities the condition of equality of the derivatives fails, i.e.,
![]()
which is a consequence of equation (see Equation (10)); therefore, the use of through-counting schemes for the wave equation for ![]() is difficult.
is difficult.
Moreover, reformulation of the boundary conditions for Equations (1.39), with electric field strength being eliminated from the boundary conditions, does not even allow prediction of the surface current direction. Indeed, magnetic field strength ![]() is an axial vector which on substitution
is an axial vector which on substitution ![]() must remain constant. The value of the surface current also cannot be determined without knowledge of the polar vector of electric field strength.
must remain constant. The value of the surface current also cannot be determined without knowledge of the polar vector of electric field strength.
The generalized wave equation for ![]() contains the term
contains the term ![]() which directly allows for the influence of induced surface charges on the propagation of waves, the right-hand side of the generalized wave equation has the same form as the equations of the linear elasticity theory, hydrodynamics. We note that the proposed method of calculation can be used on condition that there are no built-in space charges and extraneous electro- motive forces [13] (Grinberg, G. A. & Fok, V. A., 1948).
which directly allows for the influence of induced surface charges on the propagation of waves, the right-hand side of the generalized wave equation has the same form as the equations of the linear elasticity theory, hydrodynamics. We note that the proposed method of calculation can be used on condition that there are no built-in space charges and extraneous electro- motive forces [13] (Grinberg, G. A. & Fok, V. A., 1948).
By virtue of what has been stated above, for modeling of the propagation of electromagnetic waves in glasses having roughness and defects, we used system (see Equations (13)-(15)) with boundary conditions (see Equa- tions (24)-(34)).
2.2.3. Results of Numerical Simulation
The physicomathematical model developed can also efficiently be used in modeling the propagation of electromagnetic waves in media with complex geometries and strong electromagnetic field discontinuities.
The transverse cut of a cellular structure represents a set of parallelepipeds and triangular prisms of various cross sections, as depicted in Figure 10 and Figure 11. An electromagnetic wave propagates across the direction of parallelepipeds and triangular prisms (channels) along the coordinate x.
The size of the investigated two-dimensional object is 14 × 20 ´ 10‒6 m, and the sizes of the domains are 2 - 4 μm. The frequency of the influence of the magnetic field is ω = 2π ×106, and the strength of the field is
![]() (40)
(40)
The electrophysical properties are as follows: of the large parallelepiped, μ = 1, ε = 8, σ = 10‒9 Ω∙m; of domains, μ = 1, ε = 6, σ = 10‒8 Ω∙m. They correspond to the electrophysical properties of glasses.
It was assumed that in a layer of thickness 15 - 20 μm an electromagnetic wave propagates without attenuation; therefore, on all the faces of the large parallelepiped the fulfillment of condition (see Equation (40)) was considered valid. On the faces of the parallelepiped that are parallel to the OX axis condition (see Equation (40)) corresponded to the “transverse” tangential component of the wave; on the faces parallel to OY condition (see Equation (40)) corresponded to the normal component of the field.
The calculations were carried out with a time step of 10‒13 sec up to a time instant of 10‒10 sec.
Figure 10 and Figure 11 present the amplitude values of the magnetic field strength along Hx and Hy with a comparison scale, present the corresponding isolines. An analysis of these Figures shows that at the places of discontinuity, on the wedges, force lines of the electromagnetic field concentrate. According to [32] (Akulov, N. S., 1939), precisely wedges are often the sources and sinks of the vacancies that determine, for example, the
![]()
Figure 10. Amplitude Hx of the magnetic field strength.
![]()
Figure 11. Amplitude Hy of the magnetic field strength.
![]()
![]() (a) (b)
(a) (b)
Figure 12. Amplitude Hx and Hy of the magnetic field strength.
hardness and plasticity of a solid body.
Also, we modeled the propagation of waves in media, when domains possess magnetic properties. We as- sumed, in the calculations, that μ = 100; the remaining parameters correspond to the previous example of solution (Figure 12).
Of interest is the interaction of the electromagnetic wave with the rough surface shown in Figure 13 and Figure 14. As in the previous examples, we observe the concentration of electromagnetic energy on angular structures.
From Figure 13 and Figure 14, it is seen that electromagnetic heating of tapered structures may occur in addition to mechanical heating in magnetic abrasive machining.
As we have mentioned above, for investigation of the propagation of electromagnetic waves in nonmagnetic materials, it is more expedient to use the generalized equation for![]() . For the purpose of illustration we give an example of numerical calculation of an optical knife with the wave equation for
. For the purpose of illustration we give an example of numerical calculation of an optical knife with the wave equation for ![]() (Figure 15).
(Figure 15).
From Figure 15, it is seen that the actual problem of diffraction on the optical knife remains to be solved, i.e., there is no “glow” on the optical-knife section, which is inconsistent with experimental data.
As is known [33] (Bazarov, 1991), in thermodynamically equilibrium systems the temperature T and the electrical φ and chemical μc potentials are constant along the entire system:
![]() (41)
(41)
If these conditions are not fulfilled (grad T ≠ 0, grad φ ≠ 0, grad μc ≠ 0), irreversible processes of the transfer
![]()
Figure 13. Amplitude Hx of the magnetic field strength.
![]()
Figure 14. Amplitude Hy of the magnetic field strength.
of mass, energy, electrical charge, etc. appear in the system.
The chemical potential of the j-th component is determined, for example, as a change of the free energy with a change in the number of moles:
![]() (42)
(42)
where
![]() (43)
(43)
The last term in equation (see Equation (43)) takes into account the change in the free energy of a dielectric due to the change in the magnetic induction. The free energy of a unit volume of the dielectric in the magnetic field in this case has the form
![]() (44)
(44)
We assume that changes in the temperature and volume of the dielectric are small. Then the mass flux is determined by a quantity proportional to the gradient of the chemical potential or, according to equation (see
![]()
![]() (a) (b)
(a) (b)
Figure 15. Amplitude Hx and Hy of the magnetic field strength.
Equation (43)), we obtain
![]() (45)
(45)
where ![]() is the density of the magnetic field in the unit volume of the dielectric.
is the density of the magnetic field in the unit volume of the dielectric.
In magnetic abrasive polishing on the sharp protrusions of domains the gradients of magnetic energy are great, which can lead to the origination of vacancy flows.
An analysis of the results shows that the nonstationary component of the full electromagnetic energy is also concentrated in the region of fractures and wedges, i.e., at the sharp angles of domains, which may lead to the improvement of the structure of the sublayer of the treated surface due to the “micromagnetoplastic” effect. Maximum values of the nonstationary part of the total electromagnetic energy Wmax in the sublayer correspond to a maximum value of the function sin (2π ´ 106t) and occur for the time instants t = (n/4)10‒6 sec, where n is the integer, with the value of Wmax for a neodymium magnet and a magnetoabrasive particle on the basis of carboxyl iron amounting to a value of the order of (see Equations (5)-(6)) × 106 J/m3 . Having multiplied Wmax by the volume of a domain, vacancy, or atom, we may approximately obtain the corresponding energy. The density of the electromagnetic energy in all of the cases is muchsmaller than the bonding energy of atoms, 10‒18 - 10‒19 J. However, a periodic change in the magnetic field in one direction leads to a ponderomotive force that may influence the motion of various defects and dislocations to create a stable and equilibrium structure of atoms and molecules in magnetic abrasive polishing and, in the long run, in obtaining a surface with improved characteristics due to the “micromagnetoplastic” effect. The result of Para 2.2 were published in part [34] (Grinchik, N. N. et al., 2010).
3. Ion Conductors. New Closing Relations on the Boundaries of Adjacent Media
3.1. Diffusion Electric Phenomena in Electrolytes
The medium under discussion is assumed to consist of a non-ionized solvent, an electrolyte in the form of ions and uncharged components. At first we consider infinitely diluted electrolytes when molecules are completely dissociated into cations and anions.
In a solution, ions are transferred by convection, diffusion, and migration in the presence of an electric field. Derivation of the equation for ion migration is based on the following considerations. In a solution with molar concentration n and diffusion coefficient Di let there be ions with charge zi. When an ion is exposed to an electric field with intensity E applied to the solution, the ion experiences the force zieE, which brings it into motion. The ion velocity is related to this force by the usual expression known for the motion of particles in a viscous medium:
![]() (46)
(46)
where ![]() is the ion mobility. The latter may be expressed in terms of the diffusion coefficient using the known Einstein relation:
is the ion mobility. The latter may be expressed in terms of the diffusion coefficient using the known Einstein relation:
![]() (47)
(47)
The total flux of ions of the i-th kind in a moving medium in the presence of diffusion and migration is determined by the Nernst-Planck equation:
![]() (48)
(48)
Formulas (see Equations (46) and (47)) have, in fact, a limited sphere of applicability. Indeed, A. Einstein’s work [35] (Einstein, 1966) is concerned only with the diffusion of a neutral impurity with its small concentration in a solution when the usual relations of hydrodynamics are valid for a flow around a sphere.
In the physics of plasma, formulas (see Equations (46) and (47)) are based on other considerations and pro- vided the plasma is weakly ionized, i.e., particles move independently of each other. Here, only the collision of charged particles with neutral ones is taken into account [36] (Golant, V. E. et al., 1977).
In [37] [38] (Kharkats, 1988; Sokirko, A. & Kharkats, Yu., 1989), for describing the diffusion and migration of ions in a partially dissociated electrolyte it is suggested to take into consideration their transfer by neutral molecules. In the theory developed by Yu. I. Harkats (Kharkats, 1988) [37] the expression for the total flux of ions is
![]() (49)
(49)
The last term in equation (see Equation (49)) takes into account ion transfer by a flux of neutral molecules; here the concentrations of anions, cations, and neutral dissociated molecules are determined by the chemical equilibrium conditions
![]() (50)
(50)
where β is the dissociation equilibrium constant. If the degree of dissociation at the prescribed total concentra- tion n is α, then nA = (1 ‒ α)n and, consequently,
![]() (51)
(51)
The dissociation constant β, unlike the degree of dissociation, must not depend on concentration. However, in real partially dissociated electrolytes those arguments for α and β are in rather poor agreement with experiment. In [39] (Gibbs, 1982) the dissociation degree for HCl is listed in Table 1 as a function of concentrations, calcu- lated in terms of measured electric conductivity α1 and e.m.f. α2.
Inspection of the table reveals that the dissociation degrees obtained by different experimental methods coin- cide best in the case of dilute solutions. In the high-concentration range of the electrolyte, α2 even exceeds unity, which, naturally, has no physical sense.
According to the Arrhenius theory the dissociation constant β for the given electrolyte at the prescribed tem- perature and pressure must remain constant independently of the solution concentration. In [40] (Antropov, L. N., 1984), the dissociation constants of some electrolytes are given at their different concentrations. Only for very weak electrolytes (solutions of ammonia and acetic acid) does the dissociation constant remain more or less constant on dilution. For strong electrolytes (potassium chloride and magnesium sulfate), it changes by several- fold and in no way may be considered a constant.
![]()
Table 1. The degree of HCl electrolytical dissociation in terms of measured electric conductivity α1 and e.m.f. α2.
Of course, one may formally take into account the dependence of the dissociation constant on the electrolyte concentration and use it in the modified Nernst-Planck equation (see Equations (49) and (50)) but the main drawback in describing separately the diffusion and migration of ions in an electrolyte, in D. I. Mendeleev’s opinion, lies in the fact that the interaction of particles of a dissolved substance between each other as well as with solvent molecules is neglected. Also, he has pointed out that not just the processes of formation of new compounds with solvent molecules are of importance for solutions. D. I. Mendeleev’s viewpoints have been extended by A. I. Sakhanov (Antropov, L. N., 1984), who believed that in addition to the usual dissociation reaction in an electrolyte solution there also proceeds associating of simple molecules. Molecular associations dissociate, in their turn, into complex and simple ions. In this case equation (see Equation (49)) will not hold mainly because of the fact that the expressions for diffusion, migration, and nondissociated flows of molecules must be determined relative to some mean liquid velocity. In concentrated solutions, this velocity does not coincide with the solvent velocity and must be determined from the fluid dynamics equations of a multicomponent mixture in which characteristics of its components (physical density, charge, diffusion coefficient of a complex ion) are, in fact, unknown. This is a reason why the theory of diffusion and migration of ions for a partially dissociated electrolyte solution, with a current traversing through it, encounters crucial difficulties. Besides, it is rather dif- ficult to take an account of the force interaction of complex cations and anions between each other and with an external electric field. Therefore Einstein’s formula (see Equation (46)) will also change its form.
The main drawbacks of the theory of electrolytic dissociation are fully defined in collected papers “Funda- mental Principles of Chemistry” by D. I. Mendeleev as well as in [40] [41] (Antropov, L. N., 1984; Hertz, 1980).
In our opinion, the principal disadvantage of the approaches considered above lies in the fact that the Nernst- Planck equation as well as its modified form for a partially dissociated electrolyte (see Equation (49)) are based on the hydrodynamic theory of diffusion. We shall substantiate below that it is more reasonable to use the equa- tions of thermodynamics of irreversible processes.
When applying the Nernst-Planck equation (see Equation (48)) and its modified forms (see Equation (49)), it is implicitly postulated that cations and anions in the electrolyte solution are different components. The equa- tions of transfer of cations and anions are written separately. On the other hand, the commonly used equation of electroneutrality does not ensure, according to Gibbs [39] (Gibbs, 1982), the independence of differentials of cations dni and anions dne in a volumetric electrolyte solution their changes are functionally related and there- fore they are identical, indiscernible components.
3.1.1. The Case of a Current Traversing a Binary Fully Dissociated Electrolyte
Let us write system of equations (see Equation (48)) in the form
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
Analogously to [39] (Gibbs, 1982), instead of concentrations ne and ni we introduce the molar concentration related to ne and ni by the expressions
![]() (55)
(55)
Expressing ne and ni in equations (see Equations (52) and (53)) in terms of the molar concentration, we arrive at the following expression for the function C:
![]() (56)
(56)
where
![]() (57)
(57)
is the diffusion coefficient of a salt or the effective diffusion coefficient of a binary electrolyte. Expressing the concentrations ne and ni in terms of the molar concentration C we find the expression for the vector of current density J (Levich, 1959) [42] :
![]() (58)
(58)
In [43] (Neumann, 1977) it is shown that by its meaning Def is a coefficient of molecular diffusion. For instance, the diffusion coefficients of copper sulfate have an intermediate value between the diffusion coefficients of copper and sulfate ions; if De = 0.173 ´ 10‒9 m2/sec and Di = 1.065 ´ 10‒9 m2/sec, then Def = 0.854 ´ 10‒9 m2/sec. However, expression (see Equation (57)) does not offer an explanation of the abnormally high mobility of H and OH ions when their displacement proceeds by a croquet-like mechanism (Skorcheletti, 1969) [44] .
In the system of equations (see Equations (56)-(58)) no symmetry of cross terms is observed; therefore, it is difficult to take into account “the superposition effects”. Indeed, from equation (see Equation (58)) it is evident that the molar concentration gradients VC exert an influence on the current J. On the other hand, one can see from equation (see Equation (56)) that an electric field has no effect on the diffusion of the molecules, and therefore the Onsager reciprocal relation is disturbed.
One may raise the objection that according to the Nernst-Planck equations it follows that the concentration gradients of cations and anions exert an influence on the potential distribution of an electric field (Levich, 1959) [42] :
![]() (59)
(59)
However relation (see Equation (59)) itself has been derived by Neumann [43] (Neumann, 1977) on the assumption that the resultant current does not depend on the mass flow.
On derivation of the equations for diffusion and migration of ions in a volumetric electrolyte solution we shall employ the relations of the thermodynamics of irreversible processes.
Finally, it is worthy of note that in plasma physics there is also no symmetry of “the superposition effects” in describing the ambipolar diffusion of ions, and the theory is based on the hydrodynamic model [36] (Golant, V. E. et al., 1977).
In investigating the dynamics of an electron-hole semiconductor plasma, the hydrodynamic model (see Equations (52)-(54)) is also used.
In our opinion, electric field-induced transfer of charges entails transfer of their kinetic energy as well as of heat and mass, and conversely, mass or heat transfer may simultaneously cause, if we are concerned with the system of charged particles, charge transfer and give rise to an electromotive force.
3.1.2. Conclusion
To phenomenologically describe diffusional-electrical phenomena in electrolytes it is suggested to use the me- thods of the thermodynamics of irreversible processes, rather than the hydrodynamic theory of diffusion of ions, for the experimentally observable thermodynamic flows and forces without clear discernment and identification of real ion flows and mobilities.
3.2. Landau Model
In what follows we consider ion conductors that contain the electrolytic plasma with a fairly high concentration of charged particles. The interaction of the charged plasma particles with the external electromagnetic field and their collective interaction can theoretically be investigated completely only on the basis of the Boltzmann ki- netic equation with a self-consistent field. In this probabilistic approach to the phenomena under study, one in- troduces characteristics that are average over a large ensemble of particles and are always related to the intro- duction of additional hypotheses on the properties of particles and their interactions and to the simplification of these properties and interactions. We note that in many cases, e.g., when the electrolytic plasma in liquid elec- trolytes is considered, there is even no basis for constructing such methods. The developed methods are usually not an efficient means of solving problems by virtue of the excessive complexity of corresponding equations.
Another general method is construction of a phenomenological macroscopic theory based on the general regularities and hypotheses obtained experimentally; this precisely method will be developed in the present work. For many problems of applied character, consideration of a plasma as a conducting gas is sufficient. Such approximation is strictly justified only in the case of a dense plasma when the free path of charged particles is much smaller than the characteristic dimension of the system and particle collisions are of crucial importance. The velocity distribution of particles is Maxwellian; at each point, it is fully determined by the local values of density, temperature, and macroscopic velocity. With these conditions being observed, we can carry out, in a unified context, macroscopic phenomenological description of a gas medium, a metal and dielectric plasma, a plasma in a liquid electrolyte, or an electrolytic plasma.
The necessary condition of existence of the state of local thermodynamic equilibrium (LTE) of a plasma is high frequency of collisions of plasma particles (maxwellization) so that the plasma state undergoes no marked changes over the period between collisions on the mean free path. The observance of this condition means the following: 1) the electrons have time to transfer the energy received from the electrostatic field to heavy parti- cles; 2) ionization processes are nearly totally counterbalanced by recombination (the Saha equation holds true); 3) the overwhelming part of excited atoms gives up its energy in collisions; 4) energy exchange between parti- cles dominates the processes in which the plasma energy markedly grows or diminishes.
In the LTE plasma state, it is only the radiation field (photons) that is not in equilibrium with the plasma, but the energy loss by radiation is minor in a number of cases compared to other mechanisms of energy transfer. With allowance for the assumptions enumerated above, the plasma electrodynamics can be described by Max- well continuity, motion, and energy equations [45] (Landau, L. D. & Lifshits, E. M., 1982). For macroscopic description of transfer processes in ion conductors, we will use the equations of thermodynamics of irreversible processes without separating explicitly ion carriers.
The possibility of such description was first suggested by L.D. Landau. This approach which has been sub- stantiated above does not provide for the introduction and determination of the coefficients of molecular diffu- sion of cations and anions and of the degree of dissociation in an ion conductor. It is conditioned by the interac- tion of the mass and charge fluxes. The ion fluxes are not determined. The density of the conduction current Jq, the mass flux Jm, and the heat flux JT for the medium’s nonequilibrium state has the form (Landau, L. D. & Lifshits, E. M., 1982) [45] .
![]() (60)
(60)
where DM is the coefficient of molecular diffusion, ![]() is the coefficient of ambipolar diffusion,
is the coefficient of ambipolar diffusion, ![]() is the coefficient allowing for heat transfer by the impurity motion, β is the coefficient of specific electrical ambipolar conductivity due to
is the coefficient allowing for heat transfer by the impurity motion, β is the coefficient of specific electrical ambipolar conductivity due to![]() , and П is the Peltier coefficient.
, and П is the Peltier coefficient.
3.3. Interaction of Nonstationary Electric, Thermal, and Diffusion Fields with Allowance for Mass Transfer in a Layered Medium with the Example of an Electrochemical Cell
3.3.1. Introduction
Investigation of the interaction of electric and thermal fields with allowance for mass transfer and contact phenomena is a complex and topical problem of the theory and practice of various fields of natural science and technology.
The work seeks to construct a physicomathematical model of the interaction of nonstationary electric fields in a layered medium with allowance for nonstationary thermal phenomena and mass transfer without explicit separation of charge carriers. The media in contact are considered to be homogeneous. For the sake of clear representation, we will consider two-layer one-dimensional models.
3.3.2. Interaction of Electric and Thermal Fields
In different substances, the processes of transfer of charge and energy are interrelated. The quantity of the released heat is determined by Joule heating and by the effects of Thomson and Peltier. The problem of interaction of nonstationary thermal phenomena has been considered in [46] (Tsurko, 1999) without taking into account the Thomson effect.
According to [45] (Landau, L. D. & Lifshits, E. M., 1982), the expressions for the conduction-current density and the energy-flux density in the absence of an external magnetic field or in the case of its slight influence have, respectively, the form
![]()
where a(T) is the specific thermoelectromotive force, П = αT is the Peltier coefficient, φ is the potential, and k(T) is the thermal-conductivity coefficient. We note that the problem is always nonlinear.
Having eliminated the magnetic-field strength from system (see Equations (13)-(15)) according to one method of [47] -[49] (Shvab, 1994; Shvab, A. I. & Imo, F., 1994; Grinchik, N. N. et al., 1997), we obtain the equation for the electric-field strength
![]() (61)
(61)
The heat-balance equation has the form [45] (Landau, L. D. & Lifshits, E. M., 1982)
![]() (62)
(62)
At the interface, the following relation [50] (Tamm, 1976) holds:
![]() (63)
(63)
Here ε is the permittivity, c2 = l/(ε0・μ0), μ is the magnetic permeability, ε0 is the electric constant, μ0 is the magnetic constant, cpρ is the product of the specific heat of the medium by its density, and β(T) = ∂α(T)/∂T.
In deriving equation (see Equation (62)), use has been made of the condition of local electroneutrality of the substance. We give a differential formulation of the problem and the method of its solution in greater detail.
Let us investigate, on the segment![]() , the contact of homogeneous media 1 and 2 with different electrophysical properties. The quantities ε, λ, μ, E, and φ have discontinuities of the first kind at the point of the interface x = ξ. We will consider the case of plane contact where the influence of surface currents can be disregarded and the thickness of the electric double layer is much smaller than the characteristic dimension of the object. We set E = ?gradφ. Equations (see Equations (61) and (62)) for the one-dimensional problem will take the form
, the contact of homogeneous media 1 and 2 with different electrophysical properties. The quantities ε, λ, μ, E, and φ have discontinuities of the first kind at the point of the interface x = ξ. We will consider the case of plane contact where the influence of surface currents can be disregarded and the thickness of the electric double layer is much smaller than the characteristic dimension of the object. We set E = ?gradφ. Equations (see Equations (61) and (62)) for the one-dimensional problem will take the form
![]() (64)
(64)
![]() (65)
(65)
Conditions (see Equations (41) and (63)) will be written, respectively, in the form
![]() (66)
(66)
![]() (67)
(67)
By differentiating (see Equation (66)) with respect to time and taking into account (see Equation (67)), at the phase boundary we obtain the condition of equality of the total currents
![]() (68а)
(68а)
Here and in what follows, for the arbitrary function f we adopt the notation
![]()
Equality (see Equation (66)) is a corollary of the relation ![]() [50] (Tamm, 1976). Taking into
[50] (Tamm, 1976). Taking into
consideration the finiteness of the value of the space electric charge and the continuity of it, in the one-dimen- sional case we obtain
![]() (68b)
(68b)
Relations (see Equation (68)) reflect the laws of conservation and continuity of electric charge [45] [50] (Landau, L. D. & Lifshits, E. M., 1982; Tamm, 1976). At the contact point, we also have the equality of the temperatures and the energy fluxes (Landau, L. D. & Lifshits, E. M., 1982):
![]() (69a)
(69a)
![]() (69b)
(69b)
Thus, in the presence of the interaction of the electric and thermal fields in a layered medium, the equality of the charge fluxes (see Equation (68a)), the equality of the charges (see Equation (68b)) (when the conditions of quasineutrality of the contacting media beyond the electric double layer are satisfied), the equality of the tem- peratures (see Equation (69a)), and the equality of the energy fluxes must be fulfilled at the interface of the me- dia. In the relations for the charge and energy fluxes, we take into account cross thermoelectrical phenomena.
The process of charge of the electric field is considered on the finite time interval [0 ≤ t ≤ t0]. The initial con- ditions have the form
![]() (70)
(70)
We give the boundary conditions, for example, for the value x = 0. We set the value of the total-current den- sity to be known
![]() (71)
(71)
and take into account the heat exchange at the boundary using the Newton relation
![]() (72)
(72)
where γ1 is the coefficient of heat exchange and T* is the ambient temperature. We consider the analogous relations at the right-hand boundary.
3.3.3. Interaction of Electric and Thermal Fields with Allowance for Mass Transfer
Let us consider the nonstationary model of heat and mass transfer for electrochemical systems with the example of electrolysis. For this problem, an electric double layer occurs at the site of contact of the electrolyte with the metallic anode and cathode. Let us set the density of the space charge beyond the electric double layer of the metal-electrolyte contact to be zero at the initial instant and hence, according to [51] (Stratton, 1938), remain constant in the future while the voltage drop in the electrodes and leads is small. The influence of the electrodes on the temperature field of the electrolyte will be taken into account in terms of the coefficient of heat exchange.
Two approaches to modeling of diffusion-electrical phenomena have currently been developed, each of which has certain disadvantages and advantages. The first approach [37] [38] [42] (Levich, 1959; Kharkats, 1988; Sokirko, A. & Kharkats, Yu., 1989) is characterized by consideration of the flows of ions of the corresponding sort in a completely or partially dissociated electrolyte. The equations derived contain many parameters, the re- liable procedure of determination of which is absent in the majority of cases. Furthermore, the proposed theory fails to provide for taking into account the interaction of the cations and the anions of the dissolved substance with each other and with the molecules of the solvent. It must also be borne in mind that, apart from the disso- ciation reaction, we have the association of simple molecules which in turn are dissociated into complex and simple ions. It is difficult to determine the diffusion coefficients of complex ions; it is also difficult to take into account the force interaction of complex cations and anions with each other and with the external electric field. The difficulties in question become more serious when a multicomponent electrolyte is described. We note that such difficulties also arise in modeling, for example, certain problems of plasma physics.
The second approach [52] -[56] (Grinchik, 1993; Grinchik, N. N. et al., 2000; Grinchik, N. N.; Muchinskii, A. N. et al., 1998; Grinchik, N. N. et al., 1998) fails to provide for the introduction and determination of the coeffi- cients of molecular diffusion of cations and anions and the degree of dissociation of the electrolyte. It is based on the interaction of the mass and charge fluxes. The ionic flows are not determined.
The system of equations describing the electrodynamic processes in the electrolyte is as follows:
![]() (73)
(73)
Here Iq, Im, and IT are the densities of the conduction current and of the mass and heat fluxes which (in the case of the nonequilibrium state of the medium) have, respectively, the form (see Equation (60)) [45] (Landau, L. D. & Lifshits, E. M., 1982), where DM is the molecular diffusion coefficient, ![]() is the ambipolar diffusion coefficient, DT is the thermal diffusion coefficient,
is the ambipolar diffusion coefficient, DT is the thermal diffusion coefficient, ![]() is the coefficient taking into account the transfer of heat due to the motion of the impurity, and n is the concentration of the impurity.
is the coefficient taking into account the transfer of heat due to the motion of the impurity, and n is the concentration of the impurity.
We give the initial
![]() (74)
(74)
and boundary conditions (anode-electrolyte, x = 0)
![]() (75)
(75)
![]() (76)
(76)
![]()
in modeling the one-dimensional problem in the region![]() . Here ka is the electroche- mical equivalent of a substance which deposits at the anode. The analogous conditions hold for x = l as well.
. Here ka is the electroche- mical equivalent of a substance which deposits at the anode. The analogous conditions hold for x = l as well.
The constructed system of differential equations makes it possible to model the processes of transfer in the electrochemical system with allowance for the influence of an electric double layer; this influence directly de- termines the thermoelectrical and ambipolar electrodiffusion phenomena at the boundary of the metal-electrolyte contact.
3.3.4. Numerical Modeling of Electrochemical Systems. Heating of an Electrochemical Cell in the Case of Constant-Current and Pulse Electrolysis
In electrochemical systems, the electrodes are metals as a rule. The electrical conductivity of metals is hundreds of times higher than the specific electrical conductivity of electrolytes; therefore, one can disregard the voltage drop in electrodes and leads. In highly conductive metals, one can also disregard the displacement currents and the coefficients of ambipolar diffusion and thermal diffusion and restrict oneself to consideration of the system of equations (see Equations (73)-(76)) just in the electrolyte itself.
Let us consider the process of heating of an electrochemical medium in the case of passage of an electric cur- rent with density Iq(t) through a solution of copper sulfate CuSO4・5H2O. We use copper (99.78%) as the anode. The copper from the solution is deposited at the cathode. We set the current efficiencies for the copper equal to 100% and the electrochemical equivalent ke equal to 0.6588 ´ 10−6 kg/C. The dependence of the specific elec- trical conductivity λ(n) of the copper-plating electrolyte on the concentration of the copper sulfate in water is given in [57] (L. N. Antropov, 1989); the dependence of λ and k on the temperature will be considered to be in- significant. In the calculations for CuSO4, we set DM = 5 ´ 10‒10 m2/sec, ![]() ,
, ![]() , ε = 70, and μ = 1 and disregard the effects of thermal diffusion. The distance between the cathode and the anode is L = 0.05 m. The heat capacity, the density, and the thermal-conductivity coefficient of the electrolyte are taken to be 4.2 ´ 103 J/(kg・K), 103 kg/m3, and 0.6 V/(m・K) respectively. We note that the regimes of pulse action have been con- sidered in (Kostin, N. A. &Labyak, O. V., 1995) as applied to the processes of electrodeposition of alloys. This investigation has been carried out on the basis of a separate description of the transport of ions and the employment of the Kirchhoff law for quasistationary currents in a cell. With such an approach, the displacement currents are taken into account indirectly through introduction of the capacitive current of the electrode and determination of the experimental dependence of the polarization capacitance of the electrode on the character of the pulse action. In [58] (Kostin, N. A. & Labyak, O. V., 1995), it has been noted that neglect of the capacitive current in pulse electrolysis involves significant errors. The employment of system (see Equations (73)-(76)) to model the process of copper plating makes it possible to consider the problems without introducing the concepts of inductance and capacitance.
, ε = 70, and μ = 1 and disregard the effects of thermal diffusion. The distance between the cathode and the anode is L = 0.05 m. The heat capacity, the density, and the thermal-conductivity coefficient of the electrolyte are taken to be 4.2 ´ 103 J/(kg・K), 103 kg/m3, and 0.6 V/(m・K) respectively. We note that the regimes of pulse action have been con- sidered in (Kostin, N. A. &Labyak, O. V., 1995) as applied to the processes of electrodeposition of alloys. This investigation has been carried out on the basis of a separate description of the transport of ions and the employment of the Kirchhoff law for quasistationary currents in a cell. With such an approach, the displacement currents are taken into account indirectly through introduction of the capacitive current of the electrode and determination of the experimental dependence of the polarization capacitance of the electrode on the character of the pulse action. In [58] (Kostin, N. A. & Labyak, O. V., 1995), it has been noted that neglect of the capacitive current in pulse electrolysis involves significant errors. The employment of system (see Equations (73)-(76)) to model the process of copper plating makes it possible to consider the problems without introducing the concepts of inductance and capacitance.
The obtained nonlinear system of equations is solved by the finite-difference method analogously to [54] (Grinchik, N. N. et al., 2000).
We have modeled numerically the process of copper plating for a constant current and a pulse current (Figure 16). The density of the constant current was equal to 300 A/m2. The maximum density of the pulse current was also 300 A/m2, while the period of traversal of the current and the break were equal to 0.01 sec.
Figure 16 gives the results of modeling the distributions of the concentration of CuS04 and the temperature for different regimes of electrolysis. The measurements were carried out within 60 sec after switching on the current. It is seen from the figure that the concentration gradients near the cathode surface (x = 1) are different and depend on the regime of copper plating. In the case of nonstationary action they are substantially smaller than in the case of electrolysis in the regime of constant current. As has been shown in [58] (Kostin, N. A. & Labyak, O. V., 1995), this tendency also holds in the case where one and the same total charge passes through the electrochemical cell.
The analysis of the temperature field (Figure 16(b)) shows that the temperatures of the electrolyte in the vi- cinity of the anode and the cathode differ significantly. Nonsymmetric heating of the electrochemical cell attrib- uted to the am-bipolar diffusion and electrical ambipolar conductivity occurs. The modeling results are in agreement with the data of (Dikusar, A. I. et al., 1989).
With the aim of measuring the temperature in the surface layer of the electrolyte solution near the cathode and comparing the results to the calculated data, we developed and manufactured an experimental setup. Copper anode and cathode were placed in an electroplating bath with a sulfuric-acid copper-plating electrolyte. In the 1-mm-thick cathode, a hole was made into which we placed a temperature-sensitive element. As the latter we employed a thermal resistor. The current strength in the bath was prescribed by a variable resistor.
Figure 17 gives the results of numerical modeling and the experimental data on heating of the cathode region in relation to the regime of current. It is seen that the increase in the density of the current (both constant and pulse) causes the temperature near the cathode surface to increase. In the anode, no increase in the temperature was observed either in the calculations or in the experiment, which is in agreement with the data of [59] (Dikusar, A. I. et al., 1989). The surface temperature obtained in solving equations (see Equations (73)-(76)) in the regime of constant current is 10% - 15% higher than the temperature recorded in the experiments.
A more complicated situation occurs when we compare the experimental data and the results of numerical modeling in the regime of pulse electrolysis. The results of the experiments demonstrate that in the regime of pulse current the temperature of the electrolyte in the cathode region increases more than in the regime of constant current. At the same time, the numerical calculations of the pulse electrolysis show that the heating of the
![]()
Figure 16. Distribution of the normalized concentration of CuSO4 and the temperature in an electrochemical cell within 60 sec after switching on the current. The solid curve, at constant current; the dashed curve, at pulse current. T, ˚C; x, mm. Distribution of the normalized concentration of CuSO4; (b) Distribution of the temperature.
![]()
Figure 17. Heating of the electrolyte in the cathode region as a function of the value and kind of polarizing current: 1) constant current; 2) pulse current; 3, 4) corresponding experimental data. ΔT, ˚C; Iq, A/m2.
cathode region here is smaller than for the regime of constant current. The difference is, apparently, attributed to concentration convection [60] (Bark, F.; Kharkats,Yu. & Vedin, R., 1998), whose influence is substantial for high densities of the current for pulse electrolysis.
In a longer term, one must take into account natural and concentration convection and heat exchange with the ambient medium. Nonetheless, despite the errors in determination of the coefficients and the assumptions made in the model, the calculation results are in qualitative agreement with the experimental data, which makes it possible, in certain cases, to use the proposed approach for modeling of nonstationary processes.
The result of Para 3 were published in part (Grinchik, N. N., 1993; Grinchik, N. N. et al., 1998; Grinchik, N. N.; Tsurko, V. A., 2002) [52] [53] [55] [56] [61] .
4. Interaction of Nonstationary Electric and Thermal Fields with Allowance for Relaxation Processes
We investigate electric and thermal fields created by macroscopic charges and currents in continuous media. Of practical interest is modeling of local heat releases in media on exposure to a high-frequency electromagnetic field. We should take into account the influence of the energy absorption on the propagation of an electromagnetic wave, since the transfer processes are interrelated.
In an oscillatory circuit with continuously distributed parameters, the energy dissipation is linked [62] (Kolesnikov, 2001) to the dielectric loss due to the dependence of the relative permittivity ε(ω) on frequency. In the general case ε is also complex, and the relationship between the electric displacement and electric field vec- tors has the form D = ε(ω)E, where![]() ; here, ε' and ε'' are determined experimentally. As of now, the problems of dielectric heating of a continuous medium are reduced in many cases to consideration of an equivalent circuit based on lumped parameters, such as capacitance, inductance, loss angle, and relative-die- lectric-loss factor [63] [64] (Skanavi, 1949; Perre, P.; Turner, I. W., 1996), that are established experimentally.
; here, ε' and ε'' are determined experimentally. As of now, the problems of dielectric heating of a continuous medium are reduced in many cases to consideration of an equivalent circuit based on lumped parameters, such as capacitance, inductance, loss angle, and relative-die- lectric-loss factor [63] [64] (Skanavi, 1949; Perre, P.; Turner, I. W., 1996), that are established experimentally.
With this approach, there arise substantial difficulties in determining the temperature field of equivalent cir- cuits. Also, we have polarization and the occurrence of an electric double layer of a prescribed electric moment in contact of media with different properties. Equivalent circuits in lamellar media additionally involve empiri- cal lumped parameters: surface capacitance and surface resistance [65] (Jaeger, 1977). The total current can al- ways be separated into a dissipative, or conduction current which is in phase with the applied voltage and a dis- placement current shifted in time relative to the voltage. The exact physical meaning of these components of the current is largely dependent on selection of an equivalent electric circuit. A unique equivalent circuit―series or parallel connection of the capacitor, the resistor, and the inductor―does not exist; it is determined by a more or less adequate agreement with experimental data.
In the case of electrolytic capacitors, the role of one plate is played by the electric double layer with a specific resistance much higher than the resistance of metallic plates. Therefore, decrease in the capacitance with fre- quency is observed, for such capacitors, even in the acoustic-frequency range [65] (Jaeger, 1977). Circuits equivalent to an electrolytic capacitor are very bulky: up to 12 R, L, and C elements can be counted in them; therefore, it is difficult to obtain a true value of, e.g., the electrolyte capacitance. In [65] (Jaeger, 1977) experi- mental methods of measurement of the dielectric properties of electrolyte solutions at different frequencies are given and ε' and ε'' are determined. The frequency dependence of dispersion and absorption are essentially dif- ferent consequences of one phenomenon: “dielectric-polarization inertia” [65] (Jaeger, 1977). In actual fact, the dependence ε(ω) is attributable to the presence of the resistance of the electric double layer and to the electro- chemical cell in the electrolytic capacitor being a system with continuously distributed parameters, in which the signal velocity is a finite quantity.
Actually, ε' and ε'' are certain integral characteristics of a material at a prescribed constant temperature, which are determined by the geometry of the sample and the properties of the electric double layer. It is common knowledge that in the case of a field arbitrarily dependent on time any reliable calculation of the absorbed en- ergy in terms of ε(ω) turns out to be impossible [45] (Landau, L. D. & Lifshits, E. M., 1982). This can only be done for a specific dependence of the field E on time. For a quasimonochromatic field, we have [45] (Landau, L. D. & Lifshits, E. M., 1982)
![]() (77)
(77)
![]() (78)
(78)
The values of Е0(t) and Н0(t), according to (Barash, Yu. & Ginzburg, V. L., 1976), must very slowly vary over the period Т = 2π/ω. Then, for absorbed energy, on averaging over the frequency ω, we obtain the expres- sion [66] (Barash, Yu. & Ginzburg, V. L., 1976)
![]() ((79)
((79)
where the derivatives with respect to frequency are taken at the carrier frequency ω. We note that for an arbi- trary function Е(t), it is difficult to represent it in the form
![]() (80)
(80)
since we cannot unambiguously indicate the amplitude а(t) and the phase φ(t). The manner in which Е(t) is de- composed into factors а and cosφ is not clear. Even greater difficulties appear in the case of going to the com- plex representation ![]() when the real oscillation Е(t) is supplemented with the imaginary part V(t).
when the real oscillation Е(t) is supplemented with the imaginary part V(t).
We have
![]()
where the amplitude![]() , the phase
, the phase![]() , and the instantaneous frequency
, and the instantaneous frequency ![]() are determined by the expressions
are determined by the expressions
![]() (81)
(81)
Consequently, the amplitude, phase, and frequency of the vibration (81) are as arbitrary as the imaginary part. If we want to accurately determine the amplitude, phase, and frequency, we must indicate the operator making the function ![]() correspond to each function
correspond to each function![]() .
.
In many cases (in particular, when a quasistationary approximation is used) one needs the slowness, smooth- ness of the functions![]() ,
, ![]() , and
, and![]() . Such smoothness is obtained in solving many prob- lems in particular, in the nonlinear vibration theory when the method of averaging or related method are used. However, the amplitude, the phase, and the frequency determined here have only been comprehended within the framework of the averaging method and have no broader meaning.
. Such smoothness is obtained in solving many prob- lems in particular, in the nonlinear vibration theory when the method of averaging or related method are used. However, the amplitude, the phase, and the frequency determined here have only been comprehended within the framework of the averaging method and have no broader meaning.
We dwell on this in greater detail. Using the representation of vibrations on a phase with coordinates
![]() , one determines the amplitude, the phase, and the frequency from the position of the representation
, one determines the amplitude, the phase, and the frequency from the position of the representation
point at it instant, i.e., from the system of the equations
![]() (82)
(82)
This is equivalent to the general definition (81) at![]() . From definition (82) it follows, however, that for
. From definition (82) it follows, however, that for
any narrow-band vibration, the functions ![]() and
and ![]() contain fast components of the frequency
contain fast components of the frequency![]() ; therefore, they are not slow (compared to
; therefore, they are not slow (compared to ![]() or
or![]() ).
).
We restrict ourselves to a simple example. For the vibration with a slow modulation amplitude
![]()
It is natural to set ![]() and
and![]() . But definition (81) leads to other expressions: accurate to terms of the order of
. But definition (81) leads to other expressions: accurate to terms of the order of![]() , we obtain
, we obtain
![]()
Thus, in the amplitude and the phase, there are fast “vibrational” terms not inherent in the initial vibration and compensating each other in the product![]() . It is axiomatic that these vibrations disappear in averaging and smooth functions
. It is axiomatic that these vibrations disappear in averaging and smooth functions ![]() and
and ![]() are obtained. However vibrational corrections should be allowed for even as a first (in
are obtained. However vibrational corrections should be allowed for even as a first (in![]() ) approximation; one has to additionally find them and frequently to redefine [67] (D. E. Vakman and L. A. Vanshtein, 1977).
) approximation; one has to additionally find them and frequently to redefine [67] (D. E. Vakman and L. A. Vanshtein, 1977).
The arising problems have been considered in [67] (Vakman, D. E. & Vanshtein, L. A., 1977) in detail. In the indicated work, it has been emphasized that certain methods using a complex representation and claiming higher-than-average accuracy become trivial without an unambiguous determination of the amplitude, phase, and frequency.
The amplitude and frequency modulation of the signals is widely used in radio engineering. As of now, there are radio-engineering devises, e.g., sweep generators, whose frequency varies by a certain law in an established frequency band. Today’s sweep generators are multipurpose devices; they have found wide use in automatic meters of SHF-channel parameters (damping, impedance). Wide-band sweep generators as solo devices are em- ployed most frequently in the range 100 - 200 mHz; here sweep generators must have various forms of modula- tion depending on the field of application.
Automatic meters of the parameters of the SHF channels must have meander modulation with a frequency of the order of 100 kHz as a rule, more rarely of 1.10 kHz.
A monochromatic wave is infinite in space and time; therefore, it carried no information and transfers no en- ergy. Under actual situations, waves, including spectral lines, have an amplitude and/or frequency modulation.
The broadening of spectral lines may be due to the interaction between the radiating atom and the surrounding particles, i.e., other atoms (molecules, ions, and electrons). Shock theory (Lorenz, Lenz, and Weiskopf) is un- derlain by the assumption that a decisive factor of line. Broadening is the violation of the coherence of vibra- tions of an atomic oscillator, and also its motion, i.e., the Doppler Effect; therefore, in actual practice, a laser beam has the broadening spectral-line, too, and is not strictly monochromatic. In developing methods and tech- niques for measurement of, e.g., relative permittivity, in particular, complex permittivity and permeability, one usually determines the resistance and the phase shift between the real imaginary parts of the resistance; volt-ampere characteristics are also studied. However, here, the signal is assumed to be monochromatic; the in- fluence of the amplitude and frequency modulation is disregarded as a rule. The influence of modulation has an effect on measurements; therefore, under other experimental conditions with another “depth” of the amplitude and/or frequency modulation (![]() and
and![]() ), electrophysical properties of a material will be different. An electromagnetic sine monochromatic wave is fiction, since transfers no energy; therefore, the characteristics of a modulated signal should be allowed for during the measurement.
), electrophysical properties of a material will be different. An electromagnetic sine monochromatic wave is fiction, since transfers no energy; therefore, the characteristics of a modulated signal should be allowed for during the measurement.
We emphasize that, generally speaking, the wave (81) does not satisfy the wave equation, i.e., the dependence on the coordinates is disregarded. In the case![]() , in passing to a complex variable for the function to be analytical, differentiable, and integrable it is necessary that Cauchy?Riemann conditions be observed. Refer- ence: if the function
, in passing to a complex variable for the function to be analytical, differentiable, and integrable it is necessary that Cauchy?Riemann conditions be observed. Refer- ence: if the function ![]() is differentiable at the point
is differentiable at the point![]() , at the point
, at the point ![]() there exist partial derivatives of the function
there exist partial derivatives of the function ![]() and
and ![]() with respect to the variables x and y ; here, we have the Cauchy-Riemann relations
with respect to the variables x and y ; here, we have the Cauchy-Riemann relations
![]()
In the case of a modulated vibration of the form
![]()
where ![]() and
and![]() , passage to a complex variable is incorrect, since no Cauchy-Riemann condi- tions are observed for the function
, passage to a complex variable is incorrect, since no Cauchy-Riemann condi- tions are observed for the function![]() ;
; ![]() is not a differentiable function and it cannot be used in Maxwell equations. In this case it is necessary to introduce a complex modulation frequency; the introduction of a complex surface current is also required, since all the functions used in Maxwell equations must be analytical.
is not a differentiable function and it cannot be used in Maxwell equations. In this case it is necessary to introduce a complex modulation frequency; the introduction of a complex surface current is also required, since all the functions used in Maxwell equations must be analytical.
Radio-engineering measurement for determinate of the multitude formal coefficients are not practical. The complex permittivity has been introduced and is used in Maxwell equations for a monochromatic field; therefore, it is difficult to allow for the “depth” of the amplitude and/or frequency pulse modulation using a complex vari- able.
Summing up the aforesaid, we can state that calculation of the dielectric loss is mainly empirical in character. Construction of the equivalent circuit and allowance for the influence of the electric double layer and for the dependence of electrophysical properties on the field’s frequency are only true of the conditions under which they have been modeled; therefore, these are fundamental difficulties in modeling the propagation and absorp- tion of electromagnetic energy.
As we believe, the release of heat in media on exposure to nonstationary electric fields can be calculated on the basis of allowance for the interaction of electromagnetic and thermal fields as a system with continuously distributed parameters from the field equation and the energy equation which take account of the distinctive features of the boundary between adjacent media. When the electric field interacting with a material medium is considered we use Maxwell equations (see Equations (6)-(7)). We assume that space charges are absent from the continuous medium at the initial instant of time and they do not appear throughout the process. The energy equation will be represented in the form
![]() (83)
(83)
where Q is the dissipation of electromagnetic energy.
According to (Choo, 1962), the electromagnetic energy converted to heat is determined by the expression
![]() (84)
(84)
In deriving this formula, we used the nonrelativistic approximation of Minkowski’s theory. If ε, μ, and ρ = const, there is no heat release; therefore, the intrinsic dielectric loss is linked to the introduction of ε'(ω) and ε''(ω). The quantity Q is affected by the change in the density of the substance ρ(T).
A characteristic feature of high frequencies is the lag of the polarization field behind the charge in the electric field in time. Therefore, the electric-polarization vector is expediently determined by solution of the equation ![]() with allowance for the time of electric relaxation of dipoles τe. Restricting ourselves to the first term of the expansion P(t + τe) in a Taylor series, from this equation, we obtain
with allowance for the time of electric relaxation of dipoles τe. Restricting ourselves to the first term of the expansion P(t + τe) in a Taylor series, from this equation, we obtain
![]() (85)
(85)
The solution (see Equation (85)), on condition that Р = 0 at the initial instant of time, will take the form
![]() (86)
(86)
It is noteworthy that equation (see Equation (85)) is based on the classical Debay model. According to this model, particles of a substance possess a constant electric dipole moment. The indicated polarization mechanism involves partial arrangement of dipoles along the electric field, which is opposed by the process of disorientation of dipoles because of thermal collisions. The restoring “force”, in accordance with equation (see Equation (85)), does not lead to oscillations of electric polarization. It acts as if constant electric dipoles possessed strong damping.
Molecules of many liquids and solids possess the Debay relaxation polarizability. Initially polarization ag- gregates of Debay oscillators turn back to the equilibrium state![]() .
.
A dielectric is characterized, as a rule, by a large set of relaxation times with a characteristic distribution func- tion, since the potential barrier limiting the motion of weakly coupled ions may have different values [63] (Skanavi, 1949); therefore, the mean relaxation time of the ensemble of interacting dipoles should be meant by τe in equation (see Equation (85)).
To eliminate the influence of initial conditions and transient processes we set t0 = ‒∞, Е(∞) = 0, Н(∞) = 0, as it is usually done. If the boundary regime acts for a fairly long time, the influence of initial data becomes weaker with time owing to the friction inherent in every real physical system. Thus, we naturally arrive at the problem without the initial conditions:
![]() (87)
(87)
Let us consider the case of the harmonic field Е = Е0sinωt; then, using equation (see Equation (87)) we have, for the electric induction vector
![]() (88)
(88)
The electric induction vector is essentially the sum of two absolutely different physical quantities: the field strength and the polarization of a unit volume of the medium.
If the change in the density of the substance is small, we obtain, from formula (see Equation (82)), for the local instantaneous heat release
![]() (89)
(89)
when we write the mean value of Q over the total period Т:
![]() (90)
(90)
For high frequencies (ω → ∞), heat release ceases to be dependent on frequency, which is consistent with formula (see Equation (90)) and experiment [63] (Skanavi, 1949).
Formula (90) can also be obtained in a regular manner with introduction of a complex variable, but the intro- duction and use of the relaxation time ![]() enable us to compute the dissipation of electromagnetic energy (di- electric loss) for an amplitude and/or electromagnetic frequency-modulated wave.
enable us to compute the dissipation of electromagnetic energy (di- electric loss) for an amplitude and/or electromagnetic frequency-modulated wave.
Electrophysical properties depend on temperature as a rule; therefore, the system of Maxwell equations be- comes substantially nonlinear and it becomes impossible to use a complex variable in practice.
Changes in ![]() may be as high as tens percent for high-frequency ceramics, paper, and radio-engineering
may be as high as tens percent for high-frequency ceramics, paper, and radio-engineering
capacitors with variations in the temperature from ![]() to
to![]() . For ferroelectrics,
. For ferroelectrics, ![]() changes 3 to 5 times [68] with variations in the temperature from
changes 3 to 5 times [68] with variations in the temperature from ![]() to
to![]() . The left-hand side of Equation (12) will have the form
. The left-hand side of Equation (12) will have the form
![]()
therefore, the problems become nonlinear. Temperature variations cause the induced surface charge and the sur- face current to change; we do not know of the procedure of taking account of the influence of temperature on the charge and the surface current.
When the relaxation equation for the electric field is used we must also take account of the delay of the mag- netic field, when the magnetic polarization lags behind the change in the strength of the external magnetic field:
![]() (91)
(91)
Formula (see Equation (90)) is well known in the literature; it has been obtained by us without introducing complex parameters. In the case of “strong” heating of a material where the electrophysical properties of the material are dependent on temperature expression (see Equation (83)) will have a more complicated form and the expression for Q can only be computed by numerical methods. Furthermore, in the presence of strong field discontinuities, we cannot in principle obtain the expression for Q because of the absence of closing relations for the induced surface charge and the surface current on the boundaries of adjacent media; therefore, the issue of energy relations in macroscopic electrodynamics is difficult, particularly, with allowance for absorption.
Energy relations in a dispersive medium have repeatedly been considered; nonetheless, in the presence of ab- sorption, the issue seems not clearly understood (or at least not sufficiently known), particularly in the determi- nation of the expression of released heat on the boundaries of adjacent media.
Indeed, it is known from the thermodynamics of dielectrics that the differential of the free energy F has the form
![]() (92)
(92)
If the relative permittivity and the temperature and volume of the dielectric are constant quantities, from equation (see Equation (92)) we have
![]() (93)
(93)
where F0 is the free energy of the dielectric in the absence of the field.
The change of the internal energy of the dielectric during its polarization at constant temperature and volume can be found from the Gibbs-Helmholtz equation, in which the external parameter D is the electric displacement. Disregarding F0 which is independent of the field strength, we can obtain
![]() (94)
(94)
If the relative dielectric constant is dependent on temperature (ε(T)), we obtain
![]() (95)
(95)
Expression (see Equation (95)) determines the change in the internal energy of the dielectric in its isothermal polarization but with allowance for the energy transfer to a thermostat, if the polarization causes the dielectric temperature to change. A more detailed substantiation of equation (see Equation (95)) will be given in the book. In the works on microwave heating, that we know, expression (see Equation (95)) is not used.
A characteristic feature of high frequencies is that the polarization field lags behind the change in the external field in time; therefore, the polarization vector is expediently determined by solution of the equation
![]() (96)
(96)
With allowance for the relaxation time, i.e., restricting ourselves to the first term of the expansion ![]() in a Taylor series, we obtain
in a Taylor series, we obtain
![]() (97)
(97)
In the existing works on microwave heating with the use of complex parameters, they disregard the dependence ε''(T). In [69] (Antonets, I. V.; Kotov, L. N.; Shavrov, V. G. & Shcheglov, V. I., 2009), consideration has been given to the incidence of a one-dimensional wave from a medium with arbitrary complex parameters on one or two boundaries of media whose parameters are also arbitrary. The amplitudes of waves reflected from and transmitted by each boundary have been found. The refection, transmission, and absorption coefficients have been obtained from the wave amplitudes. The well-known proposition that a traditional selection of deter- minations of the reflection, transmission, and absorption coefficients from energies (reflectivity, transmissivity, and absorptivity) in the case of complex parameters of media comes into conflict with the law of conservation of energy has been confirmed and exemplified. The necessity of allowing for ε''(T) still further complicates the problem of computation of the dissipation of electromagnetic energy in propagation of waves through the boundaries of media with complex parameters.
The proposed method of computation of local heat release is free of the indicated drawbacks and makes it possible, for the first time, to construct a consistent model of propagation of nonmonochromatic waves in a het- erogeneous medium with allowance for frequency dispersion without introducing complex parameters.
In closing, we note that a monochromatic wave is infinite in space and time, has infinitesimal energy absorp- tion in a material medium, and transfers infinitesimal energy, which is the idealization of real processes. How- ever with these stringent constraints, too, the problem of propagation of waves through the boundary is open and far from being resolved even when the complex parameters of the medium are introduced and used. In reality, the boundary between adjacent media is not infinitely thin and has finite dimensions of the electric double layers; therefore, approaches based on through-counting schemes for a hyperbolic equation without explicit separation of the boundary between adjacent media are promising.
5. Ponderomotive Forces in Heterogeneous Lamellar Media with Absorption
It is common knowledge that the electric field strength E is equal to the ponderomotive mechanical force per unit charge acting at a given point of the field on a test charge (charged body). The issue of the force acting on induced surface charges on the boundaries remains to be solved, since there are no closing equations for σ and the charge is not determined on the interface itself. According to [45] (Landau, L. D. & Lifshits, E. M., 1982), the tension tensor of ponderomotive forces for media with dispersion and absorption due to the dipole relaxation cannot be found in general form in a macroscopic manner at all. As we believe, solution of this problem lies in computing the induced surface charge on the boundaries and the resultants of all tensions applied externally to the surface without the necessity of reducing bulk ponderomotive forces to tensions. The reduction of bulk forces to tensions is not necessarily possible; therefore, this issue will be considered in greater detail.
Reduction of Bulk Ponderomotive Forces to Tensions
If f is the bulk density of ponderomotive forces, the resultant of all forces applied to the bodies within the vol- ume V is
![]() (98)
(98)
On the other hand, if bulk forces can be reduced to tensions at all, the set of tensions acting externally of a closed surface S must be equal to the same quantity. We denote by Tn a force acting externally per unit surface the external normal to which is directed along n; the components of this force along the coordinate axes are Txn, Tyn and Tzn. Then the resultant of all tensions applied externally to the surface will be
![]() (99)
(99)
Using the Ostrogradski-Gauss theorem and equating (see Equations (99) and (100)), we obtain
![]()
![]() (100)
(100)
![]()
For the bulk forces and tensions to be equivalent, it is necessary that not only the resultant of forces applied to an arbitrary volume remain constant but the moment of these forces be invariant as well (Tamm, I., 2003). This circumstance imposes an additional constraint on the tension-tensor components. The moment of bulk forces applied to an arbitrary volume V is:
![]() (101)
(101)
where R is the distance from point O for which the moment of forces is determined to the element dV. Consequently, the component Nx must satisfy relation (see Equation (101)):
![]() (102)
(102)
The surface integral on the right is equal to the moment of tension forces Tn applied to the surface S of volume V. The moment of these tension forces will be equal to the moment of bulk forces only in the case where the last integral on the right is equal to zero. In view of the arbitrariness of the volume V, this will occur only when the integrand
![]() (103)
(103)
is equal to zero.
By repeating the same considerations for Ny and Nz, we obtain Tzx = Txy, Txy = Tyx. Consequently, for the bulk forces and surface ponderomotive forces to be equivalent, the tension tensor must be symmetric. In anisotropic media, the tension tensor is asymmetric; therefore, direct computation of the resultant of forces in terms of tensions from Formula (100) is expedient. We note that Maxwell was the first to reduce the field’s ponderomotive forces to tensions. Replacement of ponderomotive forces by an equivalent system of tensions makes it much easier to determine forces applied to the volume of the electric field.
The force applied to a charged layer, given the uncompensated surface charge, has the form
![]() (104)
(104)
If the layer is not charged, we have σ = 0 and![]() . The resultant force applied to the boundary of a cell is
. The resultant force applied to the boundary of a cell is
![]() (105)
(105)
The projections of fx, fy, and fz are determined according to equation (see Equation (101)), and in a variable electromagnetic field, we must take into account that fx, fy, and fz are expended in changing the density of the momentum flux of the substance and the electromagnetic field alike. If the forces acting only on the substance are meant by![]() , according to (Tamm, I., 2003), we have
, according to (Tamm, I., 2003), we have
![]() (106)
(106)
The expression ![]() is known to be called the Abraham force [70] (Tamm, I., 2003).
is known to be called the Abraham force [70] (Tamm, I., 2003).
If the medium is heterogeneous and the transmission of the electromagnetic wave involves its absorption and heating, we propose the following scheme of calculating ponderomotive forces:
1) the domain under study is subdivided into N cells with constant properties;
2) by the method presented in Para 1 and Para 2, we compute the surface charge σ and the surface ponderomotive force for each cell.
In this approach, we disregard the influence of striction forces and tensions acting only on the force distribution over the body’s volume but exerting no influence on the value of the resultant of all forces and on their moment [70] (Tamm, I., 2003). Allowance for ponderomotive forces is important, e.g., for biomechanics problems.
The history of the problem of ponderomotive forces developed into a paradoxical situation where the issues of certain basic propositions of classical electrodynamics have been discussed to date [66] (Barash, Yu. & Ginz- burg, V. L., 1976).
6. Maxwell Equations―Reformulation of Experiment Facts
In researchers’ daily life, it is agreed that reformulations of the already established proposition and ideas can only be trivial in essence. However an example of passage to a concentration formulation of the laws of elec- trodynamics in the form of Maxwell equations argues against this opinion. This is a brilliant achievement serv- ing as a basis for the development of the contemporary physics. An analysis (following the formulation of Maxwell equations) of the nature of an electromagnetic field and of the properties of the system of Maxwell equations became the contributor of relativity theory, of the corresponding fundamental revision of the previous ideas of the inertial frames of reference of the space and time.
Generalized Wave Equation―Reformulation of Maxwell Equations
A generalized wave equation is a reformulation of Maxwell equations. In this case, for solution of the problem, we must prescribe not only the value of the function but its time derivative as well. We must check the obser
vance of the condition ![]() in the absence of charge or
in the absence of charge or![]() ―with allowance for the
―with allowance for the
change in the charge. At the interface of adjacent media, 12 conditions, not six, must be observed.
The obtained conjugation conditions, e.g., the equality of total currents, equality of tangential projections of the vortex of an electric field, and other, hold true in each cross section of the specimen under study; therefore, it is promising to use schemes of through calculation without separating explicitly the interface of adjacent media. The use of the Dirichlet mean-value theorem for determination of the electric field strength in the presence of a strong discontinuity of the function is substantiated.
7. High-Frequency Electrodynamics of Slowly Moving Media
In the previous chapter, a study was made of the electromagnetic field of fixed bodies. A successive theory of electromagnetic phenomena in moving media can only be based on Einstein’s relativity theory. However we will consider the case of slowly moving media where![]() , i.e., with neglect of all effects that are propor- tional to the square and to high degrees of the ratio
, i.e., with neglect of all effects that are propor- tional to the square and to high degrees of the ratio![]() . From the relativity theory, we borrow just two rela- tions [71] :
. From the relativity theory, we borrow just two rela- tions [71] :
![]()
and the expression for the conduction current disregarding the Hall effect
![]()
The condition of slowness of the motion of material media is observed in most phenomena and processes of practical interest. It is not only sufficient slowness of the medium’s motion but also the requirement of con- stancy of![]() , that is the condition of applicability of the above relations [71] . The effects related to the depend- ence
, that is the condition of applicability of the above relations [71] . The effects related to the depend- ence ![]() are disregarded. In particular, the Tolman effect manifesting itself on sudden acceleration of semiconductors cannot be explained on the basis of the presented theory. The field equations were reduced to the equation of telegraphy (telegraph equation) for the electric field strength. The influence of the medium’s motion on the propagation of the waves also occurs in a simpler situation, e.g., in acoustics problem; therefore, first we consider the simulation of aeroacoustics problems and thereafter the distinctive features of the electro- dynamics problem with account taken of the Fresnel drag coefficient for the velocity of an electromagnetic wave in a moving medium.
are disregarded. In particular, the Tolman effect manifesting itself on sudden acceleration of semiconductors cannot be explained on the basis of the presented theory. The field equations were reduced to the equation of telegraphy (telegraph equation) for the electric field strength. The influence of the medium’s motion on the propagation of the waves also occurs in a simpler situation, e.g., in acoustics problem; therefore, first we consider the simulation of aeroacoustics problems and thereafter the distinctive features of the electro- dynamics problem with account taken of the Fresnel drag coefficient for the velocity of an electromagnetic wave in a moving medium.
7.1. Modeling of Unsteady Wave Processes in Moving Media
In problems of acoustics, electrodynamics, and heat conduction involving intense heat release momentum trans- fer is accompanied, as a rule, by medium motion, and, therefore, the corresponding hyperbolic equations must be solved in a moving medium.
The processes under consideration are described by a wave equation of the form
![]() (107)
(107)
where medium motion must be taken into account. The modified linear wave equation, when![]() , in a moving medium has been considered, with some limitations, by D. I. Blokhintsev [72] [73] . In [74] -[78] , equations are derived that have a wider field of application but, unfortunately, are rather complicated for calcu- lations.
, in a moving medium has been considered, with some limitations, by D. I. Blokhintsev [72] [73] . In [74] -[78] , equations are derived that have a wider field of application but, unfortunately, are rather complicated for calcu- lations.
The present work is devoted to modeling of sound propagation in a moving inhomogeneous medium by con- structing a difference scheme that accounts for the medium motion.
It is known [71] that downstream and upstream disturbances are propagated at different velocities. This effect will be accounted for when constructing a difference scheme for wave Equation (107) with the aid of deforma- tion of a difference cell.
We shall consider the interrelationship of space and time measurements in a moving medium. Let us intro- duce a uniform network in the medium at rest![]() , where
, where ![]()
![]() (Figure l(a)). In the case of medium motion, each node replaces a relatively motionless observer with velocity
(Figure l(a)). In the case of medium motion, each node replaces a relatively motionless observer with velocity ![]() and, therefore, for the time of signal propagation, within which the observer is continuously recording the amplitude and frequency of pressure or flow-velocity variation, the node is displaced by same additional distance (Figure l8(b)). For the motionless observer at node i sending or receiving a signal (a change in pressure or velocity), downstream and upstream paths of signal transmission for a cell with length
and, therefore, for the time of signal propagation, within which the observer is continuously recording the amplitude and frequency of pressure or flow-velocity variation, the node is displaced by same additional distance (Figure l8(b)). For the motionless observer at node i sending or receiving a signal (a change in pressure or velocity), downstream and upstream paths of signal transmission for a cell with length ![]() (
(![]() is the cell length in the Lagrange reference system) will be different.
is the cell length in the Lagrange reference system) will be different.
We now consider two cases: a) signal propagation to the right of node i and b) signal propagation to the left of node i. Assume that the flow velocity within the limits of the difference cell as well as the wave velocity are constant quantities. The dependence of the medium velocity V and the sound velocity С on the coordinate and time will be taken into account in the difference scheme.
1) Let a motionless observer be at the node i. Then a signal sent downstream has total velocity С + V, and for the time of signal propagation ![]() from node i to node i + 1, node i + 1 itself is displaced by an additional distance
from node i to node i + 1, node i + 1 itself is displaced by an additional distance![]() ; therefore (Figure 18(b))
; therefore (Figure 18(b))
![]()
where
![]()
![]() (a) (b)
(a) (b)
Figure 18. Deformation of a difference cell: a) medium at rest; b) moving medium.
2) A motionless observer is at the node i. Then a signal sent upstream has total velocity C ? V, and for the time of signal propagation ![]() from node i to node i ? 1, the latter approaches the former by distance
from node i to node i ? 1, the latter approaches the former by distance![]() ; therefore (Figure l8(b)).
; therefore (Figure l8(b)).
![]()
where
![]()
whence
![]() (108)
(108)
where ![]() and
and ![]() are the cell dimensions in the Euler reference system. Consequently, for a motionless observer at node i in the Euler reference system the initially uniform network undergoes deformation.
are the cell dimensions in the Euler reference system. Consequently, for a motionless observer at node i in the Euler reference system the initially uniform network undergoes deformation.
For the difference scheme, we apply relations (108), which lead, in fact, to deformations of the Euler calculation region due to medium motion.
The size of the cell (body) must be independent of the sign of the velocity; therefore, in constructing a difference scheme we shall use the condition of independence of cell size of the direction and the velocity sign of the moving medium. This means that a signal sent by an observer at time j ? 1 downstream (or upstream) must be received at moment j + 1 at the same node i when the signal direction is reversed, i.e., the measurements become time-averaged. In other words, the procedure of time averaging of measurements reflects the fact that one and the same node is an emitter and a receiver of waves at the same moment in time.
The constructing the difference scheme, we assume that wave Equation (107) holds for a medium at rest and for a moving medium in a local comoving Lagrange reference system for a given individual difference cell with a sufficiently small step![]() . Having solved (108) for
. Having solved (108) for![]() , we pass to Euler variables and select a space step equal, for convenience, to
, we pass to Euler variables and select a space step equal, for convenience, to ![]() and obtain
and obtain
![]() (109)
(109)
where![]() .
.
We write the initial wave equation not for a segment but for difference spatial nodes of the network
![]() (110)
(110)
where ![]() are the deformed nodes built in accordance with relations (109).
are the deformed nodes built in accordance with relations (109).
The boundary and initial conditions are as follows
![]()
![]()
We designate an approximate value of the function P at the nodes ![]() by
by![]() . Equation (110) will be approximated by the scheme with allowance for nonreciprocity relation (108) and independence of the mesh width from the direction of medium motion (time-averaging of measurements):
. Equation (110) will be approximated by the scheme with allowance for nonreciprocity relation (108) and independence of the mesh width from the direction of medium motion (time-averaging of measurements):
![]() (111)
(111)
where
![]()
![]()
The conditions at the boundaries are
![]() (112)
(112)
The initial conditions are
![]() (113)
(113)
Difference scheme (111) is implemented in the following iteration process
![]() (114)
(114)
![]()
where, for instance:
![]()
Iteration is carried out until the following condition is fulfilled
![]()
The values of each successive approximation are found by the elimination technique. It is easy to verify that the elimination algorithm is stable for any h and![]() .
.
Examples of Numerical Solution of the Wave Equation in Moving Media. A flat infinite membrane vi- brating in a gas causes periodic gas compression and rarefaction around it and thus is a source of acoustic waves. Consider the case when a membrane performs harmonic oscillations of the type Asin(wt) and the pressure at distance l is equal to zero. For instance, such a problem can be observed when acoustic waves propagate along a narrow long tube of constant cross-section whose width is small as compared with wavelength. Under these conditions we can assume that all quantities (velocity, density, pressure, etc.) are constant in each tube cross section and the direction of wave propagation coincides with that of the tube axis. The pressure difference be- tween the gas at the tube end and the surrounding space is small as compared with the pressure difference inside the tube. Therefore with a sufficient degree of accuracy, we assume equality of the gas pressure to zero as a boundary condition [72] .
In the presence of wind V(x,t) along the axis x, the pressure satisfies wave Equation (110) with boundary conditions
![]()
and initial conditions
![]()
The initial conditions correspond to a medium at the rest at the initial moment of time. For the example under consideration, Equation (107) acquires a linear form with the coefficients![]() . In this case, a solu- tion is sought directly from approximation relations of type (114) at s = 0. Calculations were carried out for dif- ferent space and time steps.
. In this case, a solu- tion is sought directly from approximation relations of type (114) at s = 0. Calculations were carried out for dif- ferent space and time steps.
Figure 19 shows the time-dependent amplitudes of the acoustic pressure at different gas velocities. As seen, with an increase in gas velocity, the build-up of pressure amplitude decreases. In this case, the most pronounced decrease in the amplitude and, consequently, in the intensity of acoustic radiation is observed at points far from the membrane (Figure 19(b)). Figure 20 shows pressure versus time at the point x = 0.66 at V = 0. In the pressure of velocity, the dependence preserves its character. In the calculations, we adopted the following values of the parameters: A = 0.5 Pa, l = 20 m, С = 320 m/sec, where С is the sound velocity.
The dependence of acoustic pressure on the coordinate is shown in Figure 21, which is also indicative of a decrease in the amplitude and, consequently, in the intensity of radiation of acoustic waves with an increase of gas velocity, since the medium under consideration does not dissipate and energy dissipation proceeds only due to gas motion. Curves 3 and 4 are obtained for the case when the gas velocity depends linearily on the coordinate and is directed along the axis x. According to [72] , sound audibility decreases in the presence of wind. Naturally, in a real atmosphere this effect can be associated with atmosphere turbulence, but it has been also observed in the presence of weak wind (1 - 2 m/sec).
We consider one more problem, i.e., the occurrence of sound vibrations in a resonator. The simplest examples of such resonators are tubes open on one or both ends, Helmholtz resonators (in the form of bottles), etc. It is easy to make all resonators of such kind “sound” in an air flow by blowing over their mouth. An open end is identical to an absolutely soft cover when the pressure (acoustic not atmospheric) is practically equal to zero. At the left-hand boundary of the resonator ![]() we have the condition
we have the condition![]() ; at the right-hand boundary.
; at the right-hand boundary.
![]()
Figure 19. Amplitude of the acoustic pressure vs time: = 800 sec−1, a) x = 0.33: 1) V = 0; 2) 10 m/sec; b) x = 0.66: 1) V = 0; 2) 10 m/sec; 3) 20 (dashed line, the calculated amplitude value; solid line, the time-averaged absolute amplitude value). ,Pa; t, sec.
![]()
Figure 20. Acoustic pressure vs time at V= 0, x= 0.66, = 800 sec−1. P,Pa.
![]()
Figure 21. Acoustic pressure vs the coordinate: 1) V =10 m/sec; 2) 20 m/sec at t = 0.4002 sec, = 800 sec−1; 3) V = 0, and 4) V =×3x + 5 at t = 0.3 sec, = 900 sec−1; curves 3, 4) the absolute amplitude value.
![]()
Let the tube have intrinsic noise with a set of harmonics. Then in the presence of wind whose velocity is di- rected along the resonator axis the phenomenon of resonance accompanied by a strong build-up of wave ampli- tude a sound enhancement has been observed.
The results of calculations for sound attenuation in the presence of wind and sound enhancement in resonator tube, with air flowing in it, correspond to experimental data [71] .
7.2. Electromagnetic Wave Velocity in a Slowly Moving Medium. The Fresnel Drag Coefficient
We consider a plane light wave of frequency ω in a homogeneous isotropic nonmagnetic dielictric. We choose the z axis in the direction of wave propagation:
![]() (115)
(115)
under the following assumption: the velocity ![]() coincides with the wave direction, i.e.,
coincides with the wave direction, i.e.,![]() . In this case, taking into account, that the wave velocity
. In this case, taking into account, that the wave velocity![]() , we obtain [71]
, we obtain [71]
![]() (116)
(116)
It follows from Equation (116) that if![]() ,
, ![]() ,
, ![]() ,
, ![]() differ from zero, then
differ from zero, then![]() ; since
; since ![]() is the refractive index of the medium, we finally write
is the refractive index of the medium, we finally write
![]() (117)
(117)
Perfoming calculations for the case of an arbitrary angle between ![]() and
and![]() , we may see that (117) remains valid in the general case too. Equation (117) was derived by the first by O. Fresnel in 1818. According to H. A. Lorentz (1895), a correction accounting for the medium dispersion should be introduced into Fresnel’s formula. Fresnel’s formula was confirmed by experimental data in 1851 by A. I. L. Fizeau and in 1914 by P. Zeeman.
, we may see that (117) remains valid in the general case too. Equation (117) was derived by the first by O. Fresnel in 1818. According to H. A. Lorentz (1895), a correction accounting for the medium dispersion should be introduced into Fresnel’s formula. Fresnel’s formula was confirmed by experimental data in 1851 by A. I. L. Fizeau and in 1914 by P. Zeeman.
7.3. Electromagnetic Waves in a Slowly Moving Medium
In the subsequent presentation, the wave velocity ![]() will be determined by the Fresnel Formula (117). In high- frequency electrodynamics the “aeroacoustics” equation derived by D. I. Blokhintsev [71] [72] can be recommended for taking account of the medium’s motion when changes in the flow state are rather slow compared to the frequency of the electromagnetic wave propagating through the medium, and
will be determined by the Fresnel Formula (117). In high- frequency electrodynamics the “aeroacoustics” equation derived by D. I. Blokhintsev [71] [72] can be recommended for taking account of the medium’s motion when changes in the flow state are rather slow compared to the frequency of the electromagnetic wave propagating through the medium, and![]() . In this case the telegraph equation will have the form
. In this case the telegraph equation will have the form
![]() (118)
(118)
In the presence of convective motion with a constant velocity ![]() in a one-dimensional case it
in a one-dimensional case it![]() . We have
. We have
![]() (119)
(119)
Note that (118) holds true it the velocity of the medium ![]() depends on time but does not depend on coordinates. When the medium’s velocity is determined by coordinates, too, (118) fails. In this case, for the problem to be solved, we can recommend a numerical method based on the use of local Riemann invariants in a difference cell analogously to Item 7.1 together with the courant condition which relates the time and space step:
depends on time but does not depend on coordinates. When the medium’s velocity is determined by coordinates, too, (118) fails. In this case, for the problem to be solved, we can recommend a numerical method based on the use of local Riemann invariants in a difference cell analogously to Item 7.1 together with the courant condition which relates the time and space step:
![]() (120)
(120)
where ![]() is the rate of transfer of a disturbance in a quiescent medium and
is the rate of transfer of a disturbance in a quiescent medium and ![]() and
and ![]() are the length of the difference cell and the time step in a Lagrangian frame of reference. Actually, we solved Equation (119) nu- merically for acoustic problems in the absence of the conduction current. The upwind “audibility” of sound de- creases, whereas the downwind audibility grows. These well-known experimental facts were confirmed by nu- merical calculations. A comparison of the data in quiescent and moving media has shown that is only the inten- sity of sound that changes, but no phase shift is observed.
are the length of the difference cell and the time step in a Lagrangian frame of reference. Actually, we solved Equation (119) nu- merically for acoustic problems in the absence of the conduction current. The upwind “audibility” of sound de- creases, whereas the downwind audibility grows. These well-known experimental facts were confirmed by nu- merical calculations. A comparison of the data in quiescent and moving media has shown that is only the inten- sity of sound that changes, but no phase shift is observed.
Which is consistent with the data of Michelson-Morley experiments.
Using Equation (119) we can simulate the appearance of electric fields due to the medium’s motion.
The idea of construction of a difference scheme to Equation (118) with account of the medium’s motion is based on the works of M. Laue [79] and A. Einstein [80] in which it is proved that a light pulse propagating in the form of an individual wave packet may be transformed as the velocity of a material point. By virtue of the singularity of this proposition and because of the fact that it is little-known, we cite M. Laue ([79] ): “Imagine a light pulse propagating in the form of a wave packet and moving with a velocity c relative to a viewer mo- tionless in the medium. With this packet, these moves a certain object which is in the field of a light beam at all times and hence remains illuminated by this beam at all times. Clearly, for the other viewer moving with a cer- tain arbitrary velocity relative to the first one this object will also seem illuminated at all times.
For this condition to be observed, it is necessary that the velocity of the packet of light waves, in passing from the frame of reference of the first viewer (in which he is motionless) to the frame “of the second viewer” be transformed as the velocity of a material point”. Also, we give A. Einstein’s reasoning [80] : “Let, at an instant of time ![]() (here “time” means the “time of a quiescent frame”―A. Einstein), a light beam emerge from A, be re- flected at B at an instant of time
(here “time” means the “time of a quiescent frame”―A. Einstein), a light beam emerge from A, be re- flected at B at an instant of time![]() , and return to A at an instant of time
, and return to A at an instant of time![]() . Taking into account the principle of constancy of the light velocity, we find
. Taking into account the principle of constancy of the light velocity, we find
![]()
where ![]() is the length of a moving rod, measured in the “quiescent frame”. Here
is the length of a moving rod, measured in the “quiescent frame”. Here ![]() is the light velocity; the notation is preserved according to [80] . Next: “Let, at an instant of time
is the light velocity; the notation is preserved according to [80] . Next: “Let, at an instant of time![]() , a light beam be sent from the origin of the frame
, a light beam be sent from the origin of the frame ![]() along the
along the ![]() axis to a point
axis to a point ![]() and be reflected from it, at an instant of time
and be reflected from it, at an instant of time![]() , back, to the origin where it arrives at an instant of time
, back, to the origin where it arrives at an instant of time![]() ; then these must exist the relation
; then these must exist the relation
![]()
or, writing the arguments of the function ![]() and applying the principle of constancy of the light velocity in the quiescent frame, we have
and applying the principle of constancy of the light velocity in the quiescent frame, we have
![]()
it ![]() is assumed to be infinitesimal, it follows that
is assumed to be infinitesimal, it follows that
![]()
or
![]()
It should be noted that we could have taken, instead of the origin, any other point as the reference point of the light beam; therefore, the equation just obtained holds true for any values of![]() ,
, ![]() and
and![]() .
.
If it is taken into account that the light along the ![]() and
and ![]() axes, being viewed from quiescent frame, al- ways propagates with a velocity
axes, being viewed from quiescent frame, al- ways propagates with a velocity![]() , an analogous reasoning applied to these axes fields
, an analogous reasoning applied to these axes fields
![]()
Since is the linear function, it follows from these equations that
![]()
where ![]() is still the unknown function
is still the unknown function ![]() and it is assumed for brevity that in the origin of the frame
and it is assumed for brevity that in the origin of the frame![]() , we also have
, we also have ![]() at
at![]() .
.
The necessity of giving this reasoning stems from the fact that it is the case of two moving bodies, not of a continuum, that is proposed in [80] . For a continuum (as has been shown), the introduction of at least one more point and the use of two-layer time difference schemes for a hyperbolic equation are necessary (see Item 3.1).
The concepts of space and time developed by A. Einstein were generated on the experimental-physical basic. This is their strength. However the reasoning indicated above [80] is absent, in fact, from recent publications and textbooks on field theory.
Considering that the concept of simultaneity of not-single-site events is relative, A. Einstein introduced the actually novel concept of time which is used in relativity theory.
In our case we have![]() , but the principle of discrete consideration of propagation of waves [80] is as- sumed to be promising for the electrodynamics of a slowly moving continuum with the results of Item 3.1 for aeroacoustics problems (the wave velocity is determined from Fresnel formula).
, but the principle of discrete consideration of propagation of waves [80] is as- sumed to be promising for the electrodynamics of a slowly moving continuum with the results of Item 3.1 for aeroacoustics problems (the wave velocity is determined from Fresnel formula).
The proposed method of numerical solution of the wave equation in a moving medium may, of course, be generalized to such phenomena that propagate with a superlight velocity. Geometrically, e.g., this is quite sim- ply done, but such phenomena cannot serve as signals.
This means that it is impossible to arbitrarily use them to actual, e.g. a diode at a distant site. There can exist optical media in which the “light velocity” is lager then![]() . But in this case by the light velocity we mean the propagation of phase in an infinite periodic wave flow. This velocity can never be used for signaling. Con- versely, the wave front, in all circumstances and for any properties of the optical medium, propagates with a ve- locity
. But in this case by the light velocity we mean the propagation of phase in an infinite periodic wave flow. This velocity can never be used for signaling. Con- versely, the wave front, in all circumstances and for any properties of the optical medium, propagates with a ve- locity![]() .
.
These features of determination of a signal were noted even by A. Sommerfeld [81] (the wave velocity is de- termined from the Fresnel formula).
Boundary Conditions: At the inlet and the outlet of a continuous slowly moving medium, the conditions of equality of total currents discussed earlier must hold. With account taken of the medium’s motion, an expression for expression for the total current has the form
![]() (121)
(121)
In a general sense, in the presence of diffusion and heat transfer, we must use a more general expression for the total current, which is necessary to employ in electrolytes and plasma.
When classical conditions with the introduction of a surface current and a surface charge are used it is difficult to take account of the convective transfer of a medium not only at the interfaces of adjacent media but in the continuum as well, since the classical Maxwell equations are local.
Conclusions: We have developed the “aeroacoustics” algorithm of solution of the problem of propagation of an electromagnetic field in a slowly moving medium. When a signal propagates we introduce the Fresnel drag coefficient and use local Riemann invariants in a difference cell. The calculation results show the absence of the influence of the medium’s motion on the phase shift of waves, which is consistent with experimental data.
8. Conclusions
The consistent physicomathematical model of propagation of an electromagnetic wave in a heterogeneous me- dium has been constructed using the generalized wave equation and the Dirichlet theorem. Twelve conditions at the interfaces of adjacent media were obtained and justified without using a surface charge and surface current in explicit form. The conditions are fulfilled automatically in each section of the heterogeneous medium and are conjugated, which made it possible to use through-counting schemes for calculations. For the first time the effect of concentration of “medium-frequency” waves with a length of the order of hundreds of meters at the fractures and wedges of domains of size 1 - 3 μm has been established. Numerical calculations of the total electromagnetic energy on the wedges of domains were obtained. It is shown that the energy density in the region of wedges is maximum and in some cases may exert an influence on the motion, sinks, and the source of dislocations and vacancies and, in the final run, improve the near-surface layer of glass due to the “micromagnetoplastic” effect.
The results of these calculations are of special importance for medicine, in particular, when microwaves are used in the therapy of various diseases. For a small, on the average, permissible level of electromagnetic irradia- tion, the concentration of electromagnetic energy in internal angular structures of a human body (cells, mem- branes, neurons, interlacements of vessels, etc) is possible.
For the first time, we have constructed a consistent physicomathematical model of interaction of nonstation- ary electric and thermal fields in a layered medium with allowance for mass transfer. The model is based on the methods of thermodynamics and on the equations of an electromagnetic field and is formulated without explicit separation of the charge carriers and the charge of an electric double layer. We have obtained the relations for the electric-field strength and the temperature, which take into account the equality of the total currents and the energy fluxes, to describe the electric and thermal phenomena in layered media where the thickness of the elec- tric double layer is small compared to the dimensions of the object under study.
We have modeled numerically the heating of an electrochemical cell with allowance for the influence of the electric double layer at the metal-electrolyte interface. The calculation results are in satisfactory agreement with experimental data.
It should be mentioned that Equation (8) is actually the boundary condition only in the case of electrostatic processes, when the surface charge density s is specified at the interface. In the presence of alternating currents in the medium the density s will change with time; therefore relation (8) is not a boundary condition for Dn. In this case, the surface charge density s(t) should be calculated from the solution of the conjugate problem for an electromagnetic field, i.e., in the case where the electric field distribution has been already found, which we tried to do in this work and also in [82] [83] .
We have developed the “aeroacoustics” algorithm of solution of the problem of propagation of an electro- magnetic field in a slowly moving medium. When a signal propagates, we introduce the Fresnel drag coefficient and use local Riemann invariants in a different cell. The calculation results show the absence of the influence of the medium’s motion on the phase shift of waves, which is consistent with experimental data.
Sections 1-5 of the present work have been earlier published partially in [82] [83] .
Acknowledgements
The authors express their gratitude to Corresponding Member of the National Academy of Sciences of Belarus N.V. Pavlyukevich, Corresponding Member of the National Academy of Sciences of Belarus Prof. V. I. Korzyuk for a useful discussion of the work.
This work war carried out with financial support from the Belarusian Republic Foundation for Basic Research (grant T10P-122) and from the Science Support Foundation of Poland “Kassa im. Myanowski” (2005).
Notation
B, magnetic induction, Wb/m2; D, electric displacement, C/m2; DM, molecular diffusion coefficient, m2/sec; Di, diffusion coefficients of anions and cations, m2/sec; DA, ambipolar diffusion coefficient, A/(m・kg);![]() , ambipolar diffusion coefficient, kg/(A・sec); E, electric field strength, V/m; F, free energy of the unit volume of a dielectric, J/m3; F, Faraday’s constant, 96.985 C/Equation; F0, free energy of a dielectric in the absence of a field, J/m3; J, current density, A/m2; H, magnetic field strength, A/m; h, thickness of the electric double layer, m; Iq, Iq, normal components of the conduction current in media 1 and 2, C/(m2∙sec); iτ, surface current, A/m; i, j, k, unit vectors of the orthonormalized basis; jtot, total current, A/m ; L, length, m; l, average distance between ferroparticles, m; n, unit vector normal to the interface; n, concentration, kg/m3; nA, concentration of neutral molecules, kg/m3; ni, concentration of dissociated molecules, kg/m3; nm, molar concentration, g・Equation/liter; R, universal gas constant; R, resistance, Ω∙m; P, pressure, Pa; q, mass flux, kg/(m2∙sec); r, radius of a particle, μm; S, interface between adjacent media; T, temperature, ˚C; t, time, sec; V, volume, m3; v, velocity of the slip of a ferroparticle over the treated surface, m/sec; U, voltage, V; W, magnetic field density, J/m3; x, y, z, Cartesian coordinates; β, equilibrium constant; α, degree of dissociation; ε, relative permittivity; ε0, electric constant equal to 8.58 ´ 10‒12 F/m; φ, electric potential, V; k, Boltzmann constant; λ, electrical conductivity, Ω∙m; ke, electrochemical equivalent of copper, kg/C;
, ambipolar diffusion coefficient, kg/(A・sec); E, electric field strength, V/m; F, free energy of the unit volume of a dielectric, J/m3; F, Faraday’s constant, 96.985 C/Equation; F0, free energy of a dielectric in the absence of a field, J/m3; J, current density, A/m2; H, magnetic field strength, A/m; h, thickness of the electric double layer, m; Iq, Iq, normal components of the conduction current in media 1 and 2, C/(m2∙sec); iτ, surface current, A/m; i, j, k, unit vectors of the orthonormalized basis; jtot, total current, A/m ; L, length, m; l, average distance between ferroparticles, m; n, unit vector normal to the interface; n, concentration, kg/m3; nA, concentration of neutral molecules, kg/m3; ni, concentration of dissociated molecules, kg/m3; nm, molar concentration, g・Equation/liter; R, universal gas constant; R, resistance, Ω∙m; P, pressure, Pa; q, mass flux, kg/(m2∙sec); r, radius of a particle, μm; S, interface between adjacent media; T, temperature, ˚C; t, time, sec; V, volume, m3; v, velocity of the slip of a ferroparticle over the treated surface, m/sec; U, voltage, V; W, magnetic field density, J/m3; x, y, z, Cartesian coordinates; β, equilibrium constant; α, degree of dissociation; ε, relative permittivity; ε0, electric constant equal to 8.58 ´ 10‒12 F/m; φ, electric potential, V; k, Boltzmann constant; λ, electrical conductivity, Ω∙m; ke, electrochemical equivalent of copper, kg/C;![]() , coefficient of specific electrical ambipolar conductivity, V・m3/kg;
, coefficient of specific electrical ambipolar conductivity, V・m3/kg;![]() , average value of electrical conductivity, Ω∙m; μ, relative permeability; μ0, magnetic constant equal to 4π ´ 10‒7 gf/m; μc, chemical potential; ξ, discontinuity point; ρ, specific electric charge, C/m2; ρR, conductance; σ, surface-
, average value of electrical conductivity, Ω∙m; μ, relative permeability; μ0, magnetic constant equal to 4π ´ 10‒7 gf/m; μc, chemical potential; ξ, discontinuity point; ρ, specific electric charge, C/m2; ρR, conductance; σ, surface-
density of a charge, C/m2; ω, angular frequency, 1/sec;![]() , symbolic operator;
, symbolic operator;
![]() , Subscripts: 0, constant component of a magnetic field H; 1, first medium; 2, second
, Subscripts: 0, constant component of a magnetic field H; 1, first medium; 2, second
medium; n, normal; q, charge; m, impurity mass; a, anode; A, ambipolar; M, molecular; e, equivalent; c, concentration; i, number of the grid node; j, component; max, maximum; n, τ, directions normal and tangential to the interface; x, normal component of a vector; y, z, tangential components of a vector at the interface between adjacent media; tot, total.