Quantum-Mechanical Information Content of Multiples Hartree-Fock Solutions. The Multi-Reference Hartree-Fock Configuration Interaction Method ()
1. Introduction
The repulsive coulomb term in the electronic Hamiltonian of atoms, molecules and solids introduces a hard difficult to determine stationary electronic states. It is possible only to obtain approximate solutions of the Schrö- dinger’s equation and there are several procedures for this goal. Two important and general approaches to achieve this purpose are the variational and perturbative methods. In this essay, we are primarily concerned with the approximate variational methods, in particular, with the configuration interaction (CI) methods.
An initial variational approach to study electronic structure of atoms and molecules is the Hartree-Fock (HF) approximation. This approximation can be used as starting-point for other variational and perturbative methods. Although the HF approximation provides the most part of the electronic ground state energy of the system, the rest of this energy is very important to understand several phenomena involving these systems. Rigorously, in practice it is impossible to determine the HF limit as well the exact electronic ground state energy because the atomic bases are finite. Thus, the quantity of correlation energy that is possible to rescue is limited by the atomic base and other truncations or approximations employed. But it is possible for some systems to obtain very accu- rate values. Beside this, an error in the electronic energy means an error in the correspondent state vector with consequences on the calculated values of other dynamical variables, in particular on the non-variational dynam- ical variables.
In molecular electronic problems, there is a variety of observables that depend of the charge distribution and that are not variational dynamical variables as, for instance, the electrical multipolar moments. Non-variational dynamical variables do not exhibit the decrescent monotonical behavior of the energy with the augmentation of the variational class of functions. In contrast, they display an irregular behavior. This means that in the scope of the approximate variational methods better values for electronic energy do not implicate in better values of non- variational observables. This introduces difficulties in the determination of non-variational properties in the ambit of these approximate methods. Over the last twenty years, multi-reference configuration interaction (MRCI) methods have been developed and used in molecular quantum mechanics to study this question [1] . In this communication we present some aspects of the content of quantum information of multiples HF solutions re- lated with this problem using a MRCI method based on multiple HF solutions.
2. Theory
The traditional CI method uses a single reference, the HF ground state, and your excited configurations to ex- pand the state function. However, the HF equation is non-linear and has, in principle, multiple solutions [2] and each HF extremum and its associated virtual spin-orbitals, generate the same full Configuration Interaction (full CI) space. Thus with each HF extremum we can formulate an orthogonal CI problem. It is possible also to for- mulate a non-orthogonal multi-reference CI using these multiple HF references. In the CI problem the variation- al class of functions to search the extrema is a vector space. So the equation of necessary condition to obtain the extrema is linear. It is a usual eigenvalue problem or a generalized eigenvalue problem if the base employed of the vector space is orthogonal or not, respectively. This equation is the matrix representation of the Schrödinger’s stationary equation in this base.
In previous works [3] - [5] we have introduced a new multi-reference configuration interaction method, based on the multiple solutions of the HF problem, called the multi-reference Hartree-Fock configuration interaction (MRHFCI) method. In the MRHFCI method, instead of a single reference one uses several HF extremes as ref- erences in order to expand the state function. The detailed formulation of the MRHFCI method to study a singlet ground state is presented in the references above. The basic aspects of the method can be summarized as follow.
For the restricted HF (RHF) problem of a molecule with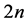 
electrons, represented in the atomic base
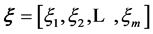, the 
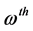HF solution is a set of functions
; 
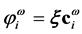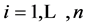where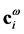 
is a column vector with components
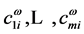. These functions, 
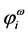, are the occupied molecular orbitals (MOs). It is po- ssible to generate an additional set of functions
; 
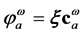called virtual MOs of the ![]()
so- lution. Associated with the MOs of the ![]()
solution, there is the set of m orbital energies, ![]()
,![]()
.
In a molecular HF problem, formulated in any class of symmetry of point and spin, it is possible, in principle, to obtain several HF solutions. And from these solutions to construct several HF references and your corre- spondent excited configuration state functions (CSFs)![]()
, ![]()
, ![]()
, … (single, double, triple excited, …) which belong to the irreducible representation of point and spin of interest. The sets of these CSFs define the
sub-bases![]()
, ![]()
, ![]()
, ![]()
, ××× and the corresponding subspaces![]()
, ![]()
, ![]()
, ![]()
, ×××. The bases ![]()
of the full CI space![]()
, associated with the HF solution, is defined as![]()
, and ![]()
can be written as the direct sum ![]()
of the subspaces![]()
, ![]()
, ![]()
, ![]()
, ×××.The set of the bases![]()
, ![]()
, form a
system of generators of the full CI space. From the set ![]()
one can form the multi-reference HF (MRHF) bases for MRHFCI calculations. These bases contain CSFs originated from different HF references, which, in general, are not orthogonal.
The motivation for using the MRHF bases lies on the following consideration. Let ![]()
and ![]()
be two bases of the full CI space. The state function ![]()
can be written as,
![]()
or as,
![]()
where,
![]()
However,
![]()
Thus, in spite of the fact that the bases ![]()
and ![]()
generate the same CI space, the corresponding CSFs of each ![]()
base have distinct quantum-mechanical information contents (QMIC). This implies a lack of uniformity of QMIC distribution in the vectors of the several bases. This fact suggests the use of MRHF bases for the generation of sub-domains in the formulation of the CI problem, i.e. basis formed with configurations originated from distinct HF references. The use of these “mixed basis” may allow a better extraction of quantum mechanical information from the several ![]()
bases for the calculation of molecular properties while simultaneously producing energy values comparable to the ones of full CI calculations.
3. Results
3.1. Previous Results
The MRHFCI method was applied to calculate the permanent electrical dipole moment of some small molecules, LiH, BH, FH, CO and H2O and the quadrupole moment of the FH [3] - [5] , using the standard STO-6G and a new minimal-6G bases [6] . For LiH molecule were performed MRHFCI calculations with the double-zeta (dz), triple- zeta (tz) and polarized dz (dzp) bases. In all cases was possible, using a reduced number of CSFs, to obtain di- pole and quadrupole moments in close agreement with the experimental values and energies without compro- mising the energy of the state function. The corresponding full CI calculations do not provide good results for the dipole and quadrupole moments. Two other interesting aspects were observed. It was possible to obtain good dipole and quadrupole values using minimal bases considered as “poor” bases in the literature. These bases are much smaller than the vast majority of the atomic bases used in the calculations of the dipole and quadrupole moments. In the LiH calculations was verified a significant relative reduction of the size of the MRHF base as the dimension of the full CI base increases.
3.2. New Results
In the current stage of development of the MRHFCI method, the results are still obtained through trials but this requires too much computational effort. To extend these calculations for larger systems and atomic bases it is necessary to develop criteria to build the MRHF bases. With this purpose, we begin this project with a systemat- ic study of the non-uniform distribution of QMIC of the ![]()
bases with regard to energy and permanent elec- trical dipole moment. We will use as initial tests the LiH molecule and Be atom using a new dz base [7] and the traditional bases dz, tz and dzp. We start this analysis determining a set of three HF solutions of the Be atom and twelve HF solutions of the LiH molecule using the new dz basis [8] . The Table 1(a) and Table 1(b) show or- thogonal CI calculations of the energy with several combinations of excited CSFs, for each these twelve LiH HF solutions. The headers of these tables indicate which and how many CSFs were employed in each of the ortho- gonal CI calculations. The Table 2 presents MRHFCI calculations of the dipole moment for the LiH. All the in- dicated energies in the Table 1(a) and Table 1(b) and Table 2 are electronic energy plus nuclear repulsion energy. The Table 3 shows an energy obtained with the MRHFCI method for the Be atom. In the Table 2 and
(a) ![]()
Table 1. (a) Non-uniform distribution of QMIC of the HF solutions of the LiH molecule; (b) Non-uniform distribution of QMIC of the HF solutions of the LiH molecule.
S, D, T and Q indicate single, double, triple and quadruple excited CSFs; Li–H distance: 3.015 bohr; All the HF solutions are ![]()
and were obtained using the new double-zeta base [7] ; The total energies (electronic + nuclear repulsion) of the HF solutions are indicated in the first column; The full CI energy is −8.01152345 hartree.
(b)
In the last column R indicates HF reference; S, D, T and Q indicate single, double, triple and quadruple excited CSFs; Li-H distance: 3.015 bohr; All the HF solutions are ![]()
and were obtained using the new double-zeta base [7] ; The total energies (electronic + nuclear repulsion) of the HF solutions are indicated in the first column; The full CI energy is −8.01152345 hartree.
![]()
Table 2. MRHFCI calculations of the dipole moment for the LiH molecule.
Total energies (electronic + nuclear repulsion) of the HF solutions: A = −7.98066895 hartree; B = −7.42164900 hartree; D = −5.46835770 hartree; L = 3.09788624 hartree; All the HF solutions are ![]()
and were obtained using the new double-zeta base [7] ; Experimental Dipole Moment value: 5.8280 debye.
![]()
Table 3. MRHFCI calculation of the energy of the Be atom.
Energies of the HF solutions: A = −14.57125146 hartree; B = −13.78788831 hartree; C = −3.47143646 hartree; All the HF solutions are 1S and were obtained using the new double-zeta base [7] .
Table 3 the first column indicates the number of CSFs employed in the MRHFCI calculation. The second and third columns indicate the HF solutions used and the MRHFCI energy obtained, respectively. The fourth column in the Table 2 presents dipole moment value obtained by the MRHFCI method. The last row in the Table 2 and Table 3 presents the full CI calculation. All the calculations presented in the Table 1(a) and Table 1(b), Table 2 and Table 3 were performed using the new dz base.
4. Conclusions
As observed in Section 2, in spite of the fact that the bases ![]()
generate the same CI space, the corresponding CSFs of each ![]()
base have distinct quantum in formation contents. The Table 1(a) and Table 1(b) show clearly this non-uniform distribution of QMIC with regard to energy of the twelve LiH HF solutions.
Table 2 and Table 3 show the possibility to make good use of this non-uniform distribution of QMIC using the reduced MRHF bases. As presented in Table 2 is possible to obtain the dipole moment of the LiH molecule in close agreement with the experimental value without prejudice to the energy of the state function. The MRHFCI energies differ less than ![]()
of the full CI energy. Besides, as shows in Table 3, the energy of the Be atom was obtained using only 25 CSFs and differs ![]()
of the full CI energy, which uses 102 CFSs. These results confirm the positive effect of the use of the MRHF bases already shown in our previous results.
A second step in this project, now in progress, is to study the composition of the CSFs of the system of generators ![]()
in terms of valence-bond and generalized valence-bond structures of interest [2a]. Future steps include search possible correlations between the CSFs of the MRHF bases that provided good values of the energies and one-electron properties. Data mining is a possible auxiliary tool to be employed [9] [10] .
Acknowledgements
L. A. C. Malbouisson thanks Professor M. A. Chaer Nascimento (Instituto de Química—Universidade Federal do Rio de Janeiro—Brazil) for his hospitality during the written of this work.
NOTES
*Corresponding author.