Opening of a Gap in Graphene Due to Supercell Potential: Group Theory Point of View ()
1. Introduction
Graphene is a two-dimensional crystal of carbon atoms, which form a honeycomb lattice with the point symmetry described by the group . The first Brillouin zone (BZ) has a hexagonal form, and the conduction band touches the valence band in six BZ corners which form two non-equivalent triads of BZ corners,
. The first Brillouin zone (BZ) has a hexagonal form, and the conduction band touches the valence band in six BZ corners which form two non-equivalent triads of BZ corners,  and
and . One of the routes toward tailoring the electronic properties of graphene is through the adsorption of metals [1] [2] . Recently, several types of adatoms were used to dope graphene in attempts to tailor properties of graphenebased devices [3] -[7] . The gap opening in the high symmetry points for the hexagonal lattices due to interaction with the interface was considered in [8] . In Ref. [9] , it was shown that, using ab initio density functional ory calculations, the adsorption of an alkali-metal submonolayer ongraphene occupying every third hexagon of the honeycomb lattice in a commensurate
. One of the routes toward tailoring the electronic properties of graphene is through the adsorption of metals [1] [2] . Recently, several types of adatoms were used to dope graphene in attempts to tailor properties of graphenebased devices [3] -[7] . The gap opening in the high symmetry points for the hexagonal lattices due to interaction with the interface was considered in [8] . In Ref. [9] , it was shown that, using ab initio density functional ory calculations, the adsorption of an alkali-metal submonolayer ongraphene occupying every third hexagon of the honeycomb lattice in a commensurate  arrangement induces an energy gap in the spectrum of graphene. We decided to analyze this opening of the gap in the framework of the group theory. In our previous publications [10] -[12] we summed up the classification of the energy bands in graphene on the basis of the point group analysis. The only fact from that analysis we need in the present work, is the fact that the little group at the point
arrangement induces an energy gap in the spectrum of graphene. We decided to analyze this opening of the gap in the framework of the group theory. In our previous publications [10] -[12] we summed up the classification of the energy bands in graphene on the basis of the point group analysis. The only fact from that analysis we need in the present work, is the fact that the little group at the point  is
is  and the bands
and the bands  and
and  realize
realize  representation of the group. The same can be said about the point
representation of the group. The same can be said about the point . This fact by itself means that the bands
. This fact by itself means that the bands  and
and  touch each other at the points
touch each other at the points  and
and , and the electron states in the vicinity of these points are described by massless Dirac equation [11] .
, and the electron states in the vicinity of these points are described by massless Dirac equation [11] .
For the purpose of the present paper, we should put the abovementioned fact into the framework of the theory of the space group symmetry [13] [14] , from which we will need only a few basic ideas. According to the theory of the space group symmetry, the bands  and
and  should be considered at the points
should be considered at the points  and
and  (these two points can be considered as the stars of the wave vector
(these two points can be considered as the stars of the wave vector , and designated
, and designated 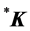 together, thus realizing a 4-dimensional representation of the
together, thus realizing a 4-dimensional representation of the  group. Due to the identity
group. Due to the identity
 (1)
(1)
any element of the group  can be presented as an element of the group
can be presented as an element of the group , or as a product of
, or as a product of  and such element. Representation of the point group
and such element. Representation of the point group  realized at the point
realized at the point 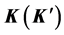 defines representation of the space group realized at
defines representation of the space group realized at . The matrix representing an element
. The matrix representing an element  is a super-matrix
is a super-matrix 
 (2)
(2)
super-indices 1 and 2 referring to the points  and
and  respectively. The matrix representing an element
respectively. The matrix representing an element  is
is
 (3)
(3)
We will not need the exact form of the non-diagonal matrix elements in Equation (3); what we need is the fact that the trace of the matrix  is equal to zero. Naturally, when we consider dispersion in grapheme as it is, space group symmetry point of view adds very little in comparison to point group symmetry point of view, because the Hamiltonian, which has the symmetry
is equal to zero. Naturally, when we consider dispersion in grapheme as it is, space group symmetry point of view adds very little in comparison to point group symmetry point of view, because the Hamiltonian, which has the symmetry , is block-diagonal.
, is block-diagonal.
Now we apply the group theory to analyze what happens at the points  in grapheme with a perfectly commensurate superlattice potential (which appears either because of the substrate or because of the absorbed atoms), which has the same point symmetry
in grapheme with a perfectly commensurate superlattice potential (which appears either because of the substrate or because of the absorbed atoms), which has the same point symmetry  as graphene. We consider explicitly a
as graphene. We consider explicitly a  superlattice, known as the Kekule distortion of the honeycomb lattice [9] . In this case we may consider the Bril-louine zone (BZ) of the superlattice as the folding of the original [9] [15] . The folding leads to the identification of the corners of the original BZ (
superlattice, known as the Kekule distortion of the honeycomb lattice [9] . In this case we may consider the Bril-louine zone (BZ) of the superlattice as the folding of the original [9] [15] . The folding leads to the identification of the corners of the original BZ ( and
and ) with the center
) with the center  of the new BZ. The Hamiltonian is no longer block diagonal and, because the points
of the new BZ. The Hamiltonian is no longer block diagonal and, because the points  and
and  are now identical, has the full symmetry
are now identical, has the full symmetry . We thus observe a paradox situation: due to decrease of the translational symmetry the point symmetry of the Hamiltonian has increased.
. We thus observe a paradox situation: due to decrease of the translational symmetry the point symmetry of the Hamiltonian has increased.
Because of the symmetry of the Hamiltonian, we need to decompose representation realized by Matrices (2) and (3) with respect to the irreducible representations of the group .To obtain the decomposition, it is convenient to use equation
.To obtain the decomposition, it is convenient to use equation
 (4)
(4)
which shows how many times a given irreducible representation 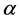 is contained in a reducible one [16] . In Equation (4)
is contained in a reducible one [16] . In Equation (4)  is the number of elements in the group,
is the number of elements in the group,  is the character of an operator
is the character of an operator  in the irreducible representation
in the irreducible representation  and
and  is the character of the operator
is the character of the operator  in the representation being decomposed. Actually, even without using Equation (4), just by inspection of the two lowest line of Table 1 we obtain the decomposition
in the representation being decomposed. Actually, even without using Equation (4), just by inspection of the two lowest line of Table 1 we obtain the decomposition
 (5)
(5)
We see that due to supercell potential two degenerate Dirac points disappear. At the point  we have two merging bands realizing representation
we have two merging bands realizing representation  and another two merging bands realizing representation
and another two merging bands realizing representation . We
. We

Table 1. Characters table for irreducible representations of  point groups.
point groups.
may expect that representation , as being more symmetrical, is realized at the top of the valence band, and the representation
, as being more symmetrical, is realized at the top of the valence band, and the representation  is realized at the bottom of the conduction band.
is realized at the bottom of the conduction band.
To get the form of the energy spectrum of the electrons in the vicinity of the point  let us consider both the
let us consider both the  term [17] and the supercell potential as a perturbation. The effective Hamoltonian is
term [17] and the supercell potential as a perturbation. The effective Hamoltonian is
 (6)
(6)
where
 (7)
(7)
and  reduces to two independent real constants
reduces to two independent real constants
 (8)
(8)
The specific form of the operator  follows from the symmetry of the base functions realizing representations
follows from the symmetry of the base functions realizing representations  and
and . By shifting origin of the energy axis these two constants can be chosen as
. By shifting origin of the energy axis these two constants can be chosen as
 (9)
(9)
Forming and solving the secular equation from these matrix elements, we obtain
 (10)
(10)
the sign plus corresponding to an upper pair of bands, and the sign minus corresponding to a lower pair of bands.
To resolve between the branches in each pair we should take into account  corrections to the operator
corrections to the operator . The first order in
. The first order in  corrections is equal to zero because the symmetry group contains the center of inversion. To the second order in
corrections is equal to zero because the symmetry group contains the center of inversion. To the second order in  we have
we have 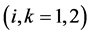
 (11)
(11)
where  is an Hermitian tensor operator (symmetrical in the suffixes
is an Hermitian tensor operator (symmetrical in the suffixes  and
and ). These include the corrections from the terms linear in
). These include the corrections from the terms linear in  in the Hamiltonian in the second-order perturbation theory and the corections from the terms quadratic in
in the Hamiltonian in the second-order perturbation theory and the corections from the terms quadratic in  in the first-order perturbation theory [17] . Notice that
in the first-order perturbation theory [17] . Notice that  is small relative to both
is small relative to both  (because we consider the states in the vicinity of the point
(because we consider the states in the vicinity of the point ), and with respect to
), and with respect to .
.
The relations exist between the matrix elements of the operator because of the requirements of symmetry. As regards their transformation law under the symmetry operations, the wave functions which form the basis of the representation  (1, 2 branches) can be taken in the form
(1, 2 branches) can be taken in the form
 (12)
(12)
and the wave functions which form the basis of the representation  can be taken in the form
can be taken in the form
 (13)
(13)
From this, we easily conclude that in the first case the matrix elements of the  reduce to three independent real constants
reduce to three independent real constants
 (14)
(14)
The matrix elements of the operator  are
are
 (15)
(15)
In the second case the matrix elements of the  also reduce to three independent real constants
also reduce to three independent real constants
 (16)
(16)
The matrix elements of the operator  are
are
 (17)
(17)
Forming and solving the secular equation from these matrix elements, we obtain the  branches of the spectrum
branches of the spectrum
 (18)
(18)
The sign of  is determined by the fact whether we are dealing with the lower or upper bands. The formula for the
is determined by the fact whether we are dealing with the lower or upper bands. The formula for the  branches of the spectrumcan is obtained similarly.
branches of the spectrumcan is obtained similarly.
The folding of the BZ, together with the destruction of previously existing gapless Dirac points, leads to appearance of the new ones. In fact, the new BZ is still a hexagon, and the same symmetry arguments used for graphene can be used to explain appearance of the gapless Dirac points at the corners of the new BZ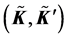 . However, these new Dirac points are situated deep below or high above the Fermi level, hence, less of them manifest themselves than Dirac points of unreconstructed graphene.
. However, these new Dirac points are situated deep below or high above the Fermi level, hence, less of them manifest themselves than Dirac points of unreconstructed graphene.