Nondegeneracy of Solution to the Allen-Cahn Equation with Regular Triangle Symmetry ()
1. Introduction
We are interested in the following Allen-Cahn equation
 (1.1)
(1.1)
There have been a lot of work on this equation during the last two decays (see for example [1] -[5] and the references there in). An important class of solutions to (1.1) is the multiple-end solutions. By definition, a solution  to (1.1) is called a multiple-end solution, if outside a large ball, the nodal curves of
to (1.1) is called a multiple-end solution, if outside a large ball, the nodal curves of  are asymptotic to finitely many half straight lines. One knows that these solutions have finite Morse index, and one also expects that any solution with finite Morse index should be a multiple-end solution. The most simple example of a multiple-end solution is
are asymptotic to finitely many half straight lines. One knows that these solutions have finite Morse index, and one also expects that any solution with finite Morse index should be a multiple-end solution. The most simple example of a multiple-end solution is , where
, where ,
,  , and
, and  is the heteroclinic solution:
is the heteroclinic solution:
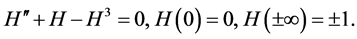 It is also well known ([6] ) that for each
It is also well known ([6] ) that for each ,
,  , (1.1) has a solution
, (1.1) has a solution  with regular polygon symmetry. More precisely, the nodal set of
with regular polygon symmetry. More precisely, the nodal set of  consists of
consists of 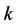 straight lines
straight lines
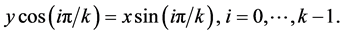
In the polar coordinate  (we abuse the notation and use the same symbol for the function
(we abuse the notation and use the same symbol for the function  in the
in the or
or  coordinate):
coordinate):
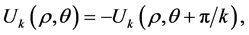
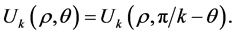
We could also assume . In the special case
. In the special case , the solution
, the solution  is called saddle solution. It turns out that
is called saddle solution. It turns out that  is not isolated in the set of 4-end solutions. Actually, there is a family of 4-end solutions to (1.1) containing
is not isolated in the set of 4-end solutions. Actually, there is a family of 4-end solutions to (1.1) containing  and the solutions
and the solutions  whose nodal lines are two almost parallel curves which are close to the solutions of the Toda system, see [7] [8] . In [9] , it is shown that for each
whose nodal lines are two almost parallel curves which are close to the solutions of the Toda system, see [7] [8] . In [9] , it is shown that for each , there is a family of 2k-end solutions whose nodal lines are close to suitable solutions of the classical Toda system. Intuitively, these solutions are in some sense on the boundary of the moduli space of 2k-end solutions and it is natural to expect that they are on the same connected component as
, there is a family of 2k-end solutions whose nodal lines are close to suitable solutions of the classical Toda system. Intuitively, these solutions are in some sense on the boundary of the moduli space of 2k-end solutions and it is natural to expect that they are on the same connected component as . In particular, one expects that around
. In particular, one expects that around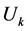 , there should be a family of 2k-end solutions to (1.1). While this is true for
, there should be a family of 2k-end solutions to (1.1). While this is true for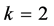 , in this paper, we will focus our attention on the solution
, in this paper, we will focus our attention on the solution .
.
To state our result in a precise way, let us introduce some notations.
We will use 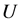 to denote
to denote . Let
. Let  be the linearized operator around
be the linearized operator around :
:
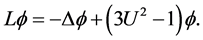
Our main theorem is the following nondegeneracy result:
Theorem 1.1 Assume  is a
is a  solution of the equation
solution of the equation  and
and
 .
.
Suppose furthermore that in the polar coordinate ,
,
 ,
,
 .
.
Then .
.
With the help of this theorem and the moduli space theory developed in [10] , we have the following Corollary 1.1 There is a family of 6-end solutions , different from
, different from , such that
, such that  in
in  as
as  and in the polar coordinate,
and in the polar coordinate,
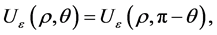
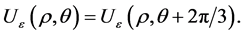
2. Proof of Theorem 1.1
To prove our main theorem, we will use the ideas developed in [11] . Assume to the contrary that  is not identically zero. As a first step, we show that
is not identically zero. As a first step, we show that  has the same symmetry as the function
has the same symmetry as the function .
.
Lemma 2.1 Under the assumption of Theorem 1.1,
 .
.
Proof. The crucial observation is that since ,
,
 (2.1)
(2.1)
Note that the Laplacian operator is taken with respect to the 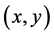 variable and in the Equation (2.1) the function is expressed in the polar coordinate.
variable and in the Equation (2.1) the function is expressed in the polar coordinate.
Consider the function

It follows from (2.1) that 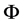 is also in the kernel of
is also in the kernel of , that is,
, that is,
 (2.2)
(2.2)
It will then suffice to show 
By the definition of  and the symmetric of
and the symmetric of , we have
, we have
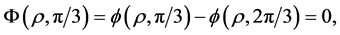
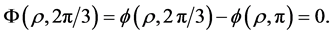
On the other hand, the solution  itself satisfies
itself satisfies
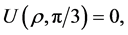
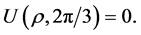
Moreover, in the region ,
,  is positive and is a supersolution of the operator
is positive and is a supersolution of the operator :
:
 (2.3)
(2.3)
Denoting , then it is well defined in
, then it is well defined in . From (2.2) and (2.3), we get
. From (2.2) and (2.3), we get
 (2.4)
(2.4)
Following similar arguments as that of Lemma 2.1 in [11] , with slight modification (one should take care of the fact that the right hand side of (2.4) is not identically zero), we could obtain 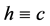 for some constant
for some constant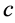 , which implies that
, which implies that
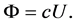
Since  decays to zero at infinity, we conclude
decays to zero at infinity, we conclude  and then
and then  This completes the proof of this lemma.
This completes the proof of this lemma.
Let  be the nodal set of
be the nodal set of . We proceed to show that
. We proceed to show that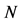 is bounded.
is bounded.
Lemma 2.2 There exists a constant  such that
such that
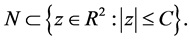
Proof. We first show that for each connected component 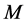 of
of , there exists a constant
, there exists a constant  such that
such that  is contained in the ball of radius
is contained in the ball of radius :
:
 .
.
We argue by contradiction and assume that  is unbounded.
is unbounded.
Case 1. 
In this case, we will consider . By the symmetry property of
. By the symmetry property of ,
,  is still connected and unbounded. Therefore, one could find a continuous and piecewise smooth curve contained in
is still connected and unbounded. Therefore, one could find a continuous and piecewise smooth curve contained in :
:
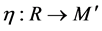
such that , as
, as . One then could consider the nodal domain
. One then could consider the nodal domain  of
of  contained in
contained in  whose boundary is the image
whose boundary is the image  of
of  (one could assume without loss of generality that
(one could assume without loss of generality that  does not have self intersection, otherwise, the presence of the supersolution
does not have self intersection, otherwise, the presence of the supersolution  yields a contradiction). Since
yields a contradiction). Since  is a positive supersolution of
is a positive supersolution of  in
in  similar arguments as Lemma 2.1 implies that
similar arguments as Lemma 2.1 implies that 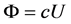 in
in  for some constant
for some constant , which is a contradiction.
, which is a contradiction.
Case 2. 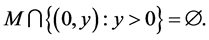
In this case, consider the region  Using symmetries of
Using symmetries of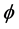 , we could assume
, we could assume But in
But in  (This follows from a moving plane argument, see for example [12] ) and
(This follows from a moving plane argument, see for example [12] ) and
 , in particular, it is a positive supersolution. Hence similar arguments as in Lemma 2.1 imply that
, in particular, it is a positive supersolution. Hence similar arguments as in Lemma 2.1 imply that , a contradiction.
, a contradiction.
Hence each connected component  is contained in a ball. To prove the assertion of this lemma, it will be suffice to show that there are only finite many connected components. We will assume to the contrary that there are infinite many of them. Then for each
is contained in a ball. To prove the assertion of this lemma, it will be suffice to show that there are only finite many connected components. We will assume to the contrary that there are infinite many of them. Then for each  large, one could find a nodal domain of
large, one could find a nodal domain of 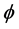 which is contained in
which is contained in
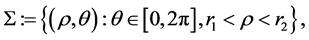
for some 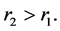 But when
But when  is large, since multiple-end solutions have finite Morse index, there is a positive supersolution
is large, since multiple-end solutions have finite Morse index, there is a positive supersolution  in
in :
:
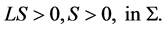
This contradicts with the maximum principle. The proof is thus completed. □
Now we are ready to prove our main theorem.
Proof of Theorem 1. Suppose  is not identically zero. By the previous lemmas, we could assume that
is not identically zero. By the previous lemmas, we could assume that when
when  is large enough, say for
is large enough, say for .
.
Let us consider the projection of  onto
onto . That is, we define the function
. That is, we define the function
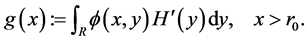
Note that 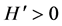 and hence
and hence .
.
We compute
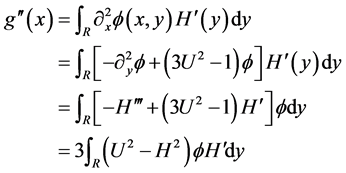
Since  (This could be seen from the construction of
(This could be seen from the construction of ), we find that
), we find that  for
for  large. On the other hand, by the assumption,
large. On the other hand, by the assumption,  , as
, as . Therefore as
. Therefore as 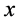 goes to infinity,
goes to infinity,  goes to zero. This contradicts with the fact that
goes to zero. This contradicts with the fact that  and the proof is thus completed. □
and the proof is thus completed. □
A simple application of Theorem 1.1 is Corollary 1.1.
Proof of Corollary 1.1 By Theorem 1.1, the solution  is nondegenerated in the class of functions having regular triangle symmetry. Then we could use the moduli space theory developed in [10] , in suitable functional spaces having these symmetry. This theory tells us that locally around
is nondegenerated in the class of functions having regular triangle symmetry. Then we could use the moduli space theory developed in [10] , in suitable functional spaces having these symmetry. This theory tells us that locally around  (in certain natural topology), the solution set has a structure of one dimensional real analytic manifold. Hence we get a family of 6-end solution
(in certain natural topology), the solution set has a structure of one dimensional real analytic manifold. Hence we get a family of 6-end solution  satisfying the property stated in Corollary 1.1. □
satisfying the property stated in Corollary 1.1. □
Remark 2.1 By the moduli space theory, the angles of consecutive ends of  will be close to
will be close to . We conjecture that these angles should be exactly equal to
. We conjecture that these angles should be exactly equal to . But this seems to be a difficult problem.
. But this seems to be a difficult problem.
Acknowledgements
Y. Liu is partially supported by NSFC grant 11101141 and the Fundamental Research Funds for the Central Universities 13MS39.