On the Structure of Infinitesimal Automorphisms of the Poisson-Lie Group SU(2,R) ()
1. Introduction
Let  be a Lie group. A Poisson-Lie structure on
be a Lie group. A Poisson-Lie structure on  is a Poisson structure on
is a Poisson structure on  for which the group multiplication is a Poisson map. Then as is usual in [1] -[3] , this is equal to giving an antisymmetric contravariant 2-tensor
for which the group multiplication is a Poisson map. Then as is usual in [1] -[3] , this is equal to giving an antisymmetric contravariant 2-tensor  on
on  which satisfies Jacobi identity and the relation
which satisfies Jacobi identity and the relation
 (1)
(1)
where  and
and  respectively denote the left and right translations in
respectively denote the left and right translations in  by
by  and
and . We note that a Poisson-Lie structure
. We note that a Poisson-Lie structure  has rank zero at a neutral element
has rank zero at a neutral element  of
of , i.e.,
, i.e., .
.
If we choose local coordinates  in a neighborhood
in a neighborhood 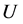 of neutral element
of neutral element  of
of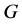 , the Poisson-Lie structure
, the Poisson-Lie structure  reads
reads
 (2)
(2)
where  are smooth functions vanishing at
are smooth functions vanishing at  and
and
 (3)
(3)
where  is the Poisson bracket associated to
is the Poisson bracket associated to . By this Poisson bracket,
. By this Poisson bracket,  becomes a Lie algebra.
becomes a Lie algebra.
Let  be a Lie algebra of
be a Lie algebra of . The derivative of
. The derivative of  at
at  defines a skewsymetric co-commutator map
defines a skewsymetric co-commutator map 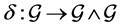 such that:
such that:
1) The map  is a 1-cocycle, i.e.,
is a 1-cocycle, i.e.,
 (4)
(4)
2) The dual map  is a Lie bracket on
is a Lie bracket on .
.
The map  is said a Lie bialgebra structure associated to
is said a Lie bialgebra structure associated to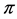 . Conversely, if
. Conversely, if  is simply connected, any Lie bialgebra structure
is simply connected, any Lie bialgebra structure  on the Lie algebra
on the Lie algebra  can be integrated to define a unique Poisson-Lie structure
can be integrated to define a unique Poisson-Lie structure  on
on  such that
such that .
.
The bialgebra structure  is called a coboundary one when there exists an skewsymmetric element
is called a coboundary one when there exists an skewsymmetric element  of
of  (the classical r-matrix) such that
(the classical r-matrix) such that
 (5)
(5)
Both properties 1) and 2) imply that the element  has to be a constant solution of the modified classical Yang-Baxter equation (mCYBE) [4] -[6] :
has to be a constant solution of the modified classical Yang-Baxter equation (mCYBE) [4] -[6] :
 (6)
(6)
Therefore, a constant solution of mCYBE  on a given Lie algebra
on a given Lie algebra  provide a coboundary Poisson-Lie structure
provide a coboundary Poisson-Lie structure  on (connected and simply connected) group
on (connected and simply connected) group  given by
given by
 (7)
(7)
where  and
and  denote respectively the left and right translations in
denote respectively the left and right translations in  by
by .
.
Finally, recall that for semisimple Lie algebras, all Lie bialgebra structures are coboundaries, and the corresponding Poisson-Lie structures can be fully solved through the classical r-matrices.
In this work, We shall treat the case of the Poisson-Lie group . We will calculate, firstly, all Poisson-Lie structures through the correspondence with Lie bialgebra; secondly, we will show that these Poisson-Lie structures are linearizable in a neighborhood of the unity
. We will calculate, firstly, all Poisson-Lie structures through the correspondence with Lie bialgebra; secondly, we will show that these Poisson-Lie structures are linearizable in a neighborhood of the unity 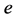 of the group
of the group  and, finally, we shall study infinitesimal automorphism of
and, finally, we shall study infinitesimal automorphism of  with a linear Poisson-Lie structure, and show that the Lie algebra
with a linear Poisson-Lie structure, and show that the Lie algebra , consisting of all infinitesimal automorphisms is strictly contained in the Lie algebra
, consisting of all infinitesimal automorphisms is strictly contained in the Lie algebra  consisting of Hamiltonian vector fields.
consisting of Hamiltonian vector fields.
2. The Group  and Lie Algebra
and Lie Algebra 
The special unitary group  is defined by
is defined by

Let  and
and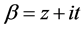 .
.  can be identified with the unit sphere
can be identified with the unit sphere  in
in 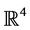 with the unity
with the unity .
.
The Lie algebra  of group
of group  is defined by
is defined by

Let

a basis of . The Lie bracket on
. The Lie bracket on  is defined by
is defined by
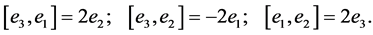
Through a straightforward computation, the left invariant fields associated to this basis had this local expression

3. The Lie Bialgebra Structure on  and the Poisson Lie Structure on
and the Poisson Lie Structure on 
3.1. Lie Bialgebra Structures on 
Recall that the Lie algebra  is semisimple. Then, all Lie bialgebra structures on
is semisimple. Then, all Lie bialgebra structures on  are coboundaries, there exists an skew symmetric element r of
are coboundaries, there exists an skew symmetric element r of  such that the cocommutator
such that the cocommutator  is given by
is given by

We stress that the element  satisfies the classical Yang-Baxter Equation (CYBE) (6). Through a long but straightforward computation, we show that these solutions are of the form
satisfies the classical Yang-Baxter Equation (CYBE) (6). Through a long but straightforward computation, we show that these solutions are of the form
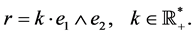 (8)
(8)
So any Lie bialgebra structure of  can be written as
can be written as
 (9)
(9)
3.2. Poisson-Lie Structures on 
Since the Lie bialgebra structures  on
on  are coboundaries, the Poisson-Lie structures on
are coboundaries, the Poisson-Lie structures on  corresponding to
corresponding to  are given by
are given by

where  is the solution of Yang-Baxter equation given by (8) and
is the solution of Yang-Baxter equation given by (8) and  and
and  respectively denote the right and left translations in
respectively denote the right and left translations in  by
by . Then, using
. Then, using ,
,  and
and  one gets
one gets
 (10)
(10)
Let
 (11)
(11)
be the components of  in the basis
in the basis  of the bivector field.
of the bivector field.
4. Linearization of Poisson-Lie Structures on 
By taking back the formula (2), The Taylor series of the functions 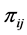 reads
reads
 (12)
(12)
where  are the structure constants of a Lie algebra
are the structure constants of a Lie algebra , dual of a Lie algebra
, dual of a Lie algebra , and the
, and the  are smooth functions vanishing at
are smooth functions vanishing at .
.
The term  of (12) definines a linear Poisson structure, called the linear part of
of (12) definines a linear Poisson structure, called the linear part of . The linearization problem for a structure
. The linearization problem for a structure  around
around  is the following [7] [8] :
is the following [7] [8] :
Linearization problem. Are there new coordinates where the functions  vanish identically, so that the Poisson structure is linear in these coordinates?
vanish identically, so that the Poisson structure is linear in these coordinates?
Let us notice that the Lie bialgebra structure  associated to
associated to  defines a linear Poisson-Lie structure on the additive group
defines a linear Poisson-Lie structure on the additive group 
 that can be expressed as follows
that can be expressed as follows
 (13)
(13)
where  is the canonical basis of
is the canonical basis of .
.
Let us notice that (13) coincides with the linear part of , so, the linearization problem would be the following:
, so, the linearization problem would be the following:
There is a local Poisson diffeomorphism  of a neighborhood in
of a neighborhood in  of G to a neighborhood of 0 in
of G to a neighborhood of 0 in ?
?
If 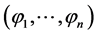 are the components of
are the components of , then
, then  is solution of the system of equations
is solution of the system of equations
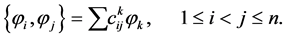 (14)
(14)
For the Poisson-Lie structure on  given by (10), the system of equations (14) would be
given by (10), the system of equations (14) would be
 (15)
(15)
With the identification of the subgroups of the singular points and the symplectic leaves of  and
and , we have:
, we have:
Proposition 1. The map :
: 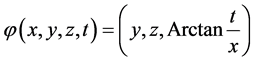 is a diffeomorphism in the neighborhood of
is a diffeomorphism in the neighborhood of  such that
such that  and
and

So, the Poisson-Lie structure  on
on  is linear in the new variables
is linear in the new variables
 (16)
(16)
and will be written
 (17)
(17)
The Poisson bracket associated to  reads
reads
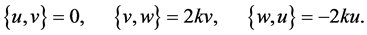 (18)
(18)
5. Casimir Functions and Infinitesimal Automorphisms on 
Recall that for ,
,  defines a derivation of
defines a derivation of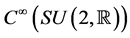 . Hence there corresponds a vector field
. Hence there corresponds a vector field , which we call the Hamiltonian vector field. We denote by
, which we call the Hamiltonian vector field. We denote by  the Lie algebra of Hamiltonian vector fields.
the Lie algebra of Hamiltonian vector fields.
A Casimir function on  is a function
is a function  such that
such that  for all function
for all function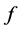 . On the other words,
. On the other words, 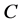 is an element of the center of the Lie algebra
is an element of the center of the Lie algebra . By simple consideration, we know that for each Casimir function
. By simple consideration, we know that for each Casimir function  there exists a function
there exists a function 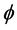 of one variable such that
of one variable such that .
.
Each symplectic leaf is the common level manifold of casimir functions. So, these have for equation:

and hence are spheres.
By an automorphism of , we mean a smooth vector field
, we mean a smooth vector field  on
on  such that
such that
 (19)
(19)
where  denotes the Lie derivative along
denotes the Lie derivative along .
.
If we denote by  the Lie algebra consisting of all infinitesimal automorphism, it is easy to see that
the Lie algebra consisting of all infinitesimal automorphism, it is easy to see that  is an ideal of
is an ideal of . Let
. Let  be a vector field of
be a vector field of . Then three function
. Then three function  and
and  must satisfy:
must satisfy:
 (20)
(20)
Now we shall clarify the gap between  and
and .
.
We consider the vector field
 (21)
(21)
where  are the components of the structure
are the components of the structure  in the basis
in the basis  given by (11).
given by (11).
In the local coordinates  given by (14), this vector field reads
given by (14), this vector field reads
 (22)
(22)
A simple check shows that the components of  satisfy the relations (20). So, the vector field
satisfy the relations (20). So, the vector field  belongs to
belongs to . In other hand,
. In other hand,  is locally Hamiltonian if and only if there exist a smooth function
is locally Hamiltonian if and only if there exist a smooth function  in a neighborhood of the unity
in a neighborhood of the unity  of the group
of the group  such that
such that , this is translated by the fact that
, this is translated by the fact that  is a solution of the following system of equations
is a solution of the following system of equations
 (23)
(23)
It is easy to see that (23) does not admit solutions. Hence  does not belong
does not belong . Thus we have proved:
. Thus we have proved:
Proposition 2. The ideal  is strictly contained in the Lie algebra
is strictly contained in the Lie algebra .
.
In terms of Poisson cohomology [9] , recall that the first Poisson cohomology group  is the quotient of the Lie algebra
is the quotient of the Lie algebra  by its ideal
by its ideal . Then, by Proposition 2, we show that the vector field
. Then, by Proposition 2, we show that the vector field  defines a non trivial class
defines a non trivial class . On the other hand, this result shows that the classical result due to Conn [10] [11] stating that for a Poisson structure formally linearizable around a singular point any local Poisson automorphism is Hamiltonian, and not just in the
. On the other hand, this result shows that the classical result due to Conn [10] [11] stating that for a Poisson structure formally linearizable around a singular point any local Poisson automorphism is Hamiltonian, and not just in the  category.
category.