Conformal Evolution of Waves in the Yang-Mills Condensate: The Quasi-Classical Approach

Roman Pasechnik, George Prokhorov, Grigory Vereshkov

1Research Institute of Physics, Southern Federal University, Rostov-on-Don, Russia 2Institute for Nuclear Research of Russian Academy of Sciences, Moscow, Russia.
Research Institute of Physics, Southern Federal University, Rostov-on-Don, Russia.
Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund University, Lund, Sweden.

DOI: 10.4236/jmp.2014.55032                

Abstract

We have constructed a consistent system of equations for the Yang-Mills quantum-wave fluctuations in the classical Yang-Mills condensate based on canonical quantization in the Heisenberg representation. Such a quasi-classical system has been thoroughly analyzed in the conformal limit in the linear and quasi-linear approximations, both analytically and numerically. We have found that interaction between waves and condensate triggers a significant transfer or swap of energy from the condensate to the wave modes in the SU(2) gauge theory. Remarkably, a similar energy swap effect has been found in the maximally-supersymmetric N=4 Yang-Mills theory, as well as in the two-condensate SU(4) gauge theory. Such a generic feature of Yang-Mills dynamics opens up vast phenomenological implications in ultra-relativistic Yang-Mills plasma physics.

Keywords

Gauge Theories; Canonical Quantization; Relativistic Yang-Mills Plasma; Quantum-Wave Fluctuations; Classical Yang-Mills Condensate

1. Introduction

A consistent non-perturbative theory of the Yang-Mills (YM) vacuum responsible e.g. for spontaneous chiral symmetry breaking and color confinement phenomena in quantum chromodynamics (QCD) [1] - [4] , has not yet been created. Self-interacting YM fields play an important role in yet poorly known quark-gluon plasma dynamics at high and low temperatures, including the problem of QCD phase transition, as well as complicated QCD dynamics at large distances. Also, the role of non-Abelian gauge fields in the early Universe evolution has been intensively studied in many different aspects, in particular, in the context of the Dark Energy [5] - [9] and non-Abelian fields driven inflation without the presence of a scalar field (“gauge-flation”) [10] [11] . Moreover, the modern dark energy can be in principle generated by quantum gravity corrections to the QCD vacuum energy [12] [13] . Very recently, it was understood that the unknown non-perturbative dynamics of the quantum- topological and quantum-wave modes of the YM vacuum could also be responsible for (partial or complete) compensation of the QCD instanton vacuum energy to the ground state energy of the Universe at cosmological scales [13] [14] . Thus, yet poorly known non-perturbative dynamics of the YM vacuum is one of the biggest theoretical issues of modern quantum field theory, and this situation strongly motivates us to search for a proper dynamical approach to the YM vacuum physics.

The major goal of our paper is to study dynamical properties of the spatially-inhomogeneous wave modes in the homogeneous YM condensate (YMC) incorporating interactions between the waves and the condensate in the simplest one-condensate 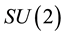YM theory. The wave modes are interpreted as particles after quantization procedure which constitute the ultra-relativistic YM plasma, and our purpose is to study the plasma properties taking into account its interactions with the condensate in a theoretically consistent way.

We work in Hamilton gauge―the only known gauge which allows to formulate the YM theory in the Heisen- berg representation beyond the perturbation theory (for more details, see e.g. Reference [15] ). Moreover, it is a ghost-free gauge which is important for our study since the Faddeev-Popov ghosts [16] do not have a physical interpretation in plasma physics. In the considered case we analyze the evolution of the homogeneous YMC in real time, and the Heisenberg representation is the most useful one for this purpose.

Let us mention a few aspects of the YM theory in Hamilton gauge which are important for our analysis. Typically, the YM theory is formulated in terms of the functional (or path) integral [15] . After introducing the Hamilton gauge into the functional integral for YM fields, one defines the S-matrix and all the incident propagators. As one of the attractive features of Hamilton gauge, the asymptotic states of such S-matrix automatically contain transverse modes only, without introducing extra selection rules. In the functional integral approach, the propagators in the YM theory are defined as Green functions of the equations of motion in Hamilton gauge, and the longitudinal modes of the YM field give a certain contribution to these propagators while they disappear in asymptotic states.

In our analysis, we take the following theoretically consistent pathway¹ which has certain methodological advantages for interacting systems of YM waves and YM condensates compared to the standard functional integral formulation:

• First, one starts with the YM Lagrangian in Hamilton gauge and writes down the Lagrange equations of motion in the operator form following to the Bohr’s correspondence principle;

• Second, since the zeroth component of the YM field 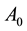is absent in the YM Lagrangian written in Hamilton gauge, there are no explicit constraint equations in the system of corresponding Lagrange equations. But this does not lead to any loss of information since the equations of constraint can be obtained as integrals of motion of the system of Lagrange equations;

• Third, from the Lagrange formulation of the YM theory one can turn to the Hamilton (or canonical) formulation and canonical quantization in a theoretically consistent way.

Let us discuss the third point of the above scheme in more detail. In the case of free YM field (without its interactions with the condensate), free longitudinal YM mode does not have any proper frequency and dispersion, thus in the Minkowski space without the condensate this mode is aperiodic. The latter has three consequences: 1) it does not contribute to the Hamiltonian; 2) it is impossible to calculate its contribution to the YM propagator as a vacuum expectation value of time-ordered operator product; 3) there is a problem with canonical quantization. The first consequence is essentially one of the advantages of the Hamilton gauge which excludes any non-physical degrees of freedom from the Hamiltonian. The other two consequences point out to the fact that the YM theory in Hamilton gauge cannot be constructed according to standard algorithms of a non- degenerate field theory. We found a simple alternative way to resolve the latter issue: in a system without the YMC we introduce extra “virtual” infinitesimal terms, which are proportional to an infinitesimal parameter, into the YM Lagrangian in Hamilton gauge. These terms are chosen in such a way that the longitudinal mode acquires a small dispersion proportional to the infinitesimal parameter which allows to perform canonical quantization in the standard way and to calculate a contribution of this mode to the YM propagator as a vacuum expectation value of time-ordered operator product. After canonical quantization procedure and construction of the YM propagator, the infinitesimal parameter is safely turned to zero leading to exactly the same S-matrix as the one defines in the standard functional integral formulation. This methodological trick therefore leads to theoretically consistent results and allows to realize the scheme described above in practice.

Consider now physically interesting case of the YM wave modes interacting with the YMC. Here, the situa- tion changes significantly, namely, in this case an important physical effect of dynamical generation of the lon- gitudinal plasma waves as collective excitations (also known as plasmons) of macroscopic medium takes place. The latter effect is well-known in physics of ordinary plasma [17] [18] as well as quark-gluon plasma [19] [20] (see also Reference [21] and references therein). These longitudinal waves acquire both proper frequency (proportional to density of the medium) and dispersion (proportional to thermal wave velocity squared).

A complete theory of quark-gluon plasma accounting for interactions between waves is very complicated and is not yet constructed. In this paper, we consider a simple one-condensate toy-model as our starting point where interactions between wave modes and condensate are taken into account only while interactions between differ- ent wave modes are not included. Physically, this situation corresponds to a YM system in the beginning of its time evolution with a few wave modes interacting with the condensate such that the interactions between waves are negligibly small compared to interactions of the waves with the condensate. Noticeably enough it turns out that even in this model the longitudinal modes acquire proper frequencies providing their periodic dynamics in agreement with previous considerations in the literature. Moreover, it turns out that as soon as one extracts the homogeneous condensate in the initial YM Lagrangian in Hamilton gauge, the canonical quantization of longi- tudinal modes automatically appears to be natural and theoretically consistent without introducing any “virtual” infinitesimal terms discussed above. Of course, the longitudinal (plasma) waves in the condensate get excited together with transverse ones so they contribute to observable quantities and must be taken into consideration on the same footing to the transverse ones. Based on the canonical framework we present in this paper and play out in the simplest one-condensate model, one may further extend this study incorporating effects of mutual interac- tions between different wave modes. Certainly, the latter have to be taken into account in a complete theory of ultra-relativistic gluon plasma.

The effect of dynamical generation of longitudinal modes in a YM medium and their dynamical role described above is well-known in the literature [21] and we discuss it here only for completeness and validation of our approach. The basic new result of our study is observation that the interactions between the YM waves and the condensate in a simple 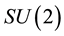YM theory trigger a significant energy transfer in one particular direction, namely, from the condensate to the wave modes². Such a specific energy swap effect between the two vacuum subsystems may have serious consequences to the theory of non-perturbative YM vacuum and, in particular, may have important phenomenological implications e.g. in the theory of QCD phase transition in early Universe and in particle production mechanisms in the hot cosmological plasma.

To start with, we have constructed the exact quasi-classical equations for the wave modes and the condensate, and investigated them in the linear approximation (in small wave amplitudes limit). In this case, the equations of motion have a characteristic form of Mathieu equations having certain regions of parametric resonance instabil- ity which leads to an increase of amplitude of the waves. As was argued above, the constraints written for the system of interacting homogeneous YMC and inhomogeneous waves do not allow to exclude the longitudinal modes, such that these extra d.o.f. acquire their own dynamical properties due to interactions between the two subsystems.

As a consequence of energy conservation, an increase of the YM waves energy reflected in a corresponding increase of their amplitudes has to be accompanied by a corresponding decrease of the YMC energy. In particu- lar, this fact must be taken into account in derivation of the quasi-linear YMC equation of motion where the “back reaction” effect of the wave modes to the YMC is consistently incorporated. The numerical analysis of the resulting system of equations has indeed revealed the energy swap effect satisfying the energy conservation: a decrease of the YMC energy is exactly compensated by an increase of energy attributed to the wave modes, which is an important test of our calculations. In addition, we have investigated the energy spectrum of the free YMC steady-state solutions of the corresponding Schrödinger equation. Interestingly enough, it has been found that its energy spectrum corresponds to a potential well of the fourth power.

Further, we have generalized our study to the maximally 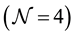supersymmetric YM (SYM) theory (see e.g. Reference [22] ). As one of the specific features of this theory is its conformality such that its 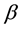-function disappears (i.e. the coupling constant does not acquire radiative corrections and therefore does not run), which significantly simplifies our calculations. The 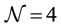SYM theory includes four different fermion fields, three scalar and pseudoscalar fields. We have shown, both numerically and analytically, that interactions of supersymmetric wave modes with the YMC lead to similar energy swap effect from the YMC to the (pseudo) scalar wave modes as it was earlier observed for the vector wave modes. We also studied the heterogenic system of two interacting YMCs in the 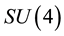gauge theory and similar energy swap effect has been found. These findings strongly suggest that the observed dynamics in energy balance of the interacting YM system (wave + condensate) is a general phenomenon and specific property inherent to YM theories. Inclusion of colored fermion modes into our quasi-classical analysis is relevant for particle production mechanisms in early Universe and will be done elsewhere.

The paper is organized as follows. In Section II we derive the equations of motion for the YMC and YM wave modes in the first (linear) approximation. An extension to the quasi-linear case accounting for the leading-order “back reaction” effect of the wave modes to the YMC has been performed and thoroughly investigated in Section III. In Section IV we apply our quasi-classical approach to the 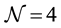super-Yang-Mills theory. Section V contains a discussion of the two-condensate 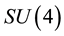model. A few concluding remarks were made in Section VI. Appendix A is devoted to details of the Hamilton formulation of the YM theory where the YM propagator has been derived by using the method of infinitesimal parameter. Finally, canonical quantization of the YM wave modes in the classical YMC has been performed in Appendix B as a consistency check of our quasi-classical analysis.

2. Yang-Mills Dynamics in the Linear Approximation

2.1. An Overview of Degenerate Yang-Mills Theory

For a comprehensive introduction to the theory of YM fields we refer to the standard quantum field theory textbooks [15] [23] . At first, we would like to remind a few important basics of the classical degenerate YM theory useful for our analysis below.

The Lagrangian of a pure YM field is

(1)

where

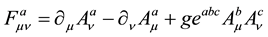
is the YM stress tensor as usual. Here, we work with the 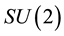symmetry group with isotopic 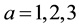and Lorentz indices. There are twelve equations of motion in the degenerate case given by

(2)

Imposing the Hamilton (or Weyl) gauge

(3)

we end up with nine equations of motion

(4)

and three constraints in the form of first integrals of motion

(5)

The total time derivative here can be removed in degenerate case, i.e.

(6)

2.2. First-Order Yang-Mills Equations of Motion

It has been demonstrated in Refs. [5] - [7] that due to isomorphism of isotopic and spatial symmetry groups the unique (up to scaling) YM configuration can be parameterized in terms of a sca- lar time-dependent field. This field contains both electric and magnetic components. One can therefore introduce a mixed space-isotopic basis such that in this basis the YM vector field transforms into a tensor field with two spatial indices³ and. The isotopic symmetry group and the group of spatial 3-rotations are isomorphic which allows to introduce the mixed orthonormal space-isotopic basis as follows

(7)

Thus, a trivial projection of the Yang-Mills vector field in the basis can be represented as follows [5] - [7]

(8)

Here, the spatially-homogeneous time-dependent scalar field corresponds to the YM vacuum condensate (YMC). The quantum-wave part is spatially-inhomogeneous and describes motion of YM quanta, namely, physical particles after quantization.

The representation (8) enables us to rewrite the YM equation of motion (4) through the YMC, , and the wave modes, , separately as follows

(9)

The constraint Equation (6) provides an extra condition:

(10)

The Equation (9) is separable by averaging over the Heisenberg state vector. To the leading (zeroth) order in fields, the equation for the YMC becomes

(11)

which has to be fulfilled in order to find the equations of motion for the free YM wave modes in the first (linear) approximation. It is convenient to turn to Fourier transforms for modes and expand them over the tensor basis [24] . In terms of symmetric and antisymmetric parts, the tensor field reads

(12)

Then, we expand the Fourier transforms of antisymmetric and symmetric modes into the tensor basis as

(13)

and

(14)

respectively, where the coefficients satisfy the following conditions

(15)

Thus, instead of nine components of the tensor, we have introduced nine new d.o.f. In Equations (13) and (14), 3-vectors and are the longitudinal and transverse unit vectors, respectively, and is the corresponding Fourier 3-momentum. In what follows, we omit the Fourier momentum index. Next, let us rewrite the general equation of motion (9) (after a proper subtraction of the YMC Equation (11)) through new d.o.f. to the linear approximation as the following system of equations

(16)

and

(17)

where we introduced the following shorthand notations:

(18)

Therefore, one arrives at the system of nine equations of motion for nine d.o.f. Finally, the equations of constraint (10) can be conveniently transformed to the following explicit form in terms of new d.o.f.

(19)

(20)

It is straightforward to check that these two constraints are automatically satisfied for a solution of the system of YM Equations (16) and (17). Note, in a degenerate YM theory, these constraints do not explicitly contain time derivatives, i.e.

(21)

(22)

which are thus the first integrals of motion in this case.

For further considerations and consistency checks, it is instructive to represent quadratic Lagrangian and Hamiltonian densities of the YM wave modes interacting with the YM condensate in terms of the new d.o.f. as follows

(23)

(24)

It is straightforward to check that the system of Equations (16) and (17) can be obtained directly from Equations (23) or (24) in usual way. Finally, the complete effective YM Hamiltonian density properly including the YMC dynamics can be represented in terms of (24) as follows:

(25)

which will be used below in studies of the dynamical properties of the “waves + condensate” system below.

2.3. Free Yang-Mills Condensate

The equation of motion which determines dynamical properties of the YMC, , has been derived to the leading order in the previous subsection and is given by Equation (11). Its numerical solution is shown in Figure 1(a). To a good accuracy, the latter exhibits a non-linear oscillation pattern and can be approximated by a quasi- harmonic function with frequency of oscillations depending on their amplitude, e.g.

(26)

where is the Euler beta function. The maximal error of this approximation is limited by.

The energy spectrum of quasi-harmonic YMC fluctuations can be found in standard way from the Schrö- dinger steady-state equation and is shown in Figure 1(b). Starting from the Hamiltonian density for free YMC

one arrives at the Schrödinger equation

(27)

It straightforward to show that the free YMC spectrum corresponds to a potential well of the fourth power. Numerical calculation provides us with the first few energy levels in the spectrum (see also, Reference [25] ), e.g.

(28)

For practical use, it is convenient to come up with an approximate analytic formula for the lower end of this

(a) (b)

Figure 1. Numerical solution of the YM equation of motion (11) for the time dependence of free YMC potential, , and its analytical approximation (26) for a fixed initial phase (a) and numerical result for the energy spectrum of free YMC, , and its continuous analytical approximation (29) (b).

spectrum, e.g. in the following form

(29)

The maximal error of this formula for the first thirty energy levels does not exceed 4%.

2.4. Wave Modes

Now, consider dynamics of the wave modes in the linear approximation (without taking into account for the “back reaction” of wave modes to condensate) encoded in the system of YM Equations (11), (16) and (17). In fact, Equation (16) is a closed system of two equations for two functions, and thus can be analyzed separately. By an appropriate choice of the frame of reference, the matrices and vector can be represented in the following simple form:

Further, introducing superpositions

Equation (16) in the above basis falls apart into two independent equations for

which are recognized as Mathieu equations. Here, is a solution of YMC Equation (26). Notably, the parametric resonance (or instability) domains are well known for this type of equations. In particular, for the tensor mode the first such parametric resonance instability domain can be found approximately as

where is an initial value of YMC. Other wave modes have different resonance-like instability domains which can be found numerically.

An analytical analysis of remaining Equation (17) is less feasible due to the presence of quadratic term in YMC,. In addition, our numerical study has shown that one should not use the approximation (26) in this case such that dynamics of the wave modes becomes very different from the well-known picture of parametric resonance in the case of Mathieu equations. Nevertheless, exact numerical analysis of the complete system of equations reveals the existence of the resonance-like instability domains for all of the wave d.o.f. analogical to the rigorous parametric (Mathieu) resonance one of the mode.

As an example, in Figure 2 we represent the normalized numerical solution for one of the wave modes, , for two distinct cases: a solution with monotonically growing amplitude for (left) and a solution from the parametric resonance-type instability domain with harmonic impulses for a particular value of momentum (right). The observed growth of amplitude or, equivalently, its energy is triggered by its interactions with the YMC. The same effect has been observed for all other modes as well. We thus conclude that the particles energy dynamically increases in the course of time evolution of “particles + condensate” system due to parametric resonance-like instability of numerical solutions of the non-linear YM equations.

2.5. Free Yang-Mills Field and Longitudinal d.o.f.

Let us consider the limiting case of free YM field without taking into account its interactions with the YMC, i.e. setting in Equations (16) and (17). In this case we have the following reduced system

(a) (b)

Figure 2. Example of normalized numerical solution of the system of YM Equations (11), (16) and (17) for one of the wave modes, , in the case of monotonic growth of oscillations for (a), and in the resonance-like instability domain with harmonic impulses for a particular value (b).

and two constraints

since the considered case with corresponds to a degenerate YM theory. Notably, now the constraints allow to eliminate three d.o.f., namely, and, which can be associated with three unphysical longitudinal polarisations of free gauge field such that

(30)

Thus, in the considering limiting case the constraints reduce the number of physical d.o.f. from nine down to six transverse ones. Note, such a reduction is not possible for non-zeroth interactions with the YMC, e.g. when in Equations (16) and (17). This is because in the general case the constraints (21) and (22) cannot be represented in the form of motion integrals as it used to take place in the standard case without the YMC such that the longitudinal d.o.f. cannot be eliminated anymore. This fact essentially means that interactions of the wave modes with the homogeneous YMC dynamically generate three additional d.o.f. and, such that both the longitudinal and transverse polarisations of interacting YM field have the status of physical d.o.f. and therefore must be treated on the same footing. The latter statement is in a good agreement with the canonical quantization procedure (see Appendices A and B) and is confirmed by numerical analysis of the complete system (16) and (17).

3. “Back Reaction” of the Wave Modes to the Condensate

3.1. Dynamics of YMC in Quasi-Linear Approximation

Due to energy conservation the growth of energy of the wave modes observed in the previous Section has to be followed by a certain redistribution of energy between YMC and wave modes. In order to take into account this effect consistently it is necessary to incorporate second-order contributions to the YMC equation for (11) which account for interactions between condensate and particles as follows

(31)

Here, the averaging is performed over the Heisenberg vector state. Since equal wave modes with different momenta do not interact with each other then all their products disappear upon the averaging, so only products of different (interacting) modes remain. Besides, all linear and cubic terms in waves also disappear in the considering quasi-linear approximation as well.

The effective second-order Hamiltonian density incorporating the “back reaction” effect of the wave modes to the YMC can be represented as a sum of three components corresponding to the free YMC, , free wave modes (or particles), , and the term accounting for interactions between these two subsystems, , respectively. Let us consider for simplicity interactions of the YMC with three wave modes, and only which form a closed subsystem of equations and hence can be considered separately. In this case extracting the corresponding contributions from the effective Hamiltonian density given by Equation (25) we obtain

where dots stand for omitted contributions from other modes. It can be seen from these expressions that interaction term is not sign-definite in distinction to positively-definite condensate and waves contributions.

In our numerical analysis and in all the plots in this paper we consider the complete system of all nine wave d.o.f. and YMC including interactions between them. We found that wave-condensate interactions lead to a decrease of amplitude of the YMC oscillations in time as is seen in Figure 3(a). An analogical picture of damping of the condensate oscillations is observed in the reduced (closed) system of, and wave modes and the YMC. We have also calculated the energy evolution of particles and condensate shown in Figure 3(b). These plots clearly illustrate the energy transfer (swap) effect from the YMC to particles due to interac- tions between them.

In addition, interactions between the YMC and wave modes (particles) lead to a redistribution of energy between the modes with different impulses which rather strongly depends on particles momentum due to para- metric resonance-like instability of YM solutions. The latter happens because the interaction strength, and hence the energy transfer intensity, depends on amplitude of impulses which is different for different modes and particles momenta (for a given mode). As an illustration of this effect, in Figure 4 we show the particle momen-

(a) (b)

Figure 3. Time dependence of the YMC in the quasilinear approximation in the complete system of wave modes (a), and the evolution of condensate, YM wave modes (or particles), and interaction term contributions to the total energy in the complete system of wave modes (b). The illustrated numerical solutions are physical for relatively small wave amplitudes, i.e. corresponding to.

Figure 4. Particle momentum dependence of the ratio of averaged absolute value of the wave amplitude at a fixed final (when most of the energy of the system is concentrated in waves) to the initial amplitude at (when all energy of the system is concentrated in the YMC). The latter ratio accounts for the maximal deviation in the wave amplitudes within the time interval between and. The results are shown for transverse and longitudinal modes.

tum dependence (in dimensionless units) of the ratio of averaged absolute value of the wave amplitude at a fixed final (when most of the energy of the system is concentrated in waves) to the initial amplitude at (when all energy of the system is concentrated in the YMC). The results are shown for transverse and longitudinal modes and are qualitatively the same for all the other modes. We notice that an increase in wave amplitude due to parametric instability may be rather strong close to the peak regions in corresponding energy spectra. One therefore observes the ultra-relativistic particles production effect with momenta close to the resonant momenta in a vicinity of maxima points in Figure 4.

As the main physical result to be emphasized here, we have found the significant energy swap effect between the YMC and particle-like modes of the ultrarelativistic YM plasma due to their interactions in quasilinear approximation. Due to energy conservation it is clear that the parametric resonance for the mode or a resonance-like instability for other modes in general is accompanied by an energy flow from the YMC to the waves. So the resonance-like instability of the quantum-wave solutions in the classical condensate is the physical reason of the energy swap effect. Note, that in Figure 3(b) we should restrict ourselves to maximal time scales of about one period of YMC fluctuations,. At larger time scales the amplitude of the wave fluctuations becomes comparable to the amplitude of condensate fluctuations so the considering quasilinear approximation breaks down there. Let us study sensitivity of our solutions with respect to higher- order corrections in detail.

3.2. Stability of Results with Respect to Higher-Order Corrections

So far we have considered the YM wave dynamics in the classical YM condensate in the first (leading or linear) approximation, while the YMC dynamics―in the leading (linear) and next-to-leading (quasi-linear) approximations. The range of applicability of our quasi-classical analysis is limited to small quantum-wave fluctuations in the condensate considered as a classical background, i.e. in the asymptotics.

It has been demonstrated above that the interactions between the wave modes and the condensate lead to an increase of energy accumulated by the wave modes at expense of a corresponding decrease of YMC energy. This means that as some point in evolution of the system the amplitude of wave modes becomes too large so that the initial approximation breaks down. Such a breakdown can be noticed in numerical results in the quasi-linear approximation, e.g. in YMC dynamics given by a numerical solution of Equations (16), (17) and (31) illustrated in Figure 5 by red line. It is clearly seen from this figure that at relatively large time scales increasing the time domain of effective energy swap from the condensate to waves, the YMC energy becomes

Figure 5. Time evolution of the YMC in the complete quasi- linear problem given by a numerical solution of Equations (16), (17) and (31) (red line) and in the problem with extra higher order terms included (36) (blue line).

singular and unbounded. The latter anomaly is due to breakdown of the quasi-linear approximation. In what follows, we show that inclusion of the principal part of the higher-order terms into the linear Equations (16) and (17) for the wave modes allows to eliminate such anomalies and reveals qualitative stability of the energy swap effect under consideration.

The equations of motion for the wave modes in a given order are normally constructed after elimination of the equation of motion for the YMC from generic Equation (9). Denote the left side of Equation (9) as such that equations for the modes take the following form

(32)

where denotes averaging over the Heisenberg state vector as usual. For simplicity, we take into account the last two terms in Equation (9) only. Omitting all other higher-order terms in Equation (32) we have

(33)

Now let us multiply by in a different space-time point in order to make the terms of the fourth order such that

(34)

due to Equation (32). Here each fourth-order term can then be transformed as follows

(35)

Omitting function and performing Fourier transform of the remaining terms we obtain

(36)

We notice here that the third-order terms have transformed to effective mass terms given by averages of various two operator products. In particular, Figure 5 (blue line) illustrates that such higher-order effective mass terms eliminate formal singularities in the YMC such that the numerical solution stabilizes and the energy swap effect discussed above remains at the qualitative level.

Certainly, this simplified analysis is not complete and is aimed only at illustrating that inclusion of the major part of higher-order terms significantly improves and stabilizes the results of the quasi-linear model. In a fully consistent model one has to take into account contributions from all the higher-order terms both in the wave equations of motion and in the YMC equation simultaneously, which will be done elsewhere.

4. Supersymmetric Extension of Pure YM Theory

Now we would like to extend our analysis to the supersymmetric Yang-Mills theory with which contains additional spinor, scalar and pseudoscalar d.o.f. (see e.g. Reference [22] ). The corresponding Lagrangian reads

(37)

Here are the isotopic indices, numerate different types of scalar and pseudoscalar fields, numerate different flavors of fermions. Next, we decompose additional supersymmetric modes into transverse and longitudinal components in momentum space as follows

Also, we perform the corresponding tensor decompositions for the YM field which enters the covariant derivative and stress tensor in the same way as is done above.

Next, let us rewrite the supersymmetric part of the Lagrangian density (37) in terms of new Fourier modes and. The supersymmetric YM Lagrangian density (23) is given in terms of wave modes and condensate by

(38)

and the corresponding Hamiltonian density (24) has a form

(39)

The equations of motion for the extra supersymmetric d.o.f. can be constructed in the standard way as Lagrange (or Hamilton) equations based upon Equation (38) (or Equation (39))

(40)

(41)

(42)

(43)

The equations for pseudoscalar modes and are the same as equations for (40) and (41), respectively. A numerical analysis of these equations in the linear approximation (with free YMC) has shown that qualitative behavior of the (pseudo)scalar modes is analogical to that of the YM wave modes discussed above. Finally, the equation of motion for the YMC in the quasi-linear approximation accounting for “back reaction” effects of the wave modes (including supersymmetric ones) to the condensate reads

Taking into consideration only additional scalar and pseudoscalar fields in numerical analysis we notice that the qualitative picture of YMC dynamics shown in Figure 3 is not changed. Also, energy of extra d.o.f. grows effectively due to the energy swap effect in the parametric resonance-like instability region similarly to other YM wave modes. Note, a consistent analysis of Equations (42) and (43) for the spinor modes can only be performed in the framework of quantum field theory approach, which is planned for further studies.

5. Two-Condensate Model

As has been pointed out in the beginning of Section II, the YMC is a dynamical vacuum object which can be introduced for the YM field in Hamilton gauge based on isomorphism of gauge and spatial symmetry groups. Let us consider a higher gauge group, which would contain a few subgroups isomorphic to. The simplest group of this type is. It contains two subgroups which means that the YM field, described by local gauge group, contains two condensates. The main focus of this Section is to discuss dynamical features of such a heterogenic vacuum system.

The generators of gauge group can be written as

(44)

The generators and correspond to subgroups, and structure constants are given by

(45)

In the Hamilton gauge, two different YMCs corresponding to each subgroup can be introduced in analogy with Equation (8), i.e.

(46)

where

(47)

The equations of motion are given by general formula from the classical YM theory (4). The equations for free (non-interacting) condensates and can be easily extracted from Equation (4)

Note, these equations do not contain mixed terms like and coincide with Equation (11). This means that the condensates and in the theory do not interact with each other directly. As we will demonstrate later, they can interact only by means of particle exchanges.

The linear equations of motion for the Fourier transformed wave modes (we omit index below) are

(48)

One can show by a direct calculation that equations for the wave modes corresponding to each of the subgroups (with and, respectively) coincide with analogical equations in the one- condensate model (9) (or with Equations (16) and (17) in terms of the tensor basis modes).

Now let us investigate the quasi-linear “back reaction” effect of the wave modes to YMCs. Including next (second) order in waves, the equation for the condensate reads

(49)

The corresponding equation for the second condensate has an analogical form. By a direct calculation it can be shown from Equation (49), analogical equation for and Equation (48) that the wave modes corresponding to the first and second subgroup interact only with its own condensate and, respectively, in the same way as they do in the one-condensate model considered above. Remarkably enough, other 27 modes corresponding generators of interact with both condensates at the same time. This means that interaction between and condensates is realized via particle exchanges only related to these remaining 27 wave modes. This effect is explicitly confirmed by a numerical analysis.

In general, time evolution of wave modes of the theory and two YMCs is analogical to the case of one-condensate system illustrated in Figure 3, i.e. energy of the both condensates is transferred into the ultra- relativistic YM plasma. This study suggests that the observed effect of energy swap is a generic feature of YM dynamics.

6. Conclusions

Starting from the basic idea about an important dynamical role of the YMC (8), we have constructed a consistent quasi-classical approach based on Hamilton formulation and canonical quantization of the wave modes in the classical YMC. This approach has been applied in analysis of the system of YM wave modes (or particles after quantization) in the ultra-relativistic plasma interacting with the YMC (in the limit of small interactions between waves).

Namely, we have derived the YM equations of motion for the waves in condensate in linear approximation (16), (17) and (11) in the gauge theory and numerically investigated their solutions. In order to understand how interactions of waves with condensate affect the energy balance between these two subsystems, we have investigated a consistent problem in the quasi-linear approximation accounting for the “back reaction” effect of particles to the condensate (31). The results of numerical analysis are presented in Figures 3 and 4 and demonstrate a specific energy swap effect, namely, an effective energy transfer from the YMC fluctuations to the YM wave modes heating up the ultra-relativistic plasma. The latter effect can be important for better understanding particle production mechanisms e.g. in the hot cosmological plasma which is the matter for further studies. Interaction of the wave modes with the YMC leads to dynamical generation of effective longitudinal d.o.f in the plasma increasing the number of physical modes from six to nine. The quantum energy spectrum of free YMC has been found from stationary Schrödinger equation. It turned out that this spectrum corresponds to a potential well of the fourth power, and a convenient analytical approximation to the discrete numerical solution has been proposed.

It has been shown that dynamics of waves and condensate in the extended supersymmetric YM theory is analogical to the one of pure YM theory discussed above. In particular, it has been indicated that interaction of the supersymmetric (pseudo)scalar wave modes with the YMC leads to a similar energy swap effect between them. We also studied the heterogenic system of two interacting YMCs in the gauge theory and similar energy swap effect has been found. These findings strongly suggest that the observed dynamics in energy balance of the interacting YM system (wave + condensate) is a general phenomenon and specific property inherent to YM theories.

As the main result of this paper, the energy redistribution effect from the YMC to the YM wave modes has been found and investigated from the first principles of quasi-classical YM theory in one- and two-condensate cases. This effect can be of major importance for cosmological processes in the early Universe, in particular, in the processes of particle production during the preheating period after cosmic inflation which is planned for further studies. In addition, an extension of the quasi-classical approach to a full quantum field theory formalism (including fermion modes) could become one of the next important steps in further theoretical understanding of dynamics of the wave modes interacting with the condensate.

Acknowledgements

This work was supported in part by the Crafoord Foundation (Grant No. 20120520). R. P. is grateful to the “Beyond the LHC” Program at Nordita (Stockholm) for support and hospitality during completion of this work.

Appendix A: Hamilton Formulation of the Yang-Mills Theory

The major difficulties of the canonical quantization of the free YM field (without the YMC) arise due to the presence of its time-retarded zero component in the Lagrangian (1). One of the ways to resolve this issue is based upon the method of expansion in configuration space elaborated in Refs. [26] [27] . Here we follow anoth- er way using the ghost-free Hamilton gauge (3) and the method of infinitesimal parameter discussed below.

Let us construct the YM propagator in the form of chronologically ordered vacuum average of operator product. In a realistic case, consider a system of a YM field and a color-charged multiplet of fermions. The Lagrangian and Hamiltonian densities of such a system are

(50)

(51)

respectively. Then, the corresponding Lagrange equations of motion read

The canonical quantization procedure is based upon the (anti)commutation relations between the field operators

where generalized momenta conjugated to the fields and are found as

respectively. Here we kept color index of a quark flavor for transparency, while it is often omitted in other places. The system of quantum equations of motion can be written in Heisenberg representation

as well as in the interaction representation

(52)

After Fourier transformation, the equations for longitudinal and transverse components of the YM field take the following form

(53)

respectively. The equation for longitudinal mode does not have a wave solution, so it is impossible to take into account its contribution in the YM propagator constructed as a vacuum average of the chronologically ordered operator product. In order to resolve this problem we can modify the Hamiltonian density by means of adding an extra small “virtual” term depending on an infinitesimal parameter and vanishing at, i.e.

After such modification the equation of motion for the longitudinal component becomes

(54)

such that it acquires an infinitesimal frequency. This modified equation enables us to incorporate the longitu- dinal mode into the YM propagator which is given by (in the limit)

(55)

where is the zeroth component of YM quantum momentum. The fermion propagator takes the standard form:

(56)

As an important test of the proposed method of infinitesimal parameter, the Formulas (55) and (56) turn out to coincide with the corresponding Green functions constructed for initial (non-modified) Equation (52).

Appendix B: Canonical Quantization of YM Wave Modes

Let us now perform canonical quantization of the YM wave modes in the classical YMC and therefore construct the quasi-classical YM theory. For this purpose, as the matter of the Bohr’s correspondence principle we introduce operators instead of field functions in the Hamiltonian density of, for example, the supersymmetric YM theory (39). Then we impose (anti)commutation relations to the field operators for each wave mode as follows

Commutation relations for pseudoscalar modes and are the same as for scalar ones and, respectively. In addition, analogical formulas for Hermitian conjugate modes etc should be added.

Finally, quantum Hamilton equations in commutators can be constructed in the standard way. For example, for the mode we have

(57)

Such equations written for all wave modes coincide with the corresponding equations of motion which were constructed previously (16), (17) and (40)-(43). The latter is an important validation of our calculations.

NOTES

^*Corresponding author.

¹Of course, we do not say anything new here for the S-matrix theory and the gain is purely methodological since this scheme can be consistently extended to an interacting system of the YM field and the YMC relevant for our purposes here.

²The existence of longitudinal modes is not critical for the observed energy transfer effect.

³Since there is not zero index in the considering gauge, in what follows one can use only lower indices for contravariant tensors and covariant derivatives, while repeated indices are assumed to be summed up.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Belavin, A.A., Polyakov, A.M., Schwartz, A.S. and Tyupkin, Y.S. (1975) Physics Letters B, 59, 85-87. http://dx.doi.org/10.1016/0370-2693(75)90163-X
[2]	Schafer, T. and Shuryak, E.V. (1998) Reviews of Modern Physics, 70, 323. http://dx.doi.org/10.1103/RevModPhys.70.323
[3]	Gogohia, V. and Toki, H. (2000) Physical Review D, 61, Article ID: 036006.
[4]	Gogohia, V. and Kluge, G. (2000) Physical Review D, 62, Article ID: 076008.
[5]	Gal’tsov, D.V. and Davydov, E.A. (2012) International Journal of Modern Physics: Conference Series, 14, 316. [arXiv:1112.2943].
[6]	Galtsov, D.V. and Volkov, M.S. (1991) Physics Letters B, 256, 17-21. http://dx.doi.org/10.1016/0370-2693(91)90211-8
[7]	Dyadichev, V.V., Gal’tsov, D.V., Zorin, A.G. and Zotov, M.Y. (2002) Physical Review D, 65, Article ID: 084007. http://dx.doi.org/10.1103/PhysRevD.65.084007
[8]	Gal’tsov, D.V. and Davydov, E.A. (2011) Proceedings of the Steklov Institute of Mathematics, 272, 119-140. [arXiv:1012.2861].
[9]	Elizalde, E., Lopez-Revelles, A.J., Odintsov, S.D. and Vernov, S.Y. (2013) Physics of Atomic Nuclei, 76, 996-1003. [arXiv:1201.4302]
[10]	Maleknejad, A. and Sheikh-Jabbari, M.M. (2013) Physics Letters B, 723, 224-228. [arXiv:1102.1513].
[11]	Maleknejad, A. and Sheikh-Jabbari, M.M. (2011) Physical Review D, 84, Article ID: 043515. [arXiv:1102.1932]. http://dx.doi.org/10.1103/PhysRevD.84.043515
[12]	Urban, F.R. and Zhitnitsky, A.R. (2010) Nuclear Physics B, 835, 135-173. [arXiv:0909.2684]. http://dx.doi.org/10.1016/j.nuclphysb.2010.04.001
[13]	Pasechnik, R., Beylin, V. and Vereshkov, G. (2013) Journal of Cosmology and Astroparticle Physics, 1306, Article ID: 011. [arXiv:1302.6456].
[14]	Pasechnik, R., Beylin, V. and Vereshkov, G. (2013) Physical Review D, 88, Article ID: 023509. [arXiv:1302.5934]. http://dx.doi.org/10.1103/PhysRevD.88.023509
[15]	Faddeev, L.D. and Slavnov, A.A. (1991) Gauge Fields. Introduction to Quantum Theory. 2nd Edition, Addison-Wesley, Boston.
[16]	Faddeev, L.D. and Popov, V.N. (1967) Physics Letters B, 25, 29-30. http://dx.doi.org/10.1016/0370-2693(67)90067-6
[17]	Jackson, J.D. (1999) Classical Electrodynamics. 3rd Edition, Wiley, Hoboken.
[18]	Griffiths, D.J. (1999) Introduction to Electrodynamics. 3rd Edition, Prentice Hall, Upper Saddle River.
[19]	Blaizot, J.P. and Iancu, E. (1994) Physics Letters B, 326, 138-144. http://dx.doi.org/10.1016/0370-2693(94)91205-X
[20]	Bannur, V.M. (2002) Pramana, 59, 671-677. http://dx.doi.org/10.1007/s12043-002-0077-5
[21]	Schenke, B. (2008) Collective Phenomena in the Non-Equilibrium Quark-Gluon Plasma. Ph.D. Thesis. [arXiv:0810.4306].
[22]	Gliozzi, F., Scherk, J. and Olive, D.I. (1977) Nuclear Physics B, 122, 253-290. http://dx.doi.org/10.1016/0550-3213(77)90206-1
[23]	Bogoliubov, N.N. and Shirkov, D.V. (1982) Quantum Fields. Addison-Wesley, Boston.
[24]	Landau, L.D. and Lifshitz, E.M. (1980) The Classical Theory of Fields. Course of Theoretical Physics Series, 4th Edition, Vol. 2, Butterworth-Heinemann, Oxford.
[25]	Hautot, A. and Magnus, A. (1979) Journal of Computational and Applied Mathematics, 5, 3-15. http://dx.doi.org/10.1016/0771-050X(79)90021-4
[26]	Batalin, I.A. and Vilkovisky, G.A. (1981) Physics Letters B, 102, 27-31. http://dx.doi.org/10.1016/0370-2693(81)90205-7
[27]	Batalin, I.A. and Vilkovisky, G.A. (1983) Physical Review D, 28, 2567. [Erratum-ibid. D 30, 508 (1984)]. http://dx.doi.org/10.1103/PhysRevD.28.2567