1. Introduction
It is usually accepted today in the literature that the physical foundations of what we shall simply call (classical) “gauge theory” (GT) can be found in the paper published by C.N. Yang and R.L. Mills in 1954 [1] . Having in mind the space-time formulation of electromagnetism (EM), the rough idea is to start with a manifold and a group in order to exhibit a procedure leading to a physical theory, namely a way to obtain fields and field equations from geometrical arguments on one side, both with a dual variational counterpart providing inductions and induction equations on the other side. Accordingly, the mathematical foundations of GT can be found in the references existing at this time on differential geometry and group theory, the best and most quoted one being the survey book [2] published by S. Kobayashi and K. Nomizu in 1963 (see also [3] -[6] ). The aim of this Introduction is to revisit these foundations and their applications with critical eyes, recalling them in a quite specific and self-contained way for later purposes.
The word “group” has been introduced for the first time in 1830 by Evariste Galois (1811-1832). Then this concept slowly passed from algebra (groups of permutations) to geometry (groups of transformations). It is only in 1880 that Sophus Lie (1842-1899) studied the groups of transformations depending on a finite number of parameters and now called Lie groups of transformations.
Let 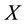 be a manifold with local coordinates
be a manifold with local coordinates  and
and 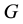 be a Lie group, that is another manifold with local coordinates
be a Lie group, that is another manifold with local coordinates 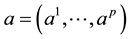 called parameters with a composition
called parameters with a composition 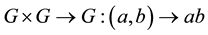 , an inverse
, an inverse  and an identity
and an identity  satisfying:
satisfying:
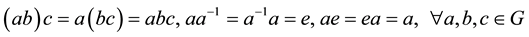
Then  is said to act on
is said to act on  if there is a map
if there is a map  such that
such that  and, for simplifying the notations, we shall use global notations even if only local actions are existing. The action is said to be effective if
and, for simplifying the notations, we shall use global notations even if only local actions are existing. The action is said to be effective if . A subset
. A subset  is said to be invariant under the action of
is said to be invariant under the action of 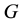 if
if 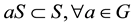 and the orbit of
and the orbit of ![]() is the invariant subset
is the invariant subset![]() . If
. If ![]() acts on two manifolds
acts on two manifolds ![]() and
and![]() , a map
, a map ![]() is said to be equivariant if
is said to be equivariant if![]() . For reasons that will become clear later on, it is often convenient to introduce the graph
. For reasons that will become clear later on, it is often convenient to introduce the graph ![]() of the action. In the product
of the action. In the product![]() , the first factor is called the source while the second factor is called the target.
, the first factor is called the source while the second factor is called the target.
We denote as usual by ![]() the tangent bundle of
the tangent bundle of![]() , by
, by ![]() the cotangent bundle, by
the cotangent bundle, by ![]() the bundle of r-forms and by
the bundle of r-forms and by ![]() the bundle of q-symmetric tensors. Moreover, if
the bundle of q-symmetric tensors. Moreover, if ![]() are two vector fields on
are two vector fields on![]() , we may define their bracket
, we may define their bracket ![]() by the local formula
by the local formula
![]() leading to the Jacobi identity
leading to the Jacobi identity
![]() allowing to define a Lie algebra. We have also the useful formula
allowing to define a Lie algebra. We have also the useful formula
![]()
where ![]() is the tangent mapping of a map
is the tangent mapping of a map![]() . Finally, when
. Finally, when ![]() is a multi-index, we may set
is a multi-index, we may set ![]() and introduce the exterior derivative
and introduce the exterior derivative ![]() with
with ![]() in the Poincaré sequence:
in the Poincaré sequence:
![]()
In order to fix the notations, we quote without any proof the “three fundamental theorems of Lie” that will be of constant use in the sequel (See [7] for more details):
FIRST FUNDAMENTAL THEOREM 1.1: The orbits ![]() satisfy the system of PD equations
satisfy the system of PD equations ![]() with
with![]() . The vector fields
. The vector fields ![]() are called infinitesimal generators of the action and are linearly independent over the constants when the action is effective.
are called infinitesimal generators of the action and are linearly independent over the constants when the action is effective.
In a rough way, we have ![]() and
and ![]() is thus a family of right invariant 1-forms on
is thus a family of right invariant 1-forms on ![]() called Maurer-Cartan forms or simply MC forms.
called Maurer-Cartan forms or simply MC forms.
SECOND FUNDAMENTAL THEOREM 1.2: If ![]() are the infinitesimal generators of the effective
are the infinitesimal generators of the effective
action of a lie group ![]() on
on![]() , then
, then ![]() where the
where the ![]() are the structure cons-
are the structure cons-
tants of a Lie algebra of vector fields which can be identified with ![]() the tangent space to
the tangent space to ![]() at the identity
at the identity ![]() by using the action as we already did. Equivalently, introducing the non-degenerate inverse matrix
by using the action as we already did. Equivalently, introducing the non-degenerate inverse matrix ![]() of right invariant vector fields on
of right invariant vector fields on![]() , we obtain from crossed-derivatives the compatibility conditions (CC) for the previous system of partial differential (PD) equations called Maurer-Cartan equations or simply MC equations, namely:
, we obtain from crossed-derivatives the compatibility conditions (CC) for the previous system of partial differential (PD) equations called Maurer-Cartan equations or simply MC equations, namely:
![]()
(care to the sign used) or equivalently ![]() (See [7] for more details).
(See [7] for more details).
Using again crossed-derivatives, we obtain the corresponding integrability conditions (IC) on the structure constants and the Cauchy-Kowaleski theorem finally provides:
THIRD FUNDAMENTAL THEOREM 1.3: For any Lie algebra ![]() defined by structure constants
defined by structure constants ![]() satisfying:
satisfying:
![]()
one can construct an analytic group ![]() such that
such that ![]() by recovering the MC forms from the MC equa- tions.
by recovering the MC forms from the MC equa- tions.
EXAMPLE 1.4: Considering the affine group of transformations of the real line![]() , the orbits are defined by
, the orbits are defined by![]() , a definition leading to
, a definition leading to ![]() and thus
and thus
![]() . We obtain therefore
. We obtain therefore ![]() and
and
![]() with .
with .
GAUGING PROCEDURE 1.5: If ![]() with
with ![]() a time depending orthogonal matrix (rotation) and
a time depending orthogonal matrix (rotation) and ![]() a time depending vector ( translation) describes the movement of a rigid body in
a time depending vector ( translation) describes the movement of a rigid body in![]() , then the projection of the absolute speed
, then the projection of the absolute speed ![]() in an orthogonal frame fixed in the body is the so-called relative speed
in an orthogonal frame fixed in the body is the so-called relative speed ![]() and the kinetic energy/Lagrangian is a quadratic function of the 1-forms
and the kinetic energy/Lagrangian is a quadratic function of the 1-forms![]() . Meanwhile, taking into account the preceding example, the Eulerian speed
. Meanwhile, taking into account the preceding example, the Eulerian speed ![]() only depends on the 1-forms
only depends on the 1-forms![]() . We notice that
. We notice that ![]() and
and ![]() are both
are both ![]() skewsymmetric time depending matrices that may be quite different.
skewsymmetric time depending matrices that may be quite different.
REMARK 1.6: An easy computation in local coordinates for the case of the movement of a rigid body shows that the action of the ![]() skewsymmetric matrix
skewsymmetric matrix ![]() on the position
on the position ![]() at time
at time ![]() just amounts to the
just amounts to the
vector product by the vortex vector ![]() (See [8] - [11] for more details).
(See [8] - [11] for more details).
The above particular case, well known by anybody studying the analytical mechanics of rigid bodies, can be generalized as follows. If ![]() is a manifold and
is a manifold and ![]() is a lie group ( not acting necessarily on
is a lie group ( not acting necessarily on![]() ), let us consider maps
), let us consider maps ![]() or equivalently sections of the trivial (principal) bundle
or equivalently sections of the trivial (principal) bundle ![]() over
over
![]() . If
. If ![]() is a point of
is a point of ![]() close to
close to![]() , then
, then ![]() will provide a point
will provide a point ![]() close to
close to ![]()
on![]() . We may bring
. We may bring ![]() back to
back to ![]() on
on ![]() by acting on
by acting on ![]() with
with![]() , either on the left or on the right, getting therefore a 1-form
, either on the left or on the right, getting therefore a 1-form ![]() or
or ![]() with value in
with value in![]() . As
. As ![]() we also get
we also get ![]() if we set
if we set ![]() as a way to link
as a way to link ![]() with
with![]() . When there is an action
. When there is an action![]() , we have
, we have ![]() and thus
and thus![]() , a result leading through the first fundamental theorem of Lie to the equivalent formulas:
, a result leading through the first fundamental theorem of Lie to the equivalent formulas:
![]()
Introducing the induced bracket![]() , we may define the curvature
, we may define the curvature ![]() -form
-form ![]() by the local formula (care again to the sign):
by the local formula (care again to the sign):
![]()
This definition can also be adapted to ![]() by using
by using ![]() and we obtain from the second fundamental theorem of Lie:
and we obtain from the second fundamental theorem of Lie:
THEOREM 1.7: There is a nonlinear gauge sequence:
![]()
Choosing ![]() “close” to
“close” to![]() , that is
, that is ![]() and linearizing as usual, we obtain the linear operator
and linearizing as usual, we obtain the linear operator ![]() leading to (See [7] for more details):
leading to (See [7] for more details):
COROLLARY 1.8: There is a linear gauge sequence:
![]()
which is the tensor product by ![]() of the Poincaré sequence.
of the Poincaré sequence.
It just remains to introduce the previous results into a variational framework. For this, we may consider a lagrangian on![]() , that is an action
, that is an action ![]() where
where ![]() and to vary it. With
and to vary it. With
![]() we may introduce
we may introduce ![]() with local coordinates
with local coordinates
![]() and we obtain
and we obtain ![]() that is
that is ![]() in local coordinates. Then, setting
in local coordinates. Then, setting![]() , we get:
, we get:
![]()
and therefore, after integration by part, the Euler-Lagrange (EL) equations [7] [12] [13] :
![]()
Such a linear operator for ![]() has non constant coefficients linearly depending on
has non constant coefficients linearly depending on![]() . However, setting
. However, setting![]() , we get
, we get ![]() while, setting
while, setting![]() , we get the gauge transformation
, we get the gauge transformation
![]() . Setting
. Setting ![]() with
with![]() ,
,
then ![]() becomes an infinitesimal gauge transformation. Finally,
becomes an infinitesimal gauge transformation. Finally, ![]() when
when ![]() with
with![]() . Therefore, introducing
. Therefore, introducing ![]() such that
such that![]() , we get the divergence-like equations
, we get the divergence-like equations![]() .
.
In 1954, at the birth of GT, the above notations were coming from electromagnetism with EM potential ![]() and EM field
and EM field ![]() in the relativistic Maxwell theory [14] . Accordingly,
in the relativistic Maxwell theory [14] . Accordingly, ![]() (unit circle in the complex plane)
(unit circle in the complex plane) ![]() was the only possibility to get a pure 1-form
was the only possibility to get a pure 1-form ![]() and a pure 2- form
and a pure 2- form ![]() when
when![]() . However, “surprisingly”, this result is not coherent at all with elasticity theory and, a fortiori with the analytical mechanics of rigid bodies where the Lagrangian is a quadratic expression of 1-forms as we saw, because the EM lagrangian
. However, “surprisingly”, this result is not coherent at all with elasticity theory and, a fortiori with the analytical mechanics of rigid bodies where the Lagrangian is a quadratic expression of 1-forms as we saw, because the EM lagrangian ![]() is a quadratic expression of the EM field
is a quadratic expression of the EM field ![]() as a 2-form satisfying the first set of Maxwell equations
as a 2-form satisfying the first set of Maxwell equations![]() . The dielectric constant
. The dielectric constant ![]() and the magnetic constant
and the magnetic constant ![]() are leading to the electric induction
are leading to the electric induction ![]() and the magnetic induction
and the magnetic induction ![]() in the second set of Maxwell equations. In view of the existence of well known and quite useful field-matter couplings such as piezoelectricity and photoelasticity [13] [15] [16] , such a situation is contradictory as it should lead to put on equal footing 1-forms and 2-forms, contrary to any unifying mathematical scheme, but no other substitute could have been provided at that time, despite the tentatives of the brothers Eugene Cosserat (1866-1931) and Francois Cosserat (1852-1914) in 1909 [13] [16] - [18] or of Herman Weyl (1885-1955) in 1918 [13] [19] .
in the second set of Maxwell equations. In view of the existence of well known and quite useful field-matter couplings such as piezoelectricity and photoelasticity [13] [15] [16] , such a situation is contradictory as it should lead to put on equal footing 1-forms and 2-forms, contrary to any unifying mathematical scheme, but no other substitute could have been provided at that time, despite the tentatives of the brothers Eugene Cosserat (1866-1931) and Francois Cosserat (1852-1914) in 1909 [13] [16] - [18] or of Herman Weyl (1885-1955) in 1918 [13] [19] .
After this long introduction, the purpose of this paper will be to escape from such a contradiction by using new mathematical tools coming from the formal theory of systems of PD equations and Lie pseudogroups, exactly as we did in [20] for general relativity (GR). In particular, the titles of the three parts that follow will be quite similar to those of this reference though, of course, the contents will be different. The first part proves hat the name “curvature” given to ![]() has been quite misleading, the resulting confusion between translation and rotation being presented with humour in [21] through the chinese saying “to put Chang’s cap on Li’s head”. The second part explains why the Cosserat/Maxwell/Weyl (CMW) theory MUST be described by the Spencer sequence and NOT by the Janet sequence, with a SHIFT by one step contradicting the mathematical foundations of both GR and GT. The third part finally presents the Poincaré duality scheme of physics [12] by means of unexpected methods of homological algebra and algebraic analysis.
has been quite misleading, the resulting confusion between translation and rotation being presented with humour in [21] through the chinese saying “to put Chang’s cap on Li’s head”. The second part explains why the Cosserat/Maxwell/Weyl (CMW) theory MUST be described by the Spencer sequence and NOT by the Janet sequence, with a SHIFT by one step contradicting the mathematical foundations of both GR and GT. The third part finally presents the Poincaré duality scheme of physics [12] by means of unexpected methods of homological algebra and algebraic analysis.
2. First Part: The Nonlinear Janet and Spencer Sequences
In 1890, Lie discovered that Lie groups of transformations were examples of Lie pseudogroups of transfor- mations along the following definition [7] [13] [22] -[24] :
DEFINITION 2.1: A Lie pseudogroup of transformations ![]() is a group of transformations solutions of a system of OD or PD equations such that, if
is a group of transformations solutions of a system of OD or PD equations such that, if ![]() and
and ![]() are two solutions, called finite transformations, that can be composed, then
are two solutions, called finite transformations, that can be composed, then ![]() and
and ![]() are also solutions while
are also solutions while ![]() is the identity solution denoted by
is the identity solution denoted by ![]() and we shall set
and we shall set![]() . In all the sequel we shall suppose that
. In all the sequel we shall suppose that ![]() is transitive that is
is transitive that is ![]()
From now on, we shall use the same notations and definitions as in [7] [16] [20] for jet bundles. In particular, we recall that, if ![]() is the q-jet bundle of
is the q-jet bundle of ![]() with local coordinates
with local coordinates ![]() for
for![]() ,
, ![]() ,
, ![]() and
and![]() , we may consider sections
, we may consider sections ![]() transforming like the sections
transforming like the sections
![]()
where both ![]() and
and ![]() are over the section
are over the section ![]() of
of![]() . The (nonlinear) Spencer operator just allows to distinguish a section
. The (nonlinear) Spencer operator just allows to distinguish a section ![]() from a section
from a section ![]() by introducing a kind of “difference” through the operator
by introducing a kind of “difference” through the operator ![]() with local components
with local components
![]() and more generally
and more generally![]() . If
. If ![]()
and ![]() with source projection, we denote by
with source projection, we denote by ![]() the open sub-bundle locally defined by
the open sub-bundle locally defined by![]() .
.
We also notice that an action ![]() provides a Lie pseudogroup by eliminating the
provides a Lie pseudogroup by eliminating the ![]() parameters
parameters ![]() among the equations
among the equations ![]() obtained by successive differentiations with respect to
obtained by successive differentiations with respect to ![]() only when
only when ![]() is large enough. The system
is large enough. The system ![]() of PD equations thus obtained may be quite nonlinear and of high order. Looking for transformations “close” to the identity, that is setting
of PD equations thus obtained may be quite nonlinear and of high order. Looking for transformations “close” to the identity, that is setting ![]() when
when ![]() is a small constant parameter and passing to the limit
is a small constant parameter and passing to the limit![]() , we may linearize the above (nonlinear) system of finite
, we may linearize the above (nonlinear) system of finite
Lie equations in order to obtain a (linear) system of infinitesimal Lie equations ![]()
for vector fields. Such a system has the property that, if ![]() are two solutions, then
are two solutions, then ![]() is also a solution. Accordingly, the set
is also a solution. Accordingly, the set ![]() of its solutions satisfies
of its solutions satisfies ![]() and can therefore be considered as the Lie algebra of
and can therefore be considered as the Lie algebra of![]() .
.
GAUGING PROCEDURE REVISITED 2.2: Setting ![]() and
and![]() ,
,
we obtain ![]() because
because ![]() and the matrix involved has rank
and the matrix involved has rank ![]() in the following commutative diagram:
in the following commutative diagram:
![]()
Looking at the way a vector field and its derivatives are transformed under any ![]() while replacing
while replacing ![]() by
by![]() , we obtain:
, we obtain:
![]()
and so on, a result leading to:
LEMMA 2.3: ![]() is associated with
is associated with ![]() that is we can obtain a new section
that is we can obtain a new section ![]() from any section
from any section ![]() and any section
and any section ![]() by the formula:
by the formula:
![]()
where the left member belongs to![]() . Similarly
. Similarly ![]() is associated with
is associated with![]() .
.
In order to construct another nonlinear sequence, we need a few basic definitions on Lie groupoids and Lie algebroids that will become substitutes for Lie groups and Lie algebras. The first idea is to use the chain rule for derivatives ![]() whenever
whenever ![]() can be composed and to replace both
can be composed and to replace both ![]() and
and ![]() respectively by
respectively by ![]() and
and ![]() in order to obtain the new section
in order to obtain the new section![]() . This kind of “composition” law can be written in a pointwise symbolic way by introducing another copy
. This kind of “composition” law can be written in a pointwise symbolic way by introducing another copy ![]() of
of ![]() with local coordinates
with local coordinates ![]() as follows:
as follows:
![]()
We may also define ![]() and obtain similarly an “inversion” law.
and obtain similarly an “inversion” law.
DEFINITION 2.4: A fibered submanifold ![]() is called a system of finite Lie equations or a Lie groupoid of order
is called a system of finite Lie equations or a Lie groupoid of order ![]() if we have an induced source projection
if we have an induced source projection![]() , target projection
, target projection![]() , composition
, composition![]() , inversion
, inversion ![]() and identity
and identity![]() . In the sequel we shall only consider transitive Lie groupoids such that the map
. In the sequel we shall only consider transitive Lie groupoids such that the map ![]() is an epimorphism. One can prove that the new system
is an epimorphism. One can prove that the new system ![]() obtained by differentiating
obtained by differentiating ![]() times all the defining equations of
times all the defining equations of ![]() is a Lie groupoid of order
is a Lie groupoid of order![]() .
.
Now, using the algebraic bracket![]() , we may obtain by bilinearity a differential bracket on
, we may obtain by bilinearity a differential bracket on ![]() extending the bracket on
extending the bracket on![]() :
:
![]()
which does not depend on the respective lifts ![]() and
and ![]() of
of ![]() and
and ![]() in
in![]() . One can prove that his bracket on sections satisfies the Jacobi identity and we set:
. One can prove that his bracket on sections satisfies the Jacobi identity and we set:
DEFINITION 2.5: We say that a vector subbundle ![]() is a system of infinitesimal Lie equations or
is a system of infinitesimal Lie equations or
a Lie algebroid if![]() , that is to say
, that is to say![]() . Such a definition can be tested by means of computer algebra.
. Such a definition can be tested by means of computer algebra.
EXAMPLE 2.6: With ![]() and evident notations, the components of
and evident notations, the components of ![]() at order zero, one and two are defined by the totally unusual successive formulas:
at order zero, one and two are defined by the totally unusual successive formulas:
![]()
![]()
![]()
For affine transformations, ![]() and thus
and thus![]() .
.
We may prolong the vertical infinitesimal transformations ![]() to the jet coordinates up to order
to the jet coordinates up to order ![]() in order to obtain:
in order to obtain:
![]()
where we have replaced ![]() by
by![]() , each component beeing the “formal” derivative of the previous one. Replacing
, each component beeing the “formal” derivative of the previous one. Replacing ![]() by
by ![]() as sections of
as sections of ![]() over the target, we obtain a vertical vector field
over the target, we obtain a vertical vector field ![]() over
over
![]() such that
such that ![]() over the target. We may then use the Frobenius theorem in order to find a generating fundamental set of differential invariants
over the target. We may then use the Frobenius theorem in order to find a generating fundamental set of differential invariants ![]() up to order
up to order ![]()
which are such that ![]() by using the chain rule for derivatives whenever
by using the chain rule for derivatives whenever ![]() acting now on
acting now on![]() . Looking at the way the differential invariants are transformed between themselves under changes of source, we may define a natural bundle
. Looking at the way the differential invariants are transformed between themselves under changes of source, we may define a natural bundle![]() . Specializing the
. Specializing the ![]() at
at ![]() we obtain the Lie form
we obtain the Lie form ![]() of
of ![]() and a section
and a section ![]() of
of![]() . If we introduce the maximum number of formal derivatives
. If we introduce the maximum number of formal derivatives ![]() that are linearly independent over the jets of strict order
that are linearly independent over the jets of strict order![]() , any other formal derivative is a linear combination with coefficients functions of
, any other formal derivative is a linear combination with coefficients functions of![]() . Applying
. Applying![]() , we get a contradiction unless these coefficients are killed by
, we get a contradiction unless these coefficients are killed by ![]() and are thus functions of the fundamental set, a result leading to CC of the form
and are thus functions of the fundamental set, a result leading to CC of the form![]() . Finally, setting
. Finally, setting![]() , we obtain a new natural bundle
, we obtain a new natural bundle ![]() as a vector bundle over
as a vector bundle over![]() .
.
THEOREM 2.7: There exists a nonlinear Janet sequence associated with the Lie form of an involutive system of finite Lie equations:
![]()
where the kernel of the first operator ![]() is taken with respect to the section
is taken with respect to the section ![]() of
of ![]() while the kernel of the second operator is taken with respect to the zero section of the vector bundle
while the kernel of the second operator is taken with respect to the zero section of the vector bundle ![]() over
over ![]() (Compare to [24] [25] ).
(Compare to [24] [25] ).
THEOREM 2.8: There is a first nonlinear Spencer sequence:
![]()
with![]() . Moreover, setting
. Moreover, setting![]() , this sequence is locally exact if
, this sequence is locally exact if ![]() and there is an induced second nonlinear Spencer sequence (See next section for definitions):
and there is an induced second nonlinear Spencer sequence (See next section for definitions):
![]()
where all the operators involved are involutive.
Proof: There is a canonical inclusion ![]() defined by
defined by ![]() and the composition
and the composition
![]() is a well defined section of
is a well defined section of ![]() over the section
over the section ![]() of
of ![]() like
like![]() . The
. The
difference ![]() is thus a section of
is thus a section of ![]() over
over ![]() and we have already noticed that
and we have already noticed that![]() . For
. For ![]() we get with
we get with![]() :
:
![]()
We also obtain from Lemma 6.3 the useful formula ![]() allowing to determine
allowing to determine ![]() inductively.
inductively.
We refer to ( [7] , p 215) for the inductive proof of the local exactness, providing the only formulas that will be used later on and can be checked directly by the reader:
![]() (1)
(1)
![]() (2)
(2)
There is no need for double-arrows in this framework as the kernels are taken with respect to the zero section of the vector bundles involved. We finally notice that the main difference with the gauge sequence is that all the indices range from 1 to ![]() and that the condition
and that the condition ![]() amounts to
amounts to ![]() because
because ![]() by assumption (See [7] [16] [23] for more details).
by assumption (See [7] [16] [23] for more details).
Q.E.D.
COROLLARY 2.9: There is a first restricted nonlinear Spencer sequence:
![]()
and an induced second restricted nonlinear Spencer sequence:
![]()
where all the operators involved are involutive and which is locally isomorphic to the corresponding gauge sequence for any Lie groups of transformations when ![]() is large enough. The action, which is essential in the Spencer sequence, disappears in the gauge sequence.
is large enough. The action, which is essential in the Spencer sequence, disappears in the gauge sequence.
DEFINITION 2.10: A splitting of the short exact sequence ![]() is a map
is a map ![]() such that
such that ![]() or equivalently a section of
or equivalently a section of ![]() over
over ![]() and is called a
and is called a ![]() -connection. Its curvature
-connection. Its curvature ![]() is defined by
is defined by![]() . We notice that
. We notice that ![]() is a connection with
is a connection with ![]() if and only if
if and only if ![]() and connections cannot be used for describing fields because we must have
and connections cannot be used for describing fields because we must have![]() . İn particular
. İn particular ![]() is the only existing symmetric connection for the Killing system.
is the only existing symmetric connection for the Killing system.
REMARK 2.11: Rewriting the previous formulas with ![]() instead of
instead of ![]() we get:
we get:
![]() (1*)
(1*)
![]() (2*)
(2*)
When ![]() and though surprising it may look like, we find back exactly all the formulas presented by E. and F. Cosserat in ( [17] , p 123 and [26] ) (Compare to [25] ).
and though surprising it may look like, we find back exactly all the formulas presented by E. and F. Cosserat in ( [17] , p 123 and [26] ) (Compare to [25] ).
Finally, setting![]() , we get
, we get
![]() .
.
With![]() , we get the gauge transformation
, we get the gauge transformation ![]() as in the Introduction, thus ACTING ON THE FIELDS
as in the Introduction, thus ACTING ON THE FIELDS ![]() WHILE PRESERVING THE FIELD EQUATIONS
WHILE PRESERVING THE FIELD EQUATIONS![]() . Setting
. Setting ![]() with
with ![]() over the source, we obtain an infinitesimal gauge transformation of the form
over the source, we obtain an infinitesimal gauge transformation of the form ![]() as in [7] [13] [16] . However, setting now
as in [7] [13] [16] . However, setting now ![]() and
and ![]() with
with ![]() over the target, we get
over the target, we get![]() . The same variation is obtained whenever
. The same variation is obtained whenever ![]() with
with![]() , a transformation which only depends on
, a transformation which only depends on ![]() and is invertible if and only if
and is invertible if and only if ![]() [7] [13] . This result proves that
[7] [13] . This result proves that ![]() is also associated with the groupoid
is also associated with the groupoid ![]() defined by
defined by![]() . With
. With![]() , we have the unusual formulas:
, we have the unusual formulas:
![]()
Accordingly, THE DUAL EQUATIONS WILL ONLY DEPEND ON THE LINEAR SPENCER OPERA- TOR![]() . Moreover, in view of the two variational results obtained at the end of the Introduction, THE CMW EQUATIONS CANNOT COME FROM THE GAUGE SEQUENCE, contrary to what mechanicians still be- lieve after more than a century.
. Moreover, in view of the two variational results obtained at the end of the Introduction, THE CMW EQUATIONS CANNOT COME FROM THE GAUGE SEQUENCE, contrary to what mechanicians still be- lieve after more than a century.
EXAMPLE 2.12: We have the formulas (Compare to [17] [19] , (76) p 289,(78) p 290):
![]() (3)
(3)
![]() (4)
(4)
Setting![]() , we have
, we have![]() .
.
EXAMPLE 2.13: (Projective transformations) With![]() , the formal adjoint of the Spencer operator brings as many dual equations as the number of parameters (1 translation + 1 dilatation + 1 elation).
, the formal adjoint of the Spencer operator brings as many dual equations as the number of parameters (1 translation + 1 dilatation + 1 elation).
![]()
Cosserat/Weyl equations : ![]() (equivalent “momenta”).
(equivalent “momenta”).
3. Second Part: The Linear Janet and Spencer Sequences
It remains to understand how the shift by one step in the interpretation of the Spencer sequence is coherent with mechanics and electromagnetism both with their well known couplings [7] [13] [16] [20] . In a word, the problem we have to solve is to get a 2-form in ![]() from a 1-form in
from a 1-form in ![]() for a certain
for a certain![]() .
.
For this purpose, introducing the Spencer map ![]() defined by
defined by![]() , we recall from [7] [20] [27] the definition of the Janet bundles
, we recall from [7] [20] [27] the definition of the Janet bundles
![]() and the Spencer bundles
and the Spencer bundles
![]() or
or ![]() with
with![]() . When
. When ![]() is an involutive system on
is an involutive system on![]() , we have the following crucial commutative diagram with exact columns where each operator involved is first order apart from
, we have the following crucial commutative diagram with exact columns where each operator involved is first order apart from![]() , generates the CC of the preceding one and is induced by the extension
, generates the CC of the preceding one and is induced by the extension
![]()
of the Spencer operator![]() . The upper sequence is the (second) linear Spencer sequence while the lower sequence is the linear Janet sequence [7] [28] and the sum
. The upper sequence is the (second) linear Spencer sequence while the lower sequence is the linear Janet sequence [7] [28] and the sum ![]() does not depend on the system while the epimorphisms
does not depend on the system while the epimorphisms ![]() are induced by
are induced by![]() .
.
![]()
For later computations, the sequence ![]() can be described by the images
can be described by the images![]() ,
, ![]() ,
, ![]() leading to the identities:
leading to the identities:
![]() (1**)
(1**)
![]() (2**)
(2**)
We also recall that the linear Spencer sequence for a Lie group of transformations![]() , which essentially depends on the action because infinitesimal generators are needed, is locally isomorphic to the linear gauge sequence which does not depend on the action any longer as it is the tensor product of the Poincaré sequence by the Lie algebra
, which essentially depends on the action because infinitesimal generators are needed, is locally isomorphic to the linear gauge sequence which does not depend on the action any longer as it is the tensor product of the Poincaré sequence by the Lie algebra![]() .
.
The main idea will be to introduce and compare the three Lie groups of transformations:
![]() The Poincare group of transformations with
The Poincare group of transformations with ![]() parameters leading to the Killing system
parameters leading to the Killing system![]() :
:
![]()
![]()
![]() The Weyl group of transformations with
The Weyl group of transformations with ![]() parameters leading to the system
parameters leading to the system![]() :
:
![]()
![]()
![]() The conformal group of transformations with 15 parameters leading to the conformal Killing system
The conformal group of transformations with 15 parameters leading to the conformal Killing system ![]() and to the corresponding Janet/Spencer diagram:
and to the corresponding Janet/Spencer diagram:
![]()
![]()
where one has to eliminate the arbitrary function ![]() and 1-form
and 1-form ![]() for finding sections, replacing the ordinary Lie derivative
for finding sections, replacing the ordinary Lie derivative ![]() by the formal Lie derivative
by the formal Lie derivative![]() , that is replacing
, that is replacing ![]() by
by ![]() when needed.
when needed.
![]()
We shall use the inclusions ![]() in the tricky proof of the next crucial proposition:
in the tricky proof of the next crucial proposition:
PROPOSITION 3.1: The Spencer sequence for the conformal Lie pseudogroup projects onto the Poincare sequence with a shift by one step.
Proof: Using ![]() as a
as a ![]() -connection and the fact that
-connection and the fact that ![]() while set- ting
while set- ting ![]() with
with ![]() and
and
![]() with
with![]() , we obtain the following commutative and exact diagram:
, we obtain the following commutative and exact diagram:
![]()
We also obtain from the relations ![]() and the previous identities (1**) + (2**):
and the previous identities (1**) + (2**):
![]()
As ![]() and
and![]() , the conformal Spencer sequence projects onto the sequence
, the conformal Spencer sequence projects onto the sequence ![]() which finally projects with a shift by one step onto the Poincaré sequence
which finally projects with a shift by one step onto the Poincaré sequence ![]() by applying the Spencer map
by applying the Spencer map![]() , because these two sequences are only made by first order involutive operators and are thus formally exact. The short exact sequence
, because these two sequences are only made by first order involutive operators and are thus formally exact. The short exact sequence ![]() has already been used in [16] [20] for exhibiting the Ricci tensor and the above result brings for the first time a conformal link between electromagnetism and gravitation by using second order jets (See [7] [13] for more details).
has already been used in [16] [20] for exhibiting the Ricci tensor and the above result brings for the first time a conformal link between electromagnetism and gravitation by using second order jets (See [7] [13] for more details).
The study of the nonlinear framework is similar. Indeed, using Remark 2.11 with![]() , we get:
, we get:
![]()
and we may finish as before as we have taken out the quadratic terms through the contraction.
Q.E.D.
This unification result, which may be considered as the ultimate “dream” of E. and F. Cosserat or H. Weyl, could not have been obtained before 1975 as it can only be produced by means of the (linear/nonlinear) Spencer sequences and NOT by means of the (linear/nonlinear) gauge sequences. We invite the reader to notice that it only depends on the Formulas (1), (2), (3), (4) and their respective (*) or (**) consequences.
4. Third Part: The Duality Scheme
A duality scheme, first introduced by Henri Poincaré (1854-1912) in [12] , namely a variational framework adapted to the Spencer sequence, could be achieved in local coordinates as we did for the gauge sequence at the end of the Introduction. We have indeed presented all the explicit formulas needed for this purpose and the reader will notice that it is difficult or even impossible to find them in [25] . However, it is much more important to relate this dual scheme to homological algebra [29] and algebraic analysis [30] [31] by using the comment done at the end of the Second Part which amounts to bring the nonlinear framework to the linear framework, a reason for which the stress equations of continuum mechanics are linear even for nonlinear elasticity [13] [16] [18] .
Let ![]() be a unitary ring, that is
be a unitary ring, that is ![]() and even an integral domain, that is
and even an integral domain, that is ![]() or
or![]() . However, we shall not always assume that
. However, we shall not always assume that ![]() is commutative, that is
is commutative, that is ![]() may be different from
may be different from ![]() in general for
in general for![]() . We say that
. We say that ![]() is a left module over
is a left module over ![]() if
if ![]() or a right module
or a right module ![]() for
for ![]() if the operation of
if the operation of ![]() on
on ![]() is
is ![]() . Of course,
. Of course, ![]() is a left and right module over itself. We define the torsion submodule
is a left and right module over itself. We define the torsion submodule ![]() and
and ![]() is a torsion module if
is a torsion module if ![]() or a torsion-free module if
or a torsion-free module if![]() . We denote by
. We denote by ![]() the set of morphisms
the set of morphisms ![]() such that
such that![]() . In particular
. In particular ![]() because
because ![]() and we recall that a sequence of modules and maps is exact if the kernel of any map is equal to the image of the map preceding it. When
and we recall that a sequence of modules and maps is exact if the kernel of any map is equal to the image of the map preceding it. When ![]() is commutative,
is commutative, ![]() is again an
is again an ![]() -module for the law
-module for the law ![]() as we have
as we have ![]() . In the non-commutative case, things are much more complicate and we have:
. In the non-commutative case, things are much more complicate and we have:
LEMMA 4.1: Given ![]() and
and![]() , then
, then ![]() becomes a right module over
becomes a right module over ![]() for the law
for the law![]() .
.
Proof: We just need to check the two relations:
![]()
![]()
Q.E.D.
DEFINITION 4.2: A module ![]() is said to be free if it is isomorphic to a (finite) power of
is said to be free if it is isomorphic to a (finite) power of ![]() called the rank of
called the rank of ![]() over
over ![]() and denoted by
and denoted by ![]() while the rank of a module is the rank of a maximum free submodule. In the sequel we shall only consider finitely presented modules, namely finitely generated modules defined by exact sequences of the type
while the rank of a module is the rank of a maximum free submodule. In the sequel we shall only consider finitely presented modules, namely finitely generated modules defined by exact sequences of the type
![]()
where ![]() and
and ![]() are free modules of finite ranks. For any short exact sequence
are free modules of finite ranks. For any short exact sequence![]() , we have
, we have![]() . A module
. A module ![]() is called projective if there exists a free module
is called projective if there exists a free module ![]() and another (projective) module
and another (projective) module ![]() such that
such that![]() . By a projective (free) resolution of
. By a projective (free) resolution of![]() , we understand a long exact sequence
, we understand a long exact sequence
![]()
where ![]() are projective (free) modules,
are projective (free) modules, ![]() and
and ![]() is the canonical projection.
is the canonical projection.
We now introduce the extension modules, using the notation ![]() and, for any morphism
and, for any morphism![]() , we shall denote by
, we shall denote by ![]() the morphism which is such that
the morphism which is such that ![]() . For this, we take out
. For this, we take out ![]() in order to obtain the deleted sequence
in order to obtain the deleted sequence
![]() and apply
and apply ![]() in order to get the sequence
in order to get the sequence![]() .
.
PROPOSITION 4.3: The extension modules ![]() and
and ![]() do not depend on the resolution chosen and are torsion modules for
do not depend on the resolution chosen and are torsion modules for![]() .
.
Let ![]() be a differential field, that is a field
be a differential field, that is a field ![]() with
with ![]() commuting derivations
commuting derivations ![]() with
with ![]() such that
such that ![]() and
and ![]() . Using an implicit summation on multi-indices, we may introduce the (noncommutative) ring of differential operators
. Using an implicit summation on multi-indices, we may introduce the (noncommutative) ring of differential operators ![]() with elements
with elements ![]() such that
such that ![]() and
and![]() . We notice that
. We notice that ![]() can be generated by
can be generated by ![]() and
and![]() . Now, if we introduce differential indeterminates
. Now, if we introduce differential indeterminates![]() , we may extend
, we may extend ![]() to
to ![]() for
for![]() . Therefore, setting
. Therefore, setting![]() , we obtain by residue the differential module or
, we obtain by residue the differential module or ![]() -module
-module![]() . Introducing the two free differential modules
. Introducing the two free differential modules![]() , we obtain equivalently the free presentation
, we obtain equivalently the free presentation![]() . More generally, introducing the successive CC as in the preceding section, we may finally obtain the free resolution of
. More generally, introducing the successive CC as in the preceding section, we may finally obtain the free resolution of![]() , namely the exact sequence
, namely the exact sequence![]() . In actual practice, we let
. In actual practice, we let ![]() act on the left on column vectors in the operator case and on the right on row vectors in the module case. Homological algebra has been created for finding intrinsic properties of modules not depending on their presentation or even on their resolution.
act on the left on column vectors in the operator case and on the right on row vectors in the module case. Homological algebra has been created for finding intrinsic properties of modules not depending on their presentation or even on their resolution.
We now exhibit another approach by defining the formal adjoint of an operartor ![]() and an operator matrix
and an operator matrix![]() :
:
DEFINITION 4.4: ![]()
![]()
from integration by part, where ![]() is a row vector of test functions and
is a row vector of test functions and ![]() the usual contraction.
the usual contraction.
LEMMA 4.5: IIf![]() , we may set
, we may set ![]() and we have the identity:
and we have the identity:
![]()
PROPOSITION 4.6: If we have an operator![]() , we obtain by duality an operator
, we obtain by duality an operator ![]() where
where ![]() is obtained from
is obtained from ![]() by inverting the transition matrix.
by inverting the transition matrix.
EXAMPLE 4.7: Let us revisit EM in the light of the preceding results when![]() . First of all, we have
. First of all, we have ![]() in the sequence
in the sequence ![]() and the field equations are invariant under any local diffeomorphism
and the field equations are invariant under any local diffeomorphism![]() . By duality, we get the sequence
. By duality, we get the sequence ![]() which is locally isomorphic (up to sign) to
which is locally isomorphic (up to sign) to ![]() and the induction equations
and the induction equations ![]() are thus also invariant under any
are thus also invariant under any![]() . Indeed, using the last lemma and the identity
. Indeed, using the last lemma and the identity![]() , we have:
, we have:
![]()
Accordingly, it is not correct to say that the conformal group is the biggest group of invariance of Maxwell equations as it is only the biggest group of invariance of the Minkowski constitutive laws in vacuum [14] . Finally, both sets of equations can be parametrized independently, the first by the potential, the second by the so- called pseudopotential (See [30] , p 492 for more details).
Now, with operational notations, let us consider the two differential sequences:
![]()
![]()
where ![]() generates all the CC of
generates all the CC of![]() . Then
. Then ![]() but
but ![]() may not gene- rate all the CC of
may not gene- rate all the CC of![]() . Passing to the module framework, we just recognize the definition of
. Passing to the module framework, we just recognize the definition of![]() . Now, exactly like we defined the differential module
. Now, exactly like we defined the differential module ![]() from
from![]() , let us define the differential module
, let us define the differential module ![]() from
from![]() . Then
. Then ![]() does not depend on the presentation of
does not depend on the presentation of ![]() [31] . More generally, changing the presentation of
[31] . More generally, changing the presentation of ![]() may change
may change ![]() to
to ![]() but we have [30] [32] :
but we have [30] [32] :
THEOREM 4.8: The modules ![]() and
and ![]() are projectively equivalent, that is one can find two projective modules
are projectively equivalent, that is one can find two projective modules ![]() and
and ![]() such that
such that ![]() and we obtain therefore
and we obtain therefore![]() .
.
THEOREM 4.9: When ![]() is a left
is a left ![]() -module, then
-module, then ![]() is also a left
is also a left ![]() -module.
-module.
Proof: Let us define:
![]()
![]()
It is easy to check that ![]() in the operator sense and that
in the operator sense and that ![]() is the standard bracket of vector fields. We finally get
is the standard bracket of vector fields. We finally get ![]() that is exactly the Spencer operator we used in the second part. In fact,
that is exactly the Spencer operator we used in the second part. In fact, ![]() is the projective limit of
is the projective limit of ![]() in a coherent way with jet theory [18] [19] [33] .
in a coherent way with jet theory [18] [19] [33] .
Q.E.D.
COROLLARY 4.10: if ![]() and
and ![]() are right
are right ![]() -modules, then
-modules, then ![]() becomes a left
becomes a left ![]() - module.
- module.
Proof: We just need to set ![]() and conclude as before.
and conclude as before.
Q.E.D.
As ![]() is a bimodule, then
is a bimodule, then ![]() is a right
is a right ![]() -module according to Lemma 4.1 and thus the module
-module according to Lemma 4.1 and thus the module ![]() defined by the ker/coker sequence
defined by the ker/coker sequence ![]() is in fact a right module
is in fact a right module![]() .
.
THEOREM 4.11: We have the side changing procedure![]() .
.
Proof: According to the above Corollary, we just need to prove that ![]() has a natural right module structure over
has a natural right module structure over![]() . For this, if
. For this, if ![]() is a volume form with coefficient
is a volume form with coefficient![]() , we may set
, we may set ![]() when
when![]() . As
. As ![]() is generated by
is generated by ![]() and
and![]() , we just need to check that the above formula has an intrinsic meaning for any
, we just need to check that the above formula has an intrinsic meaning for any![]() . In that case, we check at once:
. In that case, we check at once:
![]()
by introducing the Lie derivative of ![]() with respect to
with respect to![]() , along the intrinsic formula
, along the intrinsic formula
![]()
where ![]() is the interior multiplication and
is the interior multiplication and ![]() is the exterior derivative of exterior forms. According to well known properties of the Lie derivative, we get:
is the exterior derivative of exterior forms. According to well known properties of the Lie derivative, we get:
![]()
Q.E.D.
REMARK 4.12: The above results provide a new light on duality in physics. Indeed, as the Poincaré se- quence is self-adjoint (up to sign) as a whole and the linear Spencer sequence for a Lie group of transformations is locally isomorphic to copies of that sequence, it follows from Proposition 4.3 that ![]() parametrizes
parametrizes ![]() in the dual of the Spencer sequence while
in the dual of the Spencer sequence while ![]() parametrizes
parametrizes ![]() in the dual of the Janet sequence, a result highly not evident at first sight in view of the Janet/Spencer diagram for the conformal group of tranformations of space-time that we have presented because
in the dual of the Janet sequence, a result highly not evident at first sight in view of the Janet/Spencer diagram for the conformal group of tranformations of space-time that we have presented because ![]() and
and ![]() are totally different operators.
are totally different operators.
5. Conclusion
The mathematical foundations of Gauge Theory (GT) leading to Yang-Mills equations are always presented in textbooks or papers without quoting/taking into account the fact that the group theoretical methods involved are exactly the same as the standard ones used in continuum mechanics, particularly in the analytical mechanics of rigid bodies and in hydrodynamics. Surprisingly, the lagrangians of GT are (quadratic) functions of the curvature 2-form while the lagrangians of mechanics are (quadratic or cubic) functions of the potential 1-form. Meanwhile, the corresponding variational principle leading to Euler-Lagrange equations is also shifted by one step in the use of the same gauge sequence. This situation is contradicting the well known field/matter couplings existing between elasticity and electromagnetism (piezzoelectricity, photoelasticity). In this paper, we prove that the mathematical foundations of GT are not coherent with jet theory and the Spencer sequence. Accordingly, they must be revisited within this new framework, that is when there is a Lie group of transformations consi- dered as a Lie pseudogroup, contrary to the situation existing in GT. Such a new approach, based on new mathematical tools not known by physicists, allows unifying electromagnetism and gravitation. Finally, the striking fact that the Cosserat/Maxwell/Weyl equations can be parametrized, contrary to Einstein equations, is shown to have quite deep roots in homological algebra through the use of extension modules and duality theory in the framework of algebraic analysis.