On the Convergence of Observed Partial Likelihood under Incomplete Data with Two Class Possibilities ()
Keywords:
In this paper, we discuss the theoretical validity of the OPL which appears in a Cox-type model under incomplete data beyond the right-censored form. In this area, one advantage of the OPL is that the baseline hazard function as a nuisance included in a Cox-type model is eliminated completely in the inferential likelihood. This yields a more stable computational system for optimization than that of the SPFL. For example, in a Cox-cure model, a computational process based the EM algorithm to obtain the SPFL easily fails to converge if a suitable starting value is not provided (e.g., see [10]). The main disadvantages of the OPL are, for instance, that a great length of time is required for the exact computation and it is not clear how much the amount of computation can be reduced by the Monte Carlo (MC) method. However, even if the feasible number of MC trials is smaller than desirable to approximate the OPL, and hence the MC approximation is quite rough, it may be sufficient for a starting value in the computational process of the SPFL.
Generally, it is difficult to investigate computationally to what extent the MC approximations of the OPL are valid, since the exact computation requires a huge number of summands, as the sample size and incomplete information of data are increasing. For this reason, it is worth studying the OPL theoretically. However, it is not easy to complete such a study in one go, because standard tools to study asymptotic properties of Cox’s partial likelihood or the SPFL cannot be applied directly to an objective of the OPL. Therefore in this paper, for the sake of simplicity, we focus on the OPL constructed in incomplete data composed of unobserved two class labels. Typical cases of this type occur in a Cox-type model with incomplete data, such as missing binary covariates, a cure-mixture model or doubly censored data. As a main result, we establish the asymptotic convergence of the OPL and derive a limit form of the OPL. This result is a foundation or precondition for applying an infinite-dimensional Laplace approximation for integral on the baseline hazard. Such a Laplace approximation method will yield the other limit form of the OPL [11], which is useful in discussing the consistency and asymptotic normality of the estimators. However, the method is not convenient for showing the convergence of the OPL. For these reasons, it is also valuable to discuss the convergence of the OPL using the arguments employed in this paper.
A matter of interest in practice concerns MC approximations of the OPL. One other significant point is that the result for the convergence of the exact OPL can be easily tailored to the context of the MC approximations. Based on such an argument, we show that a suitable order of the number of MC trials is less than O(n2) Further, in Section 4 we investigate how the asymptotic properties discussed here behave in a finite sample.
In Section 2 we formulate the OPL in incomplete data with two class possibilities, providing several examples of interest; in Section 3 we develop the tools to obtain the main result and show the convergence of the OPL, and in Section 4 we discuss the performances of MC approximations.
2. Observed Full and Partial Likelihoods
2.1. Notations and Motivated Examples
Let  and
and 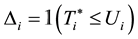 be the observed survival time and right-censoring indicator of the
be the observed survival time and right-censoring indicator of the  individual, where
individual, where 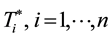 are continuous random variables independent of
are continuous random variables independent of 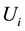 and
and  is the indicator function. Suppose that the individuals possess some difference between models or observations identified by the two classes. We define such a class variable by
is the indicator function. Suppose that the individuals possess some difference between models or observations identified by the two classes. We define such a class variable by
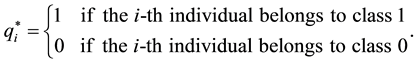
In the case that  expresses the difference between models, assume that the distribution of
expresses the difference between models, assume that the distribution of 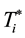 follows the proportional hazards model formulated as
follows the proportional hazards model formulated as
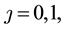
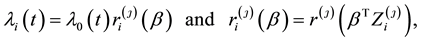
where 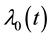 is the baseline hazard function,
is the baseline hazard function, 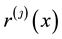 is the function given by
is the function given by
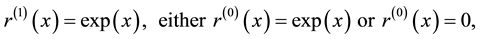
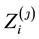 is the covariate vector
is the covariate vector 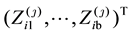 from the population of the class
from the population of the class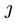 , and
, and  is the regression
is the regression
coefficient vector 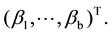 As usual, the information on
As usual, the information on 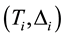 can be re-expressed using the counting processes
can be re-expressed using the counting processes ![]() and at-risk processes
and at-risk processes ![]()
In this paper, we consider incomplete data where some of the![]() ’s are treated as missing. Let
’s are treated as missing. Let
![]()
Each of these is used to construct the likelihoods. Further, if the event of ![]() can be expressed by a pro- bability, we use the following notation and assumption
can be expressed by a pro- bability, we use the following notation and assumption
![]()
where ![]() is the covariate vector
is the covariate vector ![]() related to
related to ![]() and
and ![]() is the regression coefficient vector
is the regression coefficient vector ![]() For simplicity, we will write
For simplicity, we will write ![]() hereafter.
hereafter.
Let ![]() be the collection of true
be the collection of true![]() ’s. In many cases of incomplete data with two class possi-
’s. In many cases of incomplete data with two class possi-
bilities, the observed full likelihood (OFL) can be generally written as
![]() (2.1)
(2.1)
with the elements such that
![]()
and ![]() where the space
where the space ![]() denotes the collection of all the vectors composed of 0 or 1 with length n,
denotes the collection of all the vectors composed of 0 or 1 with length n, ![]() expresses one element of
expresses one element of![]() , in which there exists one true element
, in which there exists one true element![]() ,
,
![]()
is the survival function of the ![]() individual belonging to the class
individual belonging to the class ![]()
![]() is the cumulative baseline hazard function, and
is the cumulative baseline hazard function, and ![]() is given by either of
is given by either of ![]() or
or ![]() in advance.
in advance.
In the following three examples, we show how the form of the OFL is related to the representative cases. Hereafter, we will often omit ![]() when it is clear that a function depends on
when it is clear that a function depends on ![]() e.g.
e.g. ![]()
![]()
![]()
![]() and so on.
and so on.
Example: Missing Binary Covariates. Let us assume that ![]() but
but ![]() For example, the
For example, the
first covariate is binary and may be missing, ![]() and
and ![]() Then, we can write
Then, we can write
![]()
where ![]() In this case, the OFL is
In this case, the OFL is
![]()
Using the binomial expansion, this can be rewritten as
![]() (2.2)
(2.2)
Example: Cox Cure-Mixture Model. The Cox cure-mixture model [10,12-15] is presumed to hold the proportional hazards model for uncured individuals and to be zero-hazard for cured ones. That is, we assume ![]() but
but ![]() so that we can write
so that we can write
![]()
We observe that ![]() if
if ![]() and
and ![]() is missing
is missing ![]() otherwise. The OFL is usually
otherwise. The OFL is usually
![]() (2.3)
(2.3)
note here that ![]() for all
for all ![]() Then, (2.3) can be rewritten in the same form as (2.2).
Then, (2.3) can be rewritten in the same form as (2.2).
Example: Doubly Censored Data. In doubly censored data [16,17], left-censored data may be included. Let ![]() indicate whether the
indicate whether the ![]() observation is left-censored or not, the OFL is then
observation is left-censored or not, the OFL is then
![]() (2.4)
(2.4)
In the phenomenal meaning, the common model is assumed regardless of the type of observations, but we do not define ![]() as
as ![]() Here we use the rule
Here we use the rule ![]() and
and ![]() such that
such that ![]() designates the type of model rather than an observation. Under this rule, because we have
designates the type of model rather than an observation. Under this rule, because we have ![]() for all
for all ![]() (2.4) can be expressed as
(2.4) can be expressed as
![]()
where note that ![]() is defined as missing data (i.e.
is defined as missing data (i.e.![]() ) if the
) if the ![]() observation is left-censored, and as complete data of
observation is left-censored, and as complete data of ![]() (i.e.
(i.e.![]() ) otherwise.
) otherwise.
2.2. Observed Partial Likelihood
Let ![]() be the integral operator proposed by [18] to derive the partial likelihood in the Cox model without time-dependent covariates. Without loss of generality, let us suppose that there are no ties. By operating
be the integral operator proposed by [18] to derive the partial likelihood in the Cox model without time-dependent covariates. Without loss of generality, let us suppose that there are no ties. By operating ![]() to the OFL
to the OFL ![]() we have the OPL
we have the OPL
![]()
where
![]()
Let ![]() To discuss an asymptotic form of
To discuss an asymptotic form of ![]() we will prepare some convenient expressions. First, to pack the expression of
we will prepare some convenient expressions. First, to pack the expression of ![]() into
into ![]() and
and![]() , we define
, we define
![]()
and ![]()
Using these expressions, let
![]()
where ![]() is an empirical version of the theoretical expectation
is an empirical version of the theoretical expectation![]() . Further, as an important definition, let
. Further, as an important definition, let
![]()
be the n-dimensional version of Minkowski’s measure ![]() Then, using these notations,
Then, using these notations, ![]() can be written as
can be written as
![]() (2.5)
(2.5)
where
![]()
![]() is the greatest follow-up time and
is the greatest follow-up time and ![]() The quantity of
The quantity of ![]() is the total number that the same
is the total number that the same![]() ’s are repeated on
’s are repeated on ![]() In addition, we define
In addition, we define
![]()
and ![]()
which is ![]() in which
in which![]() ’s are replaced by the true intensity
’s are replaced by the true intensity
![]()
where ![]()
![]() and
and ![]() are the true
are the true ![]() and
and ![]() In the case of
In the case of ![]()
![]() such as Cox cure-mixture model or doubly censored data, we have
such as Cox cure-mixture model or doubly censored data, we have ![]()
Remark 1. In (2.5), even if we consider a difference or quotient between ![]() and
and ![]() we cannot remove the potential increasing factor n in the summands
we cannot remove the potential increasing factor n in the summands ![]() because of the existence of the operator
because of the existence of the operator ![]() Thus, it may potentially be difficult to apply some of the standard tools in the survival analysis to the asymptotic discussion. For these reasons, our strategy to obtain a limit of
Thus, it may potentially be difficult to apply some of the standard tools in the survival analysis to the asymptotic discussion. For these reasons, our strategy to obtain a limit of ![]() is to regard all the summands of
is to regard all the summands of ![]() as a process on
as a process on ![]() We will then derive the result of a weak convergence on
We will then derive the result of a weak convergence on ![]()
![]()
3. Convergence of the Observed Partial Likelihood
We will now discuss how the mean of the log OPL converges to a deterministic function and provide Theorem 1 of the main result. The following conditions are assumed for these discussions.
Conditions A. Let ![]() be a compact set of
be a compact set of ![]() which includes
which includes ![]() where
where ![]() and
and ![]() are the true
are the true ![]() and
and ![]() The true baseline function
The true baseline function ![]() is continuous and non-decreasing on
is continuous and non-decreasing on ![]() with
with ![]()
A1: ![]() are i.i.d. vectors from the population of the class
are i.i.d. vectors from the population of the class![]() .
.
A2:![]() A3:
A3: ![]()
A4:![]() A5:
A5: ![]()
Condition A2 means ![]() for all
for all ![]() because of
because of ![]()
![]() where
where ![]() and
and ![]() and
and ![]() is the i-th survival function of
is the i-th survival function of
right-censoring time under a given ![]() By the compact condition of
By the compact condition of ![]() we have
we have ![]()
![]() on
on ![]() as a matter of course. However, in the case that there are no
as a matter of course. However, in the case that there are no ![]() as in the example of doubly censored data, such conditions on
as in the example of doubly censored data, such conditions on ![]() are omitted because
are omitted because ![]() always.
always.
Theorem 1. Suppose that Conditions A are satisfied. Then, as ![]()
![]() converges almost surely to a deterministic function uniformly on
converges almost surely to a deterministic function uniformly on ![]()
Theorem 1 is proved in Section 3.3. We prepare useful tools for such a proof in Sections 3.1 and 3.2 below. In Section 3.1, we discuss a relation needed to show that two OPL’s converge to the same limit, determining a plan (Lemmas 1 and 2) to obtain Theorem 1. In Section 3.2, following the plan, we provide a tool (Lemma 3) to give a weak convergence of all possible partial-sum processes.
3.1. Relations between Two Observed Partial Likelihoods
Note that the OPL is constructed by an integral on ![]() with the measure
with the measure ![]() Thus, to give two OPL’s with the same limit, it is predicted that the difference between the integrands of two OPL’s should converge weakly to zeros on
Thus, to give two OPL’s with the same limit, it is predicted that the difference between the integrands of two OPL’s should converge weakly to zeros on ![]() for example, by analogy of the dominated convergence theorem. Let
for example, by analogy of the dominated convergence theorem. Let
![]()
be functions that exist around ![]() where
where ![]() for simplicity. Then, we have the following lemma about some
for simplicity. Then, we have the following lemma about some ![]() and
and ![]()
Lemma 1. Suppose that
![]() (3.1)
(3.1)
with probability 1. Then, as ![]()
![]()
where ![]() denotes almost sure convergence.
denotes almost sure convergence.
(Proof of Lemma 1). Using Taylor expansions of
![]() and,
and,
the difference between ![]() and
and ![]() is derived as
is derived as
![]()
where, with some ![]() on
on ![]() and
and ![]()
![]()
Let us assume that ![]() without loss of generality. Then,
without loss of generality. Then, ![]() and
and
![]() are bounded on
are bounded on ![]() by some finite values
by some finite values ![]() and
and ![]() In fact,
In fact,
![]() and
and
are shown by ![]() Therefore, we have
Therefore, we have
![]()
Applying (3.1) to the above inequality, this lemma is proved. ![]()
Using Lemma 1, for several patterns of ![]() and
and ![]() we can investigate whether they converge to the same limit. The important problem is how to show the condition (3.1). For this purpose, we make the use of meaning that a convergence in
we can investigate whether they converge to the same limit. The important problem is how to show the condition (3.1). For this purpose, we make the use of meaning that a convergence in ![]() implicated in (3.1), since
implicated in (3.1), since ![]() is a probability measure on
is a probability measure on ![]() We have the following lemma to establish the condition (3.1).
We have the following lemma to establish the condition (3.1).
Lemma 2. Suppose that
![]() (3.2)
(3.2)
where ![]() denotes convergence in probability. Then, (3.1) is established.
denotes convergence in probability. Then, (3.1) is established.
Remark 2. For simplicity, letting
![]()
denote
![]()
as the area of![]() . We can immediately show that (3.2) provides a version of convergence in probability of (3.1), i.e.
. We can immediately show that (3.2) provides a version of convergence in probability of (3.1), i.e.
![]() (3.3)
(3.3)
because it is always satisfied that
![]()
Thus, we show that the operators of ![]() and
and ![]() are mutually exchangeable in (3.3) in a proof of Lemma 2.
are mutually exchangeable in (3.3) in a proof of Lemma 2. ![]()
(Proof of Lemma 2). Note that
![]()
because ![]() is independent of
is independent of ![]() due to the n-dimensional projection to
due to the n-dimensional projection to ![]() from
from ![]() From condition (3.2), limits of
From condition (3.2), limits of ![]() are zeros almost everywhere on
are zeros almost everywhere on ![]() which can be eventually written as
which can be eventually written as ![]() independently of
independently of ![]() The dominated convergence theorem provides
The dominated convergence theorem provides
![]()
This shows ![]() via Markov’s inequality such that
via Markov’s inequality such that
![]()
Therefore, condition (3.2) gives (3.1). ![]()
3.2. All Possible Partial-Sum Processes
Note that, by the portmanteau theorem, (3.2) is equivalent to, as ![]()
![]()
where ![]() denotes convergence in distribution. In this section, we develop a tool to show such a weak conver- gence on
denotes convergence in distribution. In this section, we develop a tool to show such a weak conver- gence on ![]()
For simplicity, let ![]()
![]() and
and ![]() An important key to obtaining (3.2) or a limit of
An important key to obtaining (3.2) or a limit of
![]() is a convergence result of
is a convergence result of ![]() on
on ![]() As representa-
As representa-
tions of more essential terms to consider in the convergence on ![]() we denote
we denote
![]()
where examples of ![]() are
are ![]() and so on. Then,
and so on. Then, ![]()
can be regarded as![]() , which is the empirical version of the conditional expectation on a unique
, which is the empirical version of the conditional expectation on a unique
![]() but is calculated letting
but is calculated letting ![]() be fixed. Let
be fixed. Let
![]()
which is the conditional expectation of ![]() on given
on given ![]() Although
Although ![]() is treated as unknown in many incomplete problems, this is not the case for terms included in the observed partial likelihood. Hence, for a fixed
is treated as unknown in many incomplete problems, this is not the case for terms included in the observed partial likelihood. Hence, for a fixed
![]() the conditional expectation of
the conditional expectation of ![]() on
on ![]() is
is ![]()
So, letting ![]()
![]() and
and ![]() be means to centralize
be means to centralize ![]()
![]() and
and![]() , then
, then
![]()
![]()
![]()
Example: Missing Binary Covariates. For simplicity, we assume that ![]() or 0 occurs independently of
or 0 occurs independently of
![]() Letting
Letting![]() , then
, then
![]()
while the expectations of terms which may form all possible partial-sums in ![]()
![]() and
and ![]() are
are
![]()
In these calculi, note that the Bayes rule is used, such as
![]()
Example: Cox Cure-Mixture Model. In this model, ![]() is usually assumed. The expectations of terms
is usually assumed. The expectations of terms
which may form all possible partial-sums are ![]() and
and
![]()
where ![]() Similarly, we have
Similarly, we have
![]()
On Weak Convergence. Let ![]() In our application, note that centred
In our application, note that centred
![]() are zero-means and mutually independent but are not sampled from an identical distribution. We will therefore discuss the partial-sum processes about
are zero-means and mutually independent but are not sampled from an identical distribution. We will therefore discuss the partial-sum processes about ![]() sampled from two populations. Lemma 3 shows that
sampled from two populations. Lemma 3 shows that ![]() converges in probability to zero uniformly on
converges in probability to zero uniformly on![]() ; recall that an n-dimensional element
; recall that an n-dimensional element ![]() means marginal collection of elements of
means marginal collection of elements of ![]() In advance, let
In advance, let
![]()
Remark 3. For example, if ![]() by Chebyshev’s inequality, we immediately have
by Chebyshev’s inequality, we immediately have
![]()
However, a result of interest here is whether ![]() and
and ![]() can be exchanged, that is, about
can be exchanged, that is, about
![]() .
.
Incidentally, we cannot obtain the almost sure convergence in this problem, since
![]()
is always apart from zero. ![]()
Lemma 3. Let ![]() be random elements on
be random elements on ![]() sampled from one of two distributions (populations) with
sampled from one of two distributions (populations) with ![]() at every
at every ![]() where the population to which the
where the population to which the ![]() element
element ![]() belongs is known and indexed by
belongs is known and indexed by ![]() or 1. Suppose that
or 1. Suppose that ![]() are mutually independent and have
are mutually independent and have ![]() at every
at every ![]() If the following three conditions are satisfied,
If the following three conditions are satisfied,
(i) The class of functions ![]() is Glivenko-Cantelli,
is Glivenko-Cantelli,
(ii) ![]() and
and
(iii) ![]() for every
for every ![]()
then, as ![]()
![]()
Lemma 3 is proved in Appendix A.1. The following examples show that the conditions needed in Lemma 3 are
satisfied for ![]() and
and ![]()
Example 1. Let ![]() From Condition A5, we have Condition (ii). Since
From Condition A5, we have Condition (ii). Since ![]() is independent of
is independent of![]() , Conditions (i) and (iii) are clearly satisfied.
, Conditions (i) and (iii) are clearly satisfied.
Example 2. Let ![]()
![]() Conditions (i) and (ii) are shown by Conditions A1 and A4. Arbitrary
Conditions (i) and (ii) are shown by Conditions A1 and A4. Arbitrary ![]() satisfies
satisfies ![]() by Condition A4 and
by Condition A4 and
![]() by Condition A3, where
by Condition A3, where ![]() means the Euclidean norm for vectors. Hence, Condition (iii) is satisfied.
means the Euclidean norm for vectors. Hence, Condition (iii) is satisfied.
3.3. Proof of Theorem 1
Consider ![]() in which the random quantities are reduced less than that of
in which the random quantities are reduced less than that of ![]() where
where ![]() and
and ![]() are
are ![]() in which
in which ![]() is replaced by
is replaced by ![]() and
and![]() ,
,
i.e. ![]() and
and
![]()
![]() : It is satisfied that
: It is satisfied that
![]()
and ![]()
by Conditions A1 and A4, similar to the standard Cox model (see [19]). Thus,
![]()
is obtained as ![]()
![]() : We have
: We have
![]()
using Lemma 3 in Example 1 and applying the strong law of large numbers (SLLN) to ![]() and
and ![]() by Conditions A1 and A5. For the latter application, note that
by Conditions A1 and A5. For the latter application, note that ![]() be- cause of
be- cause of ![]() Also, it is shown that
Also, it is shown that
![]()
by applying the SLLN on ![]() (see [1]) from Conditions A1 and A4. In addition, we have
(see [1]) from Conditions A1 and A4. In addition, we have
![]()
using Lemma 3 in Example 2. Hence, ![]() converges in probability to zero as
converges in probability to zero as![]() .
.
![]() : It satisfies that
: It satisfies that
![]()
using Lemma 3 in Example 2 and the continuous mapping theorem about log-function. For the latter application, note that ![]() is bounded away from zero on
is bounded away from zero on ![]() by Condition A2. Hence,
by Condition A2. Hence,
![]()
converges in probability to zero as ![]()
Applying the above three results to Lemmas 1 and 2, therefore, we obtain
![]()
respectively, so that we conclude
![]() (3.4)
(3.4)
Although (3.4) shows that the limit of ![]() is equivalent to that of
is equivalent to that of![]() ,
, ![]() still depends on n and
still depends on n and![]() ’s. We will therefore investigate the limit form of
’s. We will therefore investigate the limit form of ![]() further.
further.
In discussing a convergence about the form ![]() and
and ![]() included in
included in ![]() and
and ![]() of the partial sums, note that they can be written as
of the partial sums, note that they can be written as
![]()
Let ![]() Similarly to Lemma 3 (proof of s2), we show that
Similarly to Lemma 3 (proof of s2), we show that
![]()
at arbitrary point ![]() In particular, because of
In particular, because of
![]()
note that
![]()
and then![]() . We have the following lemma.
. We have the following lemma.
Lemma 4. ![]() converge in probability to
converge in probability to
![]()
uniformly on ![]()
A proof of Lemma 4 is provided briefly in Appendix A.2 since it is similar to Lemma 3. Now, applying Lemma
4 to ![]() we obtain their limits as
we obtain their limits as
![]()
![]()
![]()
Let ![]() be
be![]() , in which
, in which ![]() is replaced by
is replaced by
![]()
![]() : We obtain
: We obtain ![]()
![]()
![]()
![]() by Lemma 4 and the continuous mapping theorem about log-function. Therefore,
by Lemma 4 and the continuous mapping theorem about log-function. Therefore, ![]() converges in probability to zero as
converges in probability to zero as![]() . Hence, using Lemmas 1 and 2, we can show
. Hence, using Lemmas 1 and 2, we can show ![]() so that a triangle combi-
so that a triangle combi-
nation of this result and (3.4) yields
![]() (3.5)
(3.5)
On a Limit Form. The result of (3.5) shows only that the limit of ![]() is equivalent to that of
is equivalent to that of ![]()
Here we discuss a limit form of ![]() To consider the case of
To consider the case of![]() , let
, let ![]() and
and ![]() be the sub-
be the sub-
sets of ![]() such that
such that ![]() if
if ![]() and
and ![]() if
if ![]() For simplicity, let
For simplicity, let
![]()
Then,
![]()
![]()
Because of![]() , we have
, we have
![]() ,
,
so that, via the general binomial theorem, we can show that
![]()
Also, ![]() Therefore, because of
Therefore, because of ![]() and similar to the derivation of the
and similar to the derivation of the ![]() on the Banach space which results in the essential supremum, we conclude
on the Banach space which results in the essential supremum, we conclude
![]() (3.6)
(3.6)
In addition, (3.6) is derived in the case of![]() . Results (3.5) and (3.6) show that Theorem 1 is complete.
. Results (3.5) and (3.6) show that Theorem 1 is complete. ![]()
A limit function of ![]() is concretely provided by (3.6), which is summarized as follows.
is concretely provided by (3.6), which is summarized as follows.
Corollary 1. If Theorem 1 holds, then a limit expression to which ![]() converges almost surely as
converges almost surely as ![]() is
is ![]()
4. Additional Considerations
4.1. Monte Carlo (MC) Approximations
It usually takes a long time for the exact computation of the OPL. So, another subject of interest is the performance of its MC approximations. Let ![]() be all the elements of
be all the elements of ![]() labelled in order such that
labelled in order such that
![]()
We assign a point ![]() to
to ![]() using
using ![]() and let
and let ![]() denote the distribution
denote the distribution ![]() Using these notations, we redefine
Using these notations, we redefine ![]() as
as
![]()
Given fixed data ![]() let
let ![]() be
be ![]() random elements from
random elements from ![]()
![]() where
where ![]() and
and ![]() is either 1 or 0 with an equal probability 0.5 if
is either 1 or 0 with an equal probability 0.5 if ![]() and
and
![]() if
if ![]() An MC approximation of
An MC approximation of ![]() is
is
![]()
using ![]() and the corresponding empirical measure
and the corresponding empirical measure
![]()
By the standard asymptotic theory, as ![]() it follows that
it follows that
![]() (4.1)
(4.1)
provided ![]() exists and
exists and ![]() where
where
![]()
To evaluate the quantity of ![]() in the case of
in the case of![]() , consider
, consider![]() , then, as
, then, as ![]()
![]()
similar to the discussion for (3.6). As this result means that ![]() may increase exponentially according to n, direct use of (4.1) is not particularly productive. Therefore, although (4.1) is the rationale in this context, it will be modified, as
may increase exponentially according to n, direct use of (4.1) is not particularly productive. Therefore, although (4.1) is the rationale in this context, it will be modified, as ![]() to
to
![]() (4.2)
(4.2)
using the delta method. Now consider the other aspect of (4.2) under ![]() Applying Theorem 1 and Corollary 1 to such a problem, we obtain the following results
Applying Theorem 1 and Corollary 1 to such a problem, we obtain the following results
![]()
![]()
where ![]() This means
This means ![]() from the point of view of the k-asymp- totic variance in the second line of (4.2). Hence, we can show that the order of
from the point of view of the k-asymp- totic variance in the second line of (4.2). Hence, we can show that the order of ![]() is less than
is less than ![]() in (4.2) under
in (4.2) under ![]() That is, using the MC method, a computational load of
That is, using the MC method, a computational load of ![]() needed in the exact computation can be reduced to one of at most
needed in the exact computation can be reduced to one of at most ![]()
4.2. Numerical Examples
We will investigate two circumstances in the finite samples using the Cox cure-mixture model. One is how a relation such as (3.6) obtained as ![]() is located in the finite samples. The other is to observe numerically the practical size of the error in MC approximations,
is located in the finite samples. The other is to observe numerically the practical size of the error in MC approximations, ![]() which was shown to be less than
which was shown to be less than ![]() in the previous section.
in the previous section.
Ovarian Cancer Data: For the first purpose, we use survival data of ovarian cancer patients [20]. We set the covariates as ![]() and
and ![]()
![]() where Treat is the type of chemotherapy (0 = single, 1 = combined), Age is the age of the patient (in years) and Rdisease is the extent of residual disease (0 = complete, 1 = incomplete). The maximum of the OPL
where Treat is the type of chemotherapy (0 = single, 1 = combined), Age is the age of the patient (in years) and Rdisease is the extent of residual disease (0 = complete, 1 = incomplete). The maximum of the OPL ![]() is achieved approximately at
is achieved approximately at
![]()
Here, let ![]() Figure 1 shows plots of
Figure 1 shows plots of
![]()
and ![]() at
at ![]() where
where ![]() and the y-axis is drawn in exponential scale. Although the total number of
and the y-axis is drawn in exponential scale. Although the total number of ![]() is
is ![]() in fact
in fact![]() ’s of
’s of ![]() are sorted on
are sorted on ![]() This data are small in size
This data are small in size ![]() However, circumstances close to the relation in (3.6) are observed at least at
However, circumstances close to the relation in (3.6) are observed at least at ![]() and
and ![]()
Simulated Data: For the second purpose, we prepare simulated data with ![]() and
and ![]() where
where ![]() follows the standard uniform distribution. The latent distribution of
follows the standard uniform distribution. The latent distribution of ![]() is standard exponential and the censoring follows a uniform distribution
is standard exponential and the censoring follows a uniform distribution ![]() Under these settings, the simulated means of cure and censored rate are about 48% and 58%, respectively. We generate 100 pairs of simulated data of size n. We perform m MC approximations for each simulated data set. Let
Under these settings, the simulated means of cure and censored rate are about 48% and 58%, respectively. We generate 100 pairs of simulated data of size n. We perform m MC approximations for each simulated data set. Let ![]() be the
be the ![]() element of m
element of m![]() ’s. For each simulated data set, we estimate
’s. For each simulated data set, we estimate ![]() and
and ![]() by
by ![]() and
and![]() , where
, where
![]()
We use these to observe a better estimation performance than
![]()
Figure 2 shows simulated averages and standard errors (SEs) of 100 pairs of
![]()
computed at ![]() in simulated data of
in simulated data of ![]() under
under ![]() and
and ![]() where
where ![]()
![]() Although
Although ![]() is considerably smaller than the
is considerably smaller than the ![]() needed in the exact method,
needed in the exact method, ![]() approximates
approximates ![]() well enough.
well enough.
Further, even if the approximations were reduced to ![]() the simulated average of
the simulated average of ![]() would still yield sufficiently good approximations of
would still yield sufficiently good approximations of ![]() Based on these empirical findings,
Based on these empirical findings,
we set ![]() and
and ![]() Figure 3 shows
Figure 3 shows
![]()
computed under these settings. Although ![]() increases over an initial domain of n, Figure 3 shows that the rate of such an increase is smaller as n increases. This provides a conjecture that
increases over an initial domain of n, Figure 3 shows that the rate of such an increase is smaller as n increases. This provides a conjecture that ![]() may be bounded by some order smaller than
may be bounded by some order smaller than ![]() such as
such as ![]() for a sufficiently large
for a sufficiently large ![]() We leave further investigation of this to future research.
We leave further investigation of this to future research.
5. Concluding Remarks
A main result of this paper was to show the almost sure convergence of the OPL constructed in incomplete data with two class possibilities. To obtain this result, we discussed the principle of formulating this type of structure of the OPL, and then developed the tools based on a partial-sum processes argument. The limit function of the OPL resulting finally (Corollary 1) is the essential supremum of partial likelihoods obtained based on all the forms of complete data included in incomplete data, which is similar to ![]() on a Banach space. In Section 4.2, we showed numerically how an essential supremum approximates the OPL in real data for the Cox cure-mixture model.
on a Banach space. In Section 4.2, we showed numerically how an essential supremum approximates the OPL in real data for the Cox cure-mixture model.
Unfortunately, it will be difficult to show consistency and asymptotic normality of the maximum OPL estimator (MOPLE) using the limit function of the OPL provided in Corollary 1. However, if the consistency is
achieved (as almost expected), the global essential maximum will be accomplished around true complete data under a true regression parameter. On the other hand, for the purpose of showing the consistency of the MOPLE, there will be other convenient limit expressions, although not discussed in this paper. A future paper on this topic is based on an infinite-dimensional Laplace approximation for integral on the baseline hazard function [11]. However, in applying such a Laplace approximation to the OPL, a precondition that the OPL converges to a deterministic function is necessary. Hence, in order to obtain this precondition and for the reason that it is generally difficult to show the convergence result directly using the Laplace approximation, it is meaningful to discuss the asymptotic convergence of the OPL using the argument employed in this paper.
The results on the convergence of the exact OPL could easily suit the context of MC approximations. For example, at the end of Section 4.1 we show that, by applying Theorem 1 and Corollary 1, the size of the MC error is less than ![]() This suggests that the MC method, for which the number is at most
This suggests that the MC method, for which the number is at most![]() , achieves an appropriate approximation and can reduce the vast computational load of
, achieves an appropriate approximation and can reduce the vast computational load of ![]() implied by the exact method up to a feasible level. Further, in Section 4.2 we performed numerical experiments to investigate the practical size of the error in MC approximations using the Cox cure-mixture model. These experiments indicate that the exact OPL may be sufficiently approximated with the number of MC trials smaller than
implied by the exact method up to a feasible level. Further, in Section 4.2 we performed numerical experiments to investigate the practical size of the error in MC approximations using the Cox cure-mixture model. These experiments indicate that the exact OPL may be sufficiently approximated with the number of MC trials smaller than![]() , such as
, such as![]() , as
, as ![]() is larger.
is larger.
In future study, it is important to derive the other expression of the limit function based on an infinite-dimen- sional Laplace approximation for integral on the baseline hazard and then to discuss the consistency and asymptotic normality of the MOPLE, since the asymptotic convergence of the OPL is given in this paper. Further, it is an interesting issue how the discussion of the OPL of the binary class as considered here could be extended to that under continuous class possibilities, such as the Cox frailty model.
Acknowledgements
The author is grateful to anonymous referees for their careful reading. This work is financially supported by JSPS KAKENHI grant number 23700336.