Classification of Single Traveling Wave Solutions to the Generalized Strong Nonlinear Boussinesq Equation without Dissipation Terms in P = 1 ()
1. Introduction
There are many methods of obtaining the exact solutions for nonlinear evolution equations, such as the homogeneous balance method [1], the inverse scattering method [2], Hirotas bilinear transformation [3], the extended tanh-function method [4], the sech-function method [5] and so on. Liu introduced complete discrimination system for the polynomial method to obtain the classification of traveling wave solutions to some nonlinear evolution equations [6-8]. In [9], the generalized strong nonlinear Boussinesq equation without dissipation terms was given by
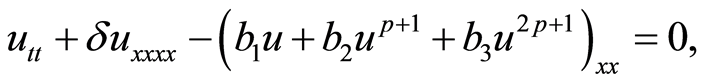 (1)
(1)
where ,
,  ,
,  are constants. When
are constants. When , Equation (1) becomes
, Equation (1) becomes
 (2)
(2)
Equation (2) is an important model equation in physics. It describes the wave propagation in the weakly nonlinear and dispersive media. When  or
or , the Equation (2) becomes good Boussinesq equation [10,11] or bad Boussinesq equation [12,13]. The good Boussinesq equation and bad Boussinesq equation have been studied by many authors [10-17]. But the classification of single traveling wave solutions to these equations hasn't been studied. In the present paper, we consider the following generalized strong nonlinear Boussinesq equation without dissipation terms in
, the Equation (2) becomes good Boussinesq equation [10,11] or bad Boussinesq equation [12,13]. The good Boussinesq equation and bad Boussinesq equation have been studied by many authors [10-17]. But the classification of single traveling wave solutions to these equations hasn't been studied. In the present paper, we consider the following generalized strong nonlinear Boussinesq equation without dissipation terms in :
:
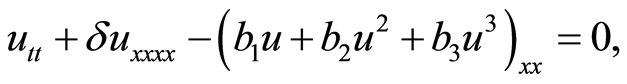 (3)
(3)
where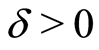 ,
,  are constants. By using Liu’s method, the classification of single traveling wave solutions to Equation (3) is obtained.
are constants. By using Liu’s method, the classification of single traveling wave solutions to Equation (3) is obtained.
2. The Traveling Wave Solutions to the Equation (3)
Take wave transformation
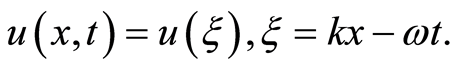 (4)
(4)
Substituting Equation (4) into Equation (3) yields the following nonlinear ordinary difference equation:
 (5)
(5)
Integrating Equation (5) once with respect to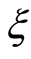 , and setting the integration constant to zero yields:
, and setting the integration constant to zero yields:
 (6)
(6)
Integrating Equation (6) twice with respect to  yields:
yields:
 (7)
(7)
where 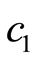 and
and  are arbitrary constants.
are arbitrary constants.
In order to find the traveling wave solutions to the Equation (3), let us solve Equation (7). In this article, there are two cases to discuss the exact solutions of Equation (7) according to the arbitrary constant .
.
Case 2.1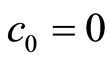 , then Equation (7) becomes
, then Equation (7) becomes
 (8)
(8)
Integrating Equation (8) once yields
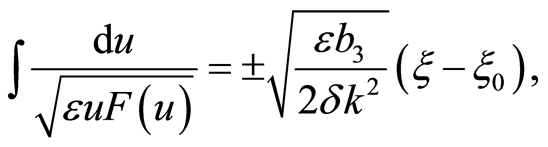 (9)
(9)
where
 (10)
(10)
If , we take
, we take ; if
; if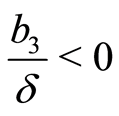 , we take
, we take . The complete discrimination system for the third order polynomial
. The complete discrimination system for the third order polynomial 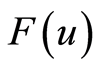 is given as follows:
is given as follows:
 (11)
(11)
In order to obtain the solutions to the Equation (9), according to the complete discrimination system for the third order polynomial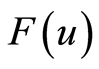 , there are four cases to be discussed.
, there are four cases to be discussed.
Case 2.1.1.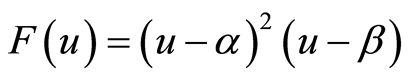
 , where
, where  are real constants,
are real constants,  ,
,  If
If
 , when
, when 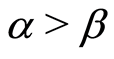 and
and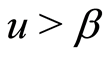 , from Equation (9), we give the solution of Equation (7) as follows:
, from Equation (9), we give the solution of Equation (7) as follows:
 (12)
(12)
when  and
and , we have
, we have
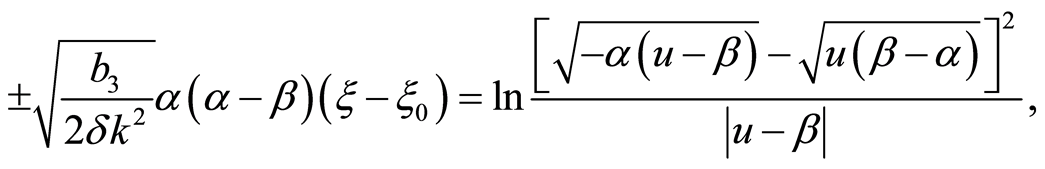 (13)
(13)
when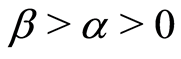 , we have
, we have
 (14)
(14)
If , when
, when 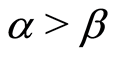 and
and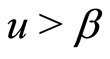 , from Equation (9), we give the solutions of Equation (7)
, from Equation (9), we give the solutions of Equation (7)
 (15)
(15)
when , and
, and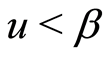 , we have
, we have
 (16)
(16)
when , we have
, we have
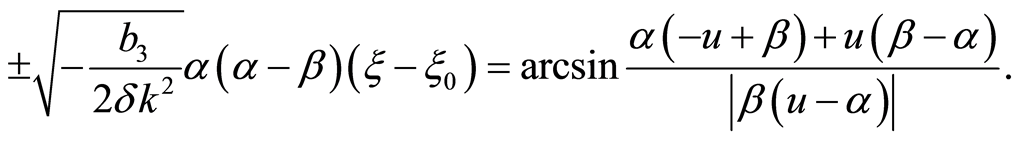 (17)
(17)
Case 2.1.2.
 , where
, where 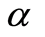 is real constant. If
is real constant. If , when
, when , we have
, we have
 (18)
(18)
If , when
, when , we have
, we have
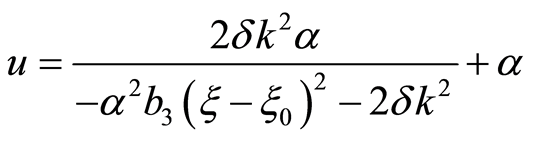 (19)
(19)
Case 2.1.3.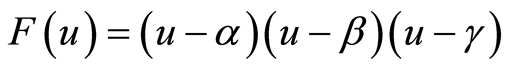
 , where
, where  are different real constants. If
are different real constants. If
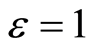 , when
, when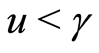 , we have
, we have
 (20)
(20)
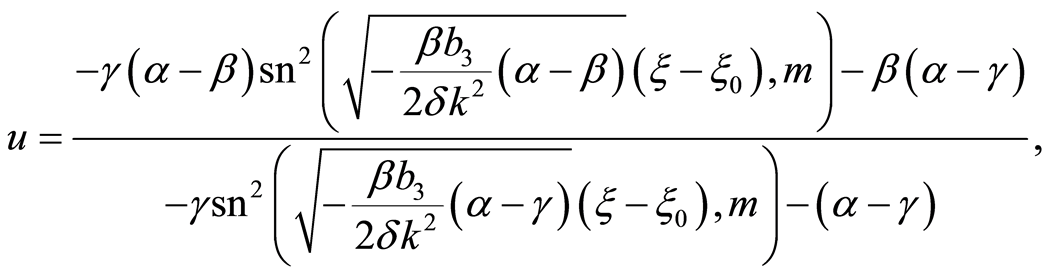 (21)
(21)
where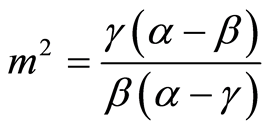 . If
. If , when
, when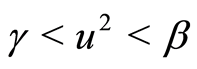 , we have
, we have
 (22)
(22)
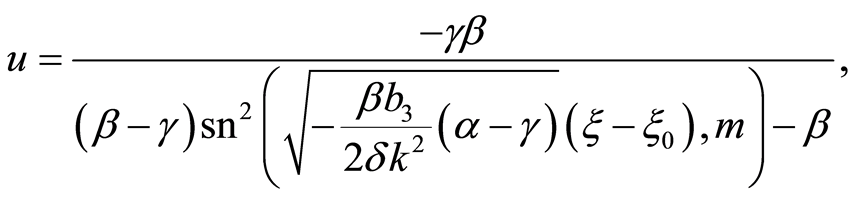 (23)
(23)
where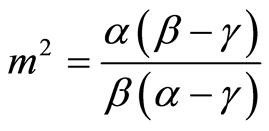 .
.
Case 2.1.4.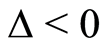 ,
,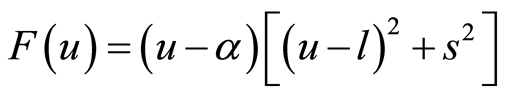 , where
, where  are all real constants, and
are all real constants, and we have
we have
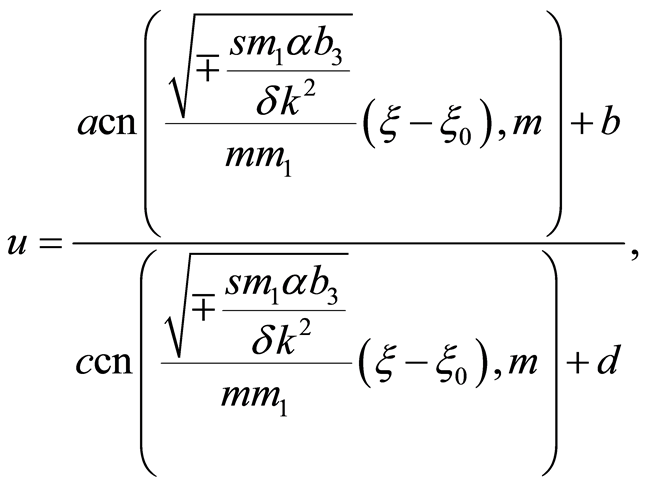 (24)
(24)
where
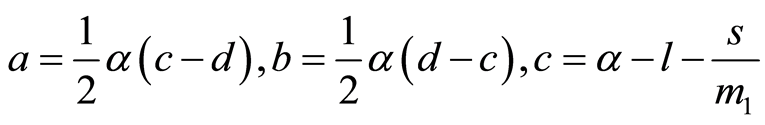 ,
, .
.
Case 2.2  In order to solve Equation (7), when
In order to solve Equation (7), when , we take the transformation as follows
, we take the transformation as follows
 (25)
(25)
Combining the expression (7) with Equation (25) yields
 (26)
(26)
where
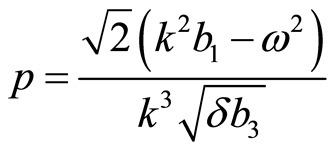 ,
, 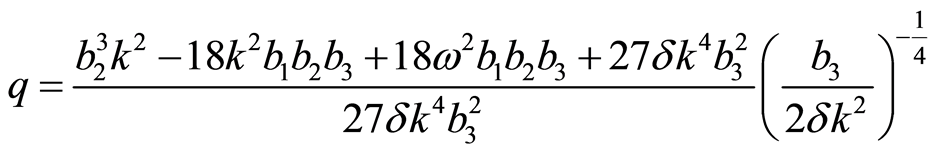 And
And 
When , we take the following transformation:
, we take the following transformation:
 (27)
(27)
Combining the expression (7) with Equation (27) yields
 (28)
(28)
where
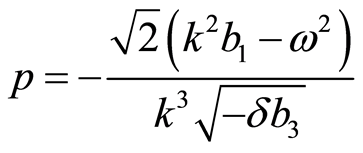 ,
,  and
and 
The complete discrimination system for the fourth order polynomial  as follows:
as follows:
 (29)
(29)
In order to obtain the solutions to Equation (26) and Equation (28), according to the complete discrimination system for the fourth order polynomial , there are nine cases to be discussed.
, there are nine cases to be discussed.
Case 2.2.1 ,
, 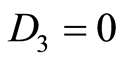 , and
, and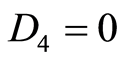 , then
, then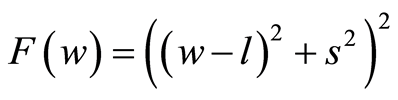 . where
. where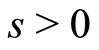 . For
. For , the solution of Equation (7) is
, the solution of Equation (7) is
 (30)
(30)
Case 2.2.2.  and
and 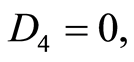 then
then  For
For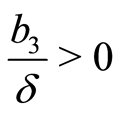 , the solution of Equation (7) is
, the solution of Equation (7) is
 (31)
(31)
Case 2.2.3. 
 and
and ,
,  , where
, where 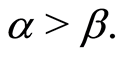 For
For when
when  or
or , the solution of Equation (7) is
, the solution of Equation (7) is
 (32)
(32)
when ,the solution of Equation (7) is
,the solution of Equation (7) is
 (33)
(33)
Case 2.2.4. 
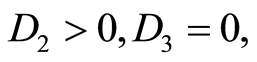 and
and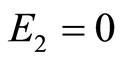 , then
, then  when
when ,
,
 or
or , the solution of Equation (7) is
, the solution of Equation (7) is
 (34)
(34)
when ,
,  or
or , the solution of Equation (7) is
, the solution of Equation (7) is
 (35)
(35)
Case 2.2.5  and
and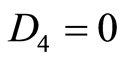 , then
, then  If
If , when
, when 
and  or when
or when  and
and , we have
, we have
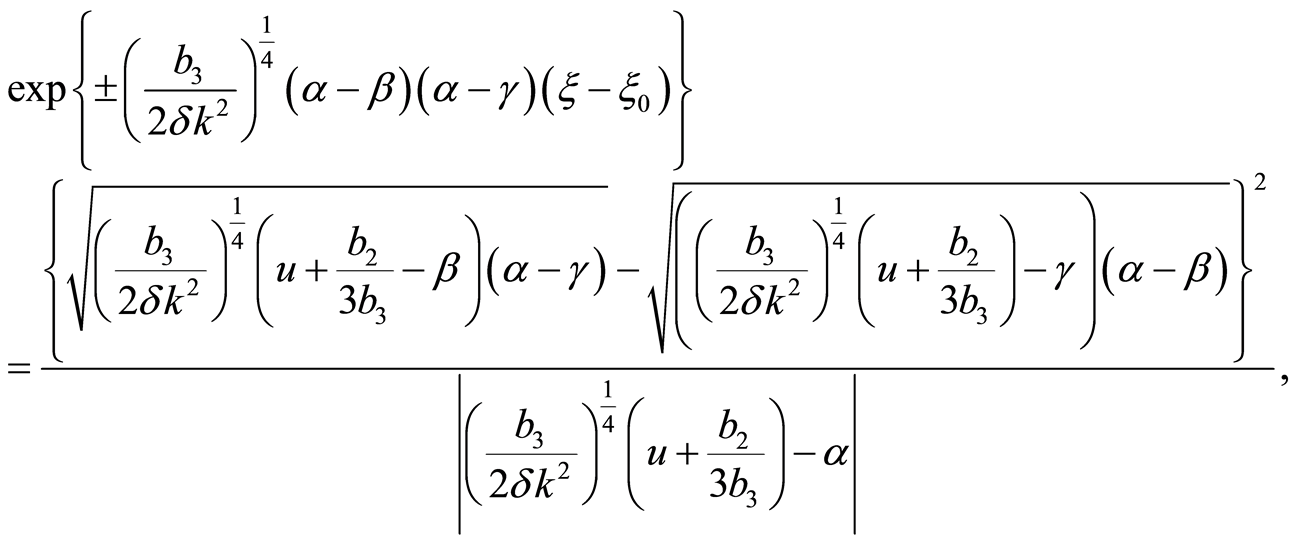 (36)
(36)
when  and
and , or when
, or when , and
, and , we have
, we have
 (37)
(37)
when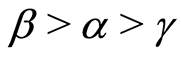 , we have
, we have
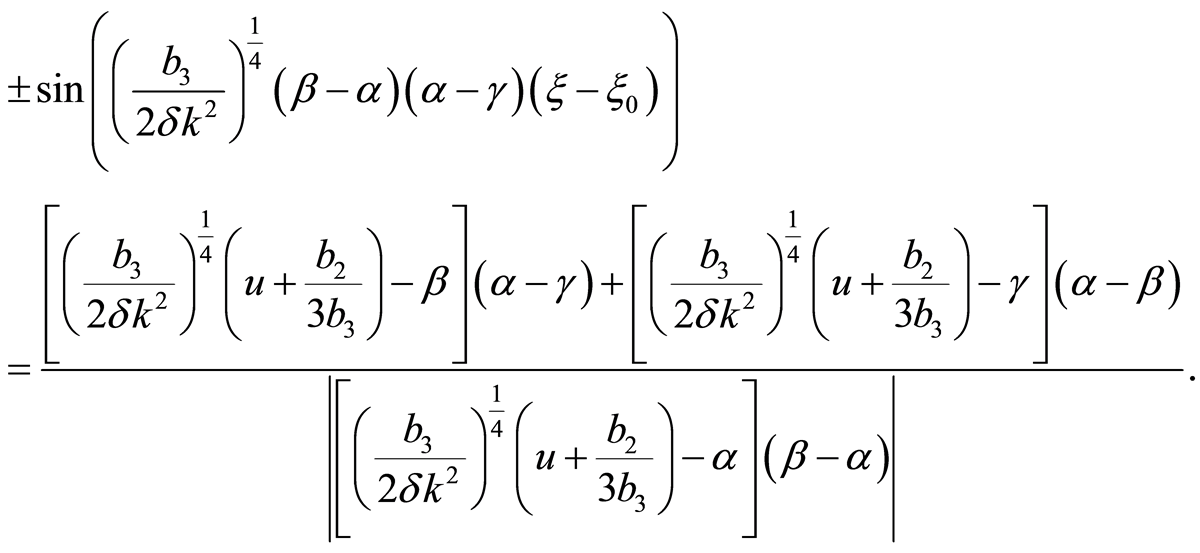 (38)
(38)
If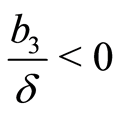 , when
, when  and
and  or when
or when  and
and , we have
, we have
 (39)
(39)
when  and
and , or when
, or when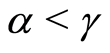 , and
, and , we have
, we have
 (40)
(40)
when , we have
, we have
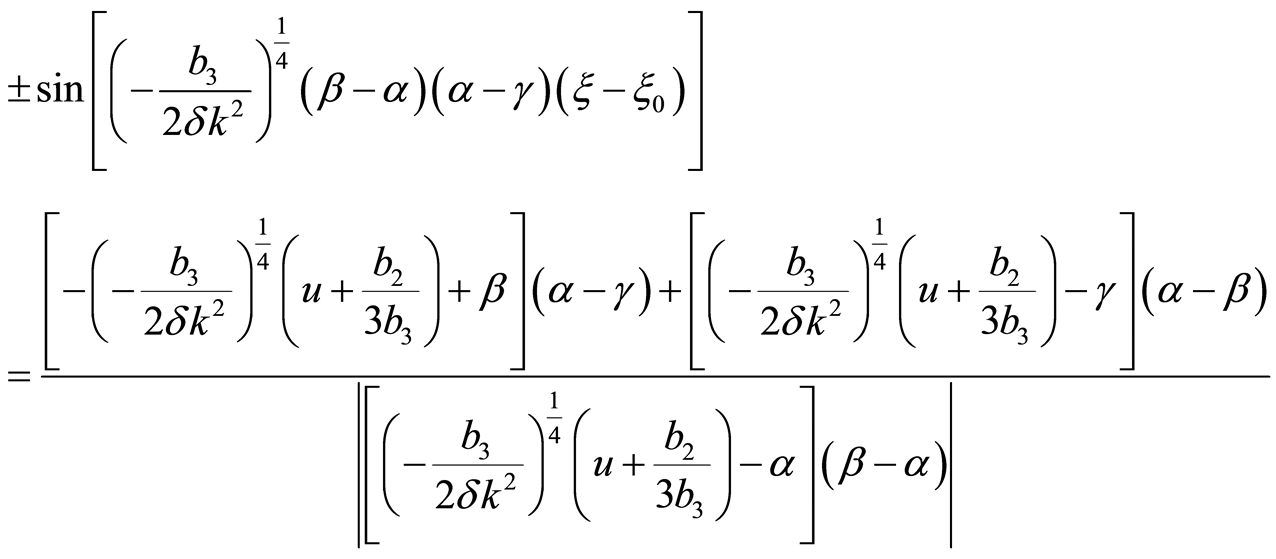 (41)
(41)
where , and
, and .
.
Case 2.2.6. 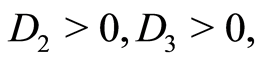 and
and ,
, 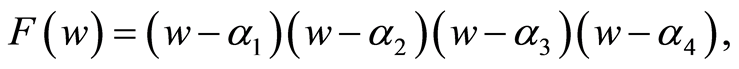
where  If
If  when
when  or
or , the solution of Equation (7) is
, the solution of Equation (7) is
 (42)
(42)
when 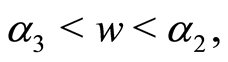 the solution of Equation (7) is
the solution of Equation (7) is
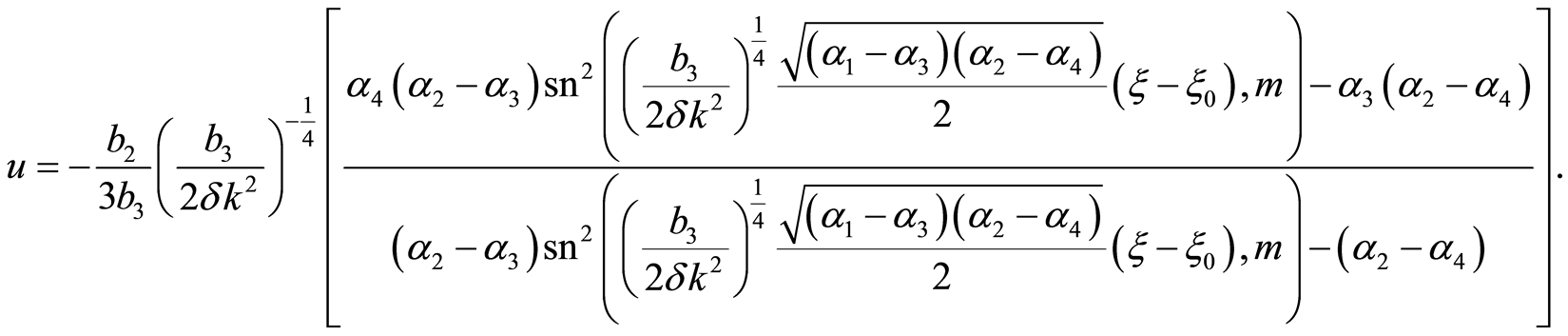 (43)
(43)
If 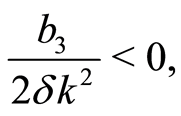 when
when 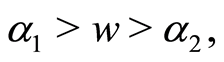 the solution of Equation (7) is
the solution of Equation (7) is
 (44)
(44)
when 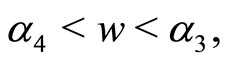 the solution of Equation (7) is
the solution of Equation (7) is
 (45)
(45)
where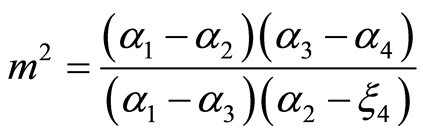 .
.
Case 2.2.7. 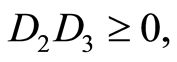 and
and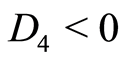 ,
, . where
. where  and
and .
.
The solution of Equation (7) (when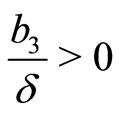 , we take the positive sign; when
, we take the positive sign; when  we take the negative) is
we take the negative) is
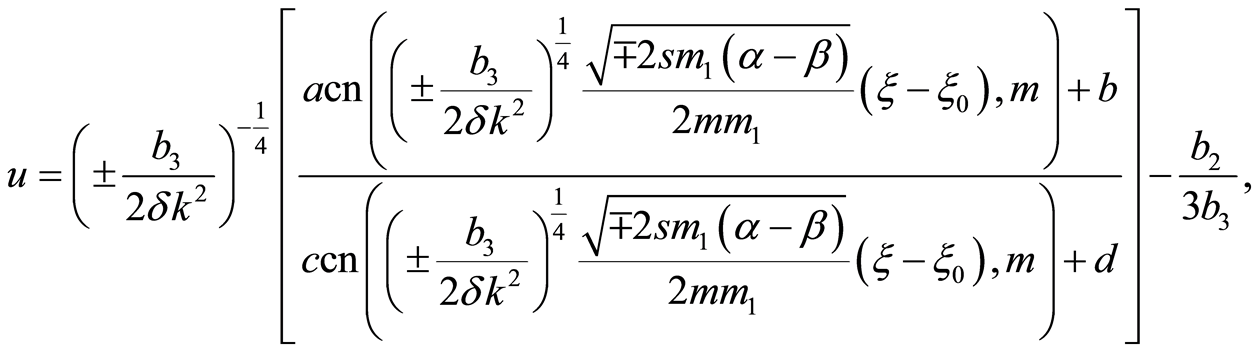 (46)
(46)
where ,
,  ,
, 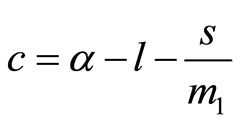 ,
, 
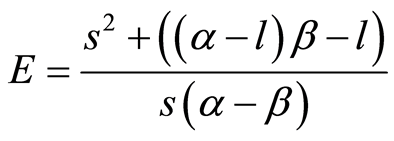 ,
,  ,
, .
.
Case 2.2.8. 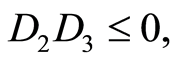 and
and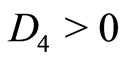 , then
, then , where
, where . The solution of Equation (7) is
. The solution of Equation (7) is
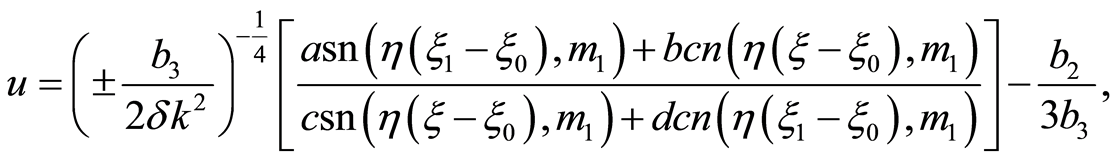 (47)
(47)
where ,
,  ,
, 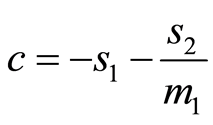
 ,
, 
 ,
, .
.
Case 2.2.9.  and
and , then
, then , where
, where  and
and 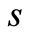 are real numbers. If
are real numbers. If , we have
, we have
 (48)
(48)
where .
.
4. Conclusion
By the complete discrimination system for polynomial method, we have obtained the classification of single traveling wave solutions to the generalized strong nonlinear Boussinesq without dissipation terms in 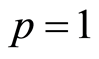 .These solutions include trigonometric periodic solutions, rational function solution, hyperbolic funtion solutions, Jacobi elliptic function solutions and so on. This method is simple and efficient.
.These solutions include trigonometric periodic solutions, rational function solution, hyperbolic funtion solutions, Jacobi elliptic function solutions and so on. This method is simple and efficient.
Acknowledgements
The project is supported by Scientific Research Fund of Education Department of Heilongjiang Province of China under Grant No. 12521049.
[1] Fan, E.G. (1998) A Note on the Homogenous Balance Method. Physics Letters A, 246, 403-406. http://dx.doi.org/10.1016/S0375-9601(98)00547-7
[2] Ablowitz, M.J. and Clarkson, P.A. (1991) Solitons, Non-Linear Evolution Equations and Inverse Scattering Transform. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511623998
[3] Hirota, R. (1973) Exact Envelope-Soliton of a Nonlinear Wave Equation. Journal of Mathematical Physics, 14, 805-813. http://dx.doi.org/10.1063/1.1666399
[4] Ma, W.X. and Fuchssteiner, B. (1996) Explicit and Exact Solutions to a Kolmogorov-Petrovskii-Piskunov Equation. International Journal of Non-Linear Mechanics, 31, 329-338. http://dx.doi.org/10.1016/0020-7462(95)00064-X
[5] Ma, W.X. (1993) Travelling Wave Solutions to a Seventh Order Generalized KdV Equation. Physics Letters A, 180, 221-224.
[6] Liu, C.S. (2010) Applications of Complete Discrimination System for Polynomial for Classifications of Traveling Wave Solutions to Nonlinear Differential Equations. Computer Physics Communications, 181, 317-324. http://dx.doi.org/10.1016/j.cpc.2009.10.006
[7] Liu, C.S. (2007) Classification of All Single Traveling Wave Solutions to Calogero-Focas Equation. Communications in Theoretical Physics (Beijing), 48, 601-604. http://dx.doi.org/10.1088/0253-6102/48/4/004
[8] Liu, C.S. (2006) Direct integral method, complete discrimination system for polynomial and applications to classifications of all single travelling wave solutions to nonlinear differential equations: a survey. arXiv: nlin/0609058v1
[9] Zhang, W.G. and Tao, T. (2008) Analysis of Solitary-Wave Shape and Solutions of the Generalized Strong Nonlinear Boussinesq Equation. Acta Mathematica Sientia, 28A, 086-095.
[10] Whitham, G.B. (1974) Linear and Nonlinear Wave. Springer, New York.
[11] Zhakarov, V.E. (1974) On Stochastization of One-Dimensional Chains of Nonlinear Oscillation. Soviet Physics-JETP, 38, 108- 110.
[12] McKean, H.P. (1981) Boussinesq’s Equation on the Circle. Pure and Applied Mathematics, 34, 599-690. http://dx.doi.org/10.1002/cpa.3160340502
[13] Manoranjan, V.S., et al. (1985) Numerical Solution of the Good Boussinesq Equation. SIAM: SIAM Journal on Scientific Computing, 5, 946-957.
[14] Weiss, J. (1985) The Painlevé Property and Backlund Transformation for the Sequence of Boussinesq Equations. Journal of Mathematical Physics, 26, 258-269. http://dx.doi.org/10.1063/1.526655
[15] Hu, X.G., Wu, Y.H. and Li, L. (2013) New Traveling Wave Solutions of the Boussinesq Equation Using a New Generalized Mapping Method. Journal of Basic and Applied Physics, 2, 68-77. http://dx.doi.org/10.5963/JBAP0202005
[16] Zakharov, V.E., et al. (1984) Theory of Solitons: The Iverse Scattering Method. Plenum Press, New York.
[17] Hirota, R. (1973) Exact N-Soliton Solutions of the Wave Equation of Long Wave Shallow-Water and in Nonlinear Lattices. Journal of Mathematical Physics, 14, 810-814. http://dx.doi.org/10.1063/1.1666400
NOTES
*Corresponding author.