2. Schematic Diagram
The following Figure 1 shows the Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR.
3. Methodology and Discussion
I plan to develop a theoretical research program in average Hamiltonian theory (AHT) to explain how periodic pulse sequences can be used to switch off or transform the symmetry of selected interactions in coupled and many-spin systems, allowing magnetic resonance spectroscopists to create effective spin Hamiltonians with a wide variety of useful properties [2,3]. The AHT via the Magnus expansion will be applied as the numerical integrator. Secondly, I propose to develop a research program in Floquet theory for studying spin systems under sample rotation and pulse crafting [4-7]. Thirdly, I intend investigate new theories including the Floquet-Magnus expansion (FME) [8-11] and the Fer expansion (FE) [12, 13] still in their infancy and recently introduced to solid-state NMR. To achieve this third goal, I will apply the FME to perform calculations in a finite-dimensional Hilbert space instead of an infinite dimensional space within the Floquet theory and provide new aspects not present in AHT and FLT such as recursive expansion scheme in Hilbert space that can facilitate the devise and improvement of pulse sequences. Next, I propose to perform

Figure 1. Flow chart of the theories, numerical simulations and applications in NMR.
more work of the possible extensions of the Fer expansion to ascertain its feasibility in handling cases involving non-periodic and non-cyclic cases which I expect to yield interesting results in the field of solid-state NMR in the future. I also plan to investigate potential future theoretical and numerical directions in solid-state NMR including (but not limited to) the Chebyshev expansion [14-16] and the transformation of Cayley [17,18].
Solid-state NMR is a powerful method to elucidate molecular structure and dynamics in systems not amenable to characterization by other methodologies and its importance stands in its ability to accurately determine intermolecular distances and molecular torsion angles.
Methods developed over the past  years enabled me to obtain simplified calculations for the common form of Hamiltonian in solid-state NMR and multimode Hamiltonian in its generalized Fourier expansion Hamiltonian. Based on these and other unpublished findings, I now believe that the FME provides a quick means to calculate higher order terms allowing the disentanglement of the stroboscopic observation and effective Hamiltonian that will be useful to describe spin dynamics processes in solid-state NMR and understand different synchronized or non-synchronized experiments. Furthermore, our preliminary applications of FE approach to study interactions in solid-state NMR when irradiated with the magic-echo sequence support this goal. The results of the first order
years enabled me to obtain simplified calculations for the common form of Hamiltonian in solid-state NMR and multimode Hamiltonian in its generalized Fourier expansion Hamiltonian. Based on these and other unpublished findings, I now believe that the FME provides a quick means to calculate higher order terms allowing the disentanglement of the stroboscopic observation and effective Hamiltonian that will be useful to describe spin dynamics processes in solid-state NMR and understand different synchronized or non-synchronized experiments. Furthermore, our preliminary applications of FE approach to study interactions in solid-state NMR when irradiated with the magic-echo sequence support this goal. The results of the first order  obtained for chemical shift, dipolar, and quadrupolar interactions might lead to the average Hamiltonian,
obtained for chemical shift, dipolar, and quadrupolar interactions might lead to the average Hamiltonian, 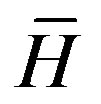 , in the sense of Magnus expansion under the circumstances:
, in the sense of Magnus expansion under the circumstances: . One major advantage of the Fer expansion over the AHT (Magnus expansion) is that only an evaluation of nested commutators is required in the calculation of
. One major advantage of the Fer expansion over the AHT (Magnus expansion) is that only an evaluation of nested commutators is required in the calculation of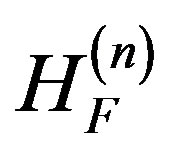 . The Magnus expansion requires the calculation of nested commutators and their integrals to obtain the correction terms of a Hamiltonian. A salient feature of the Fer and Magnus expansions stem from the fact that, when H(t) is an element in a given Lie algebra group, both approaches have the required structure and evolve in the desired group (Lie group). In addition, this is also true for their truncation to any order. I am thus poised to perform more work to ascertain the feasibility of Fer expansion in handling cases involving non-periodic and non-cyclic cases, and to use the expansion schemes of the theories therein described including the Magnus (AHT) and the Fer expansions as numerical integrators for solving the time dependent Schrodinger equation which is a central problem in quantum physics in general and solid-state nuclear magnetic resonance in particular.
. The Magnus expansion requires the calculation of nested commutators and their integrals to obtain the correction terms of a Hamiltonian. A salient feature of the Fer and Magnus expansions stem from the fact that, when H(t) is an element in a given Lie algebra group, both approaches have the required structure and evolve in the desired group (Lie group). In addition, this is also true for their truncation to any order. I am thus poised to perform more work to ascertain the feasibility of Fer expansion in handling cases involving non-periodic and non-cyclic cases, and to use the expansion schemes of the theories therein described including the Magnus (AHT) and the Fer expansions as numerical integrators for solving the time dependent Schrodinger equation which is a central problem in quantum physics in general and solid-state nuclear magnetic resonance in particular.
Theoretical approaches in NMR are challenging, but the potential payoff is substantial, and could ultimately lead not only to a more accurate and efficient spin dynamics simulation, but also to the development of sophisticated RF pulse sequences, and understanding new experiments. Therefore, theory and simulation in NMR should not only be encouraged but is essential. For instance, since the first demonstration of nuclear magnetic resonance in condensed matter in 1946 [19,20], the field of solid-state NMR has adopted only two milestones theoretical approaches in its history, theories which control the dynamics of spin systems: the average Hamiltonian theory (1968) and the Floquet theory (1982). However, compared to other spectroscopic techniques, the technique of NMR is well-established and will remain much a vibrant field of research due to its theoretical components driven by mathematicians, chemical and quantum physicists. With the possibilities of manipulating spin evolutions which can be accurately described by quantum mechanics and mathematics, and the abundance of physical, chemical and biological systems containing spins that produce NMR signals, and specific physical and chemical environments for the spins, I hope to contribute meaningfully to the qualitative improvements in the field of NMR.
The overall goals of this proposal is to support a theoretical research program in order to a) apply the average Hamiltonian theory to problems including (but not limited to): a class of symmetrical radio-frequency pulse sequences in the NMR of rotating solids [21-26], the symmetry principles in the design of NMR multiplepulse sequences [27], the Magnus expansion as numerical integrator, the composite pulses [28-30], and the problems still unsolved such as the AHT for 3 spins; b) use the Floquet theory in the study of several magic-angle spinning (MAS) NMR experiments on spin systems with a periodically time-dependent Hamiltonian. The system I intend to investigate will involve the multiple-multimode Floquet-theory in NMR and the scope of this research effort will focus on improving the diagonalization method and alternative ways of obtaining analytical solution in the form of effective Hamiltonians obtained via contact or van Vleck transformation procedure; c) enhance the performance of the Floquet-Magnus expansion by considering fundamental questions that arise when dealing with this approach. Many interesting problems such as multi-mode Hamiltonian, rotational-resonance recoupling, continuous wave irradiation on a single species, DARR and MIRROR recoupling, C-type and R-type sequences, TPPM decoupling, etc. [31,32], will be approached using the FME method. I hope to perform more quantitative work to bring out the salient features of the Floquet-Magnus expansion and explore its use in solid-state NMR and in many other theoretical areas; d) use the Fer expansion to solve similar problems such as those solved using the AHT including using the Fer expansion as numerical integrator for numerical simulation of spin systems. I also plan to tackle subtle aspects of FE, including, the convergence issue, the degree of computational involvement, and the application to coupled networks of spins, with regard to NMR; e) explore potential future theoretical and numerical directions for the calculation of the time propagation and evolution operators using Chebychev expansion (CE) and Cayley transformation (CT) methods. Simulation is very important in molecular quantum dynamics especially in the case of chemical exchange or relaxation, where line shapes can be overlapping. The main difficulty encountered in spectrum simulation is the rapid increase of computational requirements with an increasing number of spins. My motivation here to presenting the Chebyshev approximation as a potential surrogate of the popular expansions in NMR for the task of numerical simulations in spin dynamics paradigm stem from its numerical stability and high accuracy. It is noteworthy that the combinations of two or more of the theories known in NMR will continue to provide a framework for treating time-dependent Hamiltonian in quantum physics and NMR in a more efficient way that can be easily extended to all types of modulations.
4. Conclusion
The intention of this proposal is to help bring the current and future prospective theoretical aspects of spin dynamics to the attention of the NMR community and lead new interactions between NMR experts and other specialists in related fields. All of these points strongly support the idea that the Floquet-Magnus expansion, the Fer expansion, and the Chebyshev approach can also be very useful and powerful tools in quantum spin dynamics.
Acknowledgements
E.S. Mananga acknowledges assistance from Massachusetts General Hospital, Harvard Medical School, and the National Institute of Health (NIH) of USA, under Grants R01-HL110241 and T32 EB013180. The contents of this paper are solely the responsibility of the authors and do not represent the official views of NIH.