Turn Control of a Three-Dimensional Quasi-Passive Walking Robot by Utilizing a Mechanical Oscillator ()
However, it is difficult to stabilize passive walking robots in different environments because passive walking is sensitive to variations of initial condition and slope angle [3]. Moreover, passive walking robots cannot walk on flat ground or an upward slope because the robots do not have actuators to recover mechanical energy. Addition of some control and actuation is therefore necessary to stabilize passive waking robots in complex environments. The walking robot with minimum control and actuation is called quasi-passive walking robot [2,4,5]. Quasi-passive walking robots are energy-efficient and retain the feature of passive walking gait. Collins et al. demonstrated that quasi-passive walking robots can walk on a flat ground with startling human-like gait with simple controls only, such as ankle push-off or hip actuation [2]. These robots can walk straight stably, but few quasi-passive walking robots can turn because they are symmetrically controlled and actuated.
A quasi-passive walking robot that can walk and turn on flat ground was demonstrated in our previous study [6-8]. It was experimentally demonstrated that synchronization of the period of lateral motion TL with the period of swing leg motion TS was a necessary condition for stable 3D passive walking [6]. In the next step, a mechanical oscillator actuated by a motor was mounted on a 3D passive walking robot to stabilize the robot [7,8]. The mechanical oscillator was always oscillated in the frontal plane to synchronize TL with TS by utilizing forced entrainment. The target trajectory of the mechanical oscillator is periodic, and thus is planned by adjusting the period, phase and amplitude of the target trajectory. The stabilization control method was numerically and experimentally demonstrated [7,8].
In variable environments, the ability to turn is a necessity for a biped robot in order to steer and avoid obstacles, as an example. In order to improve adaptability of the robot to changing environments, a turn control method was proposed and numerically examined [9]. However, the same method cannot appropriately apply to our experimental robot because the target trajectory of the mechanical oscillator becomes discontinuous when the stance leg changes. The power of the motor of the experimental robot is so limited that the mechanical oscillator cannot follow the discontinuous target trajectory and the experimental robot fails to turn.
In this study, we propose a novel turn control method by controlling the central axis of oscillation of the mechanical oscillator to enable the robot to turn stably on flat ground with turn radius controlled. This new method is examined experimentally and numerically. Since this method does not need to increase actuators or change the construction of the robot the turn control and stabilizing methods for straight walking can switch to each other directly.
Additionally, the gait of turn is compared with that of straight walking and analyzed in terms of mechanical work and energy.
2. Experimental and Simulation Model
The experimental robot is made based on a passive walker, and the robot is composed of two straight legs, a trunk, a motor and a mechanical oscillator, as shown in Figure 1(a). The legs are connected to hip axis by two passive joints, and the relative angles between the legs and the hip axis are measured by utilizing two rotary encoders, as shown in Figure 1(b). The trunk is fixed to the hip axis, and the motor is mounted on the trunk to control the mechanical oscillator around the motor axis in the frontal plane. The batteries are fixed to the trunk to increase the moment of inertia about yaw axis and to lower the center of mass of the trunk. The center of mass of the trunk is lower than the hip axis because of the batteries, so the mechanical oscillator can keep upright. The robot’s foot sole is spherical and the center of the sphere is set higher than the center of mass of the robot to ensure that the robot is not only stable in standing posture but also robust against disturbance, initial conditions and path conditions in walking. The center of mass of the feet is adjusted backward by weights so that the swing leg can naturally swing forward even on a flat ground, as shown in Figure 1(b).
The simulation model constructed on the Open Dynamics Engine (ODE) [10] has the same structure, mass distribution as the experimental model except for the feet, as shown in Figure 2. The geometrical shape of the feet
 (a)
(a) (b)
(b)
Figure 1. Experimental robot based on a passive walker. (a) Experimental robot; (b) Back view of the legs and the hip axis.

Figure 2. Simulation model in ODE.
is set to spherical the same as the experimental model, but the mass distribution of the feet is set cubic for simplicity. The world coordinate is OXYZ, and the roll, pitch and yaw are denoted by θ, γ and ψ, respectively. The double support phase is assumed to be instantaneous, and the motion that the swing foot reaches the ground is regarded as heel-strike, which is assumed to be inelastic and without sliding in simulation. In single support phase, the spherical stance foot purely rolls on the ground without slip, and the swing leg swings ahead like a pendulum. The friction in joints is set to zero in simulation.
3. Algorithm of Turn Control
A simplified model of lateral motion in turn control is shown in Figure 3, where the trunk and legs are simplified to a block, with line AB as the central axis of the block, and line AC as the central axis of oscillation of the mechanical oscillator.
The roll angle of the lateral motion of the block is represented by θ, the inclination angle of the mechanical oscillator relative to line AB is represented by θw, the inclination angle of the central axis of oscillation relative to line AB is represented by θ1, and the inclination angle of the mechanical oscillator relative to line AC is represented by θ2.
The target trajectory of θw, θ1 and θ2 are represented by θwt, θ1t and θ2t, respectively. The target trajectory θwt is planned by θ1t and θ2t, because θwt is equal to θ1t + θ2t. The turning radius is controlled by θ1t, and the robot is stabilized by θ2t based on the stabilization control method.
In the stabilization control method, the period of lateral motion TL is controlled and always synchronized with the period of swing leg motion TS by periodic oscillation of the mechanical oscillator. Following the method, in turn control θ2t is also periodic and thus is planned by control-

Figure 3. Simplified model of lateral motion in turn control.
ling its period, amplitude and phase, respectively, as shown in Figure 4.
The period of θ2t is controlled on the basis of forced entrainment, which is an interesting phenomenon in nonlinear vibrations [11]. Forced van der Pol equation,
 , (1)
, (1)
is utilized to realize forced entrainment [7], where the roll angle θ of the robot is inputted into the Equation (1) as a periodic forcing function. The angular frequency of self-excitation of the Equation (1) is represented by ΩV and the angular frequency of θ is represented by ω. If ΩV@ω or the coefficient K is sufficiently large, the system indicates a phase-locking phenomenon and θ will entrain y. According to forced entrainment, the periods of y and  are synchronized to the period of θ. The phase of
are synchronized to the period of θ. The phase of 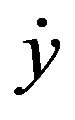 is the same as θ, but y shows a phase lead of π/2 relative to θ. The period of θ2t is controlled by y and
is the same as θ, but y shows a phase lead of π/2 relative to θ. The period of θ2t is controlled by y and 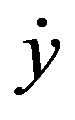 , and thus the period of target trajectory is also synchronized with the period of lateral motion of the robot.
, and thus the period of target trajectory is also synchronized with the period of lateral motion of the robot.
The amplitude β of the θ2t is determined by a proportional algorithm based on the stabilization control,
 , (2)
, (2)
where KP is the proportional gain, and α is a constant value obtained by preliminary simulation and determines the initial value of β.
According to y,  , β, and phase difference φ, The target trajectory θ2t is determined as follows [7]:
, β, and phase difference φ, The target trajectory θ2t is determined as follows [7]:
 , (3)
, (3)

Figure 4. Turn control algorithm.
where C1 and C2 are the amplitudes of y and  . When β is positive, the phase difference φ between the target trajectory θ2t and the roll angle θ is set to 90˚ or −90˚, respectively, to increase or decrease TL most efficiently. When φ is set to 90˚, the phase difference is automatically selected as 90˚ or −90˚ according to the sign of β given by Equation (2).
. When β is positive, the phase difference φ between the target trajectory θ2t and the roll angle θ is set to 90˚ or −90˚, respectively, to increase or decrease TL most efficiently. When φ is set to 90˚, the phase difference is automatically selected as 90˚ or −90˚ according to the sign of β given by Equation (2).
The target trajectory of θ1 is θ1t, which is planned to control the turning direction and turning radius r. When θ1 is positive, the robot turns right, and when θ1 is negative, the robot turns left. In order to investigate the relation between the turning radius r and θ1, r is measured when θ1 is set to a constant value in ODE simulation, as shown in Figure 5. The vertical axis is r, and the horizontal axis is θ1, the data of which is symmetric about the vertical axis. The minimum turning radius is 0.53m when θ1 is set to −60˚ or 60˚. If the absolute value of θ1 is larger than 60˚, the robot cannot turn stably.
In order to control r, based on Figure 5, the relationship between θ1 and rt is expressed by a function obtained by a curve fitting method, as
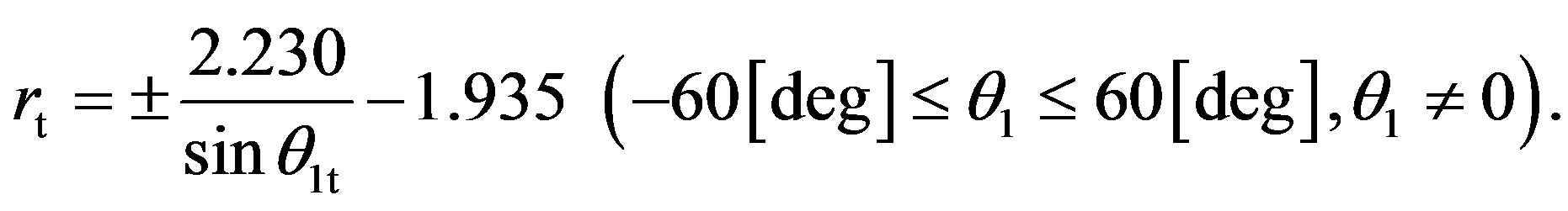 (4)
(4)
The plus and minus signs “±” in Equation (4) are used in left and right turn control, respectively.
4. Simulation and Experiment
4.1. Turn Control
The turn control is realized in the ODE simulation. The robot walks straight on a flat ground for 3 seconds to stabilize the walking gait, then θ1 is set to −60˚ and the robot begins to turn right. The trajectory of the center of mass of the robot in right turn is shown in Figure 6, where the horizontal and vertical axis are X and Y axis of the world coordinate, respectively. The turning radius is about 0.53 m, and the trajectory of the center of mass is snaky because the robot rolls in the lateral plane and the

Figure 5. Turn radiuses as a function of the inclination angle of the central axis of oscillation.
center of mass of the robot moves between the left and right foot.
The period of right lateral motion Tright is defined as the period of twice the time while θ is positive in one walking cycle, and the period of left lateral motion Tleft is defined as the period twice of the time while θ is minus in one walking cycle. In straight walking, Tright and Tleft are the same because of the symmetric left and right lateral motion.
However, Tright and Tleft become different in turn control by the inclination angle of the central axis of oscillation θ1. The relation of θ1 to the period difference “Tright - Tleft” is investigated in simulations and experiments, and the results are as shown in Figure 7, where the vertical axis is the period difference “Tright - Tleft” and the horizontal axis is the inclination angle θ1. The period difference increases when θ1 increases. The results of the simulation and experiments show that the method is effective to control the period difference “Tright - Tleft”. According to Figure 5 and Figure 7, if |Tright - Tleft| is larger, the turn radius becomes smaller, because larger |Tright -

Figure 6. Trajectory of the center of mass of the robot in right turn.

Figure 7. Period difference between the right and left lateral motion as a function of the inclination angle of the central axis of oscillation.
Tleft| leads larger difference of strides between the left and right leg and makes the robot turn with smaller turn radius.
Turn is an important ability of the robot in variable environments, so the turn control method is examined with the experimental robot and simulation model walking on a path with different turn radiuses at bends on flat ground.
In the experiment the path has two bends and the turn radiuses are 0.75 m and 2.0 m, as shown in Figure 8(a), so the robot has to switch its turn radius to adapt to the changing environment. There are no external sensors on the robot to sense the changing environment, so θ1t is calculated in advance according to the turn radiuses. According to Equation (4), θ1t is calculated and adjusted to −58˚ and 35˚ in the experiments when the turn radiuses are set to 0.75 m and 2.0 m, respectively. The robot stably walks through the path in the experiments, as shown in Figure 8(b), which shows that the turn control makes it possible for the robot to walk stably even under different conditions.
In the simulation a more complicated path is built but control method is the same as the method in the experiment, in which θ1t is also calculated in advance according to the turn radiuses. The robot walks through the path stably, as shown in Figure 9, where the location of the robot is shown in the mini map of the path.
4.2. Comparison of Turn and Straight Walking
In order to investigate the gait of the robot in turn control, the pitch angles of the right and left legs in right turn are compared with that in straight walking by simulation, as shown in Figure 10. The vertical axis is the pitch angle, and the horizontal axis is time. In straight walking the pitch angles of the two legs indicate similar wave shape, periods, and amplitudes yet opposite phase, and thus the time of left and right swing phase is the same, as shown in Figure 10(a). However, in right turn the pitch angles of the two legs indicate similar periods yet different wave shape and phases, and the time of the left swing phase is larger than the time of the right swing phase, as shown in Figure 10(b).
The lateral motion of the robot in right turn is compared with that in straight walking by using phase plane portraits, as shown in Figure 11. The vertical axis is the roll angle of the lateral motion θ, and the horizontal axis is the angular velocity of the lateral motion, with the black dot indicating the initial state, and the black arrow is the end of phase plane portraits. In straight walking the phase plane portraits are almost symmetric on the left and right half plane, and thus the lateral motion is symmetry in left and right stance phase, as shown in Figure 11(a). However, in right turn the phase plane portraits is asymmetric on the left and right half plane, as shown in
 (a)
(a) (b)
(b)
Figure 8. Experiments of turn control. (a) The path with different turn radiuses; (b) Walking on a path with different turn radiuses.
Figure 11(b), and the asymmetry comes from the inclination of the central axis of the mechanical oscillator movement. In right turn the roll angle of lateral motion in right stance phase is larger than that in left stance phase.
The unsymmetrical lateral motion of the robot can be understood from the viewpoint of mechanical work, so the positive and negative work performed by the motor on the robot in right turn are calculated and compared with that in straight walking in ODE simulation.
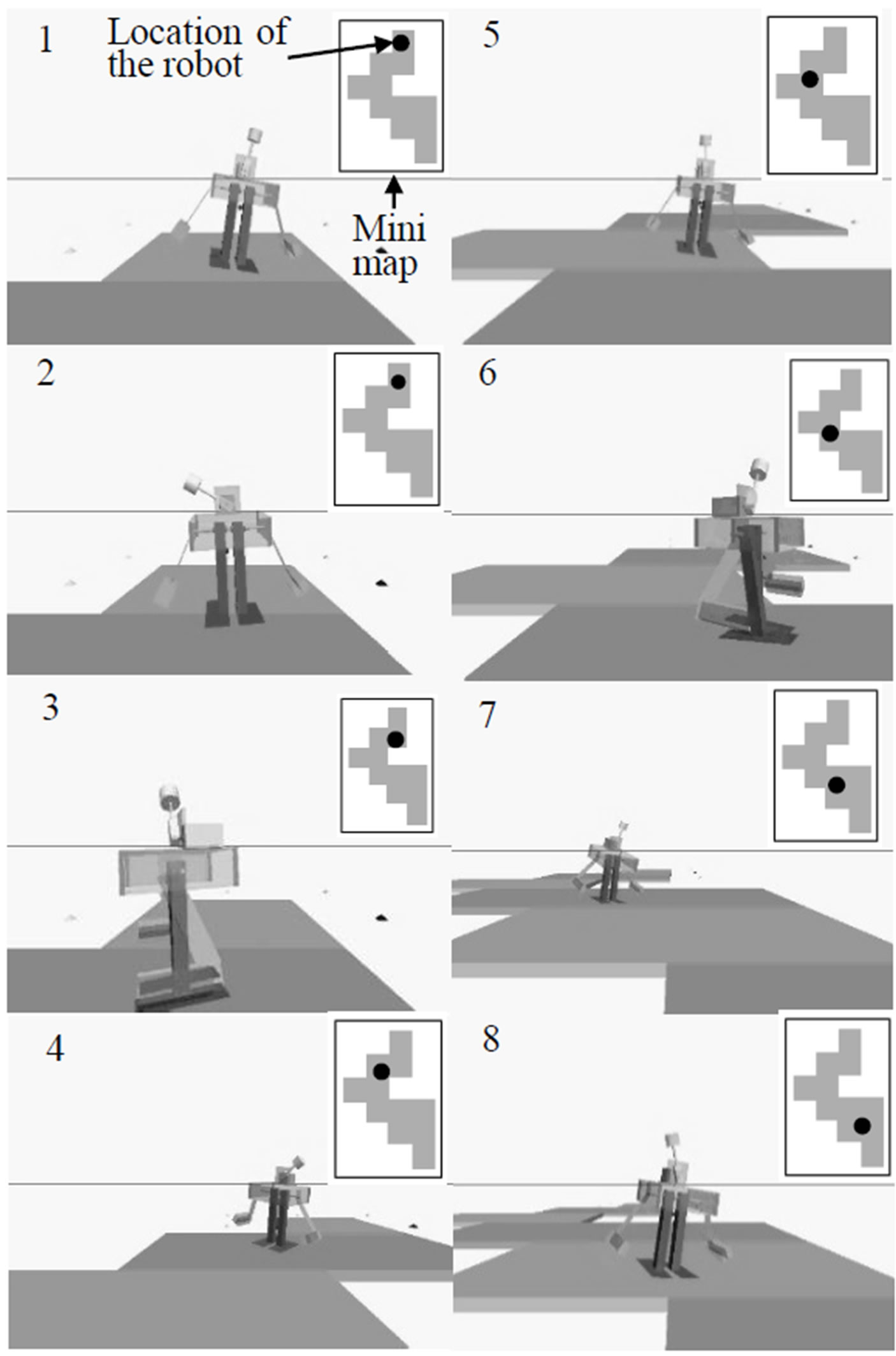
Figure 9. Simulation of turn control.


Figure 10. Pitch angles of the legs in straight walking and right turn.

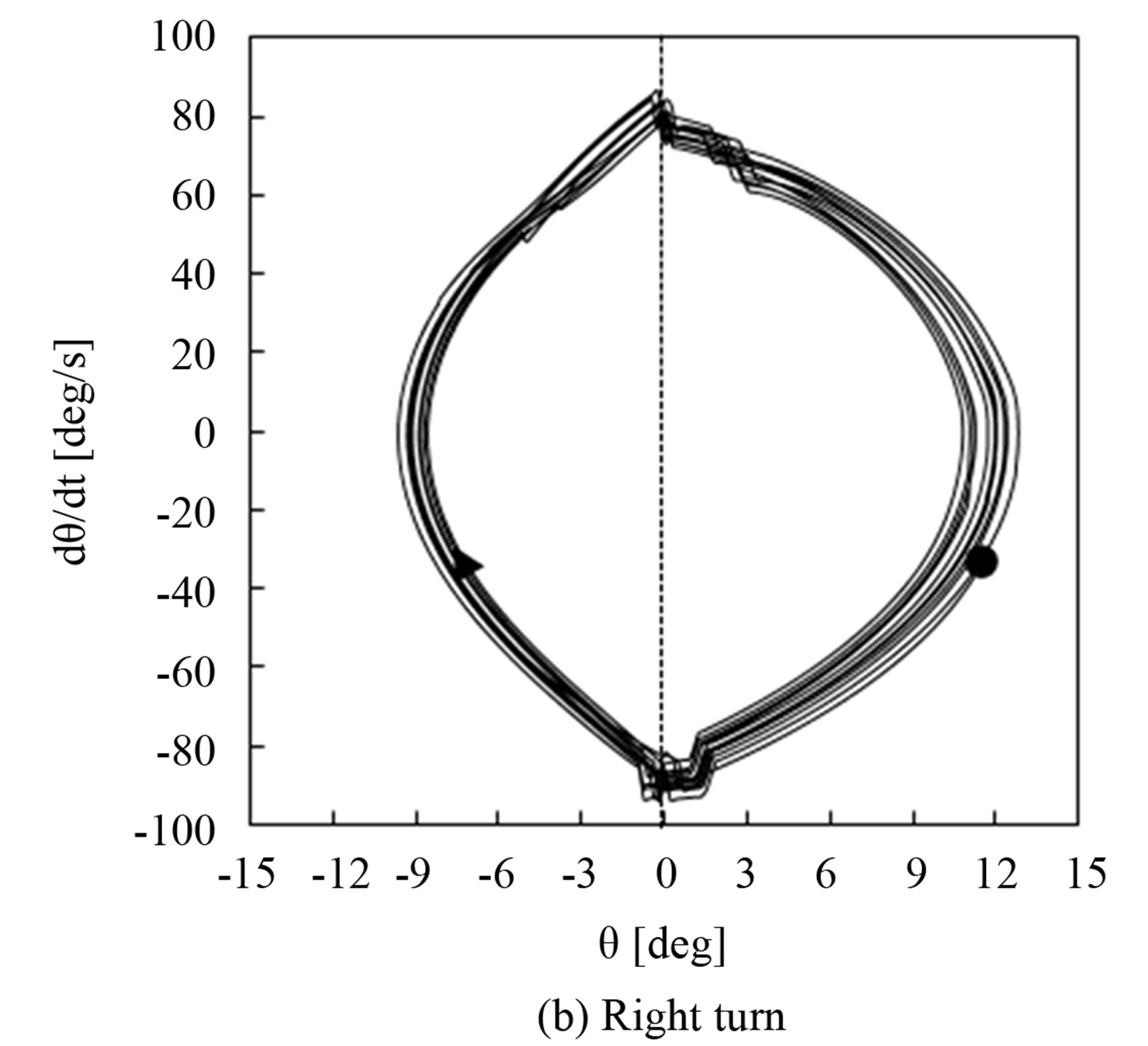
Figure 11. Phase plane portraits of lateral motion of the robot in straight walking and right turn.
The positive and negative works in right turn are shown in Figure 12(a). The positive and negative works are represented by Wp and Wn, respectively. The left vertical axis shows the work performed by the motor on the robot, and the right vertical axis shows the roll angle of the robot θ. According to the roll angle θ, the right and left stance phase can be distinguished easily, because stance leg changes when θ is 0. In the right stance phase the motor performs more positive work than negative work, thus the mechanical energy, the amplitude of lateral motion of the robot and the time of right stance phase increases. In the left stance phase the motor performs more negative work than positive work, thus the mechanical energy, the amplitude of lateral motion of the robot and the period of right lateral motion decreases. Therefore, the period difference between the right and left lateral motion can be increased, as shown in Figure 7.
The positive and negative work in straight walking is shown in Figure 12(b). Although the mechanical oscil-


Figure 12. Positive and negative work in right turn and straight walking.
lator always accelerates and decelerates to periodically sway left and right in the frontal plane, positive work accounts for 91% of total mechanical work on average in both right and left stance phase. Therefore, the right and left lateral motion of the robot are symmetric, as shown in Figure 12(b).
5. Conclusion
In this research, a novel turn control method is proposed for a 3D quasi-passive walking robot, and the method is examined both numerically and experimentally. The turn radius of the robot can be controlled by the inclination angle of the central axis of oscillation of the mechanical oscillator. Based on the turn control, the robot successfully walks through a curved path in the experiment and simulation, which indicates that it is possible for the robot to walk in variable environments. In addition, the gait and mechanical work of turn control are investigated and compared with that in straight walking.
In our future work, external sensors will be used to detect changing environments in order to guide the robot to walk in complex environments. Moreover, the amplitude of the target trajectory of the mechanical oscillator will be calculated by utilizing the relation between work and energy in turn control.