Asynchronous Secret Reconstruction and Its Application to the Threshold Cryptography ()
1. Introduction
Secret sharing schemes (SSs) were first introduced by both Blakley [1] and Shamir [2] separately in 1979 as a solution for safeguarding cryptographic keys and have been studied extensively in the literature. SS has become one of the most basic tools in cryptographic research. In Shamir’s  SS, a secret,
SS, a secret,  is divided into
is divided into 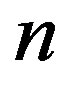 shares by a dealer and shares are sent to shareholders secretly. The security requirements of a
shares by a dealer and shares are sent to shareholders secretly. The security requirements of a  SS satisfy that (a) the secret can be reconstructed when there are
SS satisfy that (a) the secret can be reconstructed when there are  or more than
or more than  shares; and (b) the secret cannot be obtained when there are fewer than
shares; and (b) the secret cannot be obtained when there are fewer than  shares. Shamir’s
shares. Shamir’s  SS is based on the linear polynomial and is unconditionally secure. There are other types of SS. For example, Blakely’s scheme [1] is based on the geometry, Mignotte’s scheme [3] and Asmuth-Bloom’s scheme [4] are based on the Chinese Remainder Theorem (CRT).
SS is based on the linear polynomial and is unconditionally secure. There are other types of SS. For example, Blakely’s scheme [1] is based on the geometry, Mignotte’s scheme [3] and Asmuth-Bloom’s scheme [4] are based on the Chinese Remainder Theorem (CRT).
In the secret reconstruction, participating users can be either legitimate shareholders or attackers. Shamir’s scheme only considers the situation when all participating users are legitimate shareholders. When there are more than  users participating and shares are released asynchronously in the secret reconstruction, an attacker can always release his share last. In such a way, after knowing
users participating and shares are released asynchronously in the secret reconstruction, an attacker can always release his share last. In such a way, after knowing  valid shares, the attacker can obtain the secret and therefore, can successfully impersonate to be legitimate shareholder without being detected. One simple way to overcome this security problem is to authenticate every participating user to be a legitimate sharesholder before reconstructing the secret. Since all user authentication schemes are one-to-one type of interactions between one prover and one verifier, this approach may slow down the secret reconstruction significantly especially when there are a large number of users who participated in the process.
valid shares, the attacker can obtain the secret and therefore, can successfully impersonate to be legitimate shareholder without being detected. One simple way to overcome this security problem is to authenticate every participating user to be a legitimate sharesholder before reconstructing the secret. Since all user authentication schemes are one-to-one type of interactions between one prover and one verifier, this approach may slow down the secret reconstruction significantly especially when there are a large number of users who participated in the process.
In this paper, we propose a simple modification of Shamir’s scheme to fix the security problem in the secret reconstruction. Our solution does not use any user authentication. The secret can be reconstructed successfully only when all participating users are legitimate shareholders and release their shares honestly. If there are any attackers among participating users, the secret cannot be reconstructed by users since the attacker does not own any valid share. Furthermore, the attacker cannot obtain the secret from partially released valid shares of legitimate shareholders.
In Shamir’s  SS, every share can only be used for one time to recover the secret. This is because once the secret has been recovered, then all shares released and the secret are no longer secret. Therefore, the
SS, every share can only be used for one time to recover the secret. This is because once the secret has been recovered, then all shares released and the secret are no longer secret. Therefore, the  SS is not very efficient. To improve its efficiency, the
SS is not very efficient. To improve its efficiency, the  SS has been incorporated with public-key cryptography in the threshold cryptography. The group-oriented threshold cryptosystem was first introduced by Desmedt [5] in 1987. In such a system, each group, instead of each individual group member, publishes a single group public key. The corresponding private key of the group’s public key is divided into n shares and is shared among n group members following a
SS has been incorporated with public-key cryptography in the threshold cryptography. The group-oriented threshold cryptosystem was first introduced by Desmedt [5] in 1987. In such a system, each group, instead of each individual group member, publishes a single group public key. The corresponding private key of the group’s public key is divided into n shares and is shared among n group members following a 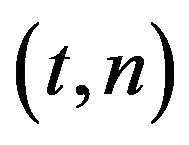 SS [1-4], where t is a predefined threshold value. Threshold cryptography is the study of efficient multiparty computation protocols for cryptographic functions (e.g. signing or decrypting), in which each group member has a share of the private key which allows the computation of such function. Threshold cryptography utilizes some computational assumptions, such as factoring a composite integer or solving the discrete logarithm, to enable shares of group members to be reused for multiple times. Similar to the
SS [1-4], where t is a predefined threshold value. Threshold cryptography is the study of efficient multiparty computation protocols for cryptographic functions (e.g. signing or decrypting), in which each group member has a share of the private key which allows the computation of such function. Threshold cryptography utilizes some computational assumptions, such as factoring a composite integer or solving the discrete logarithm, to enable shares of group members to be reused for multiple times. Similar to the  SS, participating users in a threshold cryptographic application can be either legitimate group members or attackers. All threshold cryptographic applications only consider the situation when all participating users are legitimate group members. When there are more than
SS, participating users in a threshold cryptographic application can be either legitimate group members or attackers. All threshold cryptographic applications only consider the situation when all participating users are legitimate group members. When there are more than  users participating and values of users are released asynchronously in a threshold application, an attacker can always release his computed values last. In such a way, after knowing
users participating and values of users are released asynchronously in a threshold application, an attacker can always release his computed values last. In such a way, after knowing 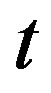 valid values of legitimate group members, the attacker can obtain the valid output of the cryptographic function and therefore, can successfully impersonate to be a legitimate group member without being detected. We also propose a modified scheme to fix this security problem.
valid values of legitimate group members, the attacker can obtain the valid output of the cryptographic function and therefore, can successfully impersonate to be a legitimate group member without being detected. We also propose a modified scheme to fix this security problem.
Related Works. The security of cryptographic schemes/protocols can be classified into two types, computational security and unconditional security. Computational security assumes that the adversary has bounded computing power that limits the adversary to solving hard mathematical problem, such as factoring a large composite integer into two primes. Unconditional security means that the security holds even if the adversary has unbounded computing power. Research on developing cryptographic schemes/protocols with unconditional security has received wide attention recently. Shamir’s  SS scheme is based on a linear polynomial and is unconditionally secure.
SS scheme is based on a linear polynomial and is unconditionally secure.
Shamir’s  SS is very simple; but if the secret reconstruction is performed over networks, possible threats make the secret reconstruction very complicate. In fact, attackers who do not own valid shares may impersonate to be shareholders who participated in the secret reconstruction. In 1985, Chor et al. [6] proposed the notion of verifiable secret sharing (VSS). VSS enables shareholders to verify that their shares are valid without revealing their shares. There are vast research papers on VSS [6-8] in the literature. VSS is a complicate process which requires additional information and processing time.
SS is very simple; but if the secret reconstruction is performed over networks, possible threats make the secret reconstruction very complicate. In fact, attackers who do not own valid shares may impersonate to be shareholders who participated in the secret reconstruction. In 1985, Chor et al. [6] proposed the notion of verifiable secret sharing (VSS). VSS enables shareholders to verify that their shares are valid without revealing their shares. There are vast research papers on VSS [6-8] in the literature. VSS is a complicate process which requires additional information and processing time.
How the secret should be reconstructed fairly is another research problem. When all other participating shareholders honestly present their shares in the secret reconstruction process, a dishonest shareholder can always exclusively get the secret by presenting a fake share and thus the others get nothing but a fake secret. Although protocols have been developed to detect fake shares [9-12], they do not prevent a dishonest shareholder from gaining this advantage. Even if the cheater is detected, this problem still persists as the cheater has already obtained the secret. The first protocol to solve this problem is proposed by Tompa et al. [10]. Most fair secret reconstruction proposals share one basic idea that utilizes a process where information is revealed slowly [13]. Chaum et al. [14], and Beaver et al. [15] considered the general problem of fair multiparty computation. Most of these works are based on a computational model, i.e., some computational assumptions are used like the existence of an oblivious transfer protocol or the quadratic residuosity assumption. In 1995, Lin et al. [16] proposed the first fair secret reconstruction protocol in which the real secret can be reconstructed as a whole entity without simultaneously releasing constraint. Cheating immune SSs through which the cheaters gain no advantage over honest participants by submitting invalid shares, are proposed in [17,18]; but secret and shares are limited to be either binary or from 
Our proposed scheme is not a VSS since in our scheme, shares are the only information of shareholders to prevent attackers from obtaining the secret and shares are not protected in the secret reconstruction. Furthermore, our proposed scheme cannot prevent a dishonest shareholder from presenting a fake share last in the secret reconstruction. In such a way, the dishonest shareholder can always exclusively get the secret but others get nothing but a fake secret. How the secret should be reconstructed fairly is a different research problem.
In a threshold signature scheme [19], when there are t or more than t group members, a group signature can be generated successfully. The group signature can be verified by any verifier using the group public key. On the other hand, in a threshold decryption scheme [20,21], any sender of a secret message can generate a cipher-text to the group using the group public key. When there are t or more than t group members, the group cipher-text can be decrypted successfully. All existing threshold cryptographic algorithms [19-26] only consider the situation when all participating users are legitimate group members. In this paper, we point out that when there are more than t participating users and computed valued are released asynchronously in a threshold application, an attacker can obtain the valid output of the application and therefore, can impersonate to be a legitimate group member without being detected.
We summarize the contributions of this paper in the following.
• We point out a security problem in Shamir’s  SS when there are more than t participating users and shares are released asynchronously in the secret reconstruction.
SS when there are more than t participating users and shares are released asynchronously in the secret reconstruction.
• A modified  SS based on Shamir’s
SS based on Shamir’s 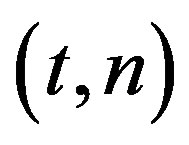 is proposed to fix the security problem.
is proposed to fix the security problem.
• We point out a similar security problem in all existing threshold algorithms when there are more than t participating users in threshold applications.
• A modified threshold decryption is proposed to fix the security problem.
The rest of this paper is organized as follows. In Section 2, we review Shamir’s  SS scheme and point out a security problem in Shamir’s
SS scheme and point out a security problem in Shamir’s  SS. In Section 3, we present a modified SS to fix the security problem when there are more than t participating users and shares are released asynchronously in the secret reconstruction. In Section 4, we point out the similar security problem and propose a solution to fix the security problem of a threshold decryption scheme. We conclude in Section 5.
SS. In Section 3, we present a modified SS to fix the security problem when there are more than t participating users and shares are released asynchronously in the secret reconstruction. In Section 4, we point out the similar security problem and propose a solution to fix the security problem of a threshold decryption scheme. We conclude in Section 5.
2. Review of Shamir’s (t, n) SS [2]
In Shamir’s (t, n) SS based on a linear polynomial, the dealer D is responsible to select a secret and generate shares of the secret to n shareholders,
 The scheme consists of two algorithms as illustrated in Figure 1.
The scheme consists of two algorithms as illustrated in Figure 1.
Shamir’s SS satisfies security requirements of the (t, n) SS, that are, (a) the secret can be reconstructed with t or more than t shares; and (b) no information about the secret can be obtained with fewer than t shares. In other words, if there are exactly t legitimate shareholders participated in the secret reconstruction, Shamir’s scheme can recover the secret. Shamir’s secret reconstruction scheme can be generalized to take more than t shares. For example, if there are j (i.e., ) participated shareholders with their shares,
) participated shareholders with their shares,  in the secret reconstruction, the secret can be recovered as follows.
in the secret reconstruction, the secret can be recovered as follows.

During secret reconstruction, participated users can be either legitimate shareholders or attackers. Shamir’s scheme only considers the situation when all participated users are legitimate shareholders. When there are more than t users participated in the secret reconstruction and shares are released asynchronously, an attacker can always release his share last. After knowing t valid shares of legitimate shareholders, since the secret polynomial,  having degree
having degree , the attacker can reconstruct the secret. Furthermore, the attacker can successfully forge a valid share on the polynomial,
, the attacker can reconstruct the secret. Furthermore, the attacker can successfully forge a valid share on the polynomial,  without being detected. Thus, Shamir’s (t, n) SS is no longer secure if there are more than t users participated in the secret reconstruction.
without being detected. Thus, Shamir’s (t, n) SS is no longer secure if there are more than t users participated in the secret reconstruction.
3. Proposed (t, n) Secret Sharing Scheme
In this section, we propose a (t, n) SS to fix the security problem of Shamir’s (t, n) SS when there are more than t participated users and shares are released asynchronously
in the secret reconstruction. The outcome of our proposed secret reconstruction is either (a) the secret if all participated users are legitimate shareholders; or (b) not the secret if there are attackers. The basic idea is that the dealer in Shamir’s (t, n) SS scheme selects  (i.e.,
(i.e.,  for example, if
for example, if 
 then
then  We will prove this condition in Theorem 1) random polynomials,
We will prove this condition in Theorem 1) random polynomials, 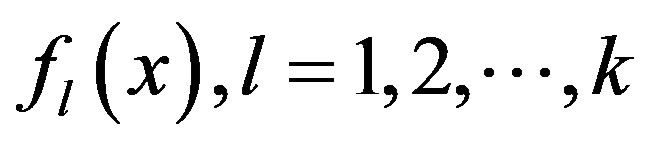 , having degree
, having degree  each, and generates shares,
each, and generates shares,  , for each shareholder,
, for each shareholder,  where
where  is the public information of shareholder,
is the public information of shareholder,  For the secret, s, the dealer can always find integers,
For the secret, s, the dealer can always find integers,  in GF(p)such that
in GF(p)such that  where
where 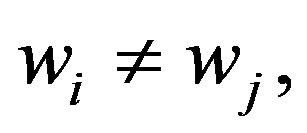 for every pair of i and j, and
for every pair of i and j, and  The dealer makes these integers,
The dealer makes these integers,  publicly known.
publicly known.
We assume that there are j (i.e., ) participated shareholders,
) participated shareholders,  in the secret reconstruction. Each shareholder
in the secret reconstruction. Each shareholder  uses his shares,
uses his shares, 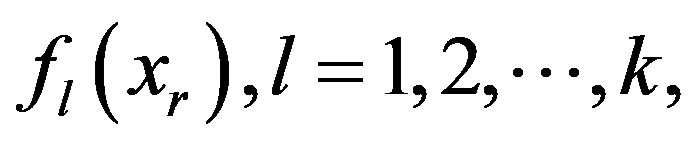 to compute and release one Lagrange component,
to compute and release one Lagrange component, 
to other participants. After knowing  each shareholder can recover the secret as
each shareholder can recover the secret as
 We outline this scheme, Scheme 1, in
We outline this scheme, Scheme 1, in
Figure 2.
Theorem 1. The outcome of Scheme 1 is either (a) the secret when all participated users are legitimate shareholders; or (b) not the secret when there are attackers.
Proof. In Scheme 1, if all participated users are legitimate shareholders and act honestly to compute their Lagrange components,  in Step 1, then in Step 2, we get
in Step 1, then in Step 2, we get

The outcome is the secret.
On the other hand, if there are attackers in the secret reconstruction, since attackers do not know any valid shares, the outcome of Scheme 1 is not the secret.
In the following discussion, we want to determine whether attackers can still recover the secret from partially released Lagrange components,  of legitimate shareholders. We analyze the security of the scenario which gives an attacker the most information to recover the secret. We assume that there are n users participated in the secret reconstruction and among them, there are
of legitimate shareholders. We analyze the security of the scenario which gives an attacker the most information to recover the secret. We assume that there are n users participated in the secret reconstruction and among them, there are 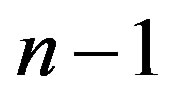 legitimate shareholders and the attacker is the last one to release his Lagrange component. Since each released Lagrange component is a linear function of kt coefficients of polynomials,
legitimate shareholders and the attacker is the last one to release his Lagrange component. Since each released Lagrange component is a linear function of kt coefficients of polynomials, 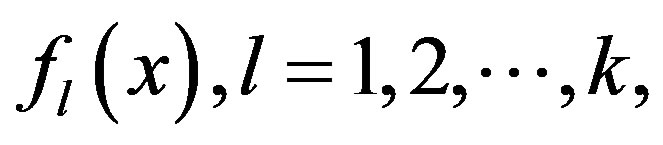 having degree
having degree  the attacker can obtain
the attacker can obtain  Lagrange components to form
Lagrange components to form  equations. The condition,
equations. The condition,  (i.e., kt is the number of unknown coefficients of polynomials,
(i.e., kt is the number of unknown coefficients of polynomials,  having degree
having degree  each), prevents the attacker solving the secret polynomials,
each), prevents the attacker solving the secret polynomials,  Thus, the attacker cannot recover the secret in Scheme 1. We have come to this conclusion without making any computational assumption. Thus, the proposed scheme is unconditionally secure.■
Thus, the attacker cannot recover the secret in Scheme 1. We have come to this conclusion without making any computational assumption. Thus, the proposed scheme is unconditionally secure.■
Remark 1. For the secret, s, the dealer needs to select  for every pair of i and j and the secret is
for every pair of i and j and the secret is
 If
If  for every pair of i and j, the attacker can still recover the secret after knowing t partially released Lagrange components,
for every pair of i and j, the attacker can still recover the secret after knowing t partially released Lagrange components,  of legitimate shareholders. This is because in this case, the secret,
of legitimate shareholders. This is because in this case, the secret,  is a share of the additive sum of polynomials,
is a share of the additive sum of polynomials,  having degree
having degree  Each participated shareholder,
Each participated shareholder,  needs to use his shares to compute and release the Lagrange component,
needs to use his shares to compute and release the Lagrange component,
 The attacker can recover the additive sum of shares,
The attacker can recover the additive sum of shares,  from each released Lagrange component
from each released Lagrange component 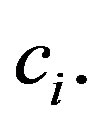 Thus, after knowing t additive sum of shares, the attacker can recover secret as,
Thus, after knowing t additive sum of shares, the attacker can recover secret as,

4. Proposed Threshold Decryption Scheme
In this section, we present two  threshold decryption schemes; one is a basic scheme and the other one is a modified scheme, in which the security of both schemes is based on the computational difficulty of solving the discrete logarithm problem. We use the basic scheme to point the security problem when there are more than t users participated in a threshold application. The threshold decryption scheme is one of the grouporiented threshold cryptographic algorithms. In this application, a group manager (GM), instead of each individual group member, publishes a single group public key. The corresponding private key of the group’s public key is divided into n shares and is shared among n group members. Then, any t or more than t group members can enable a threshold application.
threshold decryption schemes; one is a basic scheme and the other one is a modified scheme, in which the security of both schemes is based on the computational difficulty of solving the discrete logarithm problem. We use the basic scheme to point the security problem when there are more than t users participated in a threshold application. The threshold decryption scheme is one of the grouporiented threshold cryptographic algorithms. In this application, a group manager (GM), instead of each individual group member, publishes a single group public key. The corresponding private key of the group’s public key is divided into n shares and is shared among n group members. Then, any t or more than t group members can enable a threshold application.
4.1. Basic Scheme
We assume that there are  members,
members,  for
for
 forming a group.
forming a group.
Initialization
The GM selects two large public primes,  and
and , such that
, such that  divides
divides 
 is a unique subgroup of
is a unique subgroup of  with order
with order , and one public generator,
, and one public generator,  from
from  GM selects a private key,
GM selects a private key,  and computes the public key of the group,
and computes the public key of the group,  GM acts like a dealer in Shamir’s
GM acts like a dealer in Shamir’s  SS to select a random polynomial
SS to select a random polynomial 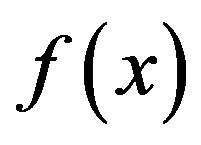 of degree
of degree
 :
:  such that the private key is
such that the private key is  and all coefficients,
and all coefficients, 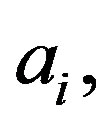 for
for  are in
are in  with
with  GM computes
GM computes  shares,
shares,  where
where  is the public information associated with group member
is the public information associated with group member  Each share,
Each share,  is sent to group member,
is sent to group member,  secretly.
secretly.
Generation of a cipher-text
We adopt the ElGamal’s encryption scheme [27]. With access to the group public key,  the sender can generate a cipher-text,
the sender can generate a cipher-text,  of message m by computing
of message m by computing  where
where 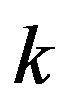 is a random integer in
is a random integer in  and
and  where
where  The sender sends the cipher-text,
The sender sends the cipher-text,  to the group.
to the group.
Decryption of a cipher-text
Let us assume that j (i.e.,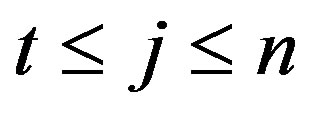 ) group members,
) group members,
 work together to decrypt a cipher-text.
work together to decrypt a cipher-text.
Each group member,  uses his private share,
uses his private share,  to compute a partial session key,
to compute a partial session key,
 The value,
The value,  is sent to other group members participated in the decryption. After collecting all partial session keys, the session key,
is sent to other group members participated in the decryption. After collecting all partial session keys, the session key,  can be computed as
can be computed as

Each participated group member can decrypt the ciphertext as 
Security discussion
In a practical application, participated users in a threshold decryption can be either legitimate group members or attackers. We assume that an attacker has collected  valid partial session keys,
valid partial session keys,
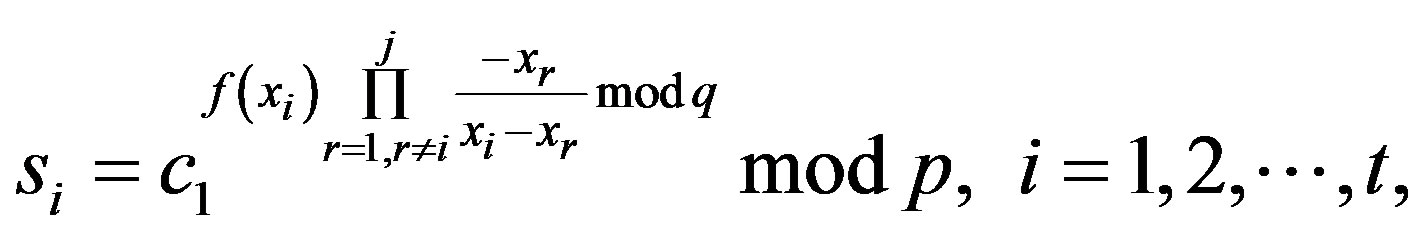
of legitimate group members. Then, the attacker can compute

The real session key,  can be obtained by computing
can be obtained by computing 
Thus, the attacker can decrypt the cipher-text as
 Furthermore, the attacker can successfully forge a valid partial session key of other legitimate group member, say
Furthermore, the attacker can successfully forge a valid partial session key of other legitimate group member, say  as
as

without being detected in this process. The security problem of this basic scheme is caused by the fact that the modular exponentiation of each share,  can be obtained from the partial session key,
can be obtained from the partial session key, 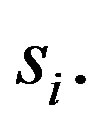 With any
With any  modular exponentiations of shares, the attacker can successfully recover the modular exponentiation of the constant term of the polynomial and to recover the session key,
modular exponentiations of shares, the attacker can successfully recover the modular exponentiation of the constant term of the polynomial and to recover the session key,  In the following subsection, we propose a simple modification to fix this security problem.
In the following subsection, we propose a simple modification to fix this security problem.
4.2. Modified Scheme
Initialization
GM selects two large public primes,  and
and , such that
, such that  divides
divides 
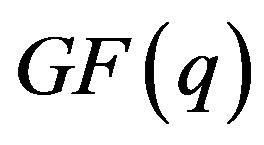 is a unique subgroup of
is a unique subgroup of  with order
with order , and one public generator,
, and one public generator,  from
from  GM selects a private key,
GM selects a private key,  and computes the public key of the group,
and computes the public key of the group,
 GM acts like a dealer in Shamir’s
GM acts like a dealer in Shamir’s  SS to select two random polynomials,
SS to select two random polynomials,  and
and  having degree
having degree  each:
each:
 and
and
 such that the private key,
such that the private key,  is divided into
is divided into  with
with  and
and  all coefficients,
all coefficients,  and
and  for
for  are in
are in  with
with 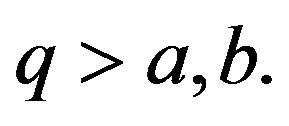 GM computes a pair of shares,
GM computes a pair of shares, 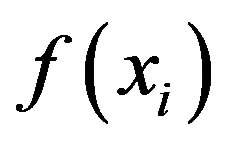 and
and  for each shareholder,
for each shareholder,  where
where  is the public information associated with
is the public information associated with  Each pair of shares,
Each pair of shares,  and
and  is sent to group member,
is sent to group member,  secretly.
secretly.
Generation of a cipher-text
This part of process is the same as the basic scheme. A group cipher-text, 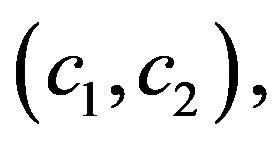 of message m is generated by computing
of message m is generated by computing  and
and  where
where  is a random integer from
is a random integer from  and
and
 The sender sends the cipher-text,
The sender sends the cipher-text,
 to the group.
to the group.
Decryption of cipher-text
Let us assume that j (i.e., ) group members,
) group members,  work together to decrypt the ciphertext. Each group member,
work together to decrypt the ciphertext. Each group member,  uses his pair of private shares,
uses his pair of private shares,  and
and  to compute a partial session key,
to compute a partial session key,  The value
The value  is sent to other participated shareholders. After collecting all partial session keys from other group members, the member can decrypt the cipher-text as
is sent to other participated shareholders. After collecting all partial session keys from other group members, the member can decrypt the cipher-text as  We outline this scheme, Scheme 2, in Figure 3.
We outline this scheme, Scheme 2, in Figure 3.
Theorem 2. In Scheme 2, if all participated users are legitimate group members and act honestly, the ciphertext,  of the message m can be decrypted successfully.
of the message m can be decrypted successfully.
Proof. If all group members act honestly, the real session key,  can be obtained as
can be obtained as


Figure 3. Scheme 2—Proposed (t, n) threshold decryption scheme.
The session key can be used to recover the message as ■
■
Security discussion
In this modified scheme, the partial session key is
 Since the exponent of each partial session key is a linear combination of two shares,
Since the exponent of each partial session key is a linear combination of two shares,  and
and  attackers cannot separate these two shares to obtain the modular exponentiation of each share. In other words, attackers need to collect all partial session keys to be able to decrypt the cipher-text of the group. Therefore, if there are attackers participated in the decryption, the cipher-text cannot be decrypted.
attackers cannot separate these two shares to obtain the modular exponentiation of each share. In other words, attackers need to collect all partial session keys to be able to decrypt the cipher-text of the group. Therefore, if there are attackers participated in the decryption, the cipher-text cannot be decrypted.
We want to determine whether attackers can still decrypt the group cipher-text from a portion of partial session keys which are released from legitimate group members. There are 2t coefficients in polynomials, 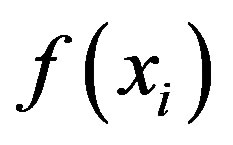 and
and  having degree
having degree 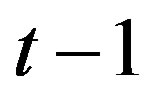 each. If an attacker can obtain
each. If an attacker can obtain  (i.e.,
(i.e., ) additive sum of shares,
) additive sum of shares, 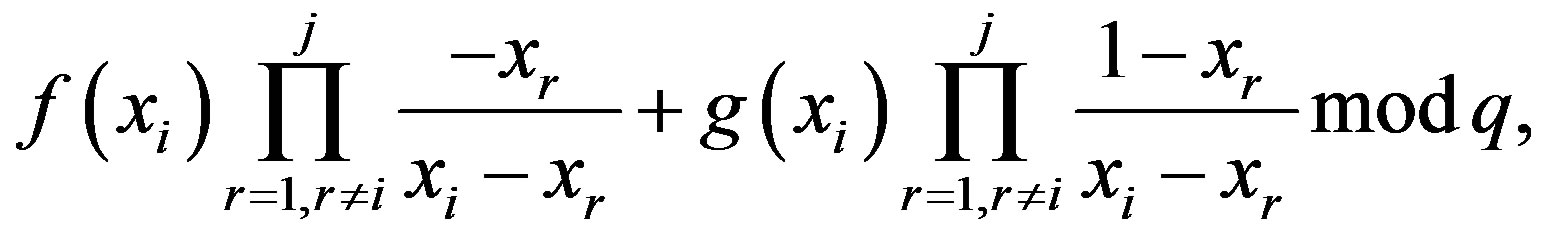
from released partial session keys, the attacker is able to solve both polynomials,  and
and  However, this attack is computational infeasible due to the difficulty of solving the discrete logarithm problem.
However, this attack is computational infeasible due to the difficulty of solving the discrete logarithm problem.
Remark 3. For any secret, s, the dealer needs to select two different points on the polynomials,  and
and 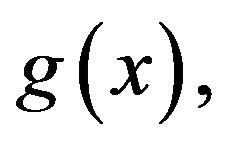 for example,
for example,  and
and  If two points are the same such as
If two points are the same such as 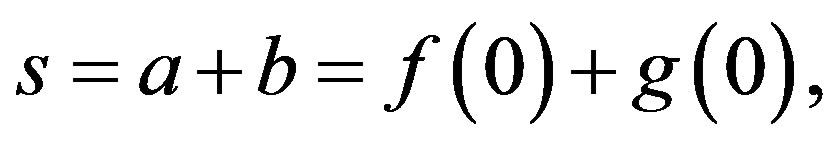 the secret,
the secret,  is a share of the additive sum of polynomials,
is a share of the additive sum of polynomials,  having degree
having degree  The partial session key of
The partial session key of  is
is  If one attacker has obtained
If one attacker has obtained  partial session keys,
partial session keys,
 of legitimate group members, the attacker can compute
of legitimate group members, the attacker can compute

Therefore, the session key,  can be obtained by computing
can be obtained by computing

5. Conclusion
We pointed out security problems of a (t, n) SS and a threshold algorithm. The security problems occurred when there are more than t participated users and shares/ values that are released asynchronously in the secret reconstruction/threshold application. Since all existing networks are asynchronous networks and we cannot exclude the probability that with more than t users participating in a secret reconstruction/threshold application, our paper has made significant contributions to addressing the security problems and proposing solutions. We believe that we have opened a new research direction in both the secret sharing and the threshold cryptography.
Acknowledgements
This research is supported by the National Natural Science Foundations of China under Grant No. 61103247.
NOTES