Shannon showed that self-information is formally de- fined as the negative expected log probability, 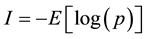 , and has meaning with both discrete and continuous probability distributions. It can even be derived from the definition of statistical entropy,
, and has meaning with both discrete and continuous probability distributions. It can even be derived from the definition of statistical entropy, 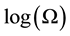 , as given by Boltzmann [8]. The natural loga- rithm is used in this analysis and thus the units of infor- mation are the natural unit, or nats [9].
, as given by Boltzmann [8]. The natural loga- rithm is used in this analysis and thus the units of infor- mation are the natural unit, or nats [9].
2. Quantum Mechanics
2.1. Schrödinger Equation
The Schrödinger equation, found during the advent of quantum mechanics, dictates how a wave function and its phase evolve through time. The Hamiltonian or energy operator, H , of a system is equal to hbar times the im- aginary derivative with respect to time; with the opera- tor’s eigenvalue, the energy,  , of the system [10].
, of the system [10].
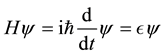
The solution to this equation is the complex exponential,
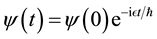
One can calculate the probability distribution associated with this wave function via its magnitude squared [10].

Note the phase information is lost. Calculating the information without considering the phase information one would conclude that the information is constant and a function only of its initial state,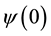 . Let me assume that
. Let me assume that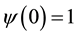 . However if we dig a little deeper an insight appears that when looked at in a few different ways proves resilient.
. However if we dig a little deeper an insight appears that when looked at in a few different ways proves resilient.
If the probability is constant, then the size of the space is equal to one over the probability, . In this case
. In this case  is the thermodynamic entropy [8],
is the thermodynamic entropy [8],
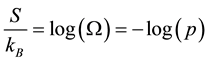
By being a little more formal we can relax the condition that 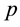 is constant and instead only need to have
is constant and instead only need to have 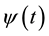 independent from
independent from . Consider a large number
. Consider a large number 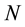 of independent steps in the particle, where
of independent steps in the particle, where . In this case, the probability of
. In this case, the probability of  is equal to
is equal to 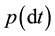 raised to the
raised to the 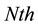 power. I next use the weak law of large numbers through the asymptotic equipartition property (AEP) to focus on the most likely states [9]. (This is important and exemplified by the Gaussian distribution, where the Gaussian has infinite range but most likely states are limited to its standard deviation. If a large number of possible outcomes can occur each with the same probability within the range
power. I next use the weak law of large numbers through the asymptotic equipartition property (AEP) to focus on the most likely states [9]. (This is important and exemplified by the Gaussian distribution, where the Gaussian has infinite range but most likely states are limited to its standard deviation. If a large number of possible outcomes can occur each with the same probability within the range ![]() of a system, then one can prove that information encoded into that system is equal to the negative log of the probability on average.) In this case
of a system, then one can prove that information encoded into that system is equal to the negative log of the probability on average.) In this case
![]()
and
![]()
The AEP and the weak law of large numbers [9] can be used to show the negative log probability approaches the incremental entropy. Calling this the differential information, dI , I have
![]()
2.2. Dueling information Rates
The insight comes by breaking up ![]() and looking at the differential information,
and looking at the differential information,
![]()
Plugging in for![]() , results in the trivial answer
, results in the trivial answer
![]()
There are two information rates that cancel each other out, one equal to the imaginary energy dived by hbar and the other a negative imaginary energy divided by hbar.
If a Minkowski transformation had been performed prior to calculating the probability distribution a different answer would result. The Minkowski transformation takes imaginary time and makes it real. We see this transformation appear in relativity and analytic continuation [11,12]. After applying the Minkowski transformation ![]() such that,
such that,
![]()
and
![]()
or,
![]()
This last equation is the governing thought of the paper. Assuming that the mass energy is not a function of time (which is not always the case), the following simple expression results,
![]()
2.3. Non-commuting operators
It is possible to remove the dependency on the Minkowski transformation and arrive at the same result by replacing the energy eigenvalue![]() , with the energy operator. When this is the case, the complex conjugate operation also requires the transpose of the operators since they do not commute. Using the power rule to expand the exponent and the logarithm, I now have, with
, with the energy operator. When this is the case, the complex conjugate operation also requires the transpose of the operators since they do not commute. Using the power rule to expand the exponent and the logarithm, I now have, with ![]() the energy operator,
the energy operator,
![]()
![]()
With this approach the negative log probability is now
![]()
Since the commutator ![]() [10], I have,
[10], I have,
![]()
I show in Section 4 that this is true of every step in the process with the appropriate step of size,![]() . For a large number of
. For a large number of ![]() independent steps (where,
independent steps (where,![]() ), the negative log probability approaches the information,
), the negative log probability approaches the information, ![]() , or
, or
![]()
3. Signals
The initial conclusion (before I introduced imaginary time or the commutator) was that there is no information contained in the phase of a wave function; however we know from our analysis of signals that sine and cosine waves are capable of transmitting information in their phases. There are differences between the phase of the wave function and the phase of a signal [4] but it is worthwhile to pursue this approach as well.
Work by Nyquist and Hartley after the turn of the 20th century [13,14] tells us that the bandwidth of the signals is in direct proportion to the width of the signal in the frequency domain.
Gabor was even closer on track in the middle of 20th century when he tiled the time-frequency plane with quantized “logons” on information [15]―see Figure 1. Each logon was one degree of freedom and is represented by a shifted and modulated Gaussian wave packet. These wave packets were used as a basis to represent a signal with bandwidth f and duration t.
A more rigorous analysis of the number of degrees of freedom of a signal limited in bandwidth and time can be found by Slepian, Pollak and Landau [16-18].
They concluded the rate of information that can be encoded into a signal is linear in the bandwidth (or frequency). With Planck’s work on black body radiation and Einstein’s equation for the photo electric effect, where ![]() [10], this proportion reduces to below
[10], this proportion reduces to below
![]()
Figure 1. Time frequency plane quantized to individual de- grees of freedom, each containing one natural unit of in- formation.
where ![]() is the information rate of the signal,
is the information rate of the signal, ![]() is the bandwidth of the signal,
is the bandwidth of the signal, ![]() is Planck’s constant times
is Planck’s constant times ![]() and
and ![]() is the duration of the signal.
is the duration of the signal.
![]()
From here I can quickly return to the governing thought a third time by solving for the direct proportion in the equation above by diving by the minimum width of the signal (the Heisenberg uncertainty relation).
![]()
In Section 5.1, I show that the Gaussian wave packet, which obtains the minimum uncertainty, contains one natural unit of information, thus completing this proof.
An important insight to interpreting this equation is seen by again returning to Figure 1 and looking at the time-frequency plane as a Venn diagram of entropy.
4. Brownian Motion
Before the two examples, I will re-derive the governing thought yet a 4th way by discretizing space and motion.
Building on the analysis by Kubo on the fluctuation dissipation theorem [19], I formalize the 2 time constants for a diffusing free particle; the collision time, ![]() and the relaxation time,
and the relaxation time,![]() . When the relaxation time is equal to the thermal time,
. When the relaxation time is equal to the thermal time, ![]() , the diffusion constant becomes,
, the diffusion constant becomes, ![]() , [19-22] and spatial variance is
, [19-22] and spatial variance is![]() .
.
4.1. Bernoulli Process
Introducing the Bernoulli process as reviewed by Reif and Chandrasekhar [8,23], one can solve for the step size, ![]() , (or the collision time). The contribution to the spatial variance is balanced between drift and diffusion; when the probability parameter is 1/2 the variance is,
, (or the collision time). The contribution to the spatial variance is balanced between drift and diffusion; when the probability parameter is 1/2 the variance is,
![]()
Here ![]() is the spatial step size,
is the spatial step size, ![]() is the number of steps,
is the number of steps, ![]() is the duration of the process and
is the duration of the process and ![]() is the variance in velocity. From Dirac, we know that
is the variance in velocity. From Dirac, we know that ![]() [24] which allows us to calculate
[24] which allows us to calculate![]() .
.
When ![]() is large, the average variance of the sum of
is large, the average variance of the sum of ![]() samples of a distribution is equal to the variance of the individual sample divided by
samples of a distribution is equal to the variance of the individual sample divided by ![]()
![]()
Equating ![]() and
and![]() , or
, or![]() , results in ,
, results in ,
![]()
Thus when the relaxation time is equal to one over twice the temperature![]() , the collision time is one over twice the energy
, the collision time is one over twice the energy![]() , and visa versa.
, and visa versa.
4.2. Information Content
With the details of the Bernoulli process defined, we can move onto the Gaussian channel. Combined with the Shannon-Nyquist’s sampling theorem one has the channel capacity per second, ![]() [9],
[9],
![]()
![]() is the signal power,
is the signal power, ![]() is the noise spectral density and
is the noise spectral density and ![]() is the bandwidth of the channel. (In this case, the channel is the vacuum which either has infinite bandwidth or some very large value.)
is the bandwidth of the channel. (In this case, the channel is the vacuum which either has infinite bandwidth or some very large value.)
Using the assumption (aided by the insight of appendix A1) that the signal spectral density is equal to the noise spectral density, the signal power, ![]() , is the noise spectral density times twice the bandwidth of the signal,
, is the noise spectral density times twice the bandwidth of the signal,![]() . Since the bandwidth of the signal is much smaller than the bandwidth of the channel,
. Since the bandwidth of the signal is much smaller than the bandwidth of the channel, ![]() , we can re-write the equation above as,
, we can re-write the equation above as,
![]()
The signal is the location of the particle performing the Bernoulli process with a step size of![]() , thus the Shannon-Nyquist sampling theorem [25] tells us that the maximum frequency that can be represented by the discrete Bernoulli process is
, thus the Shannon-Nyquist sampling theorem [25] tells us that the maximum frequency that can be represented by the discrete Bernoulli process is![]() .
.
![]()
To finish the derivation I will take one more finding from Dirac, who showed that there is both a positive and negative solution to the energy eigenvalue [24]. Because there are two independent particles diffusing and information is generated by each particle a factor of 2 must be included; returning us to the governing thought.
![]()
5. Examples
5.1. Gaussian Wave Packet
The Gaussian wave packet has many special properties, including 1) its Fourier transform is also a Gaussian [25], 2) the Gaussian obtains the minimum uncertainty relation [12], and 3) the Gaussian maximizes the differential entropy for a given variance [9]. As introduced above, Gabor [15] used the first two properties to tile the time frequency plane with shifted and modulated Gaussian wave packets. I will expand on property 3) and show that the information that can be decoded from one Gaussian wave packet is one nat.
First a result from Hirshman [26] where he proposed that to properly measure the information contained in a pair of distributions linked through the Fourier Transform (FT) one must add the differential entropy of the probability distribution in the time domain to the differential entropy of the probability distribution in the standard frequency domain. Given the scale property of the FT and the differential entropy, the sum of the two differential entropies is constant regardless of scale factor. Thus the information you can encode into a Gaussian wave packet is the same regardless of the relative width of the wave packet in the two domains.
Hirshman found that any FT pair contained at least ![]() of information and that the Gaussian has exactly
of information and that the Gaussian has exactly![]() . I believe Hirshman missed an extra
. I believe Hirshman missed an extra ![]() which nature requires. Looking at the governing thought, and applying the Heisenberg uncertainty principle when the energy is not a function of the time, shows that information in nature is greater than or equal to 1 natural unit.
which nature requires. Looking at the governing thought, and applying the Heisenberg uncertainty principle when the energy is not a function of the time, shows that information in nature is greater than or equal to 1 natural unit.
![]()
To show how this applies to the Gaussian, I again use the example of a massive particle. Dirac tells us from his work on the relativistic wave equation that there is both a positive and negative Eigen state [24]. Looking at the positive eigenvalue where the mass-energy divided by Planck’s constant equals the average frequency![]() , we have
, we have
![]()
and for the negative eigenvalue,
![]()
If ![]() the two functions don’t overlap, they don’t interfere and thus according to Feynman [10] it’s their probability distributions that add not the probability amplitudes (or wave functions). See Figure 2. The resulting probability distribution for the frequency domain
the two functions don’t overlap, they don’t interfere and thus according to Feynman [10] it’s their probability distributions that add not the probability amplitudes (or wave functions). See Figure 2. The resulting probability distribution for the frequency domain ![]() is,
is,
![]()
Taking the inverse FT we have ![]() and
and![]() . The resulting probability distribution for the time domain,
. The resulting probability distribution for the time domain, ![]() is,
is,
![]()
Given the modulation properties of the FT, ![]() and with
and with![]() ,
, ![]() reduces to
reduces to
![]()
Now using Hirshman’s sum the result is, ![]() 1,
1,
![]()
Coupling this back to Gabor’s original analysis, I would conclude that a measurement of the Gaussian wave packet requires one natural unit of classical information to describe. This finite amount is due to the inherent noise associated with the Heisenberg uncertainty principle.
5.2. Electron Spin state
1It is interesting to note that the Hirshman sum of the exponential wave function is also one natural unit.
One might jump to the conclusion that a spin 1/2 particle has one natural unit of information by taking our governing thought and applying it to the spin angular momentum. However this is not correct as spin is quantized to ![]() along of each of the three spatial dimensions. Associating one natural unit of information to each spa-
along of each of the three spatial dimensions. Associating one natural unit of information to each spa-
![]()
Figure 2. Probability distribution for Gaussian with non- overlapping positive and negative states. Hirshman sum is one natural unit.
tial dimension for a total of 3 natural units is also not correct since the measurements are not independent. The way to tackle this problem is by looking at the three spa- tial dimensions and the time dimension, then using our governing thought on the magnitude of the all four spin operators.
Let’s start with the mathematical formulism to deal with the spin operator for the time dimension. This operator maps the wave function at the instantaneous moment in time to the discrete value![]() , or
, or ![]() when
when![]() .
.
Sticking with the spin operator formulism, we need a ![]() matrix that has unity eigenvalues and returns the wave function untouched (since we are simply mapping to a discrete time value but not touching any of the spatial dimensions). You can see I have identified this Pauli matrix as the identity matrix. The spin operator
matrix that has unity eigenvalues and returns the wave function untouched (since we are simply mapping to a discrete time value but not touching any of the spatial dimensions). You can see I have identified this Pauli matrix as the identity matrix. The spin operator ![]() associated with this identity Pauli matrix is,
associated with this identity Pauli matrix is,
![]()
![]() is now a fourth spin operator similar to
is now a fourth spin operator similar to![]() ,
, ![]() , and
, and![]() .
.
One implication to adding the identity matrix to the formulism is that the magnitude of the spin angular momentum now takes on a more simple form with s the quantum spin number. Adding to the standard way of calculating ![]() [12] we have,
[12] we have,
![]()
![]()
Now applying the governing thought to angular momentum, I have the information in the spin of a particle equal to twice the magnitude divided by hbar.
![]()
Applying this to the electron with ![]() the electron should have 2 natural units of information.
the electron should have 2 natural units of information.
![]()
Let’s see how that plays out using our current understanding of quantum information theory.
We know from Schumacher and Westmoreland [4], that the probability of error in inferring a message from a quantum measurement is at least one minus the dimension of the Hilbert space divided by the number of distinct messages, Y,
![]()
We find this channel capacity is equal to ![]() when the Hilbert space is a qubit and we choose to send spins in only the
when the Hilbert space is a qubit and we choose to send spins in only the![]() , or
, or ![]() state. In this case
state. In this case ![]() and
and ![]() can be zero.
can be zero.
However nature does not just produce electrons in only the![]() , or
, or ![]() state. Sending an electron in one of only two states is a human choice and filtering or initialization is required. For nature to maintain symmetry and balance, the state must have a uniform distribution around the Bloch sphere. Thus the arbitrary state
state. Sending an electron in one of only two states is a human choice and filtering or initialization is required. For nature to maintain symmetry and balance, the state must have a uniform distribution around the Bloch sphere. Thus the arbitrary state ![]() is created
is created
![]()
We also know that if we classically measure in an arbitrary direction, the wave function collapses to the state defined by that outcome [4]. This means that if we make a measurement in one direction with zero variance, any other non-commuting observable will have maximum variance.
However there is nothing stopping us from calculating the entropy we would expect if a measurement were to happen (even though don’t make the measurement as that would collapse the state). Here I use the word entropy instead of information since a measurement of a state with ![]() will produce a partially random Boolean output that is not completely deterministic from knowledge of the initial state. Yet the term information is still relevant since it takes that much information to describe the outcome.
will produce a partially random Boolean output that is not completely deterministic from knowledge of the initial state. Yet the term information is still relevant since it takes that much information to describe the outcome.
In this way we can add the entropy in each non- commuting observable in the same way Hirshman showed us.
For ![]() to be uniformly distributed across the Bloch sphere we need to look at the Jacobian between spatial and spherical coordinates to seek how
to be uniformly distributed across the Bloch sphere we need to look at the Jacobian between spatial and spherical coordinates to seek how ![]() and
and ![]() are distributed. We find the determinant of the Jacobian is equal to
are distributed. We find the determinant of the Jacobian is equal to![]() , which means that
, which means that ![]() is uniformly distributed but
is uniformly distributed but ![]() has the distribution
has the distribution ![]() for
for![]() .
.
Defining![]() , wh- ere
, wh- ere ![]() is the probability of a positive measurement of the qubit in question, we can calculate the entropy of
is the probability of a positive measurement of the qubit in question, we can calculate the entropy of
each spin operator by averaging ![]()
over ![]() to get the average information, one will find,
to get the average information, one will find,
![]()
Since the distribution of ![]() is uniform around the Bloch sphere this calculation is the same for
is uniform around the Bloch sphere this calculation is the same for ![]() and
and![]() .
.
![]()
One might not be satisfied that each of![]() ,
, ![]() , and
, and ![]() can be separable, however if you go through the math and use the joint distribution on
can be separable, however if you go through the math and use the joint distribution on ![]() and
and ![]() and take into consideration the angle between
and take into consideration the angle between ![]() and
and![]() ,
, ![]() , and
, and![]() , one gets the same answer.
, one gets the same answer.
The entropy of the ![]() operator takes different reasoning to calculate, but the answer is the same. To start we need to review Section 4.1 on the Bernoulli process. If
operator takes different reasoning to calculate, but the answer is the same. To start we need to review Section 4.1 on the Bernoulli process. If ![]() acts to confirm a particle is occupying the time,
acts to confirm a particle is occupying the time, ![]() , where
, where ![]() is the step index and
is the step index and ![]() is the step size, the probability of a positive confirmation is equal to the relative distance the instantaneous time,
is the step size, the probability of a positive confirmation is equal to the relative distance the instantaneous time, ![]() is away from
is away from![]() . A negative confirmation would mean that the particle is found in the state
. A negative confirmation would mean that the particle is found in the state![]() .
.
Figure 3 is a picture of a particle at time ![]() uniformly distributed between
uniformly distributed between![]() . Finding the particle in the
. Finding the particle in the ![]() state is equal to
state is equal to ![]() and finding the particle in the
and finding the particle in the ![]() state is
state is![]() .
.
![]()
Without loss of generality we can set![]() . To complete the derivation I average
. To complete the derivation I average ![]() over the uniform distribution to find
over the uniform distribution to find![]() .
.
![]()
Thus, using Hirshman’s sum I find,
![]()
It is interesting to note that ![]() is described by 2 degrees of freedom. One real number from
is described by 2 degrees of freedom. One real number from ![]() and one real number from
and one real number from![]() . Thus we further support the idea that one degree of freedom is associated with one natural unit.
. Thus we further support the idea that one degree of freedom is associated with one natural unit.
6. Discussion and Conclusion
The questions that I addressed are, “how much information is in an evolving system, how does one quantify it, and how much classical information is needed to describe it?”
You might have noticed that in some cases above I used the term rate, while in other cases I used capacity. We know from Shannon’s noisy-channel coding theorem that the rate must be less than the capacity for the probability of error of decoding a message to go to zero; and conversely that if the rate is greater than the capacity, an arbitrary small probability of error is not achievable [6]. However from my analysis it appears that in nature the rate of the underlying particles equals the capacity of the channel that transmits those particles through space-time; which in turn equals the energy of the particle. This insight is another reason why I am using the word information to describe![]() .
.
I propose that the quantum state and the associated degree of freedom keep an extremely high (or possibly infinitly high) precision of its value. Yet when the wavefunction collapses and a classical measurement occurs, the capacity of that channel is only one natural until information per degree of freedom and the entropy rate of that measurement is such that one natural unit of information is needed to describe any measurement process you could ask of it per degree of freedom.
Thus, I find that precision to the infinite decimal point in the classical measurement is neither required nor possible since the classical information is finite. It thus makes sense that space is quantized. Planck showed energy is quantized [10]; Quantum Mechanics showed “action” is quantized; and from the analysis here a finite system is described by a finite amount of information; there is just not enough information in nature (or too much noise) to localize a particle to a continuous value that is not part of a finite set of values.
A broader debate is necessary to understand the physicality of classical information describing a quantum system, since its implications can be seen on both tangible qualities like the entanglement of quantum states and intangible qualities like the collaspe of the wavefunction. Yet, one advantage of knowing the governing thought is that you are able to use information theoretic tools to solve physics problems and vice versa. For example, the principle of least action (which is fundamental to mechanics) can be now looked at as a principle of least information.
There is much more work to do in these areas including application to the unsolved problems of physics [5], or for that matter other unknown unsolved problems. Still having this insight into information is a good start.
Acknowledgements
JLH would like to thank many the ground breaking contributors who built the foundations of quantum mechanics and information theory, the Professors who inspire him, and specifically his family for their love, Professor Hawking for his reminder to always move “forward” and the Lord for the opportunity to contribute.
REFERENCES
[1] J. Gantz and D. Reinsel, “The Digital Universe in 2020,” IDC, Framingham, 2012.
[2] J. Manyika, et al., “Big Data: The Next Frontier for Innovation, Competition, and Productivity,” McKinsey Global Institute, San Francisco, 2011.
[3] L. Brillouin, “Science and Information Theory,” 2nd Edition, Academic Press Inc., Waltham, 1962.
[4] B. Schumacher and M. Westmoreland, “Quantum Pro- cesses, Systems, and Information,” Cambridge University Press, Cambridge, 2010.
[5] L. Smolin, “The Trouble With Physics,” First Mariner Books, New York, 2006
[6] C. Shannon and W. Weaver, “The Mathematical Theory of Communication,” University of Illinois Press, Cham- paign, 1949.
[7] M. Volkenstein, “Entropy and Information,” Birkhauser, Berlin, 2009. http://dx.doi.org/10.1007/978-3-0346-0078-1
[8] F. Reif, “Fundamentals of Statistical and Thermal Phys- ics,” McGraw Hill, Boston, 1965.
[9] T. Cover and J. Thomas, “Elements of Information Theory,” John Wiley & Sons Inc., New York, 1991. http://dx.doi.org/10.1002/0471200611
[10] R. Feynman, “Lectures on Physics,” Addison-Wesley Publishing, Reading, 1965.
[11] A. Einstein, “The Meaning of Relativity,” Princeton Uni- versity Press, Princeton, 1953.
[12] R. Shankar, “Principles of Quantum Mechanics,” 2nd Edition, Plenum Press, New York, 1994. http://dx.doi.org/10.1007/978-1-4757-0576-8
[13] H. Nyquist, Bell System Technical Journal, Vol. 3, 1924, pp. 324-326. http://dx.doi.org/10.1002/j.1538-7305.1924.tb01361.x
[14] R. V. L. Hartley, Bell System Technical Journal, Vol. 7, 1928, pp. 535-563. http://dx.doi.org/10.1002/j.1538-7305.1928.tb01236.x
[15] D. Gabor, Journal of Institution of Electrical Engineers, Vol. 93, 1946, p. 429.
[16] D. Slepian and H. O. Pollak, Bell System Technical Jour- nal, Vol. 40, 1961, pp. 43-63. http://dx.doi.org/10.1002/j.1538-7305.1961.tb03976.x
[17] H. J. Landau and H. O. Pollak, Bell System Technical Journal, Vol. 40, 1961, pp. 65-84. http://dx.doi.org/10.1002/j.1538-7305.1961.tb03977.x
[18] H. J. Landau and H. O. Pollak, Bell System Technical Journal, Vol. 41, 1962, pp. 1295-1336. http://dx.doi.org/10.1002/j.1538-7305.1962.tb03279.x
[19] R Kubo, Reports on Progress in Physics, Vol. 29, 1966, p. 255. http://dx.doi.org/10.1088/0034-4885/29/1/306
[20] J. Haller Jr., Journal of Modern Physics, Vol. 4, 2013, pp. 85-95. http://dx.doi.org/10.4236/jmp.2013.47A1010
[21] J. Haller Jr., Journal of Modern Physics, Vol. 4, 2013, pp. 1393-1399. http://dx.doi.org/10.4236/jmp.2013.410167
[22] E. Nelson, Physical Review, Vol. 150, 1966, pp. 1079- 1085. http://dx.doi.org/10.1103/PhysRev.150.1079
[23] S. Chandrasekhar, Reviews of Modern Physics, Vol. 15, 1943, pp. 1-89.
[24] P. A. M. Dirac, “The Principles of Quantum Mechanics,” 4th Edition, Oxford University Press, Oxford, 1958, p. 262.
[25] R. N. Bracewell, “The Fourier Transform and Its Appli- cations,” 2nd Edition, McGraw-Hill Inc., New York, 1986.
[26] I. I. Hirshman Jr., American Journal of Mathematics, Vol. 79, 1957, pp. 152-156. http://dx.doi.org/10.2307/2372390
[27] H. Nyquist, Physical Review, Vol. 32, 1928, pp. 110-113. http://dx.doi.org/10.1103/PhysRev.32.110
Appendix
A1. Signal Spectral Density
It is helpful to show how the signal of Brownian motion has the same spectral density as the noise. This is shown in the example of a harmonic oscillator with a thermal energy ![]() (from two degrees of freedom) exactly equal to the quantum ground state energy,
(from two degrees of freedom) exactly equal to the quantum ground state energy, ![]() [20],
[20],
![]()
The signal power is the time derivate of the energy,![]() . As the signal is wiped-out for frequencies higher than one over twice the relaxation time,
. As the signal is wiped-out for frequencies higher than one over twice the relaxation time, ![]() we divide the power by
we divide the power by ![]() to give the signal spectral density,
to give the signal spectral density, ![]() ,
,
![]()
Here ![]() is the force, which is equal to
is the force, which is equal to![]() . Re-writing this equation and interpreting
. Re-writing this equation and interpreting ![]() and
and ![]() as operators to replace with the commutator
as operators to replace with the commutator ![]() [10], we get
[10], we get
![]()
This is purely reactive power (as one would expect from an un-damped harmonic oscillator). But for the purposes here, one will recognize the apparent power, or magnitude of the complex power, (apart from the resistive factor) as the Johnson-Nyquist noise spectral density when spread over both positive and negative frequencies [27]. Thus we support the assumption in Section 4.2.
A2. Thermodynamic Derivation
Having in appendix A1, introduced the harmonic oscillator with quantum ground state energy equal to the temperature, it is straightforward to show that, for this example, the governing thought also applies within thermodynamics. Reviewing the power, ![]() , we have
, we have
![]()
![]()
Since the power is reactive (imaginary), there is no work done and from the first law of thermodynamics [8]![]() will equal the heat,
will equal the heat,![]() . Our expression of for thermodynamic entropy is now
. Our expression of for thermodynamic entropy is now ![]()
![]()
Remembering ![]() and assuming the temperature is constant gives the result,
and assuming the temperature is constant gives the result,
![]()
It is interesting that once again imaginary time is in the picture. Since![]() , and upon making a Minkowski transformation [11,12],
, and upon making a Minkowski transformation [11,12],
![]()
Haller derives the entropy rate of thermal diffusion for one particle in [21]; here I will use a quicker derivation for both the positive and negative energy states and use the Gaussian channel capacity. The signal in this case is the width of the diffusing particle undergoing the Bernoulli process for one step, ![]() ,
,
![]()
The noise is the minimum width of the wavepacket [10],
![]()
The capacity of one step of the Gaussian channel with this signal and noise is
![]()
Taking ![]() over the step size,
over the step size, ![]() , (and including a factor of 2 for the two particles), we have the information rate,
, (and including a factor of 2 for the two particles), we have the information rate,
![]()
Assuming a non-relativistic particle, where![]() , or equivalently
, or equivalently![]() , the above reduces to,
, the above reduces to,
![]()
Replacing![]() , the governing thought is again returned,
, the governing thought is again returned,
![]()
As assumed before, the temperature is constant so by integrating, we finish with information being equal to the thermodynamic entropy calculated above in this section,
![]()