Common Fixed Points for a Countable Family of Set-Valued Mappings with Quasi-Contractive Conditions on Metrically Convex Spaces ()
1. Introduction
There have appeared many fixed point theorems for a single-valued self map of a closed subset of a Banach space. However, in many applications, the mapping under considerations is not a self-mapping on a closed subset. In 1976, Assad [1] gave sufficient condition for such single valued mapping to obtain a fixed point by proving a fixed point theorem for Kannan mappings on a Banach space and putting certain boundary conditions on the mapping. Similar results for multi-valued mappings were respectively given by Assad [2] and Assad and Kirk [3]. On the other hand, many authors discussed common fixed point problems [4-7] for finite single or multi-valued mappings on a complete 2-metric convex space or a complete cone metric space respectively. And some authors also discussed common fixed point problems [8-13] for a countable family of self-single-valued mappings with contractive or quasi-contractive conditions on a metric space or a metrically convex space respectively. These results improved and generalized many previous works.
In this paper, we will discuss the existent problems of common fixed points for a countable family of surjective set-valued mappings, which satisfy certain quasi-contractive condition, defined on a complete metrically convex space and obtain some important theorems. The main results in this paper further generalize and improve many common fixed point theorems for single valued or multi-valued mappings with quasi-contractive type conditions.
Through this paper,  (or
(or ) is a metric space. Let
) is a metric space. Let  denote the families of all bounded closed subset of
denote the families of all bounded closed subset of .
.
Let , the distance between
, the distance between  and
and .
.
Definition 1.1. ([8-10]) A metric space  is said to be metrically convex, if any
is said to be metrically convex, if any  with
with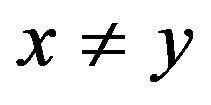 , there exists
, there exists 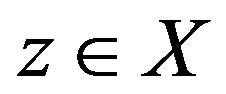 such that
such that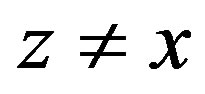 ,
,  and
and .
.
Lemma 1.1. ([3,8]) If  is a nonempty closed subset of a complete metrically convex space
is a nonempty closed subset of a complete metrically convex space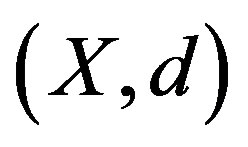 , then for any
, then for any  and
and , there exists
, there exists  which satisfies
which satisfies .
.
Lemma 1.2. ([13]) If  is a complete metric space and
is a complete metric space and , then
, then  is continuous on
is continuous on . Moreover, we have :
. Moreover, we have :
1)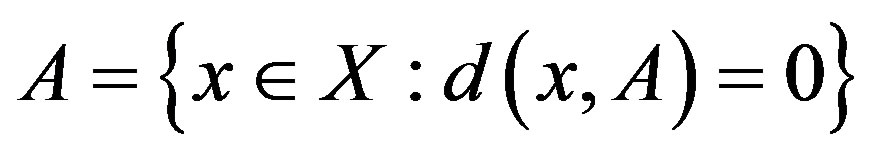 ;
;
2)  if and only if
if and only if ,
,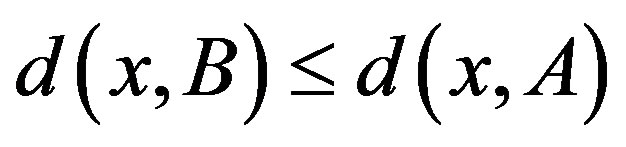 ;
;
3) for any ,
,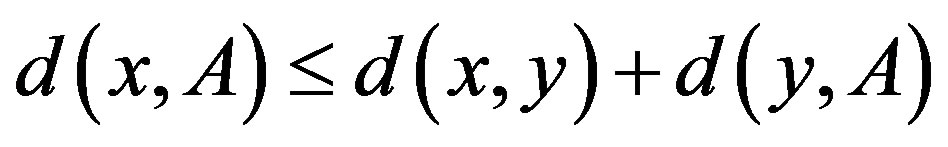 .
.
2. Main Results
Theorem 2.1. Let  be a nonempty closed subset of a complete metrically convex space
be a nonempty closed subset of a complete metrically convex space  with
with ,
, 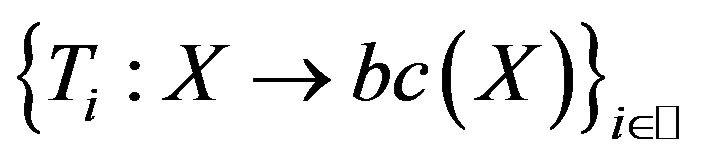 a countable family of surjective set-valued mappings with nonempty values such that for any
a countable family of surjective set-valued mappings with nonempty values such that for any  with
with , any
, any ,
,
 (1)
(1)
where  and
and  is a constant number.
is a constant number.
Furthermore, if  for all
for all , and for each
, and for each  and
and  and any
and any , there exists
, there exists  such that
such that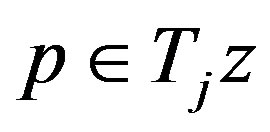 , then
, then  has a unique common fixed point in
has a unique common fixed point in .
.
Proof Take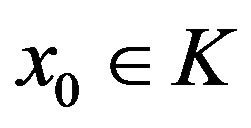 . We will construct two sequences
. We will construct two sequences 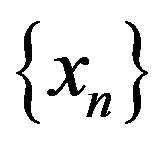 and
and  in the following manner. Since
in the following manner. Since  is on-to, there exists
is on-to, there exists 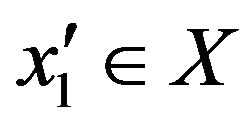 such that
such that . If
. If , then put
, then put ; if
; if , then by Lemma 1.1 there exits
, then by Lemma 1.1 there exits  such that
such that . For
. For , since
, since 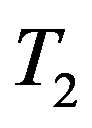 is on-to, there exists
is on-to, there exists 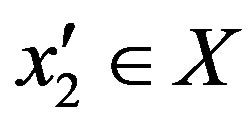 such that
such that . If
. If , then put
, then put ; if
; if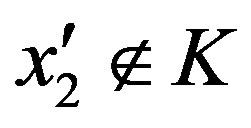 , then by Lemma 1.1 there exists
, then by Lemma 1.1 there exists  such that
such that . Continuing this way, we obtain
. Continuing this way, we obtain  and
and :
:
1) ;
;
2) if , then put
, then put ;
;
3) if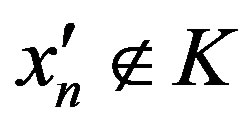 , then by Lemma 1.1 there exists
, then by Lemma 1.1 there exists  such that
such that 
4)  for all
for all 
Let  and
and . If there exists
. If there exists  such that
such that , then
, then  In fact, By 3) and the definition of
In fact, By 3) and the definition of , we have that
, we have that ,
,  ,
,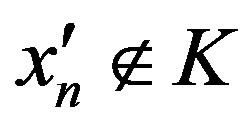 . If
. If , then
, then . On the other hand, since
. On the other hand, since  and
and , hence
, hence  which is a contradiction. If
which is a contradiction. If , then
, then 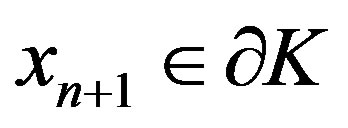 and
and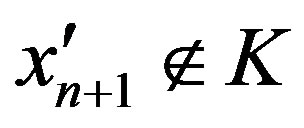 , hence
, hence , so
, so , which is another contradiction.
, which is another contradiction.
By the definitions and properties of  and
and , we can estimate
, we can estimate  into three cases:
into three cases:
Case I. . In this case,
. In this case,  ,
, 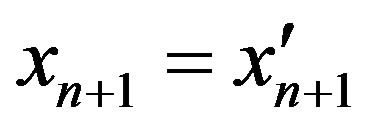 ,
,  and
and . And we have
. And we have
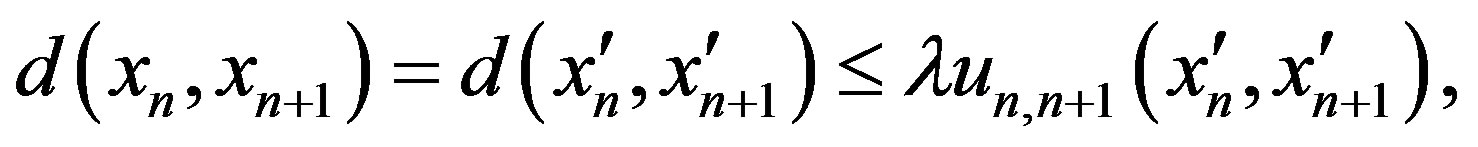
where

If  then
then

hence
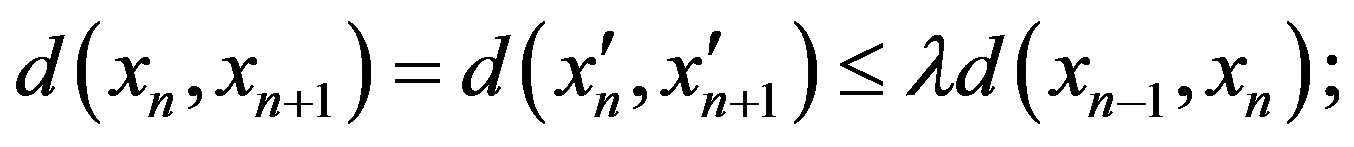
If , then
, then
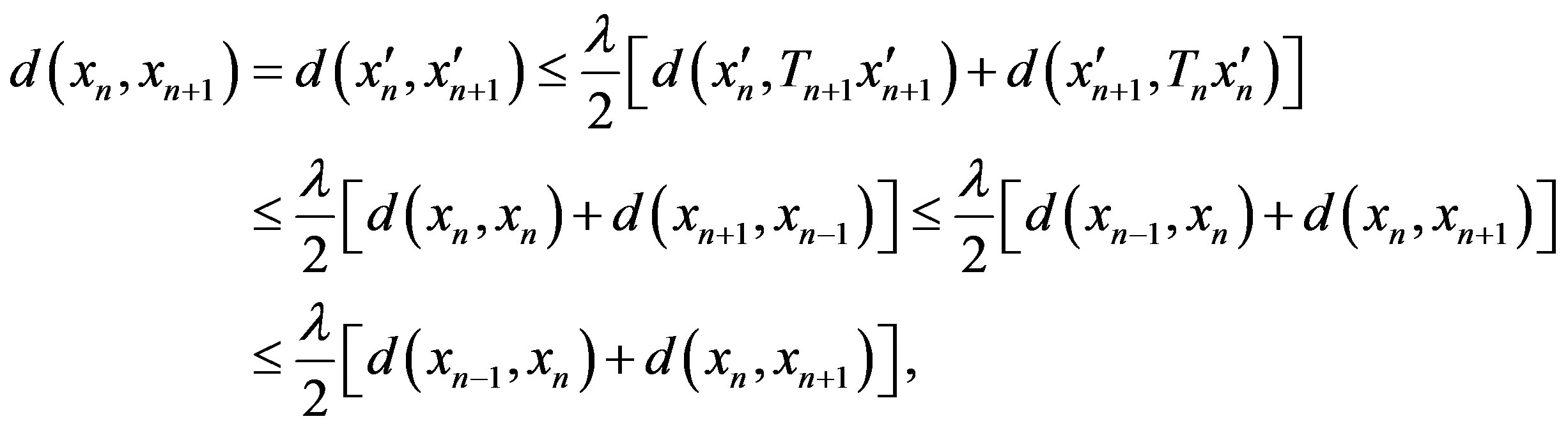
hence
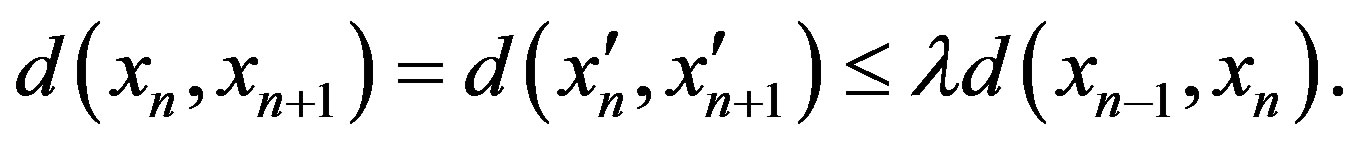
Therefore, in any situation, we have

Case II.  and
and . In this case,
. In this case,  ,
,  and
and 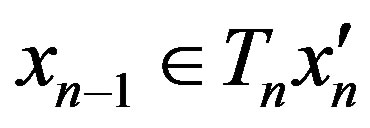 and
and . And we have
. And we have
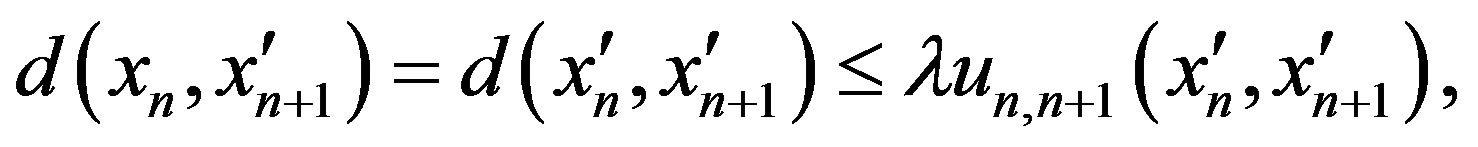
where
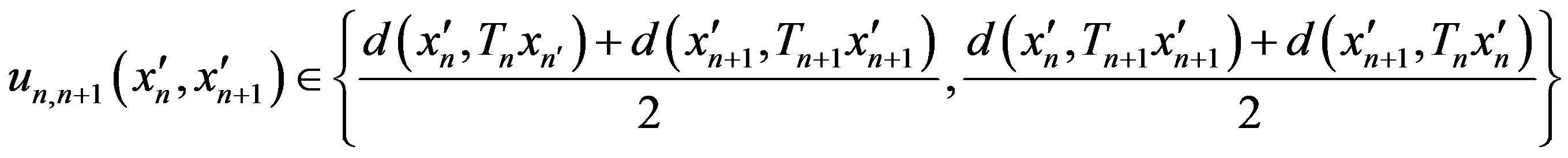
If  then
then
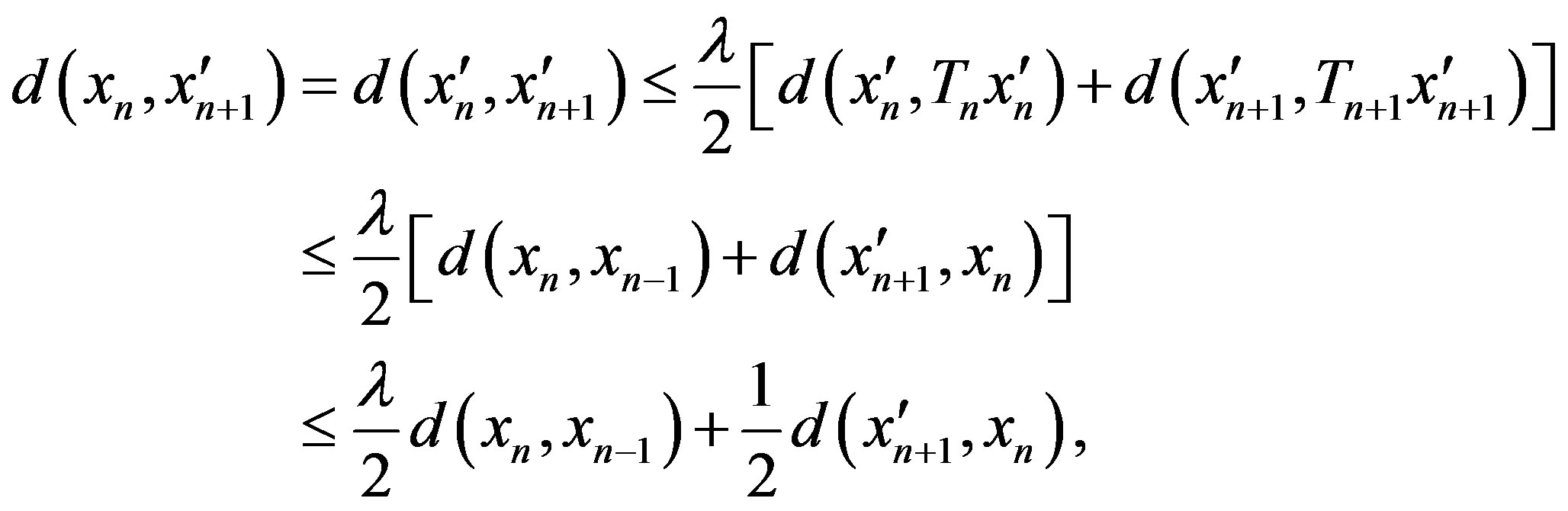
hence
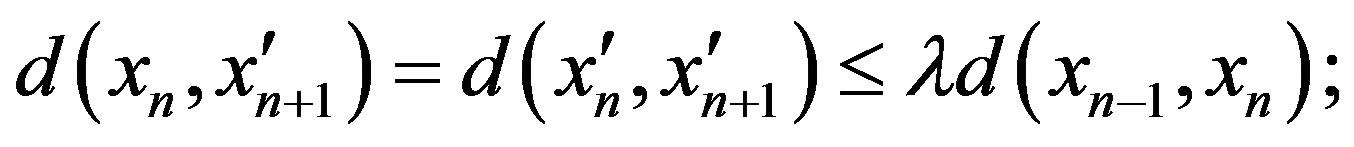
If , then
, then
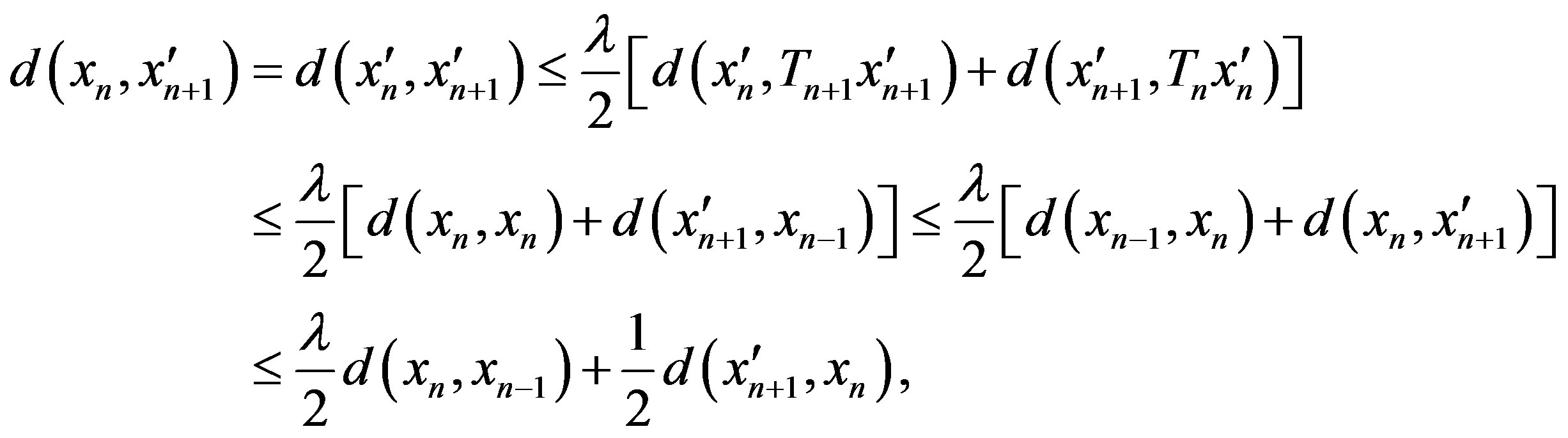
hence
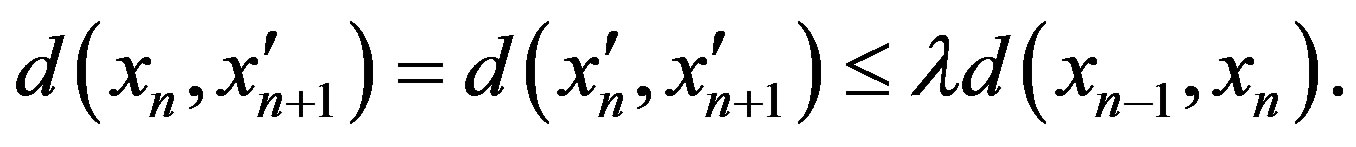
Therefore, in any situation, we have
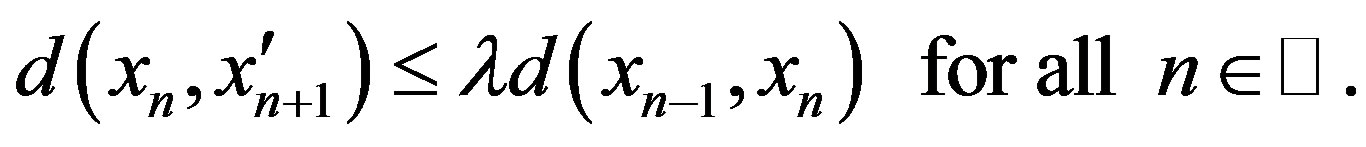
But , hence we obtain
, hence we obtain
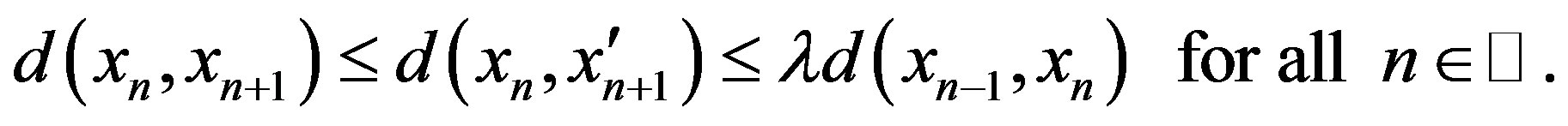
Case III.  and
and . In this case,
. In this case,  by the property of
by the property of  and
and , and
, and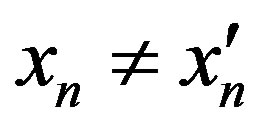 ,
,  ,
,  and
and . And we have
. And we have
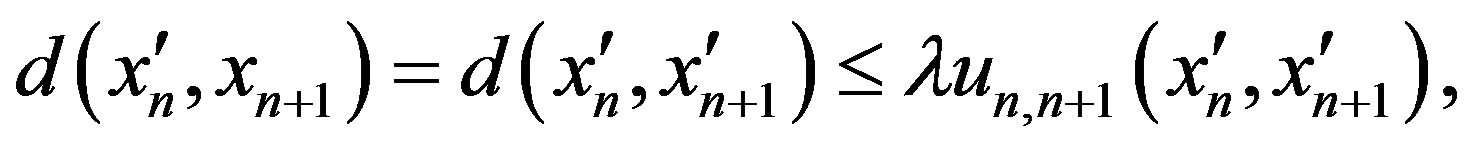
where
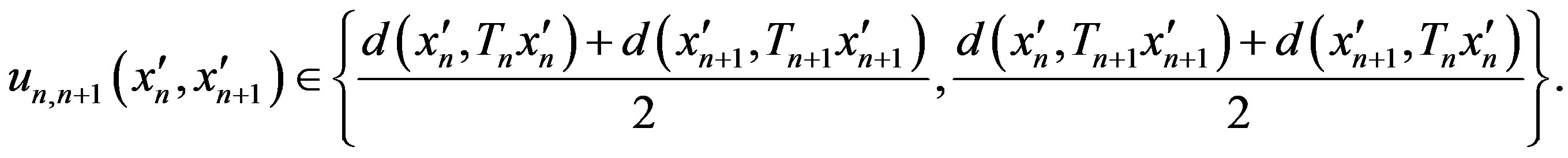
Here, we give two basic properties:
1) since  so
so  and hence
and hence 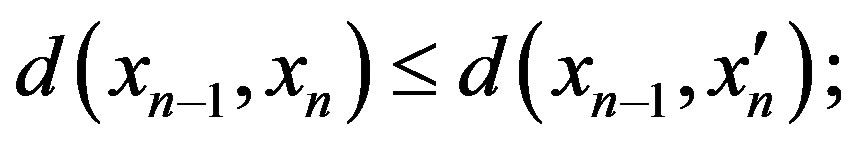
2) since
 hence
hence 
If  then
then
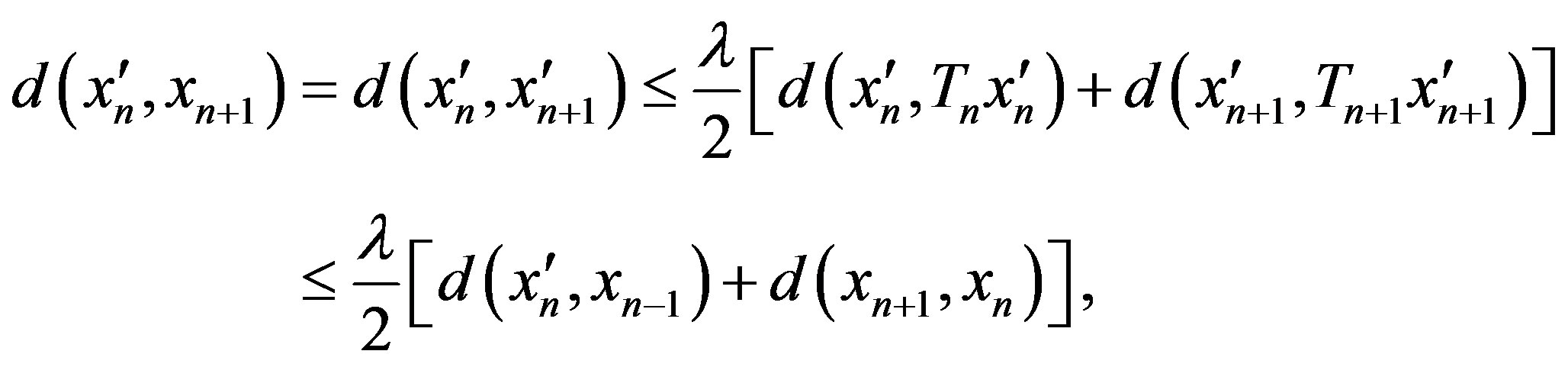
hence by 2),
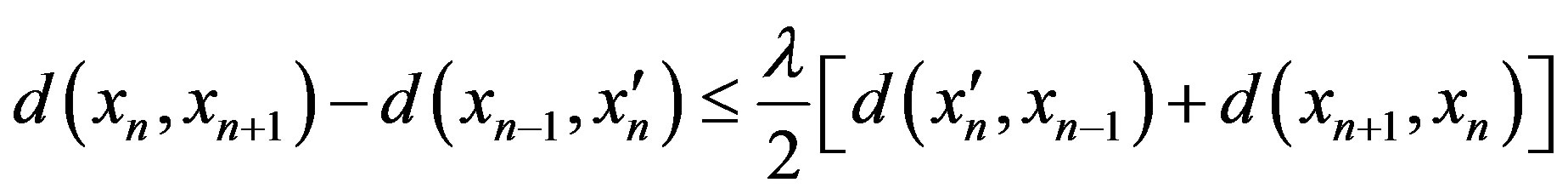
So by Case II, we obtain

If , then
, then

hence by 2),
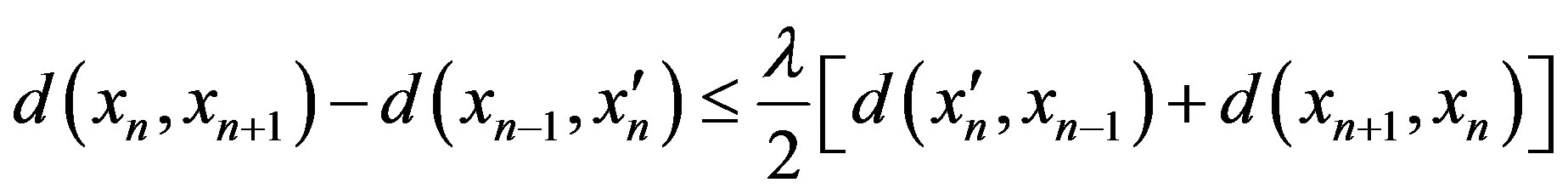
So by Case II again, we obtain
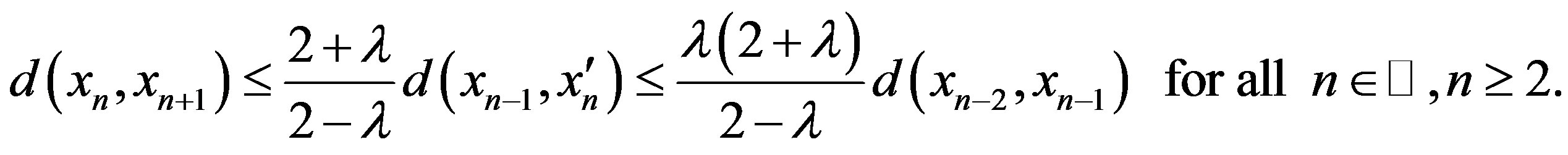
Hence in any situation, we have
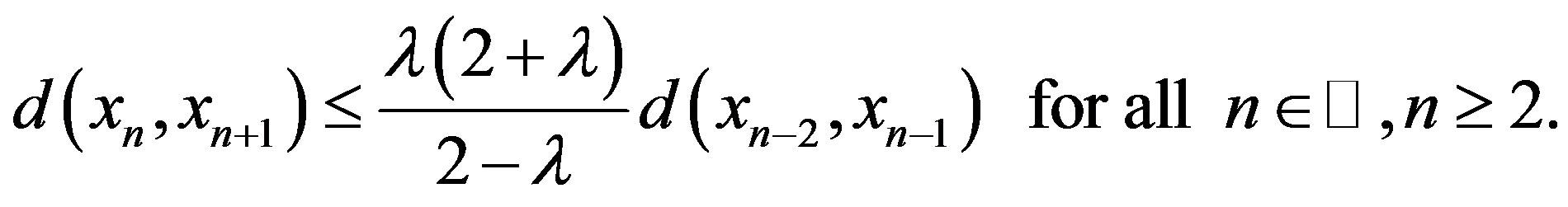
Therefore, from Case I, Case II and Case III, we obtain
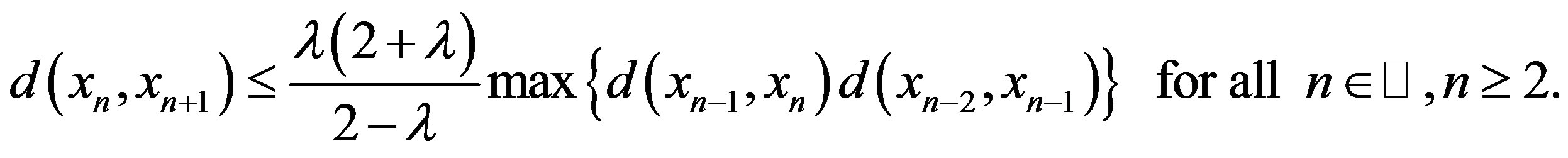
Let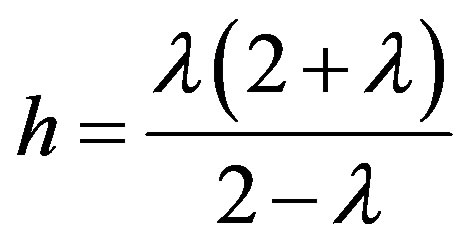 , then
, then  since
since , hence we have
, hence we have
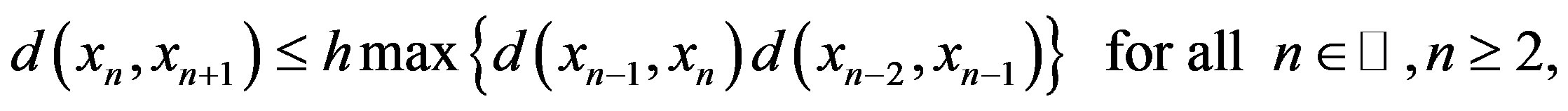
so

Let , then for
, then for ,
,
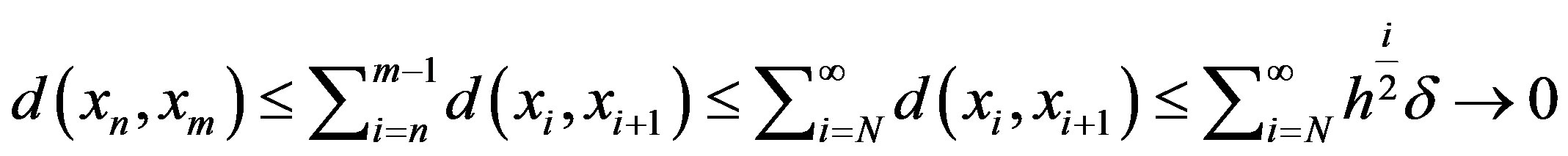 as
as . Hence
. Hence 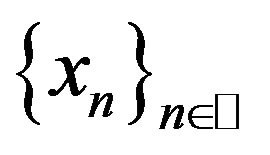 is a Cauchy sequence. Since
is a Cauchy sequence. Since  is complete,
is complete,  has a limit
has a limit . But
. But  is closed and
is closed and  for all
for all , hence
, hence .
.
By the property of  and
and , we can see that there exists an infinite subsequence
, we can see that there exists an infinite subsequence  of
of  such that
such that , hence
, hence  and
and 
Next, we will prove that 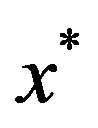 is a common fixed point of
is a common fixed point of . Fix any
. Fix any , for each fixed
, for each fixed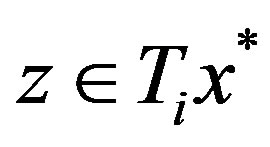 , there exists
, there exists  such that
such that  . Take an enough large
. Take an enough large  such that
such that 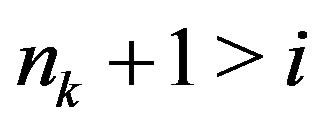 and
and . By Lemma 1.2 3) and (1), we have
. By Lemma 1.2 3) and (1), we have
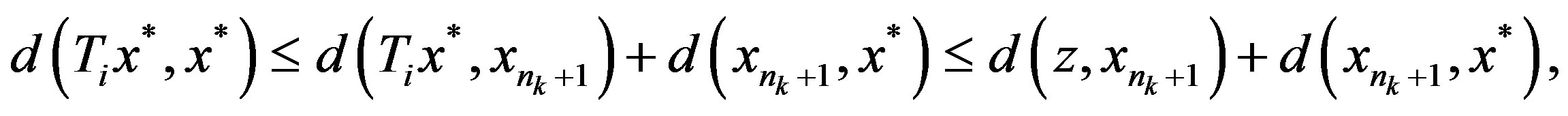
and
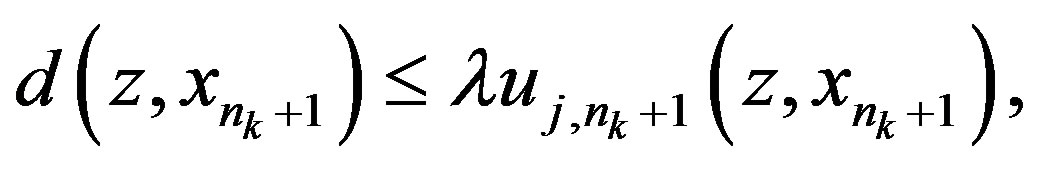
where
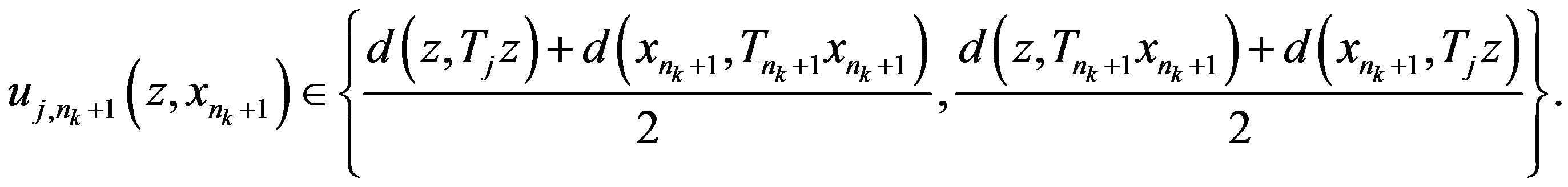
If 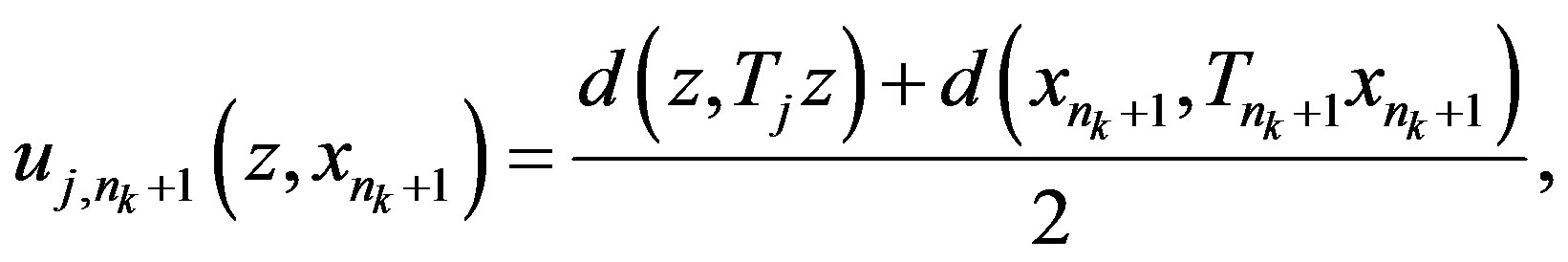 then
then
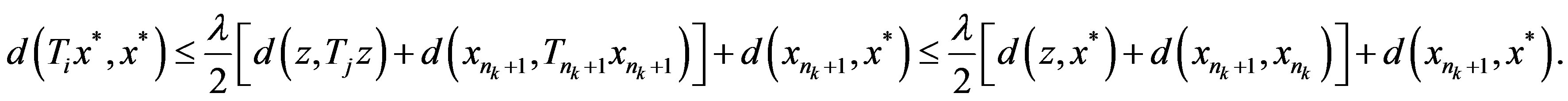
Let , then
, then  since
since , hence
, hence
 . So
. So  since
since , therefore
, therefore 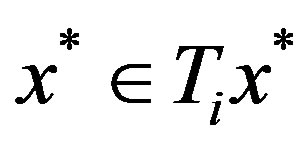 by Lemma 1.2 1).
by Lemma 1.2 1).
If , then
, then
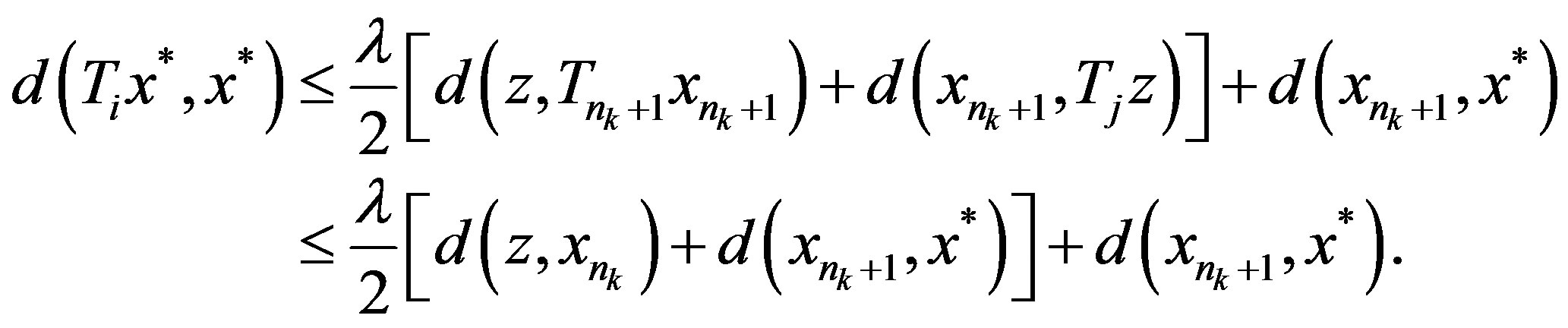
Let , then
, then  since
since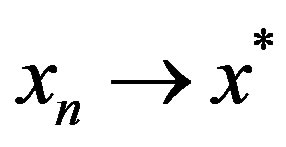 , hence similarly,
, hence similarly, 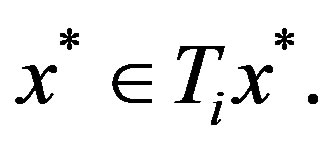
So in any situation, 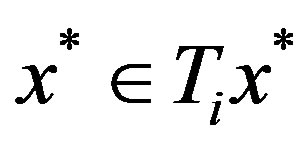 for all
for all , so
, so  is a common fixed point of
is a common fixed point of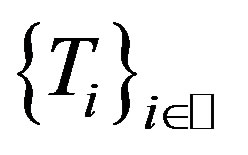 .
.
If  and
and 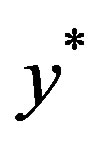 are all common fixed points of
are all common fixed points of , then we will have
, then we will have
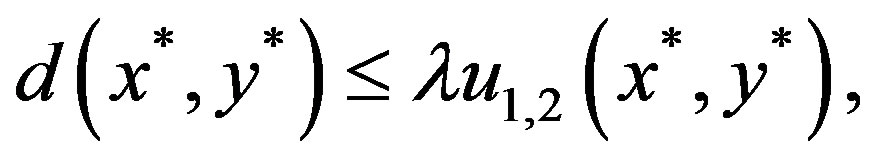
where

If , then
, then , hence
, hence ;
;
If , then
, then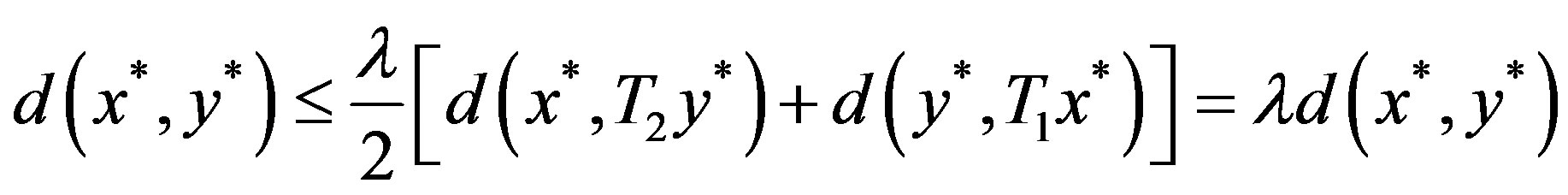 hence
hence  since
since , so
, so .
.
Hence in any situation,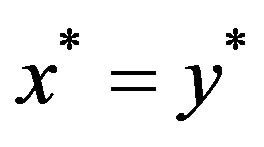 . So
. So  is the unique common fixed points of
is the unique common fixed points of 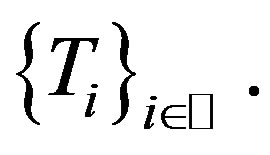
If the mappings in Theorem 2.1 are all single-valued, then Theorem 2.1 becomes the next form.
Theorem 2.2. Let  be a nonempty closed subset of a complete metrically convex space
be a nonempty closed subset of a complete metrically convex space  with
with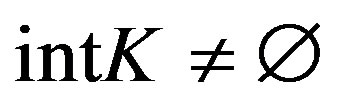 ,
, 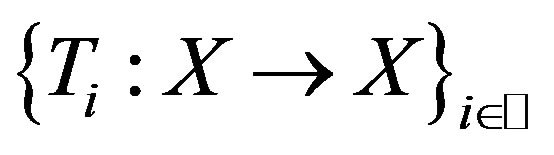 a countable family of surjective single-valued mappings such that for any
a countable family of surjective single-valued mappings such that for any  with
with , any
, any ,
,
 (2)
(2)
where  and
and 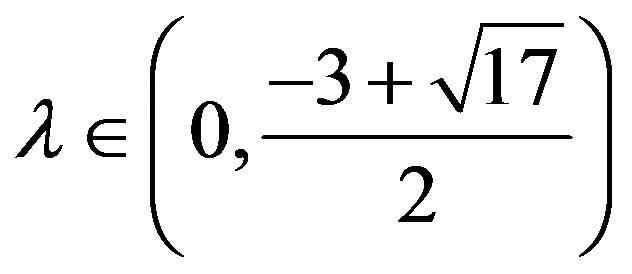 is a constant number.
is a constant number.
Furthermore, if  for all
for all , and for each
, and for each  and
and , there exists
, there exists  such that
such that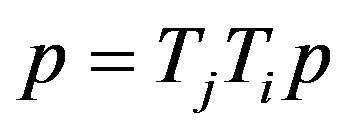 , then
, then  has a unique common fixed point in
has a unique common fixed point in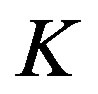 .
.
From Theorem 2.2, we can obtain the following more generalized common fixed point theorem.
Theorem 2.3. Let  be a nonempty closed subset of a complete metrically convex space
be a nonempty closed subset of a complete metrically convex space 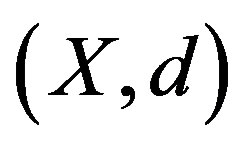 with
with ,
,  a family of subjective single-valued mappings,
a family of subjective single-valued mappings,  a family of positive integral numbers such that for any
a family of positive integral numbers such that for any ,
,  ,
,
 (3)
(3)
where  and
and  is a constant number. Furthermore, if 1)
is a constant number. Furthermore, if 1)  for all
for all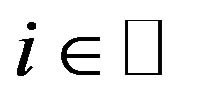 , 2) for each
, 2) for each  and
and there exists
there exists  such that
such that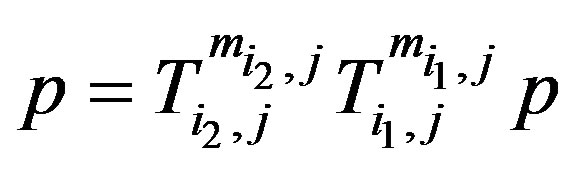 , 3) for each
, 3) for each  with
with ,
, . Then
. Then  has a unique common fixed point in
has a unique common fixed point in .
.
Proof Fix , and let
, and let , then
, then 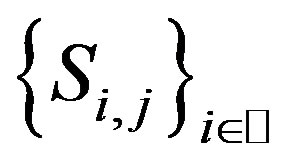 satisfies all of the conditions of Theorem 2.2, hence
satisfies all of the conditions of Theorem 2.2, hence 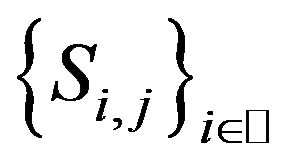 has an unique common fixed point
has an unique common fixed point 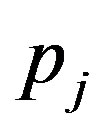 in
in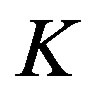 . Now, we will prove that
. Now, we will prove that  is also unique common fixed point of
is also unique common fixed point of . In fact, for any fixed
. In fact, for any fixed ,
,
 . This means that
. This means that 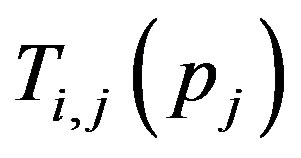 is a fixed point of
is a fixed point of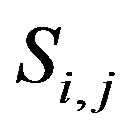 . For any
. For any  with
with , there exists
, there exists  such that
such that  by 2), and by (3) we have that
by 2), and by (3) we have that
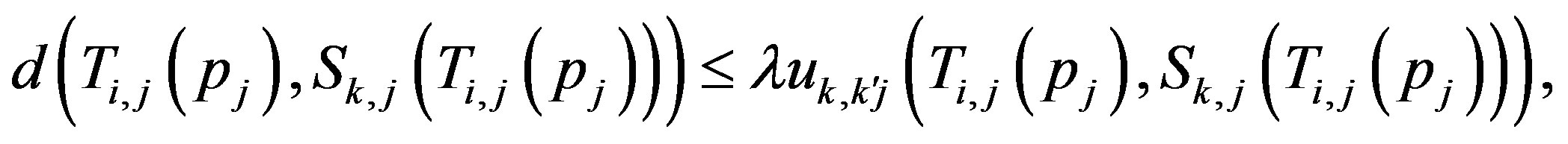
where
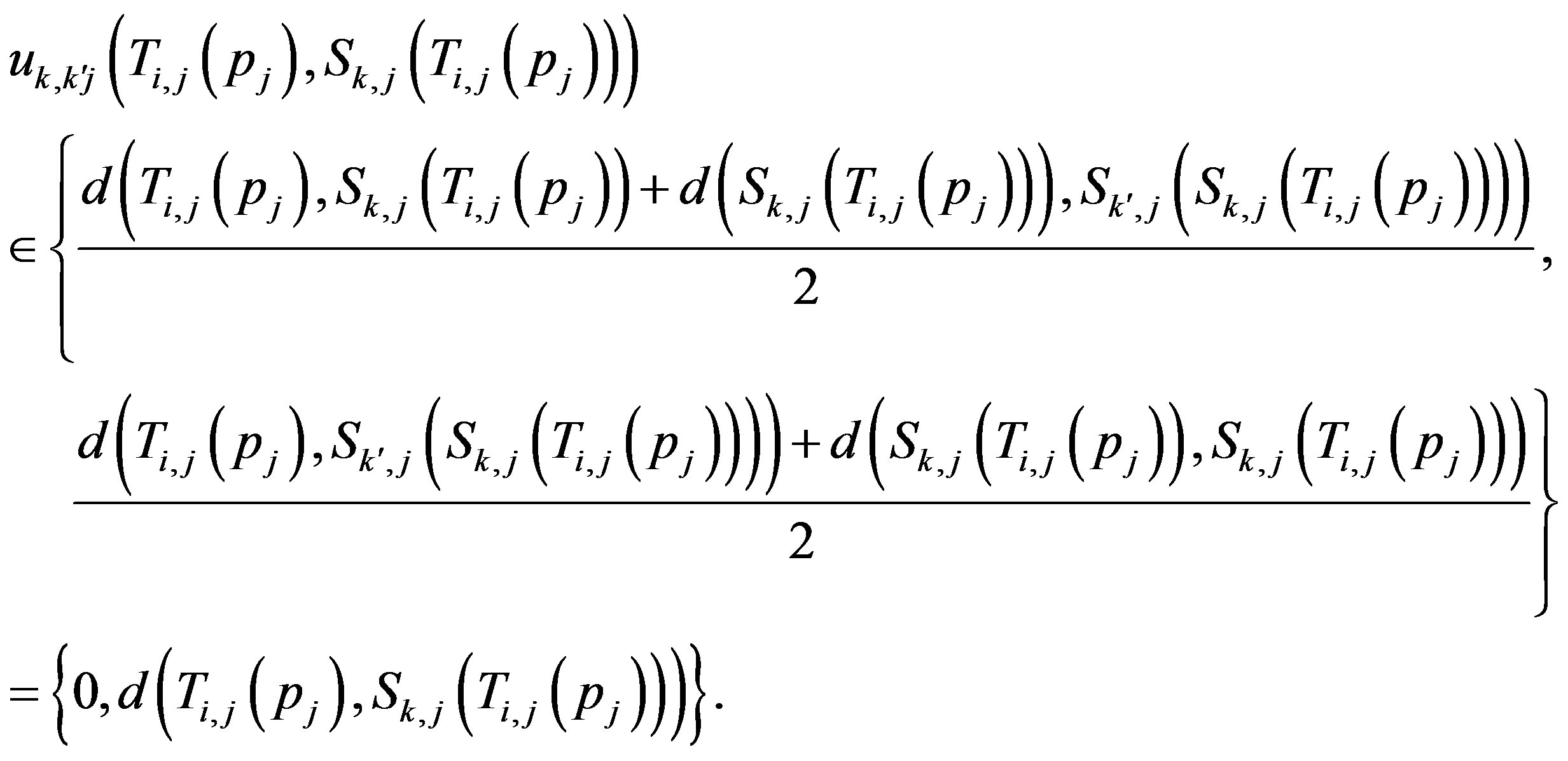
If , then
, then , hence
, hence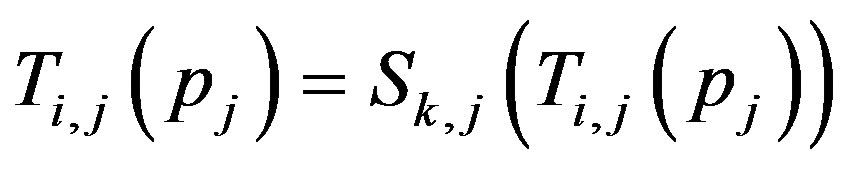 ;
;
If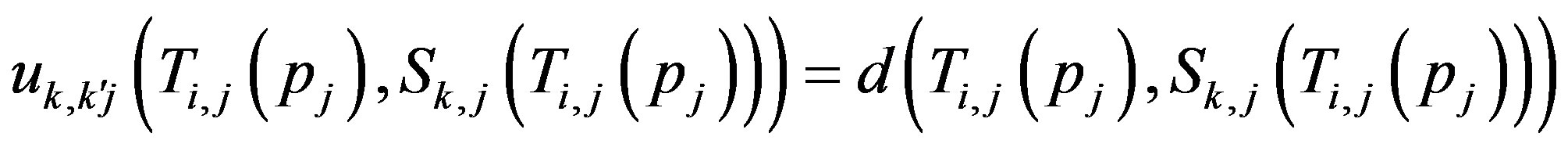 , then
, then
 , hence
, hence 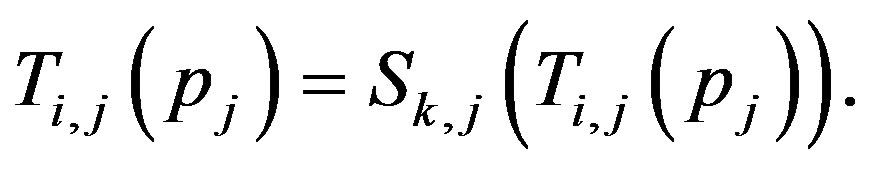
Hence in any situation, we have that  is a fixed point of
is a fixed point of  for each
for each 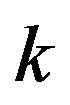 with
with . So
. So  is a common fixed point of
is a common fixed point of . By uniqueness of common fixed points of
. By uniqueness of common fixed points of , we have
, we have  for each
for each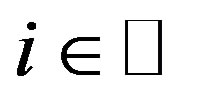 . Hence
. Hence  is a common fixed point of
is a common fixed point of .
.
If 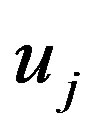 and
and  are all common fixed points of
are all common fixed points of , then they are also common fixed points of
, then they are also common fixed points of , hence by the uniqueness of common fixed points of
, hence by the uniqueness of common fixed points of , we obtain
, we obtain . This means that for each
. This means that for each 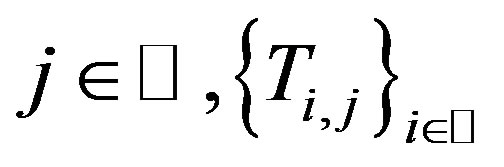 has a unique common fixed point
has a unique common fixed point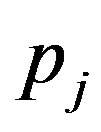 .
.
Now, we prove 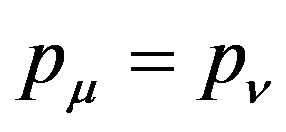 for each
for each . In fact, for any
. In fact, for any  with
with , since
, since  and
and , so
, so , hence
, hence
 by 3). Therefore,
by 3). Therefore,  is a fixed point of
is a fixed point of  for each
for each i.e.,
i.e.,  is a common fixed point of
is a common fixed point of . But
. But  has a unique common fixe point
has a unique common fixe point , hence
, hence  for each
for each , and therefore
, and therefore 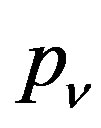 is a common fixed point of
is a common fixed point of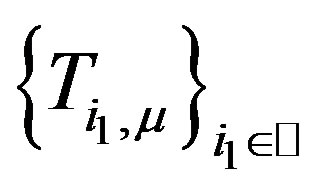 . But
. But 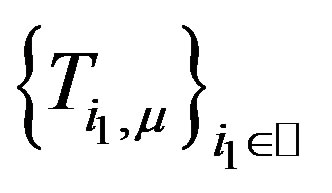
has a unique common fixed point , hence
, hence . Let
. Let , then
, then  is the common fixed point of
is the common fixed point of . The uniqueness of common fixed points of
. The uniqueness of common fixed points of  is obvious.
is obvious.
Funding
This work was supported by the National Natural Science Foundation of China (No. 11361064).
[1] N. A. Assad, “On Fixed Point Theorem of Kannan in Banach Spaces,” Tamkang Journal of Mathematics, Vol. 7, 1976, pp. 91-94.
[2] N. A. Assad, “Fixed point Theorems for Set-Valued Transformations on Compact Sets,” Bolletino della Unione Matematica Italiana, Vol. 7, No. 4, 1973, pp. 1-7.
[3] N. A. Assad and W. A. Kirk, “Fixed Point Theorems for Set-Valued Mappings of Contractive Type,” Pacific Journal of Mathematics, Vol. 43, No. 3, 1972, pp. 553-562. http://dx.doi.org/10.2140/pjm.1972.43.553
[4] X. Zhang, “Common Fixed Point Theorem of Lipschitz Type Mappings on Convex Cone Metric Spaces,” Acta Mathematica Sinica (Chinese Series), Vol. 53, No. 6, 2010, pp. 1139-1148.
[5] M. Abbas, B. E. Rhoades, et al., “Common Fixed Points of Generalized Contractive Multivalued Mappings in Cone Metric Spaces,” Mathematical Communications, Vol. 14, No. 2, 2009, pp. 365-378.
[6] S. L. Singh and B. Ram, “Common Fixed Points of Commuting Mappings in 2-Metric Spaces,” Mathematical Semester Notes, Vol. 10, 1982, pp. 197-207.
[7] Y. J. Piao and Y. F. Jin, “New Unique Common Fixed Point Results for Four Mappings with  -Contractive Type Theorems in 2-Metric Spaces,” Applied Mathematics, Vol. 3, No. 7, 2012, pp. 734-737. http://dx.doi.org/10.4236/am.2012.37108
-Contractive Type Theorems in 2-Metric Spaces,” Applied Mathematics, Vol. 3, No. 7, 2012, pp. 734-737. http://dx.doi.org/10.4236/am.2012.37108
[8] M. S. Khan, H. K. Pathak and M. D. Khan, “Some Fixed Point Theorems in Metrically Convex Spaces,” Georgian Mathematical Journal, Vol. 7, No. 3, 2000, pp. 523-530.
[9] S. K. Chatterjea, “Fixed Point Theorems,” Comptes rendus de l'Académie des Sciences, Vol. 25, 1972, pp. 727-730.
[10] O. Hadzic, “Common Fixed Point Theorem for a Family of Mappings in Convex Metric Spaces,” Univ. U. Novom Sadu, Zb. Rad. Prirod. Mat. Fak. Ser. Mat., Vol. 20, No. 1, 1990, pp. 89-95.
[11] Y. J. Piao, “Unique Common Fixed Point Theorems for a Family of Non-Self Maps in Metrically Convex Spaces,” Applied Mathematics, Vol. 22, No. 4, 2009, pp. 852-857.
[12] Y. J. piao, “Unique Common Fixed Point Theorems for a Family of Quasi-Contractive Type Maps in Metrically Convex Spaces,” Acta Mathematica Scientia, Vol. 30A, No. 2, 2010, pp. 487-493.
[13] J. R. Wu and H. Y. Liu, “Common Fixed Point Theorems for Sequences of  -Type Contraction Set-Valued Mappings,” Chinese Quarterly Journal of Mathematics, Vol. 24, No. 4, 2009, pp. 504-510.
-Type Contraction Set-Valued Mappings,” Chinese Quarterly Journal of Mathematics, Vol. 24, No. 4, 2009, pp. 504-510.
NOTES
*Corresponding author.