Keywords:Quantum Invariant; Jones Polynomial; Braid Knot
1. Introduction
The discovery of the Jones polynomial inspired many people to search for other skein relations compatible with Reidemeister moves and thus defined knot polynomials. This led to the introduction of the HOMFLY and Kauffmans polynomials. It soon became clear that all these polynomials are the first members of a vast family of knot invariants called quantum invariants.
The original idea of quantum invariants was proposed by E. Witten in [1]. Witten’s approach coming from physics was not completely justified from the mathematical viewpoint. The first mathematically definition of quantum invariants of links and 3-manifolds was given by Reshetikhin and Turaev [2,3], who used in their construction the notion of quantum groups introduced shortly before that by V. Drinfeld in [4] (see also [5]) and M. Jimbo in [6]. In fact, a quantum group is not a group at all. Instead, it is a family of algebras, more precisely, of Hopf algebras, depending on a complex parameter  and satisfying certain axioms. The quantum group
and satisfying certain axioms. The quantum group  of a semisimple Lie algebra
of a semisimple Lie algebra  is a remarkable deformation of the universal enveloping algebra of
is a remarkable deformation of the universal enveloping algebra of  (corresponding to the value
(corresponding to the value ) in the class of Hopf algebras.
) in the class of Hopf algebras.
This paper is organized as follows: In Section 2, we give the basic ideas about knots, tangles, the Jones polynomial, Lie algebra representations, and construction of quantum invariants. In Section 3, we present the main result along with its specialization to the Jones polynomial.
2. Preliminary Notions
2.1. Basic Concepts of Knots
A knot is a circle embedded in . Knots are usually studied via projecting them on a plan; a projection with extra information of overcrossing and undercrossing is called the knot diagram.
. Knots are usually studied via projecting them on a plan; a projection with extra information of overcrossing and undercrossing is called the knot diagram.



A crossing trivial knot trefoil knot Two knots are called isotopic if one of them can be transformed to the other by a diffeomorphism of the ambient space  onto itself. A fundamental result about the isotopic knot diagrams is:
onto itself. A fundamental result about the isotopic knot diagrams is:
Two unoriented knots  and
and  are equivalent if and only if a diagram of
are equivalent if and only if a diagram of  can be transformed into a diagram of
can be transformed into a diagram of  by a finite sequence of ambient isotopies of the plane and three local (Reidemeister) moves:
by a finite sequence of ambient isotopies of the plane and three local (Reidemeister) moves:



R1 R2 R3 The set of all knots that are equivalent to a knot  is called a class of
is called a class of . By a knot
. By a knot  we shall always mean a class of the knot
we shall always mean a class of the knot .
.
The main question of knot theory is Which two links are equivalent and which are not? To address this question one needs a knot invariant, a function that gives one value on all knots that belong to a single class and gives different values (but not always) on knots that belong to different classes. The present work is concerned with this question.
2.2. Tangles
A tangle is a generalization of a knot which at the same time is simpler and more complicated than a knot. On one hand, knots are a particular case of tangles, on the other hand, knots can be represented as combinations of (simple) tangles.
A tangle in a knot projection is a region in the projection plane surrounded by a circle such that the knot crosses the circle exactly at four places.

A tangle The following two operations are defined on tangles: When the bottom of a tangle  coincides with the top of another tangle
coincides with the top of another tangle , the product
, the product  is defined by putting
is defined by putting  on top of
on top of . (For oriented tangles we also require the consistency of orientations.)
. (For oriented tangles we also require the consistency of orientations.)



The second operation, tensor product, is defined by placing one tangle next to the other tangle (of the same height).



2.3. The Jones Polynomial
In 1985, V. F. R. Jones revolutionized knot theory by defining the Jones polynomial as a knot invariant via Von Neumann algebras [7]. However, in 1987 L. H. Kauffman introduced in [8] a state-sum model construction of the Jones polynomial that was purely combinatorial and remarkably simple; we follow this approach.
Definition 1 [7-9] The Jones polynomial  of an oriented link
of an oriented link  is a Laurent polynomial in the variable
is a Laurent polynomial in the variable  satisfying the skein relation
satisfying the skein relation

and that the value of the unknot is 1. Here ,
,  , and
, and  are three oriented links having diagrams that are isotopic everywhere except at one crossing where they differ as in the figure below:
are three oriented links having diagrams that are isotopic everywhere except at one crossing where they differ as in the figure below:






For instance, it is easy to verify that the Jones polynomial of the left-handed trefoil knot (which is denoted by  in the knot table) is V
in the knot table) is V =
= .
.
2.4. Lie Algebra Representations
Let  be a semisimple Lie algebra and let
be a semisimple Lie algebra and let  be its finite-dimensional representation. One can view
be its finite-dimensional representation. One can view  as a representation of the universal enveloping algebra
as a representation of the universal enveloping algebra . It is remarkable that this representation can also be deformed with parameter
. It is remarkable that this representation can also be deformed with parameter  to a representation of the quantum group
to a representation of the quantum group . The vector space
. The vector space  remains the same, but the action now depends on
remains the same, but the action now depends on . For a generic value of
. For a generic value of  all irreducible representations of
all irreducible representations of  can be obtained in this way. However, when
can be obtained in this way. However, when  is a root of unity the representation theory is different and resembles the representation theory of
is a root of unity the representation theory is different and resembles the representation theory of  in finite characteristic. It can be used to derive quantum invariants of 3-manifolds. For the purposes of knot theory it is enough to use generic values of
in finite characteristic. It can be used to derive quantum invariants of 3-manifolds. For the purposes of knot theory it is enough to use generic values of , that is, those which are not roots of unity.
, that is, those which are not roots of unity.
An important property of quantum groups is that every representation gives rise to a solution  of the quantum Yang-Baxter equation
of the quantum Yang-Baxter equation

where  (the
(the  -matrix ) is an invertible linear operator
-matrix ) is an invertible linear operator , and both sides of the equation are understood as linear transformations
, and both sides of the equation are understood as linear transformations .
.
In case of Lie algebra  and its standard two-dimensional representation, the
and its standard two-dimensional representation, the  -matrix has the form
-matrix has the form

for an appropriate basis  of the space
of the space . The inverse of
. The inverse of  is
is

2.5. Construction of Quantum Invariants
The general procedure of constructing quantum invariants is as follows (see details in [10]). Consider a knot diagram in the plane and take a generic horizontal line. To each intersection point of the line with the diagram assign either the representation space  or its dual
or its dual  depending on whether the orientation of the knot at this intersection is directed upwards or downwards. Then take the tensor product of all such spaces over the whole horizontal line. If the knot diagram does not intersect the line, then the corresponding vector space is the ground field
depending on whether the orientation of the knot at this intersection is directed upwards or downwards. Then take the tensor product of all such spaces over the whole horizontal line. If the knot diagram does not intersect the line, then the corresponding vector space is the ground field .
.
A portion of a knot diagram between two such horizontal lines represents a tangle . We assume that this tangle is framed by the black board framing. With
. We assume that this tangle is framed by the black board framing. With  we associate a linear transformation
we associate a linear transformation  from the vector space corresponding to the bottom of
from the vector space corresponding to the bottom of 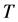 to the vector space corresponding to the top of
to the vector space corresponding to the top of . The following three properties hold for the linear transformation
. The following three properties hold for the linear transformation :
:
·  is an invariant of the isotopy class of the framed tangle
is an invariant of the isotopy class of the framed tangle ;
;
·  ;
;
·  .
.


Now we can define a knot invariant  regarding the knot
regarding the knot  as a tangle between the two lines below and above
as a tangle between the two lines below and above . In this case
. In this case  would be a linear transformation from C to C. Since our linear transformations depend on the parameter
would be a linear transformation from C to C. Since our linear transformations depend on the parameter , this number is actually a function of
, this number is actually a function of .
.
Because of the multiplicity property  it is enough to define
it is enough to define  only for elementary tangles
only for elementary tangles  such as a crossing, a minimum or a maximum point. This is precisely where quantum groups come in. Given a quantum group
such as a crossing, a minimum or a maximum point. This is precisely where quantum groups come in. Given a quantum group  and its finite-dimensional representation
and its finite-dimensional representation , one can associate certain linear transformations with elementary tangles in a way consistent with the Turaev oriented moves [11]. The
, one can associate certain linear transformations with elementary tangles in a way consistent with the Turaev oriented moves [11]. The  -matrix appears here as the linear transformation corresponding to a positive crossing. Of course, for a trivial tangle consisting of a single string connecting the top and bottom, the corresponding linear operator should be the identity transformation. So we have the following correspondence valid for all quantum groups:
-matrix appears here as the linear transformation corresponding to a positive crossing. Of course, for a trivial tangle consisting of a single string connecting the top and bottom, the corresponding linear operator should be the identity transformation. So we have the following correspondence valid for all quantum groups:




Using this one can verify that  remains invariant under all three Reidemeister moves, for details see [11].
remains invariant under all three Reidemeister moves, for details see [11].
To complete the construction of our quantum invariant we should assign appropriate operators to the minimum and maximum points. These depend on all the data involved: the quantum group, the representation and the  -matrix. For the quantum group
-matrix. For the quantum group , its standard two-dimensional representation
, its standard two-dimensional representation  and the
and the  - matrix, these operators are:
- matrix, these operators are:








where  is the basis of
is the basis of , dual to the basis
, dual to the basis  of
of .
.
In the following example we compute the quantum  -invariant for the unknot.
-invariant for the unknot.
Example 1 Let us compute the  -quantum invariant of the unknot. Represent the unknot as a product of two tangles and compute the composition of the corresponding transformations.
-quantum invariant of the unknot. Represent the unknot as a product of two tangles and compute the composition of the corresponding transformations.


So, . Therefore, in order to normalize our invariant so that its value on the unknot is equal to 1, we must divide
. Therefore, in order to normalize our invariant so that its value on the unknot is equal to 1, we must divide  by
by , and denote this normalized invariant by
, and denote this normalized invariant by . (We shall write the precise formula for
. (We shall write the precise formula for  in the main result.)
in the main result.)
3. Main Result
Here we give the general formulas of the quantum  -invariants of the braid knot
-invariants of the braid knot  for odd
for odd .
.
Proposition 1 The quantum invariant of , when
, when  is odd, is
is odd, is
 (1.1)
(1.1)
Proof 1 We prove it by induction on .
.
For , we receive the following braid knot along with its tensor product.
, we receive the following braid knot along with its tensor product.


Note that the map  sends
sends  into the tensor
into the tensor . Also, the map
. Also, the map  sends
sends  into the tensor
into the tensor
 .
.
Now applying  to each middle factor, we get
to each middle factor, we get

Finally, the two maps at the top contract the whole tensor into the linear transformation

Hence the unframed normalized  -quantum invariant of
-quantum invariant of  is
is

To get a clear picture, we also compute the quantum invariant of the knots  (which is actually the left trefoil) and
(which is actually the left trefoil) and . First of all, we proceed for
. First of all, we proceed for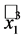 :
:


The map at the bottom sends 1  into the tensor
into the tensor 
Now the map  sends the above tensor into the tensor
sends the above tensor into the tensor

Then applying  to two tensor factors in the middle we get
to two tensor factors in the middle we get

Finally, the two maps at the top contract the whole tensor into a number

Dividing by the normalizing factor  we get
we get

The invariant  remains unchanged under the second and third reidemeister moves. However it varies under the first reidemeister move and thus depends on the framing. One can deframe it, that is, manufacture an invariant of unframed knots out of it, according to the formula
remains unchanged under the second and third reidemeister moves. However it varies under the first reidemeister move and thus depends on the framing. One can deframe it, that is, manufacture an invariant of unframed knots out of it, according to the formula

where  is the writhe of the knot diagram and
is the writhe of the knot diagram and  is the quadratic Casimir number defined by the Lie algebra
is the quadratic Casimir number defined by the Lie algebra  and its representation. For
and its representation. For  and the standard 2-dimensional representation
and the standard 2-dimensional representation . Since the writhe of the left trefoil is
. Since the writhe of the left trefoil is , the unframed normalized quantum invariant is
, the unframed normalized quantum invariant is

This can be further written as
 (1.2)
(1.2)
For , the knot and the corresponding tensor products are:
, the knot and the corresponding tensor products are:


With some computations, similar to the computations of , we get
, we get
 (1.3)
(1.3)
Similarly,
 (1.4)
(1.4)
We now assume the result (1.1) holds for , that is
, that is
 (1.5)
(1.5)
Now for  we have
we have

and the proof is finished.
Proposition 2 The Jones polynomial of the knot , when
, when  is odd, is
is odd, is

Proof 2 Nothing to prove; just substitute  in place of
in place of  in
in .
.