A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy ()
1. Introduction
A Kolmogorov-Arnold-Moser (i.e. KAM) Cantorian spacetime manifold rather than a simple fractal is the right starting point for an exact formulation of a quantumrelativity gravity theory which resolves the challenging task of explaining the increased rather than decreased rate of cosmic expansion and calculating accurately the measured 95.5% missing energy density of the universe [1-5]. Within the KAM formulation the thin fractal, i.e. zero measure random Cantor set is modelled by the zero set which is found from K-category theory to be given by the bi-dimension  and identified physically with a virtual quantum pre-particle [3-28]. On the other hand the fat fractal, i.e. the positive measure empty random Cantor set is given by
and identified physically with a virtual quantum pre-particle [3-28]. On the other hand the fat fractal, i.e. the positive measure empty random Cantor set is given by  and is identified with a virtual pre-quantum wave being the cobordism of the quantum pre-particle zero set and
and is identified with a virtual pre-quantum wave being the cobordism of the quantum pre-particle zero set and  [2-28]. Continuing the K-theoretical analysis [11-22] to encompass Penrose’s noncommutative fractal tiling which constitutes a compactified Klein modular holographic boundary for our KAM spacetime bulk [8,9], we can define mass as the inverse of isomorphic diameters of the relevant spaces, for instance
[2-28]. Continuing the K-theoretical analysis [11-22] to encompass Penrose’s noncommutative fractal tiling which constitutes a compactified Klein modular holographic boundary for our KAM spacetime bulk [8,9], we can define mass as the inverse of isomorphic diameters of the relevant spaces, for instance 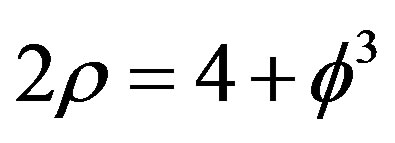 of Penrose tiling [11,16,19]. Simple analogies with positive and negative Van der Waals fluctuation, instantons dynamics and Hawking’s negative energy vacuum fluctuation as well as Rindler coordinates at a toy black hole horizon lead us to understand negative gravity and dark energy [29-59]. Our formal analysis starts with an inspiring idea due to D. Gross [1] and arrives that way at a topological Planck energy Ep and a corresponding topological Planck length
of Penrose tiling [11,16,19]. Simple analogies with positive and negative Van der Waals fluctuation, instantons dynamics and Hawking’s negative energy vacuum fluctuation as well as Rindler coordinates at a toy black hole horizon lead us to understand negative gravity and dark energy [29-59]. Our formal analysis starts with an inspiring idea due to D. Gross [1] and arrives that way at a topological Planck energy Ep and a corresponding topological Planck length  effectively scaling the Planck scale from esoterically large
effectively scaling the Planck scale from esoterically large 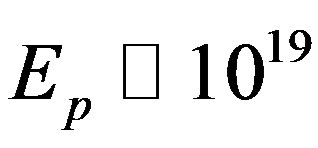 Gev and equally esoterically small
Gev and equally esoterically small  cm numbers to a manageably
cm numbers to a manageably
 where
where  is the famous Hardy’s probability for quantum entanglement which amounts to almost 9 percent and
is the famous Hardy’s probability for quantum entanglement which amounts to almost 9 percent and  [3]. Based on these results we conclude the equivalence of Einstein-Rosen “wormhole” bridges and Einstein’s Podolsky-Rosen’s spooky action at distance [21]. In turn these results are shown to be consistent with distinguishing two energy components which result in Einstein’s famous formula
[3]. Based on these results we conclude the equivalence of Einstein-Rosen “wormhole” bridges and Einstein’s Podolsky-Rosen’s spooky action at distance [21]. In turn these results are shown to be consistent with distinguishing two energy components which result in Einstein’s famous formula , namely the quantum zero set particle component
, namely the quantum zero set particle component 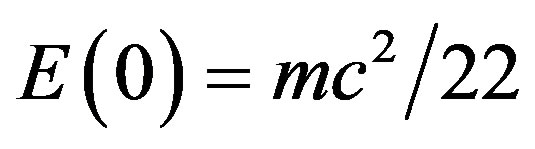 which we can measure and the quantum empty set wave component which due to state vector reduction on measurement we cannot measure
which we can measure and the quantum empty set wave component which due to state vector reduction on measurement we cannot measure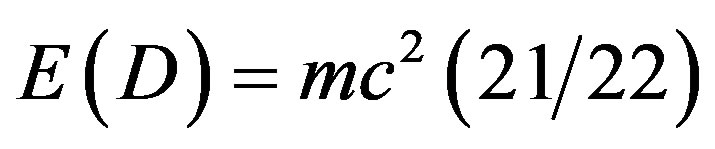 , i.e. the missing dark energy [24-28]. Together the two components add to
, i.e. the missing dark energy [24-28]. Together the two components add to  where E is the total energy, m is the mass and c is the speed of light [2-61]. In other words, the present new derivation of the world’s most celebrated formula explains in one stroke the two most puzzling problems of quantum physics and relativistic cosmology, namely the physico-mathematical meaning of the wave function and the nature of dark energy [30-68]. In essence they are one and the same when looked upon from the view point of quantum-fractal geometry and KAM theorem [2,7,19,69-83].
where E is the total energy, m is the mass and c is the speed of light [2-61]. In other words, the present new derivation of the world’s most celebrated formula explains in one stroke the two most puzzling problems of quantum physics and relativistic cosmology, namely the physico-mathematical meaning of the wave function and the nature of dark energy [30-68]. In essence they are one and the same when looked upon from the view point of quantum-fractal geometry and KAM theorem [2,7,19,69-83].
2. Motivation and Background Information
The theory advocated in this paper is a synthesis of several fundamental ideas. The first idea is the recognition that using the KAM manifold well known and quite familiar from the theory of nonlinear dynamical systems and quantum chaos [8,80] as the geometry of our quantum spacetime is by far a mathematically more firm and solid ground to build our physics upon than ordinary continuous fractal spacetime [81]. The second idea is that of scaling the Planck scale and working with topological quantities. In a remarkable essay [1] the co-founding father of Heterotic superstring theory and strong interaction asymptotic freedom, D. Gross gave a novel general direction for the unification of all fundamental forces and arriving at quantum gravity via an imaginative, unconventional and in fact revolutionary idea of scaling the almost esoteric Planck scale [1,2]. In the present work which tackles one of the currently most researched and hotly debated problems in quantum physics and cosmology [1-72], we take this idea literally and seriously to mean a mathematical topological formulation of physics starting from a unit interval spacetime with non-classical and non-smooth transfinite discrete geometry and topology [2-5]. Proceeding in this way we arrive at a quintessential, i.e. five dimensional Kaluza-Klein spacetime [26,30] and a general formula for quantum entanglement 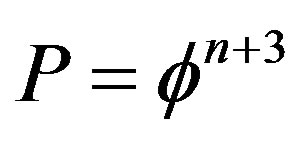 which reduces in the case of two particles
which reduces in the case of two particles  to Hardy’s famous probability [16-21] of quantum entanglement
to Hardy’s famous probability [16-21] of quantum entanglement  where
where , i.e. a quantum probability of almost 9%. This result was repeatedly verified experimentally with a very high degree of accuracy [3,4].
, i.e. a quantum probability of almost 9%. This result was repeatedly verified experimentally with a very high degree of accuracy [3,4].
In the present work we show how  is related to Gross’ proposal [1,2] and discusses its various ramifications for dark energy [2,3] and the connection between general relativity’s Einstein-Rosen bridges [24, 25] and the quantum mechanics of Einstein-PodolskyRosen nonlocality [3,4,6]. This insight leads to an effective quantum gravity theory [69,70] and an explanation for the true meaning of the quantum wave function and the missing dark energy of the cosmos by fusing Einstein’s relativity and quantum mechanics entanglement together [3,4]. Our basic philosophy and technical strategy may be summed up succinctly as follows: By facing infinity and zero head on and endorsing them we eliminate the drawback of both and suddenly everything in physics looks right [44-54]. Although the present work is reasonably self contained, for a deep understanding of the transfinite nonlinear techniques used to develop our theory it is helpful to read carefully at least Refs. [1,3,5] as well as Refs. [58-72] for a bird’s eye view of the general theory [5,16]. We may also note that the theory of quantum sets was extensively developed by D. Finkelstein who also introduced the notion of quantum relativity [69-77]. We should add at this point that the KAM Cantorian spacetime theory has wider ramifications than only physics and cosmology and has found applications in brain and consciousness research by M. Persinger, C. Lavalle [78] as well as S. Vrobel’s fundamental discourses into time, perception, music and love [79].
is related to Gross’ proposal [1,2] and discusses its various ramifications for dark energy [2,3] and the connection between general relativity’s Einstein-Rosen bridges [24, 25] and the quantum mechanics of Einstein-PodolskyRosen nonlocality [3,4,6]. This insight leads to an effective quantum gravity theory [69,70] and an explanation for the true meaning of the quantum wave function and the missing dark energy of the cosmos by fusing Einstein’s relativity and quantum mechanics entanglement together [3,4]. Our basic philosophy and technical strategy may be summed up succinctly as follows: By facing infinity and zero head on and endorsing them we eliminate the drawback of both and suddenly everything in physics looks right [44-54]. Although the present work is reasonably self contained, for a deep understanding of the transfinite nonlinear techniques used to develop our theory it is helpful to read carefully at least Refs. [1,3,5] as well as Refs. [58-72] for a bird’s eye view of the general theory [5,16]. We may also note that the theory of quantum sets was extensively developed by D. Finkelstein who also introduced the notion of quantum relativity [69-77]. We should add at this point that the KAM Cantorian spacetime theory has wider ramifications than only physics and cosmology and has found applications in brain and consciousness research by M. Persinger, C. Lavalle [78] as well as S. Vrobel’s fundamental discourses into time, perception, music and love [79].
3. Analysis
As mentioned in the introduction, the present analysis consists of several interconnected ideas and vital steps which need to be explained consecutively with a reasonable degree of logical order as follows:
3.1. KAM Spacetime Topology—The Pre-Space, Pre-Time and Pre-Matter
Let us start by constructing a random Cantor set from the unit interval [7-10]. Proceeding in the usual way well known from the theory of fractals for the classical triadic Cantor set 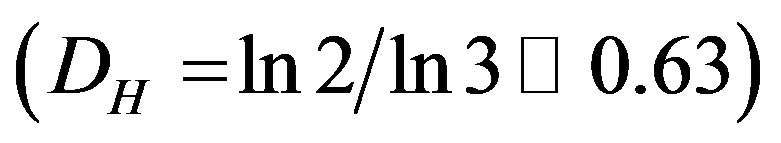 but adding uniform randomness to the construction procedure. That way we end up with a zero measure “thin” Cantor set of a topological dimension DT = 0 and a Hausdorff dimension very close to the classical deterministic set, namely
but adding uniform randomness to the construction procedure. That way we end up with a zero measure “thin” Cantor set of a topological dimension DT = 0 and a Hausdorff dimension very close to the classical deterministic set, namely  [7-10]. Notice now that the gaps left from the iterative deletion of parts of the unit interval forms a second Cantor set. By contrast to the first “thin” Cantor set this one is a “fat” Cantor set with a positive measure equal to the length of the original unit interval because
[7-10]. Notice now that the gaps left from the iterative deletion of parts of the unit interval forms a second Cantor set. By contrast to the first “thin” Cantor set this one is a “fat” Cantor set with a positive measure equal to the length of the original unit interval because . However in this case this Hausdorff dimension is not
. However in this case this Hausdorff dimension is not  but obviously
but obviously 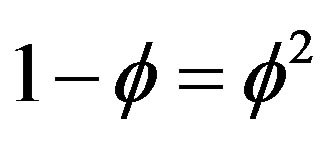 because for the original unit interval both the topological dimension and the Hausdorff dimension coincide and are equal to unity so that
because for the original unit interval both the topological dimension and the Hausdorff dimension coincide and are equal to unity so that
 as should be [7-10]. Noticing on the other hand that the thick Cantor set is made of totally empty gaps, it is clear that it is the epitome of the empty set which due to deductive dimensional and consistency reasons is assigned a topological dimension equal minus one, i.e. DT (empty) = −1 [22]. All the preceding result follows smoothly from Grothendieck K-theoretical (i.e. the general theory of classes) conception of Penrose’s fractal tiling universe [11-25] and Connes-von Neumann dimensional function [11-14] as well as E-infinity Cantorian spacetime bijection formula developed by the present author [5,16]. We showed previously how quantum physics could be formulated using a quantum set theory based on the preceding thin and thick Cantor sets [16]. These particles and waves arise naturally from a KAM-like fractal-Cantorian spacetime which is the ultimate source of matter and fields [18,22, 61]. Consequently this KAM spacetime picture is far more accurate than the ad hoc conventional picture of fractal spacetime [77-81] because we have only disjointed random sets interwoven together in an intricate manner but leaving only thin and fat Cantor sets to represent particles—zero sets and wave-empty sets respectively to form pre-space, pre-time and pre-matter to emerge from quantum spacetime geometry [10,14,18,22, 61]. In other words, quantum mechanical entanglement is what is behind the geometry of spacetime and vice versa [20,21].
as should be [7-10]. Noticing on the other hand that the thick Cantor set is made of totally empty gaps, it is clear that it is the epitome of the empty set which due to deductive dimensional and consistency reasons is assigned a topological dimension equal minus one, i.e. DT (empty) = −1 [22]. All the preceding result follows smoothly from Grothendieck K-theoretical (i.e. the general theory of classes) conception of Penrose’s fractal tiling universe [11-25] and Connes-von Neumann dimensional function [11-14] as well as E-infinity Cantorian spacetime bijection formula developed by the present author [5,16]. We showed previously how quantum physics could be formulated using a quantum set theory based on the preceding thin and thick Cantor sets [16]. These particles and waves arise naturally from a KAM-like fractal-Cantorian spacetime which is the ultimate source of matter and fields [18,22, 61]. Consequently this KAM spacetime picture is far more accurate than the ad hoc conventional picture of fractal spacetime [77-81] because we have only disjointed random sets interwoven together in an intricate manner but leaving only thin and fat Cantor sets to represent particles—zero sets and wave-empty sets respectively to form pre-space, pre-time and pre-matter to emerge from quantum spacetime geometry [10,14,18,22, 61]. In other words, quantum mechanical entanglement is what is behind the geometry of spacetime and vice versa [20,21].
3.2. The Zero Set Quantum Particle and the Empty Set Quantum Wave from a Generic Noncommutative Space and the Speed of Light as an Expectation Value
In what follows we would like to make the KAM spacetime picture more specific. As hinted at in the previous section Penrose fractal tiling universe [5,11,24] is the prototype par excellence of a noncommutative geometry reflecting the essence of K-theory [8] as well as E-infinity theory [5,16,18,79] and its bijection formula which gives the Hausdorff dimension as a function of the zero set topological dimension  and the topological dimension n [5,11]. The corresponding dimension function is given by A. Connes in [11] as
and the topological dimension n [5,11]. The corresponding dimension function is given by A. Connes in [11] as
 (1)
(1)
For a = 0 and b = 1 one finds the bi-dimensions of the zero set, i.e.
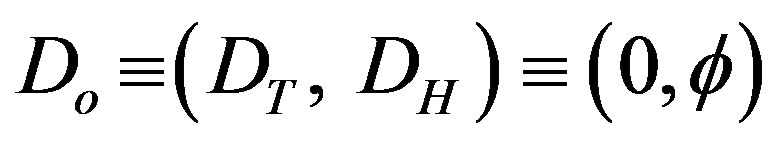 (2)
(2)
where
 (3)
(3)
Similarly for the unit set we find [11-27]
 (4)
(4)
Subsequent dimensions are found using the Fibonacci prescription. For instance D2 is found as
 (5)
(5)
and so on. For the empty set D −1 the same procedure holds true but we need to mind the correct negative sign. That way one finds the Hausdorff dimension of the empty set to be [11-27]
 (6)
(6)
The bijection formula on the other hand leads to the same result as mentioned at the beginning of this section however in a far simpler way because of the far more compact and economical notation. Thus from the bijection [5,11,27]
 (7)
(7)
we find the zero set by simply setting n = 0
 (8)
(8)
while the empty set is found by setting 
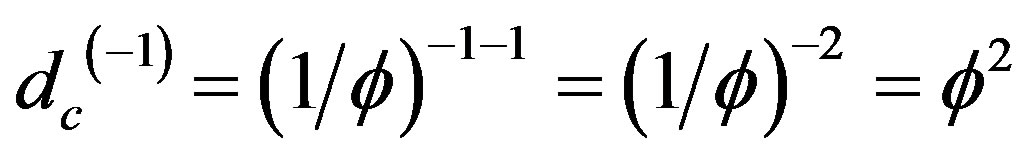 (9)
(9)
Finally we mention on passing that the same result may be found using the gap labelling DIS method [12]. It is also obvious from the above that the empty set is the cobordism i.e. the surface of the zero set. In addition both the union and the intersection of the inverse dimensions of the zero and the empty set give rise to Hilbert-He’s 4D fractal cube which is the core of our E-infinity space [5,17]. That means we are dealing with a KAM Cantorian space with indistinguishability condition [13,74]:
 (10)
(10)
Thus
 (11)
(11)
which is probably the most recognizable formula of E-infinity theory [5]. Another immensely important result of the von Neumann-Connes K-formula [11,18] and E-infinity bijection is that for  we have
we have  [55]. That means we have an infinity of empty sets with an increasing degree of emptiness. This has physical consequences regarding the speed of light. For
[55]. That means we have an infinity of empty sets with an increasing degree of emptiness. This has physical consequences regarding the speed of light. For  the speed of light must be infinite. Consequently the observed constancy of the speed of light is nothing but the average speed of light in a fractal spacetime harbouring infinitely many empty sets [57]. One could acquire an intuitive feel for the problems by thinking about the speed of light in infinitely many layers of liquids with infinitely many different dimensions. That way the effective speed of light would be the average over infinitely many different velocities. The infinitely many dimensions of Cantorian spacetime play the same role of the liquids. In this sense one could say the constancy of the speed of light is the evidence that spacetime is a KAM fractal. Some experimental evidence for the reality of Cantorian spacetime is discussed by E. Goldfain in [62, 67].
the speed of light must be infinite. Consequently the observed constancy of the speed of light is nothing but the average speed of light in a fractal spacetime harbouring infinitely many empty sets [57]. One could acquire an intuitive feel for the problems by thinking about the speed of light in infinitely many layers of liquids with infinitely many different dimensions. That way the effective speed of light would be the average over infinitely many different velocities. The infinitely many dimensions of Cantorian spacetime play the same role of the liquids. In this sense one could say the constancy of the speed of light is the evidence that spacetime is a KAM fractal. Some experimental evidence for the reality of Cantorian spacetime is discussed by E. Goldfain in [62, 67].
3.3. The Topological Invariants of KAM E-Infinity Space and Susslin Operation [29,77]
Consider a space given by an infinite number of unions and intersections of elementary Cantor sets resembling a Susslin operation [29] of the form
 (12)
(12)
so that
 (13)
(13)
where  and
and 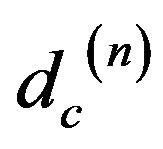 is the Hausdorff of the Cantor sets
is the Hausdorff of the Cantor sets . Since
. Since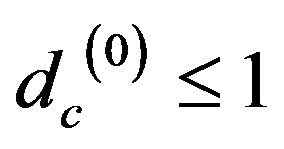 , the infinite series can be summed and one finds the topological dimension to be determined by the expectation value or a centre of gravity given by [5,15-24]
, the infinite series can be summed and one finds the topological dimension to be determined by the expectation value or a centre of gravity given by [5,15-24]
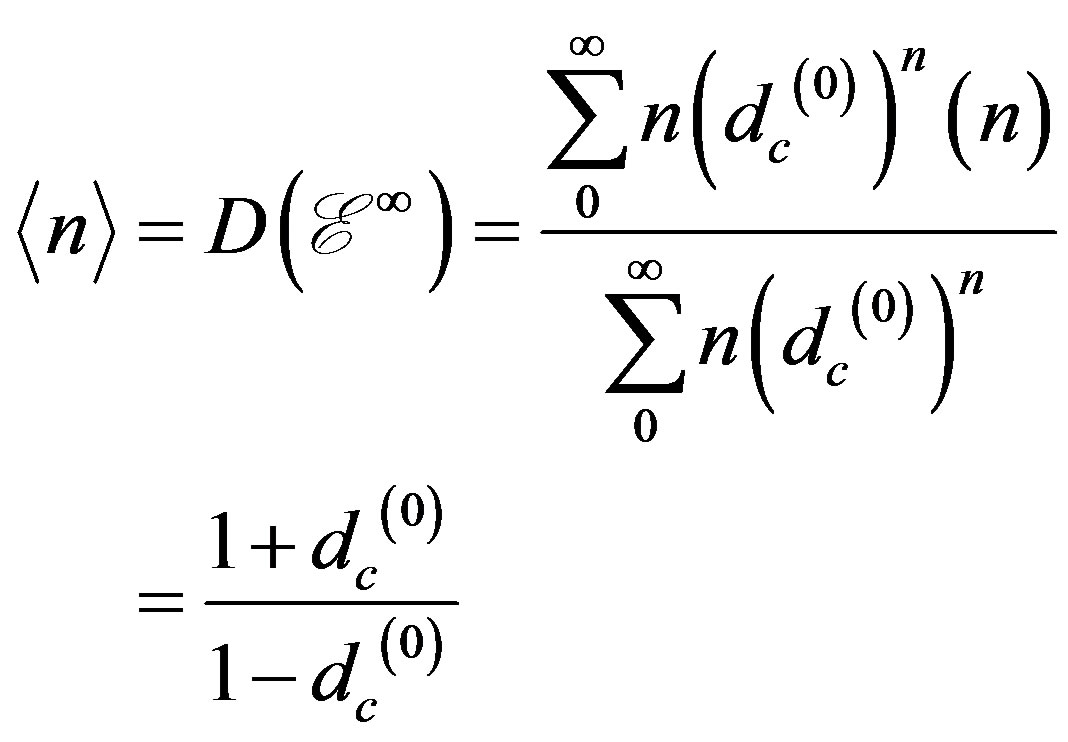 (14)
(14)
Noting that the average Hausdorff dimension is [5, 15-24]
 (15)
(15)
then by requiring space filling we see that we must have 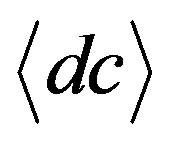 equal
equal  and one finds the following condition [5,15-24]
and one finds the following condition [5,15-24]
 (16)
(16)
This leads to a quadratic equation in  with two solutions of which the only positive one is
with two solutions of which the only positive one is
 Inserting in
Inserting in 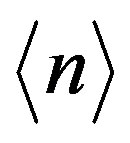 one finds that [5]
one finds that [5]
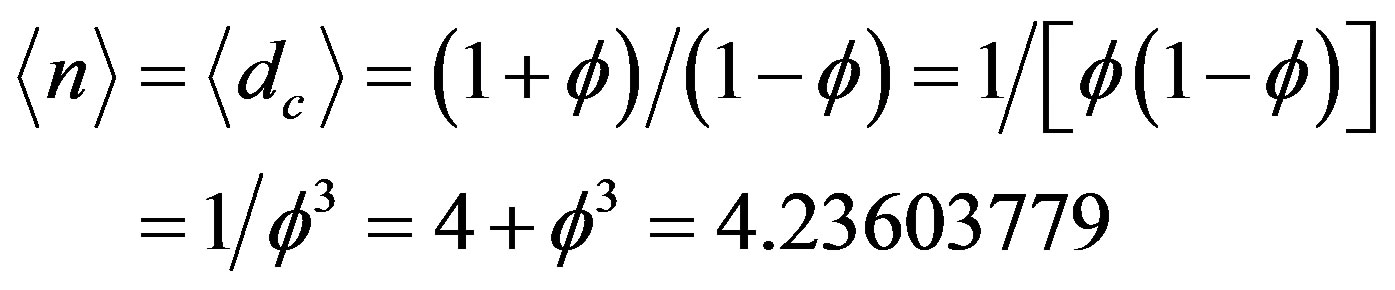 (17)
(17)
In other words our E-infinity space is essentially the same space which we gained by considering the two Cantor sets constructed from the unit interval discussed earlier on [27]. We mention here without derivation that detailed analysis of E-infinity established a remarkable result, namely the equality of the curvature of the E-infinity manifold and its Euler characteristic which amounts to 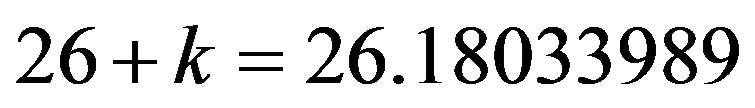 [55]. Note that
[55]. Note that  is equal to the sum of all the 17 one and two Stein spaces [2].
is equal to the sum of all the 17 one and two Stein spaces [2].
3.4. The Space E-Infinity  as a Probability Space and Quantum Entanglement—The Immrizi Parameter and Unruh Temperature
as a Probability Space and Quantum Entanglement—The Immrizi Parameter and Unruh Temperature
Let us derive a general expression for the probability that two different points in 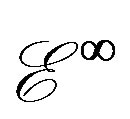 co-exist at the same location, i.e. being geometrically entangled. To do this we consider the probability of finding a single Cantor point in an isolated elementary Cantor set. The probability for that is obviously
co-exist at the same location, i.e. being geometrically entangled. To do this we consider the probability of finding a single Cantor point in an isolated elementary Cantor set. The probability for that is obviously  and for n point this is therefore given by the multiplication theorem to be [3,16,27]
and for n point this is therefore given by the multiplication theorem to be [3,16,27]
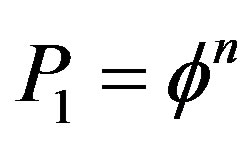 . (18)
. (18)
On the other hand the global probability and sometimes the contrafactual probability effect of finding a Cantor point in E-infinity is clearly the inverse of  namely [3,16,27]
namely [3,16,27]
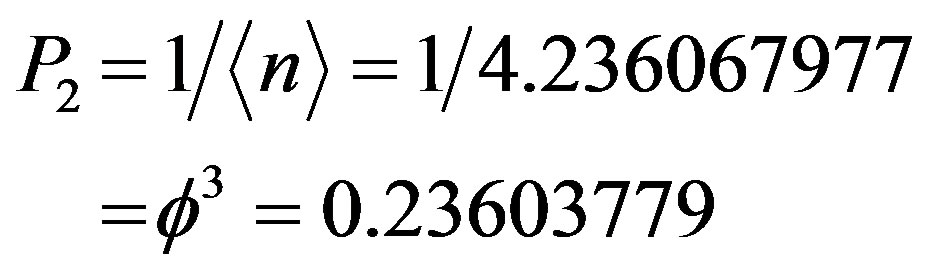 (19)
(19)
Consequently to find n point in Cantor set in E-infinity is the multiplication of the local probability  with the global “contrafactual” probability
with the global “contrafactual” probability . This means the total probability is given by [3,17-19]
. This means the total probability is given by [3,17-19]

 (20)
(20)
Now we can distinguish various cases of P with definite physical meaning corresponding to different numbers of particles n. The first is for n = 2 which means the quantum entanglement of Hardy
 (21)
(21)
This result was verified experimentally to a very high accuracy in various recognized laboratories [3,30-33]. The second value is for n = 3 which gives us the famous Immirzi parameter of loop quantum gravity [28,70]
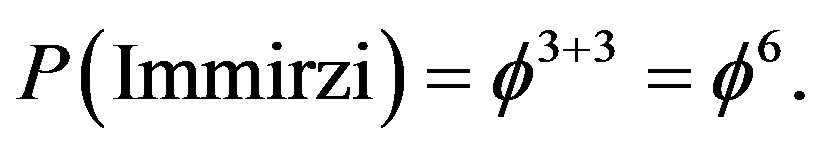 (22)
(22)
The third result is that of the celebrated Unruh temperature for which we must set  and consequently [30,34]
and consequently [30,34]
 (23)
(23)
In addition for  one finds the measurable ordinary energy density of the cosmos, i.e. the energy of the quantum particle [2,34,35]
one finds the measurable ordinary energy density of the cosmos, i.e. the energy of the quantum particle [2,34,35]
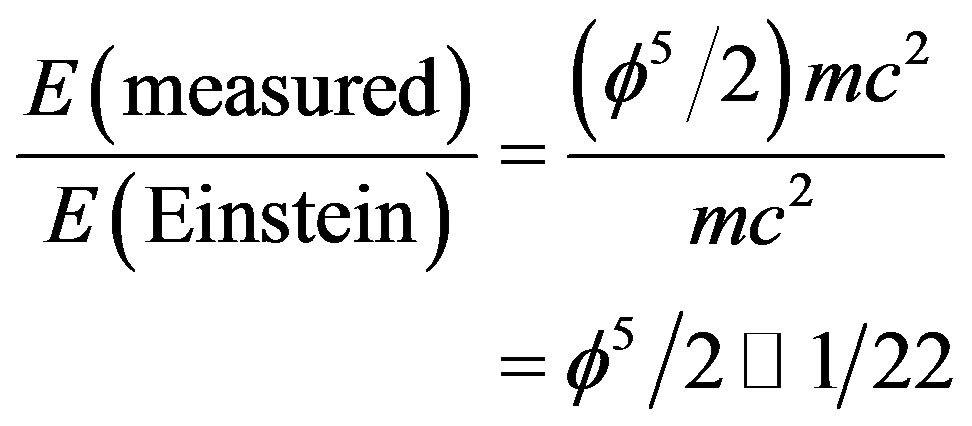 (24)
(24)
Finally the microwave background radiation of the cosmos is found for 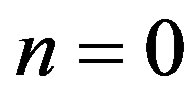 to be related to geometrical self entanglement [36-38,67]
to be related to geometrical self entanglement [36-38,67]
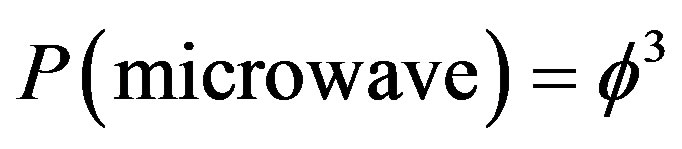 (25)
(25)
as discussed in more detail elsewhere [40-51]. Now we are actually in a position to answer Nobel Laureate G. ‘t Hooft’s deep question “What are the building blocks of Nature?” The building blocks of nature and the building blocks of spacetime are the elementary random Cantor sets [64]. In addition we conjecture that the Unruh temperature is given by  and that it is real, albeit a spacetime topological fractal effect [57].
and that it is real, albeit a spacetime topological fractal effect [57].
3.5. The Dark Energy of Quantum Kaluza-Klein Spacetime
By raising the zero set modelling the quantum particle characterized by the bi-dimension  to literally the quintessence, i.e. the 5 dimensional Kaluza-Klein core of E-infinity, one easily arrives at an expression of energy density of the universe in complete agreement with cosmic measurement of COBE, WAMP and supernova burst analysis [34,35]. To show that we calculate the pseudo Hausdorff volume of Do which is a straight forward naive generalization of classical volume to [26,27]
to literally the quintessence, i.e. the 5 dimensional Kaluza-Klein core of E-infinity, one easily arrives at an expression of energy density of the universe in complete agreement with cosmic measurement of COBE, WAMP and supernova burst analysis [34,35]. To show that we calculate the pseudo Hausdorff volume of Do which is a straight forward naive generalization of classical volume to [26,27]
 . (26)
. (26)
Using Newton’s kinetic energy as a template or simplistically speaking as a “Newtonian” rather than Hamiltonian operator one finds [26,27,61]
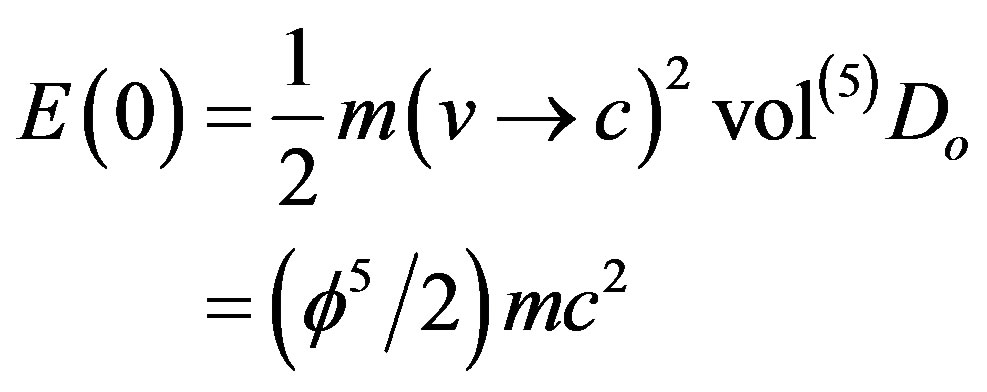 (27)
(27)
where m is the mass and c is the speed of light. Several vital points should be stressed at this stage. First while it is useful to distinguish sometime between mass, rest mass and relativistic mass the previous formula stresses that physical real mass does not change and that such concepts are only mathematical. The only “rest” quantity is the rest energy namely  itself. Second the speed of light c is quantitatively the same one we always used however its meaning here is different. The speed of light in E-infinity is variable and c is an expectation i.e. average value [10] as much as
itself. Second the speed of light c is quantitatively the same one we always used however its meaning here is different. The speed of light in E-infinity is variable and c is an expectation i.e. average value [10] as much as 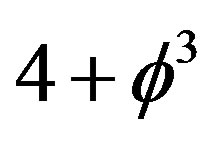 is the expectation for the formal topological dimension
is the expectation for the formal topological dimension 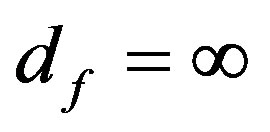 of E-infinity [5]. In this sense
of E-infinity [5]. In this sense  represents a potential energy of the momentarily at resting measured quantum particle and we are entitled to ask now where is the kinetic energy? The answer of this question is as simple as it is surprisingly because it is the energy of the EinsteinBohm “ghost” quantum wave responsible for the propagation of the quantum particle [30,61]. To find the magnitude of this energy we calculate again a corresponding volume which turned out to be the dual value for
represents a potential energy of the momentarily at resting measured quantum particle and we are entitled to ask now where is the kinetic energy? The answer of this question is as simple as it is surprisingly because it is the energy of the EinsteinBohm “ghost” quantum wave responsible for the propagation of the quantum particle [30,61]. To find the magnitude of this energy we calculate again a corresponding volume which turned out to be the dual value for 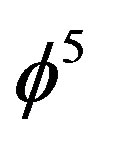 namely an additive volume of the empty set D
namely an additive volume of the empty set D 1 in D = 5 [27,61]
1 in D = 5 [27,61]
 (28)
(28)
where  is the Hausdorff component of the empty set bi-dimension
is the Hausdorff component of the empty set bi-dimension . The kinetic energy of the quantum wave in D = 5 is thus [27,61]
. The kinetic energy of the quantum wave in D = 5 is thus [27,61]
 (29)
(29)
The incredible fact which we should have noticed long ago but we did not is not only that  is the missing energy density of the cosmos (95% of the total) but that
is the missing energy density of the cosmos (95% of the total) but that 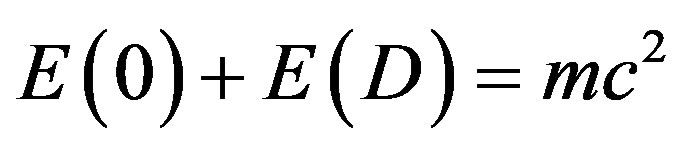 which is the classical expression found by Einstein using not solely mathematical deduction but also a quantum “leap” of “faith”. In other words Einstein included quantum mechanical features in his famous formula although at the time of
which is the classical expression found by Einstein using not solely mathematical deduction but also a quantum “leap” of “faith”. In other words Einstein included quantum mechanical features in his famous formula although at the time of  quantum mechanics was not yet invented and that later on when quantum mechanics was around Einstein did not believe in it because of the spooky action at distance of quantum entanglement. Ironically the energy expression
quantum mechanics was not yet invented and that later on when quantum mechanics was around Einstein did not believe in it because of the spooky action at distance of quantum entanglement. Ironically the energy expression  consists of two parts, namely
consists of two parts, namely  multiplied with
multiplied with  where
where  is the Hardy probability of quantum entanglement of two quantum particles so that
is the Hardy probability of quantum entanglement of two quantum particles so that  accounts for the effect of quantum entanglement of the one particle energy expression. There is an even simpler interpretation of
accounts for the effect of quantum entanglement of the one particle energy expression. There is an even simpler interpretation of  and consequently
and consequently
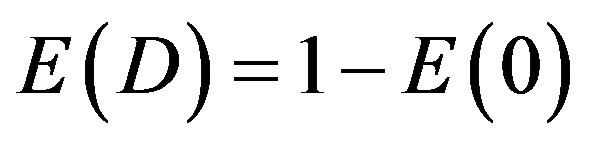 when involving the mathematics and physics of Nambu-Veneziano’s old bosonic string theory of strong interaction. According to this theory the spacetime dimensions needed are not 4 but 26. Consequently if we understand
when involving the mathematics and physics of Nambu-Veneziano’s old bosonic string theory of strong interaction. According to this theory the spacetime dimensions needed are not 4 but 26. Consequently if we understand  as a theory for D = 4 then according to the D = 26 theory we have ignored the effect of the 26
as a theory for D = 4 then according to the D = 26 theory we have ignored the effect of the 26 4 = 22 “compactified” dimensions of spacetime [27,57]. Since E is an Eigenvalue, then by Rayleigh theorem we should reduce by division
4 = 22 “compactified” dimensions of spacetime [27,57]. Since E is an Eigenvalue, then by Rayleigh theorem we should reduce by division 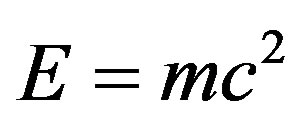 which means Weyl-Nottale scale [14] it using a scaling exponent
which means Weyl-Nottale scale [14] it using a scaling exponent 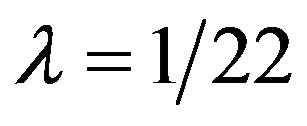 so that we find
so that we find
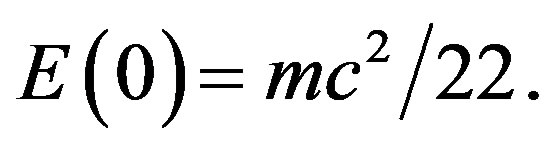 (30)
(30)
Noting that the exact value is
 (31)
(31)
We see that  is an excellent integer approximation [27,28,34,35]. Similarly the dark energy density of the quantum wave
is an excellent integer approximation [27,28,34,35]. Similarly the dark energy density of the quantum wave
 (32)
(32)
could be approximated to [27]
 . (33)
. (33)
The preceding two results are probably the most important achievements of many research efforts of many scientists [1-51] rather than a single person and could be truly said to stand on the shoulders of giants [53]. From this privileged position we can now answer a second deep question by G. Ord [63], namely “What is the wave function?” From the above it is clear that it is the empty set or the surface of the zero set quantum particle. In addition the wave function is the source of dark energy [61,63]. We conjecture or more accurately speculate using educated scientific guessing that some topological defects [72] like texture or even instantons may have an intrinsic topological dimension equal to minus one making them de facto empty sets and thus a source of negative dark energy and consequently negative gravity [2]. On the other hand we could give a more conservative interpretation by regarding E(D) as simply the energy vacuum surrounding a mini black hole, i.e. a pre-quantum particle with  being information entropy while
being information entropy while  is the lack of information complimentary entropy. This mini black hole picture could be seen as suggesting that dark energy is produced from Hawking-Beckenstein entropy leading to negative energy fluctuation at the mini black hole horizon as will be discussed next from a complimentary geometrical view point.
is the lack of information complimentary entropy. This mini black hole picture could be seen as suggesting that dark energy is produced from Hawking-Beckenstein entropy leading to negative energy fluctuation at the mini black hole horizon as will be discussed next from a complimentary geometrical view point.
3.6. Accelerated Cosmic Expansion, Anticlastic Curvature and Hawking’s Negative Vacuum Fluctuation Energy Fluctuation—Negative Van der Waals Processes [76]
To make a long story short, the surprising discovery of the accelerating rather than decelerating expansion of the universe is argued here to be due to the well known geometrical effect of anticlastic, i.e. negative curvature of the spacetime manifolds of the cosmos. In turns this anticlastic curvature accumulates at the edge of the world to a maximum as can be seen from the analogy with a long elastic thin walled cylinder squeezed at the middle as shown in Figure 14 of Ref. [2] as well as Ref. [83] Figure 2. The situation is thus analogous to that of the negative energy of vacuum fluctuation found by S. Hawking to exist at the horizon of a black hole. In other words when we look at the two dimensional projection of a ramified i.e. compactified Klein modular curve or a fractal Penrose universe [65], then at the edges being in the hyperbolic plane at infinity surrounded by a Cantorian circle we have anticlastic curvature, i.e. negative curvature producing negative dark energy causing negative gravity pushing the universe apart rather than pulling it together. The preceding geometrical picture could be translated to a topological picture by reasoning that in simplistic terms, while the visible 4 dimensions of our space produce positive curvature and ordinary gravity, the 26 − 4 = 22 compactified bosonic string dimensions are responsible for dark energy, i.e. negative curvature and consequently negative gravity which is the force behind the measured increased acceleration of cosmic expansion at the edge of the holographic Klein-Penrose universe [65]. The situation can be explained quantitatively by taking the ratio between Heterotic string theory 504 states and the 528 states of maximally symmetric spaces such as Witten’s M-theory [2-4,10,27,28]. There is also a very instructive analogy to between gravity and Van der Waals fluctuation which was proposed by the author [75] and which could be extended to negative gravity and negative Van der Waals fluctuation [76].
3.7. Scaling the Planck Scale—The Connection between Wormholes (Einstein-Rosen Bridges) and Quantum Entanglement (Einstein-Podolsky-Rosen Spooky Action at Distance)
The Planck energy  Gev and not dissimilarly the Planck length
Gev and not dissimilarly the Planck length  cm are quite esoteric scales difficult to visualize and totally outside present or near future experimental capacities if at all [30]. Never the less by going back to our initial unit interval universe and noting the unexpected result arising from Hardy’s entanglement
cm are quite esoteric scales difficult to visualize and totally outside present or near future experimental capacities if at all [30]. Never the less by going back to our initial unit interval universe and noting the unexpected result arising from Hardy’s entanglement  and related conclusions regarding Sigalotti’s critical “topological” velocity of light
and related conclusions regarding Sigalotti’s critical “topological” velocity of light  and the isomorphic length of a super symmetric compactified hyperbolic Penrose universe [65] with a Hawking black hole circular horizon given by [10, 61]:
and the isomorphic length of a super symmetric compactified hyperbolic Penrose universe [65] with a Hawking black hole circular horizon given by [10, 61]:
 (34)
(34)
we realize the following vital topological facts which amount to a realization of D. Gross’ idea of scaling the Planck scale [10]:
1) The topological Planck energy is nothing but Hardy’s quantum entanglement, i.e. the quantum glue which sticks the patches of spacetime together
 (35)
(35)
2) The topological expectation value of the speed of light in a multi-fractal spacetime medium is
 . (36)
. (36)
3) The topological Planck length is equal to the dimension of a fractal M-theory
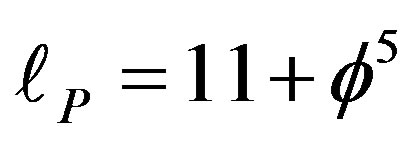 (37)
(37)
since  is equal to
is equal to  where
where  is the topological Plank energy
is the topological Plank energy  we see that E-infinity space is infinitely multi-connected and that all these fractal gaps and voids in their space are essentially wormholes [6] with length equal to an isomorphic length
we see that E-infinity space is infinitely multi-connected and that all these fractal gaps and voids in their space are essentially wormholes [6] with length equal to an isomorphic length  of a super symmetric Penrose tiling universe which constitutes Einstein-Rosen bridges [6,30]. It is ironic as well as surreal to see that the ultimate resolution of the Einstein—Podolsky-Rosen spooky action at distance existed always in the Einstein-Rosen bridges and consequently in quantum entanglement which Einstein as well as Schrö- dinger rejected so vehemently [52].
of a super symmetric Penrose tiling universe which constitutes Einstein-Rosen bridges [6,30]. It is ironic as well as surreal to see that the ultimate resolution of the Einstein—Podolsky-Rosen spooky action at distance existed always in the Einstein-Rosen bridges and consequently in quantum entanglement which Einstein as well as Schrö- dinger rejected so vehemently [52].
3.8. Ordinary and Dark Energy from Rindler Space
A truly brief derivation of dark energy which may also highlight strong evidence that the Rindler-Unruh effects [82] are real and similar to Hawking’s negative energy fluctuation at a black hole horizon [82] could run as follows:
The topological ordinary energy density is simply half the Unruh topological mass  multiplied with the square of the topological speed of light
multiplied with the square of the topological speed of light  [2]. That means it is exactly equal to the area of the fractal version of the hyperbolic Rindler triangle (see Ref. [2], Figures 1.2 to 1.6] when we realize that fractal geometry has no ordinary lines but borders between different KAM space fractal parts. Since events in this hyperbolic fractal front triangle are correlated, i.e. entangled, we half obtained half of Hardy’s
[2]. That means it is exactly equal to the area of the fractal version of the hyperbolic Rindler triangle (see Ref. [2], Figures 1.2 to 1.6] when we realize that fractal geometry has no ordinary lines but borders between different KAM space fractal parts. Since events in this hyperbolic fractal front triangle are correlated, i.e. entangled, we half obtained half of Hardy’s  quantum entanglement probability and the final result for ordinary energy density is
quantum entanglement probability and the final result for ordinary energy density is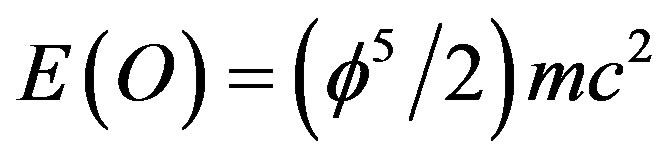 . The topological dark energy density on the other hand is equal to half of Kaluza-Klein’s topological mass 5 multiplied with the square of the topological speed of light
. The topological dark energy density on the other hand is equal to half of Kaluza-Klein’s topological mass 5 multiplied with the square of the topological speed of light  [2]. That means we have
[2]. That means we have  which is exactly equal to the area behind the hyperbolic triangle which completes it to the famous Lorentzian invariant Rindler triangular wedge [82]. The final value of the dark energy is thus
which is exactly equal to the area behind the hyperbolic triangle which completes it to the famous Lorentzian invariant Rindler triangular wedge [82]. The final value of the dark energy is thus . This dark energy is uncorrelated and cannot be observed by the Rindler observer [82].
. This dark energy is uncorrelated and cannot be observed by the Rindler observer [82].
4. Results and Discussion
At the beginning there was the word topology constituting the blueprint for existence. However for the Pythagoreans it was the number which may be golden mean number system in which the topological properties of elementary Cantor sets are expressed so that we can do calculations with them and draw general conclusions [4,17,45]. The author hopes that the present work makes it clear that we can deal with infinity without processing an infinite number of information [17,54,56]. In fact  written in decimal expansion 0.618033989… is infinite.
written in decimal expansion 0.618033989… is infinite.
However written as  we can easily work out that
we can easily work out that  and that
and that 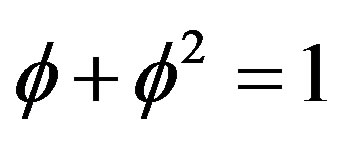 [45]. In any event we showed here beyond any reasonable doubt that
[45]. In any event we showed here beyond any reasonable doubt that  consists of two parts,
consists of two parts, 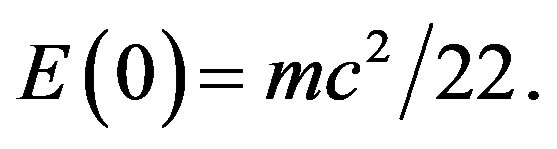 which is the position or potential energy of a quantum particle or equivalently a five dimensional “quintic” zero set at rest and
which is the position or potential energy of a quantum particle or equivalently a five dimensional “quintic” zero set at rest and  which is the absolute value of the negative kinetic energy of the quantum wave or equivalently the moving “quintic” empty set of a quasi De-Sitter five dimension space [2,61]. Together
which is the absolute value of the negative kinetic energy of the quantum wave or equivalently the moving “quintic” empty set of a quasi De-Sitter five dimension space [2,61]. Together  give Einstein’s iconic formula for the maximal total energy of a classical particle [4,26,61]. It is important to note the
give Einstein’s iconic formula for the maximal total energy of a classical particle [4,26,61]. It is important to note the 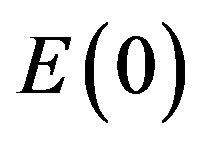 density is only 4.5% of the total expected energy density of the universe in agreement with the most recent sophisticated accurate cosmological measurements of the three physics Nobel Prize winners of 2011 [34,35,61]. On the other hand present measurement technologies do not permit direct measurement of
density is only 4.5% of the total expected energy density of the universe in agreement with the most recent sophisticated accurate cosmological measurements of the three physics Nobel Prize winners of 2011 [34,35,61]. On the other hand present measurement technologies do not permit direct measurement of  which constitutes 95.5% of the total expected energy because of the well documented but ill understood quantum wave collapse at measurement [10,20,33]. For this reason
which constitutes 95.5% of the total expected energy because of the well documented but ill understood quantum wave collapse at measurement [10,20,33]. For this reason  is dubbed dark energy and baring new developments in wave collapse free non-demolition measurement instruments [2,4,10,20], dark it will remain [30,34,35]. Negative dark energy is linked here to the anticlastic curvature at the edge of the a Rindler Wedge-like universe and is therefore a cousin of Hawking’s negative energy fluctuation of the vacuum at the horizon of a toy black hole which constitutes a circular edge of the hyperbolic compactified edge lying at infinity of a Klein-Penrose holographic universe [2,61,65]. It is this negative gravity force which is responsible for the unexpected measured accelerated expansion of the cosmos which is the only indication that repulsive gravity due to negative dark energy must really be there [10,34,35]. Technically speaking we could not have obtained accurate quantitative results for the preceding effect if it would not have been for L. Hardy’s magnificent quantum entanglement exact solutions for two particles [31-33] as well as the work of Sigalotti [10] leading to the topological speed of light
is dubbed dark energy and baring new developments in wave collapse free non-demolition measurement instruments [2,4,10,20], dark it will remain [30,34,35]. Negative dark energy is linked here to the anticlastic curvature at the edge of the a Rindler Wedge-like universe and is therefore a cousin of Hawking’s negative energy fluctuation of the vacuum at the horizon of a toy black hole which constitutes a circular edge of the hyperbolic compactified edge lying at infinity of a Klein-Penrose holographic universe [2,61,65]. It is this negative gravity force which is responsible for the unexpected measured accelerated expansion of the cosmos which is the only indication that repulsive gravity due to negative dark energy must really be there [10,34,35]. Technically speaking we could not have obtained accurate quantitative results for the preceding effect if it would not have been for L. Hardy’s magnificent quantum entanglement exact solutions for two particles [31-33] as well as the work of Sigalotti [10] leading to the topological speed of light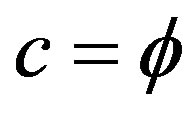 . In addition the general theory of noncommutative space of A. Connes and the realization that Penrose universe is a K-theoretical explicit realization of a generic noncommutative space played a pivotal role in reaching our conclusion [2].
. In addition the general theory of noncommutative space of A. Connes and the realization that Penrose universe is a K-theoretical explicit realization of a generic noncommutative space played a pivotal role in reaching our conclusion [2].
5. Conclusion
Finally the inspiring idea of D. Gross to scale the Planck scale [1] gave an overall intuitive justification for  and the fractal M-theory dimension
and the fractal M-theory dimension 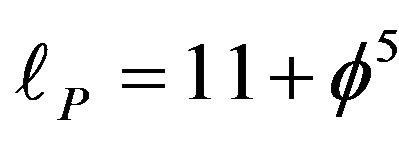 to realize that E-infinity fractal geometry is the geometry of quantum entanglement linking Einstein-Rosen bridges with quantum entanglement, zero measure geometry as well as Mielke-El Naschie-Elokaby worm holes and Magueijo-Smolin’s ingenious theory of varying speed of light [44]. The same is true for Nash Embedding of Witten’s M-Theory [83]. In fact from the fundamental work of Gutzwiller, the Russian School of Quantum Chaos led by Cherikov and the pioneering work of Berry, Casati and others on KAM [80-83], it is clear that quantum entanglement shapes quantum spacetime and glues it together giving rise to classical space and time [3]. The entire analysis and result obtained have testified once more to Einstein’s dictum “Raffiniert is der Herr Gott aber boshaft ist er nich”. Einstein added later that “Die Natur verbirgt ihre Geheimnisse durch die Erhabenheit ihres wesen, aber nicht durch List” [52]. In fact nature is simple to a degree that at least initially defies human expectation, in order not to say human comprehension. However, as H.R.H. the Prince of Wales, T. Juniper and I. Shelly emphasized in their book [53], harmony is the way to comprehension and nothing could be more harmonious than a golden ratio based number system which we used in E-infinity theory [17,53,2]. In E-infinity the most irrational number
to realize that E-infinity fractal geometry is the geometry of quantum entanglement linking Einstein-Rosen bridges with quantum entanglement, zero measure geometry as well as Mielke-El Naschie-Elokaby worm holes and Magueijo-Smolin’s ingenious theory of varying speed of light [44]. The same is true for Nash Embedding of Witten’s M-Theory [83]. In fact from the fundamental work of Gutzwiller, the Russian School of Quantum Chaos led by Cherikov and the pioneering work of Berry, Casati and others on KAM [80-83], it is clear that quantum entanglement shapes quantum spacetime and glues it together giving rise to classical space and time [3]. The entire analysis and result obtained have testified once more to Einstein’s dictum “Raffiniert is der Herr Gott aber boshaft ist er nich”. Einstein added later that “Die Natur verbirgt ihre Geheimnisse durch die Erhabenheit ihres wesen, aber nicht durch List” [52]. In fact nature is simple to a degree that at least initially defies human expectation, in order not to say human comprehension. However, as H.R.H. the Prince of Wales, T. Juniper and I. Shelly emphasized in their book [53], harmony is the way to comprehension and nothing could be more harmonious than a golden ratio based number system which we used in E-infinity theory [17,53,2]. In E-infinity the most irrational number  with infinite decimal expansion
with infinite decimal expansion  is taken as basic and integers as constructed from
is taken as basic and integers as constructed from 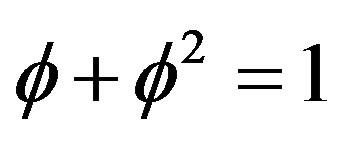 and so on. Similarly rationals are given by
and so on. Similarly rationals are given by
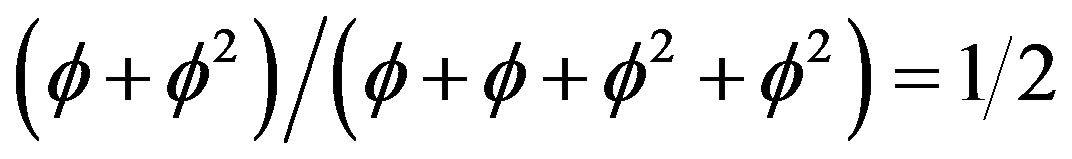 . We note on passing that the golden mean is fundamental in KAM theorem [3,8,80]. In that way we tame infinity and extend what D. Hilbert called Cantor’s paradise to physics [17,54]. The author for one firmly believes in the preceding concept of the role of infinity in physics and the incredibly deep work of Hugh Wooden [56], which is bigger than mere mathematical tradition which came from G. Cantor, a monastery in Greece and the Moscow School of Mathematics founded by Egorov and Luzin [77].
. We note on passing that the golden mean is fundamental in KAM theorem [3,8,80]. In that way we tame infinity and extend what D. Hilbert called Cantor’s paradise to physics [17,54]. The author for one firmly believes in the preceding concept of the role of infinity in physics and the incredibly deep work of Hugh Wooden [56], which is bigger than mere mathematical tradition which came from G. Cantor, a monastery in Greece and the Moscow School of Mathematics founded by Egorov and Luzin [77].