More Results on Singular Value Inequalities for Compact Operators ()
1. Introduction
Let 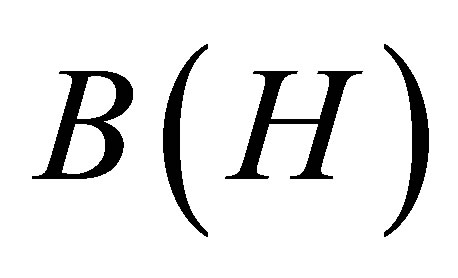 denote the space of all bounded linear operators on a complex separable Hilbert space H, and let
denote the space of all bounded linear operators on a complex separable Hilbert space H, and let 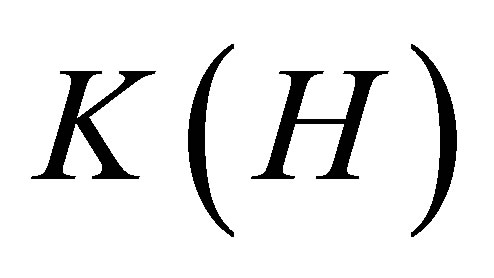 denote the two-sided ideal of compact operators in
denote the two-sided ideal of compact operators in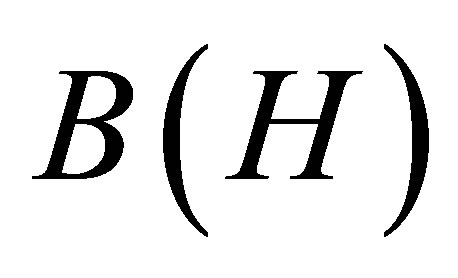 . For
. For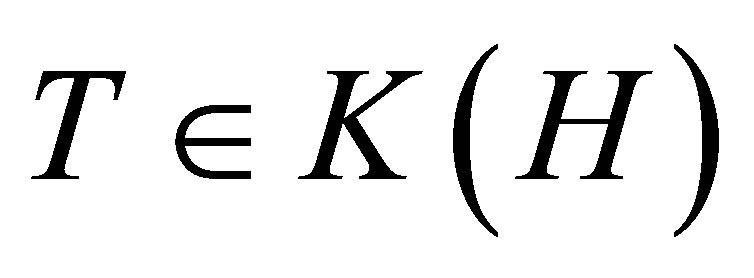 , the singular values of
, the singular values of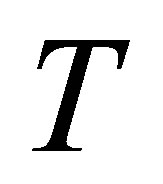 , denoted by
, denoted by 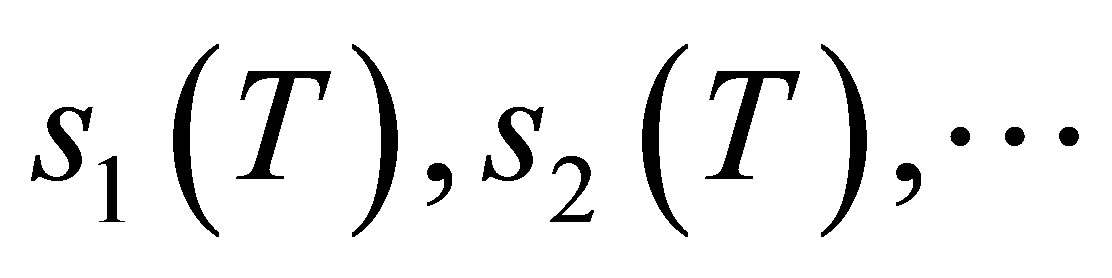 are the eigenvalues of the positive operator
are the eigenvalues of the positive operator 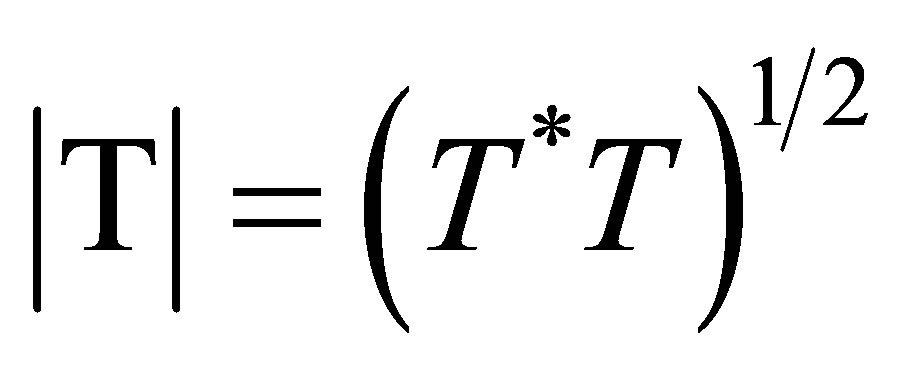 as
as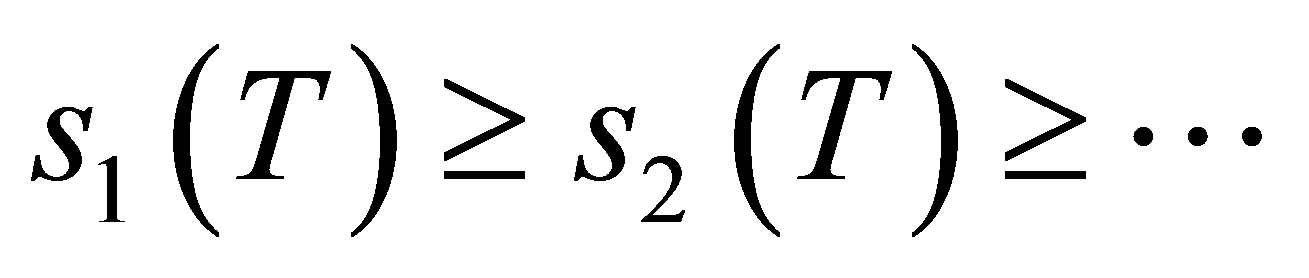
repeated according to multiplicity. Note that 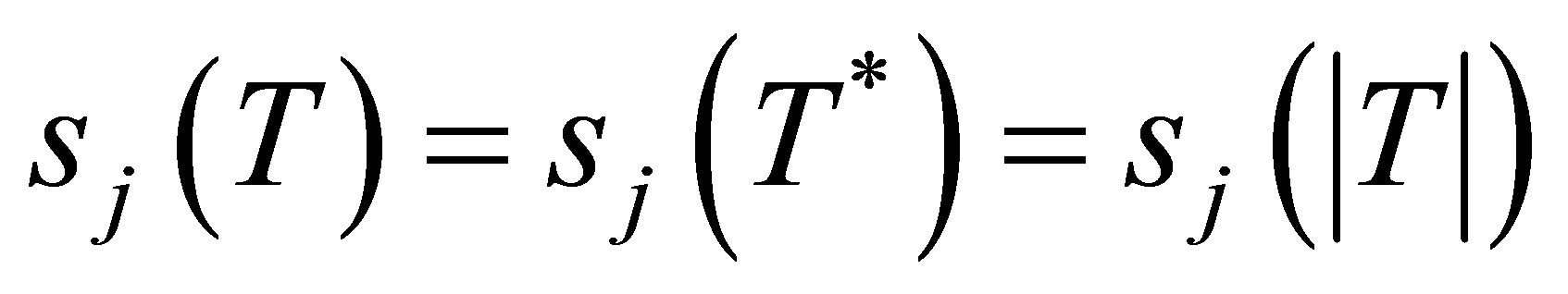
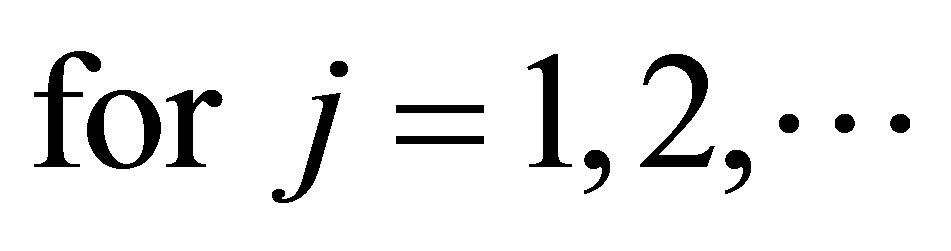 It follows Weyl’s monotonicity principle (see, e.g., [1, p. 63] or [2, p. 26]) that if
It follows Weyl’s monotonicity principle (see, e.g., [1, p. 63] or [2, p. 26]) that if 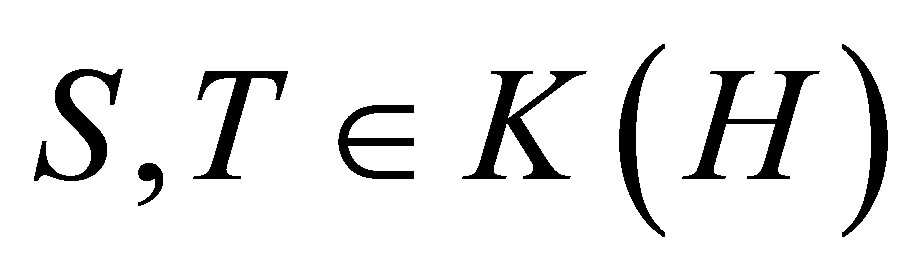 are positive and
are positive and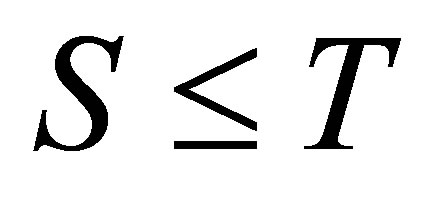 , then
, then 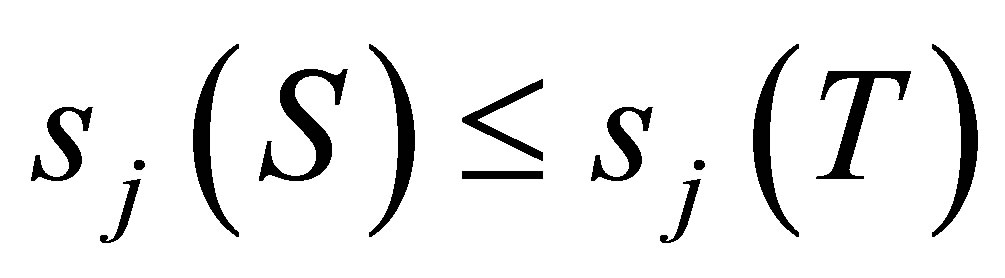
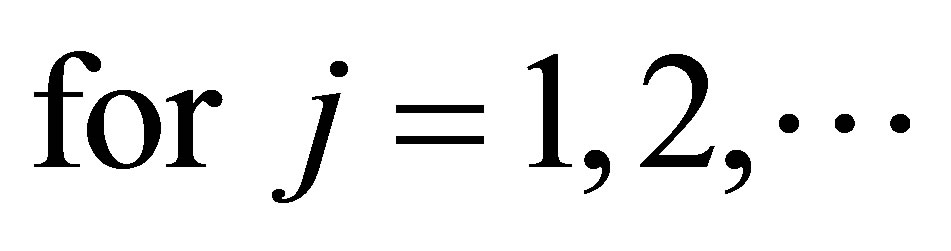 Moreover, for
Moreover, for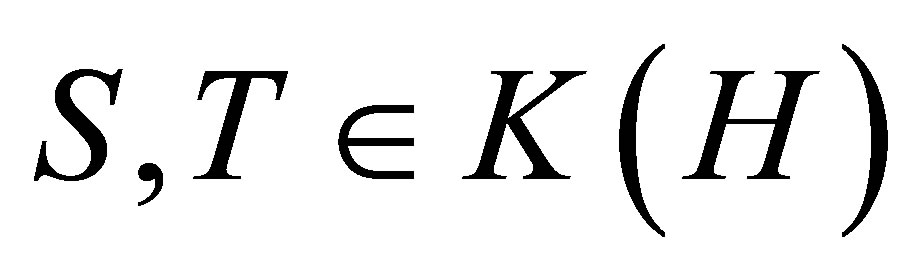 ,
, if and only if
if and only if 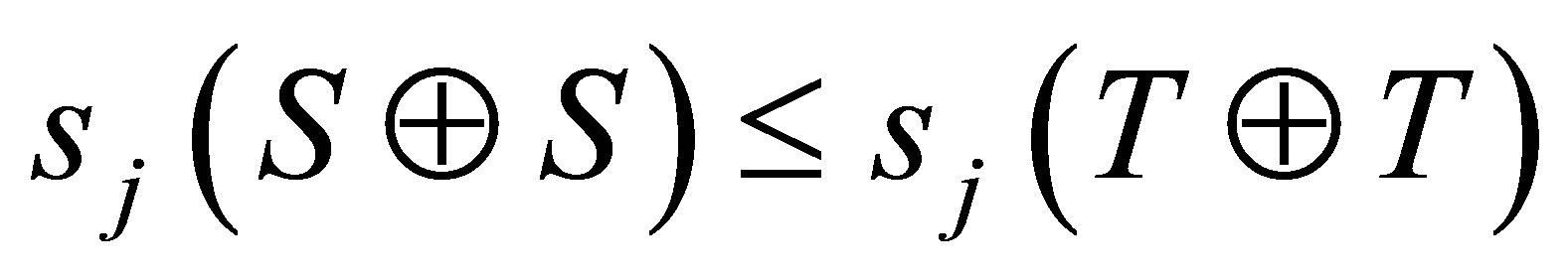
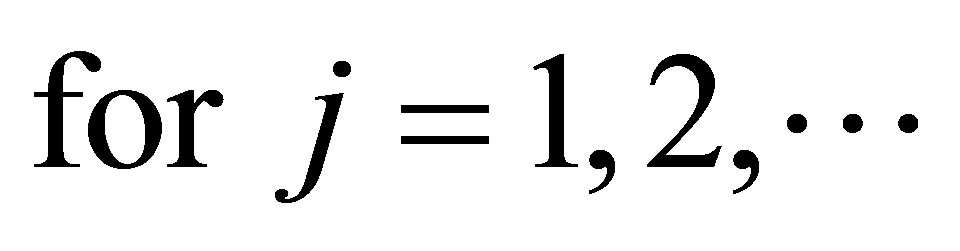 The singular values of
The singular values of 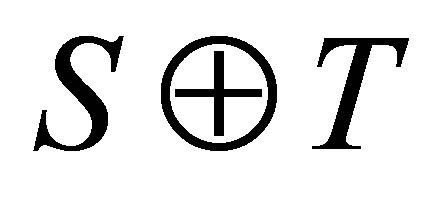 and
and 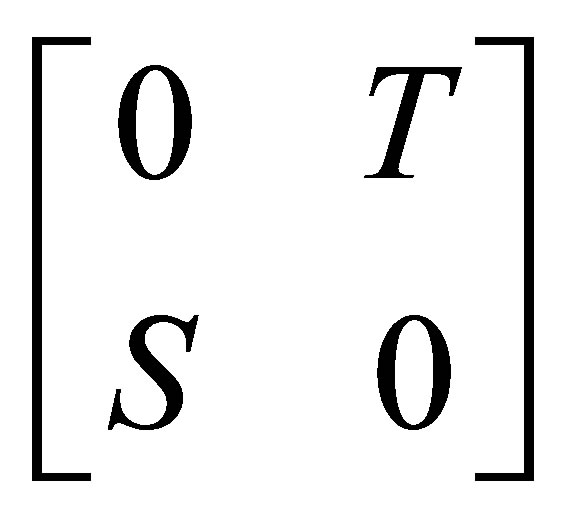 are the same, and they consist of those of
are the same, and they consist of those of 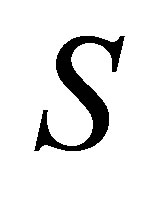 together with those of
together with those of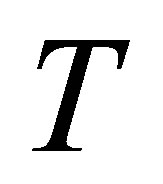 . Here, we use the direct sum notation
. Here, we use the direct sum notation 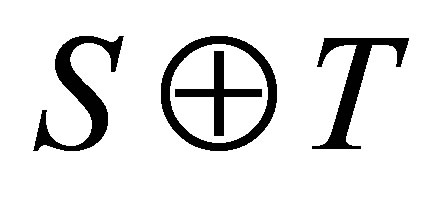 for the blockdiagonal operator
for the blockdiagonal operator 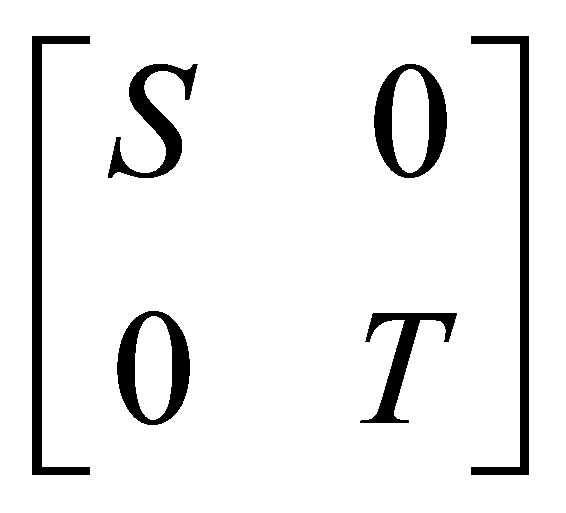 defined on
defined on .
.
The well-known arithmetic-geometric mean inequality for singular values, according to Bhatia and Kittaneh [3], says that if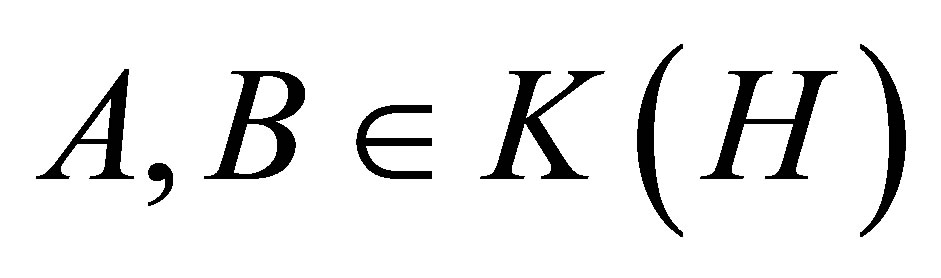 , then
, then
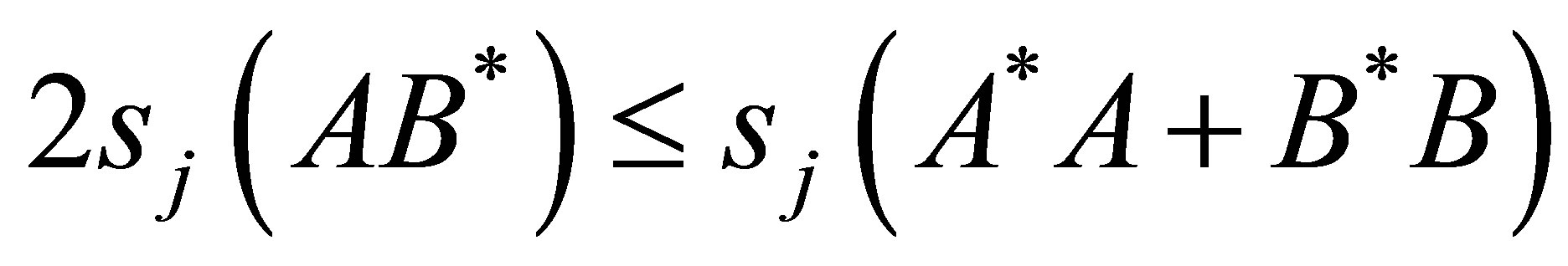 (1.1)
(1.1)
Hirzallah has proved in [4] that if 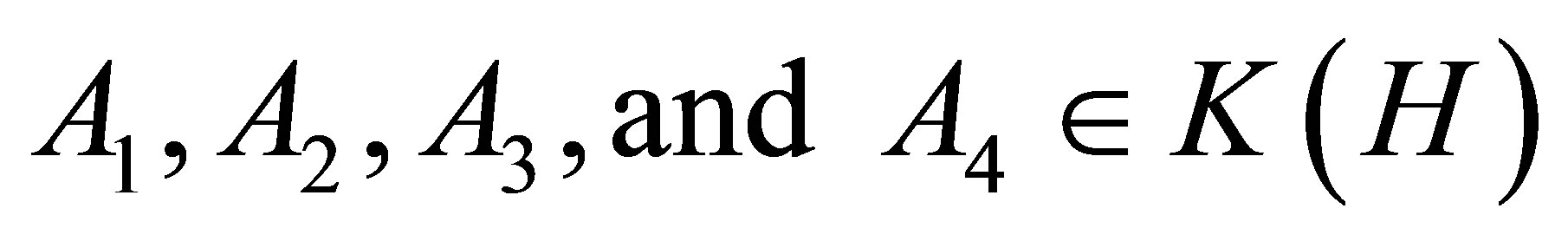 , then
, then
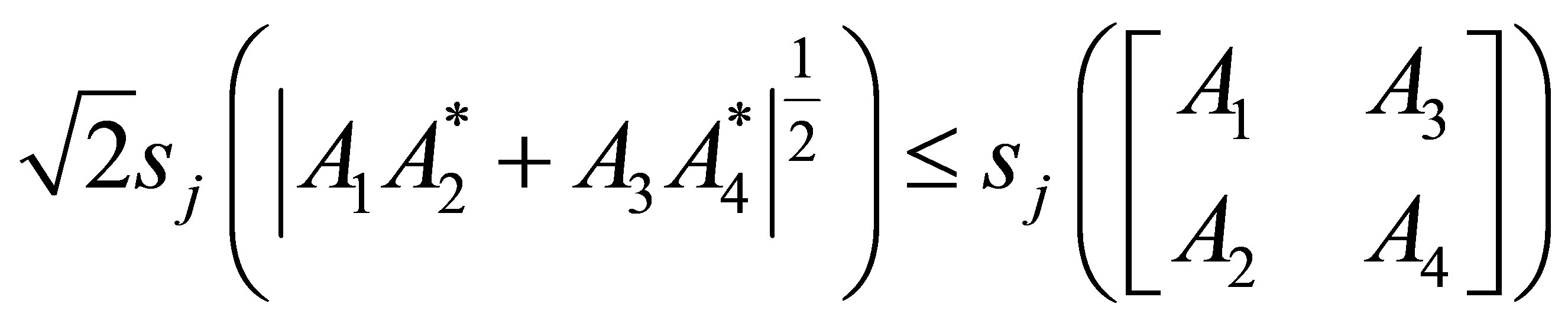 (1.2)
(1.2)
In this paper, we will give a new inequality which is equivalent to and more general than the inequalities (1.1) and (1.2):
If , then
, then
 (1.3)
(1.3)
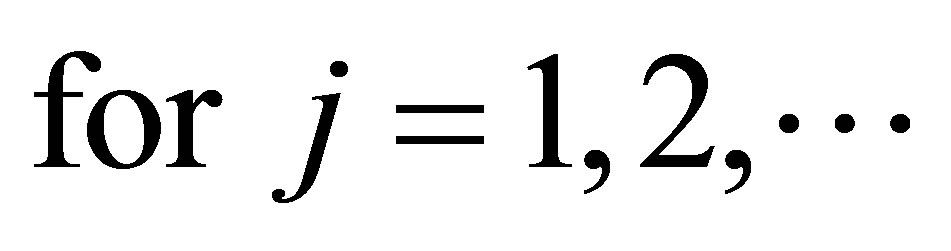
Audeh and Kittaneh have proved in [5] that if 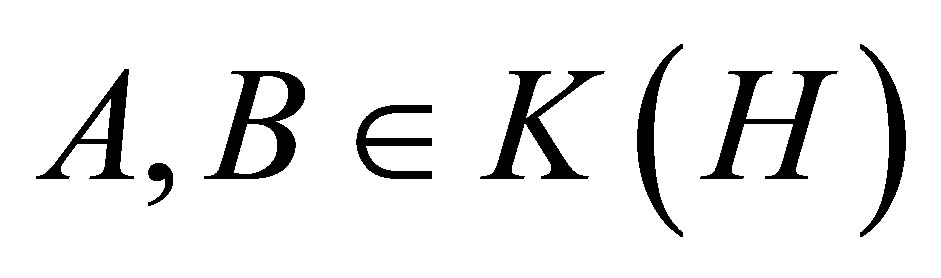 such that
such that  is self-adjoint,
is self-adjoint, 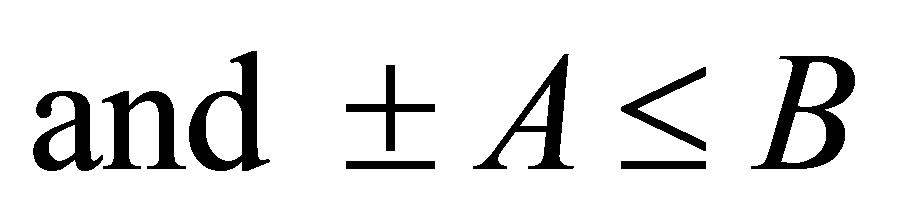
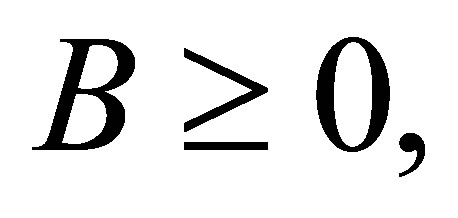 , then
, then
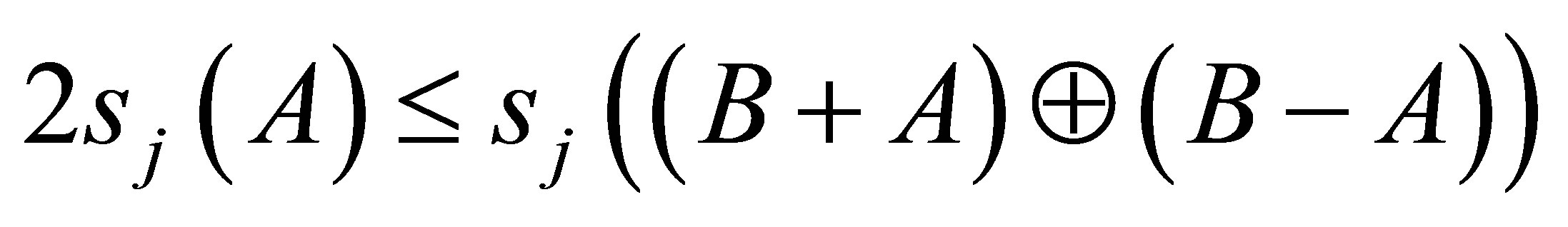 (1.4)
(1.4)
 On the other hand, Tao has proved in [6]
On the other hand, Tao has proved in [6]
that if  such that
such that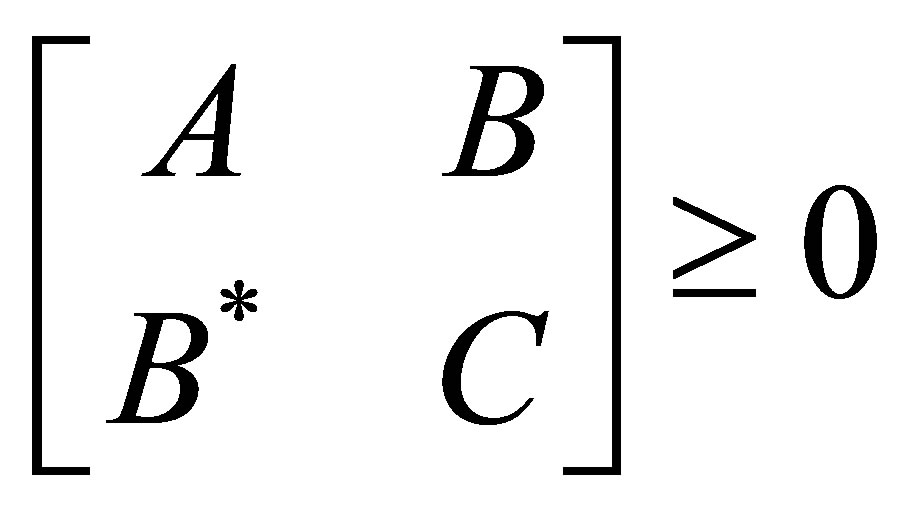 , then
, then
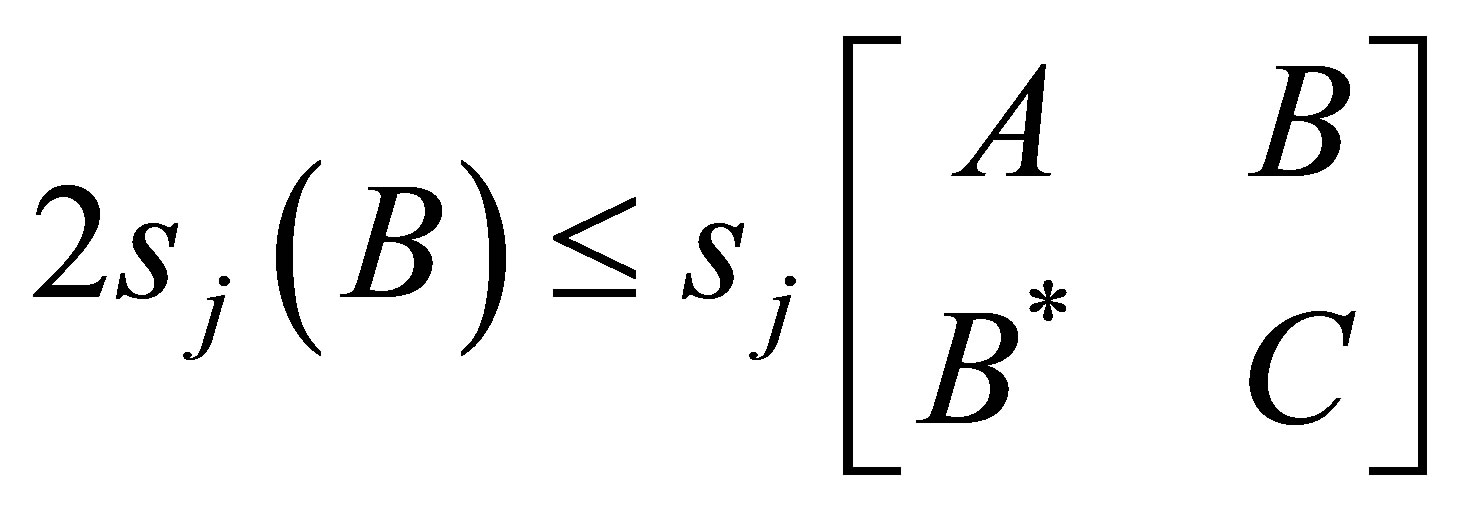 (1.5)
(1.5)
 Moreover, Zhan has proved in [7] that if
Moreover, Zhan has proved in [7] that if 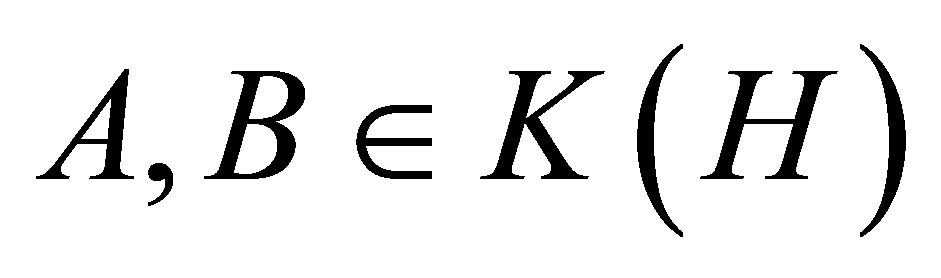 are positive, then
are positive, then
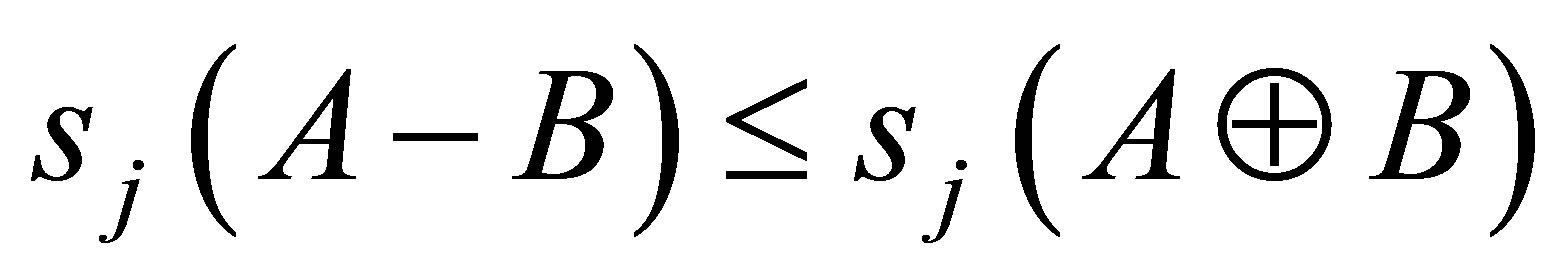 (1.6)
(1.6)
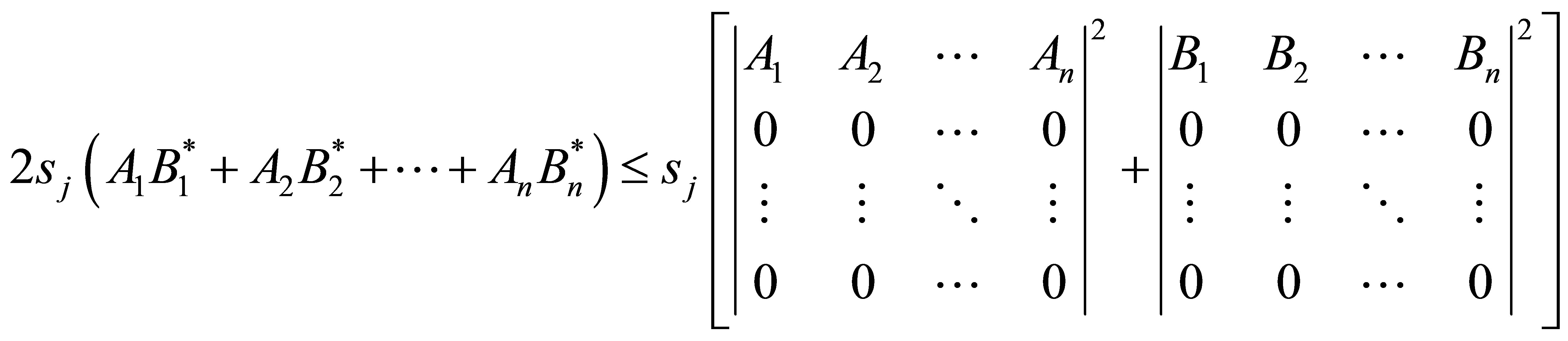
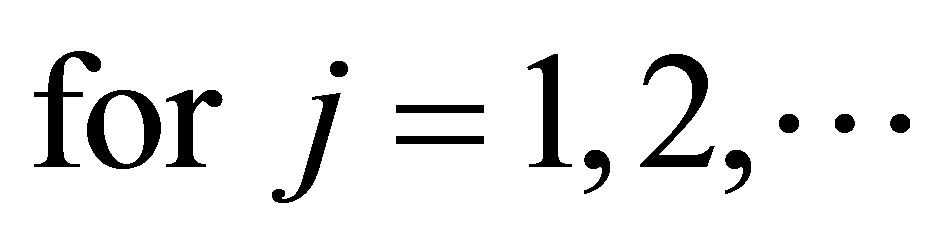 We will give a new inequality which generalizes (1.5), and is equivalent to the inequalities (1.1), (1.2), (1.3), (1.4), (1.5), and (1.6):
We will give a new inequality which generalizes (1.5), and is equivalent to the inequalities (1.1), (1.2), (1.3), (1.4), (1.5), and (1.6):
Let 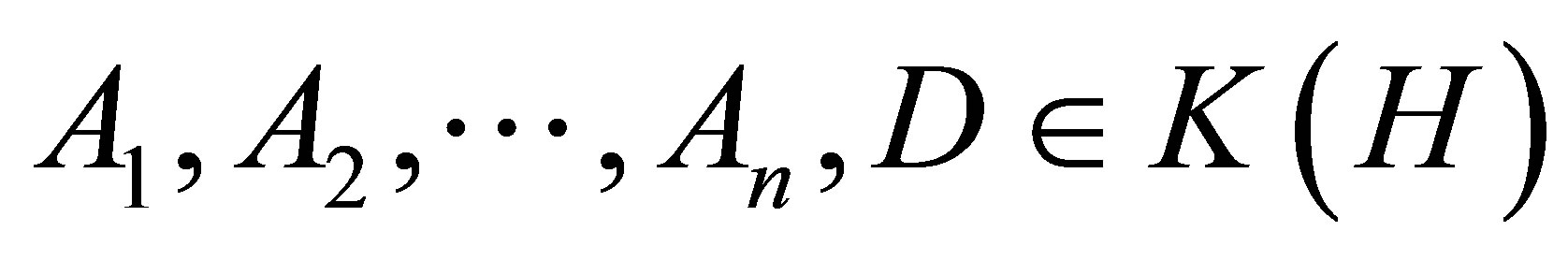 such that
such that
 , then
, then
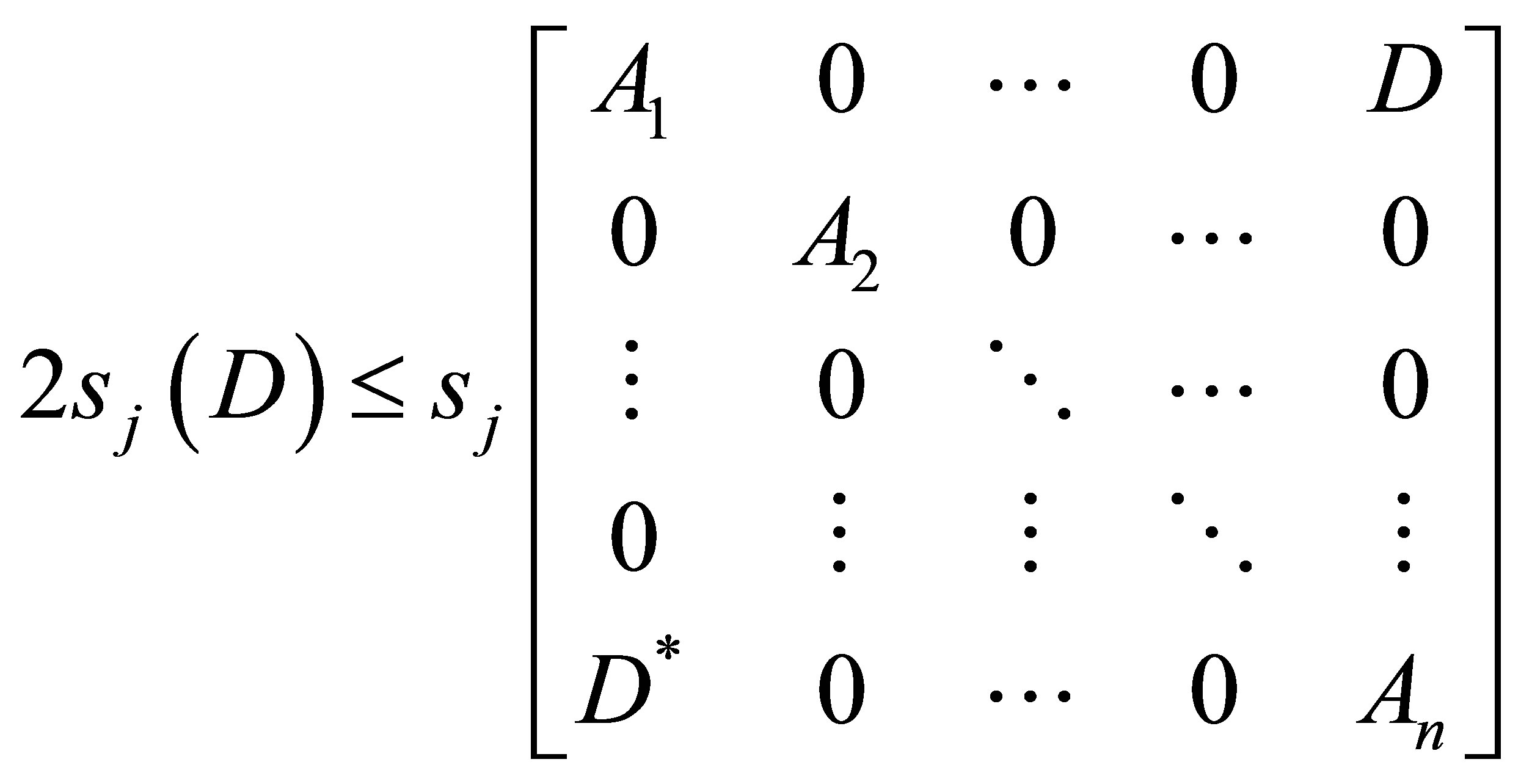 (1.7)
(1.7)
 Bhatia and Kittaneh have proved in [8] that if
Bhatia and Kittaneh have proved in [8] that if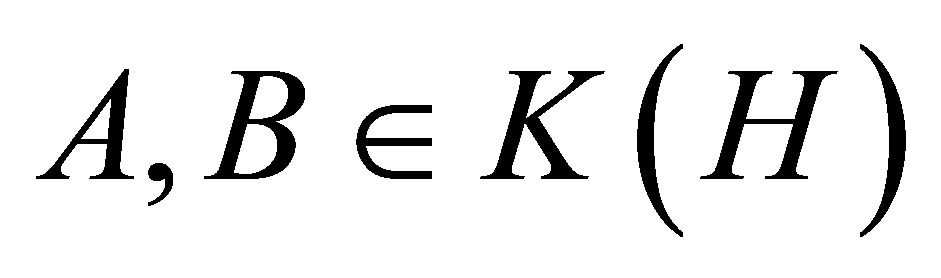 , such that
, such that  is self-adjoint,
is self-adjoint, 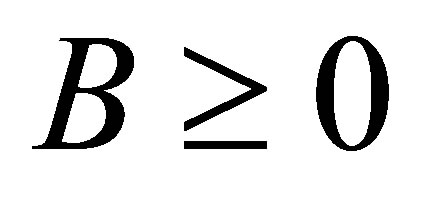 , and
, and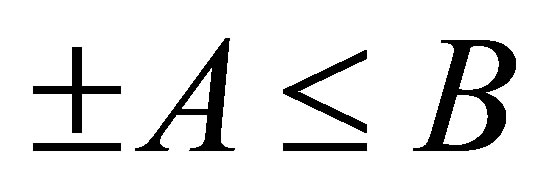 , then
, then
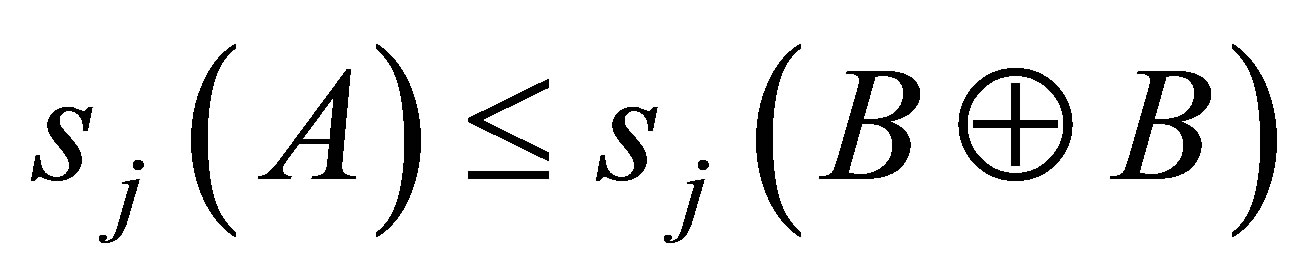 (1.8)
(1.8)
 Audeh and Kittaneh have proved in [5]
Audeh and Kittaneh have proved in [5]
that if 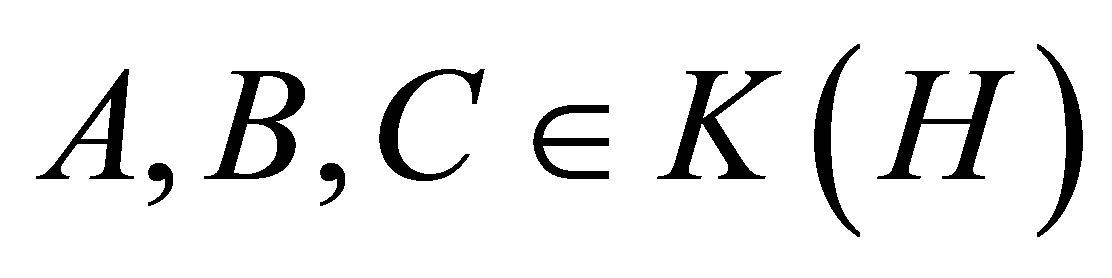 such that
such that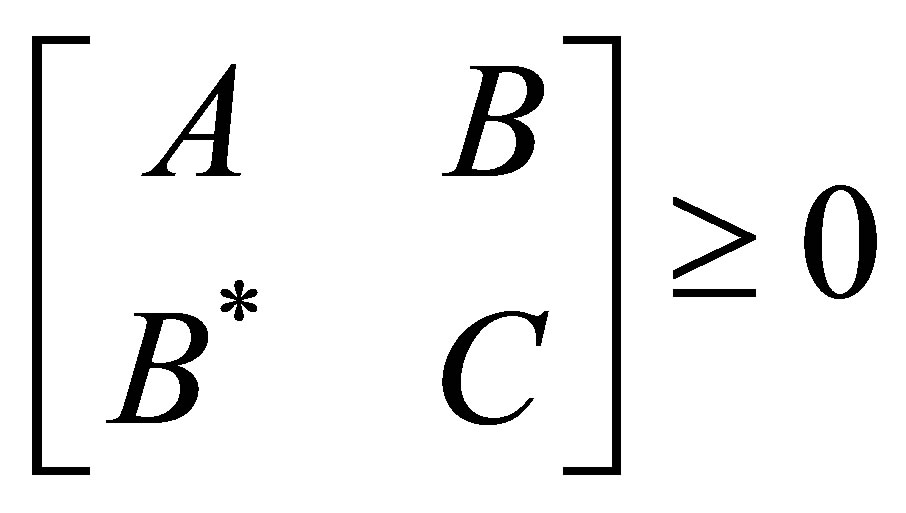 , then
, then
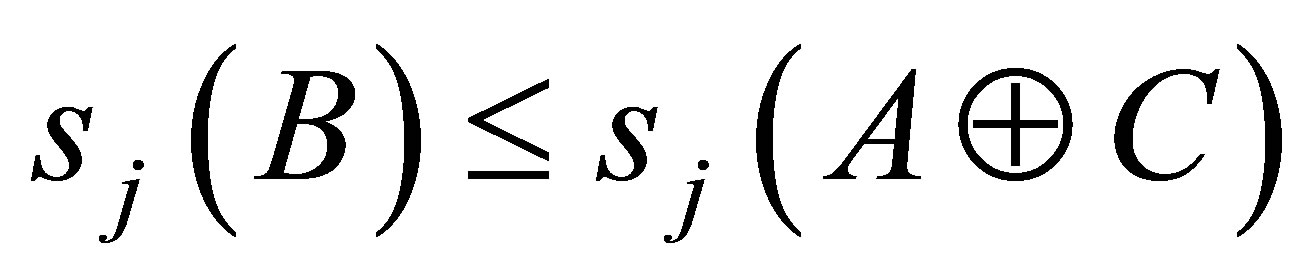 (1.9)
(1.9)
 We will prove a new inequality which generalizes (1.9), and is equivalent to the inequalities (1.8) and (1.9):
We will prove a new inequality which generalizes (1.9), and is equivalent to the inequalities (1.8) and (1.9):
If 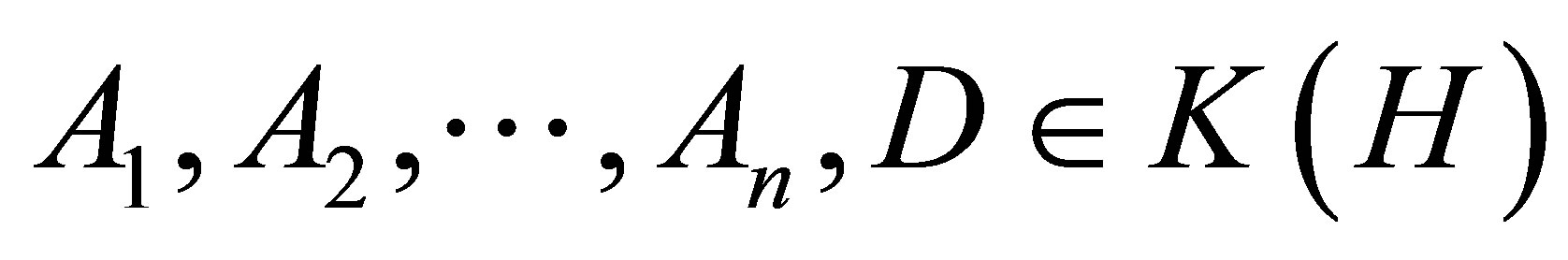 such that
such that
 , then
, then
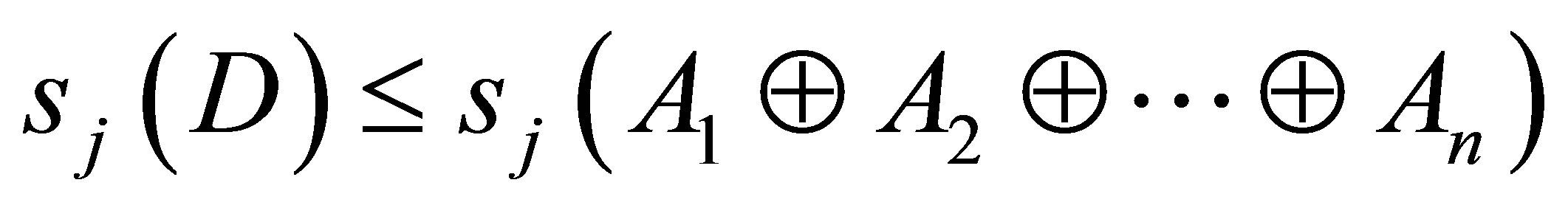 (1.10)
(1.10)
2. Main Result
Our first singular value inequality is equivalent to and more general than the inequalities (1.1) and (1.2).
Theorem 2.1 Let 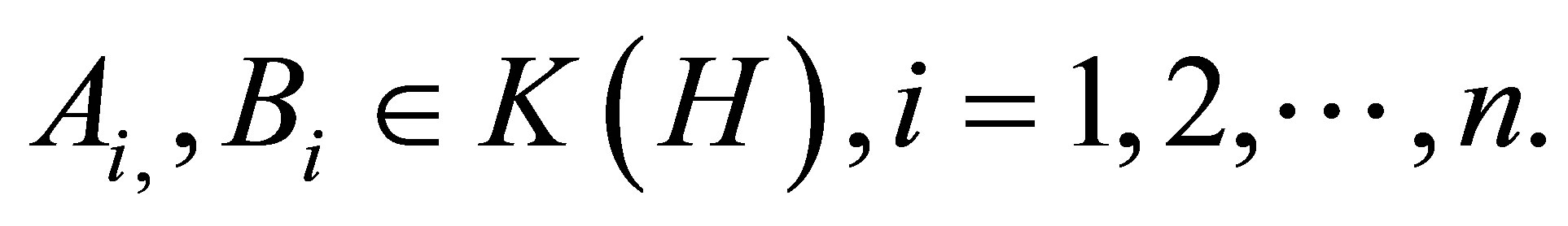 Then
Then
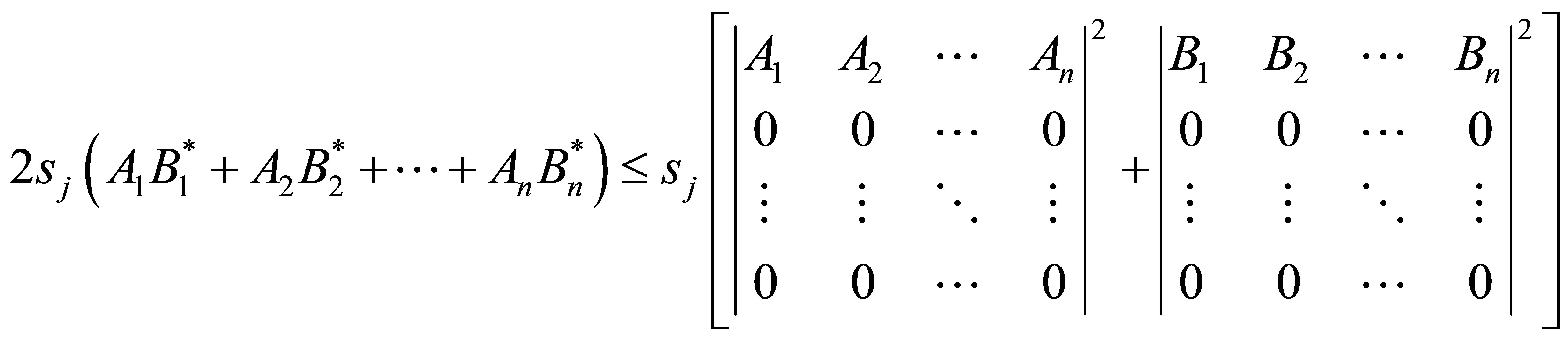
Proof. Let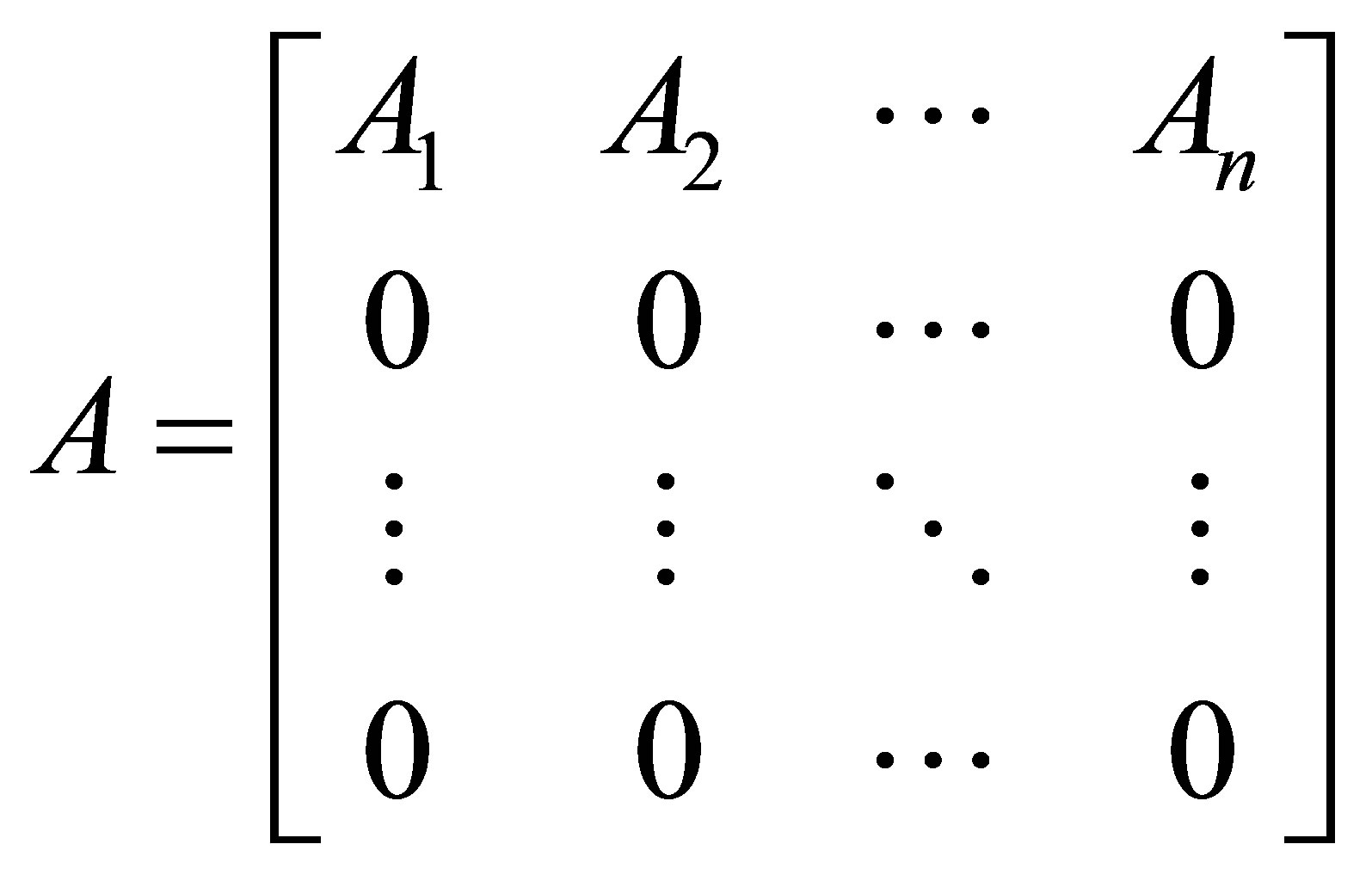 ,
, 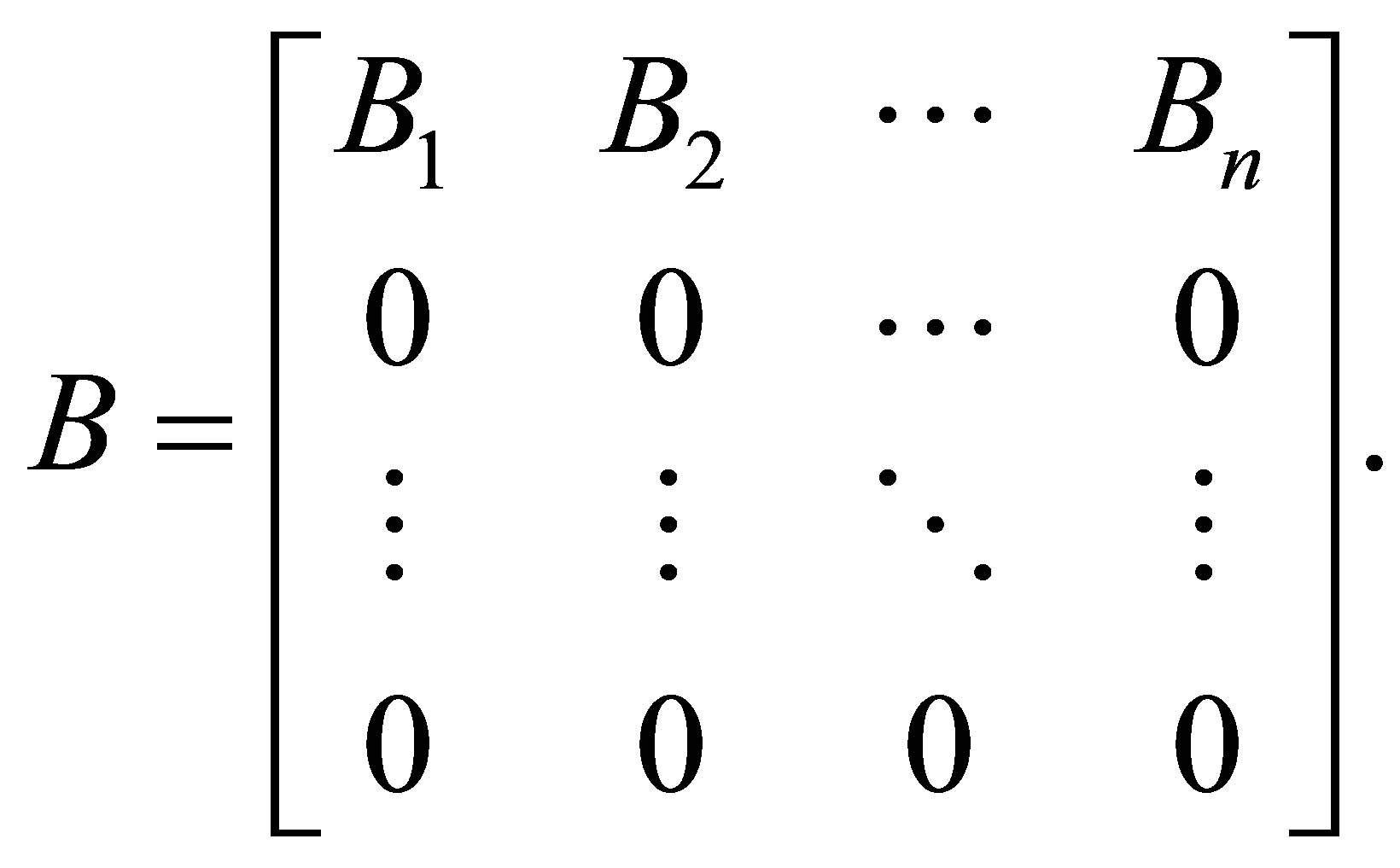 Then
Then
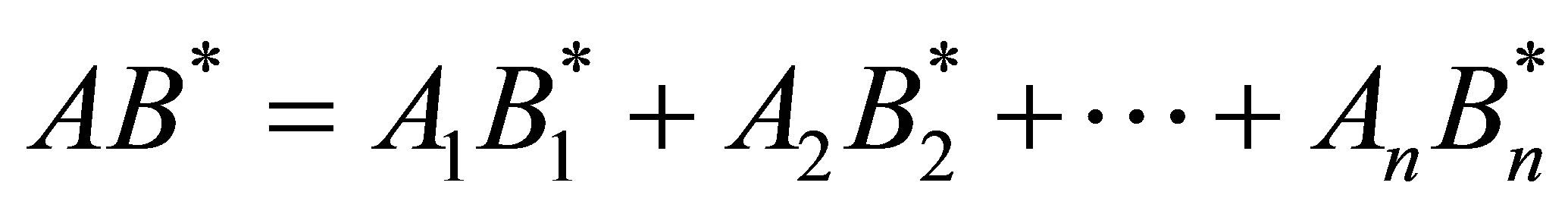 , and
, and
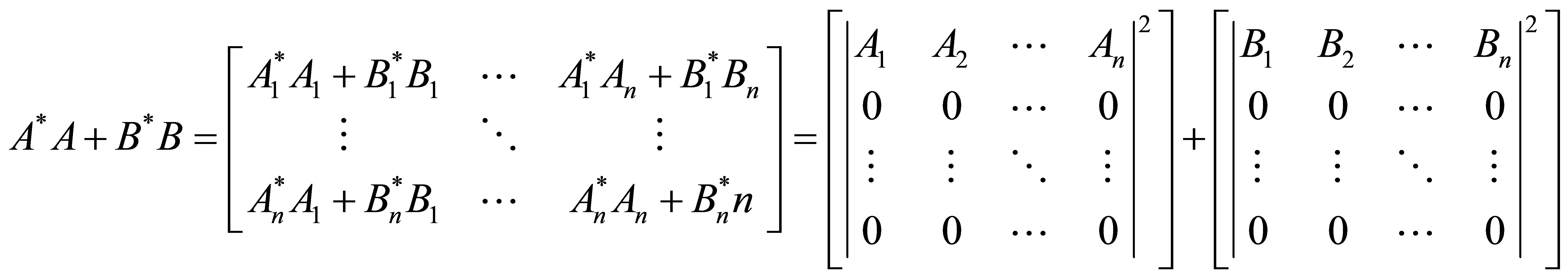
Now, using (1.1) we get
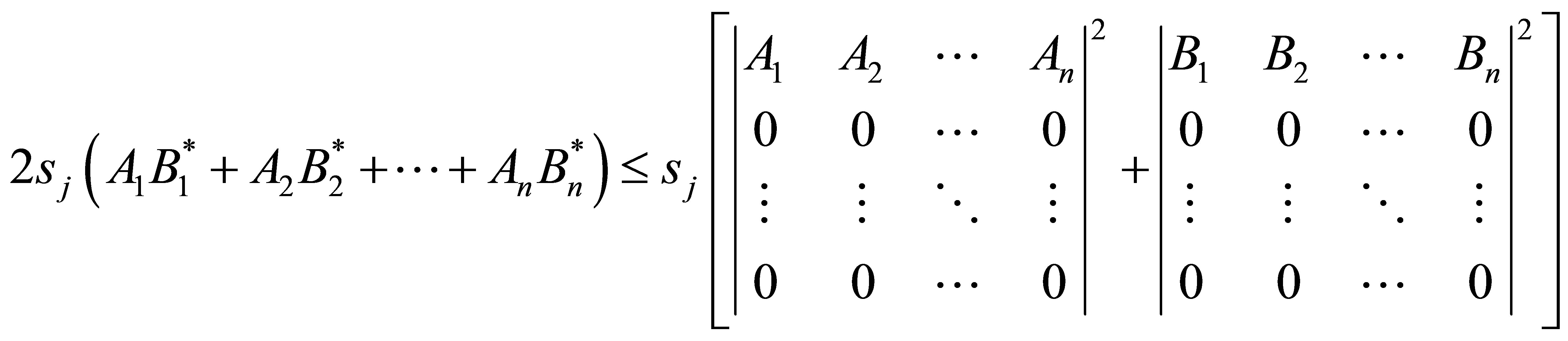
Remark 1. As a special case of (1.3), let 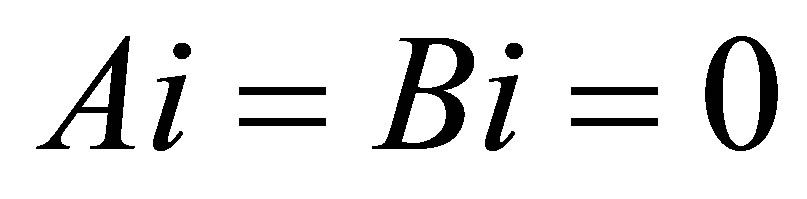
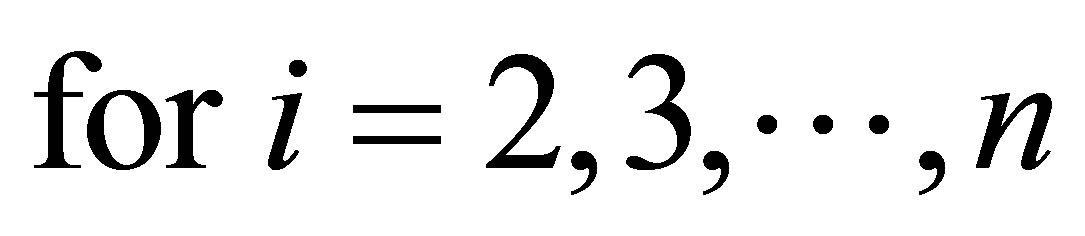 .we get (1.1)
.we get (1.1)
Remark 2. As a special case of (1.3), let 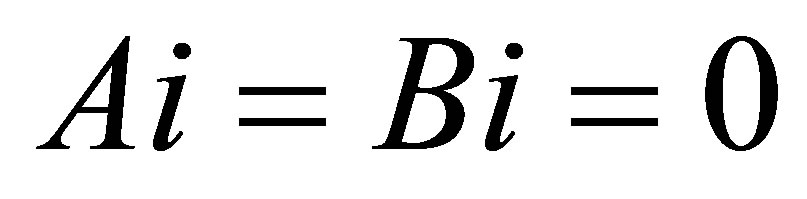
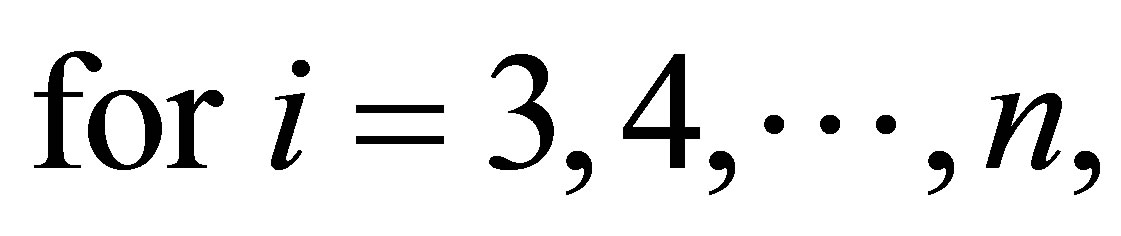 we get (1.2), to see this:
we get (1.2), to see this:
Replace 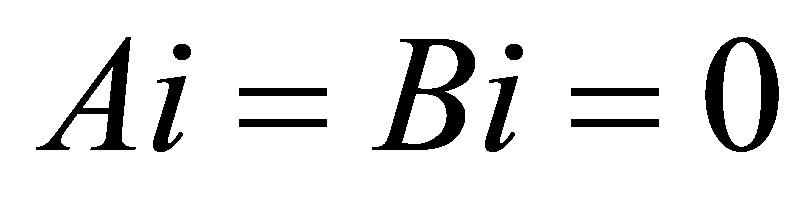
 we get
we get

Now, we prove that the inequalities (1.1) and (1.3) are equivalent.
Theorem 2.2. The following statements are equivalent:
(i) If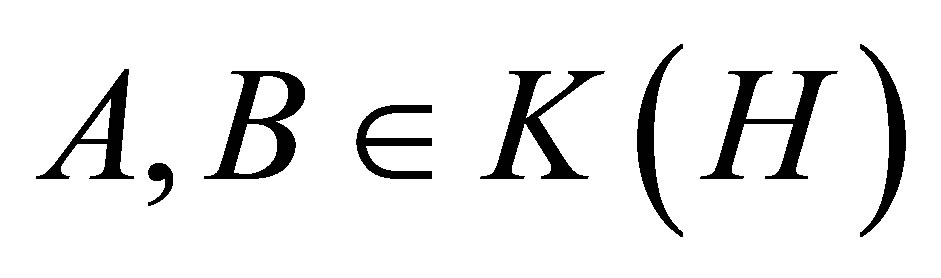 , then
, then 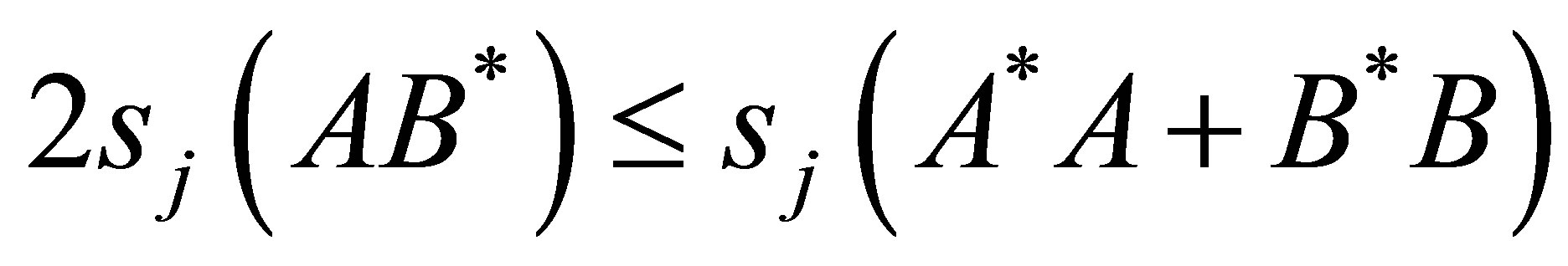
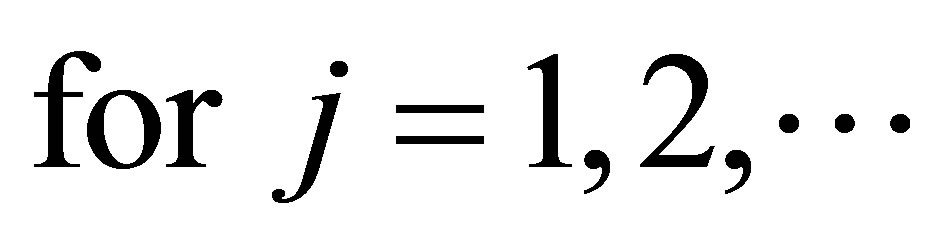
(ii) Let 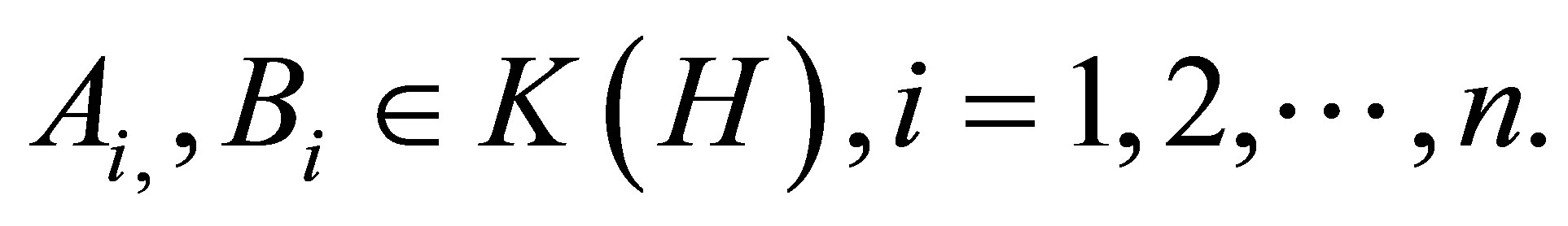 Then
Then
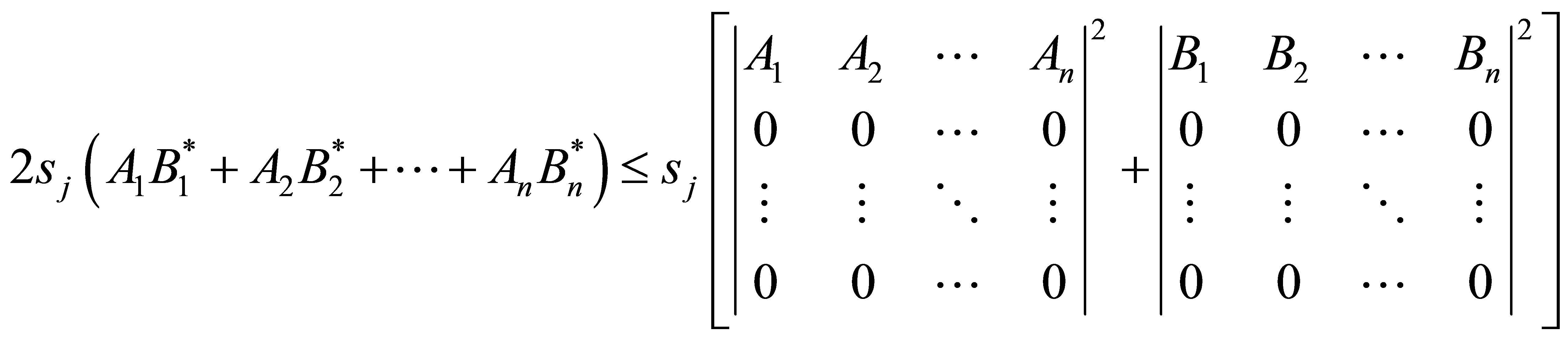
Proof.  This implication follows from the proof of Theorem 2.1.
This implication follows from the proof of Theorem 2.1.
 This implication follows from Remark 1.
This implication follows from Remark 1.
Remark 3. It can be shown trivially that (1.1) and (1.2) are equivalent. By using this with Theorem 2.2, we conclude that the inequalities (1.2) and (1.3) are equivalent. Chaining this with results in [5], we get that the inequalities (1.1), (1.2), (1.3), (1.4), (1.5), and (1.6) are equivalent.
Our second singular value inequality is equivalent to the inequality (1.4).
Theorem 2.3. Let 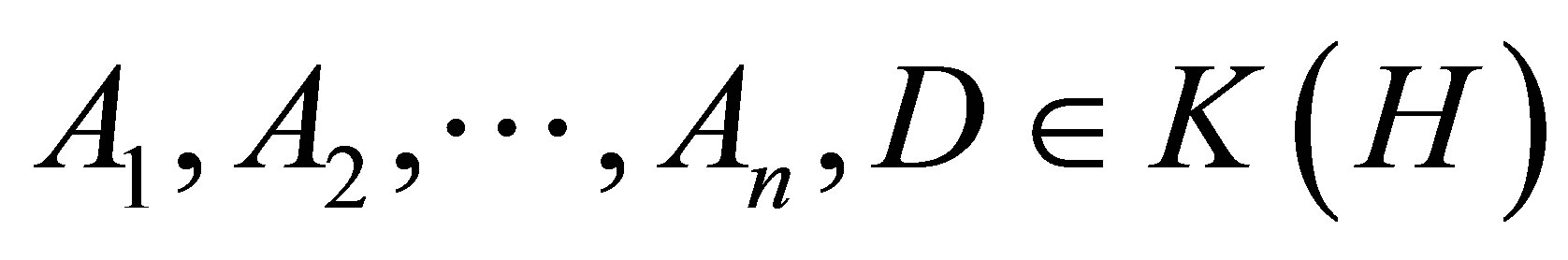 such that
such that
 Then
Then 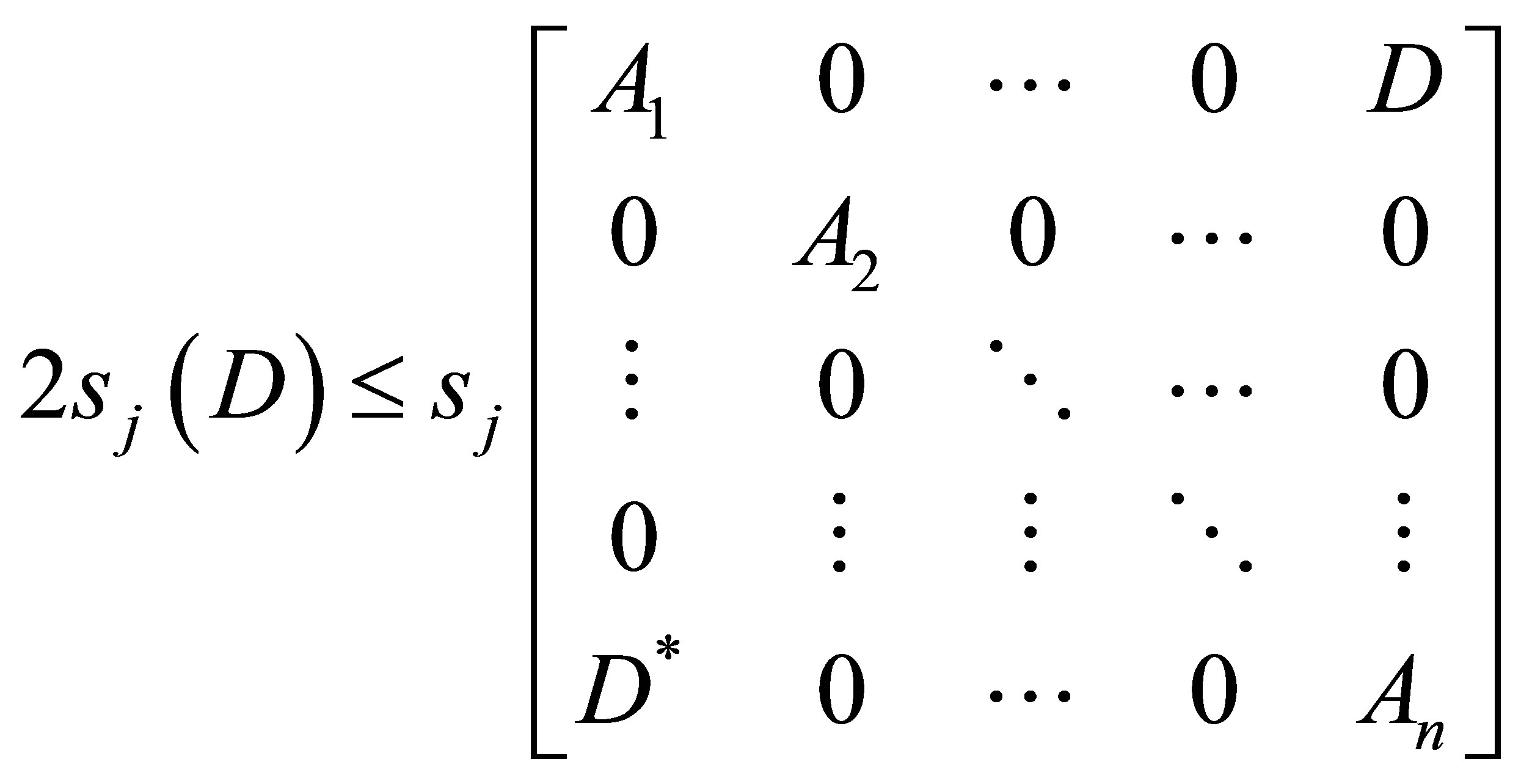
Proof. Since
 it follows that
it follows that
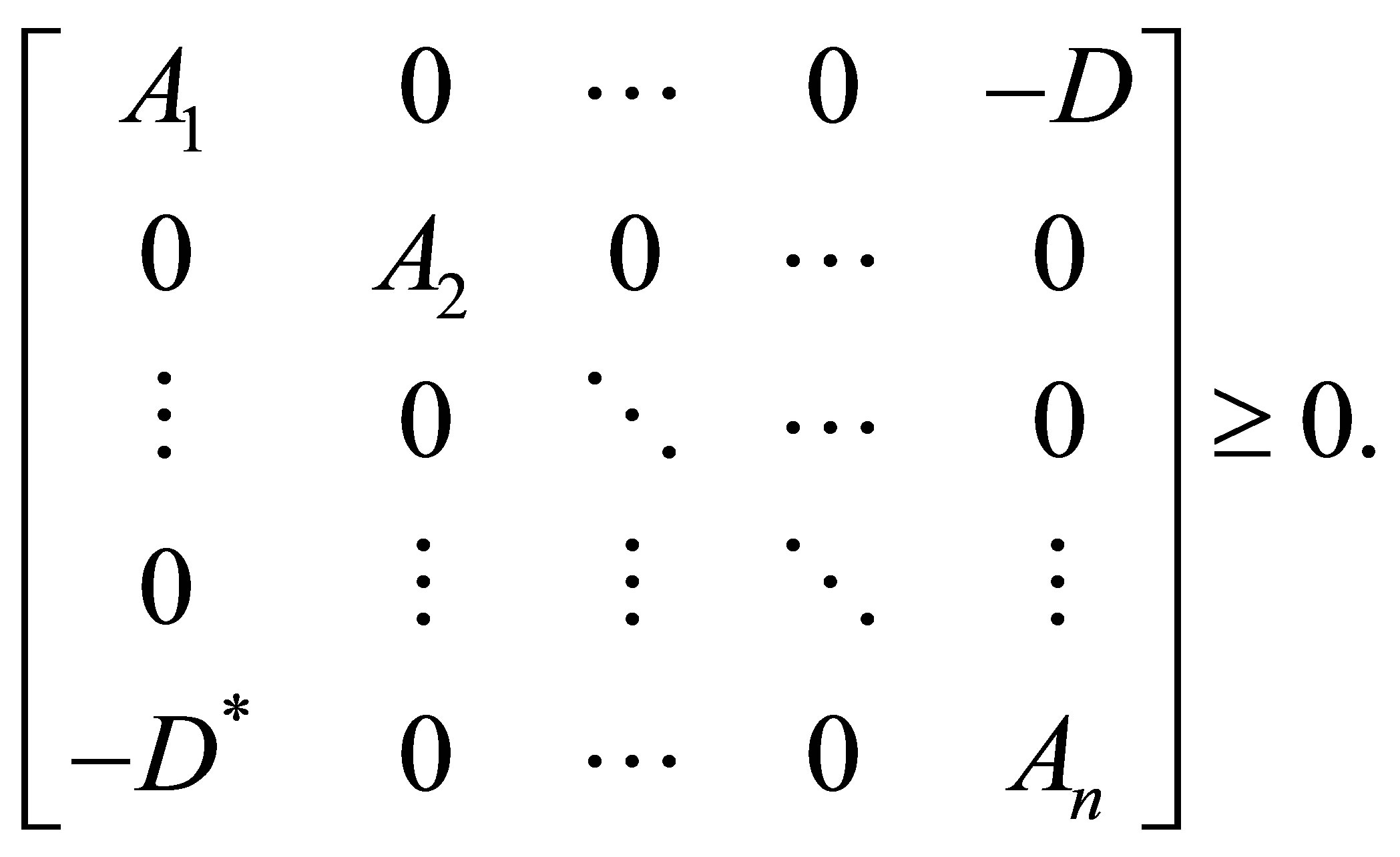
In fact, if 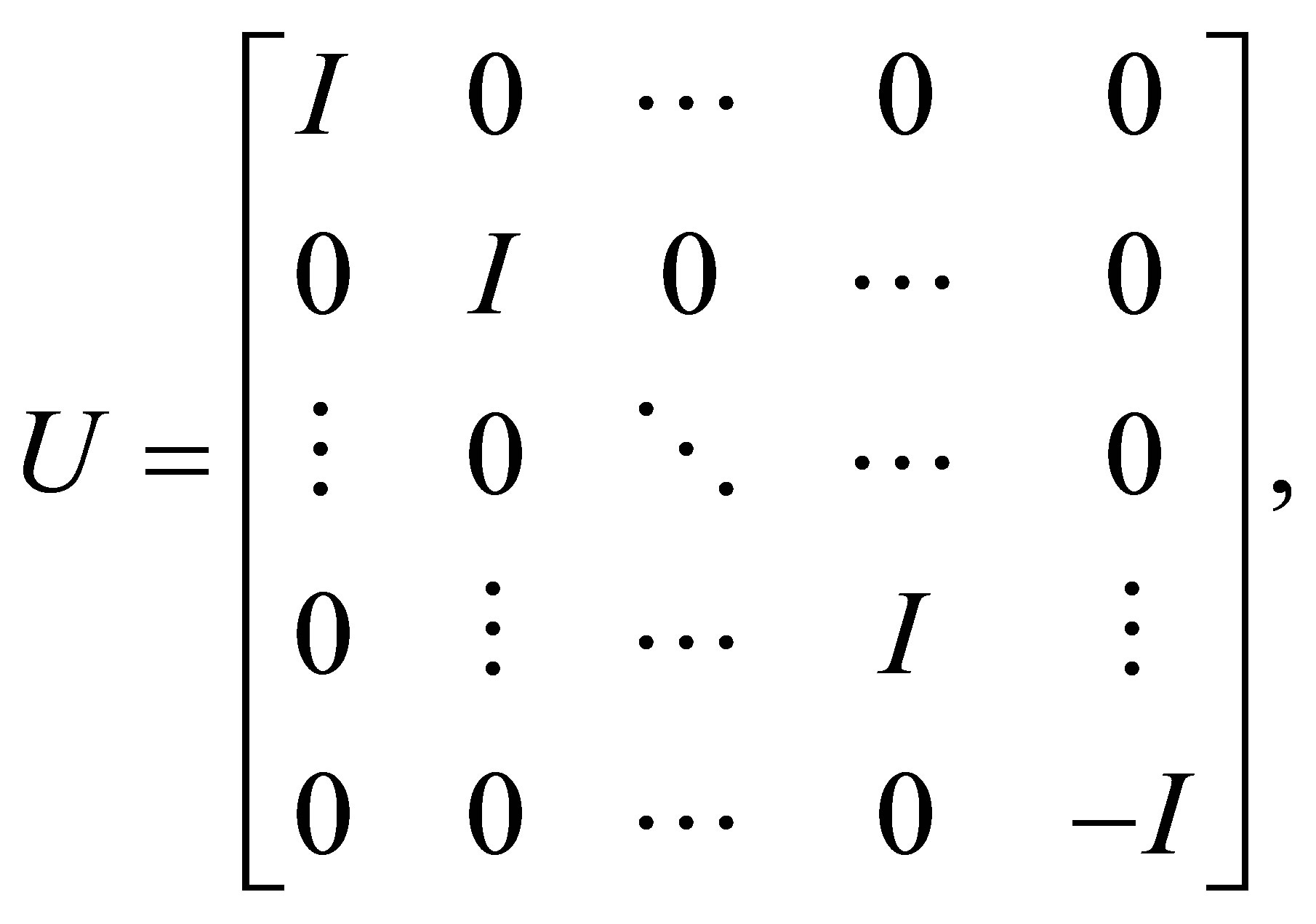 then
then 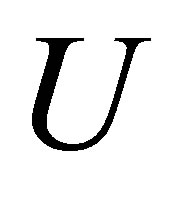 is unitary and
is unitary and
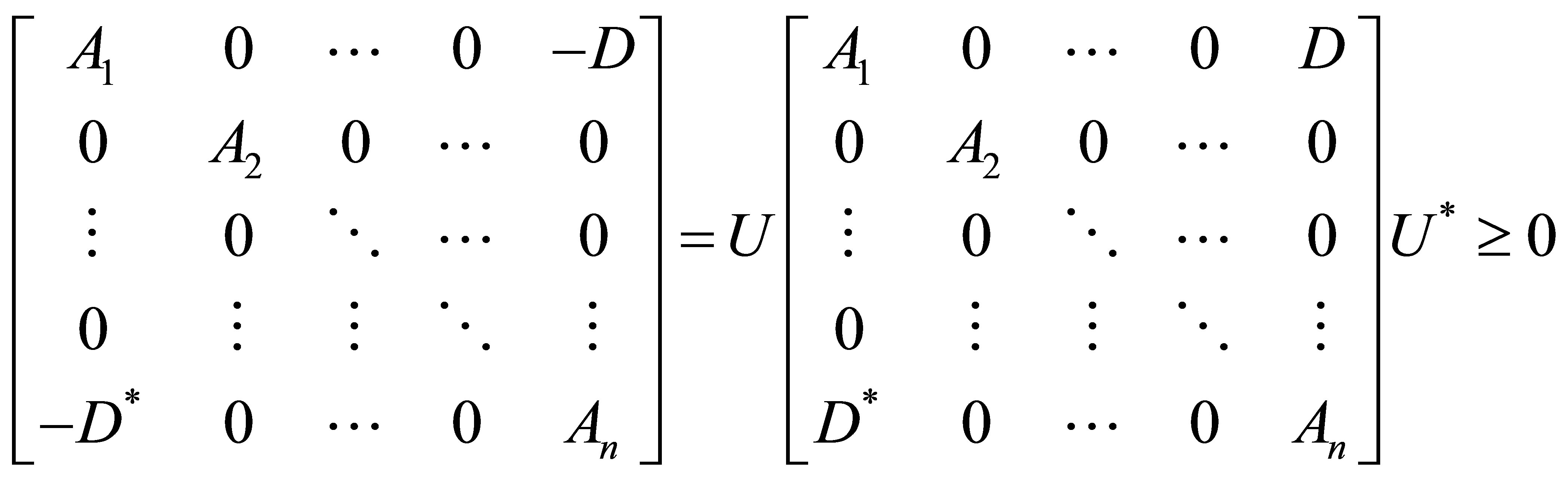
Thus
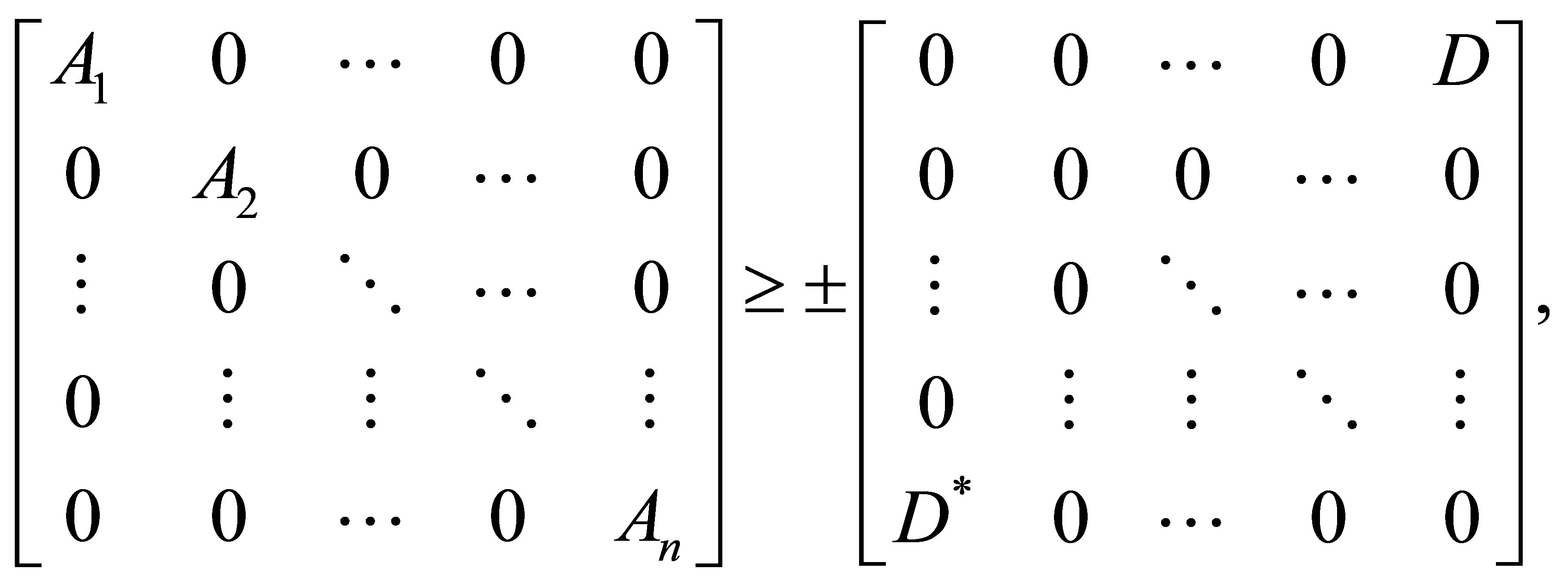
and so by applying the inequality (1.4), we get
 This is equivalent to saying that
This is equivalent to saying that 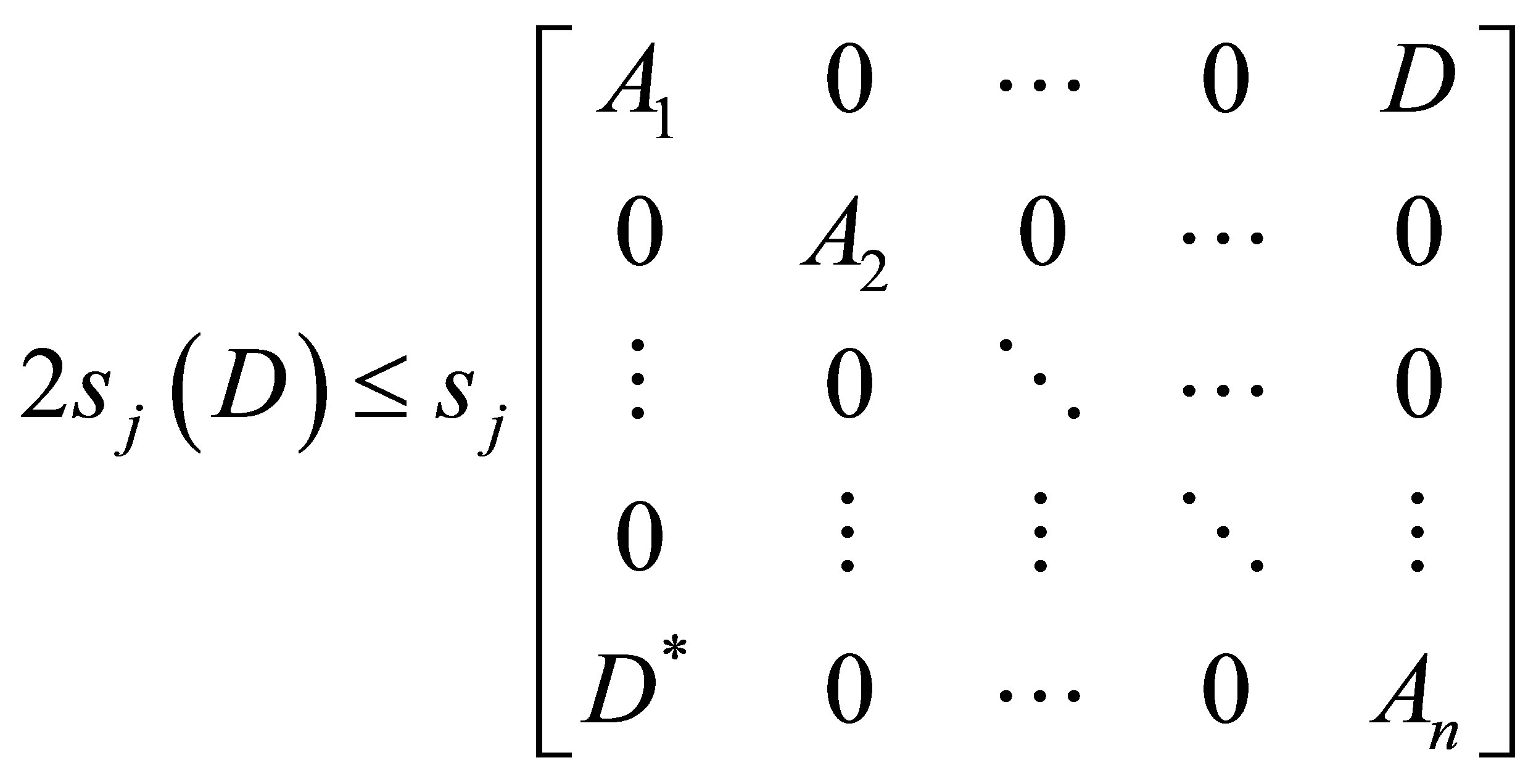
Remark 4. While the proof of the inequality (1.7), given in Theorem 2.3 is based on the inequality (1.4), it can be obtained by applying the inequality (1.6) to the positive operators
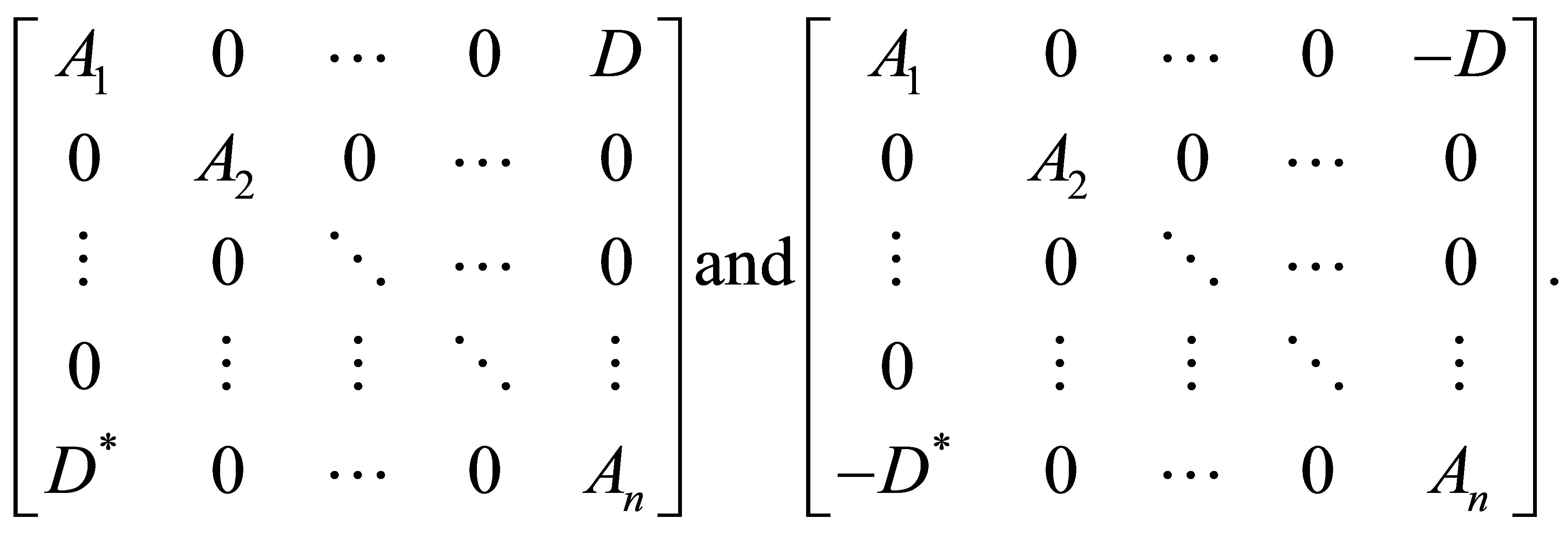
Now, we prove that the inequalities (1.4) and (1.7) are equivalent.
Theorem 2.4. The following statements are equivalent:
(i) Let 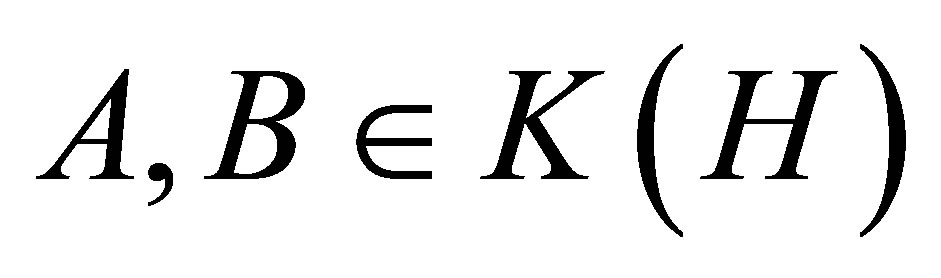 such that
such that  is self-adjoint,
is self-adjoint, 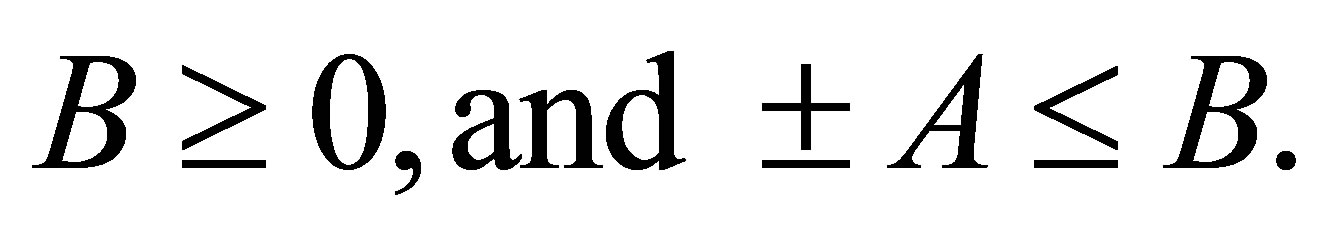 Then
Then
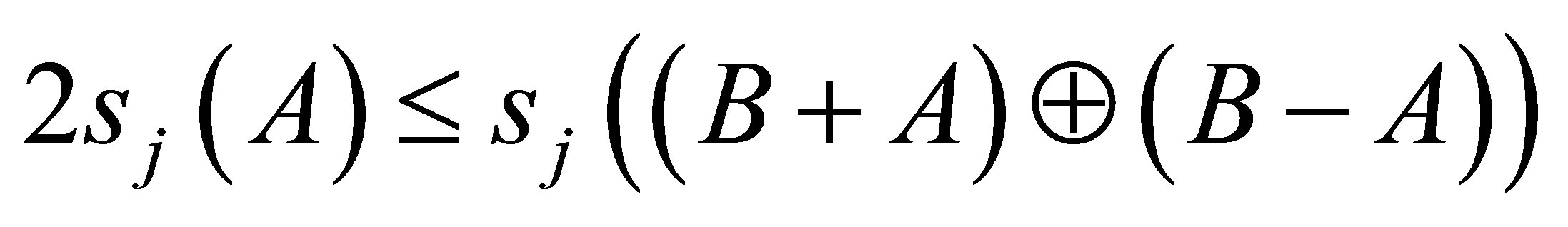
(ii) Let 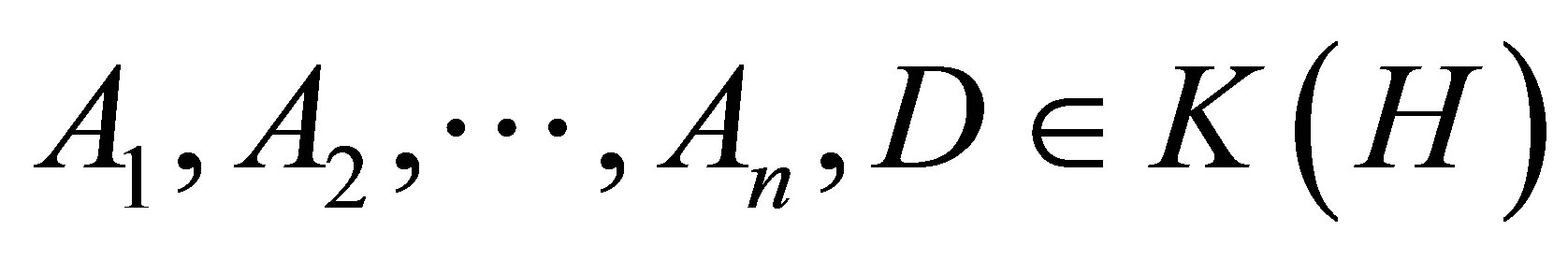 such that
such that

Then 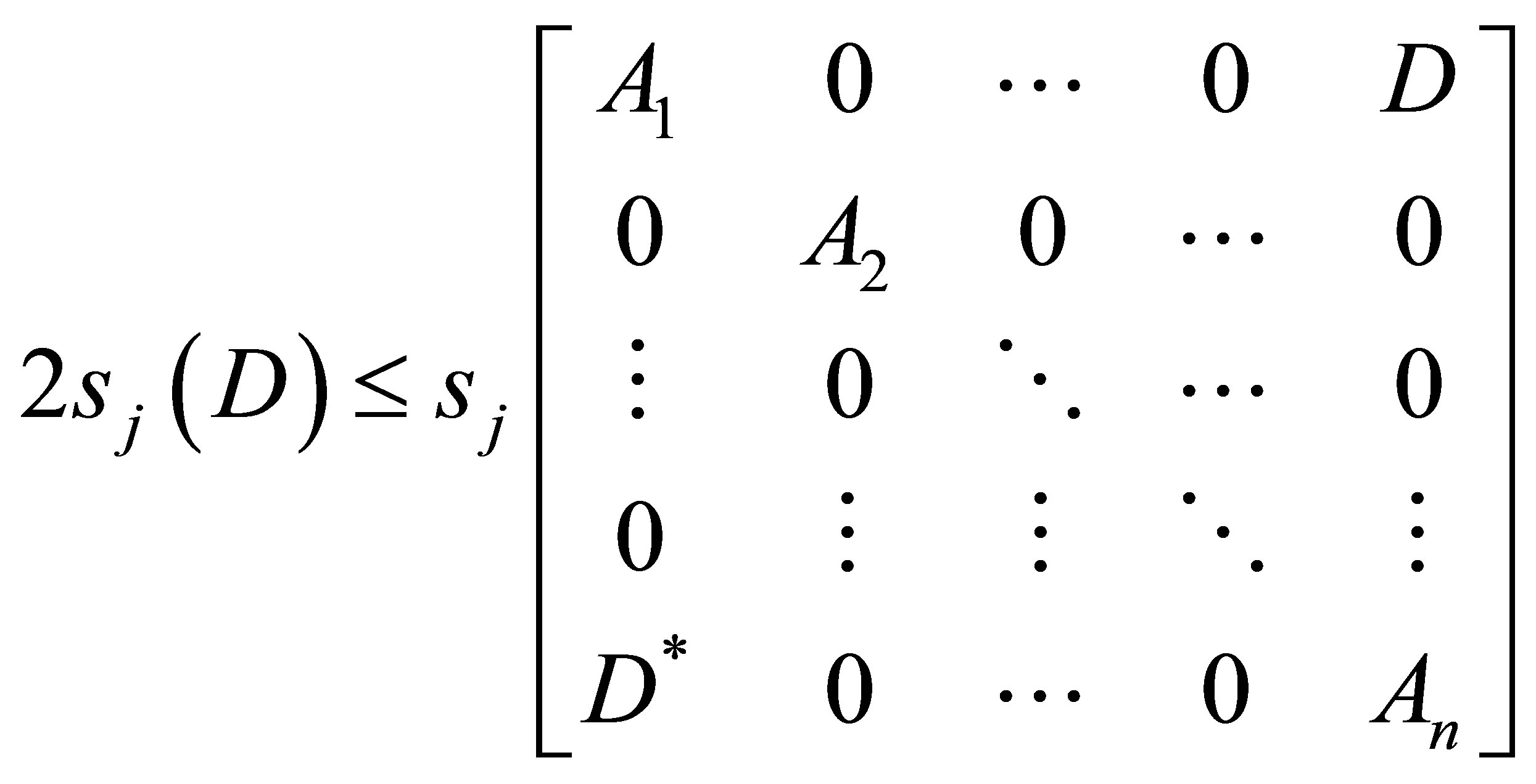
Proof.  This implication follows from the proof of Theorem 2.3.
This implication follows from the proof of Theorem 2.3.
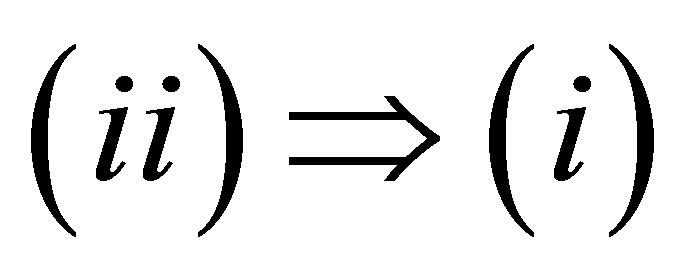 Let
Let 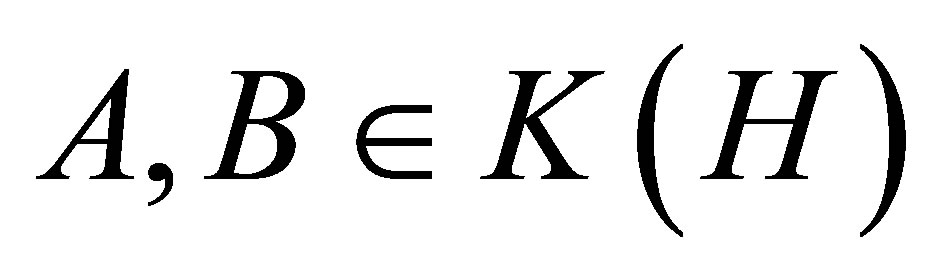 such that
such that  is selfadjoint,
is selfadjoint, 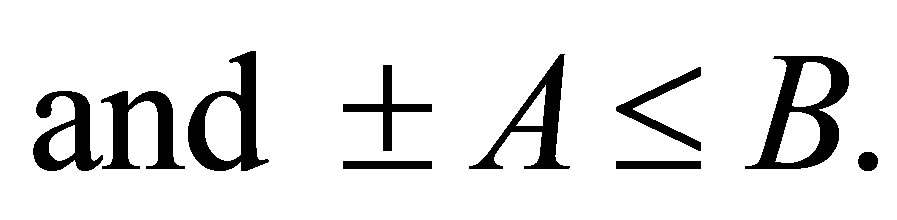
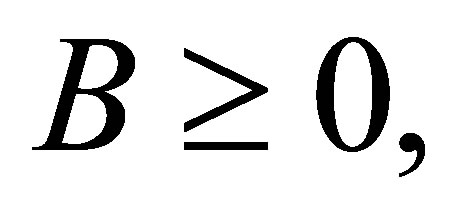 Then the matrix
Then the matrix
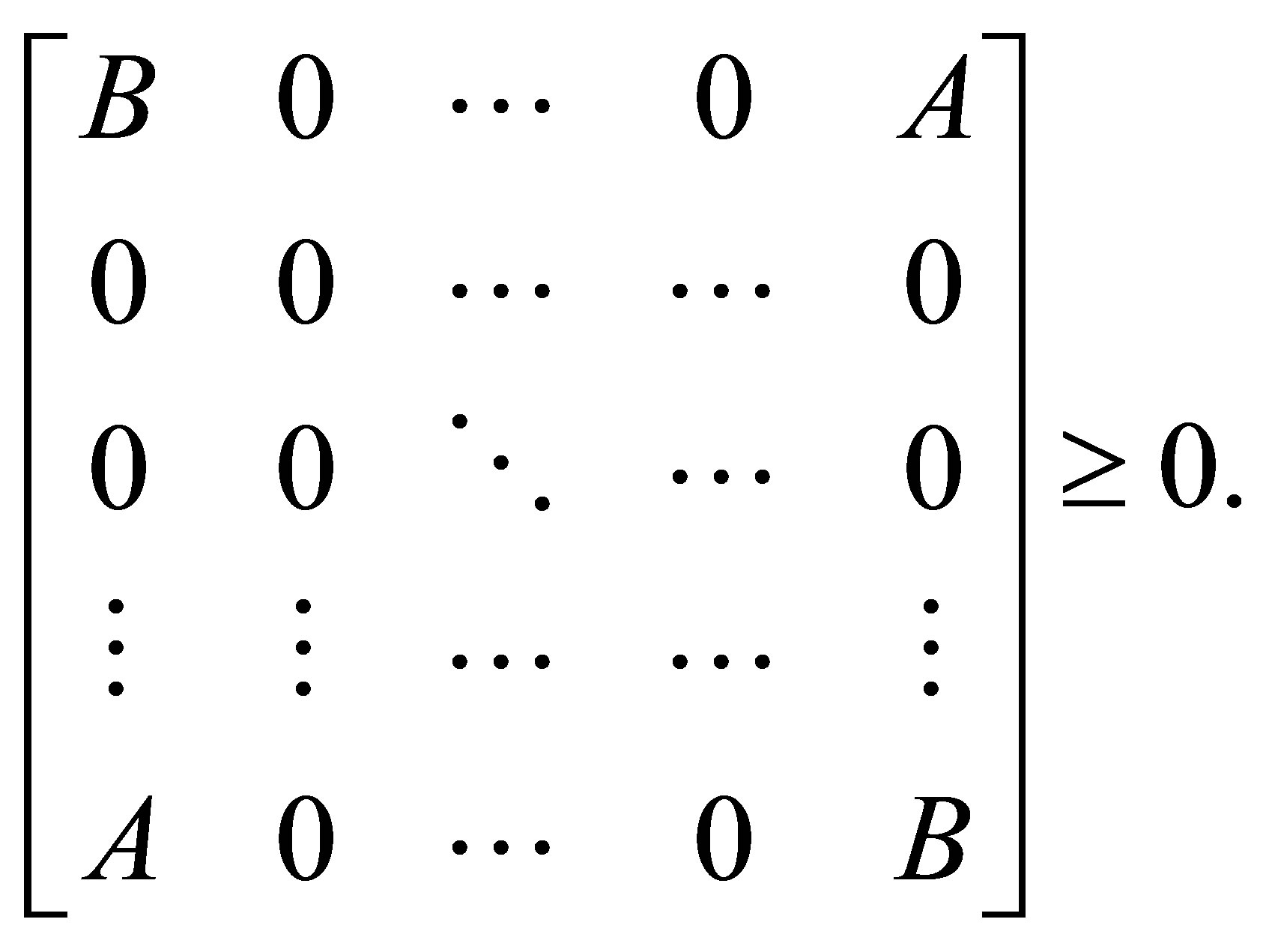
In fact, if 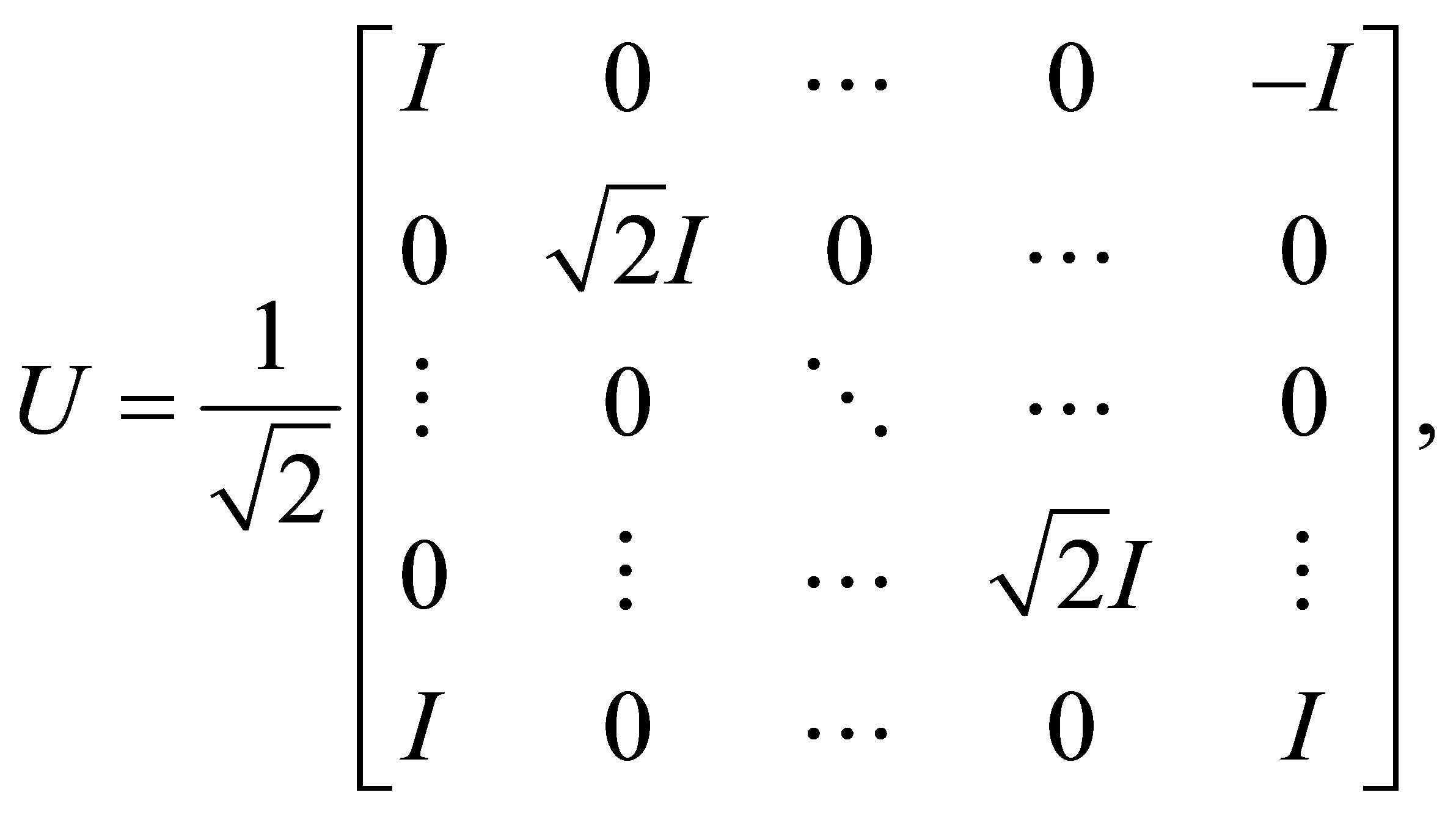 then
then  is unitary and
is unitary and
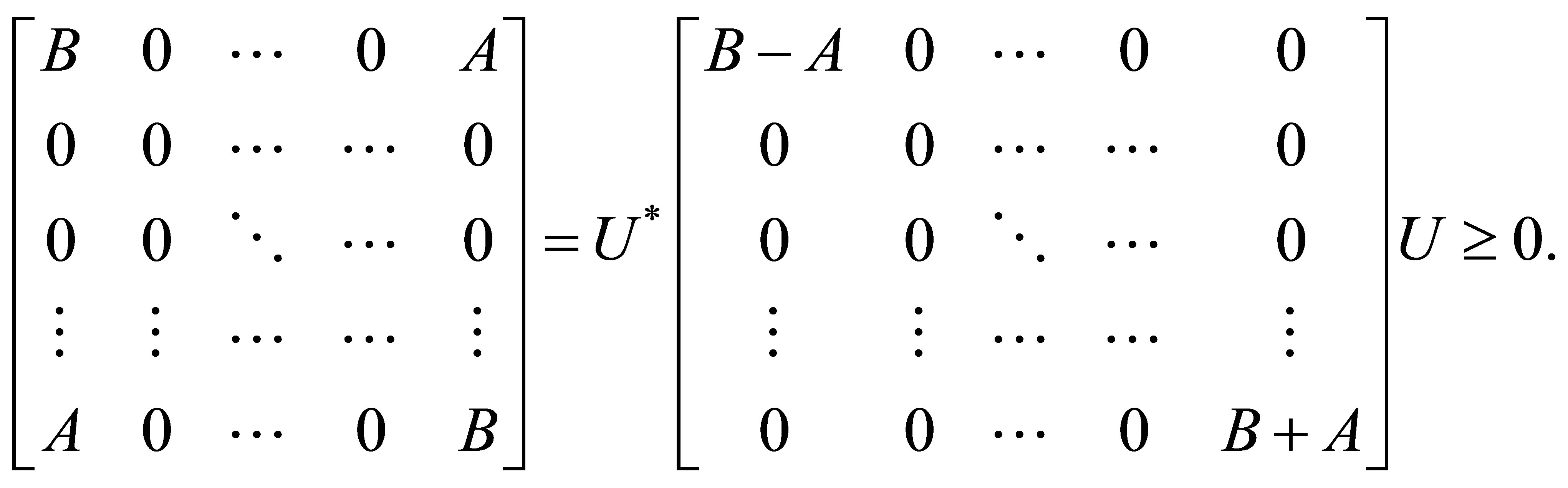
Thus, by applying (ii) we get
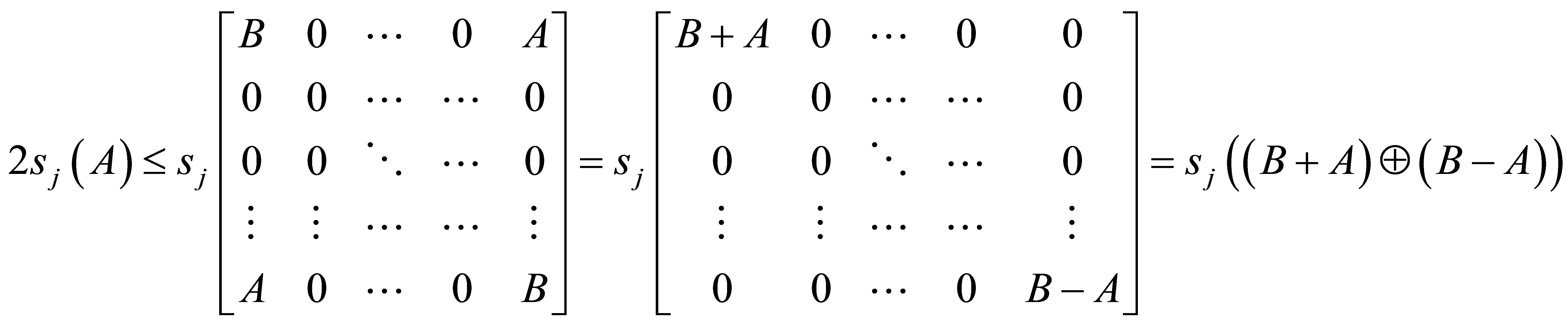
Remark 5. From equivalence of inequalities (1.4) and (1.7) in Theorem 2.4, and equivalence of the inequalities (1.1), (1.2), (1.3), (1.4), (1.5), and (1.6) in Remark 3, we get that the inequalities (1.1), (1.2), (1.3), (1.4), (1.5), (1.6) and (1.7) are equivalent.
Our third singular value inequality is equivalent to the inequalities (1.8) and (1.9).
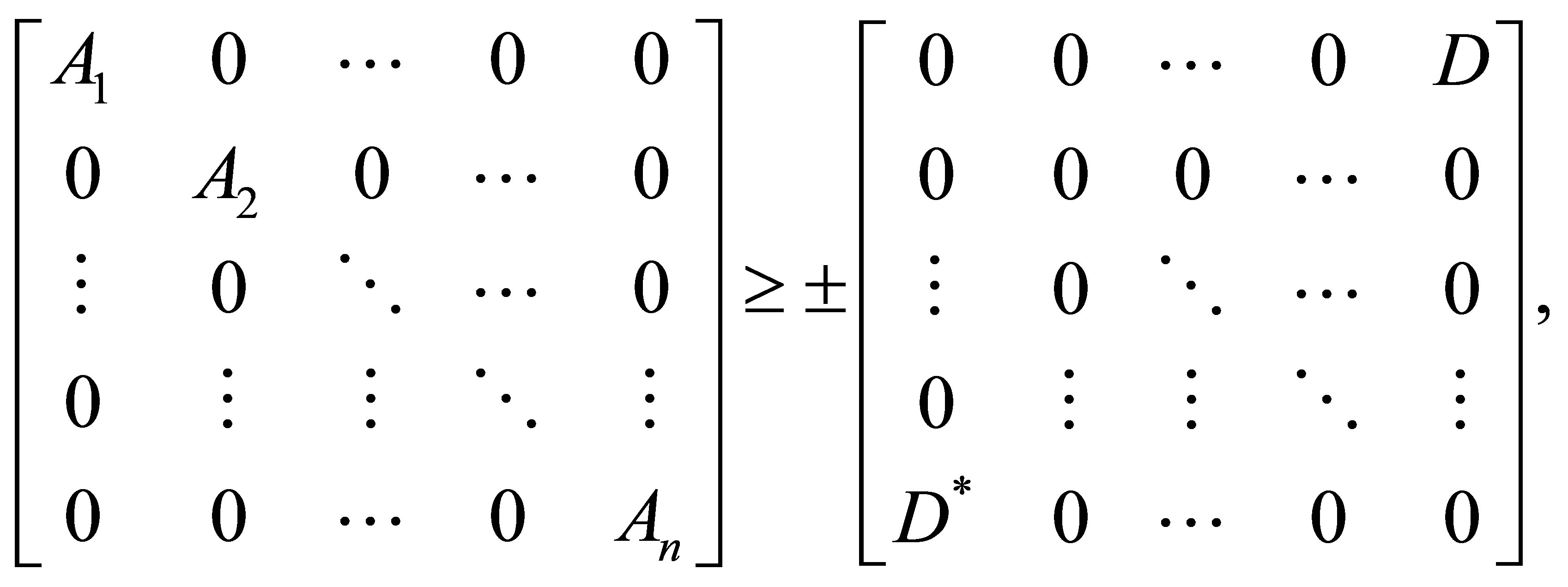
Theorem 2.5. Let 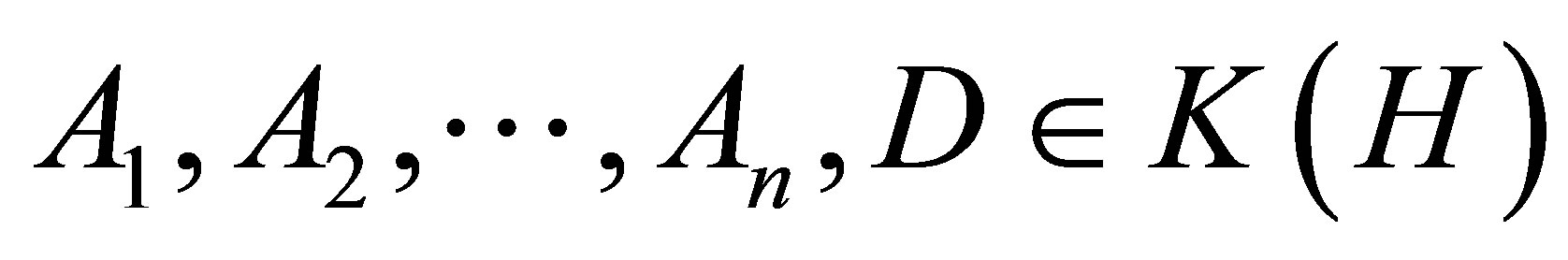 such that
such that
 Then
Then
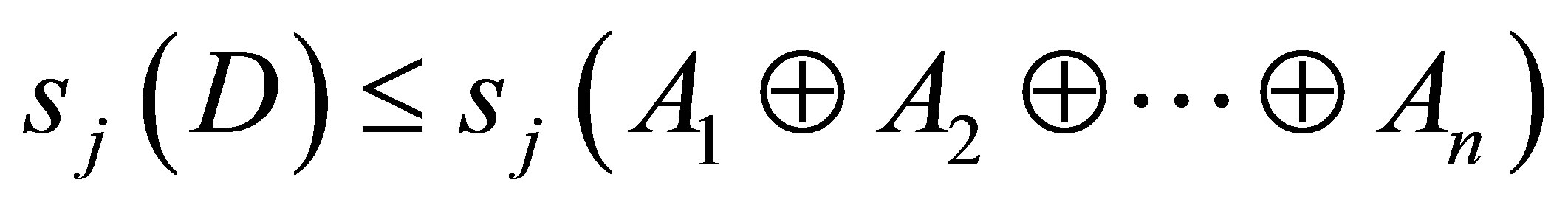
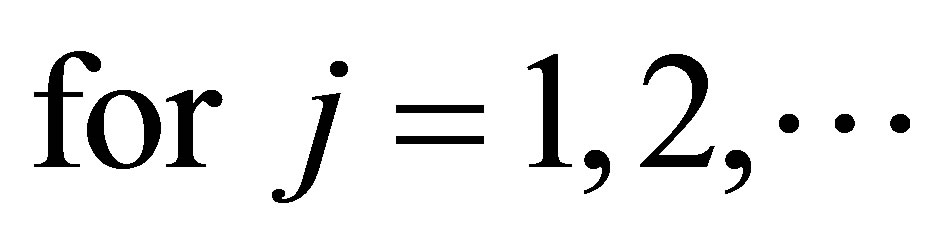
Proof. As in the proof of Theorem 2.3., we have
and so by applying the inequality (1.8), we get

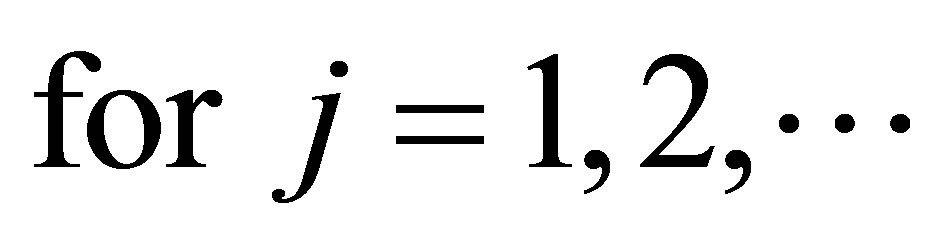 This is equivalent to saying that
This is equivalent to saying that 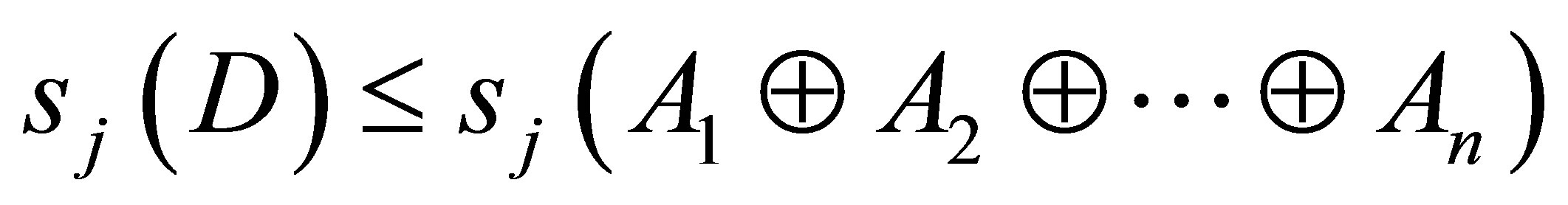
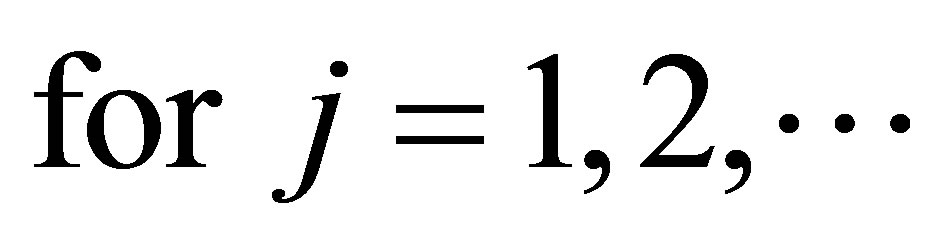
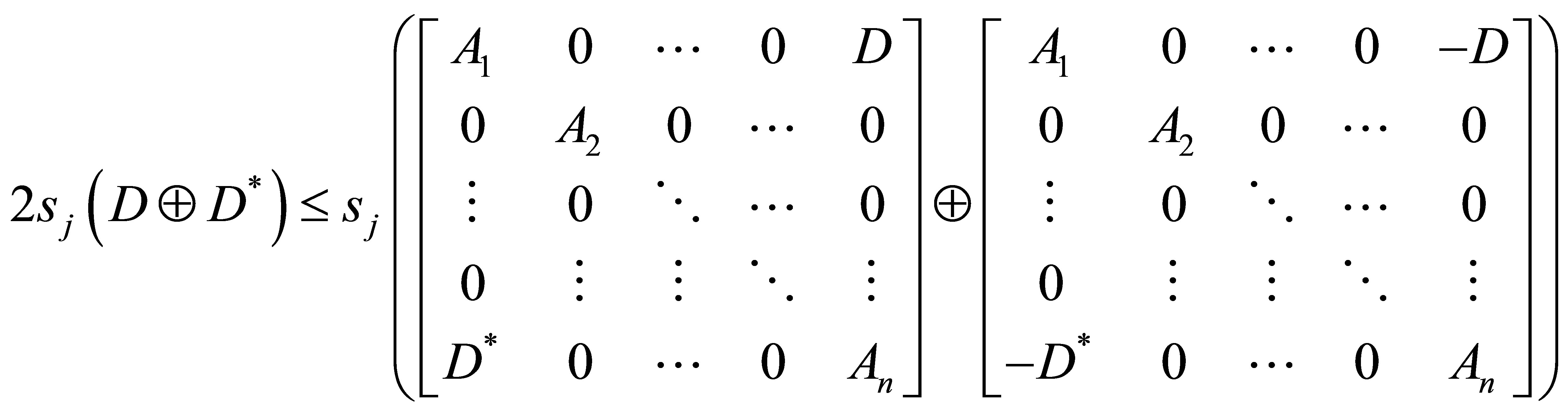
Remark 6. While the proof of the inequality (1.10), given in Theorem 2.5 is based on the inequality (1.8), it can be obtained by employing the inequality (1.7) as follows:
If  Then
Then
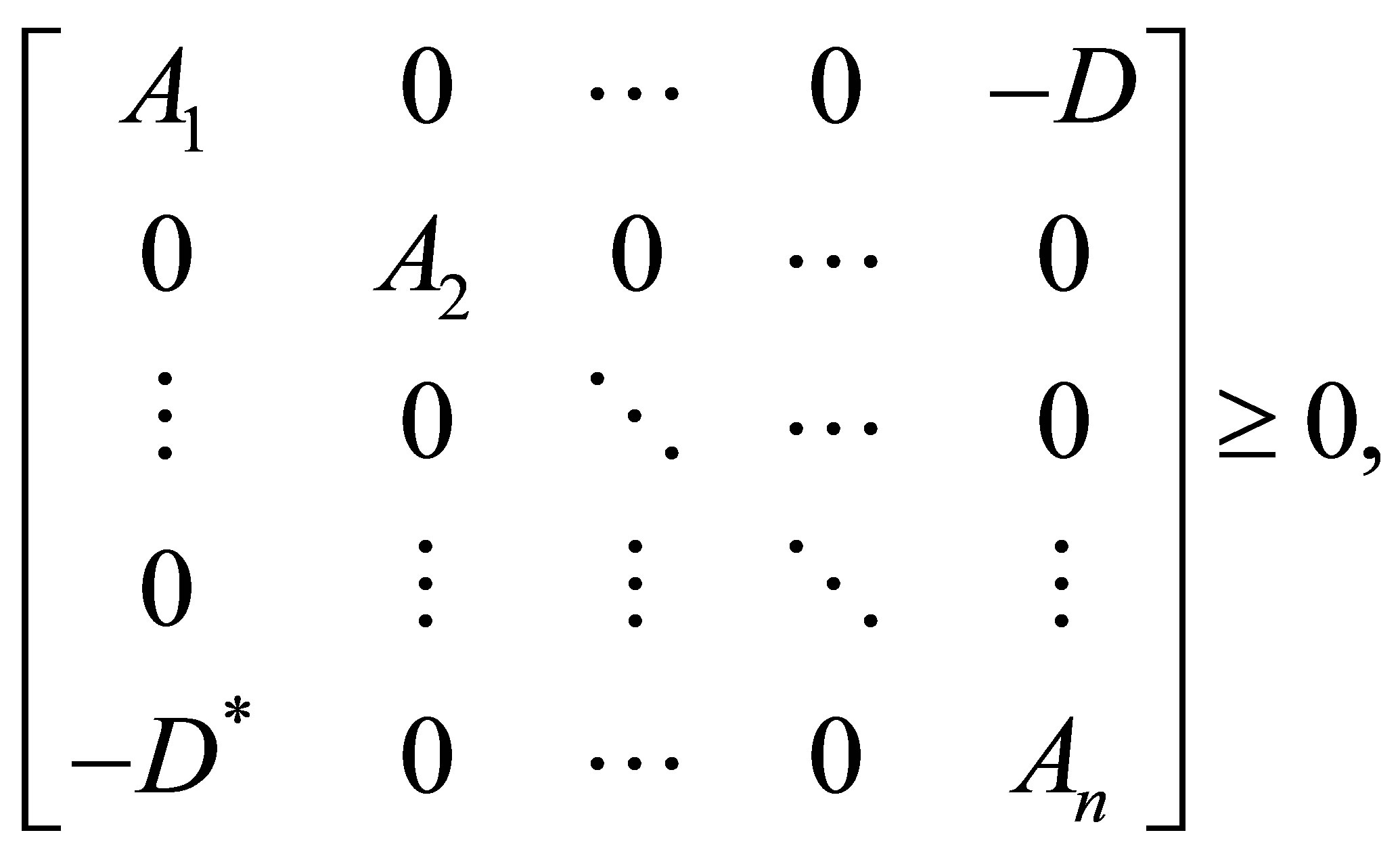 and so
and so

Following Weyl’s monotonicity principle, we have
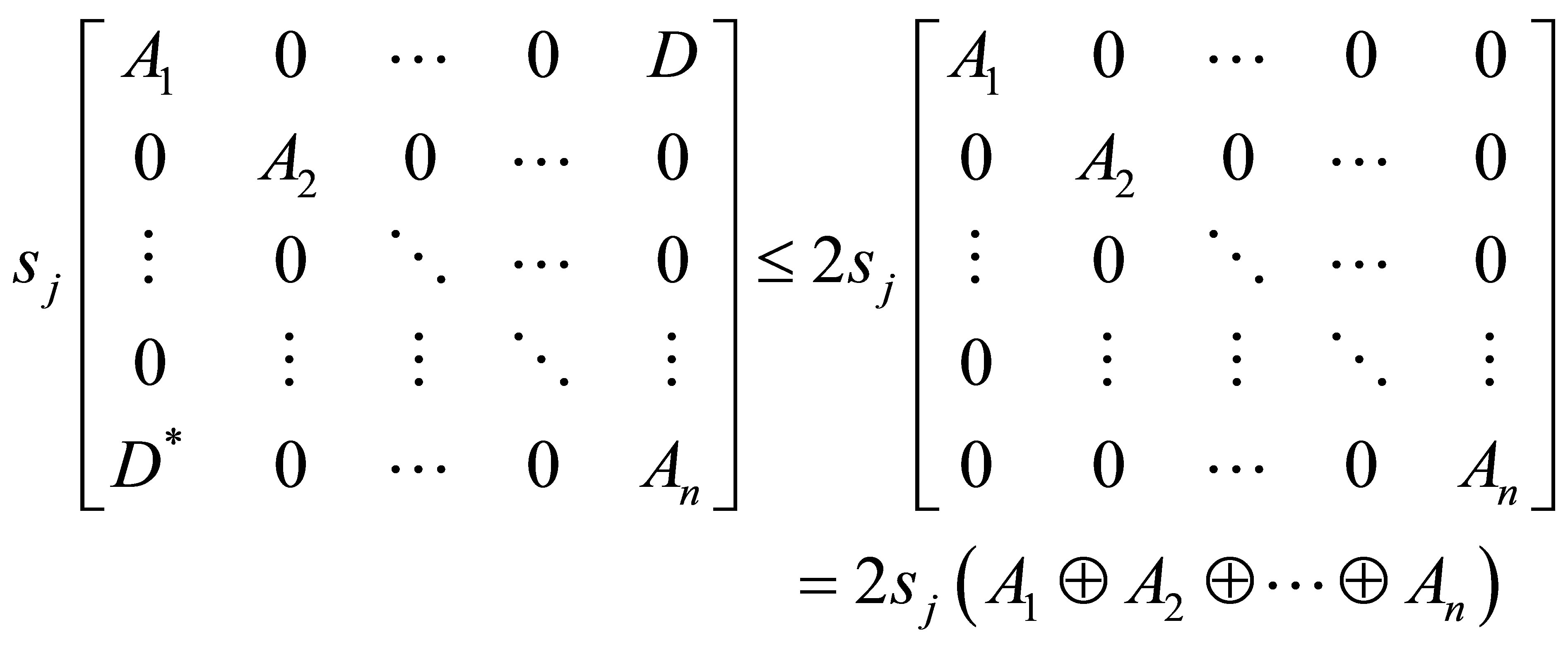
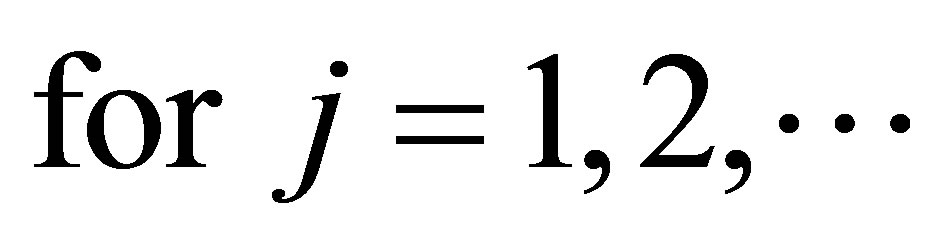 Chaining this with the inequality (1.7), yields the inequality (1.10).
Chaining this with the inequality (1.7), yields the inequality (1.10).
Now, we prove that the inequalities (1.8) and (1.10) are equivalent.
Theorem 2.6. The following statements are equivalent:
(i) Let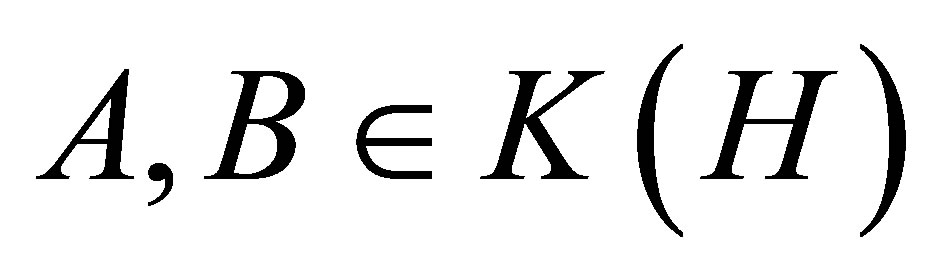 , such that
, such that  is self-adjoint,
is self-adjoint, 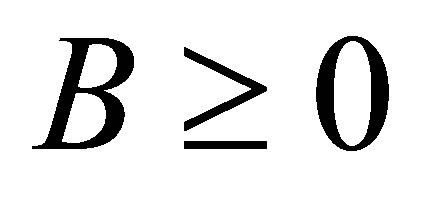 , and
, and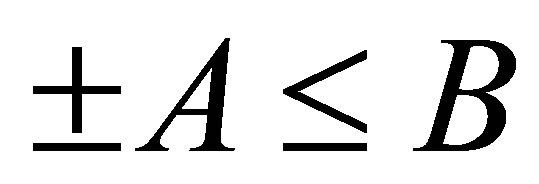 , then
, then
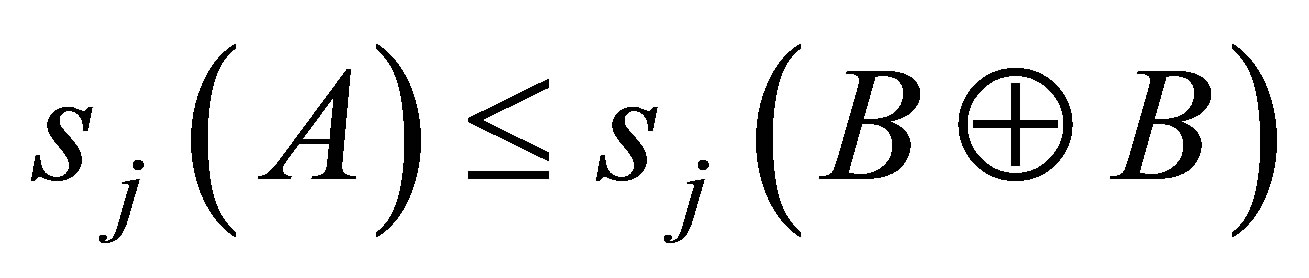
(ii) 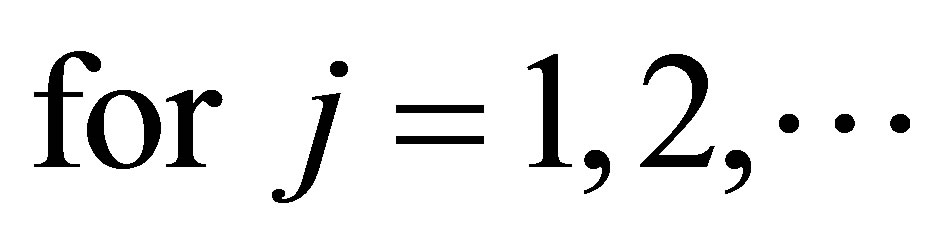
(iii) Let 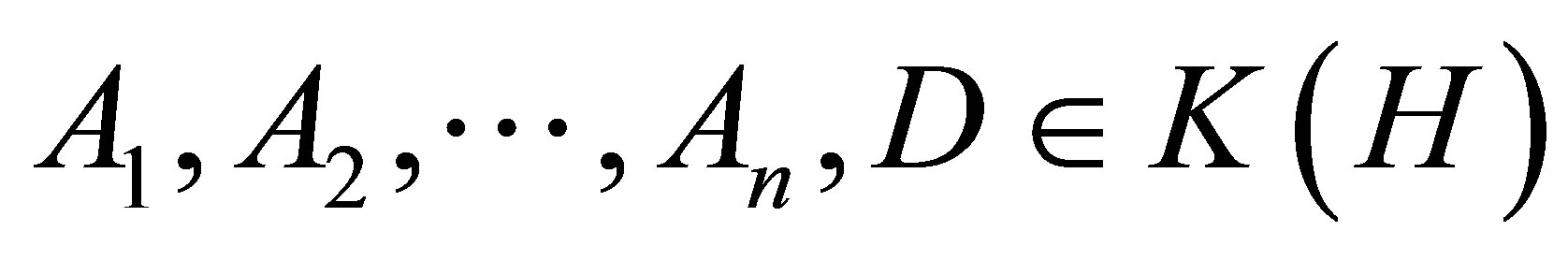 such that
such that
 Then
Then
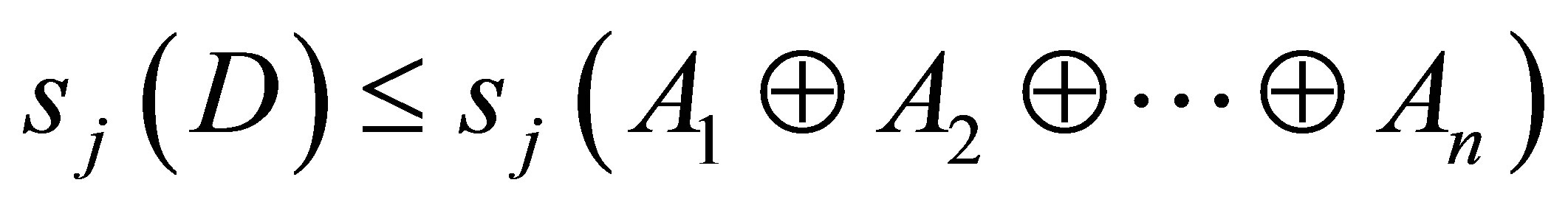
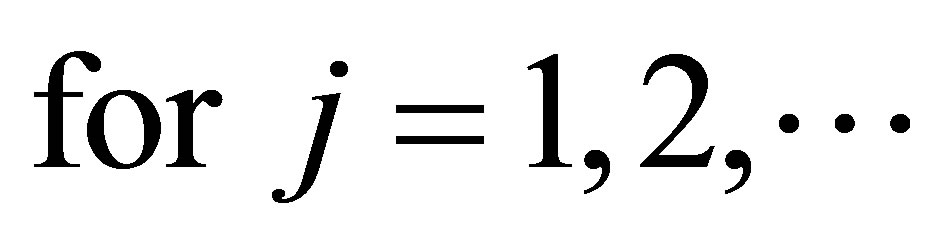
Proof.  This implication follows the proof of Theorem 2.5.
This implication follows the proof of Theorem 2.5.
 As in the proof of Theorem 2.4, if
As in the proof of Theorem 2.4, if  is self-adjoint,
is self-adjoint, 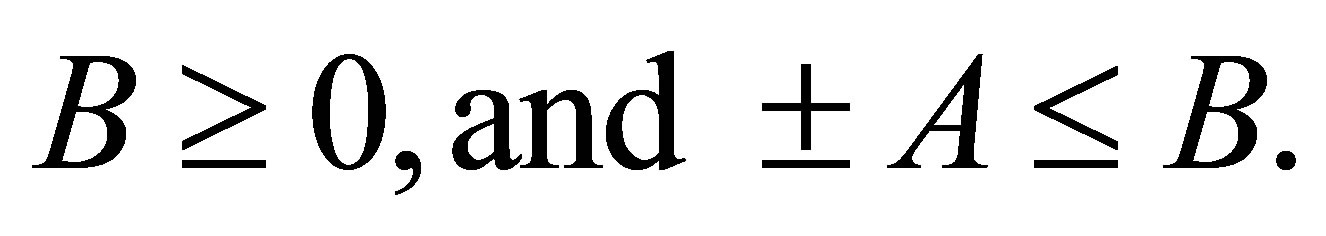 Then
Then
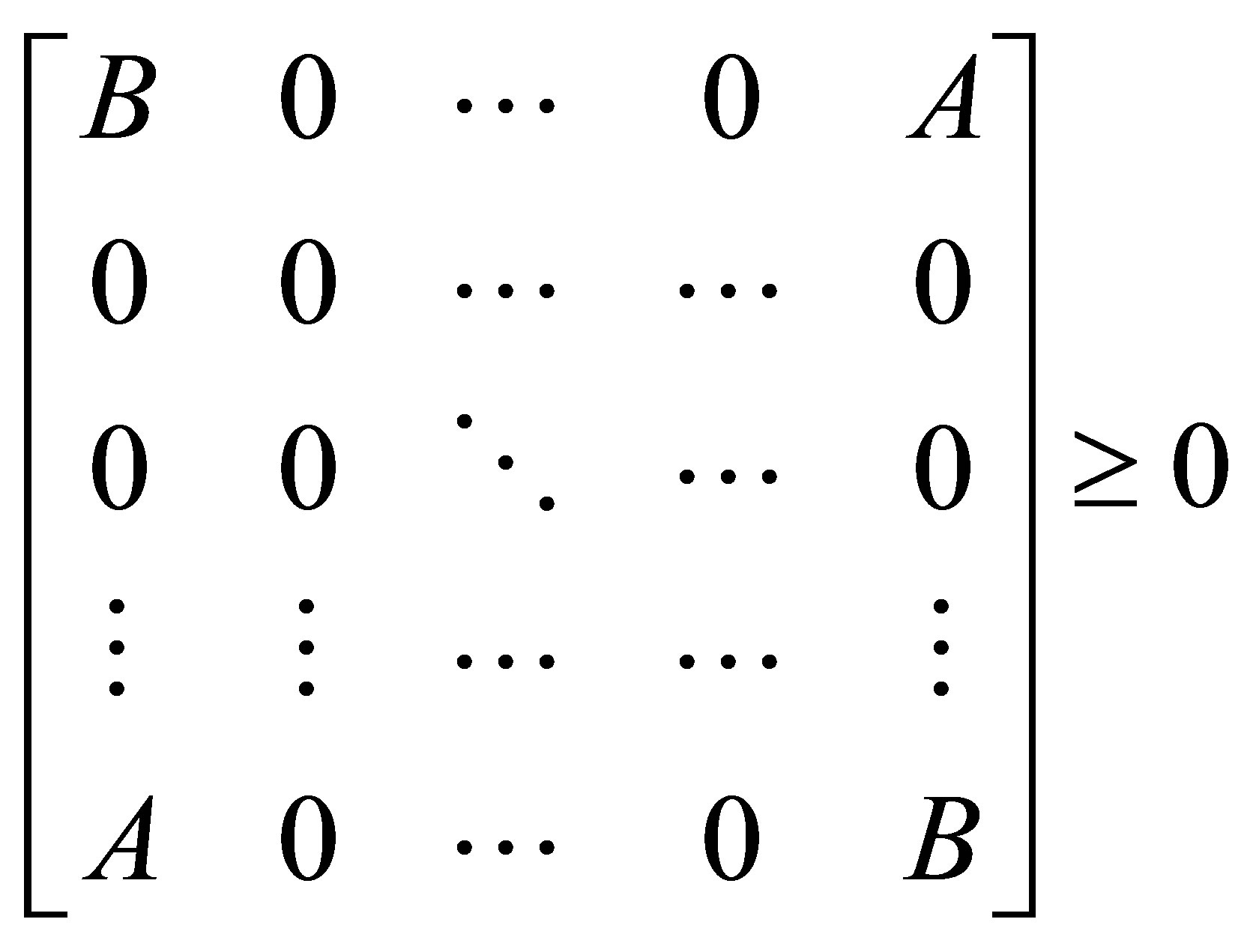 .
.
Thus, by (ii) we have 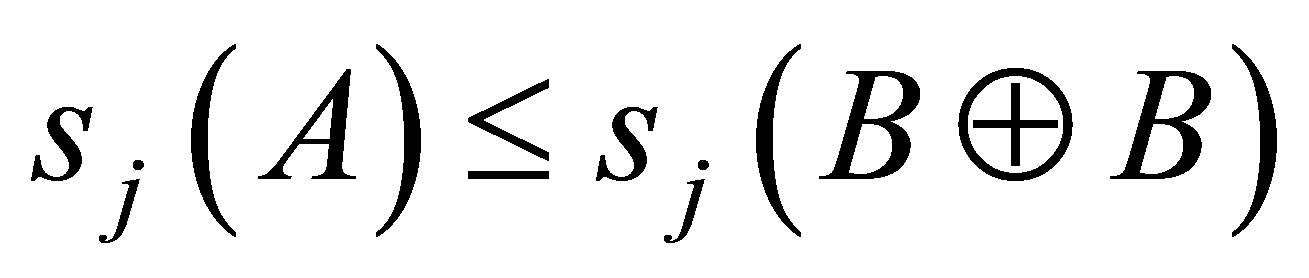
Remark 7. From equivalence of inequalities (1.8) and (1.10) in Theorem 2.6, and equivalence of inequalities (1.8) and (1.9) in [5], we get that the inequalities (1.8), (1.9), and (1.10) are equivalent.