1. Introduction
Measuring biological growth has been important in many fields. Many researchers have contributed in developing relevant models: [1] for Brody function; [2] for Von Bertalanffy function; [3,4] for Richards function; [5] for Gompertz function; [6-8] for Logistic function; [6,9-11] for Generalized Logistic; [12,13] for Weibull function; [1,14] for Monomolecular function.
The mathematical representation of the relative growth is described by the ordinary differential equation (ODE) or rate-state equation
 (1)
(1)
Here  is representing growth function and
is representing growth function and  is relative rate function at time
is relative rate function at time . This ordinary differential equation has many solutions among which some are studied in this paper. The growth models have been widely used in many biological growth problems including: in animal sciences [1,5,7,8,15,16] and in forestry [17,18]. Simulation studies by [19] indicate that such growth functions are so flexible to wrongly fit to given data set and recommends more care while selecting the models.
. This ordinary differential equation has many solutions among which some are studied in this paper. The growth models have been widely used in many biological growth problems including: in animal sciences [1,5,7,8,15,16] and in forestry [17,18]. Simulation studies by [19] indicate that such growth functions are so flexible to wrongly fit to given data set and recommends more care while selecting the models.
A number of attempts have been made to generalize the growth models. For example, [17] modified the ODE
(1) by including one parameter  as:
as:
 from which some growth models are derived. Moreover, they have shown that the model has upper limit but no inflection point when
from which some growth models are derived. Moreover, they have shown that the model has upper limit but no inflection point when ; and has both upper limit and inflection point for
; and has both upper limit and inflection point for .
.
[18] defined 9-parameters model as: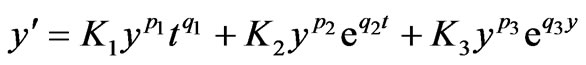 . The first two terms include all commonly known growth functions except Weibull, and so they included to the third term to account for it.
. The first two terms include all commonly known growth functions except Weibull, and so they included to the third term to account for it.
The generalized logistic function has been studied by some researchers [6,9-11]. Eberhardt and Breiwick [9] applied the models to growth of birds and mammals populations.
In the current paper, we provide a new single generalized growth model as solution of the ODE (1) consisting of eight parameters. It can also serve for model selection purposes. We also study the mathematical relationships among the models presented herein. Inflection points of the models are discussed.
2. Koya-Goshu Growth Function as a Generalization of Growth Functions
In this section we define a new generalized growth function, named as Koya-Goshu growth function and show how it accommodates the commonly known growth models such as: Logistic, Generalized Logistic, Gompertz, Brody, Monomolecular, Mitscherlich, Von Bertalanffy, Richards, Generalized Weibull and Weibull functions.
The new generalized growth function, Koya-Goshu growth function, is defined as
 (2)
(2)
Here the parameters are defined as follows:
 is derived from
is derived from 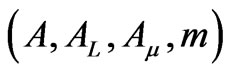
 , A is upper asymptote of
, A is upper asymptote of 
 : Lower asymptote of
: Lower asymptote of 
 Growth rate parameter
Growth rate parameter
 Time shift, a constant
Time shift, a constant
 Time scale, a constant
Time scale, a constant
 Shape parameters of the growth function,
Shape parameters of the growth function, 
2.1. Description of Koya-Goshu Growth Model
The Koya-Goshu growth model is 8-parameter  function. The model is a more general solution of the ODE (1). Note that
function. The model is a more general solution of the ODE (1). Note that  and equal at time
and equal at time  Regarding the quantity
Regarding the quantity ,
,  as
as ;
;  as
as ;
;  as
as . The quantity
. The quantity  can assume any value in the open interval
can assume any value in the open interval  for Richards, and in (0, 1) for both Von Bertalanffy and Brody. For both Logistic and Gompertz,
for Richards, and in (0, 1) for both Von Bertalanffy and Brody. For both Logistic and Gompertz,  can take any positive real number. For Weibull,
can take any positive real number. For Weibull,  while for generalized Weibull case,
while for generalized Weibull case, .
.
When time  is non-negative, the Koya-Goshu function is well defined for modeling growths. The function represents sigmoid curve for m < 0 and
is non-negative, the Koya-Goshu function is well defined for modeling growths. The function represents sigmoid curve for m < 0 and  any positive odd integer. However, if m > 0 or (m < 0 and
any positive odd integer. However, if m > 0 or (m < 0 and  is any real number other than positive odd integer), the function is well defined growth model for time
is any real number other than positive odd integer), the function is well defined growth model for time  where
where
 . This implies that the function misses lower asymptote in some cases. To account for the asymptote, modification can be made by taking
. This implies that the function misses lower asymptote in some cases. To account for the asymptote, modification can be made by taking  for
for  or can be written as:
or can be written as:

Thus, the Koya-Goshu function in (2) can be generally expressed as:
 (3)
(3)
Here * is used to denote multiplication. Also here
 is a unit step function, where
is a unit step function, where
 if
if  or
or

if
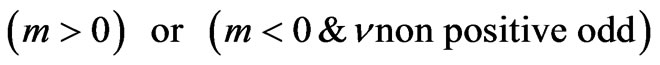
 is a lower bound for the time. Note that
is a lower bound for the time. Note that  with
with  defined by the limit of
defined by the limit of  as time t goes to
as time t goes to . It serves as a lower asymptote of
. It serves as a lower asymptote of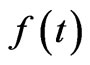 .
.
Note that the Koya-Goshu function is defined at all points  in
in  -plane. All the commonly known growth curves lay along the line
-plane. All the commonly known growth curves lay along the line  or
or  only. The function extends the inclusion of other points in the plane than these points. This means that it is so flexible that one can select any other curves than the commonly used ones.
only. The function extends the inclusion of other points in the plane than these points. This means that it is so flexible that one can select any other curves than the commonly used ones.
We show that the Koya-Goshu model accommodates all commonly known growth functions. We have given detailed analysis of the growth models and how they are related to each other. The Richards function is a general form of Brody, Von Bertalanffy, Classical Logistic and Gompertz. Brody is same as Monomolecular and Mitscherlich functions. Brody is a special case of Weibull function. All the relations are illustrated by flow chart in Figure 1. Detailed derivations of the function  and relative growth rate
and relative growth rate 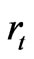 are given in Appendix A.
are given in Appendix A.
Some selected plots are illustrated in Figures 2-5.
2.2. Properties of the Koya-Goshu Function
The function represents both increasing and decaying growths (see Figure 2(a), 3(a), 4(a), 5(a)). It is increasing for  and decaying for
and decaying for . This means that increasing or decaying of the growth is influenced by sign (positive or negative) of
. This means that increasing or decaying of the growth is influenced by sign (positive or negative) of , irrespective of the values of m.
, irrespective of the values of m.
The function represents increasing growths with upper asymptote but no lower asymptote:
1) For all positive combination values of both  and
and  (see Figures 2(a), 3(a))
(see Figures 2(a), 3(a))
2) For all small negative values of  and large positive values of
and large positive values of 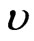 (see Figure 4(a)).
(see Figure 4(a)).
The function represents increasing growths with both upper and lower asymptotes:
1) For all negative values of m and any (small or large)

Figure 1. Flow chart illustrating the relationships among the generalized and specialized growth functions.
 (a)
(a) (b)
(b)
Figure 2. Plots of (a) growth functions and (b) rate functions with .
.
 (a)
(a)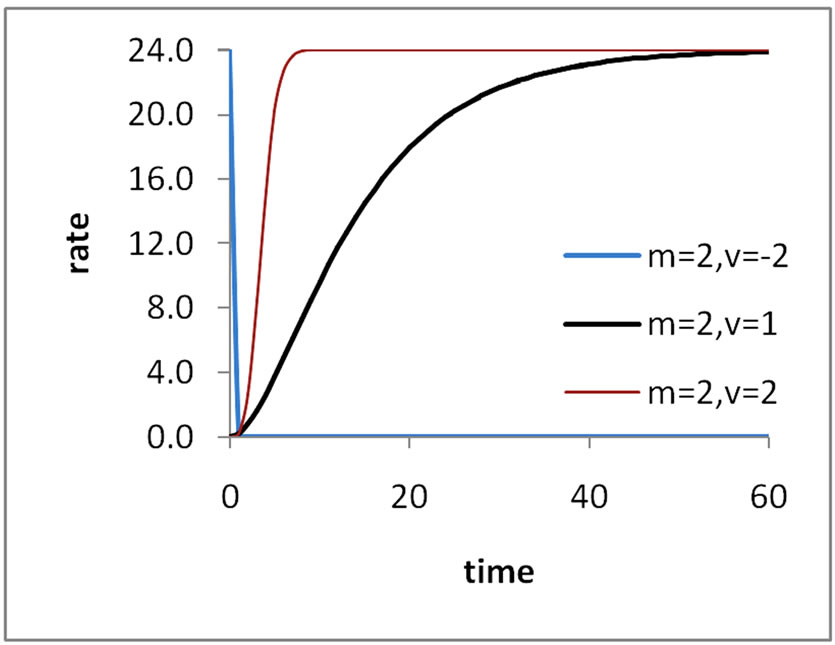 (b)
(b)
Figure 3. Plots of (a) growth functions and (b) rate functions with .
.
positive values of  (see Figure 5(a))
(see Figure 5(a))
2) For all small negative values of  and small positive values of
and small positive values of  (see Figure 4(a)).
(see Figure 4(a)).
The occurrence of either lower and upper asymptotes or only upper asymptotes is influenced by only  but not
but not . Generally, the parameter
. Generally, the parameter  influences growth behavior, while the parameter
influences growth behavior, while the parameter  influences asymptotic behavior of the function.
influences asymptotic behavior of the function.
2.3. Inflection Point of Koya-Goshu Function
We now introduce the definition of inflection points of a curve, and describe the procedure to find inflection points for the growth functions we discuss in this paper. Suppose that the function  is continuous on an open interval containing the point
is continuous on an open interval containing the point . Then the point
. Then the point  is called an inflection point of
is called an inflection point of  provided that
provided that  on one side of
on one side of  and
and  on the other side. At the inflexion point
on the other side. At the inflexion point  itself either
itself either  or
or  does not exist [20].
does not exist [20].
 (4)
(4)
 (5)
(5)
Here, we observe that
 (6)
(6)
Clearly, point of inflection exists in Koya-Goshu function provided the relation (5) is satisfied, since  at that point and also
at that point and also  and
and  are satisfied on the increasing and decreasing sides of that point.
are satisfied on the increasing and decreasing sides of that point.
Here it can be observed that the inflection points of Koya-Goshu function, when the parameters are fixed as 1) , and 2)
, and 2)  perfectly matches with the cases of Generalized logistic functions and Generalized Weibull models, respectively.
perfectly matches with the cases of Generalized logistic functions and Generalized Weibull models, respectively.
For the other cases when , the inflection point for the Koya-Goshu function can be obtained by approximations. For example, using Taylor series expansion up to first order term, the time of inflection is approximated as:
, the inflection point for the Koya-Goshu function can be obtained by approximations. For example, using Taylor series expansion up to first order term, the time of inflection is approximated as:
 (7)
(7)
3. Biological Growth Models and the Parametric Relationships
In this section we studied the parametric relationships among all the biological growth models considered in this paper viz., Koya-Goshu biological growth model, Generalized Logistic, Particular case of Generalized Logistic, Richards, Von Bertalanffy, Brody, Logistic, Gompertz, Generalized Weibull, Weibull Monomolecular, and Mitscherlich functions. The relationships identified have been exhibited through a flowchart.
3.1. Generalized Logistic Function
The Generalized Logistic function as given in [21] is expressed in its original notations as
 which we now re-express it with same notations used in this paper as
which we now re-express it with same notations used in this paper as
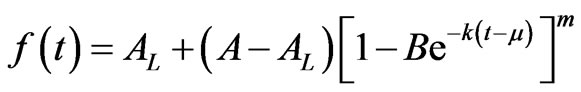 (8)
(8)
by replacing in the equation 

 and
and
 .
.
The Generalized Logistic function (7) is hereby a special case of Koya-Goshu function with  and
and . The parameter B takes the form
. The parameter B takes the form
 . The expression for the relative growth rate function can be computed as
. The expression for the relative growth rate function can be computed as  . Similarly, the expressions for
. Similarly, the expressions for  and
and  are, respectively, given by
are, respectively, given by
 and
and .
.
The single point of inflection occurs when the organism reaches the growth 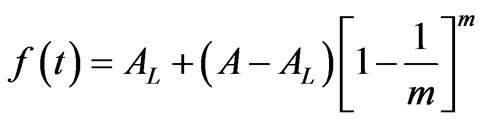
 at time
at time
where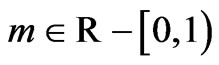 . For
. For , inflexion point does not exist.
, inflexion point does not exist.
3.2. Particular Case of the Generalized Logistic Function
A function called Particular case of the Generalized Logistic function is defined [21] as
 which we now re-express it with same notations used in this paper as
which we now re-express it with same notations used in this paper as
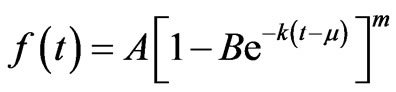 (9)
(9)
by replacing in the equation
 and
and . Note that Equation (8) is a special case of Equation (7) for Generalized Logistic function with
. Note that Equation (8) is a special case of Equation (7) for Generalized Logistic function with  In this case, the parameter
In this case, the parameter 
takes the form as . The expression for the relative growth rate function
. The expression for the relative growth rate function  can be computed as
can be computed as
 . Similarly, the expressions for
. Similarly, the expressions for  and
and  are respectively given by
are respectively given by
 and
and . The single point of inflection occurs when the organism reaches the growth
. The single point of inflection occurs when the organism reaches the growth 
 at time
at time

For , inflexion point does not exist.
, inflexion point does not exist.
3.3. Richards Function
The Richards function is defined as in the usual notations (Richards, 1959) as
 (10)
(10)
Here . The Richards function can be directly derived from the ODE or rate-state Equation (1)
. The Richards function can be directly derived from the ODE or rate-state Equation (1)
with relative rate function . The Richards function becomes special case of Koya-Goshu growth model with
. The Richards function becomes special case of Koya-Goshu growth model with . Here the parameter m can assume any non-zero real number. The expressions for
. Here the parameter m can assume any non-zero real number. The expressions for  and
and  are given by respectively
are given by respectively  and
and  The single point of inflection occurs when the growth reaches
The single point of inflection occurs when the growth reaches  of its final growth, i.e.
of its final growth, i.e. 
 at time
at time 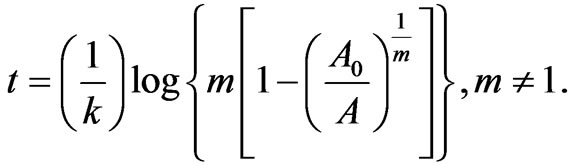
3.4. Von Bertalanffy Function
Von Bertalanffy is defined (Bertalanffy, 1957) as
 (11)
(11)
It is a special case of Richards function (5) with  and a special case of Koya-Goshu growth model with
and a special case of Koya-Goshu growth model with . Here
. Here
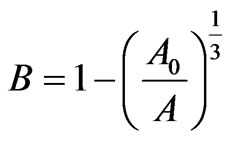 . It can also be derived from ODE (1) with relative rate function
. It can also be derived from ODE (1) with relative rate function . For Von Bertalanffy function
. For Von Bertalanffy function  and
and  are respectively given by
are respectively given by  and
and  . Here the single point of inflection occurs when the growth reaches
. Here the single point of inflection occurs when the growth reaches 
 of its final growth, i.e.
of its final growth, i.e.

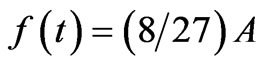 at time
at time .
.
3.5. Brody Function
Brody is defined (Brody, 1945) as:
 (12)
(12)
It is a special case of Richards function (9) with  and a special case of Koya-Goshu growth model with.
and a special case of Koya-Goshu growth model with. . It can also be derived from ODE (1) with rate function
. It can also be derived from ODE (1) with rate function . Here
. Here  and
and  are respectively given by
are respectively given by and
and
 . Brody growth function does not possess a point of inflexion since
. Brody growth function does not possess a point of inflexion since  is not satisfied for any value of
is not satisfied for any value of .
.
3.6. Logistic Function
The classical Logistic function (Nelder, 1961) is defined as:
 (13)
(13)
Here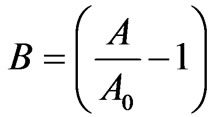 . The Logistic function is a special case of 1) Richards function (9) with
. The Logistic function is a special case of 1) Richards function (9) with 
2) Particular case of logistic function (8) with 
3) Generalized logistic function (7) with 
4) Koya-Goshu function (2) with  .
.
The Logistic function can be derived from the ODE (1) with rate function
 . Here,
. Here,  and
and  are respectively given by
are respectively given by  and
and  . The single point of inflection occurs when the growth reaches half of its final growth
. The single point of inflection occurs when the growth reaches half of its final growth  at time
at time .
.
3.7. Gompertz Function
The Gompertz function (Winsor, 1932) is defined as
 (14)
(14)
where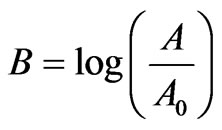 .
.
It is shown to be a special case of 1) Richards function (9) with  2) Particular case of logistic function (8) with
2) Particular case of logistic function (8) with  3) Generalized logistic function (7) with
3) Generalized logistic function (7) with ,
,  4) Koya-Goshu function (2) with
4) Koya-Goshu function (2) with . The Gompertz function can be derived from the ODE (1) with rate function
. The Gompertz function can be derived from the ODE (1) with rate function . Here,
. Here,
 ,
,
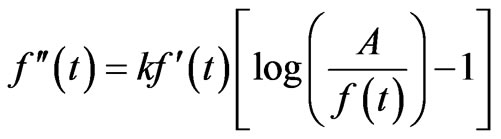 and the single point of inflection occurs when the growth reaches
and the single point of inflection occurs when the growth reaches  of its final growth, i.e.,
of its final growth, i.e.,  at time
at time
 .
.
3.8. Generalized Weibull Function
The Weibull function is generalized and named here by Generalized Weibull function as
 (15)
(15)
where . The generalized Weibull is a special case of Koya-Goshu growth function (2) with
. The generalized Weibull is a special case of Koya-Goshu growth function (2) with . Generalized Weibull functions can be derived from the ODE (1) with rate function
. Generalized Weibull functions can be derived from the ODE (1) with rate function
 . For Generalized Weibull,
. For Generalized Weibull,  and
and  are respectively given by
are respectively given by  and
and  . The single point of inflection occurs when the organism reaches the growth
. The single point of inflection occurs when the organism reaches the growth 
 at time
at time .
.
3.9. Weibull Function
The Weibull growth model (Rawlings et al., 1998) is given as
 (16)
(16)
The Weibull function can be derived from the ODE (1)
with rate function .
.
Weibull a special case of Generalized Weibull (13) function with  and that of Koya-Goshu growth function (2) with
and that of Koya-Goshu growth function (2) with
 . For Weibull,
. For Weibull,  and
and  are respectively given by
are respectively given by and
and  . For Weibull, the single point of inflection occurs when the organism reaches the growth
. For Weibull, the single point of inflection occurs when the organism reaches the growth 
 at time
at time . This fact can be verified by directly substituting
. This fact can be verified by directly substituting  in the inflection point of Generalized Weibull.
in the inflection point of Generalized Weibull.
3.10. Monomolecular and Mitscherlich Functions
Here we show that Brody, Monomolecular and Mitscherlich growth functions are the same, except that the names and notations used are different. Hence, all these three functions exhibit the same properties and behaviors and also they represent the same growth patterns.
Monomolecular growth function is defined (France et al., 1996), in its original notations, as

where  is the growth function at time
is the growth function at time ,
,  is the final (mature) value,
is the final (mature) value,  at
at  is the initial value and
is the initial value and  is rate of growth. This function can be expressed as Brody function (7) with notations
is rate of growth. This function can be expressed as Brody function (7) with notations

as . Monomolecular growth function can be derived from the ODE (1) with rate function
. Monomolecular growth function can be derived from the ODE (1) with rate function
 or
or .
.
Thus, Monomolecular growth function, just similar to Brody growth function, does not possess a point of inflexion since  is not satisfied for any value of
is not satisfied for any value of .
.
Mitscherlich growth function [22] is defined, in its original notations, as  where
where  is the growth function at time
is the growth function at time ,
,  is the final (mature) growth,
is the final (mature) growth,  is a constant and
is a constant and  is rate of growth. The Mitscherlich function can be expressed with notations
is rate of growth. The Mitscherlich function can be expressed with notations
 as Brody function
as Brody function  given by (7). It can be derived from the ODE (1) with rate function
given by (7). It can be derived from the ODE (1) with rate function
 or
or .
.
Not that the integral constant becomes  . Thus, Mitscherlich growth function, just similar to Brody growth function, does not possess a point of inflexion since
. Thus, Mitscherlich growth function, just similar to Brody growth function, does not possess a point of inflexion since  is not satisfied for any value of
is not satisfied for any value of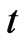 .
.
4. Other Relationships
Here we derive explicitly and present few more relationships, other than those mentioned in Section 3, among the growth models considered in this paper.
4.1. Relation between Richards and Logistic Functions
Let us now see how Richards and Logistic functions are related. Using the Richards function (9), we can derive Logistic (12) as follows:
 (17)
(17)
 (18)
(18)
where . Hence, Richards growth function with
. Hence, Richards growth function with 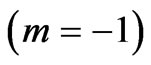 leads to the Logistic function.
leads to the Logistic function.
4.2. Relation between Richards and Gompertz Functions
We now show how Gompertz is related to Richards function, i.e., the relative growth rate function of Richards as  leads to that of Gompertz, which is now shown. Note that the relative growth rate functions of Gompertz and Richards are given respectively by
leads to that of Gompertz, which is now shown. Note that the relative growth rate functions of Gompertz and Richards are given respectively by
 and
and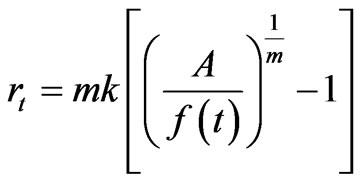 .
.
By applying the limit as  on Richards
on Richards , we get the following:
, we get the following:
 (19)
(19)
Here the last expression is obtained by a simple algebraic rearrangement of the expression. In this expression evaluation of limit leads to  and to avoid that we applying L-Hospital rule to get
and to avoid that we applying L-Hospital rule to get
 (20)
(20)
Thus, the limiting value of the Richards relative rate growth function as 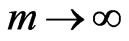 reduces to the Gompertz relative rate growth function, and hence these two functions are related.
reduces to the Gompertz relative rate growth function, and hence these two functions are related.
4.3. Relation between Particular Case of Generalized Logistic and Gompertz
We now show how Gompertz is related to the particular case of generalized Logistic function, i.e., the relative growth rate function of the particular case of generalized Logistic as  leads to that of Gompertz, which is now shown. Note that the relative growth rate functions of Gompertz and the particular case of generalized Logistic are given respectively by
leads to that of Gompertz, which is now shown. Note that the relative growth rate functions of Gompertz and the particular case of generalized Logistic are given respectively by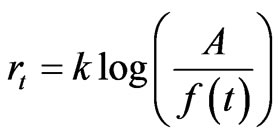 , and
, and .
.
By applying the limit as 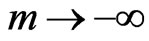 on
on  of the particular case of generalized Logistic function, we get the following:
of the particular case of generalized Logistic function, we get the following:
 (21)
(21)
Here the last expression is obtained by a simple algebraic rearrangement after the inverse functions viz, logarithmic and exponential operations are used. In this expression evaluation of limit leads to  and to avoid that we apply L-Hospital rule to get
and to avoid that we apply L-Hospital rule to get
 (22)
(22)
Thus, the relative rate growth function the particular case of generalized logistic function as  reduces to the Gompertz relative rate growth function, and hence these two functions are related.
reduces to the Gompertz relative rate growth function, and hence these two functions are related.
4.4. Relation between Brody and Gompertz Functions
We have shown in the flow chart the relationships among the growth functions by setting the parameters suitably. However, Gompertz and Brody functions can be related through a transformation of time coordinate and that goes as follows:
Let the time variables of Brody and Gompertz are represented by  and
and  respectively. Now consider the Brody function as
respectively. Now consider the Brody function as
 (23)
(23)
and the Gompertz function as
 (24)
(24)
Now on equating the  and
and  from (23) and (24), we get
from (23) and (24), we get
 (25)
(25)
and this can be expressed as
 (26)
(26)

Table 1. List of growth functions and their respective rate functions, expressions for b, integral constants and inflection points.
which is the coordinate transformation equation between the time variables of Brody and Gompertz functions.
5. Illustration for How Relative Growth Rate Function Behaves—Richards Case
The relative growth rate function  is significantly different for the models at early ages and converges to zero for the later ages. The relative growth rate
is significantly different for the models at early ages and converges to zero for the later ages. The relative growth rate  is an increasing function of
is an increasing function of  while it is a decreasing with time t. However,
while it is a decreasing with time t. However,  grows with
grows with  in the early ages allowing the parameter m to play a significant role. Subsequently,
in the early ages allowing the parameter m to play a significant role. Subsequently,  dies at later ages irrespective of
dies at later ages irrespective of . We consider Richards function as example to illustrate this.
. We consider Richards function as example to illustrate this.
Consider the Richards relative growth rate function :
:
 (27)
(27)
is a function of parameter  and time
and time , and limit gives:
, and limit gives:
 (28)
(28)
Equation (28)  is increases with
is increases with  at early times.
at early times.
Also, on taking the limit of  in (27) as
in (27) as , we get
, we get

showing that  vanishes at time of growth maturity for all
vanishes at time of growth maturity for all .
.
6. Conclusion
This paper introduces a new generalized mathematical model for biological and other growths, named as KoyaGoshu growth model. It is a generalization of the commonly used growth functions such as: Brody, Von Bertalanffy, Richards, Weibull, Monomolecular, Mitscherlich, Gompertz, Logistic and generalized Logistic functions. Koya-Goshu model is constructed as a solution of ordinary differential or rate-state equation. The function incorporates two parameters where one influences growth pattern and the other influences asymptotic behavior. The model is so flexible that it can be useful in model selections. Moreover, it generates new and useful growth functions. All of the growth models considered under the study are related to each other as illustrated in the flaw chart. As further studies, we will take up applications of this model for data fitting and prediction.
NOTES