1. Introduction
The idea of a class of sets with a continuum of grade of membership, ranging between zero and one, was first introduced by Zadeh in 1965. A larger degree of membership of an object reflects a stronger sense of belonging to a set. If A is a set in the ordinary sense of the term, then its membership takes only two values, 0 and 1. The notions of inclusion, union, intersection, complement, relation and convexity can be extended to such sets [1].
Fuzzy closure spaces were introduced by [5] in an attempt to show that fuzzy topological spaces do not constitute a natural boundary for the validity of theorems and results. The axioms used to define fuzzy closure spaces are the modified Kuratowski closure axioms that have previously been used to extend the study of the concepts of topological spaces. The class of isotonic spaces is defined using only two Kuratowski closure axioms, namely the grounded axiom  and the isotone axiom
and the isotone axiom

where  is the closure operator on a nonempty set
is the closure operator on a nonempty set .
.
2. Literature Review
2.1. Fuzzy Sets
In [2], a fuzzy set in  is defined as a function
is defined as a function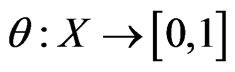 . Here
. Here  represents the degree of membership of
represents the degree of membership of  in the fuzzy set
in the fuzzy set .
.
2.2. Crisp Fuzzy Sets
Any subset  of a set
of a set  can be identified with its characteristic function
can be identified with its characteristic function  defined by;
defined by;
 (1)
(1)
Such characteristic functions are fuzzy sets in . Thus fuzzy sets generalize ordinary sets [3].
. Thus fuzzy sets generalize ordinary sets [3].
2.3. Definitions on Fuzzy Sets
Let  and
and  be
be  -valued functions defined on a fixed set, i.e fuzzy sets on
-valued functions defined on a fixed set, i.e fuzzy sets on . Then according to [3];
. Then according to [3];
1) 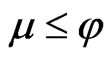 implies
implies  for every
for every .
.
2)  implies
implies 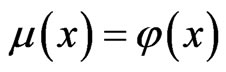 for every
for every .
.
3) Maximum function:
 .
.
4) Minimum function:
 .
.
5) Complement function: . These are [0,1]-valued functions.
. These are [0,1]-valued functions.
For two fuzzy sets  and
and  in
in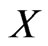 ;
;
1)  and
and  are equal if and only if
are equal if and only if .
.
2)  is contained in
is contained in  if and only if
if and only if .
.
3) The union of  and
and  is
is .
.
4) The intersection of  and
and  is
is .
.
5) The complement of  is
is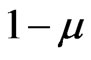 .
.
Let  be fuzzy sets. Then the union of
be fuzzy sets. Then the union of  is defined by;
is defined by;
 (2)
(2)
The intersection of  is defined by;
is defined by;
 (3)
(3)
If  are crisp, i.e. they are characteristic functions, then these suprema and infima are actually maxima and minima.
are crisp, i.e. they are characteristic functions, then these suprema and infima are actually maxima and minima.
2.4. Fuzzy Topology
According to [4], a fuzzy topology on a set  is a collection
is a collection  of fuzzy sets in
of fuzzy sets in  satisfying
satisfying
1) , where
, where  is equivalent to the empty set.
is equivalent to the empty set.
2) If  and
and  belong to
belong to , then
, then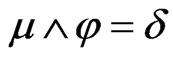 .
.
3) If  are fuzzy, then
are fuzzy, then . The members of
. The members of  are called open fuzzy sets.
are called open fuzzy sets.
The pair  is called a fuzzy topological space. Fuzzy sets of the form
is called a fuzzy topological space. Fuzzy sets of the form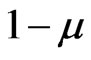 , where
, where  is fuzzy are called closed fuzzy sets.
is fuzzy are called closed fuzzy sets.
2.5. Functions and Fuzzy Continuity
Let 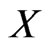 and
and 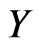 be sets and
be sets and  be a function. For a fuzzy set
be a function. For a fuzzy set  in
in , the inverse image of
, the inverse image of  under
under  is the fuzzy set
is the fuzzy set  in
in 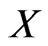 defined by;
defined by;
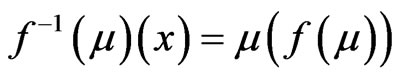
for . That is
. That is .
.
For a fuzzy set  in
in , the image of
, the image of 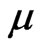 under
under  is the fuzzy set
is the fuzzy set  in
in 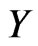 defined for
defined for  by;
by;
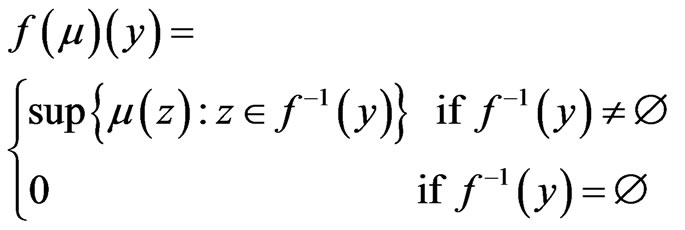 (4)
(4)
2.6. Fuzzy Continuity
Given fuzzy topological spaces  and
and , then according to [2],
, then according to [2],  is fuzzy continuous if the inverse image under
is fuzzy continuous if the inverse image under 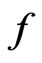 of any open fuzzy set
of any open fuzzy set 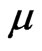 in
in  is an open fuzzy set in
is an open fuzzy set in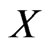 , i.e
, i.e 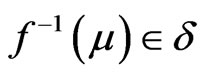 whenever
whenever .
.
The identity mapping  on a fuzzy topological space
on a fuzzy topological space  is fuzzy continuous.
is fuzzy continuous.
2.7. Closure and Interior Operation on Fuzzy Sets
Let  be a fuzzy topological space. The closure
be a fuzzy topological space. The closure  and interior
and interior  of a fuzzy set
of a fuzzy set 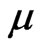 in
in  are defined respectively by [3] as follows;
are defined respectively by [3] as follows;
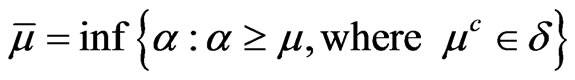
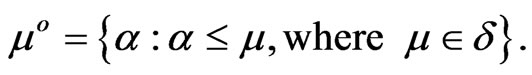
It is easily seen that  is the smallest closed fuzzy set larger than
is the smallest closed fuzzy set larger than  and that
and that  is the largest open fuzzy set smaller than
is the largest open fuzzy set smaller than . These definitions coincide with their analogous definitions on ordinary sets.
. These definitions coincide with their analogous definitions on ordinary sets.
2.8. Fuzzy Closure Spaces
Let  be the collection of all mappings from
be the collection of all mappings from  to the unit interval
to the unit interval , i.e
, i.e  is the collection of all fuzzy sets on the non-empty set
is the collection of all fuzzy sets on the non-empty set . Then from [5], an operator
. Then from [5], an operator 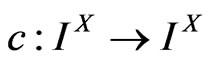 is a fuzzy closure operator if and only if
is a fuzzy closure operator if and only if
1)  constant.
constant.
2)  for every
for every .
.
3)  for every
for every .
.
4)  for every
for every .
.
The closure operator may also be used to characterize closed sets. A set  is closed if
is closed if . A fuzzy interior operator
. A fuzzy interior operator  is the dual of a closure operator. It is defined by;
is the dual of a closure operator. It is defined by;
1)  constant.
constant.
2)  for every
for every .
.
3)  for every
for every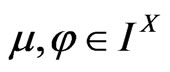 .
.
4)  for every
for every .
.
Similarly, the interior operator may also be used to characterize open sets. A set  is open if
is open if .
.
A Cech fuzzy closure operator (or CF-closure operator) on a set  is a function
is a function  satisfying the following three axioms;
satisfying the following three axioms;
1)  constant.
constant.
2)  for every
for every .
.
3)  for every
for every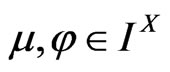 .
.
The pair  is called a fuzzy closure space or fcs. Clearly these axioms can easily be seen to be similar to the Kuratowski axioms in [6].
is called a fuzzy closure space or fcs. Clearly these axioms can easily be seen to be similar to the Kuratowski axioms in [6].
3. Results
The following are the main results of this work.
3.1. Fuzzy Isotone Space
A fuzzy isotone closure operator on a set  is a function
is a function  satisfying the following two axioms;
satisfying the following two axioms;
1)  constant.
constant.
2) For every ,
, .
.
The pair  is called a fuzzy isotone space.
is called a fuzzy isotone space.
3.2. Semi-Separated and Separated Fuzzy Sets
We would like to modify the definitions of semi-separated and separated sets in order to have their equivalent characterization on fuzzy isotone spaces. This will facilitate the definition of complete normality on fuzzy isotone spaces.
In a fuzzy isotonespace , two fuzzy subsets
, two fuzzy subsets  and
and  are called semi-separated if
are called semi-separated if
 .
.
The fuzzy subsets  and
and  are separated if there exists open fuzzy sets
are separated if there exists open fuzzy sets , V with
, V with 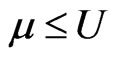 and
and  such that
such that . The openness of fuzzy sets on
. The openness of fuzzy sets on  is defined using the dual of the closure operator, i.e the interior operator.
is defined using the dual of the closure operator, i.e the interior operator.
Lemma
Let . Then
. Then  and
and  are semi-separated in
are semi-separated in  if and only if
if and only if  and
and  are semi-separated in
are semi-separated in , where
, where  is the relativization of
is the relativization of  into
into .
.
Proof
Let  be a fuzzy isotone space and
be a fuzzy isotone space and 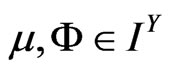 be semi-separated fuzzy sets in
be semi-separated fuzzy sets in . Then
. Then
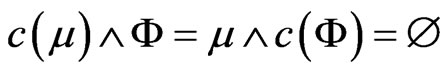 .
.
But  hence
hence
 .
.
Similarly,  hence
hence
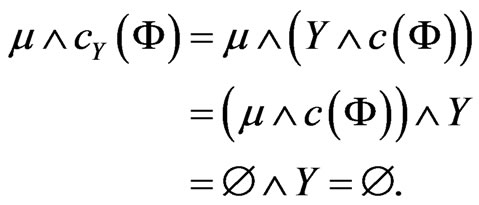
Therefore,  and
and  are semi-separated in
are semi-separated in .
.
Conversely, let  be a subspace of the fuzzy isotone space
be a subspace of the fuzzy isotone space  and
and  and
and  are semi-separated in
are semi-separated in . Of course
. Of course  and
and
 .
.
 .
.
Similarly,
 .
.
Thus  and
and  are semi-separated in
are semi-separated in .
.
3.3. Normality
A fuzzy isotone space  is normal if for every nonempty pair of fuzzy sets
is normal if for every nonempty pair of fuzzy sets  and
and  in
in  such that
such that  there exists a fuzzyopen set
there exists a fuzzyopen set  such that
such that  and
and .
.
Normality may be characterized via the existence of a fuzzy continuous real-valued function just as in topological spaces.
Let  be a normal fuzzy isotone space. Then for each pair of disjoint fuzzy subsets
be a normal fuzzy isotone space. Then for each pair of disjoint fuzzy subsets  and Ф, there exists a fuzzy continuous function
and Ф, there exists a fuzzy continuous function  such that
such that  on
on  and
and  on
on . Clearly, this characterization is analogous to the definition of normality via the existence of an Urysohn function on a normal topological space.
. Clearly, this characterization is analogous to the definition of normality via the existence of an Urysohn function on a normal topological space.
3.4. Complete Normality
A fuzzy isotone space 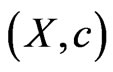 is said to be completely normal if every fuzzy subspace of
is said to be completely normal if every fuzzy subspace of  is normal.
is normal.
Theorem
A fuzzy isotone space 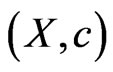 is completely normal if and only if for every pair
is completely normal if and only if for every pair  and
and  of fuzzy subsets with
of fuzzy subsets with  then there exists disjoint fuzzy sets
then there exists disjoint fuzzy sets  and
and .
.
Proof
Let 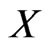 be completely normal and
be completely normal and  be fuzzy sets with
be fuzzy sets with . Denote
. Denote , a subspace of
, a subspace of  by
by . Then
. Then  since
since
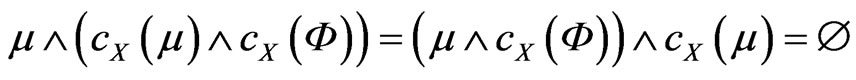 .
.
Similarly,
 .
.
Clearly  and
and 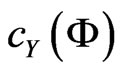 are closed sets in
are closed sets in 
such that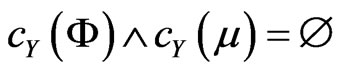 . Notice
. Notice
 .
.
Therefore, since  is completely normal, then
is completely normal, then  is normal and hence there exists
is normal and hence there exists  and
and  in
in  such that
such that 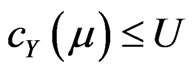 and
and .
.
Conversely, let  be a subspace of
be a subspace of  and
and 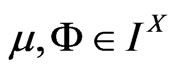 such that
such that  and
and  with
with . Then
. Then . Similarly,
. Similarly,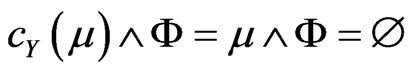 . Therefore, by the hypothesis of the theorem, there exists disjoint fuzzy sets
. Therefore, by the hypothesis of the theorem, there exists disjoint fuzzy sets
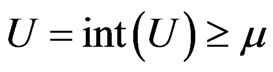 and
and .
.
The fuzzy sets  and
and  are disjoint and contained in
are disjoint and contained in  and
and . Hence
. Hence  is normal and
is normal and  is therefore completely normal.
is therefore completely normal.
3.5. Perfect Normality
Perfect normality has not been defined in fuzzy closure spaces. Therefore, different characterizations are given under this section as modifications from topological spaces. A few basic concepts have to be carried over from general topological spaces before any meaningful definition of perfectly normal isotonic spaces can be given.
3.5.1. Preliminary Definitions
It is known form point-set topology and from fuzzy topology that though the countable union of closed sets need not be closed, and the countable intersection of open sets need not be open, such sets occur frequently in analysis. The occurrence of such sets guarantees perfect normality on a space .
.
A fuzzy set  is called a
is called a  -set if and only if
-set if and only if
 where
where . A set
. A set 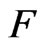 is called an
is called an  -set if
-set if
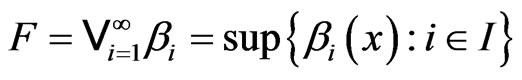
where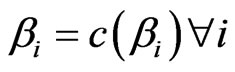 .
.
A fuzzy isotone space  is perfectly normal if
is perfectly normal if  is normal and for every fuzzy subset
is normal and for every fuzzy subset  of
of ,
,  is a
is a 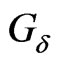 -set. That is for every closed fuzzy set
-set. That is for every closed fuzzy set 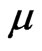 in
in ,
, . Equivalently, a normal isotonic space
. Equivalently, a normal isotonic space  is perfectly normal if every open fuzysubset of
is perfectly normal if every open fuzysubset of  is an
is an  -set. That is, for every fuzzy set
-set. That is, for every fuzzy set , then
, then
 .
.
3.5.2. Theorem
The fuzzy isotone space  is perfectly normal if for every
is perfectly normal if for every  such that
such that ,
, 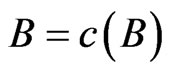 and
and , then
, then  a fuzzy continuous function
a fuzzy continuous function  that precisely separates
that precisely separates  and
and . That is
. That is  and
and 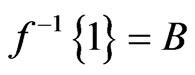
3.5.3. Theorem
Every perfectly normal fuzzy isotone space 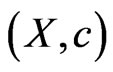 is completely normal.
is completely normal.
Proof
Since a fuzzy isotone space is completely normal if and only if every subspace is normal, then in order to show that perfect normality implies complete normality, it suffices to show the heredity of perfect normality. Let  be perfectly normal fuzzy isotone space. Then for every closed fuzzy set
be perfectly normal fuzzy isotone space. Then for every closed fuzzy set 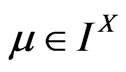 there exists a fuzzy continuous function
there exists a fuzzy continuous function  such that
such that .
.
Let  be a subspace of
be a subspace of  and
and  be closed. Then there exists a fuzzy closed set
be closed. Then there exists a fuzzy closed set  such that
such that . Since
. Since  is closed in
is closed in , then there exists a fuzzy continuous function
, then there exists a fuzzy continuous function 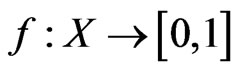
such that . But
. But  is also fuzzy continuous and
is also fuzzy continuous and . Therefore
. Therefore  is perfectly normal and hence normal. This implies that X is completely normal and hence perfect normality implies complete normality.
is perfectly normal and hence normal. This implies that X is completely normal and hence perfect normality implies complete normality.
4. Conclusion
The variants of normality naturally extend to the class of fuzzy isotone spaces and to the fuzzy closure spaces generally. Therefore, on fuzzy isotone spaces, perfect normality implies complete normality which implies normality.