1. Introduction
In the past, a huge amount of work, both theoretical and experimental, has been done in investigating the temperature dependence of acoustic attenuation in solids [1-10]. Experimental studies [3-6] reveal that the dislocation mechanism yields a negligible contribution to the ultrasonic absorption in well-annealed crystals of alkali halides, and the contribution of thermo-elastic losses, is exceedingly small, too. Thus the class of face centered cubiccrystals, it is ideally suited for the study of ultrasonic absorption by phonon-phonon interactions as the absorption is determined almost exclusively by this mechanism. An investigation of the acoustical properties provides useful information on the inter-atomic forces, inter-ionic potentials, equation of state, phonon spectra and on anharmonic properties of crystalline solids.
The calculation of temperature dependence of acoustic damping in the Akhiezer regime has been studied in NaF, NaCl, NaBr, [7-9] and LiF [10] using Mason’s theory [2]. In a study by Nava et al. [11] the attenuation was calculated at room temperature using a modified formulation of theory of Woodruff et al. [12] for 12 non-conducting cubic crystals. All these investigations employ Mason’s scheme in which the various averages of the mode Grüneisen numbers (gij) are evaluated over a small, fixed set of thermal phonon modes along the pure mode directions. A computer program developed by us [13-15] facilitates the calculation of these averages over the entire spectrum of thermal phonon modes. The motivation and aim of developing this program was that such a program would facilitate a theoretical investigation of different models in different solids on one hand, and, on the other, it could have the flexibility of incorporating new refinements in these models at any stage.
In this work, we will apply our program to estimate the temperature dependence of ultrasonic attenuation in Manganese oxide (MnO) crystal. MnO is an inorganic compound which is a simple oxide that is insoluble in water but dissolves in acids, making manganese salts. It occurs in natural surroundings as the rare mineral manganosite. MnO has the NaCl, rock salt structure, where cations and anions are both octahedrally coordinated. Below 118 K it is antiferromagnetic. MnO is one of the first compounds to have its magnetic structure determined by neutron diffraction in 1951. According to this study, the Mn2+ ions form a face centered cubic magnetic sub-lattice where there are ferromagnetically coupled sheets which are anti-parallel with adjacent sheets. MnO is a constituent of fertilizer and food additives. A lot of amount of this material are disbursed yearly for this purpose. Additional uses are: a catalyst in the production of allyl alcohol, ceramics, paints, colored glass, bleaching tallow and textile printing etc. In this work, the calculations for ultrasonic attenuation and related parameters for this significant material are presented for longitudinal and shear waves along the <100>, <110> (polarized along <001> and <1`10>) and <111> (polarized along <͞110> and <11`2>) directions in the temperature range 300 - 500 K.
2. Theory and Computation
Assuming electrostatic potential {±(e2/r)} and BörnMayer type potential Quv(r0) = A exp (−r0/q); e, r0 and q being electronic charge, nearest-neighbour distance and hardness parameter [16], and following Brügger’s [17] definition of elastic constants at absolute zero, secondand thirdorder elastic constants (SOECs and TOECs) are obtained. Leibfried et al. [18,19] have developed the theory of anharmonic properties of crystals, which has been used to obtain SOECs and TOECs at different temperatures. This theory has been used by previous investigators [7,9,13].
As elastic constants evaluation is done, Grüneisen numbers (gij) are calculated using Grüneisen number tables [4]. These parameters directly give Mason’s [20,21] non-linearity coupling constant (D) as presented below:
 (1)
(1)
where,
i
j>
2 and
i
j
2> are average Grüneisen and square average Grüneisen numbers, C
v is specific heat per unit volume, T is temperature and E
0 is the energy of the crystal.
The thermo elastic losses and attenuation [22] due to phonon-phonon interaction are given by:
 (2)
(2)
 (3)
(3)
In our case, wtth<<1, therefore the relation reduces to:
 (4)
(4)
The attenuation coefficients for longitudinal and shear waves are given by,
 (5)
(5)
and
 (6)
(6)
where, d is crystal mass density, Dl and Ds are non-linearity coupling constants, tl and ts are relaxation times, and vl and vs are acoustic wave velocities for longitudenal (l) and shear (s) waves respectively. The two relaxation times are related as
 (7)
(7)
where, tth is thermal relaxation time, K is thermal conductivity and`v is the Debye average velocity. The vl, vs,`v are given by
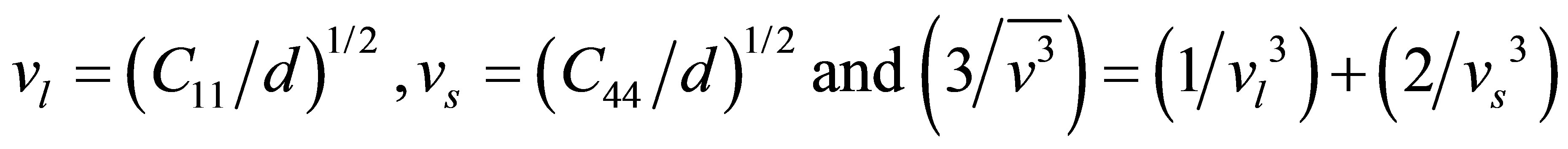
(8)
In dielectric solids an important source of acoustic absorption in the range wtth << 1 (where w is the angular frequency of the acoustic wave and tth is the thermal phonon relaxation time) is the Akhiezer mechanism, whereby the thermal phonon gas extracts energy from the acoustic wave through anharmonic interactions. Akhiezer’s original theory [23] was modified first by Woodruff and Ehrenreich and then by Mason and Bateman, using fundamentally different approaches. Woodruff’s expression for attenuation is a function of mode specific heats, and involves complex averages of the anharmonic parameters which describe the strain dependence of the lattice vibrational frequencies over the Brillouin zone. Mason’s expression, derived in the anisotropic continuum limit, involves thermal energy and non-linearity constant, which is a function of the second-and thirdorder elastic constants of the solid. Mason’s theory has been most widely used in its original format to account for the temperature dependence of attenuation in a variety of solids [7,9,10,13-15,24-27].
However, its conceptual basis has been questioned by Barrett and Holland [28] who contended that the correct derivation of the starting equation used by Mason should lead to Woodruff’s expression for attenuation coefficient. Nava et al. have suggested a modified formulation of Woodruff’s theory, based on the use of ultrasonic Grü- neisen parameter which is able to clarify the origin of the temperature dependence of attenuation. Nava et al. assume an anisotropic elastic continuum model in which the (gij) are simply given by linear combinations of SOEC and TOEC [29]. They further assume a constant phonon relaxation time deduced from the thermal conductivity by t = 3 k/Cv c2, Cv being the total specific heat. Mason’s scheme of counting these modes is followed. Thus it can be seen that although the averages of mode g’s indicated in Nava et al.’s formulation are defined by considering the mode specific heats as the weights the calculations reported by Nava et al. [11] have been performed using approximate simple numerical averages, following Mason’s scheme. Even though, the general agreements achieved by various workers are such that they do not reveal any clear pattern of superiority for a particular model.
3. Evaluation
The understanding of elastic constants is essential for many practical applications related to the mechanical properties of solids: load diffraction, thermo-elastic stress, internal strain (residual stress) and sound velocity and fracture toughness. Elastic properties are also linked thermodynamically with thermal expansion, Debye temperature and Grüneisen parameter. The SOECs and TOECs are calculated at different temperatures using the theory described [17-19]. The second and third order elastic constants play a crucial role in the investigation of ultrasonic attenuation. With the help of SOEC and TOEC data, Grüneisen parameters [4] have been evaluated using Mason’s Grüneisen tables [20] at different temperatures along <111> direction for both longitudinal wave and shear wave polarized along <͞110> direction. With the help of Equation (1), non-linearity constants have been obtained and presented in Figures 1 and 2. Thermal relaxation time has been obtained at different temperatures, taking temperature variation of thermal conductivity, as shown in Figure 3. The attenuation along <111>
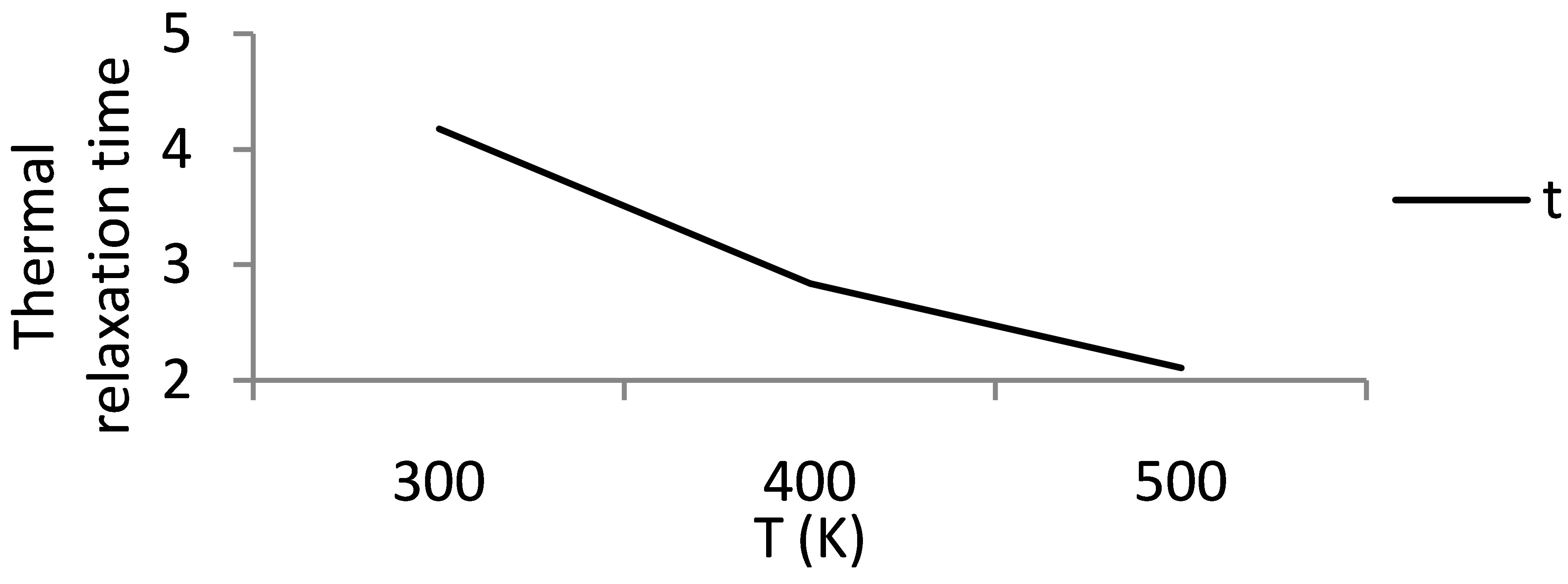
Figure 3. Temperature dependence of thermal relaxation time (in 10−12 sec.).
direction was calculated using expressions in Equations (1)-(6), by taking into account the temperature dependence of each parameter contained in these expressions. The experimental data of room temperature densities and of temperature dependence of thermal expansion coefficient and thermal conductivity were taken from the literature [30-33]. On taking specific heat and crystal energy density at different temperatures as a function of qD/T, where qD is Debye temperature, thermo elastic losses and ultrasonic attenuation at different temperatures obtained and shown in Figures 4 and 5. The input data are taken from literature [30].
4. Results and Discussion
From microstructure characterization point of view, it is well known that acoustic properties of materials are very important. The magnitude of secondand third-order elastic constants and their temperature variation plays a

Figure 4. Temperature dependence of acoustic velocities for longitudinal (l) and shear(s) waves (in 105 cm/sec).
crucial role in the investigation of ultrasonic attenuation in MnO crystals and these constants may be used for the purpose of investigating anharmonic properties. In present study, SOECs are all positive, while among TOECs, three are negative and three are positive. Among the calculated the third order elastic constants of these materials, C111s are the largest in their absolute values and an order of magnitude larger than the SOEC. Magnitude of other Cijks are markedly smaller than those of C111. The present study could also prove useful in studies of various anharmonic properties (such as thermal expansion, thermo elastic constants and thermal conductivity) of ionic solids in general. It can allow an evaluation of first order anharmonic terms of the inter-atomic potential or of generalized Grüneisen parameters, which enter the theories of all anharmonic phenomena, such as the interaction of acoustic and thermal phonons and the equation of state. The TOECs play an important role when it comes to explain anharmonic phenomena in solids (interactions of ultrasonic vibration with thermal phonons, harmonic generators, equation of state etc.). As a result of the anharmonicity of the crystal lattice vibrations, the elastic constants vary with temperature.
The temperature dependence of Grüneisen parameters are shown in Figure 1. The temperature dependence of non-linearity parameters (D) calculated for various directions of propagation are shown in Figure 2. It can be seen from this figure that the shear (s) wave exhibit larger magnitude and greater temperature dependence of D than the longitudinal wave (Table 1). The value of Ds is more than Dl which is expected [7,13]. These results are in qualitative agreement with the previous observations [34,35]. The non-linearity parameters determined in this way contain the effects of temperature on the average anharmonicity of the lattice as sampled by the sound waves.
In Figure 3, the value of the thermal relaxation time is of the order of 10−12 sec. At 300 K, its value is very high and decreases exponentially as temperature is increased. Such type of nature is as expected and also seen in other type of substances [7,13]. Figure 4 shows the variation of ultrasonic velocity with temperature.
The study of ultrasonic attenuation in the materials has gained new dimensions with the progress in material

Table 1. Comparison data of Dl/Ds (ratio of non-linearity constants) for MnO at room temperature.
science. Ultrasonic attenuation studies are used as a versatile tool in studying internal structure and inherent properties of all types of substances, viz., metallic, dielectric and semiconducting crystals. In different types of solids, the attenuation of acoustic waves is attributed due to different causes. At higher temperatures (particularly at room temperature 300 K) above 100 K, the attenuation caused by phonon-phonon interaction is most dominating in all types of crystals provided the crystal is perfect, non-ferromagnetic and non-ferroelectric. The results of our calculation of temperature dependence of ultrasonic attenuation due to phonon-phonon interaction are presented in Figure 5. It can be pointed out that attenuation is low at 300 K and increases as temperature increases for both longitudinal and shear waves. It is seen that attenuation for shear wave is more than longitudinal wave which is experimentally valid [4].
Earlier, we have successfully evaluated temperature dependency of the elastic properties and allied parameters of various compounds [35-40]. This paper contains the conclusions on some details of temperature dependent ultrasonic properties in MnO. The general observations made above in the case of MnO are true in the other crystals of the similar nature [13,14,35,39]. Therefore, it can be concluded that the present approach is correct and we can claim that our results are acceptable for further studies. More importantly, because of its relatively few assumptions, the present theory yields a reliable output. The attenuation is found to be very useful in material characterization; therefore it is expected that this study may be significant for various industrial purposes. We have shown that by obtaining the ultrasonic absorption, a deep insight into the micro structural properties can be achieved. The outcomes from this investigation can be used for advanced study of this crystal.