Pricing Options in Jump Diffusion Models Using Mellin Transforms ()
1. Introduction
Pure diffusion models are in most cases not flexible enough to fit the empirical observations concerning the movements of stock prices. Jump diffusions are a natural extension of pure diffusions since they are able to account for large and sudden changes. This is accomplished by adding a second source of uncertainty into the diffusion dynamics. The second source is discontinuous and models the jumps in the underlying asset. Also, pricing of options in jump diffusions is consistent with the volatility smile often observed in financial markets.
In his seminal paper from 1976 Merton [1] introduced a first jump diffusion process for modeling the behavior of stock prices. Since his work jump diffusions have become a very popular tool in modeling equity, foreign exchange and commodity markets. Under the assumption of log-normally distributed jumps, Merton solved the European option pricing problem explicitly in closedform in terms of an infinite series of Black-Scholes prices. Other popular pure and non-pure jump diffusion processes are those proposed in [2-6] among others. Kou [7] proposed a double exponential jump-diffusion model where jump sizes are double exponentially distributed. The model allows for an analytical pricing of some pathdependent options, such as continuously monitored barrier and lookback, and perpetual American options [8]. In [9], pricing formulas in Kou’s model for double (single) barrier and touch options with time-dependent rebates are derived applying Laplace transforms.
In many cases, however, an explicit closed-form valuation of options in jump diffusions is not possible and one is restricted to numerical procedures. These procedures rely on the fact that prices of derivatives in a jump diffusion environment satisfy partial integro-differential equations (PIDEs). The methods discretize the asset-time domain and use either binomial trees, finite difference or finites element methods to solve the PIDEs. [10], for instance, uses an explicit multinomial tree based approach for the valuation. [11] develop another pricing procedure based on a lattice framework. Further recent developments concerning the numerical evaluation include the articles [12-15].
The application of Mellin transforms for the purpose of option pricing was firstly introduced in [16] in the geometric Brownian motion economy. It was extended to the stochastic volatility model of Heston by Frontczak (2011) [17]. This paper extends the Mellin integral transform framework further to the valuation of options in jump-diffusion models. It is organized as follows: Chapter 2 reviews the problem formulation. Chapter 3 provides a solution for European derivatives as a single integral. Also simple formulas for the Greeks are derived. Although our solution is general in the sense that it does not depend on the distribution of the jump size, we choose the log-normal jump-diffusion model as an explicit example and show that our solutions for plain vanilla and digital puts may be rewritten as infinite series of Black-Scholes-Merton prices. Some numerical results are presented in Chapter 4. Chapter 5 concludes the paper and indicates possible further research projects.
2. Problem Statement
Let  be the price of a dividend paying stock at time
be the price of a dividend paying stock at time . The dividend is paid continuously at a rate
. The dividend is paid continuously at a rate  and is proportional to the price of the stock. The evolution of the stock is affected by two sources of uncertainty: a continuous part modeled as a standard Brownian motion
and is proportional to the price of the stock. The evolution of the stock is affected by two sources of uncertainty: a continuous part modeled as a standard Brownian motion  and a discontinuous part modeled as jumps with a Poisson arrival process
and a discontinuous part modeled as jumps with a Poisson arrival process . Therefore, under the physical probability
. Therefore, under the physical probability  the dynamics of the stock are given by
the dynamics of the stock are given by
 (2.1)
(2.1)
with initial value  and where
and where 
 is the time instant before
is the time instant before . The parameters
. The parameters  and
and  are the instantaneous drift and volatility, respectively. The process
are the instantaneous drift and volatility, respectively. The process 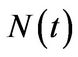 is a Poisson process with intensity
is a Poisson process with intensity  and
and

and  is the proportional change in the stock price. We also assume that the processes
is the proportional change in the stock price. We also assume that the processes ,
,  and
and  are independent. For
are independent. For  the jump diffusion process in (2.1) becomes a geometric Brownian motion as assumed in the Black-Scholes and Merton model. In order to guarantee that the discounted process is a martingale, we have
the jump diffusion process in (2.1) becomes a geometric Brownian motion as assumed in the Black-Scholes and Merton model. In order to guarantee that the discounted process is a martingale, we have
 (2.2)
(2.2)
where  is the probability density function of
is the probability density function of  and
and  is the expectation operator. It is well known that markets with jump diffusions are not complete. Hence, an equivalent martingale measure
is the expectation operator. It is well known that markets with jump diffusions are not complete. Hence, an equivalent martingale measure  is not unique. Nevertheless, if we assume that the jump risk is diversifiable as has been done in [1] we can consider the risk-neutral dynamics of
is not unique. Nevertheless, if we assume that the jump risk is diversifiable as has been done in [1] we can consider the risk-neutral dynamics of 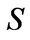
 (2.3)
(2.3)
where  is replaced by the riskless interest rate
is replaced by the riskless interest rate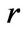 . The solution to the process above equals
. The solution to the process above equals
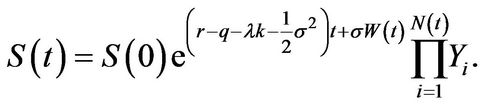
Standard arguments show that a European-style derivative written on  and time
and time  with price
with price  must solve the backward in time PIDE:
must solve the backward in time PIDE:
 (2.4)
(2.4)
for all  and where subscripts denote partial derivatives. For a derivation see [1,18]. The terminal value of the derivative equals
and where subscripts denote partial derivatives. For a derivation see [1,18]. The terminal value of the derivative equals , where
, where  is the payoff function of the contract under consideration. For a plain vanilla European put with price
is the payoff function of the contract under consideration. For a plain vanilla European put with price  we have
we have
 (2.5)
(2.5)
where  is the strike price of the put and
is the strike price of the put and  denotes the terminal stock price1. For the jump size distribution different distributions are commonly used in the financial literature. Prominent candidates are among others:
denotes the terminal stock price1. For the jump size distribution different distributions are commonly used in the financial literature. Prominent candidates are among others:
• Log-normally distributed jumps ([1]): The probability density function of  is given by
is given by
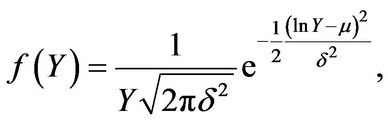 (2.6)
(2.6)
where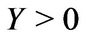 , and
, and 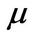 and
and  are constants.
are constants.
• Double exponentially distributed jumps ([7]): The probability density function of  is asymmetric and equals
is asymmetric and equals
 (2.7)
(2.7)
where ,
,  ,
, with
with . The restriction
. The restriction 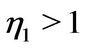 guarantees that
guarantees that 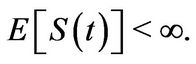
• Gamma distributed jumps: In this case  equals
equals
 (2.8)
(2.8)
where 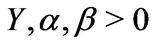 and
and  denotes the gamma function.
denotes the gamma function.
• One-sided exponentially distributed jumps2: The probability density function 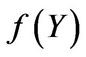 may be seen as a special case of the probability density function of gamma distributed jumps with
may be seen as a special case of the probability density function of gamma distributed jumps with . Therefore
. Therefore
 (2.9)
(2.9)
The particular choice of the distribution of  is crucial in order to solve the problem analytically in the
is crucial in order to solve the problem analytically in the  -domain. The only two models where
-domain. The only two models where  is assumed to be continuous and that have been solved explicitly in terms of an infinite series are to the best of our knowledge the Merton (1976) model and the model of Kou (2002).
is assumed to be continuous and that have been solved explicitly in terms of an infinite series are to the best of our knowledge the Merton (1976) model and the model of Kou (2002).
3. Main Results
The following theorem characterizes the solution to (2.4). The functional form of the solution is simple and is expressed as a single integral.
Theorem 3.1 The solution of the PIDE (2.4) is given by
 (3.1)
(3.1)
with ,
,  ,
,  is the imaginary unit,
is the imaginary unit,  and where
and where
 (3.2)
(3.2)
with
 (3.3)
(3.3)
In particular, for the European put 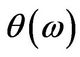 equals3
equals3
 (3.4)
(3.4)
Proof: For a locally Lebesgue integrable function  the Mellin transform
the Mellin transform  with transformation variable
with transformation variable  is defined by the relation
is defined by the relation
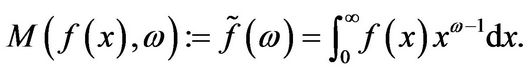
Conversely, if  is a continuous, integrable function, then the inverse of the Mellin transform is given by
is a continuous, integrable function, then the inverse of the Mellin transform is given by

Let  denote the Mellin transform of a financial derivative with price
denote the Mellin transform of a financial derivative with price . Since the Mellin transform is a linear integral operator it follows that the PIDE from (2.4) can be transformed into a homogeneous ordinary differential equation (ODE) of the form
. Since the Mellin transform is a linear integral operator it follows that the PIDE from (2.4) can be transformed into a homogeneous ordinary differential equation (ODE) of the form
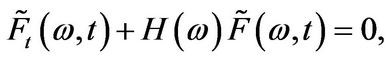 (3.5)
(3.5)
where
 (3.6)
(3.6)
The solution to this ODE equals
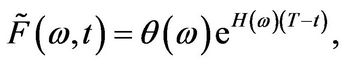
with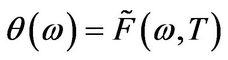 . Recalling that
. Recalling that  the expression for
the expression for  follows immediately. The final expression for the price follows from the inversion theorem for Mellin transforms.
follows immediately. The final expression for the price follows from the inversion theorem for Mellin transforms.
The previous theorem gives the analytic solution to (2.4) in a general manner, i.e. without specifying the distribution of . The solution has a simple functional form and prices are obtained very quickly using standard quadrature routines. It is also flexible to account for different jump size distributions and types of derivatives by specifying
. The solution has a simple functional form and prices are obtained very quickly using standard quadrature routines. It is also flexible to account for different jump size distributions and types of derivatives by specifying  and
and , respectively, for the contract under consideration. To give explicit examples, we state the expressions for
, respectively, for the contract under consideration. To give explicit examples, we state the expressions for  in the four special cases for
in the four special cases for 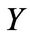 discussed above:
discussed above:
• Log-normally distributed jumps ([1]): Since for each real or complex  we have
we have
 (3.7)
(3.7)
it follows that  and
and
 (3.8)
(3.8)
• Double exponentially distributed jumps ([7]): We have
 (3.9)
(3.9)
with . Therefore
. Therefore
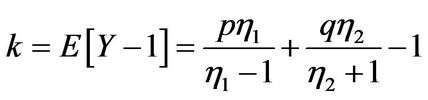
and
 (3.10)
(3.10)
• Gamma distributed jumps: In this case  and
and  From the identity
From the identity
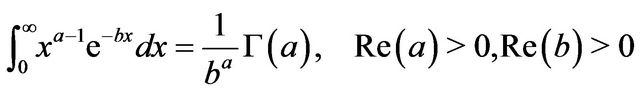
it follows that
 (3.11)
(3.11)
with .
.
• One-sided exponentially distributed jumps: Here , and
, and
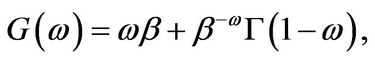 (3.12)
(3.12)
with .
.
In each of the above cases, the price  can be determined easily by a single integration. Another advantage of the approach is that hedging parameters, commonly known as Greek letters, are easily determined analytically. Popular Greeks widely used for risk management purposes are the delta, the gamma, and the vega of a contract4. The results for Greeks are summarized in the next proposition.
can be determined easily by a single integration. Another advantage of the approach is that hedging parameters, commonly known as Greek letters, are easily determined analytically. Popular Greeks widely used for risk management purposes are the delta, the gamma, and the vega of a contract4. The results for Greeks are summarized in the next proposition.
Proposition 3.2 Independently of the distribution of the jump size , the analytical expressions for the delta, gamma, and vega can be stated as follows:
, the analytical expressions for the delta, gamma, and vega can be stated as follows:
 (3.13)
(3.13)
 (3.14)
(3.14)
 (3.15)
(3.15)
where  and
and 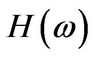 is given in Equation (3.2). In particular if
is given in Equation (3.2). In particular if  is a European plain vanilla put option the Greeks are determined as
is a European plain vanilla put option the Greeks are determined as
 (3.16)
(3.16)
 (3.17)
(3.17)
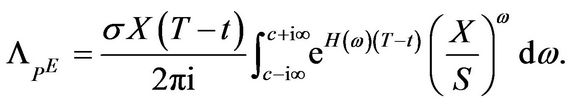 (3.18)
(3.18)
Proof: The expressions follow directly for Theorem 3.1 since we can differentiate under the integral sign. For the Greeks of a plain vanilla put one uses the Equation for  from (3.4) and simplifies.
from (3.4) and simplifies.
Similar to the derivative’s price the Greeks are characterized as a single integral which may be evaluated easily. Furthermore, hedge parameters for a range of different types of derivatives may be obtained by specifying the functional form for .
.
We complete this section by showing explicitly that Equation (3.1) with the special choices of 
 and log-normally distributed jumps is equivalent to Merton’s infinite series solution for a European put.
and log-normally distributed jumps is equivalent to Merton’s infinite series solution for a European put.
Proposition 3.3 If  and jumps are distributed log-normally with parameters
and jumps are distributed log-normally with parameters  and
and ,
,  , then (3.1) is equivalent to Merton’s solution which is formulated as an infinite series of BSMprices:
, then (3.1) is equivalent to Merton’s solution which is formulated as an infinite series of BSMprices:
 (3.19)
(3.19)
where 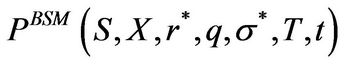 denotes the European put price due to Black, Scholes, and Merton and equals
denotes the European put price due to Black, Scholes, and Merton and equals
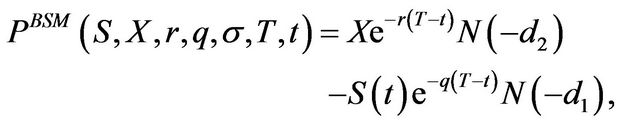
with
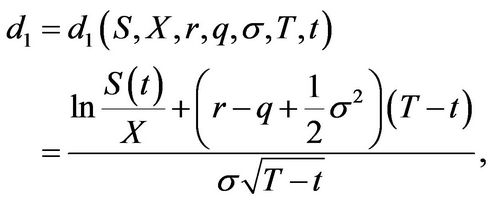
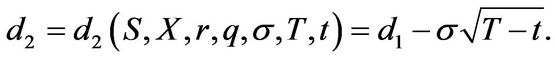
 is the cumulative standard normal distribution function and the adjusted parameters are given by
is the cumulative standard normal distribution function and the adjusted parameters are given by
 and
and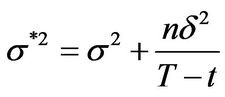 .
.
We will need the following Lemma. It gives the analytical expressions for two specific Mellin transforms.
Lemma 3.4 Let 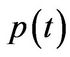 be a function of
be a function of 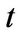 (time) and the functions
(time) and the functions 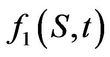 and
and  be defined as
be defined as
 (3.20)
(3.20)
and
 (3.21)
(3.21)
Then
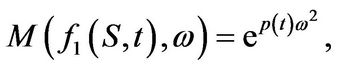 (3.22)
(3.22)
and
 (3.23)
(3.23)
Proof: Using the definition of Mellin transforms, we have that
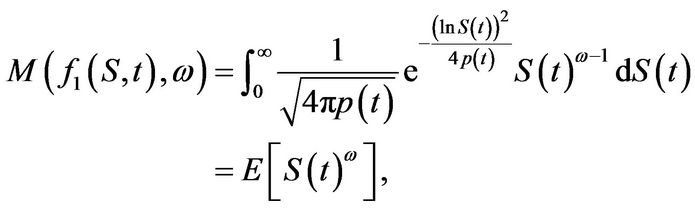
where 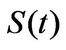 is a log-normally distributed random variable with mean 0 and variance
is a log-normally distributed random variable with mean 0 and variance . The statement follows directly from (3.7). Analogously we have for
. The statement follows directly from (3.7). Analogously we have for  after interchanging summation and integration
after interchanging summation and integration
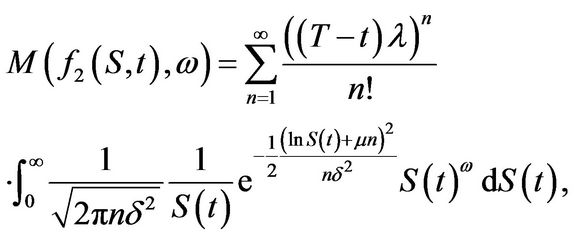
and the integral can be viewed as the  -th moment of a log-normally distributed random variable with mean
-th moment of a log-normally distributed random variable with mean  and variance
and variance . Therefore
. Therefore
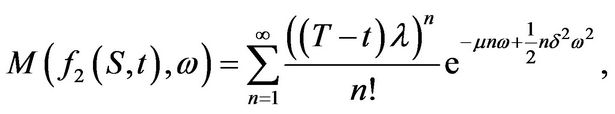
and the assertion follows.
Now we are going to prove Proposition 3.3.
Proof: Let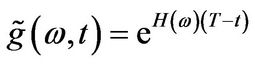 . Then
. Then
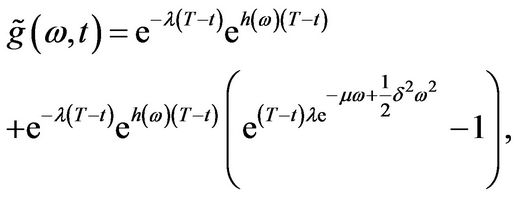 (3.24)
(3.24)
where
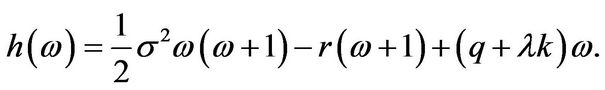
Now,
 (3.25)
(3.25)
with
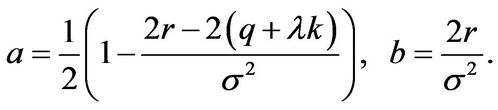 (3.26)
(3.26)
Therefore
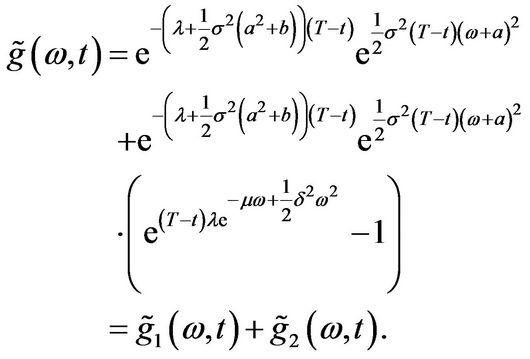
Let . Then it follows from Equations (3.20) and (3.22) that
. Then it follows from Equations (3.20) and (3.22) that
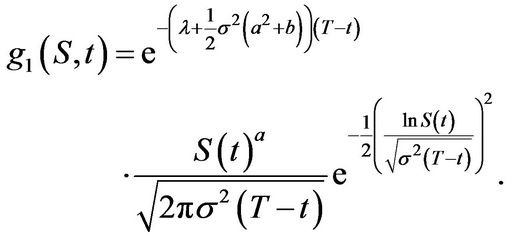 (3.27)
(3.27)
For , we apply the convolution theorem for Mellin transforms and (3.21) and (3.23) to get
, we apply the convolution theorem for Mellin transforms and (3.21) and (3.23) to get
 (3.28)
(3.28)
The transformation  gives
gives
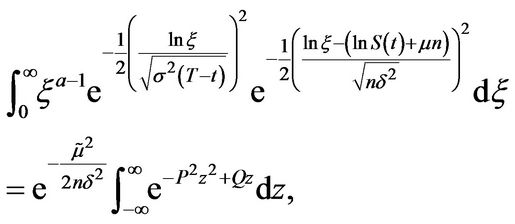
with
 (3.29)
(3.29)
 (3.30)
(3.30)
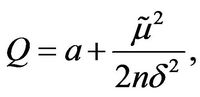 (3.31)
(3.31)
where  is defined in (3.26). From [20] p. 337,
is defined in (3.26). From [20] p. 337,
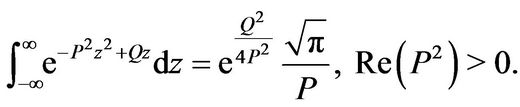
Using this result and simplifying yields after some algebra
 (3.32)
(3.32)
One observes that the expression for the summands in the Equation for  is also valid for
is also valid for . Since
. Since
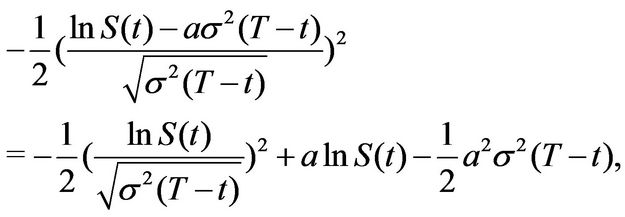
We arrive at the more compact form
 (3.33)
(3.33)
Merton’s solution follows now from the identity

where  and
and  is given in Equation (3.4). Since we have been able to derive an analytical expression for the inverse Mellin transform of
is given in Equation (3.4). Since we have been able to derive an analytical expression for the inverse Mellin transform of , convolution allows to write for the European put price
, convolution allows to write for the European put price
 (3.34)
(3.34)
The integrals above can be evaluated straightforwardly. Standard transformations convert both integrals into normal integrals. We get
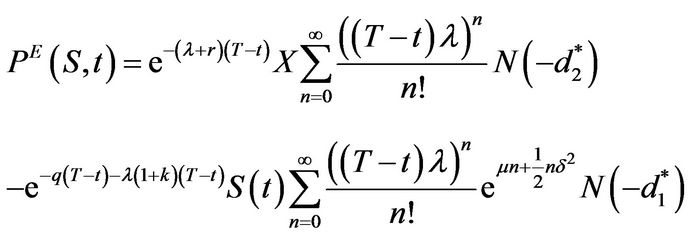 (3.35)
(3.35)
with the temporary quantities
 (3.36)
(3.36)
and
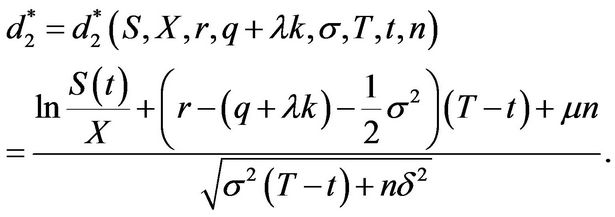 (3.37)
(3.37)
Finally, observing that
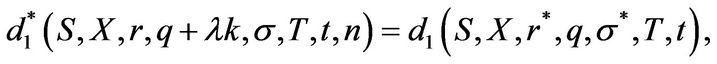
and
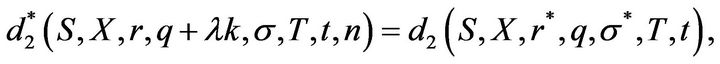
Merton’s solution follows immediately.
Corollary 3.5 The price of a European digital put 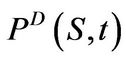 in Merton’s model equals
in Merton’s model equals

where the modified parameters  and
and  are defined in Proposition 3.3.
are defined in Proposition 3.3.
Proof: We have
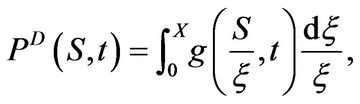
with 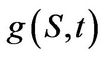 given in (3.33). The evaluation of the integral produces the result.
given in (3.33). The evaluation of the integral produces the result.
4. Numerical Results
This section presents the numerical results from implementing the analytical solutions derived in this paper. We start with options in the log-normal model of Merton (1976). The input parameters can be found in Table 1.
The parameters were found in [12] and are based on a calibration using European options on the S&P 500 stock index. Prices are determined for three different stock price levels (in-, out-, and at-the-money options). The solution based on Mellin transforms is given in Theorem 3.1. The integral is evaluated numerically using GaussLobatto quadrature. To get some information about the convergence of the results we truncate the limits of integration  gradually at
gradually at ,
,  ,
,  , and
, and  and choose
and choose . We also compute the “exact” solution using the infinite series representation with
. We also compute the “exact” solution using the infinite series representation with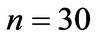 . Tables 2 and 3 show the results for the log-normal model.
. Tables 2 and 3 show the results for the log-normal model.
The next table summarizes the results for a digital put.
Our first and most important finding is that the framework proposed in this article is able to produce highly accurate prices for both types of derivatives. Even if the integration limits are truncated at  the results are correct up to the third/fourth position after decimal point
the results are correct up to the third/fourth position after decimal point
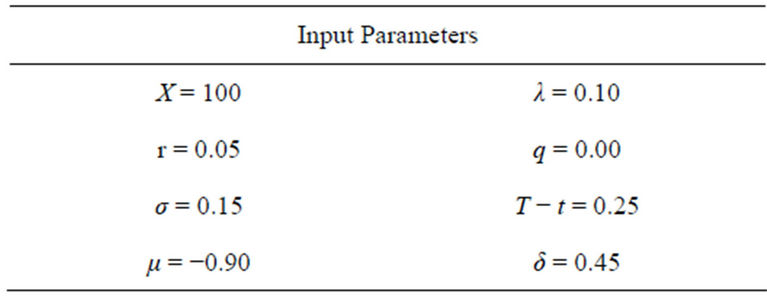
Table 1. Input parameters used for the numerical evaluation of the integral for European options in Merton’s model.

Table 2. Prices of European put options in Merton’s model using the infinite series representation with n = 30 and the integral solution from Theorem 3.1.
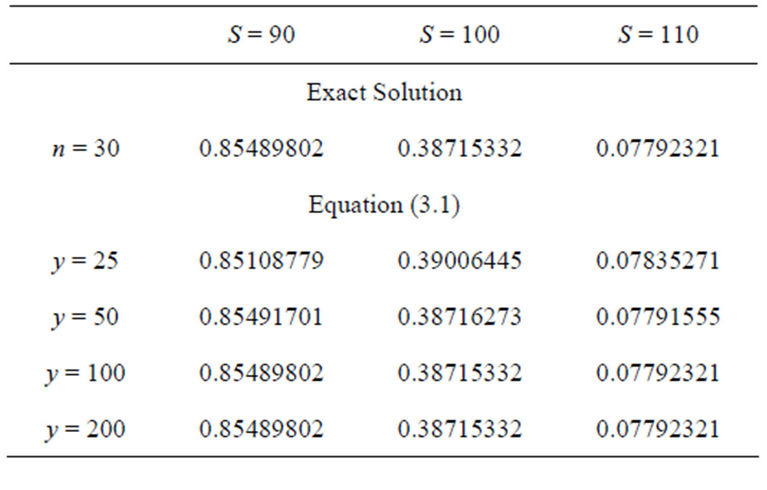
Table 3. Prices of European digital put options in Merton’s model using the infinite series representation with n = 30 and the integral solution from Theorem 3.1.
in each of the stock price scenarios. For  the prices coincide up to the eighth decimal place and there are no noteworthy differences between the two frameworks.
the prices coincide up to the eighth decimal place and there are no noteworthy differences between the two frameworks.
We conclude the numerical analysis by considering put options in Kou’s double exponential model. The “exact” solution in form of an infinite series can by found in the original article of Kou. The input parameters are the same as above except for the jump component: 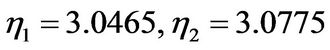 and
and . Table 4 shows the results for the double exponential model.
. Table 4 shows the results for the double exponential model.
Similar to the log-normal model, the numerical approximation of the integral solution produces satisfactory results. The convergence rate is comparable to the previous model.
In summary, the numerical experiments carried out demonstrate that the new framework besides its theoretical insights produces prices with a convincing degree of precision. The Mellin transform approach must be regarded as a capable alternative to existing methods.
5. Conclusions
The purpose of this paper is to explore the valuation of options where the underlying follows a jump-diffusion. The Mellin integral transform approach was applied to solve the homogeneous PIDE analytically. The proposed solution has a very compact form as one single integral which may be evaluated easily and quickly by quadrature. The final pricing formula offers a powerful and flexible tool for handling a variety of jump size distributions and payoff structures. For log-normally distributed jumps, it was shown explicitly that in case plain vanilla puts our integral expression equivalent to the infinite series solution of BSM-prices.
The numerical results are convincing and logically consistent. They come along with the theoretical findings.
Future research projects are multifaceted. An extension of the proposed approach to American options
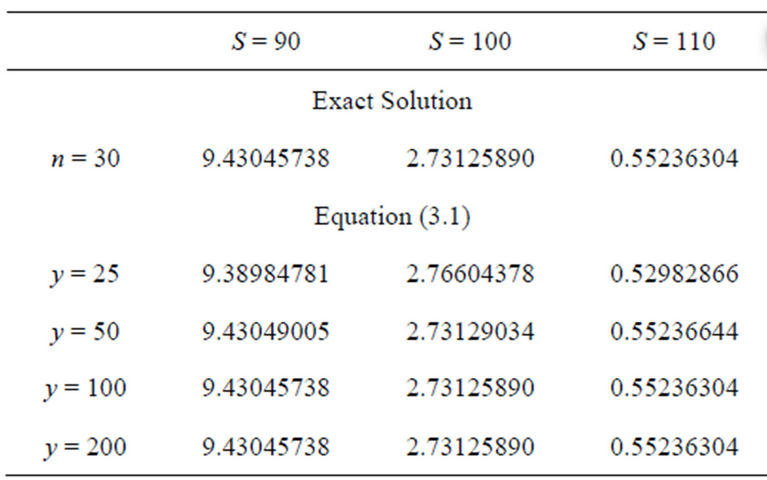
Table 4. Prices of European put options in Kou’s model using the infinite series representation with n = 30 and the integral solution from Theorem 3.1.
seems to be possible. Also multi-asset options in jumpdiffusions could be valued within this framework.
NOTES
Disclaimer: Statements and conclusions made in this article are entirely those of the author. They do not necessarily reflect the views of LBBW.
1If  is a digital European put option,
is a digital European put option,  the payoff function equals
the payoff function equals , where
, where  is a prespecified level.
is a prespecified level.
2This process was suggested in [19] to incorporate jumps into the stochastic volatility process.
3For a digital put we have .
.
4Others are for instance the theta or the rho. They are determined in the same manner as outlined in the text and therefore omitted.