Can the Abraham Light Momentum and Energy in a Medium Constitute a Lorentz Four-Vector? ()
1. Introduction
The momentum of light in a medium is a fundamental question and has kept attracting extensive interest [1-15]. There are different ways to define the light momentum, which all have their own merits [1,4,10]. However in this paper, the light momentum is defined as single photon’s momentum or electromagnetic (EM) momentum. According to this definition, the single photon’s momentum and energy are the direct result of Einstein light-quantum hypothesis of EM momentum and energy.
The plane-wave model is the simplest physical model for studying light momentum, and it can be strictly treated mathematically in the Maxwell equation frame; however, the physical results obtained are fundamental. For example, the Lorentz transformation of photon density in the isotropic-fluid model treated by sophisticated field theory is exactly the same as that in the plane-wave model [15].
As a fundamental hypothesis in the special theory of relativity, the principle of relativity requires that the laws of physics be the same in form in all inertial frames of reference. Therefore, all inertial frames are equivalent and there is no preferred inertial frame for descriptions of physical phenomena. For example, Maxwell equations, Fermat’s principle, and the conservation laws of global momentum and energy are all valid in any inertial frames, no matter whether the medium is moving or at rest, and no matter whether the space is partially or fully filled with a medium.
For an ideal plane wave (phase velocity equal to group velocity or energy velocity), the phase function characterizes the propagation of energy and momentum of light. 1) The light momentum is parallel to the wave vector, and 2) the phase function is a Lorentz invariant. As physical laws, according to the principle of relativity, the above two basic properties are valid in any inertial frames. From this we can conclude that the correct light momentum and energy must constitute a Lorentz covariant four-vector, and the Minkowski’s momentum is the unique correct light momentum [15].
Why should the light momentum be parallel to the wave vector? Conceptually speaking, the direction of photon propagation is the direction of photon’s momentum and energy propagation. The plane-wave phase function defines all equi-phase planes of motion, with the wave vector as their normal vector. From one equi-phase plane to another equi-phase plane, the path parallel to the normal vector is the shortest. Fermat’s principle indicates that, light follows the path of least time. Thus the direction of photon propagation must be parallel to the wave vector, and so must the light momentum. The phase function is Lorentz symmetric, namely it has exactly the same form in all inertial frames. Consequently, this property of light momentum must be valid in all inertial frames.
In a recent Letter by Barnett [7], a widely-accepted total-momentum model is analyzed for resolution of the Abraham-Minkowski debate, where both Abraham’s and Minkowski’s momentums are shown to be the correct light momentums, with the former being the kinetic momentum and the latter the canonical momentum.
In this paper, by analyzing the total momentum model [7] with the principle of relativity for a dielectric-medium Einstein-box thought experiment (also called “Balazs thought experiment”) [11,12], it is shown that the Abraham’s momentum and energy in a medium cannot constitute a Lorentz four-vector, and they consequentially break the global momentum and energy conservation laws when a photon enters the medium box from vacuum. Accordingly, it is not justifiable to take the Abraham’s momentum as the correct light momentum. In contrast, Minkowski’s momentum and energy always constitute a Lorentz four-vector no matter whether in a medium or in vacuum; thus the Minkowski’s momentum is the unique correct light momentum. A new kind of mass, momentum-associated photon mass in a medium is exposed, which explains why the Abraham’s momentum is obtained in the traditional “center-of-mass-energy” analysis of this thought experiment [7]. The EM boundary-condition matching approach, combined with Einstein light-quantum hypothesis, is proposed to analyze this thought experiment, and it is found for the first time that only from Maxwell equations without resort to the principle of relativity, the correctness of light momentum definitions cannot be identified. Optical pulling effect is studied as well.
2. Abraham’s Photon Momentum Breaking the Global Momentum and Energy Conservation Laws
As a physical law, according to the principle of relativity, the total momentum model [7] should be valid in any inertial frames. When applying this model to the Einstein-box thought experiment, with a slightly different process from that in [7], where a single photon has entered a block of transparent medium with a dimension much larger than the photon’s wavelength, observed in the medium-rest frame the total momentum is equal to Abraham’s photon momentum, because the medium kinetic momentum is zero. However, as shown in Appendix A, the Abraham’s photon momentum cannot be used to constitute a Lorentz covariant momentum-energy fourvector; consequently, the total momentum cannot either. Similarly, observed in the lab frame, the momentum and energy of the medium box independently constitute a four-vector while the Abraham’s photon momentum and energy do not. Thus the four-vector Lorentz covariance of the total momentum and energy is questionable.
It is a well-known postulate that the total (global) momentum and energy are conservative for an isolated physical system [13], which is valid in all inertial frames. The photon and the medium box form an isolated system in the Einstein-box thought experiment. Based on the Lorentz property of Abraham’s photon momentum, we have shown in above that the total momentum and energy cannot constitute a Lorentz four-vector after the photon has entered the medium box. In fact, by taking advantage of the initial conditions, we can further show that the Abraham’s photon momentum in a medium is not compatible with the momentum and energy conservation laws. The derivations are given below.
1) Suppose that before the photon enters the medium box, the photon initially is located far away from the medium box in vacuum. Thus initially the photon’s Abraham (= Minkowski) momentum and energy
 constitute a Lorentz four-vector.
constitute a Lorentz four-vector.
2) The medium box is made up of massive particles, and its kinetic momentum and energy  constitute a Lorentz four-vector no matter before or after the photon enters the medium box.
constitute a Lorentz four-vector no matter before or after the photon enters the medium box.
3) From 1) and 2), initially the total momentum and energy constitute a four-vector, namely

is a four-vector.
4) According to the momentum and energy conservation laws, the total momentums and energies are equal before and after the photon enters the box, namely
 .
.
From 3), we know that  is a fourvector, and thus
is a fourvector, and thus

also is a four-vector. Further, because 
is a four-vector resulting from 2), 
must be a four-vector. However  cannot be a four-vector according to the principle of relativeity [confer Equation (A-3) in Appendix A]. Thus we conclude that the Abraham’s photon momentum contradicts the momentum and energy conservation laws in the principle-of-relativity frame, which means that the Abraham’s photon momentum cannot make the conservation laws holding in all inertial frames—the direct physical consequences of Abraham’s light momentum.
cannot be a four-vector according to the principle of relativeity [confer Equation (A-3) in Appendix A]. Thus we conclude that the Abraham’s photon momentum contradicts the momentum and energy conservation laws in the principle-of-relativity frame, which means that the Abraham’s photon momentum cannot make the conservation laws holding in all inertial frames—the direct physical consequences of Abraham’s light momentum.
From the above relativity analysis of Einstein-box thought experiment, we can see that the correct light momentum and energy must constitute a Lorentz fourvector when the global momentum and energy conservation laws are taken to be the fundamental postulates [13], which actually is a criterion of identifying the correctness of light momentum definitions. This conclusion is completely in agreement with that obtained from a plane wave in a moving uniform medium [15], as stated in Section 1.
It is interesting to point out that, it is the Fermat’s principle and the principle of relativity that require the light momentum and energy to constitute a Lorentz fourvector for a plane wave in a moving uniform medium where there is no momentum transfer taking place [15], while it is the global momentum and energy conservation laws that require the light momentum and energy to constitute a Lorentz four-vector in the Einstein-box thought experiment where there is a momentum transfer taking place when the photon goes into a medium box.
3. Einstein-Box Thought Experiment Analyzed by EM Boundary-Condition Matching Approach
It has been shown that the Abraham’s light momentum and energy for a plane wave in a uniform medium is not Lorentz covariant [15]. The plane wave is a strict solution of Maxwell equations in the macro-scale electromagnetic theory, and this solution indicates that the Minkowski’s momentum density vector  and energy density
and energy density  constitute a Lorentz fourvector in the form of
constitute a Lorentz fourvector in the form of , with
, with  the “EM-field-cell density” or “photon density” in volume [15], and c the vacuum light speed. When Einstein’s light-quantum hypothesis
the “EM-field-cell density” or “photon density” in volume [15], and c the vacuum light speed. When Einstein’s light-quantum hypothesis  is imposed,
is imposed,  is restored to a single photon’s momentum-energy four-vector, namely
is restored to a single photon’s momentum-energy four-vector, namely 
 , with
, with  the wave vector; thus
the wave vector; thus  denotes the unique correct light momentum. For the plane wave in a uniform medium,
denotes the unique correct light momentum. For the plane wave in a uniform medium, 
 holds in all inertial frames, where
holds in all inertial frames, where  is the refractive index and
is the refractive index and  is the unit wave vector [15].
is the unit wave vector [15].
Now let us apply the Minkowski’s momentum to analysis of a plane-wave light pulse perpendicularly incident on the above transparent medium box without any reflection [12,14]. The pulse space length is assumed to be much larger than the wavelength but less than the box length. To eliminate any reflection, the wave-impedance matching must be reached between vacuum and the medium [12], namely the wave impedance  with
with  and
and  is continuous on the boundary (confer Figure A1 in Appendix B).
is continuous on the boundary (confer Figure A1 in Appendix B).
Since there is no reflection, there is no energy accumulation in the sense of time average. Thus “no-reflection” can be expressed as “equal energy flux density” on the both sides of the vacuum-medium interface inside the light pulse, given by

or
 . (1)
. (1)
The above Equation (1) is indeed equivalent to the wave-impedance matching condition

when the perpendicularly-incident plane-wave boundary condition  is considered, because in such a case we have
is considered, because in such a case we have

namely Equation (1), where  is employed.
is employed.
From Equation (1), we have
 (2-1)
(2-1)
namely
 . (2-2)
. (2-2)
The momentum flux density in the medium is , while the momentum flux density in the vacuum is
, while the momentum flux density in the vacuum is . Thus from Equation (2-2) we have
. Thus from Equation (2-2) we have
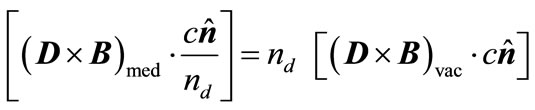 . (3)
. (3)
Equation (3) tells us that, after the Minkowski’s EM momentum (in unit area and unit time) flows into the medium from vacuum, the momentum grows by  times. To keep the total momentum unchanged, there must be a pulling force acting on the medium when the plane-wave light pulse goes into the medium box (see Appendix B), which is the result from macro-electromagnetic theory based on the assumption of “no reflection”. This pulling force can be qualitatively explained as the Lorentz force produced by the interaction of the dielectric bound current with the incident light pulse [12].
times. To keep the total momentum unchanged, there must be a pulling force acting on the medium when the plane-wave light pulse goes into the medium box (see Appendix B), which is the result from macro-electromagnetic theory based on the assumption of “no reflection”. This pulling force can be qualitatively explained as the Lorentz force produced by the interaction of the dielectric bound current with the incident light pulse [12].
Now let us examine the result from Einstein lightquantum theory. The photon energy (frequency) is supposed to be the same no matter whether in vacuum or in a medium. Einstein light-quantum hypothesis requires that
 and
and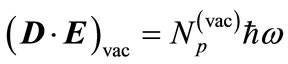 with
with  the photon density in medium and
the photon density in medium and  the photon density in vacuum. Inserting them into Equation (1), we have
the photon density in vacuum. Inserting them into Equation (1), we have
 . (4)
. (4)
Supposing that  and
and 
are the photon momentums in medium and in vacuum respectively, from the definition of momentum density we have
 (5-1)
(5-1)
 . (5-2)
. (5-2)
Inserting Equations (4) and (5) into Equation (3), we have the photon momentum in the medium, given by

or
 . (6)
. (6)
From Equation (6) we can see that when a single photon goes into the medium box, the medium box also gets a pulling force to keep the total momentum unchanged.
From Equation (3) and Equation (6) we find that a light pulse and a single photon in the medium-box thought experiment both have the pulling effect. How do we explain the fiber recoiling experiment then [5]? The recoiling could be resulting from the transverse radiation force because of an azimuthal asymmetry of refractive index in the fiber [9].
4. Implicit Assumption of Photon’s Mass in the Traditional “Center of Mass-Energy” Argument
It is worthwhile to point out that, the widely-recognized “center of mass-energy” argument for Abraham’s photon momentum [7] is questionable. As shown in Appendix C, this argument neglects the difference between the “momentum-associated mass” and “energy-associated mass” for a photon in a medium. Specifically speaking, this argument has implicitly assumed that the relation between photon’s “momentum-associated” mass and its momentum in a dielectric is the same as that in vacuum. The photon momentum-associated mass in vacuum, formulated by , is derived from “vacuum” Einstein-box thought experiment [16,17], and whether the formulation still holds in a “dielectric” remains to be confirmed. Now that this assumption has already resulted in contradictions with the covariance of relativity, the justification of the assumption should be re-considered.
, is derived from “vacuum” Einstein-box thought experiment [16,17], and whether the formulation still holds in a “dielectric” remains to be confirmed. Now that this assumption has already resulted in contradictions with the covariance of relativity, the justification of the assumption should be re-considered.
5. Conclusion
In summary, by analysis of the total momentum model [7] with the principle of relativity for a medium Einstein-box thought experiment, we have shown that the Abraham’s light momentum and energy in a medium do not constitute a Lorentz four-vector, and they break the global momentum-energy conservation law; accordingly, it is not justifiable to take the Abraham’s momentum as the correct light momentum. In contrast, Minkowski’s momentum and energy always constitute a four-vector no matter whether in a medium or vacuum, and the Minkowski’s momentum is the unique correct light momentum. This result of the relativity principle is important, because only based on the Maxwell equations one cannot judge which formulation of light momentum is correct. For example, inserting

and

into Equation (3), we directly obtain the conversion equation for Abraham’s momentum flux density from vacuum to medium, given by
 , (7)
, (7)
and similarly, inserting
 ,
,
 and
and  into above Equation (7), we have the Abraham’s photon momentum in medium, given by
into above Equation (7), we have the Abraham’s photon momentum in medium, given by

or
 . (8)
. (8)
Thus in the Maxwell-equation frame, the medium Einstein-box thought experiment supports both light momentum formulations, instead of just Abraham’s [7]. However, the two formulations cannot be “both correct”; otherwise it is not determinate whether the medium box gets a pulling force or a pushing force when a specific photon goes into the medium from vacuum. In other words, without resort to the principle of relativity, this thought experiment cannot be used to identify the correctness of light momentum definitions.
Appendix A. Lorentz Property of the Abraham’s Photon Momentum and Energy
In this Appendix, by analysis of the Lorentz property of the total momentum model in the dielectric-medium Einstein-box thought experiment [7], a specific proof is given of why the Abraham’s photon momentum and energy cannot constitute a Lorentz four-vector.
According to the total-momentum model [7], the total momentum and the total energy are assumed to constitute a momentum-energy four-vector.
Suppose that the total momentum  and the total energy
and the total energy  in the lab frame are written as
in the lab frame are written as
 ,
,  with
with  a four-vector, (A-1)
a four-vector, (A-1)
where  and
and  are, respectively, the medium-box kinetic momentum and energy, while
are, respectively, the medium-box kinetic momentum and energy, while  and
and  are, respectively, the Abraham’s photon momentum and energy.
are, respectively, the Abraham’s photon momentum and energy.
After the single photon has entered the Einstein’s medium box, according to the principle of relativity (the laws of physics are the same in form in all inertial frames), the total momentum and energy in the mediumrest frame can be written as
 ,
,  with
with  a four-vector, (A-2)
a four-vector, (A-2)
where  and
and  are, respectively, the medium-box kinetic momentum and energy, while
are, respectively, the medium-box kinetic momentum and energy, while  and
and  are, respectively, the Abraham’s photon momentum and energy.
are, respectively, the Abraham’s photon momentum and energy.
Since  is assumed to be a Lorentz four-vector,
is assumed to be a Lorentz four-vector,

can be obtained from

by Lorentz transformation.
Now let us examine whether the total momentum  [7] can really make
[7] can really make  become a Lorentz four-vector.
become a Lorentz four-vector.
In the medium-rest frame, the medium kinetic momentum is equal to zero, namely , and the total momentum is reduced to
, and the total momentum is reduced to
 .
.
1) The medium-box kinetic momentum  and its rest energy
and its rest energy  independently constitute a Lorentz four-vector, namely
independently constitute a Lorentz four-vector, namely  is a fourvector.
is a fourvector.
2) The Abraham’s photon momentum and energy is given by
 , (A-3)
, (A-3)
where  is the refractive index of medium,
is the refractive index of medium,  is the photon’s frequency,
is the photon’s frequency,  is the unit vector of the photon’s moving direction, and
is the unit vector of the photon’s moving direction, and  is the Planck constant. We have known that, the wave four-vector
is the Planck constant. We have known that, the wave four-vector  must be a Lorentz four-vector and the Planck constant
must be a Lorentz four-vector and the Planck constant  must be a Lorentz invariant [15], and thus the Abraham’s photon momentum and energy Equation (A-3) cannot be a four-vector; otherwise, contradictions would result mathematically [18].
must be a Lorentz invariant [15], and thus the Abraham’s photon momentum and energy Equation (A-3) cannot be a four-vector; otherwise, contradictions would result mathematically [18].
From 1) and 2) we conclude that the total momentum and energy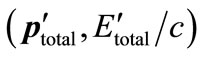 , which are the combinations of two parts respectively, cannot be a Lorentz fourvector.
, which are the combinations of two parts respectively, cannot be a Lorentz fourvector.
If  is not a Lorentz four-vector observed in one inertial frame, then it is never a Lorentz four-vector observed in any inertial frames.
is not a Lorentz four-vector observed in one inertial frame, then it is never a Lorentz four-vector observed in any inertial frames.
The above reasoning is based on the following facts:
1) General math results. a) If  and
and  are both Lorentz four-vectors, then
are both Lorentz four-vectors, then  must be Lorentz four-vectors. b) If
must be Lorentz four-vectors. b) If  is a known Lorentz four-vector in one inertial frame, then it is always a Lorentz fourvector observed in any inertial frames.
is a known Lorentz four-vector in one inertial frame, then it is always a Lorentz fourvector observed in any inertial frames.
2) In the medium Einstein-box thought experiment, like a massive particle the medium-box kinetic momentum and energy independently constitute a Lorentz fourvector because the medium box is made up of massive particles, of which each has a kinetic momentum-energy four-vector.
In summary, when applying the principle of relativity to the total momentum model [7] for the dielectricmedium Einstein-box thought experiment, we obtain the following conclusion. Observed in any inertial frames1) The total momentum and energy is the combination of the medium-box and Abraham’s momentums and energies, namely
 ;
;
2) The medium-box momentum and energy  must be a Lorentz four-vector;
must be a Lorentz four-vector;
3) The Abraham’s photon momentum and energy  cannot be a Lorentz four-vector.
cannot be a Lorentz four-vector.
Therefore, the total momentum and energy  is not a Lorentz four-vector.
is not a Lorentz four-vector.
One might argue that in stead of Equation (A-3) the photon’s momentum and energy should be
 where the photon energy is replaced by Chu’s energy
where the photon energy is replaced by Chu’s energy  [13]. However it can be shown that this kind of momentum and energy also contradicts the wave fourvector
[13]. However it can be shown that this kind of momentum and energy also contradicts the wave fourvector . That is because the Lorentz transformation of frequency (Doppler formula) and the transformation of refractive index are already defined by
. That is because the Lorentz transformation of frequency (Doppler formula) and the transformation of refractive index are already defined by  [15]. Defining a four-momentum will introduce new Lorentz transformations of the frequency and refractive index, which contradict the formers unless the four-momentum is compatible with
[15]. Defining a four-momentum will introduce new Lorentz transformations of the frequency and refractive index, which contradict the formers unless the four-momentum is compatible with . The Minkowski’s four-momentum
. The Minkowski’s four-momentum , no matter whether in a medium or in vacuum, is only different from
, no matter whether in a medium or in vacuum, is only different from  by a Planck constant
by a Planck constant , which is a Lorentz scalar [15], and it is completely compatible with
, which is a Lorentz scalar [15], and it is completely compatible with . Thus only the Minkowski’s momentum is the unique correct light momentum in the Einstein-box thought experiment.
. Thus only the Minkowski’s momentum is the unique correct light momentum in the Einstein-box thought experiment.
One might question whether a) the medium-box kinetic momentum  and energy
and energy  can really independently constitute a Lorentz four-vector and b) there is any medium-rest frame, because there must be relative motions between the elements of medium (fluid), which, even if quite small, could not be ignored in the sense of strict relativity.
can really independently constitute a Lorentz four-vector and b) there is any medium-rest frame, because there must be relative motions between the elements of medium (fluid), which, even if quite small, could not be ignored in the sense of strict relativity.
In fact, even if there are relative motions between the elements of the dielectric medium, the medium-box kinetic momentum and energy also independently constitute a four-vector, which is elucidated below.
According to the total momentum model [7, Equation (7) there], the total momentum and energy are given by
 and
and , which are conservative.
, which are conservative.  and
and  denote the medium kinetic momentum and energy, and they are only contributed by all the massive particles of which the dielectric medium is made up, while
denote the medium kinetic momentum and energy, and they are only contributed by all the massive particles of which the dielectric medium is made up, while  and
and  denote the EM kinetic momentum and energy and they are only contributed by all EM fields or waves.
denote the EM kinetic momentum and energy and they are only contributed by all EM fields or waves.
One essential difference between massive particles and photons is that any massive particle has its fourvelocity defined by 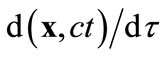 with
with  its proper time, while the photon does not [15]. Because the medium box is made up of massive particles and each of the particles has a four-velocity, no matter whether there are any relative motions between the particles, the mediumbox total kinetic momentum
its proper time, while the photon does not [15]. Because the medium box is made up of massive particles and each of the particles has a four-velocity, no matter whether there are any relative motions between the particles, the mediumbox total kinetic momentum  and energy
and energy  should constitute a four-vector. For a better understanding, specific calculations are given below.
should constitute a four-vector. For a better understanding, specific calculations are given below.
Suppose that observed in the lab frame, the fourvelocity of a massive particle is given by , and the medium-box total kinetic momentum-energy fourvector can be written as
, and the medium-box total kinetic momentum-energy fourvector can be written as
 , (A-4)
, (A-4)
where
 , and
, and , (A-5)
, (A-5)
with ,
, , and
, and , respectively, the individual particles’ rest mass, relativistic factor, and velocity.
, respectively, the individual particles’ rest mass, relativistic factor, and velocity.
Now we can define the moving velocity of the whole medium box with respect to the lab frame, given by [19]
 , (A-6)
, (A-6)
and its relativistic factor  and the medium-box rest mass
and the medium-box rest mass , given by
, given by
 ,
, . (A-7)
. (A-7)
The medium-box kinetic momentum-energy fourvector now can be re-written as
 . (A-8)
. (A-8)
From above we can see that, a) the medium-box kinetic momentum and energy indeed independently constitute a four-vector, and b) there is a medium-rest frame for the box, which moves at the velocity v with respect to the lab frame defined by Equation (A-6).
If all particles could always keep the same velocity, this medium box would become a “rigid body”; thus possibly causing the controversy of the compatibility with relativity. However it should be emphasized that, in the uniform-medium model [15], it is the dielectric parameters ( and
and ) that are assumed to be real scalar constants observed in the medium-rest frame, instead of the medium being “rigid”; thus this model is completely compatible with the relativity. In fact, the uniform-medium model is widely used in literature [7,20], although all atoms or molecules in dielectric materials used as a uniform medium are always in constant motion or vibration. Especially, the uniform-medium model is also strongly supported by the wellknown relativity experiment, Fizeau running-water experiment, where the refractive index of the water in the water-rest frame is taken to be a constant [21].
) that are assumed to be real scalar constants observed in the medium-rest frame, instead of the medium being “rigid”; thus this model is completely compatible with the relativity. In fact, the uniform-medium model is widely used in literature [7,20], although all atoms or molecules in dielectric materials used as a uniform medium are always in constant motion or vibration. Especially, the uniform-medium model is also strongly supported by the wellknown relativity experiment, Fizeau running-water experiment, where the refractive index of the water in the water-rest frame is taken to be a constant [21].
Appendix B. Optical Pulling Effect in the Einstein-Box Thought Experiment
In the medium Einstein-box thought experiment for a light pulse, the pulling force per unit cross-section area acting on the medium box can be directly obtained from the EM boundary conditions of “no reflection”, as shown below.
The momentum flowing through the inner medium surface per unit area and time, observed in the “instant medium-rest frame”, is given by
 , (B-1)
, (B-1)
and the momentum flowing through the inner vacuum surface per unit area and time is given by
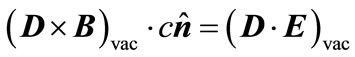 , (B-2)
, (B-2)
where  is the relativity-legitimate Minkowski’s momentum density, and
is the relativity-legitimate Minkowski’s momentum density, and  and
and  are, respectively, the propagation velocities of EM momentum and energy in the medium and vacuum. The “instant medium-rest frame” means the frame in which the medium is at rest from time
are, respectively, the propagation velocities of EM momentum and energy in the medium and vacuum. The “instant medium-rest frame” means the frame in which the medium is at rest from time  to
to .
.
Considering  given by Equation (1), which results from the electromagnetic boundary conditions, we obtain
given by Equation (1), which results from the electromagnetic boundary conditions, we obtain
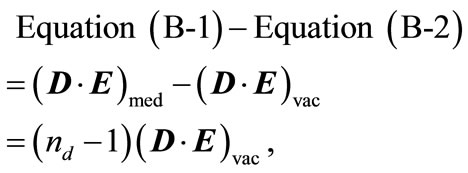
which is the momentum gained by the light pulse in unit cross-section area and unit time. From this we directly obtain the Minkowski’s force acting on the box, as shown in Figure A1, given by
 [N/m2], (B-3)
[N/m2], (B-3)
where  means that the force direction is opposite to the direction of wave propagation, namely a pulling force.
means that the force direction is opposite to the direction of wave propagation, namely a pulling force.
For a plane wave, after taking time average the pulling force is given by
 , (B-4)
, (B-4)
where , and
, and  is the plane-wave electric field amplitude in vacuum.
is the plane-wave electric field amplitude in vacuum.
Light-quantizing Equation (B-3) by 
 and considering that
and considering that  is the photon number flux density (photon number through unit cross-section area in unit time in vacuum), we obtain the transferred momentum from a single photon to the medium when the photon goes into the box, given by
is the photon number flux density (photon number through unit cross-section area in unit time in vacuum), we obtain the transferred momentum from a single photon to the medium when the photon goes into the box, given by
 . (B-5)
. (B-5)
It should be indicated that the pulling force Equation (B-3) is obtained without any ambiguity based on the momentum conservation law; however, some ambiguity will show up if using the surface bound current  and the magnetic field B to calculate the force by
and the magnetic field B to calculate the force by , because B is not continuous on the vacuum-medium interface [12].
, because B is not continuous on the vacuum-medium interface [12].
One might argue that the leading edge of the light pulse would also produce a force to cancel out the pulling force resulting from the momentum transfer on the vacuum-medium interface so that no net momentum transfer would take place [12]. However, such an argument does not seem consistent with the dielectric property of an isotropic uniform medium.
An ideal isotropic uniform medium has no dispersion and losses; accordingly, any part of the pulse within the medium always keeps the same shape and the same wave momentum during propagation within the medium, as illustrated in Figure A1. Thus there is no additional momentum transfer happening except for on the vacuummedium interface.
In calculations of the Lorentz force caused by polarization and magnetization, how to appropriately approximate a light pulse is tricky. As shown in Figure A1, the basic physical condition, which the pulse is required to satisfy, is the “moving boundary condition”, namely the EM fields E and B on the leading and trailing pulse edges must be equal to zero, because the EM fields Dielectric medium box
should, at least, be continuous at any locations and any times within a uniform medium (even if the medium had dispersion). As implicitly shown in the calculations by Mansuripur, the pulse edges, which meet the “moving boundary condition”, will not produce additional Lorentz forces in the sense of time average [12; see the author’s Equation (10) by setting  and T = an integer of wave periods]. In other words, the momentum transfer from the light pulse to the box only takes place on the vacuum-medium interface, while the pulse edges located inside the uniform medium do not have any contributions to momentum transfer.
and T = an integer of wave periods]. In other words, the momentum transfer from the light pulse to the box only takes place on the vacuum-medium interface, while the pulse edges located inside the uniform medium do not have any contributions to momentum transfer.
Appendix C. Photon’s Energy-Associated Mass and Momentum-Associated Mass in a Dielectric Medium
It is worthwhile to point out that, there are two kinds of mass: 1) energy-associated mass , defined through
, defined through  (Einstein’s energy-mass equivalence formula), and 2) momentum-associated mass
(Einstein’s energy-mass equivalence formula), and 2) momentum-associated mass , defined through
, defined through , where
, where ,
,  , and
, and  are, respectively, the particle energy, momentum, and velocity, with
are, respectively, the particle energy, momentum, and velocity, with 
 its four-momentum. For classical particles and photons in vacuum,
its four-momentum. For classical particles and photons in vacuum,  holds, while for photons in a medium,
holds, while for photons in a medium,  and
and  are valid, which lead to a Lorentz covariant Minkowski’s four-momentum. Thus we have
are valid, which lead to a Lorentz covariant Minkowski’s four-momentum. Thus we have 
 for classical massive particles,
for classical massive particles,  for photons in vacuum, and
for photons in vacuum, and  for photons in a medium. Because of
for photons in a medium. Because of  in a medium, the photon mass-vs-momentum relation is different from that in vacuum where
in a medium, the photon mass-vs-momentum relation is different from that in vacuum where  holds. In other words, only
holds. In other words, only  is the Lorentz covariant photon momentum in a medium, instead of
is the Lorentz covariant photon momentum in a medium, instead of .
.
For an isolated system, the total momentum and energy are both conserved, namely
 and
and leading to the holding of
leading to the holding of
 .
.
Thus we have the mass-energy center

moving uniformly. Note that in 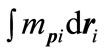 the momentum-associated mass
the momentum-associated mass  is involved, instead of the energy-associated mass
is involved, instead of the energy-associated mass . To calculate
. To calculate

in the dielectric Einstein-box thought experiment,  should be assumed to be known, including the box’s and the photon’s. In the typical analysis by Barnett [7],
should be assumed to be known, including the box’s and the photon’s. In the typical analysis by Barnett [7], 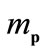
for the photon in the medium is replaced by 
(the same as that in vacuum). However if  for the photon in the medium is known, then the photon momentum is actually known, equal to
for the photon in the medium is known, then the photon momentum is actually known, equal to , with no further calculations needed, which is the straightforward way used by Leonhardt, except that he also uses
, with no further calculations needed, which is the straightforward way used by Leonhardt, except that he also uses  to replace
to replace  [20]. From above, we can see that the Abraham’s momentum in the dielectric Einstein-box thought experiment is derived actually by assuming an Abraham’s momentum in advance.
[20]. From above, we can see that the Abraham’s momentum in the dielectric Einstein-box thought experiment is derived actually by assuming an Abraham’s momentum in advance.
To better understand why the Abraham’s momentum is derived in the traditional analysis of the Einstein-box thought experiment [7], specific illustrations are given below.
Figure A2 shows the thought experiment consisting of a short light pulse and a transparent medium box. Case-1 is for the pulse not going through the box, while case-2 is for the pulse going through the box. The two cases have the same initial conditions and thus they have the same center of mass-energy.
Case-1. Since the pulse does not go through the medium box and the box always keeps at rest, the massenergy center for the system is given by
 (C-1)
(C-1)
where  is the initial mass-energy center, the pulse energy is
is the initial mass-energy center, the pulse energy is , and the box energy is
, and the box energy is . In the vacuum, the pulse momentum-associated mass and energy-associated mass are the same, equal to
. In the vacuum, the pulse momentum-associated mass and energy-associated mass are the same, equal to , and the pulse momentum is given by
, and the pulse momentum is given by .
.
Case-2. The mass-energy center for the pulse going through the box is given by
 ,
, (C-2)
(C-2)
 for t1 ≤ t ≤ t2 (C-3)
for t1 ≤ t ≤ t2 (C-3)
 for t ≥ t2 (C-4)
for t ≥ t2 (C-4)
where  is the pulse momentum-associated mass in the medium, thus leading to the pulse momentum given by
is the pulse momentum-associated mass in the medium, thus leading to the pulse momentum given by  with
with  the pulse energy velocity; the pulse energy is
the pulse energy velocity; the pulse energy is , the same as in the vacuum;
, the same as in the vacuum;  is the box momentum, with
is the box momentum, with  the box moving velocity, when the pulse is within the medium box.
the box moving velocity, when the pulse is within the medium box.
When  for the case-2, the pulse has entered the
for the case-2, the pulse has entered the
box, or just left the box, or has left the box and goes forward an additional distance, as shown in Figure A2. Comparing Equation (C-1) with Equation (C-3) or Equation (C-4) we obtain the same equation of conservation of momentum, given by
 . (C-5)
. (C-5)
Namely, the sum of the momentums of the medium box and the light pulse, when the pulse enters the box, is equal to the momentum of the pulse in vacuum.
When the pulse just leaves the box, the box has moved a distance, as shown in Figure A2, given by
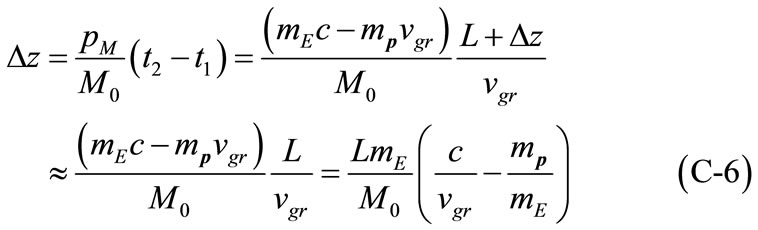
where Equation (C-5) and  are used.
are used.
From above Equation (C-6) we can see that, to obtain  we have to assume that
we have to assume that  is known. In the traditional analysis,
is known. In the traditional analysis,  (
( for a photon) is assumed, which leads to [7,10]
for a photon) is assumed, which leads to [7,10]
 . (C-7)
. (C-7)
However, as mentioned before, if  is known, then the pulse momentum
is known, then the pulse momentum 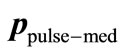 is actually known, equal to
is actually known, equal to , without any further calculations. Since
, without any further calculations. Since  is taken in the traditional analysis,
is taken in the traditional analysis,

is Abraham’s momentum [10].
For the single photon-medium box thought experiment, we have the Abraham photon momentum

if  is taken [7], while we have the Minkowski photon momentum
is taken [7], while we have the Minkowski photon momentum

if  is set.
is set.