The Conservation of Energy Space-Time Metric for Space Outside Matter ()
1. Introduction
With the passage of time, Einstein’s gravitational field equations [1-4], now often written as
 (1)
(1)
where Rμν is the Ricci curvature tensor, gμν is the metric tensor, R is the scalar curvature, G is Newton’s universal gravitational constant, c is the speed of light and Tμν is the stress energy tensor, remain the only theory of gravity to correctly predict observations against which they were tested [The cosmological constant term  is often included on the left hand side of Equation (1)]. Among the features Einstein predicted from his theory were:
is often included on the left hand side of Equation (1)]. Among the features Einstein predicted from his theory were:
• Photons leaving the sun would be redshifted by the time they reached Earth;
• The orbit of the planet Mercury would undergo a precession due to the sun’s mass curving space-time;
• The sun’s mass would deflect the path of photons that travelled close to it;
• Photons leaving the surface of a star or planet would be redshifted.
His subsequent predictions of gravity waves and gravitational lensing have also been confirmed.
Schwarzschild [5] was the first to attempt to solve them. Later solutions [6-11] yielded the now accepted exact solution [12]
 (2)
(2)
where s is the space-time geometry co-ordinate, t is time, r is distance from the centre of mass, θ and φ are angles and  where M is the mass of the body that is distorting space-time, G is Newton’s universal gravitational constant and c is the speed of light. It is rather obvious that Equation (2) behaves badly at r = α and this is the source of the concept of black holes with an event horizon at radius r = α.
where M is the mass of the body that is distorting space-time, G is Newton’s universal gravitational constant and c is the speed of light. It is rather obvious that Equation (2) behaves badly at r = α and this is the source of the concept of black holes with an event horizon at radius r = α.
Einstein’s gravitational field equations were based upon mass distorting space-time. The success of the general theory of relativity in predicting gravitational effects has been highly significant. As well as explaining the effects mentioned above, Einstein also predicted that gravity waves would be produced by rotating non symmetric objects, gravitational lensing and moving mass dragging space-time with it. These were subsequently observed. A prediction from Equation (2) was that anything originating at a distance r < α from a massive object could not pass through the barrier at r = α because it would need to travel at faster than c, which led to the concept of black holes. Subsequent studies have suggested that black holes lost all properties except mass and rotation. Kerr [13] studied the properties of rotating black holes and was able to predict a spreading of photon wavelengths when seen by outside observers.
The developments of the general theory of relativity have been very good at explaining most planetary and stellar gravitational effects as well as many galactic phenomena and some inter galactic effects. There is no doubt as to the validity of the derivations of the spacetime metric of Equation (2) from Einstein’s field Equations (1). Einstein showed the relationship between his work and Newtonian gravity. Newton [14] unified potential energy with stellar behavior and gravitational effects on planet Earth. His theory successfully described the behavior of objects under the influence of large masses such as planets and stars. In particular it enabled gravitational effects to be calculated mathematically, explaining all effects observed to that time.
Despite its success, the general theory of relativity still has its critics, particularly those aspects dealing with the predictions of an event horizon associated with collapsed matter forming black holes. From Equation (2) it is obvious that a black hole will form with an event horizon at r = α, beyond which even light cannot travel. In the case of matter collapsing to a point singularity the event horizon requires gravity to have an action at a distance. There is no physical principle in which action at a distance can occur. One of the early criticisms of Newton’s theory of gravity was that it required action at a distance for two objects to attract each other across space. Despite that criticism, Newton’s calculations dominated all gravitational studies for over two hundred years. Einstein’s general relativity theory overcame the problem of action at a distance by showing that mass distorted space-time and in turn, space-time determined how mass moved. That has allowed general relativity to successfully describe all situations against which it has been tested since its introduction.
All theories are attempts to describe reality. That does not mean that a theory is reality even if it successfully describes all situations against which it has been tested. When it comes to gravitational effects, the theory of general relativity gives the best description, having successfully predicted the outcome of all measurements against which it has been tested. Despite almost a century passing since it was first published, its format is still regarded as entirely mathematical. Some of its predictions, such as a black hole having an event horizon, are seen as predictions from the mathematics of an accurate theory for which no physical explanation is invoked. This lack of a physical explanation and the complexity of the mathematics has led many to question the integrity of general relativity, despite the accuracy of its experimentally tested predictions. General relativity has its supporters and its detractors. None of its supporters appear to have been able to offer a physical explanation for its effect. None of its detractors appear to have come up with an alternative that can satisfy all the measurements that general relativity has successfully predicted.
Reality is the result of gravity determined by measuring such properties as potential energy. It is beneficial for measurements on planet Earth that Newton’s theory of gravity gives a means of calculating potential energy. With or without Newton’s theory, potential energy is still a measurable property associated with mass, which effect can be calculated by using Newton’s universal gravitational constant G. In his derivation of general relativity, Einstein still used the same universal gravitational constant associated with mass. Gravity and potential energy are inseparably associated with mass. It is an aim of this manuscript to show that gravitational effects can be calculated from the well known physical principle of conservation of energy.
2. The Conservation of Energy Metric
Potential energy (PE) is associated with mass through the relationship
 (3a)
(3a)
where r1 and r2 are the different distances r from the centers of mass of an object of mass m from another object of mass M. When , this simplifies to
, this simplifies to
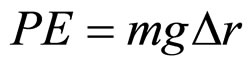 (3b)
(3b)
where g is the average acceleration due to gravity over the distance Δr. No experiment or observation has yet been made in which Equation (3a) does not hold. As such it is a suitable starting point for a study of the behavior of photons in space outside matter. A photon is a particle of energy E = hν, where h is Planck’s constant and ν is its frequency. From Einstein’s special theory of relativity [15,16] it is known that E = mc2, which yields the mass m of a photon as  [17-21]. It is known from experiment that an object of mass m with kinetic energy (KE) moving up against a gravitational field will lose kinetic energy as it gains potential energy. This is illustrated in Figure 1, for a photon of mass
[17-21]. It is known from experiment that an object of mass m with kinetic energy (KE) moving up against a gravitational field will lose kinetic energy as it gains potential energy. This is illustrated in Figure 1, for a photon of mass  moving distance Δr against a gravitational field of strength g. This was recognized by Einstein [22,23] when he discussed the effect of gravity upon the propagation of light. He expressed the relationship between the frequencies of light at different vertical positions by the equation
moving distance Δr against a gravitational field of strength g. This was recognized by Einstein [22,23] when he discussed the effect of gravity upon the propagation of light. He expressed the relationship between the frequencies of light at different vertical positions by the equation
 (4)
(4)
where ν1 and ν2 are the frequency of the light at vertical

Figure 1. Illustration of the gain in potential energy when a photon travels a distance Δr against gravity.
distances r1 and r2, separated by height Δr = r2 − r1, in a gravitational field of strength , as illustrated in Figure 1. With a photon being a constant velocity particle, a loss in kinetic energy can only occur by a loss of mass and hence frequency. Equation (4) was used by Einstein [22,23] and was subsequently verified by the work of Pound, Rebka and Snider [24-26]. Equation (4) is based upon experimental observation and has been adequately calculated using Newtonian mechanics. To date no observation has been made in which Equations (3) and (4) do not hold true.
, as illustrated in Figure 1. With a photon being a constant velocity particle, a loss in kinetic energy can only occur by a loss of mass and hence frequency. Equation (4) was used by Einstein [22,23] and was subsequently verified by the work of Pound, Rebka and Snider [24-26]. Equation (4) is based upon experimental observation and has been adequately calculated using Newtonian mechanics. To date no observation has been made in which Equations (3) and (4) do not hold true.
The conservation of energy as the light travels away from the centre of mass, as illustrated in Figure 1, yields
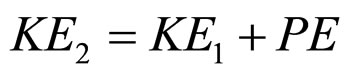 which becomes
which becomes
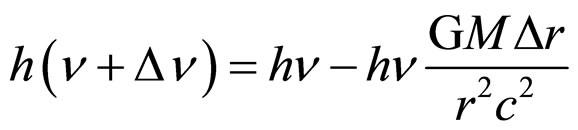 (5)
(5)
Setting the limit as Δr tends to zero in Equation (4), while allowing that G and c are constants and M is the mass of a gravitationally attracting body, enables Equation (5) to be rearranged to give
 (5a)
(5a)
for which there is no experimental evidence to suggest that it is not applicable for all values of r from the centre of mass of M. Newton [14] showed that mass distributed throughout space behaves gravitationally as if all the mass were concentrated at the centre of mass, when observed from outside the mass, allowing r to be used as the distance from the center of mass M.
Introducing a constant  and integrating from r1 to r2 (>r1) gives
and integrating from r1 to r2 (>r1) gives

or
 (6)
(6)
Equation (6) is an exact expression for the variation of frequency of light when the energy of an individual photon remains constant as it moves away from the centre of mass M. An observer at a distance from M will see the light coming away from the object as being red shifted. To such an observer, it would appear as if time was slowing down the closer the observation was made to the centre of mass. If we apply this to the case of the red shift from the sun, r1 = 700,000 km,  km and α = 2.95 km, a photon leaving the surface of the sun would be red shifted by an amount equal to
km and α = 2.95 km, a photon leaving the surface of the sun would be red shifted by an amount equal to
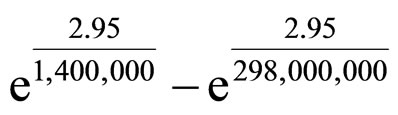 (6a)
(6a)
by the time it reaches the surface of planet Earth. This equates to , which agrees with the result reported by Einstein [22,23]. Such a change in frequency has been observed [27,28]. It should be noted that others have used Newtonian mechanics in the same manner to calculate the redshift of photons from the sun, reaching the same answer [29,30]. Those authors did not continue the study in the manner reported in the following work.
, which agrees with the result reported by Einstein [22,23]. Such a change in frequency has been observed [27,28]. It should be noted that others have used Newtonian mechanics in the same manner to calculate the redshift of photons from the sun, reaching the same answer [29,30]. Those authors did not continue the study in the manner reported in the following work.
From knowledge that c is constant to all observers and the relationship
 (7)
(7)
where λ is the wavelength of the photon, it follows that this change of frequency will generate an inverse change in wavelength. The only method we have of measuring the properties of distant objects is with photons. If the frequency of photons has changed, the distance measured using photons will also change. Equation (7) can now be substituted into Equation (6) to determine the corresponding variation of length with distance, yielding
 (8)
(8)
Equations (6) and (8) can now be used to define the exact nature of the variation of time and length with distance from the centre of mass of a body. This is equivalent for each of the coordinates, x, y and z enabling the exact nature of the space-time continuum to be calculated in any direction radially out from the centre of mass of a massive object M. We can now go directly to the Minkowski space-time equation [31,32], which is applicable to flat space-time that is well away from significant mass, which using the most common convention is expressed as

Following the work of Schwarzschild [5], when mass is involved, we need to change the form to take into account the distortion of space, giving
 (9)
(9)
where F, H and J are functions of r when .
.
Equation (9) can be transformed from Cartesian to polar co-ordinates to yield
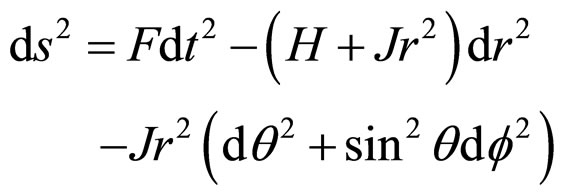 . (10)
. (10)
Allowing that the distortion of space and time is measured by variations to the frequency and wavelength of photons, it is apparent from Equation (7) that the product of . From Equations (6) and (8) this gives
. From Equations (6) and (8) this gives
 ,
, 
and  yielding
yielding
 . (11)
. (11)
Equation (11) describes how space-time varies around an object of mass
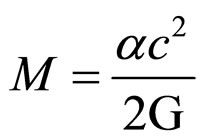
based upon the principle of conservation of energy. The only way we have of observing space-time is the detection of photons that have traveled through it. The distortion of space-time is both a measure of and is measured by the distortion of the photons that have traveled through it.
3. Comparison with Other Metrics
From his field equations for space outside matter, Einstein derived his approximate solutions of  and
and . He then used those approximations to solve for the deviation of a photon by the gravitational field of the sun and the precession of the orbit of the planet Mercury. Schwarzschild [5] provided a solution to them, which solution had the form
. He then used those approximations to solve for the deviation of a photon by the gravitational field of the sun and the precession of the orbit of the planet Mercury. Schwarzschild [5] provided a solution to them, which solution had the form

 .
.
It should also be noted that Schwarzschild introduced a co-ordinate change from r to R to simplify his calculations. In his answer, the singularity at R = α equates to a singularity at r = 0.
Equation (2) is an exact solution to Einstein’s field Equations. Equation (11) is an exact derivation of the space-time geometry equation using the principle of conservation of energy. Equations (2) and (11) are different. Although Einstein was aware of Equation (5) and used it in his first paper to derive the effect of mass upon space-time, his further work that led to the general relativity theory, was based upon the effect of the gravitational field upon space-time. This has led some general relativity practitioners to conclude that his field equations hold for all values of α/r, i.e., all gravitational field strengths, while Newtonian mechanics, which Einstein showed was a first approximation of general relativity, was only a weak field solution and as such could not be extended to high field strengths. This author contends that the principle of conservation of energy applies at all values of α and r, i.e., all gravitational field strengths. Until experimental evidence shows that Equations (3) and (4) do not hold, Equation (11) must be considered to be valid.
Further it should be noted that  can be expressed by the Maclaurin/Taylor series as:
can be expressed by the Maclaurin/Taylor series as:
 making
making  the first approximation to
the first approximation to .
.
The only mechanism for separating those two solutions is to make measurements well within the difference between the two terms, namely approximately . This can be done either by performing measurements on planet Earth that are accurate to better than 1 part in 1021, or making independent observations of the Schwarzschild radius α, the radius r and measuring the distortions of space-time at distances r less than 10 α to an accuracy of better than 1:100. Many experiments have been forwarded as verifying Equation (2). Each of those observations and subsequent verifications has been based upon only knowledge of Equation (2) only and not of Equation (11). To date no observation has been made that can distinguish between the predictions of Equations (2) and (11) [33].
. This can be done either by performing measurements on planet Earth that are accurate to better than 1 part in 1021, or making independent observations of the Schwarzschild radius α, the radius r and measuring the distortions of space-time at distances r less than 10 α to an accuracy of better than 1:100. Many experiments have been forwarded as verifying Equation (2). Each of those observations and subsequent verifications has been based upon only knowledge of Equation (2) only and not of Equation (11). To date no observation has been made that can distinguish between the predictions of Equations (2) and (11) [33].
It should be noted that Eddington [30] pointed out that light had mass and that using Newtonian mechanics as the basis of calculation, the deflection of light rays by the sun would be half that due to Einstein’s space-time distortion, the same as was originally calculated by Einstein [22,23]. The other half of the distortion comes about because a change in frequency automatically means a change in time as well as length. Eddington [34] spoke of light pulses and accepted that they behaved according to what is now called the Schwarzschild metric given in Equation (2). It is equally clear that his original work on the influence of gravity upon the propagation of light, Einstein [22,23] considered the effect of Newtonian calculations of gravity upon particles of light, now called photons. Under the Einstein-de Broglie model of photons, they are considered as particles that have relativistic mass given by .
.
4. Calculating Some Gravitational Effects
The ability of photons to be treated in the conservation of energy as particles of constant velocity and variable mass makes it somewhat easier to grasp the mechanism involved in the general theory of relativity. The redshift of photons leaving a massive object is done in the same manner as was done by Einstein [22,23] and gives the same answer, namely  for photons leaving the sun, as shown in the derivation of Equation (6).
for photons leaving the sun, as shown in the derivation of Equation (6).
Consider the situation shown in Figure 2, in which a photon passes at distance r0 from the origin O of an object of mass M. From Equation (4) the photon experiences a distortion of time at distance r given by  as it travels from −∞ to +∞. The total time distortion it experiences is given by summing all distortions, namely
as it travels from −∞ to +∞. The total time distortion it experiences is given by summing all distortions, namely

where r0 is the distance of closest approach. From Equations (7) and (11) it is obvious that there is a similar term for the distortion of space, but with opposite sign. Equation (11) shows that the total distortion of space-time is obtained by subtracting these two, which gives a spacetime distortion that shows up as a deflection given by
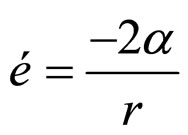 (12)
(12)
with the negative sign indicating that the distortion is towards the massive object. Using α of the sun = 2.95 km and the radius of the sun as r0 = 700,000 km, gives é = 1.74 arc seconds which agrees with Einstein’s prediction [1,3,4] and was subsequently observed [34,35].
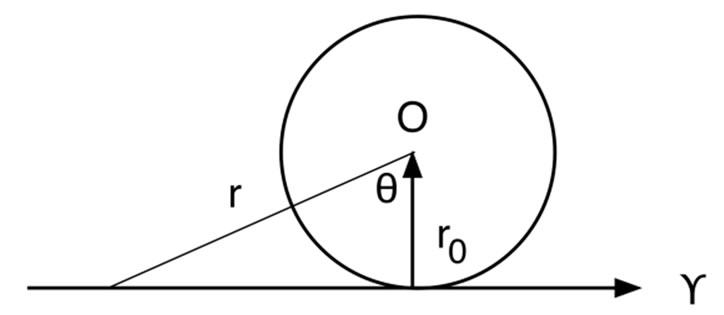
Figure 2. Illustration of the passage of a photon ϒ close to the surface of a massive object, making its closest approach at distance r0.
A study of the derivation of the precession of the orbit of planet Mercury, also predicted by Einstein [2] may help to illustrate the easier understanding of this “relativistic” effect. Mercury is the innermost planet and has an elliptical orbit, moving between distances of 46.6 million kilometers and 69.8 million kilometers from the sun, giving it an orbit eccentricity e of 0.2056, taking approximately 88 Earth days to travel once around the sun, meaning that it makes 415 orbits per Earth century.
From Equation (12), we know that a photon passing by the sun at the orbit of Mercury, will be deflected by an amount, é, equal to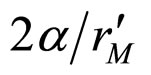 , where
, where  is the corrected radius for Mercury’s orbit. Under this presentation é is the distortion of space-time at this distance, as viewed from infinity. On planet Earth, from where these observations are made, there is a time distortion of
is the corrected radius for Mercury’s orbit. Under this presentation é is the distortion of space-time at this distance, as viewed from infinity. On planet Earth, from where these observations are made, there is a time distortion of where rE is radius of planet Earth’s orbit, see Equation (6). This is illustrated in Figure 3, which shows the time dilation, vertical scale, plotted against distance. When measured from Earth, this must be included in the spacetime distortion Δs at Mercury’s orbit, to give
where rE is radius of planet Earth’s orbit, see Equation (6). This is illustrated in Figure 3, which shows the time dilation, vertical scale, plotted against distance. When measured from Earth, this must be included in the spacetime distortion Δs at Mercury’s orbit, to give
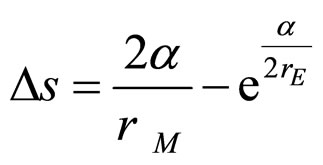
which simplifies to
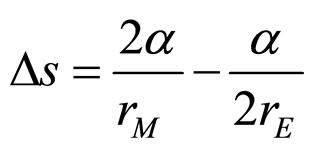
when  and
and .
.
Note that this calculation only takes planet Earth’s time distortion into account and not the space-time distortion because all measurements are made by photons travelling from Mercury to Earth, which, to a first approximation, is at a fixed distance rE from the sun. We need to consider the distortion at those distances for the whole circle of radius r. Figure 4 illustrates photons moving at a distance r from mass M. In each case a photon passing at distance r will be distorted Δs to move in a slightly different direction. Another photon passing at the new point will be distorted by the same Δs, this time starting at a different point. To determine the space-time distortion over a complete orbit, we must consider the deflection of the photon over angle φ. This is given by

Figure 3. Schematic illustration of the relationship between time dilation and distance for the sun and planets Mercury and Earth.

Figure 4. Schematic illustration of the passage of a photon past a massive object centered at point M. Summing the series of those segments yields the complete trajectory.

where e is the eccentricity of Mercury’s orbit and rM is its semi-major axis. To obtain the space-time distortion at Mercury’s orbit, we set the limit of φ tends to zero, yielding sinφ = φ, and integrate φ from 0 to 2π, which gives

yielding
 (13)
(13)
where ε is the distortion of space-time that leads to the precession of Mercury’s orbit in its direction of rotation. Using the above information, α = 2.95 km and , gives the precession ε of Mercury’s orbit as ε = 42.15 arc seconds per century.
, gives the precession ε of Mercury’s orbit as ε = 42.15 arc seconds per century.
This is slightly less than that predicted from Einstein’s calculation, which gives ε = 42.98 arc seconds per century. Part of these differences can be attributed to the uncertainties in e, α, rE and rM. It should also be noted that the total precession of Mercury’s orbit is 5599.7 arc seconds per century [36]. Of this, 5560.26 arc seconds per century is explained by other factors [37], leaving 39.44 arc seconds per century unexplained. At 42.98 arc seconds per century, Einstein’s explanation is too large by about 3.5 arc seconds per century. At 42.15 arc seconds per century, this derivation leaves about 2.7 arc seconds per century unexplained.
The ease of understanding this approach could be compared to the more complex approaches used by others. For example Trencèvski et al. [38] used flat Minkowski space to calculate their equivalent to Equation (13), yielding


which equates to 35.6 arc seconds per century when applied to the precession of the orbit of the planet Mercury. It should be noted that when Einstein derived his explanation for the motion of Mercury’s perihelion, he also derived that same expression. Trencèvski et al. [38] calculation of the equivalent of Equation (12) gave the same answer as Equation (12).
The accuracy of Einstein’s field equations from his general theory of relativity in predicting gravitational effects should not be overlooked. Einstein [39] made a further prediction that non-symmetrical rotating massive bodies would radiate gravity waves and hence loose energy. That loss of energy would be detected by the slowing down of the rotating body. Hulse and Taylor [40] reported a binary pulsar, PSR B1913 + 16, two neutron stars rotating about each other, which seemed to fit the situation of a non-symmetrical rotating body. Observation by Weisberg and Taylor [41-43] showed it was indeed slowing down according to Einstein’s predictions. Consequently it is generally believed that Einstein’s general theory of relativity been verified to an accuracy of approximately 1 part in 1014. The decay rate is independent of whether the metric used is Equation (2) or Equation (11). The same situation applies for other verifications of Einstein’s field equations. Unless independent measurements of r and α are made to the accuracy required to separate the two metrics, there is no experimental evidence to suggest that Equation (2) is accurate and Equation (11) is not.
5. Discussion
The above has demonstrated that treating photons as particles of variable mass and constant velocity while calculating the effect of conservation of energy upon them, has produced the space-time metric for space outside matter. These calculations, based upon the experimenttally verified principles of conservation of mass/energy and the existence of potential energy associated with massive objects, were done without any approximations. The relationship between the general relativity and conservation of energy metrics is illustrated in Figure 5.
Figure 5(A) suggests that mass generates potential energy, leading to gravity, which in turn distorts spacetime, as derived in this presentation. Figure 5(B) suggests that mass distorts space-time, causing gravity, which in turn leads to potential energy. In both cases, the central theme is mass, from which potential energy, gravity and space-time distortion cannot be separated, as suggested in Figure 5(C). The pathway for the calculation of gravity from mass can be either conservation of
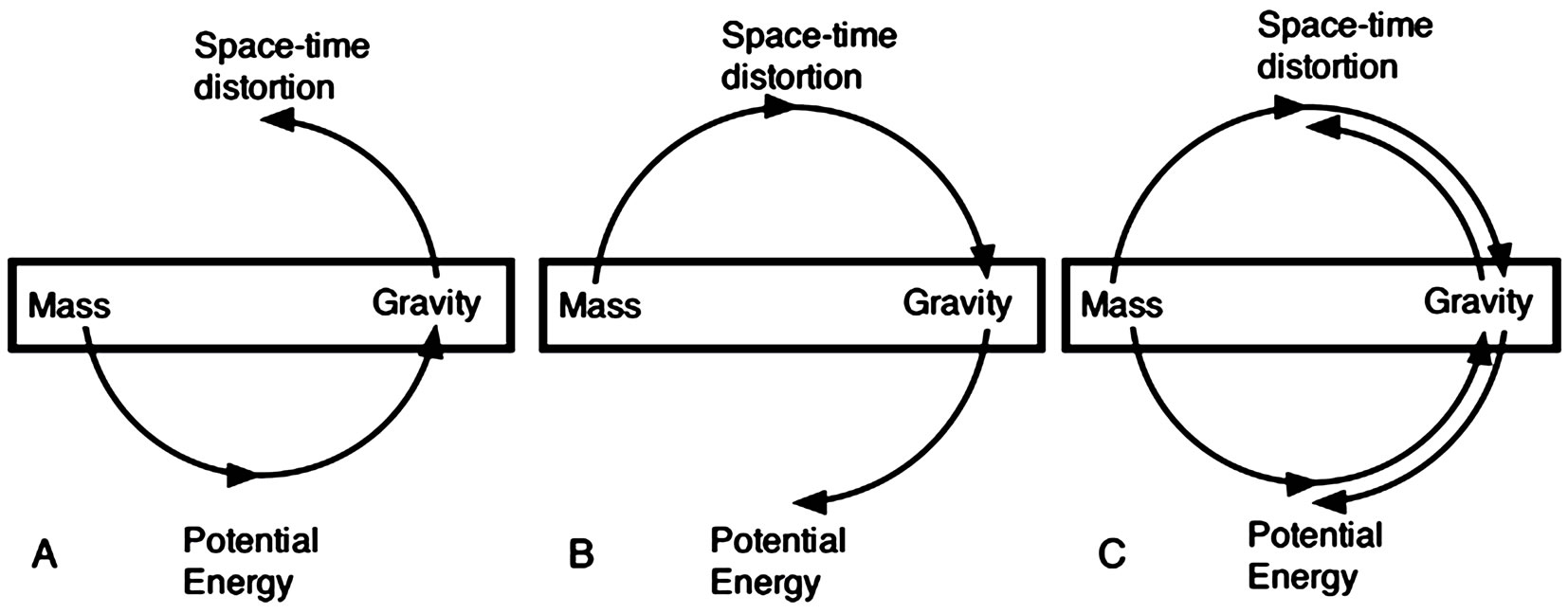
Figure 5. Schematic illustration of the possible relationships between mass, potential energy, gravity and space-time distortion. A illustrates the pathway that gravity arises from mass by potential energy, with gravity distorting space-time, as shown in this presentation. B illustrates the pathway that mass distorts space-time, which leads to gravity that generates potential energy. C suggests that both pathways will lead to the same result.
energy or space-time distortion. In either pathway the answers should always be the same because their effect, namely gravity, is the same. The important question is “which pathway offers the best means of calculating gravitational effects?” General relativity predicts a singularity at the Schwarzschild radius, which requires “action at a distance” when the Schwarzschild radius is larger than the radius of the massive body. This conservation of energy metric does not use any approximations and does not require “action at a distance” to explain any gravitational effect. Without independent determinations of r and α at r < 10α and the measurement of gravitational effects to an accuracy of ≈ 1%, there is no experimental evidence to suggest that the Schwarzschild metric better describes gravitational effects than those described by this conservation of energy metric. Lasky [33] has shown that current observations are several orders of magnitude away from being able to verify the accuracy of general relativity predictions under all conditions. Until measurements are made that can distinguish between the two metrics, there is no experimental evidence to suggest that the predictions of gravitational effects using general relativity are better than those obtained using conservation of energy.
The relationship between the three descriptions of gravity, Newtonian mechanics, general relativity and conservation of energy was shown above. It is contended that the conservation of energy metric will accurately predict all gravitational phenomena for space-time outside matter. The Schwarzschild metric from general relativity is the first approximation to the conservation of energy metric in which  is approximated to
is approximated to . Newtonian mechanics is based upon the speed of light being infinite and the mass of a photon being zero. It accurately describes local situations where experimental error is not sufficient to distinguish between c and ∞ or measure the change in mass (and hence frequency) of photons. As this presentation shows, giving photons a mass and a finite velocity enables Newtonian mechanics to predict relativistic effects when conservation of energy is applied to the photons. The differences are between the predictions of general relativity and the conservation of energy metrics.
. Newtonian mechanics is based upon the speed of light being infinite and the mass of a photon being zero. It accurately describes local situations where experimental error is not sufficient to distinguish between c and ∞ or measure the change in mass (and hence frequency) of photons. As this presentation shows, giving photons a mass and a finite velocity enables Newtonian mechanics to predict relativistic effects when conservation of energy is applied to the photons. The differences are between the predictions of general relativity and the conservation of energy metrics.
Figure 6 illustrates the difference expected when photons of frequency  are emitted at different distances r from a massive object at O and detected by an observer at infinity. The conservation of energy metric predicts that a photon emitted at r will have a frequency at infinity given by
are emitted at different distances r from a massive object at O and detected by an observer at infinity. The conservation of energy metric predicts that a photon emitted at r will have a frequency at infinity given by
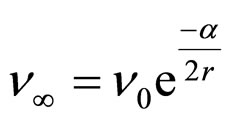 (14)
(14)
where r is the distance from the centre of mass. The Schwarzschild metric predicts that the photon will have a frequency given by
 . (15)
. (15)
For photons emitted at distances , the predictions of the two metrics will be the same for observations at infinity. As the emission distance approaches the Schwarzschild radius the predictions become significantly different. The Schwarzschild metric predicts that photons emitted at r = α will have no frequency left when they reach infinity. The conservation of energy metric predicts that photons emitted at r = α will have a redshift of ≈ 0.6065 and still be detected. Until observations are made at distances r < 10α to an accuracy of ≈ 1%, this conservation of energy metric matches all observations that have confirmed the accuracy of general relativity predictions.
, the predictions of the two metrics will be the same for observations at infinity. As the emission distance approaches the Schwarzschild radius the predictions become significantly different. The Schwarzschild metric predicts that photons emitted at r = α will have no frequency left when they reach infinity. The conservation of energy metric predicts that photons emitted at r = α will have a redshift of ≈ 0.6065 and still be detected. Until observations are made at distances r < 10α to an accuracy of ≈ 1%, this conservation of energy metric matches all observations that have confirmed the accuracy of general relativity predictions.
Equations (14) and (15) make different predictions for the detected frequency of photons leaving the surface of a massive compact object when seen by an observer in free space. It is apparent that these differences are only significant for distances of r close to α, a situation that

Figure 6. Illustration of the differences predicted by the conservation of energy and Schwarzschild metrics for photons of frequency ν0 emitted at distances r from an object, as detected by an observer at infinity.
can only apply for very massive objects, such as neutron stars. A neutron star of solar mass  will have α = 2.95 km and a physical radius r0 = 13.4 km based upon an average neutron star density of
will have α = 2.95 km and a physical radius r0 = 13.4 km based upon an average neutron star density of  [44], giving it
[44], giving it . The redshift of spectral lines emitted from the surface of non rotating neutron stars gives an opportunity to determine the accuracy of Equation (11), provided the density of the neutron star, and hence r0, is accurately known. The Schwarzschild radius α increases linearly with mass while the physical radius of the neutron star, rN, increases with the cube root of mass.
. The redshift of spectral lines emitted from the surface of non rotating neutron stars gives an opportunity to determine the accuracy of Equation (11), provided the density of the neutron star, and hence r0, is accurately known. The Schwarzschild radius α increases linearly with mass while the physical radius of the neutron star, rN, increases with the cube root of mass.
Figure 7 shows a plot of  for neutron star masses less than 10
for neutron star masses less than 10 . Using Equations (14) and (15) for the relationship of frequency versus distance for the conservation of energy and Schwarzschild metrics, Figure 8 shows a plot of the variation of frequency of photons emitted from the surface of a non rotating neutron star when plotted under these metrics. As can be seen from Figure 8, there is a region above ≈ MN ≈ 0.5
. Using Equations (14) and (15) for the relationship of frequency versus distance for the conservation of energy and Schwarzschild metrics, Figure 8 shows a plot of the variation of frequency of photons emitted from the surface of a non rotating neutron star when plotted under these metrics. As can be seen from Figure 8, there is a region above ≈ MN ≈ 0.5  where there are significant differences between the frequencies of photons emitted from the surface of the neutron star as predicted by the different metrics. This still requires measurements to be made of the MN, which determines α, and either the density or radius rN of the neutron star. If this can be done, it provides one means of discriminating between the two metrics. It is postulated that when observations are made with the required accuracy, the predictions from the conservation of energy metric will match all gravitational measurements made in space outside matter.
where there are significant differences between the frequencies of photons emitted from the surface of the neutron star as predicted by the different metrics. This still requires measurements to be made of the MN, which determines α, and either the density or radius rN of the neutron star. If this can be done, it provides one means of discriminating between the two metrics. It is postulated that when observations are made with the required accuracy, the predictions from the conservation of energy metric will match all gravitational measurements made in space outside matter.
6. Conclusion
This paper has shown that gravitational effects can be calculated from the physical principal of conservation of energy. Potential energy is a measurable properties associated with mass, which, in the case of photons, is given by . It can be calculated using Newtonian mechanics and Newton’s universal gravitational constant G. The resultant space-time metric matches all experimental
. It can be calculated using Newtonian mechanics and Newton’s universal gravitational constant G. The resultant space-time metric matches all experimental
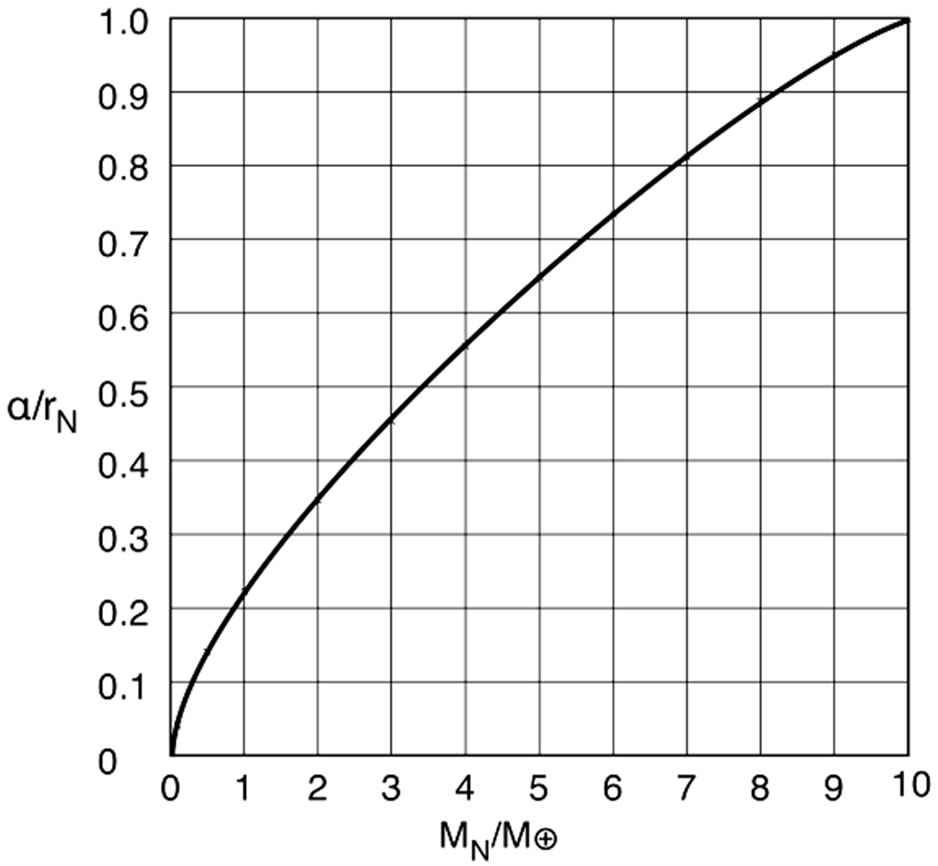
Figure 7. Plot of Schwarzschild radius α divided by the neutron star radius rN, versus the mass of the neutron star expressed as a proportion of the solar mass .
.

Figure 8. Plot of the detected frequency variation expected from photons emitted from the surface of a neutron star as calculated from the Schwarzschild metric and the conservation of energy metric, as indicated, for neutron star masses up to 10 .
.
observations that currently support the predictions of the general relativity theory. It predicts that there is no singularity at the Schwarzschild radius and hence no black holes. It also overcomes the problem of gravitational action at a distance associated with the Schwarzschild radius being outside the mass of a collapsed object.