Series Solution of Non-Similarity Boundary-Layer Flow in Porous Medium ()
1. Introduction
Heat transfer continues to be a major field of interest to engineering and scientific researchers, as well as designers, developers, and manufacturers. Heat transfer plays a major role in not only virtually all man made devices, but natural systems as well. Considerable effort has been devoted to research in traditional applications such as chemical processing, general manufacturing, energy devices, including general power systems, heat exchangers, and high performance gas turbines.
The study of boundary-layer flow along surfaces embedded in fluid saturated porous media has received considerable interest, especially in the enhanced recovery of petroleum resources, packed bed reactors and geothermal industries. The fluid flow along a stationary plate is a classical problem of fluid mechanics known as the Blasius problem [1]. In this case the free stream is parallel to the plate and its velocity is constant. If the wall makes a positive angle with the free stream, then the free stream is accelerated along the wall and we have the Falkner? Skan flow along a wedge. Falkner and Skan [2] showed that this problem admits similarity solution as happens with the Blasius problem. Hartree [3] solved this problem and gave numerical results for the wall shear stress for different values of the wedge angle. The heat transfer similarity solution can be developed in the same way by substituting the Falkner-Skan similarity momentum equation into the boundary layer energy equation. Eckert [4] solved the Falkner? Skan flow along an isothermal wedge and gave the first wall heat transfer values. Thereafter, many solutions have been obtained for different aspects of this class of boundary layer problems. Lin and Lin [5] provided very accurate solutions for wall heat transfer from either an isothermal or uniform flux wedge to fluids for any Prandtl number. When the fluid is assumed to have constant properties then the problem is uncoupled, that is, the momentum equation has an influence on the energy equation but the energy equation has not any influence on the momentum equation.
A wide range of applications and a wide variety of analytical and numerical methods have been used to study the heat transport over permeable or impermeable wedge. Elbashbeshy and Dimian [6] investigated the effect of variable viscosity and radiation on flow and heat transfer over a wedge with constant surface temperature but only for  and assuming that the Prandtl number is constant inside the boundary layer. Koh and Hartnett [7] have solved the skin friction and heat transfer for incompressible laminar flow over porous wedges with suction and variable wall temperature. Hsu et al. [8] studied the combined effects of the shape factor, suction/injection rates and viscoelasticity on the flow and temperature fields of the flow past a wedge. Magyari and Keller [9] obtained the exact solutions for the two dimensional similarity boundary-layer flows induced by permeable stretching surfaces. Rajagopal et al. [10] gave non-similarity solutions for the flow of a second grade fluid over wedge. Hossain et al. [11] studied the flow of a fluid with temperature dependent viscosity past a permeable wedge with uniform surface heat flux.
and assuming that the Prandtl number is constant inside the boundary layer. Koh and Hartnett [7] have solved the skin friction and heat transfer for incompressible laminar flow over porous wedges with suction and variable wall temperature. Hsu et al. [8] studied the combined effects of the shape factor, suction/injection rates and viscoelasticity on the flow and temperature fields of the flow past a wedge. Magyari and Keller [9] obtained the exact solutions for the two dimensional similarity boundary-layer flows induced by permeable stretching surfaces. Rajagopal et al. [10] gave non-similarity solutions for the flow of a second grade fluid over wedge. Hossain et al. [11] studied the flow of a fluid with temperature dependent viscosity past a permeable wedge with uniform surface heat flux.
From mathematical viewpoints, it is much more difficult to solve a non-linear PDE than ODE. Generally speaking, it is difficult to solve nonlinear PDEs, especially by means of analytic method. Using the perturbation methods or the traditional non-perturbation methods such as Lyapunov’s small parameter method [12], the δ-expansion method [13] and Adomian’s decomposition method [14], it is difficult to get analytic approximations convergent for all physical parameters in the infinite domain of the flows, because all of these techniques can not ensure the convergence of approximation series. Currently, Cimpean et al. [15] applied the perturbation techniques, combined with numerical techniques, to solve a free convection non-similarity boundary-layer problem over a vertical flat sheet in a porous medium. Like most of perturbation solutions, their results are valid only for small and large x, which are regarded as perturbation quantities. Among analytic methods, the method of local similarity is most frequently used. Many researchers [16-19] have obtained the non-similarity solutions by using the method of local similarity. In some cases, the results given by this method agree with numerical solutions. However, the results given by this method are not very accurate and besides are valid only for small ξ in general.
The objective of this paper is to present complete analytic solution to the temperature distribution by means of the homotopy analysis method (HAM). To the best of our knowledge no attempt has been made to present such type of analytic solution to the temperature profile in the non-similarity boundary-layer flows. The HAM aims to solve the various types of nonlinear equations including ordinary differential equations and partial differential equations analytically. Different from perturbation techniques, the HAM is independent of any small/large physical parameters and thus is more general. Besides, it provides us great freedom to choose the initial guess and the auxiliary linear operator so that we can use different types of base functions to approximate the solution. More importantly, the freedom on the choice of the auxiliary parameter provides us a convenient way to ensure the convergence of the solution series. The homotopy analysis method has been successfully applied to complicated nonlinear problems by many researchers [20-29] and so on. In [30] the authors have used the same technique to get the series solutions of of non-similarity boundarylayer flows over the porous wedge. The solutions obtained in [30] are uniformly valid for all physical parameters in the whole domain 0 ≤ x < ∞ and 0 ≤ y < ∞. In this paper we have performed heat transfer analysis of steady non-similarity boundary-layer flows over the porous wedge.
2. Mathematical Formulations
The equation governing the steady-state, two dimensional, incompressible boundary-layer flow along a porous wedge is given by [30]
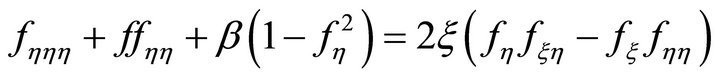 (1)
(1)
subject to the boundary conditions
 (2)
(2)
where ,
,
 , and
, and , are constants. Here,
, are constants. Here,  is the suction/injection parameter, where
is the suction/injection parameter, where ,
,  and
and 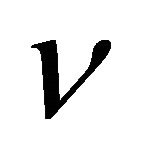 is the kinematic viscosity, and
is the kinematic viscosity, and  defines the relation between the injection index n and the wedge angle parameter m. The dimensionless variables are defined through
defines the relation between the injection index n and the wedge angle parameter m. The dimensionless variables are defined through




Using the boundary-layer approximations and neglecting the viscous dissipation, the energy equation for temperature T is given by
 (3)
(3)
subject to the boundary conditions
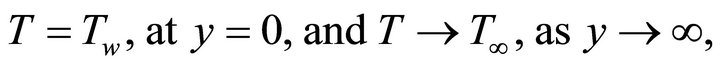 (4)
(4)
where, 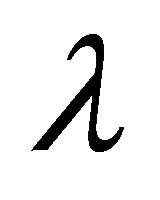 is the thermal diffusivity and
is the thermal diffusivity and  and
and 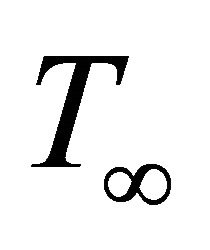 are constant temperatures near and far from the surface, respectively.
are constant temperatures near and far from the surface, respectively.
Introducing the dimensionless temperature 
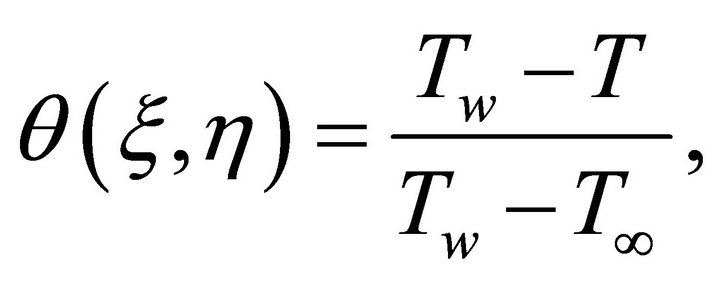
Equations (3) and (4) readily takes the forms
 (5)
(5)
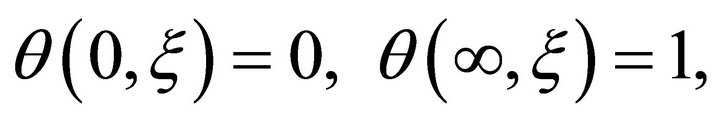 (6)
(6)
where 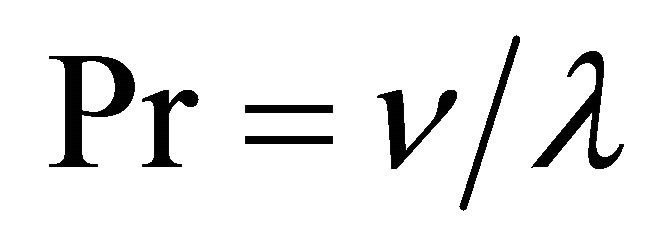 is the Prandtl number.
is the Prandtl number.
3. HAM Deformation Equations
Mathematically, the essence to approximate a nonlinear differential equation is to find a set of proper base functions to fit its solutions. Physically, it is well-known that most viscous flows decay exponentially at infinity (i.e. as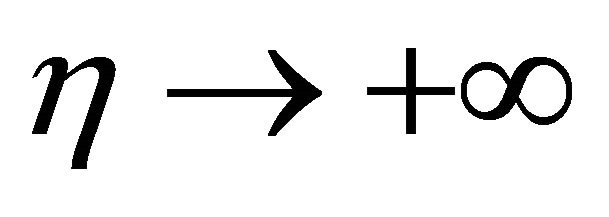 ). So, for non-similarity boundary-layer flows, the velocities
). So, for non-similarity boundary-layer flows, the velocities  and
and  should decay exponentially at infinity. According to the boundary conditions (2), and (6),
should decay exponentially at infinity. According to the boundary conditions (2), and (6), 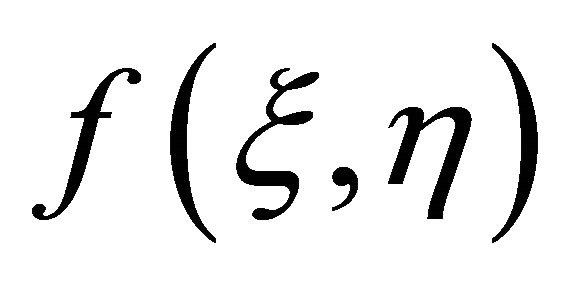 and
and 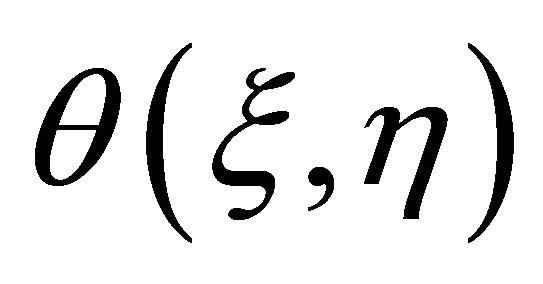 can be expressed by the set of base function
can be expressed by the set of base function

in the form
 (7)
(7)
 (8)
(8)
where ,
, 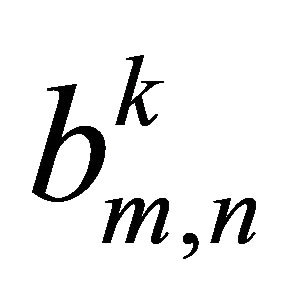 are coefficients and
are coefficients and  is a scale parameter to be determined. They provide us with the so-called rule of solution expressions for
is a scale parameter to be determined. They provide us with the so-called rule of solution expressions for  and
and . According to the rule of solution expressions (7), (8) and from the Equations (2), and (6), it is straight forward to choose the initial approximations
. According to the rule of solution expressions (7), (8) and from the Equations (2), and (6), it is straight forward to choose the initial approximations
 (9)
(9)
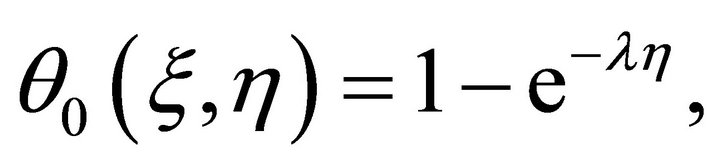 (10)
(10)
In the frame of HAM, we have great freedom to choose the auxiliary linear operator. However, this freedom is restricted by the solution expression and the boundary conditions, which we must consider in the choice of linear operators. Note that the original governing equations are nonlinear PDEs. In general, PDEs are more difficult to solve than ODEs. So, mathematically, it is much easier to solve a system of nonlinear PDEs if we could choose linear operators which contain derivatives with respect to  or
or 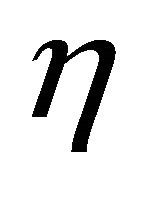 only. Physically, for boundary-layer flows, the velocity variation across the flow direction is much larger than in the flow direction.
only. Physically, for boundary-layer flows, the velocity variation across the flow direction is much larger than in the flow direction.
Therefore, the derivatives ,
, 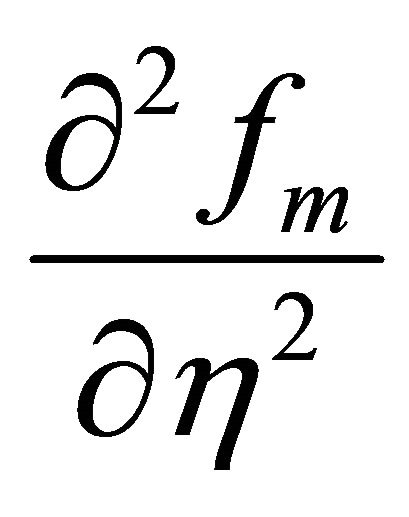 ,
,  are considerably larger and thus physically more important than
are considerably larger and thus physically more important than
 ,
, . Considering all of these, we choose the auxiliary operators
. Considering all of these, we choose the auxiliary operators
 (11)
(11)
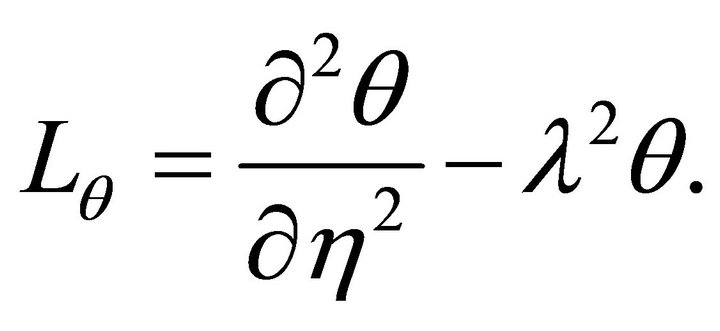 (12)
(12)
 and
and  have the following properties
have the following properties
 (13)
(13)
 (14)
(14)
where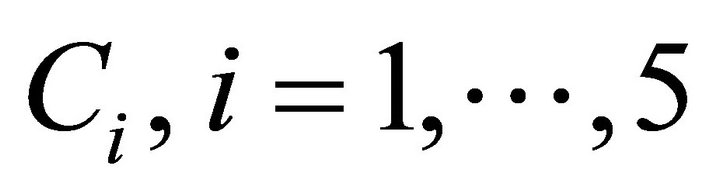 , are arbitrary constants.
, are arbitrary constants.
From Equations (1) and (5), we define the nonlinear operators  and
and

 (15)
(15)
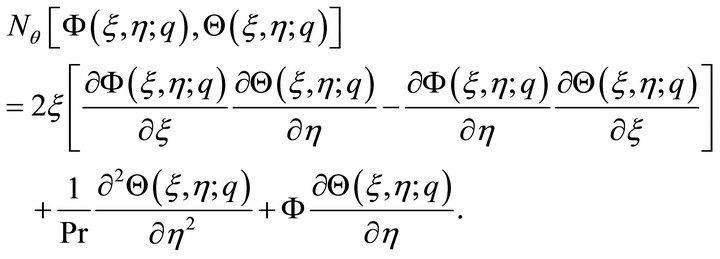 (16)
(16)
respectively.
Let  and
and  denote the convergence-control parameters [31]. We construct the so-called zeroth-order deformation equations
denote the convergence-control parameters [31]. We construct the so-called zeroth-order deformation equations
 (17)
(17)
 (18)
(18)
subject to the boundary conditions
 (19)
(19)
 (20)
(20)
 (21)
(21)
where  is the homotopy-parameter. Clearly, when
is the homotopy-parameter. Clearly, when  and
and , we have from (17) and (18)
, we have from (17) and (18)
 (22)
(22)
and
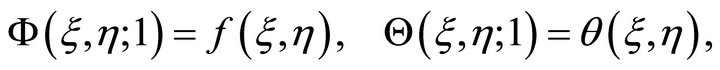 (23)
(23)
Thus, as the homotopy-parameter  increases from 0 to 1,
increases from 0 to 1,  and
and 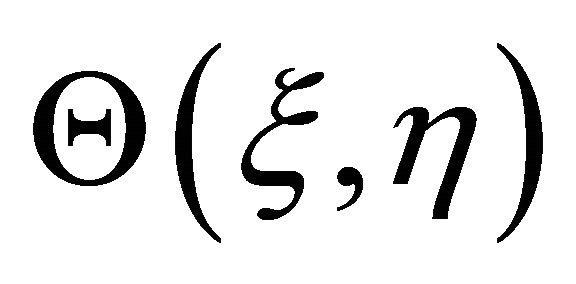 move from the initial approximations
move from the initial approximations 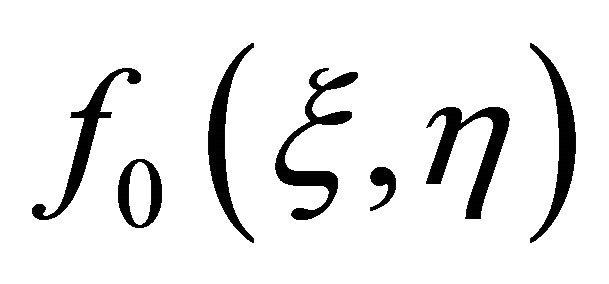 and
and  to the final solutions
to the final solutions  and
and 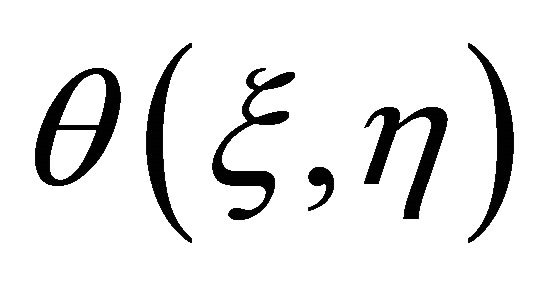 of Equations (1) and (5), respectively. Assume that the convergence-control parameters are so properly chosen that the Taylor’s series of
of Equations (1) and (5), respectively. Assume that the convergence-control parameters are so properly chosen that the Taylor’s series of  and
and  expanded with respect to homotopy-parameter
expanded with respect to homotopy-parameter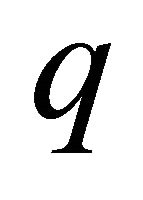 , i.e.
, i.e.
 (24)
(24)
 (25)
(25)
where

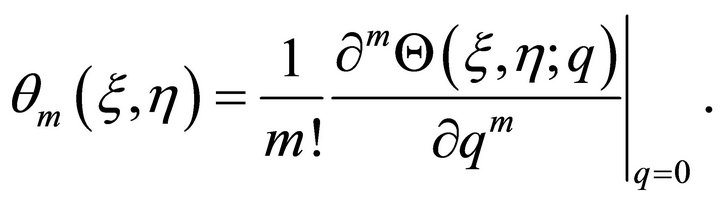
converge at . Then we have from Equations (22) and (23) that
. Then we have from Equations (22) and (23) that
 (26)
(26)
 (27)
(27)
To get the mth-order deformation equations, we first differentiate the zeroth-order deformation Equations (17) and (18) m-times with respect to the homotopy-parameter  at
at , and then divide the resulting expression by
, and then divide the resulting expression by , so that
, so that
 (28)
(28)
 (29)
(29)
subject to the boundary conditions on the wedge
 (30)
(30)
 (31)
(31)
 (32)
(32)
where
 (33)
(33)
 (34)
(34)
and
 (35)
(35)
Now, it is easy to solve the system of linear ordinary differential Equations (28) and (29), subject to the linear boundary conditions (30)-(32). Let  and
and 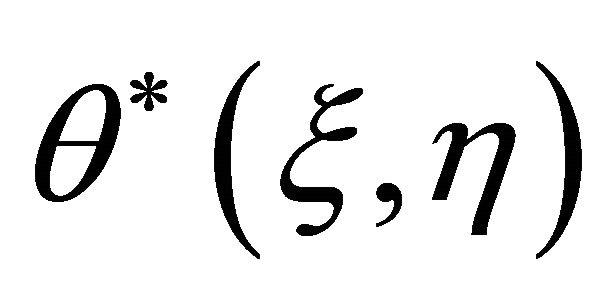 denote the particular solutions of (28)-(29). Using (14), we have the general solutions
denote the particular solutions of (28)-(29). Using (14), we have the general solutions
 (36)
(36)
 (37)
(37)
where


and
 (38)
(38)
 (39)
(39)
where  and
and  are inverse operators of
are inverse operators of 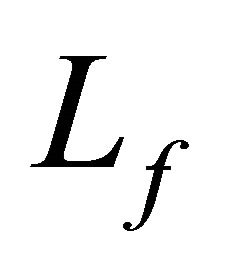 and
and , respectively. Therefore, high-order approximations of
, respectively. Therefore, high-order approximations of  and
and 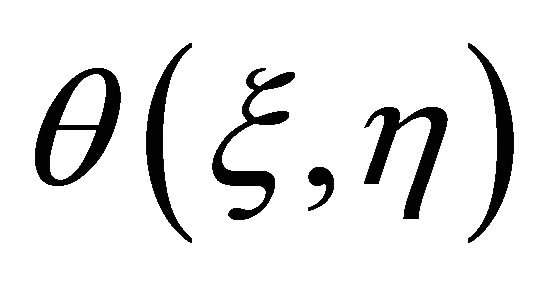 can be obtained, especially by means of symbolic computation.
can be obtained, especially by means of symbolic computation.
In many practical applications, the heat transfer rate at the surface, are vital since they influence the quality of the final products. The graphical representation of the results is very useful to discuss the physical features presented by the solutions. The influence of physical parameters on the skin friction coefficient and displacement thisckness are discussed in detail in [30]. Therefore, we confined our attention only on the temperature distribution in the flow field and the effects of physical parameters on the local Nusselt number and momentum thickness. The local Nusslet number and momentum thickness for non-similarity boundary-layer flows are defined

 (40)
(40)
4. Results and Discussion
As Liao [32,33] proved in general that, as long as a homotopy-series solution given by the homotopy analysis method is not divergent, it must converge to the exact solution of original nonlinear problems under investigation. The convergence of homotopy-series strongly depend on the convergence-control parameter . Therefore, the convergence-control parameter provides us a simple way to ensure the convergence of the homotopyseries. Mathematically, the series solutions are dependent upon
. Therefore, the convergence-control parameter provides us a simple way to ensure the convergence of the homotopyseries. Mathematically, the series solutions are dependent upon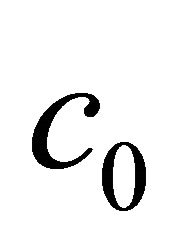 . But, physically, the solution is independent of the convergence-control parameters. As a result, the homotopy-series must converge to the same result for all corresponding values of
. But, physically, the solution is independent of the convergence-control parameters. As a result, the homotopy-series must converge to the same result for all corresponding values of  which ensures the convergence. As mentioned by Liao [32], the admissible values of
which ensures the convergence. As mentioned by Liao [32], the admissible values of  for which the homotopy-series converges can be determined by plotting the so-called
for which the homotopy-series converges can be determined by plotting the so-called  -curves or by plotting the residual error verses
-curves or by plotting the residual error verses . Besides, the optimal homotopy-analysis approach [31] can be used to find the optimal convergence-control parameters. The problem under consideration was solved by Kousar and Liao [30] for velocity field over permeable wedge. In [30] the authors have shown that the homotopy-series (24) converges at
. Besides, the optimal homotopy-analysis approach [31] can be used to find the optimal convergence-control parameters. The problem under consideration was solved by Kousar and Liao [30] for velocity field over permeable wedge. In [30] the authors have shown that the homotopy-series (24) converges at  for all physical parameters in the whole domain
for all physical parameters in the whole domain  and
and . Therefore, in the present analysis, we need only to investigate the convergence of the series (25). In order to make series (25) convergent, let
. Therefore, in the present analysis, we need only to investigate the convergence of the series (25). In order to make series (25) convergent, let  denotes the residual error of the mth-order homotopy-series (25), and
denotes the residual error of the mth-order homotopy-series (25), and
 denotes the integral of the residual error. Plotting the curves of
denotes the integral of the residual error. Plotting the curves of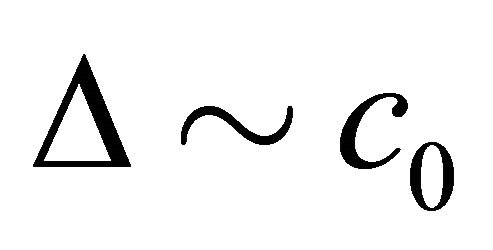 , it is straight forward to find a region of
, it is straight forward to find a region of 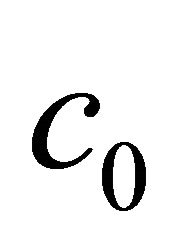 in which
in which  decreases to zero as the order of approximation increases. In this way, we can get the best value of
decreases to zero as the order of approximation increases. In this way, we can get the best value of  corresponding to the minimum of the residual error of the original governing equation.
corresponding to the minimum of the residual error of the original governing equation.
For example, the approximate region for the convergence of the homotopy-series is about  as shown in Figure 1 for different values of the Prandtl numbers when given
as shown in Figure 1 for different values of the Prandtl numbers when given ,
,  ,
, 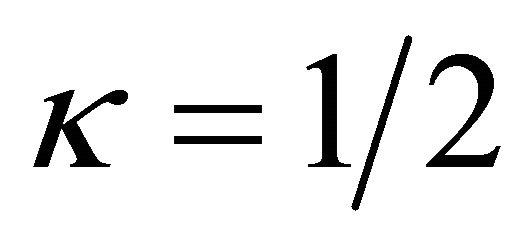 and
and .
.
In general, we can substitute the series solutions for the governing equations and evaluate the square residual error so as to check the convergence of the solutions.
Table 1 shows the square residual error of (5). It is
seen that by increasing the order of approximation the square residual error decreases. This indicates that our HAM series solution is convergent. Similarly, in case of  with
with ,
,  and
and , our series solution converges by means of
, our series solution converges by means of  and
and . It is found that, in general, our series solutions converge by means of
. It is found that, in general, our series solutions converge by means of 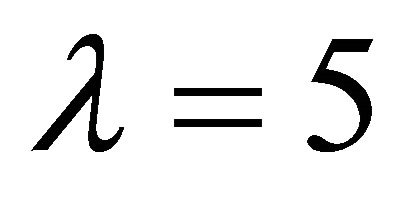 and
and  in the whole spatial domain. Besides, the so-called homotopy-Padé technique [32] is used to accelerate the convergence of the homotopy-series solution.
in the whole spatial domain. Besides, the so-called homotopy-Padé technique [32] is used to accelerate the convergence of the homotopy-series solution.
Figures 2 and 3 represent the effect of the parameter 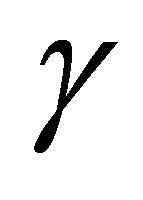 on the local Nusslet number and momentum thickness for
on the local Nusslet number and momentum thickness for ,
,  ,
, 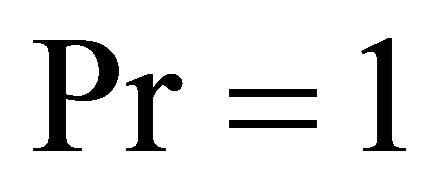 by means of
by means of 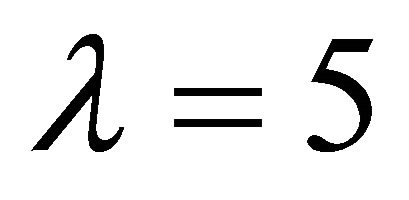 and
and . It is clear from the figures that the injection increases the momentum thickness and decreases the heat transfer rate at surface, but the suction decreases thickness and increases the heat transfer rate. This is due to the fact that the shear stress increases when introducing suction, which in turn increases the local Nusselt number.
. It is clear from the figures that the injection increases the momentum thickness and decreases the heat transfer rate at surface, but the suction decreases thickness and increases the heat transfer rate. This is due to the fact that the shear stress increases when introducing suction, which in turn increases the local Nusselt number.
The heat transfer parameter increases significantly with the Prandtl number, as highjer Prandtl number has lower thermal conductivity, which results in thinner thermal boundary-layer and hence, higher heat transfer rate at the surface. It is also noted that the non-similarity solutions are very close to the similarity ones as  for
for .
.
Figures 4 and 5 show the influence of  on the momentum thickness and the local Nusselt number when
on the momentum thickness and the local Nusselt number when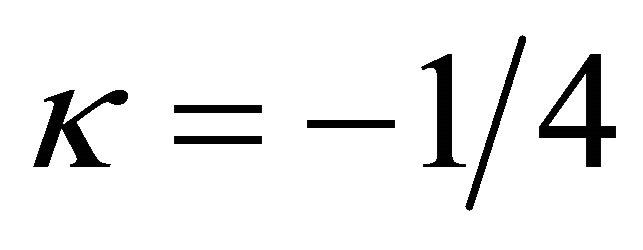 , β = 1, Pr = 1 by means of λ = 5 and c0 = c1 = −1. Again, it is observed from these figures that the suction decreases the thickness but increases the local Nusselt number while the injection increases the thickness but decreases the local Nusselt number. It is also observed that the non-similarity flows are close to the similarity ones as
, β = 1, Pr = 1 by means of λ = 5 and c0 = c1 = −1. Again, it is observed from these figures that the suction decreases the thickness but increases the local Nusselt number while the injection increases the thickness but decreases the local Nusselt number. It is also observed that the non-similarity flows are close to the similarity ones as . Hence, the non-similarity flows in the region
. Hence, the non-similarity flows in the region  for
for  and
and  for
for 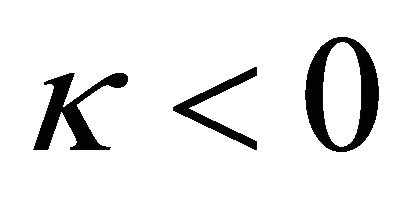 are very close to the similarity ones, respectively.
are very close to the similarity ones, respectively.
Figure 6 shows the heat transfer parameter for various values of Prandtl numbers  when the other physical parameters are fixed. It is observed that heat transfer parameter increases as Pr increases. This is because the fluid with higher Prandtl number has a relatively low thermal conductivity, which reduces the conduction and thereby reduces the thermal boundary-layer thickness. As a consequence the heat transfer rate at the surface increases.
when the other physical parameters are fixed. It is observed that heat transfer parameter increases as Pr increases. This is because the fluid with higher Prandtl number has a relatively low thermal conductivity, which reduces the conduction and thereby reduces the thermal boundary-layer thickness. As a consequence the heat transfer rate at the surface increases.