1. Introduction and Motivation
It is well known that for a family of orthogonal polynomials  the so-called “generating functions” corresponding to this class of functions are a useful tool for their study, see [2,3]. Usually, a generating function is a function of two variables
the so-called “generating functions” corresponding to this class of functions are a useful tool for their study, see [2,3]. Usually, a generating function is a function of two variables , analytic in some set
, analytic in some set , so that
, so that

For example, we have the following generating function of Hermite polynomials , because we can write:
, because we can write:

Note that it is important to specify the subset where the function  is well defined and analytic. For example, for Legendre polynomials we have
is well defined and analytic. For example, for Legendre polynomials we have
 (1)
(1)
where it is important to specify the domain of the variables , because, in other case, for example with the choise
, because, in other case, for example with the choise , formula (1) is meaningless.
, formula (1) is meaningless.
The extension to the matrix framework for the classical case of Gegenbauer [4], Laguerre [5], Hermite [6], Jacobi [7] and Chebyshev [8] polynomials has been made in recent years, and properties and applications of different classes for these matrix polynomials are given in several papers, see [9-13] for example. The importance of the generating function for orthogonal matrix polynomials is similar to the scalar case, taking into account the possible additional spectral restrictions (for a matrix  we will denote by
we will denote by  the spectrum set
the spectrum set ). For example:
). For example:
• For a matrix  such that
such that ,
,  , i.e, A is say positive stable matrix, the Hermite matrix polynomials sequence
, i.e, A is say positive stable matrix, the Hermite matrix polynomials sequence  is defined by the generating function [6]:
is defined by the generating function [6]:
• 
• For a matrix  such that
such that  for every integer
for every integer , and
, and  is a complex number with
is a complex number with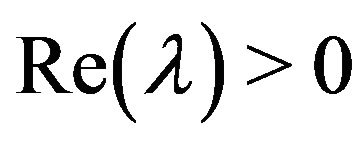 , the Laguerre matrix polynomials sequence
, the Laguerre matrix polynomials sequence  is defined by the generating function [5]:
is defined by the generating function [5]:

2. The Detected Error
Recently, in Ref. [1], the Humbert matrix polynomials of two variables are defined using the generating matrix function given in Formula (7):
 (7)
(7)
where  is a positive stable matrix, i.e., satisfies
is a positive stable matrix, i.e., satisfies  for all eigenvalue
for all eigenvalue , and m is a positive integer. This Formula (7) turns out to be the key for the development of the properties mentioned in the paper [1]. However, we will see that Formula (7) is incorrect. For this, first we have to observe that for a matrix A, we define
, and m is a positive integer. This Formula (7) turns out to be the key for the development of the properties mentioned in the paper [1]. However, we will see that Formula (7) is incorrect. For this, first we have to observe that for a matrix A, we define

where  is the exponential matrix. Of course,
is the exponential matrix. Of course,  has sense only for
has sense only for . Thus, Expression (7) is meaningless if the term
. Thus, Expression (7) is meaningless if the term  is zero. Then, we only need to consider, for example,
is zero. Then, we only need to consider, for example,  ,
,  and
and  and with this choice we have
and with this choice we have . Thus, (7) is meaningless.
. Thus, (7) is meaningless.
Therefore, I ask the authors of Ref. [1] to clarify the domain of choice for the variables t, s in Formula (7) in order to guarantee the validity of the remaining formulas which are derived from (7) and are used in the remainder of [1].