1. Introduction
Image recognition is one of the basic problems in artificial intelligence [1]. A short glance at an ordinary object, which usually suffices for the human brain to recognize and interpret as a known image, is not a trivial task for a computer to accomplish. The computer takes a quick glance but needs a much more time consuming analysis to arrive at the same conclusions. This is particularly the case if the image does not have an accurate shape. Consider a handwritten template: What seems to be relatively easy for the human brain to interpret can pose numerous difficulties in computer image recognition.
In order to overcome this difficulty, it was shown that the task of finding and identifying certain patterns in an otherwise unstructured picture can be accomplished efficiently by a quantum computer [2]. In addition, a suggested manner of handling compatibility between an image and a set of templates (like adjusting a template to a known face, for example) was shown with a set of special classifiers, such as a Fourier analysis, or neural networks (see for example ref. [1]). Another approach of addressing the recognition problem is presented in ref. [3] and in ref. [4] where it is shown that a fully quantum matching procedure exists that is strictly superior to the straightforward semi-classical extension of the conventional matching strategy based on learning process.
Quantum coherence is a basic concept in quantum computer science research [5]. The relation between coherence and image recognition was presented in ref. [6]. It proposes a probabilistic quantum algorithm that decides whether a monochrome image matches a given template.
Quantum coherence, together with the superposition principle, gives rise to the parallelism concept for which processing a single state is like acting simultaneously on all states that participate in the superposition [6,7]. It is also known that a key role in speeding up quantum algorithms is played by multi-particle entanglement [8]. These entanglement and parallelism concepts enable quantum algorithms such as Shor’s factoring, which provides options for very fast computers [9].
In addition, quantum superposition of coherence qubits has the advantage of maintaining enormous databases by a single state. It was shown that this superposition of qubits can be applied to an efficient database-finding algorithm [10-12], and the advantage of using quantum memory was shown in refs. [13-15].
However, despite of all these advantages, implementing the enormous database state is always restricted by the need for quantum measurement at the output stage. Clearly, a state that is originally composed of many qubits randomly collapses into one of its components and the coherence between the qubits is violated.
In this paper we demonstrate that what seems to be a collapse drawback may turn into an advantage if the collapse represents the observer interpretation. The traditional approach for figuring paints is by dividing them into pixels and using sophisticated algorithms to process in order to figure the paints significance. This corresponds to a situation with multi-pixel states. In our approach we propose that the observer defines a quantum basis of states (which are defined as a superposition of the pixel states) rather than using the pixel basis. In quantum mechanics any quantum basis of states can be associated with a measuring device. Thus, the observer possesses the ability of building a device that measures directly the desired figure. Selecting the figure basis depends on the observer determination. Consequently, the collapse can be regarded as the observer interpretation of the original paint. Thus, working within the figure basis allows us to measure and interpret the paint’s multi-pixel state directly in a single measurement and the result of any figure’s multi-data state will be an interpretation into one of the device figure states.
The goal of our approach is to find a device that recognizes figures as close as possible to a single pure quantum measurement by reducing the logical operators (gates) as much as it can. In theory, we show that it is possible to recognize images solely by a single pure measurement.
In the area of pattern recognition an important and central issue is the location problem [16]. Since we concentrate on the interpretation approach, we avoid the location problem by assuming that the photon representing the paint is coherent all over the entire surface of the paint. Furthermore, the paint fills the entire surfaced, thereby eliminating the need to locate it within the surface.
2. Definitions
We propose the following terminology:
Paint state: Refers to the coherent light sources that generate the quantum measuring device input. This state refers to the raw image prior to any attempt at interpretation, similar to a painting before an art critic offers an interpretation. The corresponding state is denoted by  (“
(“ aint”). We will refer to the paint state by the term paint.
aint”). We will refer to the paint state by the term paint.
Figured state: The quantum measurement output that was interpreted (figured out) by the quantum measuring device, similar to the explanation about a painting given by an art critic. The corresponding state is 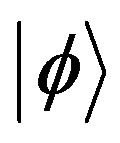 (“
(“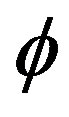 gure”).
gure”).
3. Interpretation Verses Revealing
We recall that the observer selection of the measurement device is equivalent to an interpretation in a sense that the basis of states defines the way a paint is described. The goal of this article is to present a methodology specifically dealing with that subject, i.e., instead of revealing some objective meanings of the paint, the paint is interpreted into a figure. The advantage of this approach is that the observer can define a small number of figures and in that sense it can speed up dramatically the paint interpretation. By selecting the measuring device all paints will collapse to the predefined figures. Moreover, the representation of the whole paint by a single photon enables us to interpret the paint into a figure in a single measurement. We present a conceptual scheme demonstrating how, in a single measurement, an image is interpreted directly into a known image.
4. The Single Photon State Description
In the Fock space a photon state is defined by the photon’s number 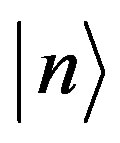 and the photon energy which we refer as the photon color,
and the photon energy which we refer as the photon color,
 . We define a monochromatic single-colored paint, skipping the color state
. We define a monochromatic single-colored paint, skipping the color state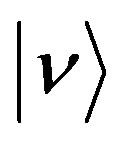 . In our analysis we consider a single photon, that is, the states are
. In our analysis we consider a single photon, that is, the states are 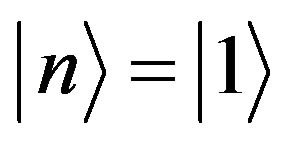 for a single photon existence or
for a single photon existence or  for the photon absence.
for the photon absence.
5. Simple Example—The “Positive” and “Negative” Paints
Before we introduce a single photon state that represents a complex paint, let us start with a simple example that demonstrates the interpretation advantage of paints by a single measurement.
In our description we refer the photon state 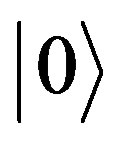 to a black color and the photon state
to a black color and the photon state 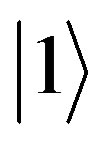 refers to a definite color and we assume the photon to be coherent allover the paint surface [17]. Quantum mechanics allows us to describe paint with superposition of the two single photon states:
refers to a definite color and we assume the photon to be coherent allover the paint surface [17]. Quantum mechanics allows us to describe paint with superposition of the two single photon states:
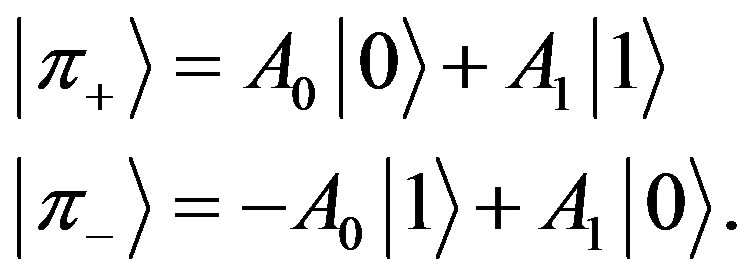 (1)
(1)
With the single photon normalization condition  We now show that the interpretation of the paint is subject to the observer selection of measuring device:
We now show that the interpretation of the paint is subject to the observer selection of measuring device:
Suppose that the observer decides to measure the amounts of colors in each paint. He therefore uses the following projective operator
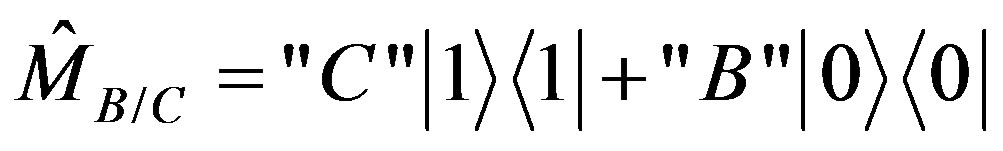 (2)
(2)
We find no specific reason to describe the measurement output by the numerical eigenvalues, in particular when the output is a color concept. Therefore we introduce the eigensymbols 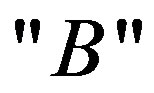 and
and 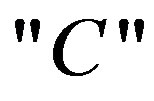 that symbolize the black and the definite colors,respectively. The states
that symbolize the black and the definite colors,respectively. The states  and
and  stand for the photon presence or absence, respectively. The minus sign that appears in the
stand for the photon presence or absence, respectively. The minus sign that appears in the 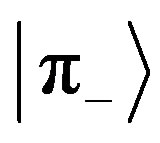 is a phase that is responsible for the states orthogonality. Although the phase is in a way obscured through the measuring process, it provides the measuring device the ability of distinguishing between the states.
is a phase that is responsible for the states orthogonality. Although the phase is in a way obscured through the measuring process, it provides the measuring device the ability of distinguishing between the states.
The expectation values of the measurements are
 (3)
(3)
Clearly the 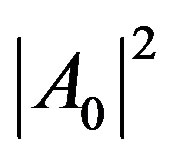 and
and 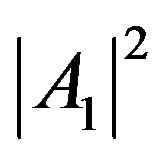 are the different amounts of black and the defined colors. It is also seen that the difference between the two expressions is a color flipping; that is, if the
are the different amounts of black and the defined colors. It is also seen that the difference between the two expressions is a color flipping; that is, if the  and
and  color amounts for
color amounts for
 are
are 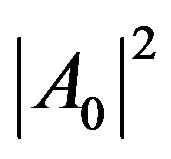 and
and , respectively, then the
, respectively, then the 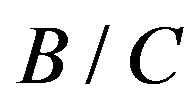 color amounts for
color amounts for 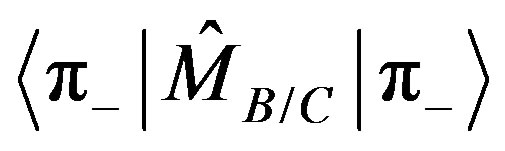 are
are 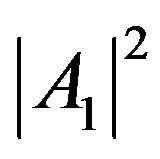
and 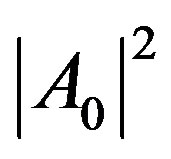 in the same order. This means that the two states
in the same order. This means that the two states 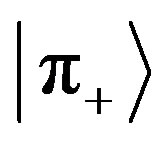 and
and 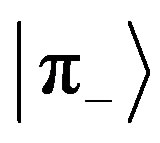 have opposite colors, like positive and negative paints.
have opposite colors, like positive and negative paints.
Selecting a measurement device is like making an interpretation, or, selecting the language to describe the phenomena. The measuring device 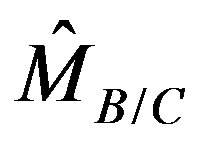 describes the paint by the amounts of the black and the definite colors. A measuring device that directly detects the states
describes the paint by the amounts of the black and the definite colors. A measuring device that directly detects the states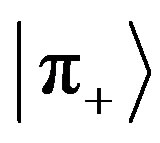 ,
,  through the operator
through the operator
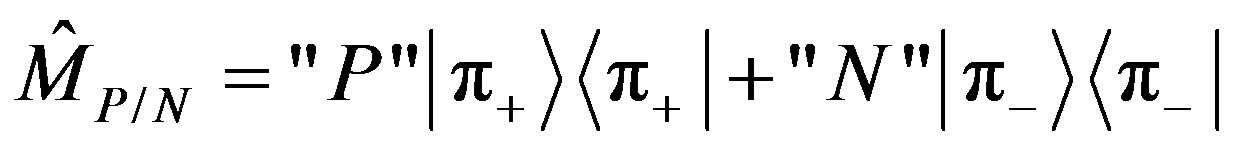 (4)
(4)
distinguishes between a positive or negative paint as indicated by the “eigensymbols” letters selection  and
and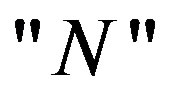 , respectively. For example if we choose the two pictures as described in Figure 1 then, by the use of the device as presented in Equation 4, a single measurement will distinguish between the two paints. It will not reveal the headline “paint” but it will distinguish between the positive and negative paint in a single measurement without the necessity of a complicated analysis. Note that this measurement requires an input photon that is coherent all over the paint.
, respectively. For example if we choose the two pictures as described in Figure 1 then, by the use of the device as presented in Equation 4, a single measurement will distinguish between the two paints. It will not reveal the headline “paint” but it will distinguish between the positive and negative paint in a single measurement without the necessity of a complicated analysis. Note that this measurement requires an input photon that is coherent all over the paint.
An impaortant quality of this measuring method is the

Figure 1. Example of positive and negative paints. Black color can be considered as the photon absence while the white color can stand for the photon existence. These two paints are distinguished in a single measurement.
full interpretation output. We should bear in mind that the observer does not seek for an absolute truth, he rather seeks for a clear observation between the paints: Positive or negative? Eventually, even paints that are not clearly distinguishable as positive or negative paints will collapse during the measurement process into one of the categories.
5.1. Measurement Correction (Interpretation)-Stressing the Paint Details
Let us assume that the paint is described by means of superposition of the  -states:
-states:
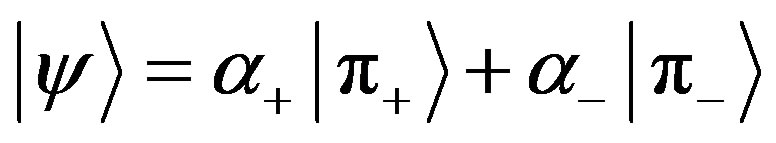 (5)
(5)
which means that we have a white and gray paint (see Figure 2). An observer that uses the 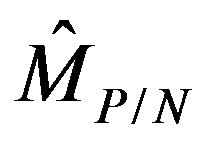 measuring device (Equation (4)) is blind to gray colors and therefore he will measure only the states
measuring device (Equation (4)) is blind to gray colors and therefore he will measure only the states 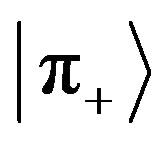 or
or 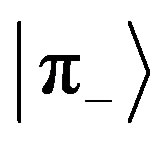 with probabilities
with probabilities  and
and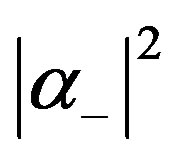 , respectively. This kind of measurement can be applicative if one needs to stress details in a fuzzy paint.
, respectively. This kind of measurement can be applicative if one needs to stress details in a fuzzy paint.
5.2. The Detailed Paint State
In order to obtain a significant paint we have to describe the colors distribution across the canvas. This is performed by dividing the paint into an  small squares matrix (pixels) represented by the states
small squares matrix (pixels) represented by the states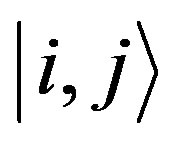 , where
, where 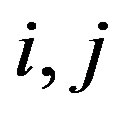 describes the pixel location. To avoid confusion we note that the states
describes the pixel location. To avoid confusion we note that the states 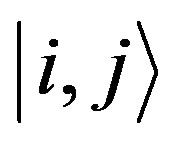 refer to a a single particle state that for convenience reason was expressed in this form in order to appear in a matrix form (see, for example, the right side of Figure 3).
refer to a a single particle state that for convenience reason was expressed in this form in order to appear in a matrix form (see, for example, the right side of Figure 3).
With a tensor product we assign the photon state such that 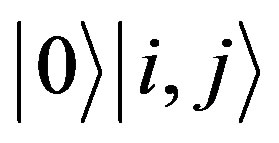 and
and 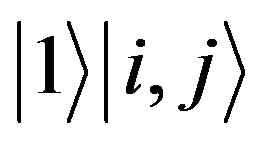 represent black and colored pixels in the
represent black and colored pixels in the  location, respectively The paint is described by the following superposition
location, respectively The paint is described by the following superposition
 (6)
(6)
By selecting various coefficients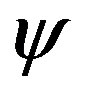 , it is possible to form a set of paints to serve as the measuring device input. There is no particular demand regarding this set and the state members can be nonorthogonal provided that the paint and the figure states belong to the same Fock space, meaning that every single photon state possesses the same number of pixels.
, it is possible to form a set of paints to serve as the measuring device input. There is no particular demand regarding this set and the state members can be nonorthogonal provided that the paint and the figure states belong to the same Fock space, meaning that every single photon state possesses the same number of pixels.

Figure 2. A gray paint example. Clearly it does not fall under the category of positive or negative paint. Yet, the measuring output will be one of the figures of Figure 1.
For the definition of the paint set we add superscripts 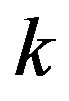 such that
such that
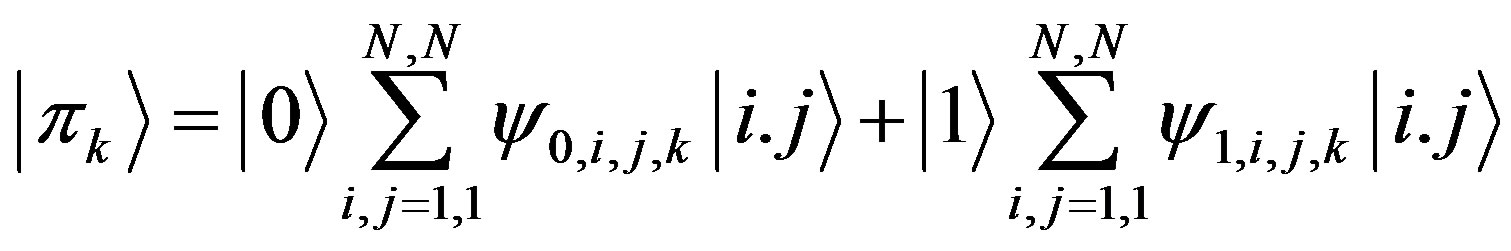 (7)
(7)
6. The Measuring Process
In order to understand the measurement role in the paint interpretation process we recall few essential issues:
1) The measuring device possesses a set of eigenstates that span the Fock space. We referred those states as to the figure states (figured out by the measuring device).
2) The measuring device does not reveal some objective meaning of the paint. It simply projects the arriving photon paint state into the device eigenstates.
3) In the collapse process the measuring device forces the measurement output to be one of device eigenstates. This collapse is responsible for the interpretation.
4) Since the single photon arrives already “dressed” in the paint state and by assuming that the paint states are similar to the figure states we can assume that a single measurement can interpret (figure out) the paint into a figure state with reasonable reliability.
5) In case of a paint that is different from the figure states, the vague paint state will collapse into clear figure identification as expected by the observer.
6.1. The Orthogonality of the Figure States
We pointed out that there is no necessity for the paints set to be orthogonal. However, when collapsing into the figure states, the new figure basis must be become orthogonal, otherwise the measuring results will be indistinguishable.
As we need the figure state to resemble the paint state as much as possible, we introduce a formalism of alternating nonorthogonal states into an orthogonal set with the introduction of relative phases.
Suppose we have a states set like in Equation (7) that are nonorthogonal.
We propose that in the measurement process the coefficients gain a phase such that
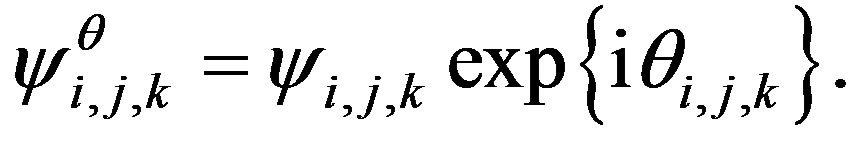 (8)
(8)
The term 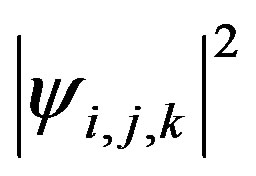 is the amount of color at the matching pixel (see Equations (6) and (7)). Therefore, the addition phase does not change the paint nature. However, we can select phases that can impose orthogonality between the states.
is the amount of color at the matching pixel (see Equations (6) and (7)). Therefore, the addition phase does not change the paint nature. However, we can select phases that can impose orthogonality between the states.
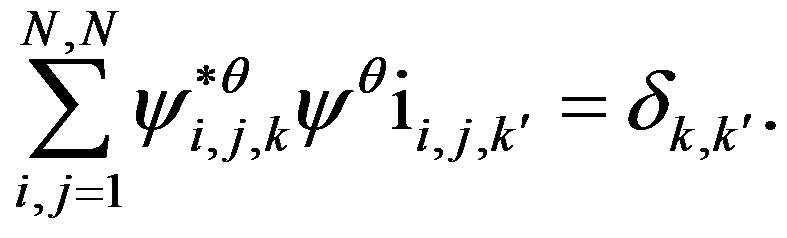 (9)
(9)
For example we can choose the following 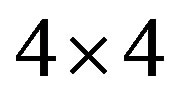 states representing the letters
states representing the letters 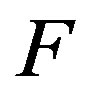 and
and  (Figure 3).
(Figure 3).
The corresponding states are:
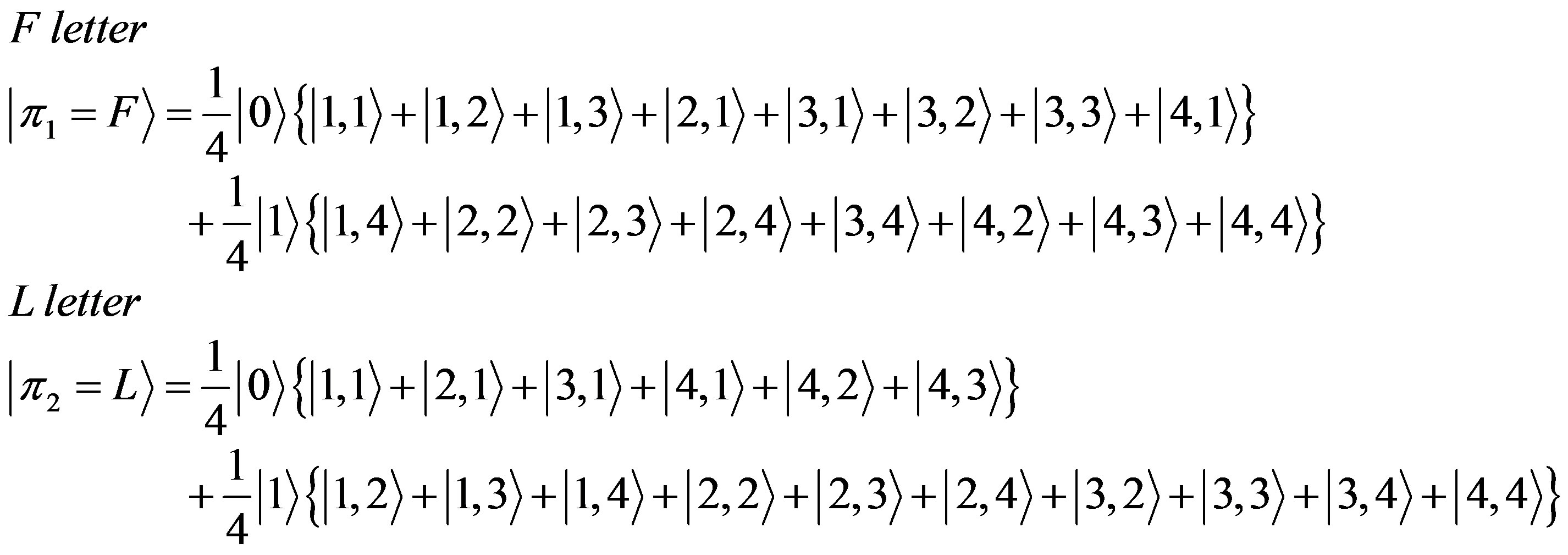 (10)
(10)
These are nonorthogonal states. Yet, by introducing the following relative phases (the  signs)
signs)
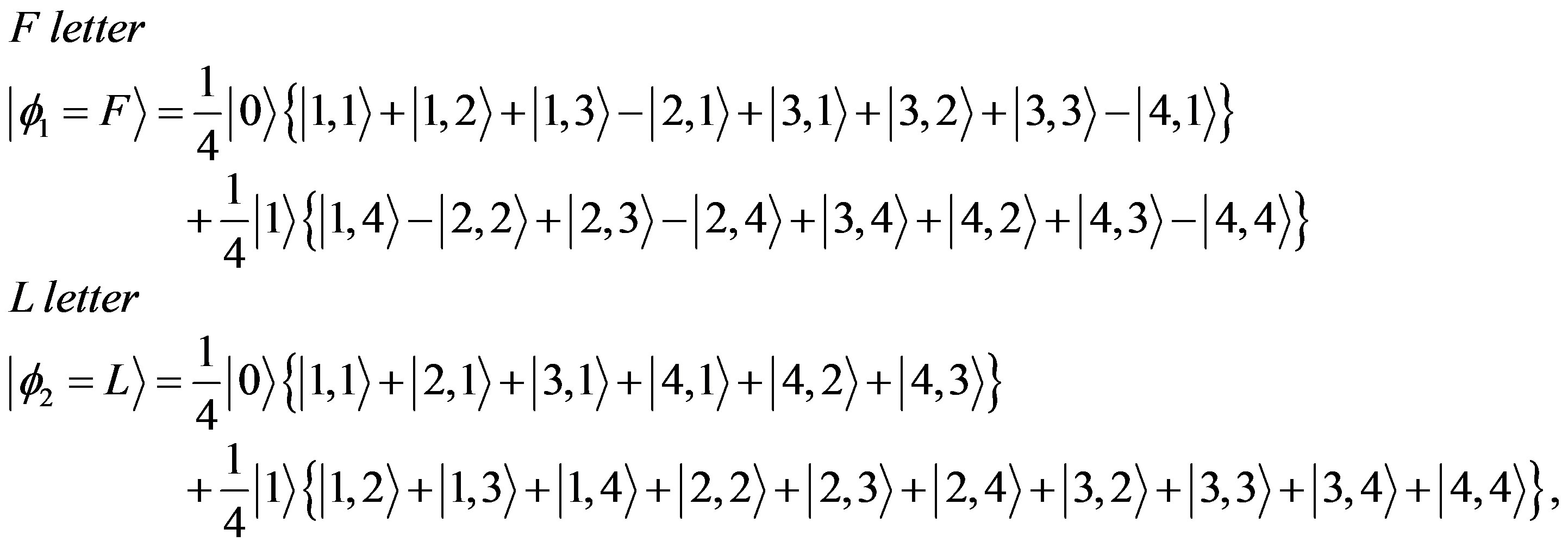 (11)
(11)
We obtain orthogonal states. We note that now the states are denoted by the letter  since now they are the measurement related states.
since now they are the measurement related states.
6.2. The Measuring Device Scheme
The measuring device is composed of two components: The Translating Slide and, behind it, the Determination Plane (see illustration in Figure 4).
The Translating Slide is the component in which the paint state  is interpreted into the figure language
is interpreted into the figure language 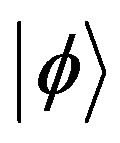 through the superposition
through the superposition
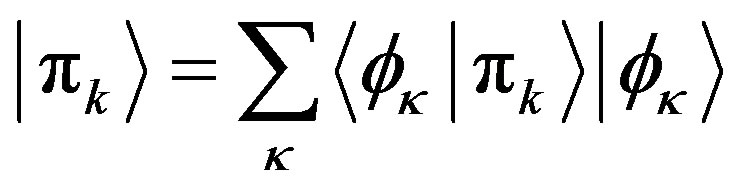 (12)
(12)
and the Determination Plane is a macroscopic device that is responsible for the original state collapsing into one of the figure states.
Let us assume a paint, located at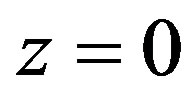 , emitting a plane wave photon
, emitting a plane wave photon . The Interpretation Slide is located at
. The Interpretation Slide is located at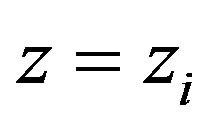 , perpendicular to the wave function direction. The Translating Slide is a varying transparency slide that is locally adjusted into the desired measured figures. In addition, in order to force orthogonality, each part of the slide can locally shift the phase of the arriving paint photon.
, perpendicular to the wave function direction. The Translating Slide is a varying transparency slide that is locally adjusted into the desired measured figures. In addition, in order to force orthogonality, each part of the slide can locally shift the phase of the arriving paint photon.
The slide is divided into 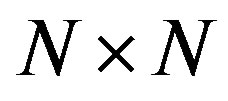 squares where each square represents a miniature of a figure. In order to form a miniature, each square is subdivided into smaller squares that play the part of pixels in the figure miniature.
squares where each square represents a miniature of a figure. In order to form a miniature, each square is subdivided into smaller squares that play the part of pixels in the figure miniature.
We define the pixels in each miniature by the subscripts 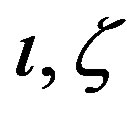 (in analogy to the
(in analogy to the 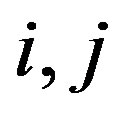 pixels of the paint state) to obtain the miniature states
pixels of the paint state) to obtain the miniature states
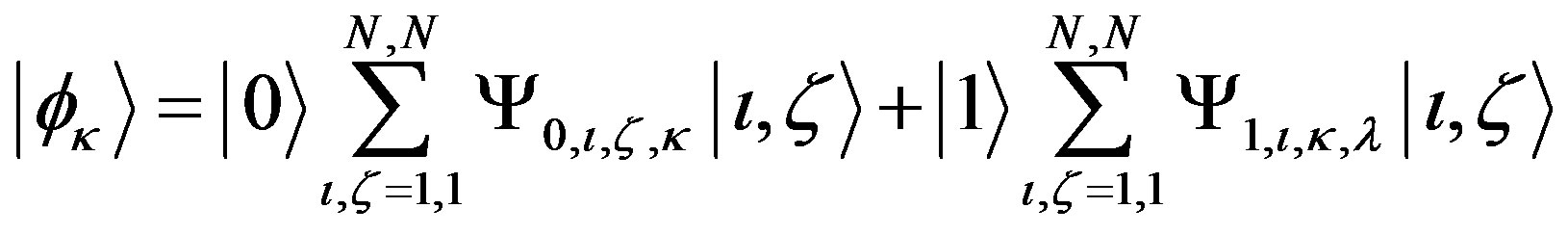 (13)
(13)
where 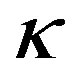 marks the miniatures. Now the coefficients
marks the miniatures. Now the coefficients  and
and 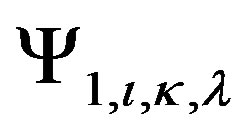 that represent the relative amount of photons amplitude can be interpreted as the pixel relative transparency and phases. We design the pixels to form orthogonal figure states.
that represent the relative amount of photons amplitude can be interpreted as the pixel relative transparency and phases. We design the pixels to form orthogonal figure states.
Thus, a photon that passes through a single miniature indicates that originally it was in a paint state that
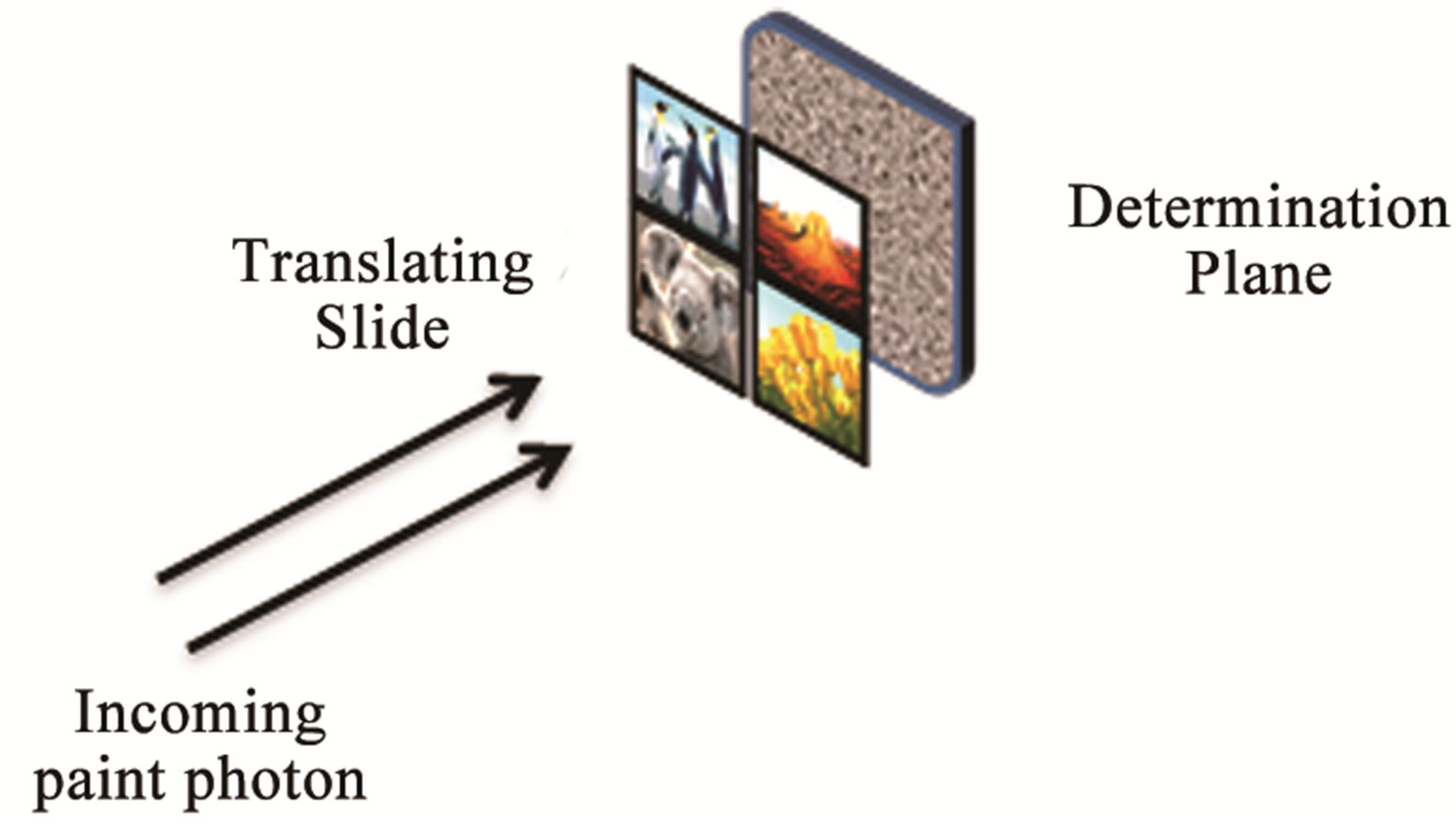
Figure 4. An illustration of the measuring device.
matches the figure state. However, a paint photon that is not a member of the figure basis will be described by the superposition of all the miniature states, described in Equation (12), that is, extended all over the Translating Slide, meaning, no conclusive interpretation regarding the photon figure state is obtained. For that scenario we introduced the Determination Plane. The Determination Plane is a macroscopic object located behind the Translating Slide. An extended photon that passes through the slide when interacting with the Determination Plane will collapse to exhibit a single location in the plane. The miniature against that location will be regarded as the figure interpretation.
7. Figure Composed of Template Pixel
In this paper we introduced the concept of an image that is represented by a single photon in contrast to the multiphoton approach for which each pixel is represented by a photon state and the image state is composed of the pixel-photon-states product.
A middle way is to compose the image from template pixels.
We define a template pixel as a figure basic element that instead of being single-colored, is a complicated figure by itself. In many ways this template image composition resembles the way a painter describes his image. He describes it as composed of templates such as lines or other shapes rather then small single colored squares.
The image states 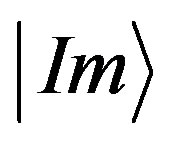 that are composed of
that are composed of 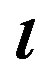 number of templates, are composed from all the template states
number of templates, are composed from all the template states 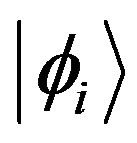 product combinations
product combinations
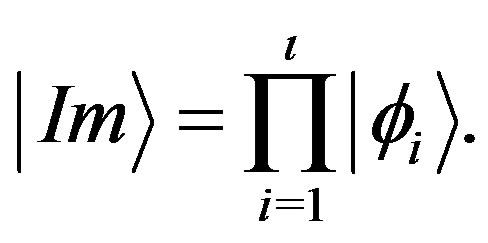 (14)
(14)
8. Summary
Rapid figure recognition is a crucial requirement in artificial intelligence. The ability of a future artificial intelligence machine to function independently depends on its ability to swiftly recognize and interpret its surroundings. It should be noticed that a robot interacting within human society must have the ability of interpreting its surroundings correctly, rather than just displaying some objective reality.
A figure interpreted within the coordinate’s basis may contain an enormous database. Therefore, in order to reduce the time consumed by the interpretation process, the multi-database is usually analyzed with sophisticated algorithms. The shorter the running time the more efficient the algorithm will be. In our approach, interpreting was analyzed strictly within the figure basis with no concern for the time-consuming algorithms. This corresponded with the single measurement that measures the figure as a whole. In the same manner as we reduced the time-consuming interpretation by replacing the sophisticated algorithms with almost a single measuring device, we can design a robot for which the interpretation capabilities are also physically embedded within its electronic brain with a measuring device as we described here in order to reduce the time-consuming algorithm components.
Let us conclude with a philosophical thought. Gestalt is a psychology term that refers to theories of visual perception. It attempts to describe how to organize visual elements as a whole. Here we proposed a kind of quantum Gestalt theory that by almost a single measurement detects the image as a whole.