Portfolio Size in Stochastic Portfolio Networks Using Digital Portfolio Theory ()
1. Introduction
The choice of financial risk measures is very important in the assessment of the riskiness of financial positions. For this reason, several classes of financial risk measures have been proposed in the literature. Among these are coherent and convex risk measures, Choquet expectations and Peng’s g-expectations. Coherent risk measures were first introduced by Artzner, Delbaen, Eber and Heath [1] and Delbaen [2]. As an extension of coherent risk measures, convex risk measures in general probability spaces were introduced by Föllmer & Schied [3] and Frittelli & Rosazza Gianin [4]. g-expectations were introduced by Peng [5] via a class of nonlinear backward stochastic differential equations (BSDEs), this class of nonlinear BSDEs being introduced earlier by Pardoux and Peng [6]. Choquet [7] extended probability measures to nonadditive probability measures (capacity), and introduced the so called Choquet expectation.
Our interest in this paper is to explore the relations among risk measures and expectations. To do so, we restrict our attention of coherent and convex risk measures and Choquet expectations to the domain of g-expectations. The distinctions between coherent risk measure and convex risk measure are accounted for intuitively in the framework of g-expectations. We show that 1) in the family of convex risk measures, only coherent risk measures satisfy Jensen’s inequality; 2) coherent risk measures are always bounded by the corresponding Choquet expectation, but such an inequality in general fails for convex risk measures. In finance, coherent and convex risk measures and Choquet expectations are often used in the pricing of a contingent claim. Result 2) implies coherent pricing is always less than Choquet pricing, but the pricing by a convex risk measure no longer has this property. We also study the relation between static and dynamic risk measures. We establish that if g-expectations are coherent (convex) risk measures, then the same is true for the corresponding conditional g-expectations or dynamic risk. In order to prove these results, we establish in Section 3, Theorem 1, a new converse comparison theorem of g-expectations. Jiang [8] studies gexpectation and shows that some cases give rise to risk measures. Here we are able to show, in the case of gexpectations, that coherent risk measures are bounded by Choquet expectation but this relation fails for convex risk measures; see Theorem 4. Also we show that convex risk measures obey Jensen’s inequality; see Theorem 3.
The paper is organized as follows. Section 2 reviews and gives the various definitions needed here. Section 3 gives the main results and proofs. Section 4 gives a summary of the results, putting them into a Table form for convenience of the various relations.
2. Expectations and Risk Measures
In this section, we briefly recall the definitions of g-expectation, Choquet expectation, coherent and convex risk measures.
2.1. g-Expectation
Peng [5] introduced g-expectation via a class of backward stochastic differential equations (BSDE). Some of the relevant definition and notation are given here.
Fix  and let
and let  be a
be a 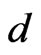 -dimensional standard Brownian motion defined on a completed probability space
-dimensional standard Brownian motion defined on a completed probability space . Suppose
. Suppose  is the natural filtration generated by
is the natural filtration generated by , that is
, that is  We also assume
We also assume . Denote
. Denote


Let 
 satisfy
satisfy
(H1) For any  is a continuous progressively measurable process with
is a continuous progressively measurable process with
 .
.
(H2) There exists a constant  such that for any
such that for any

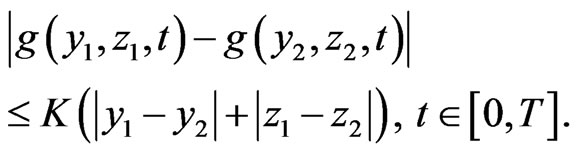
(H3) 
In Section 3, Corollary 3 we will consider a special case of  with
with .
.
Under the assumptions of (H1) and (H2), Pardoux and Peng [6] showed that for any , the BSDE
, the BSDE
 (1)
(1)
has a unique pair solution
 .
.
Using the solution  of BSDE (1), which depends on
of BSDE (1), which depends on , Peng [5] introduced the notion of g-expectations.
, Peng [5] introduced the notion of g-expectations.
Definition 1 Assume that (H1), (H2) and (H3) hold on g and . Let
. Let  be the solution of BSDE (1).
be the solution of BSDE (1).
 defined by
defined by 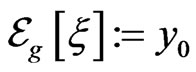 is called the g-expectation of the random variable
is called the g-expectation of the random variable .
.
 defined by
defined by  is called the conditional g-expectation of the random variable
is called the conditional g-expectation of the random variable .
.
Peng [5] also showed that g-expectation  and conditional
and conditional  -expectation
-expectation  preserve most of basic properties of mathematical expectation, except for linearity. The basic properties are summarized in the next Lemma.
preserve most of basic properties of mathematical expectation, except for linearity. The basic properties are summarized in the next Lemma.
Lemma 1 (Peng) Suppose that
 .
.
1) Preservation of constants: For any constant 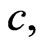
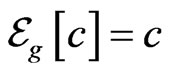 .
.
2) Monotonicity: If , then
, then .
.
3) Strict monotonicity: If , and
, and , then
, then .
.
4) Consistency: For any ,
,
 .
.
5) If  does not depend on
does not depend on , and
, and 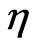 is
is  - measurable, then
- measurable, then

In particular, .
.
6) Continuity: If  as
as  in
in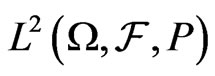 , then
, then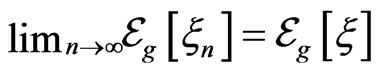 .
.
The following lemma is from Briand et al. [9, Theorem 2.1]. We can rewrite it as follows.
Lemma 2 (Briand et al. ) Suppose that  is of the form
is of the form 
 where
where  is a continuous bounded process. Then
is a continuous bounded process. Then

where the limit is in the sense of .
.
2.2. Choquet Expectation
Choquet [7] extended the notion of a probability measure to nonadditive probability (called capacity) and defined a kind of nonlinear expectation, which is now called Choquet expectation.
Definition 2
1) A real valued set function 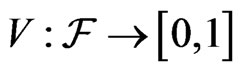 is called a capacity if a)
is called a capacity if a) 
b)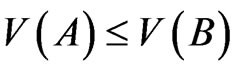 , whenever
, whenever 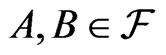 and
and .
.
2) Let  be a capacity. For any
be a capacity. For any , the Choquet expectation
, the Choquet expectation  is defined by
is defined by

Remark 1 A property of Choquet expectation is positive homogeneity, i.e. for any constant 

2.3. Risk Measures
A risk measure is a map  where
where  is interpreted as the “habitat” of the financial positions whose riskiness has to be quantified. In this paper, we shall consider
is interpreted as the “habitat” of the financial positions whose riskiness has to be quantified. In this paper, we shall consider .
.
The following modifications of coherent risk measures (Artzner et al.[1]) is from Roorda et. al. [10].
Definition 3 A risk measure  is said to be coherent if it satisfies 1) Subadditivity:
is said to be coherent if it satisfies 1) Subadditivity: ,
, ;
;
2) Positive homogeneity:  for all real number
for all real number 
3) Monotonicity:  whenever
whenever 
4) Translation invariance:  for all real number
for all real number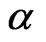 .
.
As an extension of coherent risk measures, Föllmer and Schied [3] introduced the axiomatic setting for convex risk measures. The following modifications of convex risk measures of Föllmer and Schied [3] is from Frittelli and Rosazza Gianin [4].
Definition 4 A risk measure is said to be convex if it satisfies 1) Convexity:
 ,
,

 ;
;
2) Normality: ;
;
3) Properties (3) and (4) in Definition 3.
A functional  in Definitions 3 and 4 is usually called a static risk measure. Obviously, a coherent risk measure is a convex risk measure.
in Definitions 3 and 4 is usually called a static risk measure. Obviously, a coherent risk measure is a convex risk measure.
As an extension of such a functional  Artzner et al. [11,12], Frittelli and Rosazza Gianin [13] introduced the notion of dynamic risk measure
Artzner et al. [11,12], Frittelli and Rosazza Gianin [13] introduced the notion of dynamic risk measure  which is random and depends on a time parameter
which is random and depends on a time parameter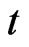 .
.
Definition 5 A dynamic risk measure

is a random functional which depends on , such that for each
, such that for each  it is a risk measure. If
it is a risk measure. If  satisfies for each
satisfies for each 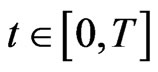 the conditions in Definition 3, we say
the conditions in Definition 3, we say  is a dynamic coherent risk measure. Similarly if
is a dynamic coherent risk measure. Similarly if  satisfies for each
satisfies for each  the conditions in Definition 4, we say
the conditions in Definition 4, we say  is a dynamic convex risk measure.
is a dynamic convex risk measure.
3. Main Results
In order to prove our main results, we establish a general converse comparison theorem of g-expectation. This theorem plays an important role in this paper.
Theorem 1 Suppose that  and
and 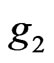 satisfy (H1), (H2) and (H3). Then the following conclusions are equivalent.
satisfy (H1), (H2) and (H3). Then the following conclusions are equivalent.
1) For any 

2) For any 
 (2)
(2)
Proof: We first show that inequality (2) implies inequality 3).
Let 
 and
and  be the solutions of the following BSDE corresponding to the terminal value
be the solutions of the following BSDE corresponding to the terminal value  and
and  and the generator
and the generator  and
and , respectively
, respectively
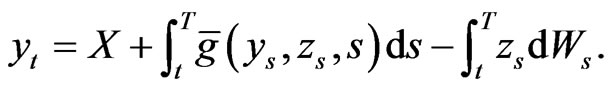 (3)
(3)
Then 


For fixed , consider the BSDE
, consider the BSDE
 (4)
(4)
It is easy to check that 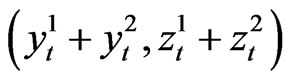 is the solution of the BSDE (4).
is the solution of the BSDE (4).
Comparing BSDEs (4) and (3) with 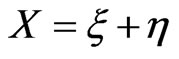 and
and , assumption (2), (2) then yields
, assumption (2), (2) then yields

Applying the comparison theorem of BSDE in Peng [5], we have  Taking
Taking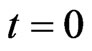 , thus by the definition of
, thus by the definition of  -expectation, the proof of this part is complete.
-expectation, the proof of this part is complete.
We now prove that inequality (1) implies (2). We distinguish two cases: the former where  does not depend on
does not depend on , the latter where
, the latter where  may depend on
may depend on .
.
Case 1,  does not depend on
does not depend on . The proof of this case 1 is done in two steps.
. The proof of this case 1 is done in two steps.
Case 1, Step 1: We now show that for any , we have
, we have

Indeed, for , set
, set

If for all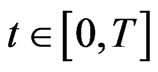 , we have
, we have  then we obtain our result.
then we obtain our result.
If not, then there exists  such that
such that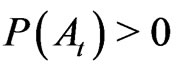 . We will now obtain a contradiction.
. We will now obtain a contradiction.
For this ,
,

That is

Taking g-expectation on both sides of the above inequality, and apply the strict monotonicity of  -expectation in Lemma 1 (3), it follows
-expectation in Lemma 1 (3), it follows

But by Lemma 1 (4) and (5),

Note that by Lemma 1(v)

Thus

This induces a contradiction, thus concluding the proof of this Step 1.
Case 1, Step 2: For any  with
with  and
and , let us choose
, let us choose 
 . Obviously,
. Obviously, 
By Step 1,

Thus

Let  applying Lemma 2, since g does not depend on
applying Lemma 2, since g does not depend on  we rewrite
we rewrite  simply as
simply as 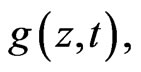 thus
thus  The proof of Case 1 is complete.
The proof of Case 1 is complete.
Case 2, g depends on y. The proof is similar to the proof of Theorem 2.1 in Coquet et al. [14]. For each  and
and  define the stopping time
define the stopping time

Obviously, if for each 
 , for all
, for all  then the proof is done. If it is not the case, then there exist
then the proof is done. If it is not the case, then there exist 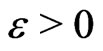 and
and

such that
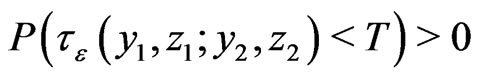 .
.
Fix  and consider the following (forward) SDEs defined on the interval
and consider the following (forward) SDEs defined on the interval 
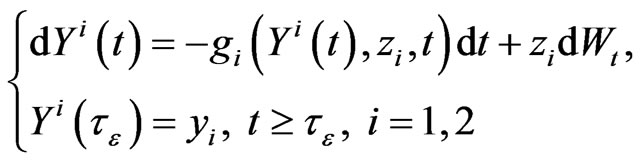
and

Obviously, the above equations admit a unique solution 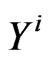 which is progressively measurable with
which is progressively measurable with

Define the following stopping time

It is clear that  and note that
and note that  whenever
whenever  thus,
thus, 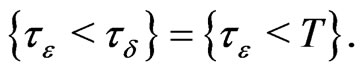 Hence
Hence .
.
Moreover, we can prove

In fact, setting
 then
then

Thus 
It follows that on ,
,  This implies
This implies
 (5)
(5)
By the definition of  and
and , the pair processes
, the pair processes  and
and  are the solutions of the following BSDEs with terminal values
are the solutions of the following BSDEs with terminal values 
 and
and ,
,

and

Hence,


and

Applying the strict comparison theorem of BSDE and inequality (5), by the assumptions of this Theorem, we have

This induces a contradiction. The proof is complete.
Lemma 3 Suppose that g satisfies (H1), (H2) and (H3). For any constant , let
, let
 .
.
Then for any ,
, 
Proof: Letting , then
, then  is the solution of BSDE
is the solution of BSDE

Since
 the above BSDE can be rewritten as
the above BSDE can be rewritten as
 (6)
(6)
Let , then
, then  satisfies
satisfies
 (7)
(7)
Comparing with BSDE (6) and BSDE (7), by the uniqueness of the solution of BSDE, we have

Let  then
then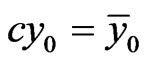 . The conclusion of the Lemma now follows by the definition of g-expectation. This concludes the proof.
. The conclusion of the Lemma now follows by the definition of g-expectation. This concludes the proof.
Applying Theorem 1 and Lemma 3, immediately, we obtain several relations between g-expectation  and
and . These are given in the following Corollaries.
. These are given in the following Corollaries.
Corollary 1 The g-expectation  is the classical mathematical expectation if and only if g does not depend on
is the classical mathematical expectation if and only if g does not depend on  and is linear in
and is linear in .
.
Proof: Applying Theorem 1,  is linear if and only if
is linear if and only if 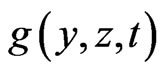 is linear in
is linear in . By assumption (H3), that is
. By assumption (H3), that is  for all
for all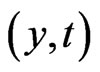 . Thus
. Thus  does not depend on
does not depend on . The proof is complete.
. The proof is complete.
Corollary 2 The  -expectation
-expectation  is a convex risk measure if and only if
is a convex risk measure if and only if  does not depend on
does not depend on  and is convex in
and is convex in .
.
Proof: Obviously,  -expectation
-expectation  is convex risk measure if and only if for any
is convex risk measure if and only if for any 
 (8)
(8)
For a fixed , let
, let

Applying Lemma 3,

Inequality (8) becomes

Applying Theorem 1, for any


which then implies that g is convex. By the explanation of Remark for Lemma 4.5 in Briand et al. [9], the convexity of 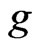 and the assumption (H3) imply that
and the assumption (H3) imply that  does not depend on
does not depend on . The proof is complete.
. The proof is complete.
The function  is positively homogeneous in
is positively homogeneous in  if for any
if for any ,
, .
.
Corollary 3 The  -expectation
-expectation  is a coherent risk measure if and only if
is a coherent risk measure if and only if  does not depend on
does not depend on  and it is convex and positively homogenous in
and it is convex and positively homogenous in . In particular, if
. In particular, if ,
, 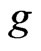 is of the form
is of the form
 with
with .
.
Proof: By Corollary 2, the  -expectation
-expectation 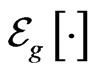 is a convex risk measure if and only if
is a convex risk measure if and only if 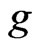 does not depend on
does not depend on  and is convex in
and is convex in . Applying Theorem 1 and Lemma 3 again, it is easy to check that
. Applying Theorem 1 and Lemma 3 again, it is easy to check that  -expectation
-expectation  is positively homogeneous if and only if
is positively homogeneous if and only if  is positively homogeneous (that is for all
is positively homogeneous (that is for all  and
and 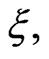
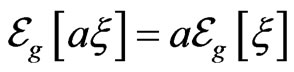 if and only if for any
if and only if for any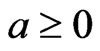 ,
, .
.
In particular, if , notice the fact that
, notice the fact that 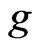 is convex and positively homogeneous on
is convex and positively homogeneous on , and that
, and that  does not depend on
does not depend on . We write it as
. We write it as  then
then
 (9)
(9)
Note that ,
,  , but
, but

Thus from (9)

Defining
 ,
, .
.
Obviously  since the convexity of
since the convexity of  yields
yields

The proof is complete.
Remark 2 Corollaries 2 and 3 give us an intuitive explanation for the distinction between coherent and convex risk measures. In the framework of g-expectations, convex risk measures are generated by convex functions, while coherent measures are generated only by convex and positively homogenous functions. In particular, if d = 1, it is generated only by the family  with
with . Thus the family of coherent risk measures is much smaller than the family of convex risk measures.
. Thus the family of coherent risk measures is much smaller than the family of convex risk measures.
Jensen’s inequality for mathematical inequality is important in probability theory. Chen et al. [15] studied Jensen’s inequality for g-expectation.
We say that 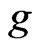 -expectation satisfies Jensen’s inequality if for any convex function
-expectation satisfies Jensen’s inequality if for any convex function  then
then
 (10)
(10)
Lemma 4 [Chen et al. [15] Theorem 3.1] Let 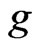 be a convex function and satisfy
be a convex function and satisfy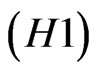 ,
,  and
and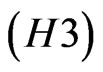 . Then 1) Jensen’s inequality (10) holds for
. Then 1) Jensen’s inequality (10) holds for  -expectations if and only if
-expectations if and only if  does not depend on
does not depend on  and is positively homogeneous in
and is positively homogeneous in ;
;
2) If  the necessary and sufficient condition for Jensen’s inequality (10) to hold is that there exist two adapted processes
the necessary and sufficient condition for Jensen’s inequality (10) to hold is that there exist two adapted processes  and
and  such that
such that
 .
.
Now we can easily obtain our main results. Theorem 2 below shows the relation between static risk measures and dynamic risk measures.
Theorem 2 If  -expectation
-expectation 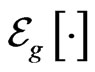 is a static convex (coherent) risk measure, then the corresponding conditional g-expectation
is a static convex (coherent) risk measure, then the corresponding conditional g-expectation  is dynamic convex (coherent) risk measure for each
is dynamic convex (coherent) risk measure for each 
Proof: This follows directly direct from Theorem 1.
Theorem 3 below shows that in the family of convex risk measure, only coherent risk measure satisfies Jensen’s inequality.
Theorem 3 Suppose that  is a convex risk measure. Then
is a convex risk measure. Then  is a coherent risk measure if and only if
is a coherent risk measure if and only if  satisfies Jensen’s inequality.
satisfies Jensen’s inequality.
Proof: If  is a convex risk measure, then by Corollary 2,
is a convex risk measure, then by Corollary 2,  is convex. Applying Lemma 4,
is convex. Applying Lemma 4,  satisfies Jensen’s inequality if and only if
satisfies Jensen’s inequality if and only if  is positively homogenous. By Corollary 2, the corresponding
is positively homogenous. By Corollary 2, the corresponding  is coherent risk measure. The proof is complete.
is coherent risk measure. The proof is complete.
Theorem 4 and Counterexample 1 below give the relation between risk measures and Choquet expectation.
Theorem 4 If  is a coherent risk measure, then
is a coherent risk measure, then  is bounded by the corresponding Choquet expectation, that is
is bounded by the corresponding Choquet expectation, that is  where
where . If
. If  is a convex risk measure then inequality above fails in general. By construction there exists a convex risk measure and random variables
is a convex risk measure then inequality above fails in general. By construction there exists a convex risk measure and random variables 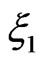 and
and  such that
such that

The prove this theorem uses the following lemma.
Lemma 5 Suppose that  does not depend on
does not depend on . Suppose that the
. Suppose that the  -expectation
-expectation  satisfies (1)
satisfies (1)  (2) For any positive constant
(2) For any positive constant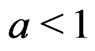 ,
,

Then for any 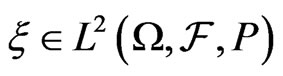 the
the  -expectation
-expectation  is bounded by the corresponding Choquet expectation, that is
is bounded by the corresponding Choquet expectation, that is
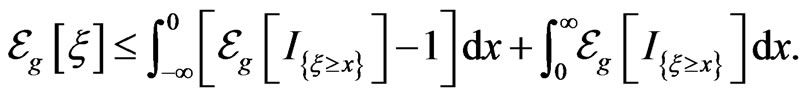 (11)
(11)
Proof: The proof is done in three steps.
Step 1. We show that if  is bounded by
is bounded by , then inequality (11) holds.
, then inequality (11) holds.
In fact, for the fixed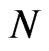 , denote
, denote 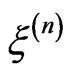 by
by

Then  in
in 
Moreover,  can be rewritten as
can be rewritten as

But by the assumptions (1) and (2) in this lemma, we have
 (12)
(12)
Note that

and 
Thus, taking limits on both sides of inequality (12), it follows that  The proof of Step 1 is complete.
The proof of Step 1 is complete.
Step 2. We show that if  is bounded by
is bounded by , that is
, that is , then inequality (11) holds.
, then inequality (11) holds.
Let  then
then  Applying Step 1,
Applying Step 1,
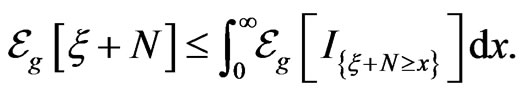 (13)
(13)
But by Lemma 1(v),  On the other hand,
On the other hand,

Thus by (13)

Therefore

Step 3. For any  let
let 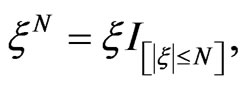 then
then . By Step 2,
. By Step 2,

Letting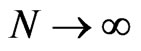 , it follows that
, it follows that

The proof is complete.
Proof of Theorem 4: If the  -expectation
-expectation  is a coherent risk measure, then it is easy to check that the
is a coherent risk measure, then it is easy to check that the  -expectation
-expectation  satisfies the conditions of Lemma 5.
satisfies the conditions of Lemma 5.
Let 
 . By Lemma 5 and the definition of Choquet expectation, we have
. By Lemma 5 and the definition of Choquet expectation, we have  The first part of this theorem is complete.
The first part of this theorem is complete.
Counterexample 1 shows that this property of coherent risk measures fails in general for more general convex risk measures. This completes the proof of Theorem 4.
Counterexample 1 Suppose that  is 1-dimensional Brownian motion (i.e. d = 1). Let
is 1-dimensional Brownian motion (i.e. d = 1). Let 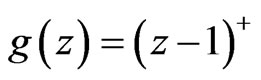 where
where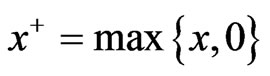 . Then
. Then  is a convex risk measure. Let
is a convex risk measure. Let  and
and  Then
Then
 However
However  Here the capacity
Here the capacity  in the Choquet expectation
in the Choquet expectation 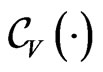 is given by
is given by 
Proof of the Inequality in Counterexample 1: The convex function 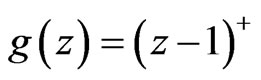 satisfies (H1), (H2) and(H3). Thus, by Corollary 2,
satisfies (H1), (H2) and(H3). Thus, by Corollary 2,  -expectation
-expectation  is a convex risk measure. This together with the property of Choquet expectation in Remark 1 implies
is a convex risk measure. This together with the property of Choquet expectation in Remark 1 implies

Moreover, since  by Corollary 3,
by Corollary 3,  is a convex risk measure rather than a coherent risk measure. We now prove that
is a convex risk measure rather than a coherent risk measure. We now prove that  In fact, since
In fact, since

we only need to show

Let  be the solution of the BSDE
be the solution of the BSDE
 (14)
(14)
First we prove that
 (15)
(15)
where  is Lebesgue measure on
is Lebesgue measure on 
If it is not true, then  a.e.
a.e.  and BSDE (14) becomes
and BSDE (14) becomes

Thus

By the Markov property,

Recall that  and
and  are independent and
are independent and . Thus
. Thus

where  is the density function of the normal distribution
is the density function of the normal distribution . Thus
. Thus  where
where  is the Malliavin derivative. Thus
is the Malliavin derivative. Thus  can be greater than 1 whenever
can be greater than 1 whenever  is near 0 and
is near 0 and 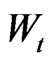 is near 0. Thus (15) holds, which contradicts the assumption
is near 0. Thus (15) holds, which contradicts the assumption  a.e.
a.e. .
.
Secondly we prove that

Let  be the solution of the BSDE
be the solution of the BSDE
 (16)
(16)
Obviously,

which means  is the solution of BSDE
is the solution of BSDE

But  Thus by the uniqueness of the solution of BSDE,
Thus by the uniqueness of the solution of BSDE,  On the other hand, let
On the other hand, let 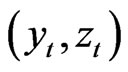 be the solution of the BSDE
be the solution of the BSDE
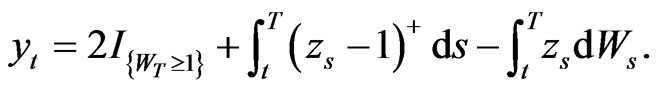 (17)
(17)
Comparing BSDE(17) with BSDE (16), notice (15) and the fact
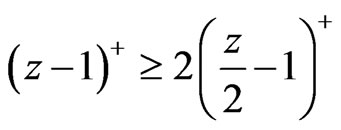 and
and 
whenever z >1. By the strict comparison theorem of BSDE, we have 
Setting , thus
, thus

The proof is complete.
Remark 3 In mathematical finance, coherent and convex risk measures and Choquet expectation are used in the pricing of contingent claim. Theorem 4 shows that coherent pricing is always less than Choquet pricing, while Counterexample 1 demonstrates that pricing by a convex risk measure no longer has this property. In fact the convex risk price may be greater than or less than the Choquet expectation.
4. Summary
Coherent risk measures are a generalization of mathematical expectations, while convex risk measures are a generalization of coherent risk measures. In the framework of  -expectation, the summary of our results is given in Table 1. In that Table, the Choquet expectation is
-expectation, the summary of our results is given in Table 1. In that Table, the Choquet expectation is .
.
Counterexample 1 shows that convex risk may be  or
or  Choquet expectation. Only in the case of coherent
Choquet expectation. Only in the case of coherent

Table 1. Relations among coherent and convex risk measures , choquet expectation and Jensen’s inequality.
, choquet expectation and Jensen’s inequality.
risk there is an inequality relation with Choquet expectation.
NOTES
This work has been supported by grants from the Natural Sciences and Engineering Research Council (NSERC) of Canada.