Nondifferentiable Multiobjective Programming with Equality and Inequality Constraints ()
1. Introduction
A number of researchers have discussed optimality and duality for a class of nondifferentiable problem containing the square root of a positive semi-definite quadratic form. Mond [1] presented Wolfe type duality while Chandra et al. [2] investigated Mond-Weir type duality for this class of problems. Later, Zhang and Mond [3] validated various duality results for the problem under generalized invexity conditions, it is observed that the popularity of this kind of problems seems to originate from the fact that, even through the objective functions, and/or constraint function are non-smooth, a simple and elegant representation for the dual to this type of problems may be obtained. Obviously non-smooth mathematical programming with more general type functions by means of generalized sub differentials. However, the square root of positive semi-definite quadratic form is one of some of a nondifferentiable function for which sub differentials can be explicitly be written.
Multiobjective optimization problems have been applied in various field of science, where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Researchers study multiobjective optimization problems from different viewpoints and, then there exist different goals when setting and solving them. The goal may be finding a representation set of Pareto optimal solutions, and/or qualifying the trade-offs in satisfying the different objectivesand/or finding a single solution that satisfies the preferences of a human decisions making. Motivated with these observations, there has been an increasing interest in studying optimality and duality for nondifferentiable multiobjective programming problems. Duality results for nondifferentiable multiobjective programming problems with square root term appearing in each component of the vector objective derived by Lal et al. [4]. In nondifferentiable multiobjective programming problems, having a support function in each component of the vector objective, further developments for duality results are found in Kim et al. [5] and Yang et al. [6].
In this paper, we obtain optimality conditions for a class of nondifferentiable multiobjective programming problems with equality and inequality involving a square root terms in each component of the objective. For this class of problems, Mond-Weir type dual is formulated and usual duality results are obtained. In the end a special case is generated.
2. Related Pre-Requisites and Expression of the Problem
In [1], the following problem is considered:
Problem (EP): Minimize
subject to 
where 1) ,
, 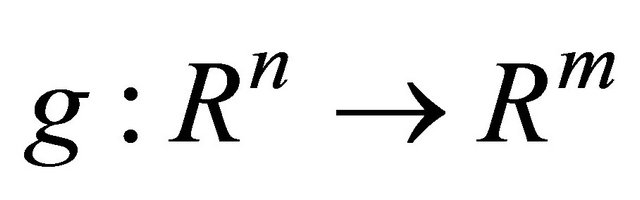 and
and  are continuously differentiable.
are continuously differentiable.
2) B is an  symmetric positive semi definite matrix.
symmetric positive semi definite matrix.
The following generalized Schwartz inequality [7] will be needed in the present analysis:
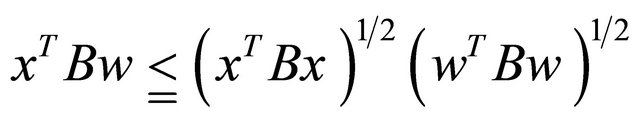
The equality in the above holds if, for 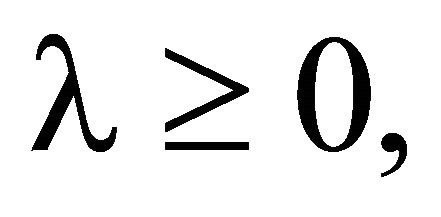
 .
.
The function , being convex and everywhere finite, has a subdifferential in the sense of convex analysis. The subdifferential of
, being convex and everywhere finite, has a subdifferential in the sense of convex analysis. The subdifferential of 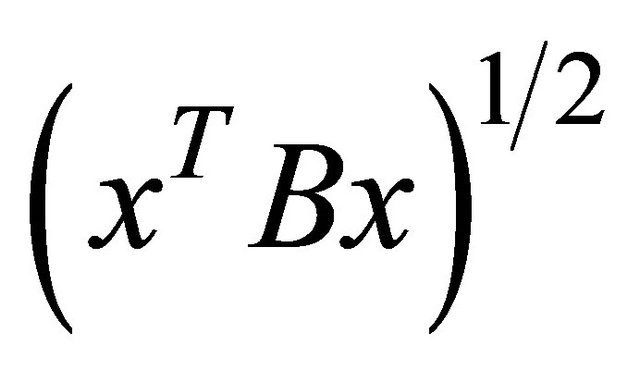 is given by
is given by

We also require the Mangasarian-Fromovitz constraint qualification which is described as the following:
Let 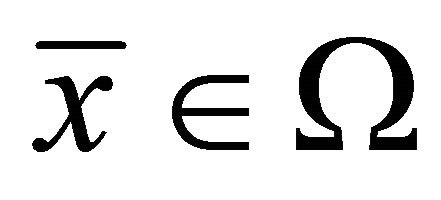 be the set of feasible solution of the problem (EP), that is,
be the set of feasible solution of the problem (EP), that is,
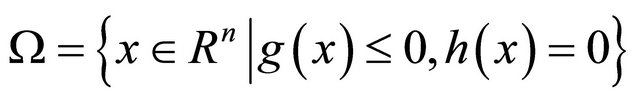
and by 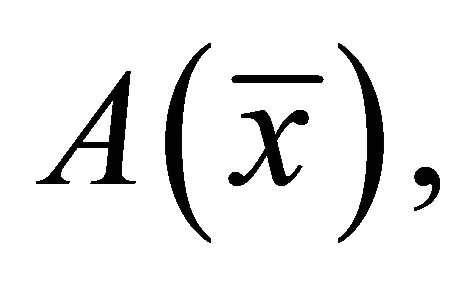 the set of inequality active constraint indices, that is,
the set of inequality active constraint indices, that is,

where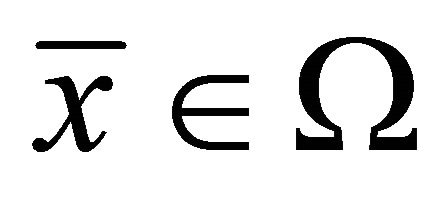 . We say the Mangasarian-Fromovitz constraint qualification holds at
. We say the Mangasarian-Fromovitz constraint qualification holds at  when the equality constraint gradients
when the equality constraint gradients 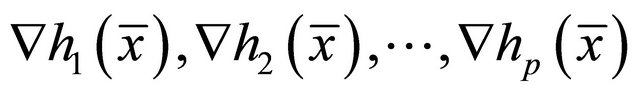 are linearly independent and there exist a vector
are linearly independent and there exist a vector such that
such that

The following theorems (Theorem 2.1 and Theorem 2.2) give Fritz John and Karush-Kuhn-Tucker type optimality conditions using the concept of sub differential obtained by Husain and Srivastav [8] using the concept of subdifferential:
Theorem 2.1 (Fritz John Optimality Conditions): If  is an optimal solution of (EP), then there exist Lagrange multipliers
is an optimal solution of (EP), then there exist Lagrange multipliers 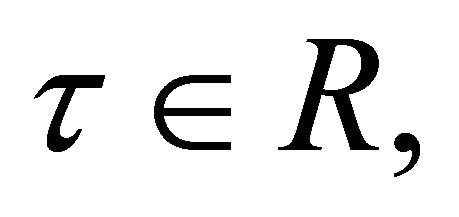

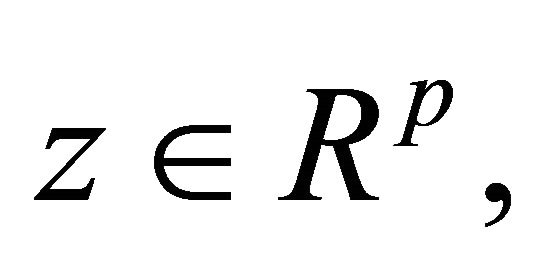
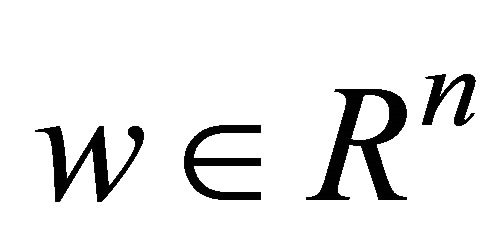 such that
such that


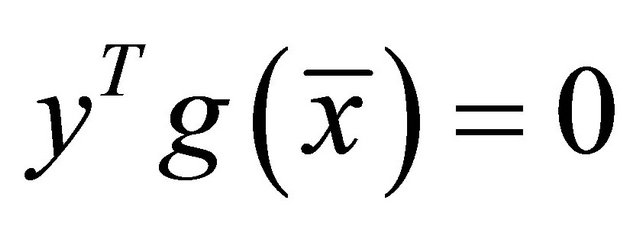
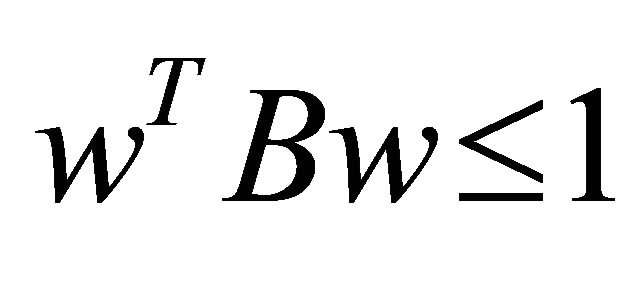

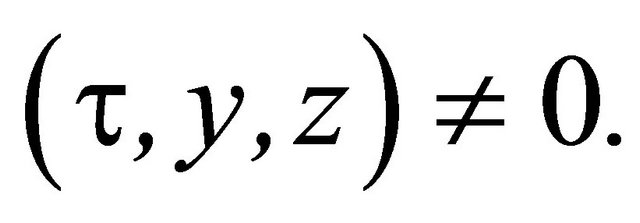
If Mangasarian-Fromovitz constrain qualification (MFCQ) holds at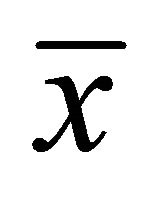 , then the above theorem reduces to the following theorem giving Karush-Kuhn-Tucker optimality conditions:
, then the above theorem reduces to the following theorem giving Karush-Kuhn-Tucker optimality conditions:
Theorem 2.2 (Karush-Kuhn-Tucker optimality conditions): If 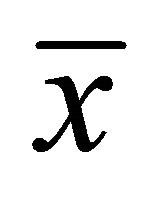 is an optimal solution of (EP) and MFCQ holds at
is an optimal solution of (EP) and MFCQ holds at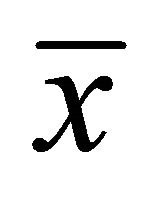 , then there exist
, then there exist 
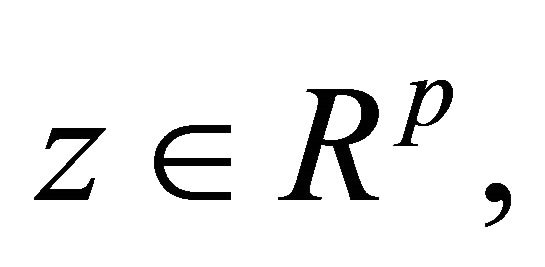
 such that
such that


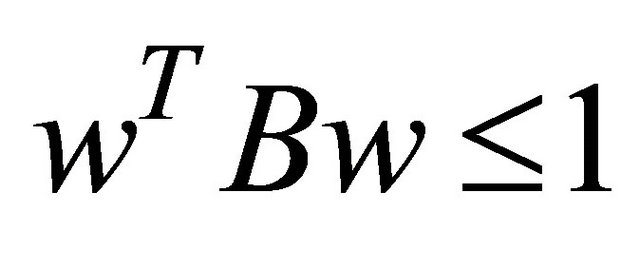
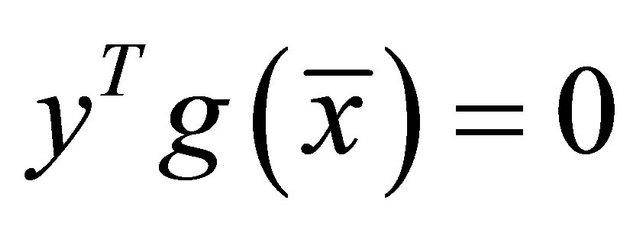

The following conventions for inequalities will be used in the subsequent analysis: If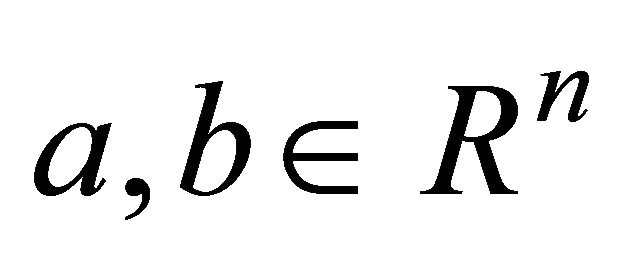 , then
, then
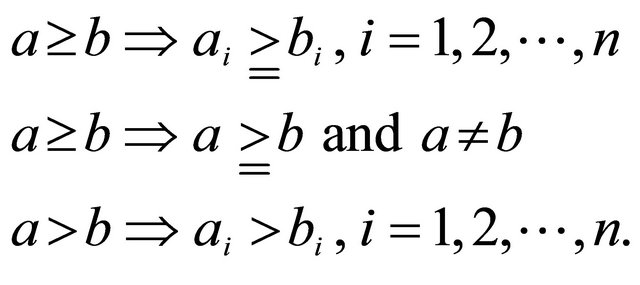
Consider the following multiobjective programming problem containing square root of a certain quadratic form in each component of the objective.
(VEP): Minimize
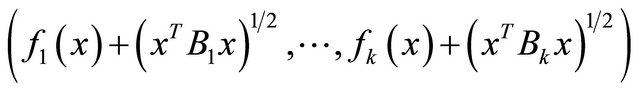
Subject to
 (1)
(1)
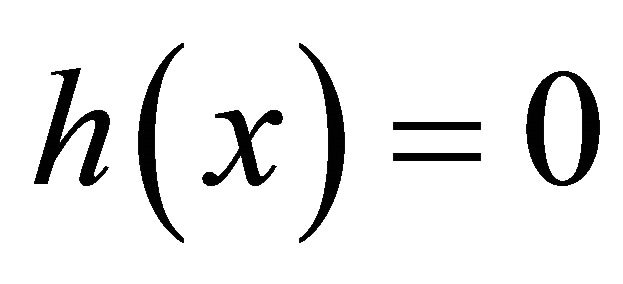 (2)
(2)
where f, g and h are the same as in (EP).
Let 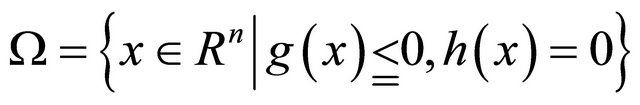
Definition 2.1 A point  is said to be an efficient solution of (EP) if there exists no
is said to be an efficient solution of (EP) if there exists no  such that
such that
 for some
for some  and
and
 for
for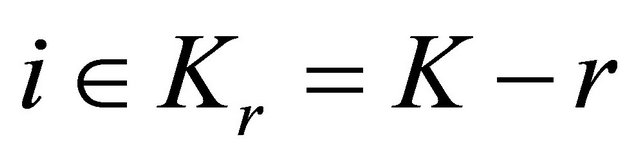 .
.
The following results relate an efficient solution of (EP) of k-scalar objective programming problems.
Lemma 2.2 (Chankong and Haimes [9]): A point 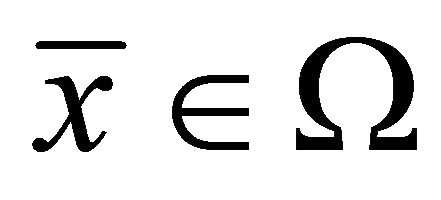 is an efficient solution of (EP) if and only if
is an efficient solution of (EP) if and only if 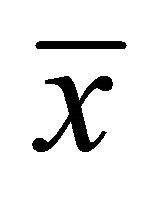 is an optimal solution of
is an optimal solution of  for each
for each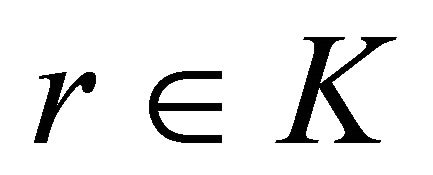 .
.
 : Minimize
: Minimize 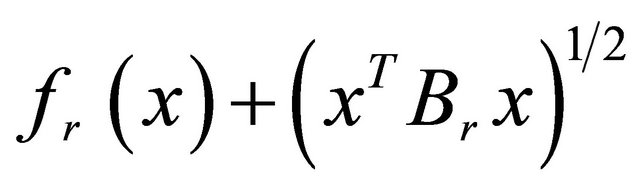
subject to 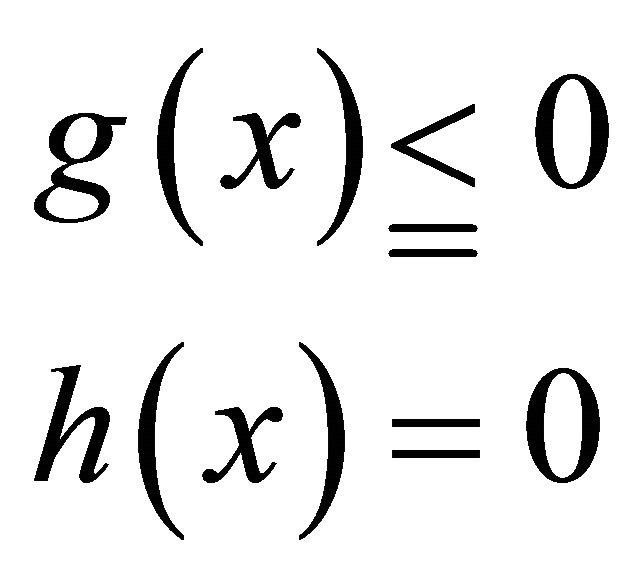

We recall the following definitions of generalized invexity which will be used to derive various duality results.
Definitions 2.2: 1) A function 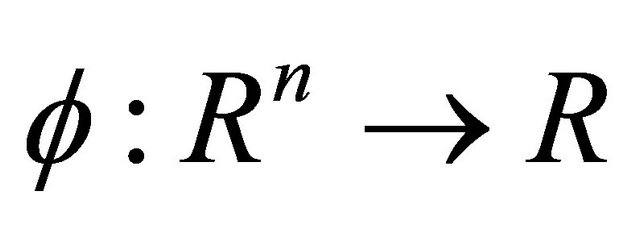 is said to be quasi-invex with respect to a vector function
is said to be quasi-invex with respect to a vector function 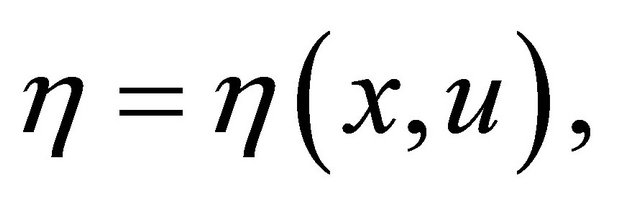 if
if

2) A function  is said to be pseudo-invex with respect to a vector function
is said to be pseudo-invex with respect to a vector function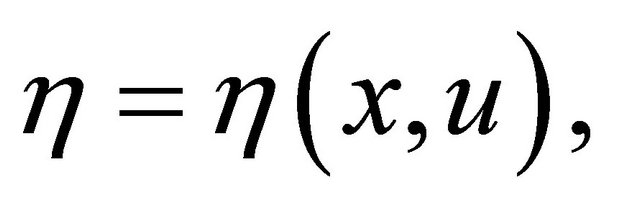 if
if
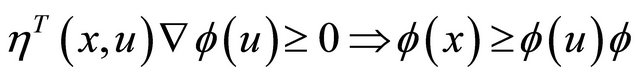 .
.
3)  is said to be the strictly pseudoinvex with respect to
is said to be the strictly pseudoinvex with respect to 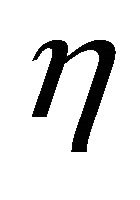 if
if 
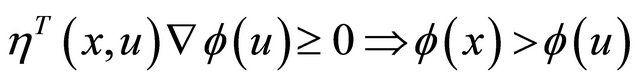 .
.
Equivalently, if
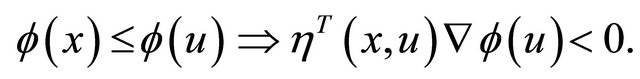
3. Optimality Conditions
In this section, the optimality conditions for the problem (EP) are obtained.
Theorem 3.1 (Fritz John Type Optimality Conditions): If 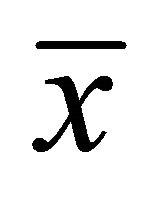 be an efficient solution of (EP), then there exist
be an efficient solution of (EP), then there exist 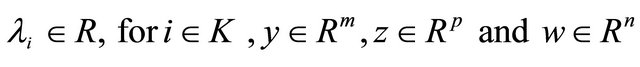 such that
such that


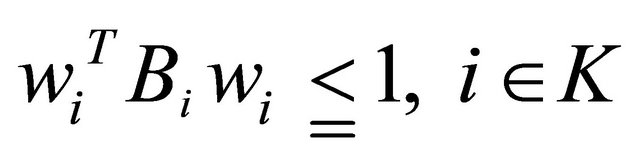
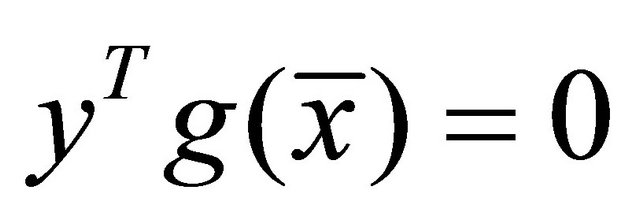

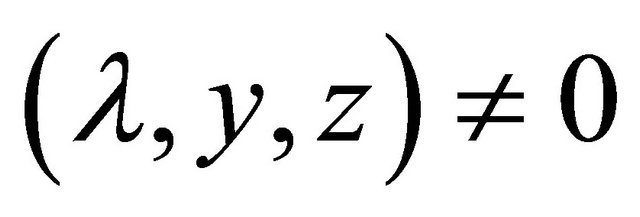
Proof: Since  is an efficient solution of (EP), by Lemma 2.1
is an efficient solution of (EP), by Lemma 2.1 is an optimal solution of
is an optimal solution of 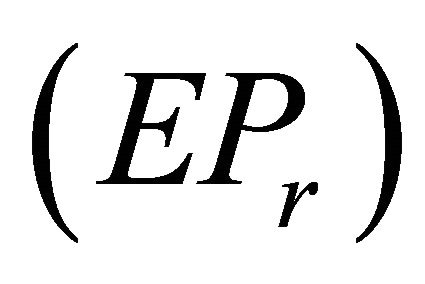 for each
for each 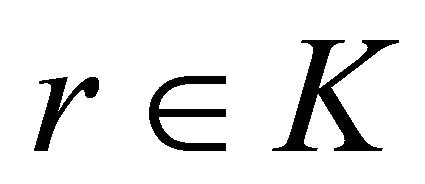 and hence in particular of
and hence in particular of . Therefore by Theorem 2.1 there exist
. Therefore by Theorem 2.1 there exist 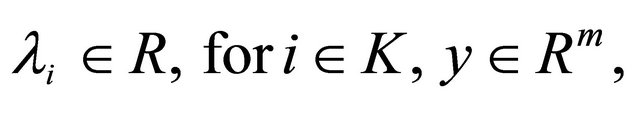
 such that
such that
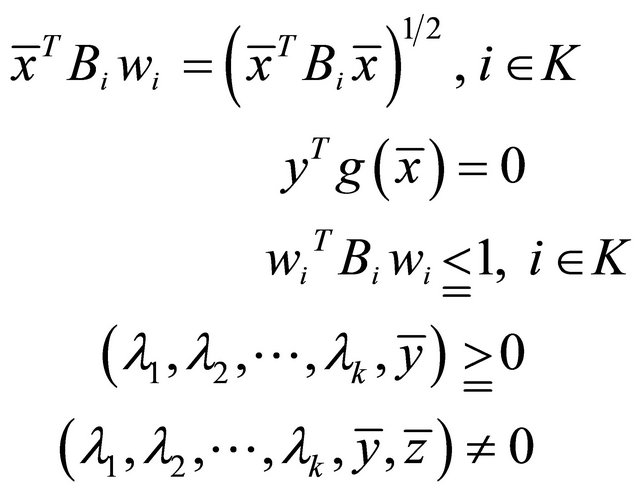
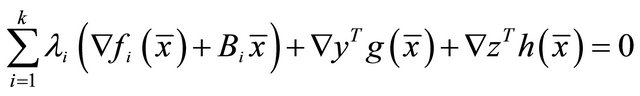
The theorem follows.
Theorem 3.2 (Kuhn-Tucker type necessary optimality conditions): If  be an optimal solution of (VEP) and let for
be an optimal solution of (VEP) and let for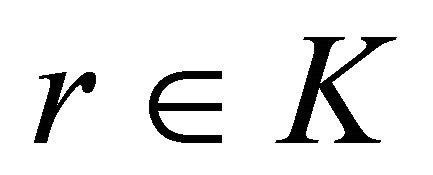 , the constraints of
, the constraints of 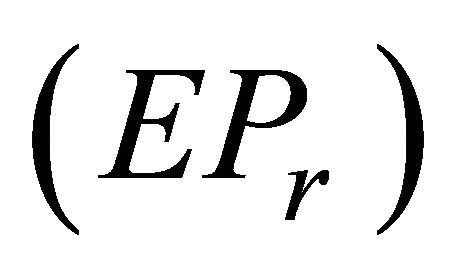 satisfy MECQ. Then there exist
satisfy MECQ. Then there exist 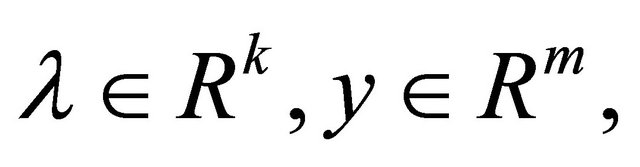
 and
and  such that
such that
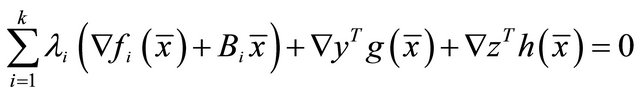
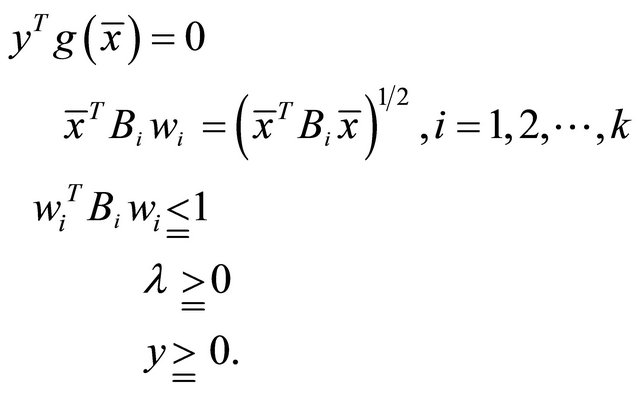
Proof: Since  is an optimal solution of (VEP), by Lemma 3.1,
is an optimal solution of (VEP), by Lemma 3.1,  is an optimal solution of
is an optimal solution of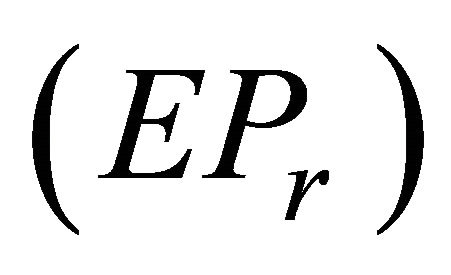 for each r. As for some r, the constraint of
for each r. As for some r, the constraint of 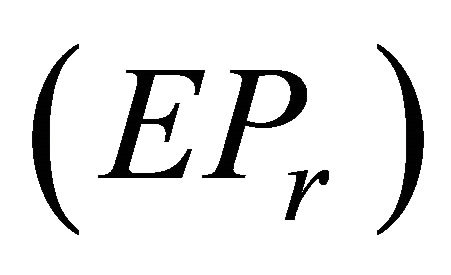 satisfy MFCQ at
satisfy MFCQ at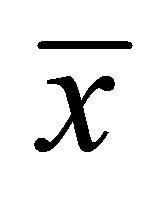 , by Theorem 2.2 of their exist
, by Theorem 2.2 of their exist 
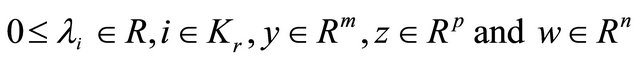 such that
such that
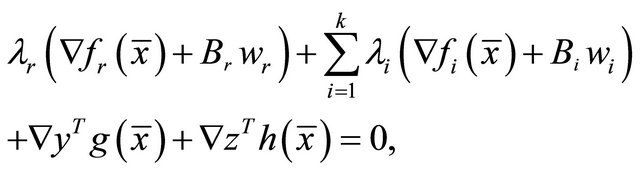
yielding

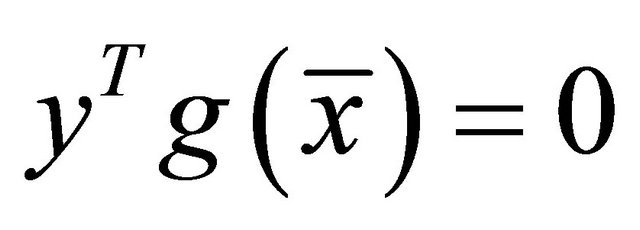

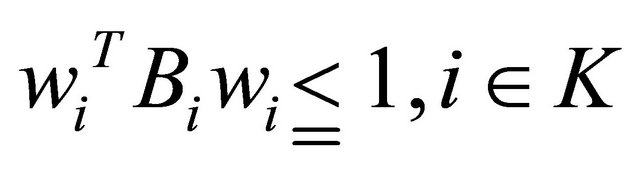

From the above relation it is obvious that the theorem follows.
In Theorem 3.2, we assume MFCQ for some , which implies
, which implies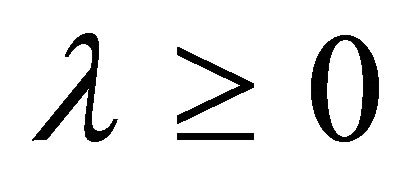 . In the following theorem, we assume MFCQ for every
. In the following theorem, we assume MFCQ for every  and obtain
and obtain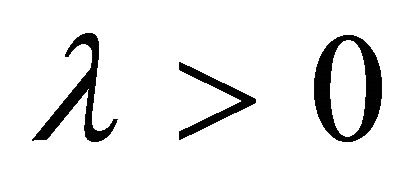 .
.
Theorem 3.3 (Kuhn-Tucker type optimality conditions): If  be an efficient of (VEP) and let for each
be an efficient of (VEP) and let for each , the constraints of
, the constraints of 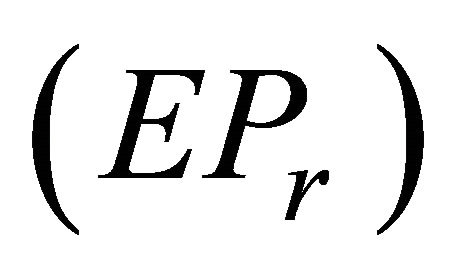 satisfy MECQ at
satisfy MECQ at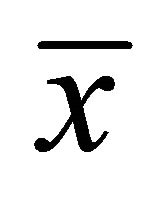 . Then there exist
. Then there exist 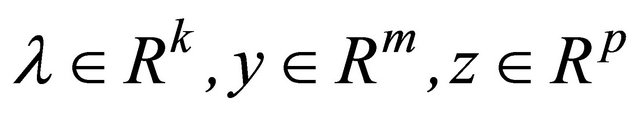 and
and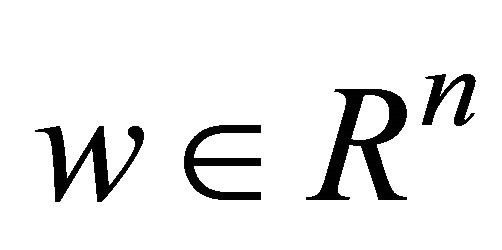 such that
such that

Proof: Since 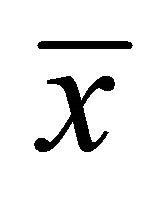 is an efficient of (VEP) by Lemma 3.1,
is an efficient of (VEP) by Lemma 3.1,  is an optimal solution of
is an optimal solution of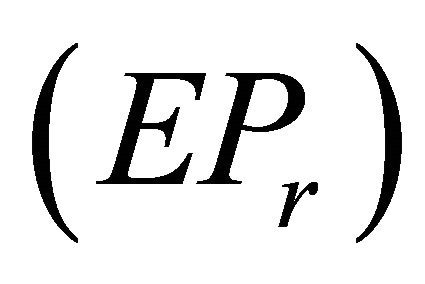 , by Kuhn-Tucker type necessary optimality conditions, for each
, by Kuhn-Tucker type necessary optimality conditions, for each , there exist
, there exist 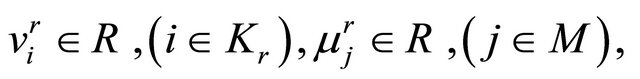
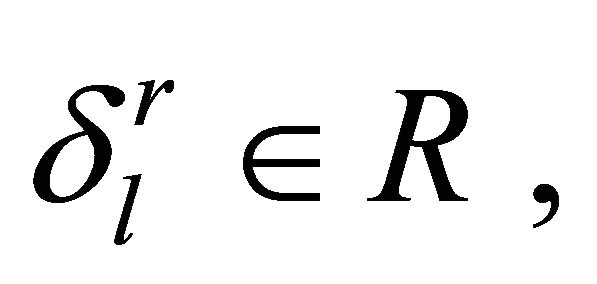
 such that
such that

Summing over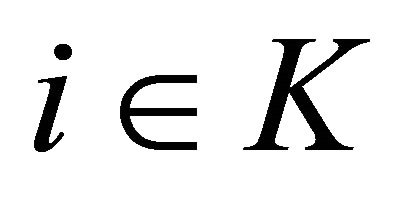 , we get
, we get


where 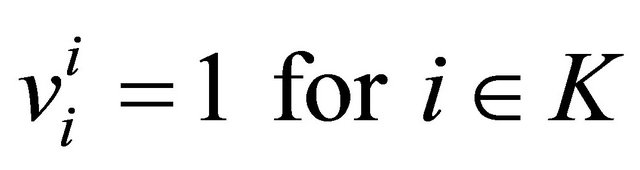
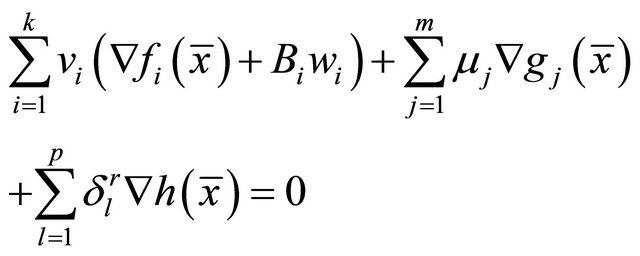
where 

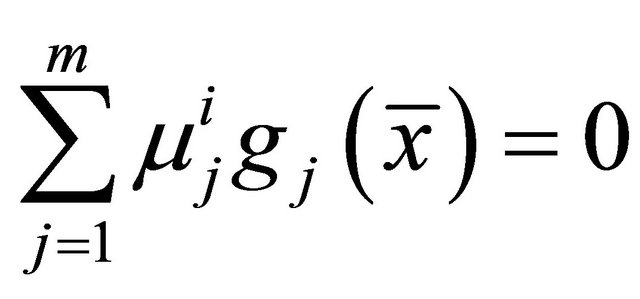
Dividing throughout the above relation and setting, by

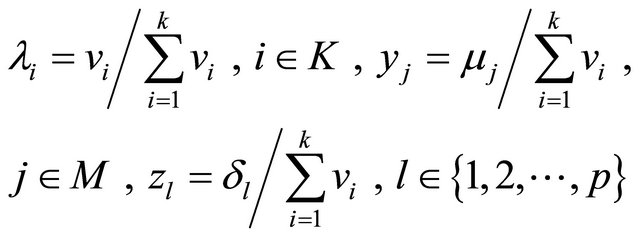
We obtain,
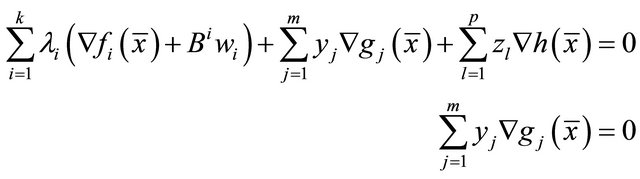
or
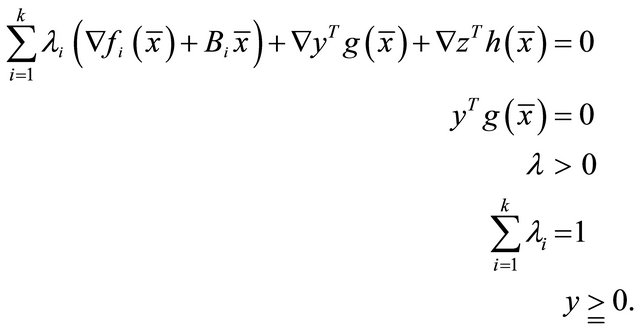
4. Mond-Weir Type Duality
We formulate the following differentiable multiobjective dual nonlinear problem for (VEP):
(M-WED): Maximize 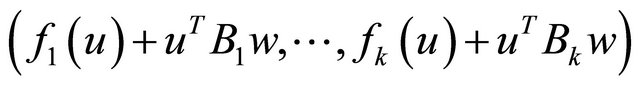
subject to
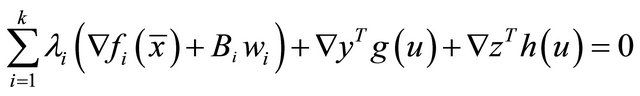 (3)
(3)
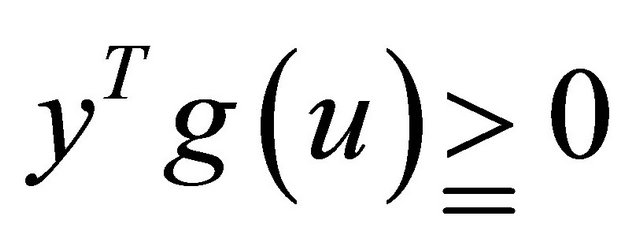 (4)
(4)
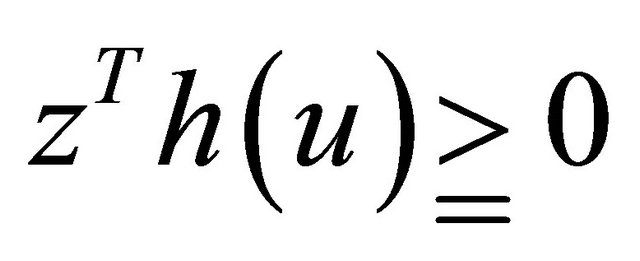 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
In the following, we shall use  for the set of feasible solutions of (M-WED)
for the set of feasible solutions of (M-WED)
Theorem 4.1 (Weak Duality): Let 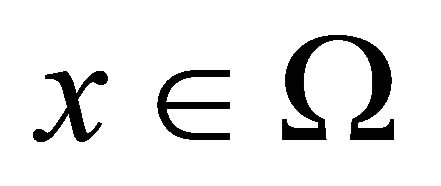 and
and 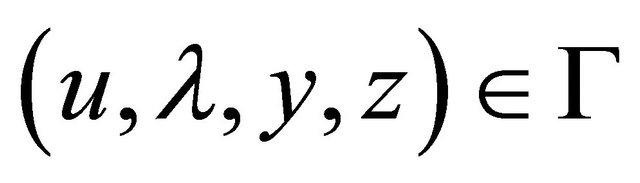 such that with respect to the same
such that with respect to the same 
1) 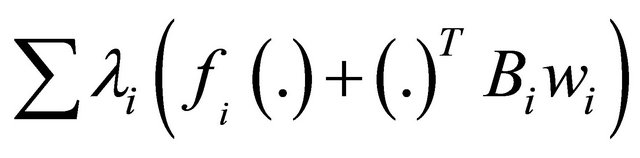 is pseudoinvex 2)
is pseudoinvex 2) 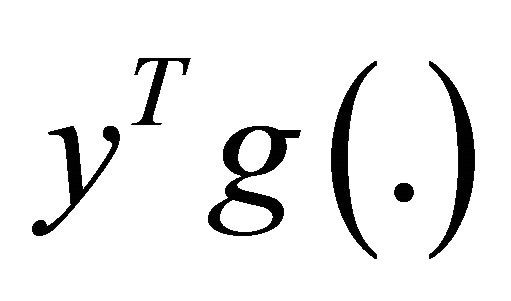 is quasi-invex, and 3)
is quasi-invex, and 3) 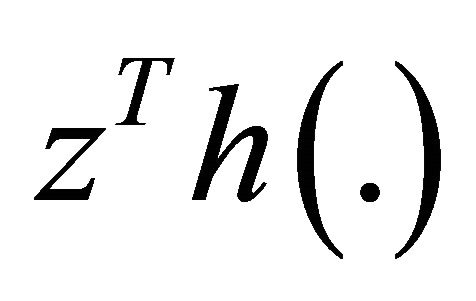 is quasi-invex.
is quasi-invex.
Then
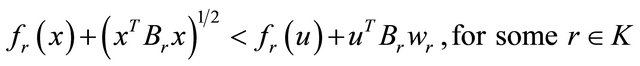 (9)
(9)
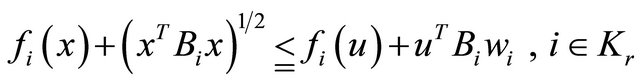 (10)
(10)
cannot hold.
Proof: Suppose the contrary that (9) and (10) hold. Since  the above inequalities (9) and (10) give
the above inequalities (9) and (10) give
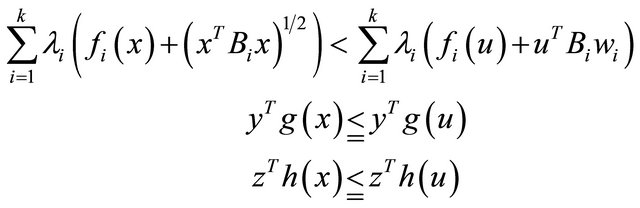
These inequalities because of quasi-invexity of  and
and 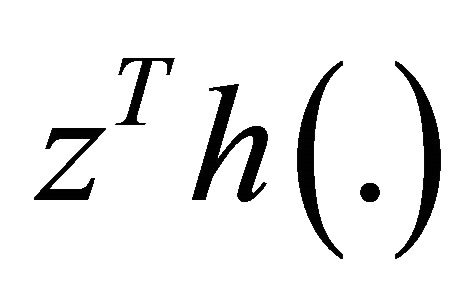 imply
imply

Combining these, we give

Using the equality constraint of (M-WED), this yields,
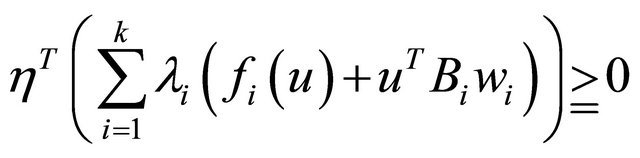
This, because of 1), implies
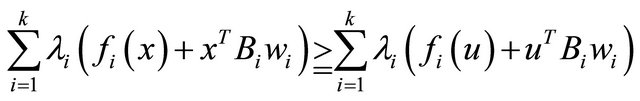
Using 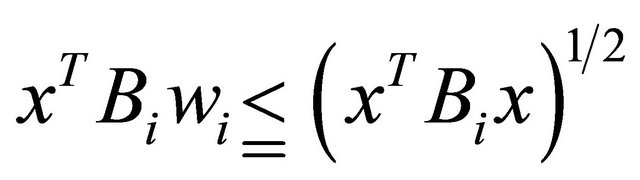 this yields,
this yields,
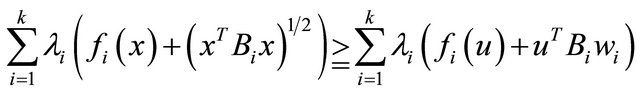
Hence the result follows.
Theorem 4.2 (Strong Duality): Let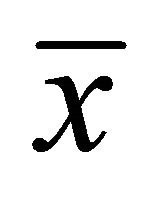 satisfy MFCQ and be an efficient solution (VEP). Then there exist
satisfy MFCQ and be an efficient solution (VEP). Then there exist 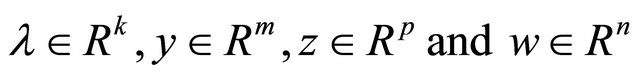 such that
such that 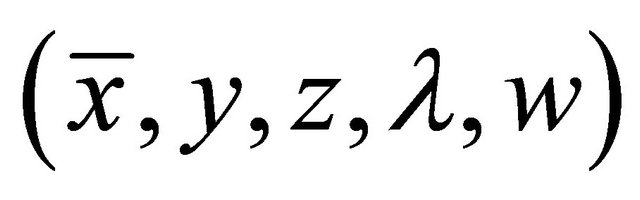 is feasible for (M-WED) and the two objective functions are equal. Furthermore, if the weak duality holds for all feasible solution of (VEP) and (M-WED), then
is feasible for (M-WED) and the two objective functions are equal. Furthermore, if the weak duality holds for all feasible solution of (VEP) and (M-WED), then  is an efficient solution of the (M-WED).
is an efficient solution of the (M-WED).
Proof: Since is an efficient solution (VEP) satisfy MFCQ, therefore by Theorem (3.3), there exist
is an efficient solution (VEP) satisfy MFCQ, therefore by Theorem (3.3), there exist 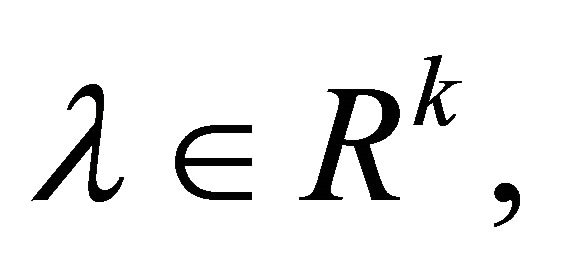
 satisfy
satisfy
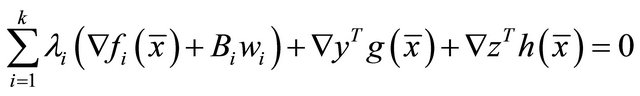

Hence 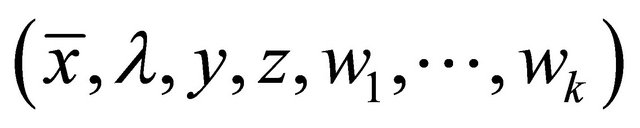 satisfies the constraints of (M-WED) and
satisfies the constraints of (M-WED) and

i.e. the two objective functions have the same value.
Now we claim that 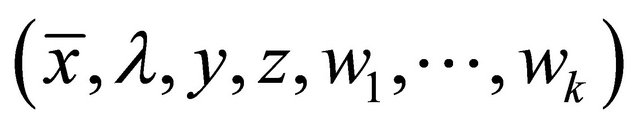 is an efficient solution of (M-WED). If not, then there exist
is an efficient solution of (M-WED). If not, then there exist 
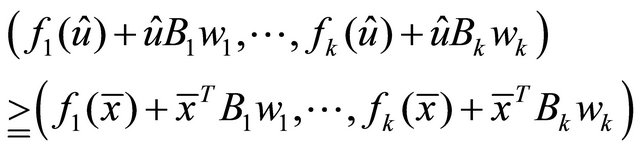
As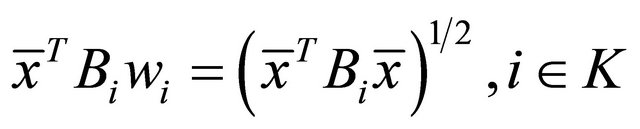 , we have
, we have

This contradicts Theorem 4.1 Hence  is an efficient solution.
is an efficient solution.
Theorem 4.3 (Strict-converse duality): Let 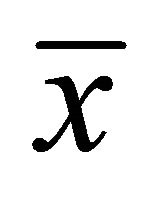 and
and  be an efficient solution of (VEP) and (M-WED), such that
be an efficient solution of (VEP) and (M-WED), such that
 (11)
(11)
If with respect to the same 
(A1) 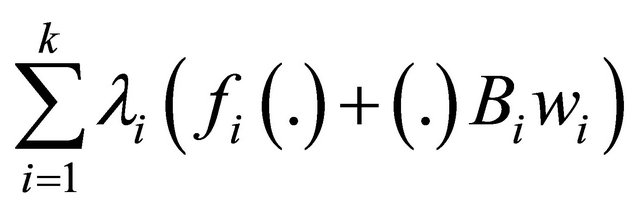 is strictly pseudoinvex(A2)
is strictly pseudoinvex(A2) 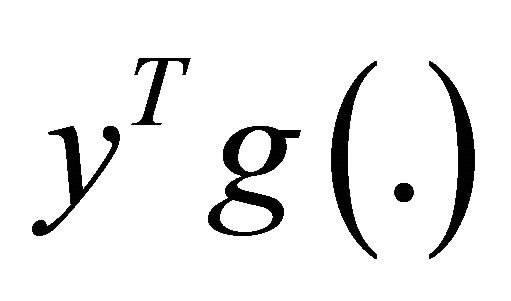 is quasi-invex, and
is quasi-invex, and
(A3) 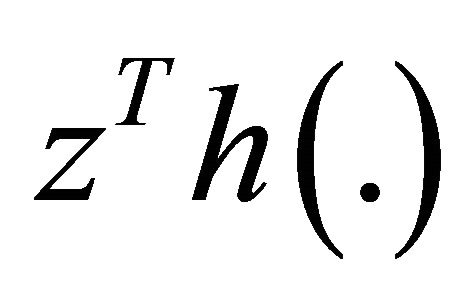 is quasi-invex then
is quasi-invex then 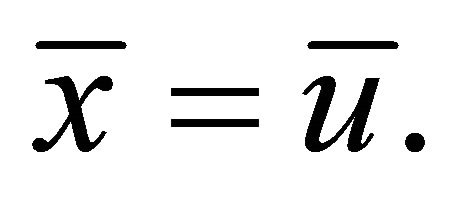
Proof: Let 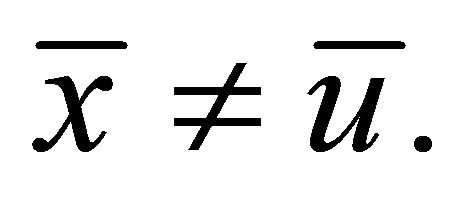 By hypothesis (A1), we have from (11)
By hypothesis (A1), we have from (11)
 (12)
(12)
By hypothesis (A2) and (A3) we have
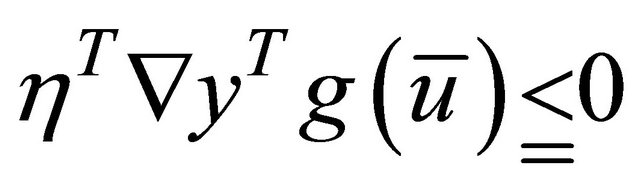 (13)
(13)
 (14)
(14)
Combining (12), (13) and (14), we have
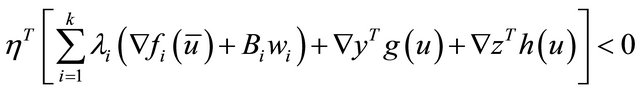
which contradict the equality constraint of (M-WED). Hence 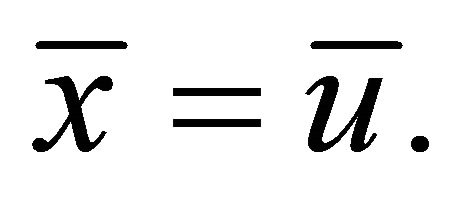
Theorem 4.4 (Converse duality):
Let  be an efficient solution of
be an efficient solution of
(M-WED) at which 1) the matrix  is positive or negative definite and 2) the vectors
is positive or negative definite and 2) the vectors  are linearly independent .
are linearly independent .
If, for all feasible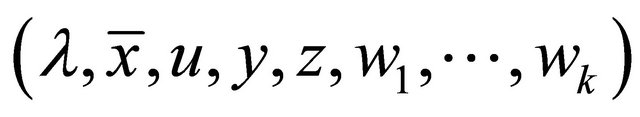 ,
,
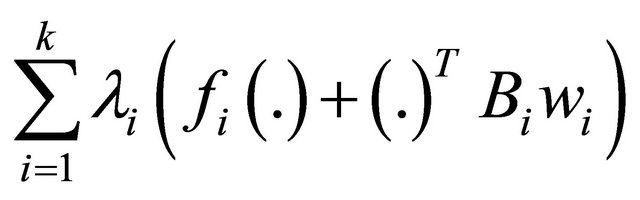 is pseudoinvex,
is pseudoinvex,  is qausi-invex and
is qausi-invex and 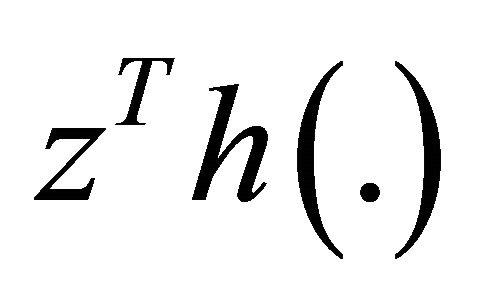 is quasi-invex with respect to the same
is quasi-invex with respect to the same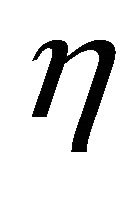 , then
, then 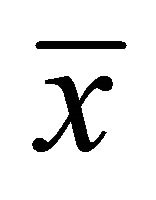 is an efficient solution (EP).
is an efficient solution (EP).
Proof: By Theorem 3.3, there exist 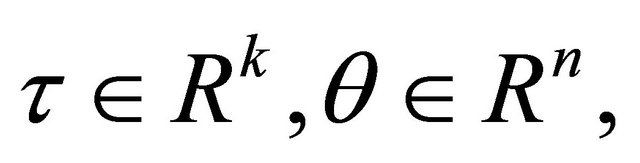
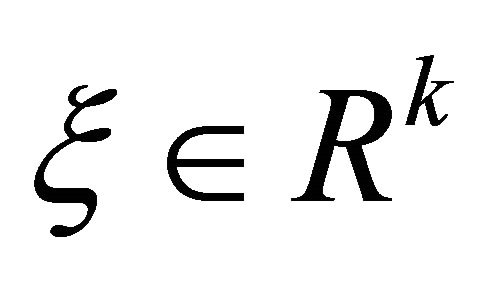
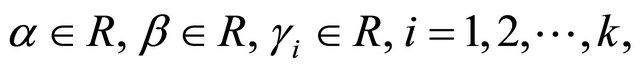 and
and 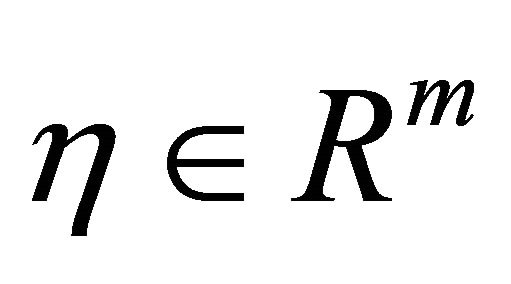 such that
such that
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
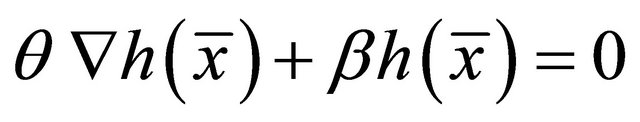 (19)
(19)
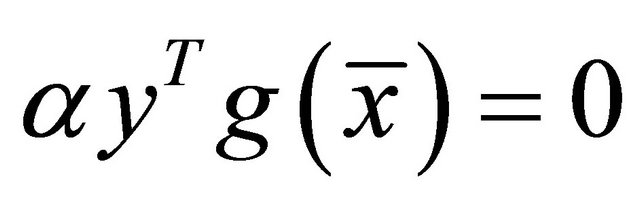 (20)
(20)
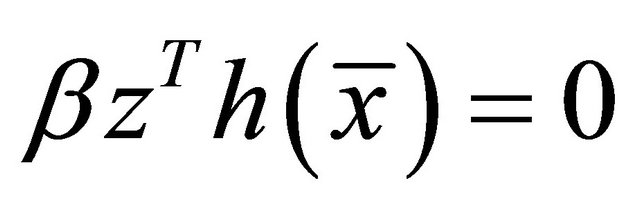 (21)
(21)
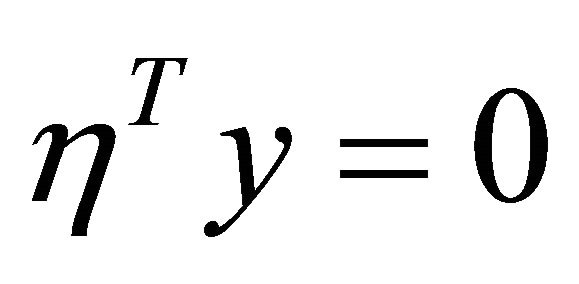 (22)
(22)
 (23)
(23)
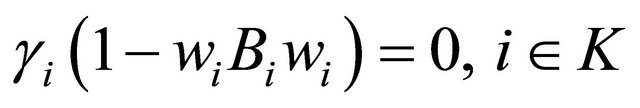 (24)
(24)
 (25)
(25)
 (26)
(26)
Multiplying (15) by 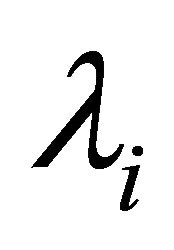 and summing over i, we have
and summing over i, we have
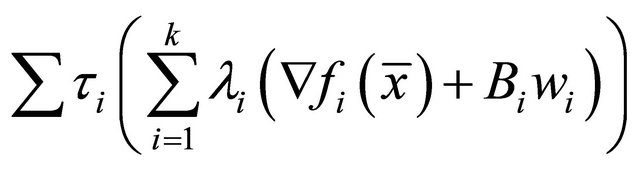
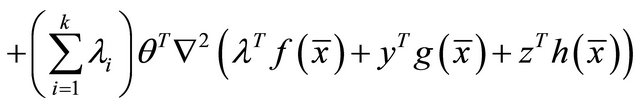
 (27)
(27)
Using the equality constraint, we have
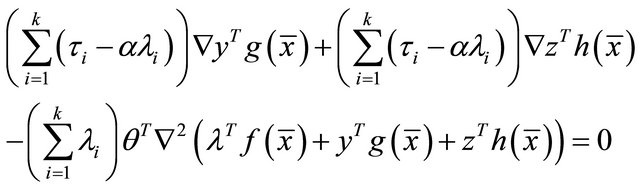 (28)
(28)
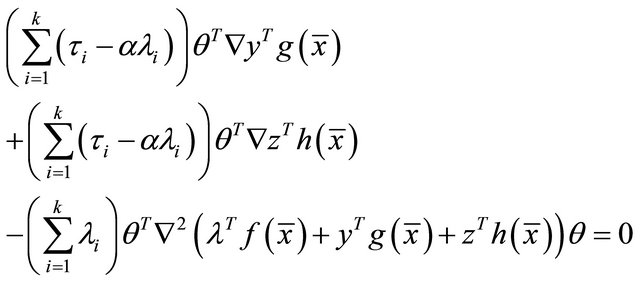 (29)
(29)
From (18) and (19), we have
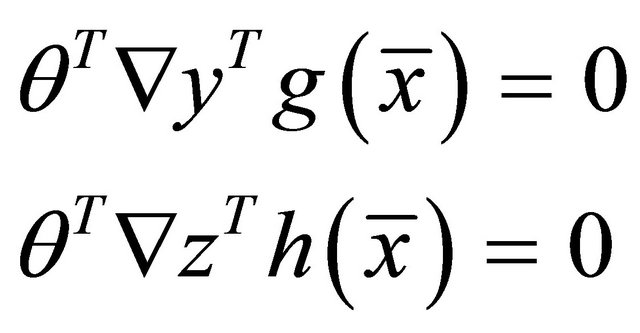
Using these in (15), we have

which because of the hypothesis 1) gives 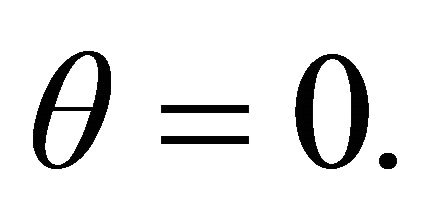
Using  and the hypothesis 2), we have
and the hypothesis 2), we have
 (30)
(30)
Let , i = 1, 2, ∙∙∙, k. Then (30) implies
, i = 1, 2, ∙∙∙, k. Then (30) implies  The relations (17) and (18) implies
The relations (17) and (18) implies 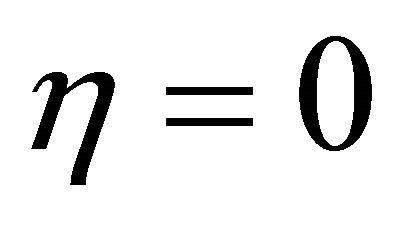 and
and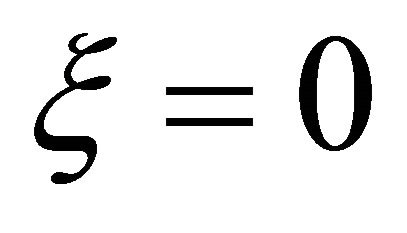 . Using
. Using 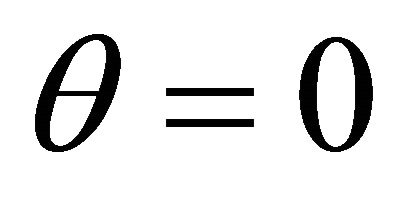 and
and 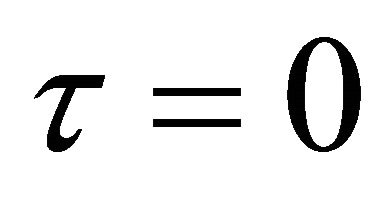 along with (24) in (16), we get
along with (24) in (16), we get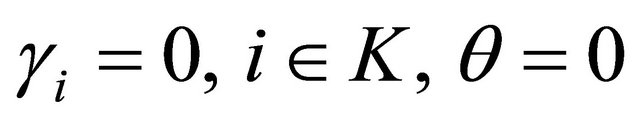 .
.
Thus  a contradiction to (26). Hence
a contradiction to (26). Hence  Consequently
Consequently  Using
Using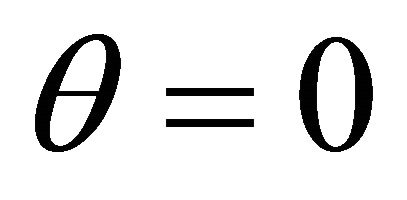 ,
,  , in (18) and (19), we have
, in (18) and (19), we have
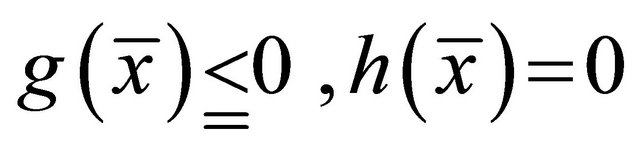
This implies that .
.
If 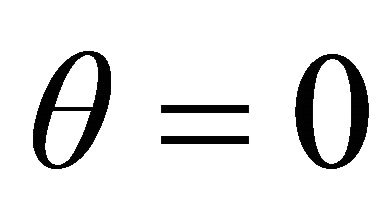 in (16), we have
in (16), we have
 (31)
(31)
Hence by Schwartz inequality
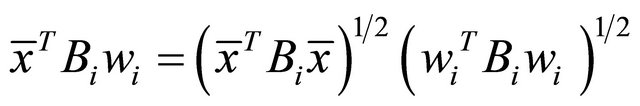 (32)
(32)
If 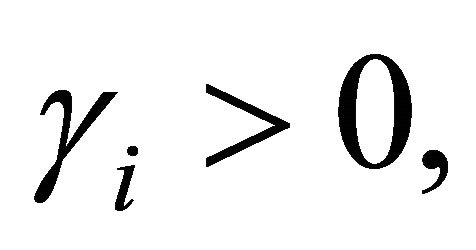 then (24) implies
then (24) implies
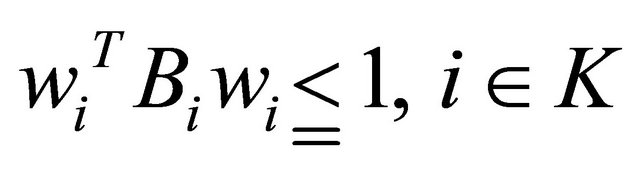
Consequently (32) yields
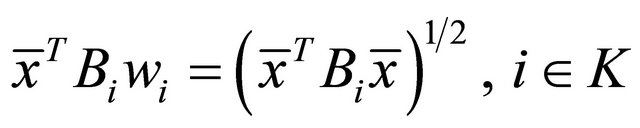
If  then (31) implies
then (31) implies 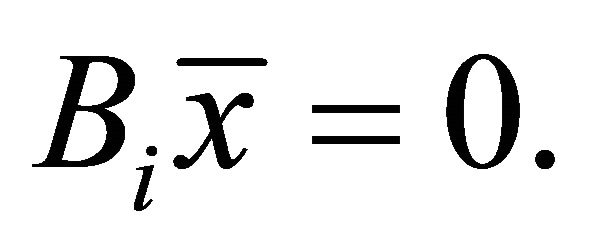 So we still get
So we still get
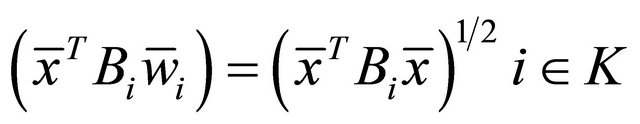 (33)
(33)
Thus by (33), we have
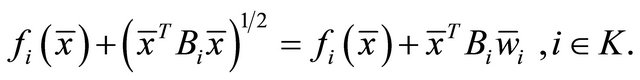
implying the two objective functions have the same value.
Now, assume that  is not an efficient solution of (VEP), then there exists
is not an efficient solution of (VEP), then there exists 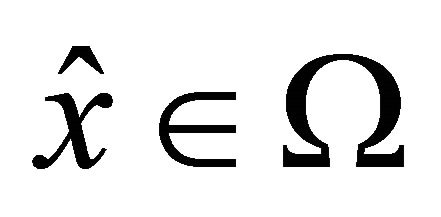 such that
such that
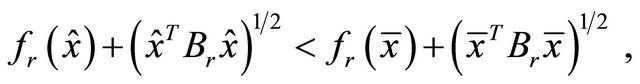
for some 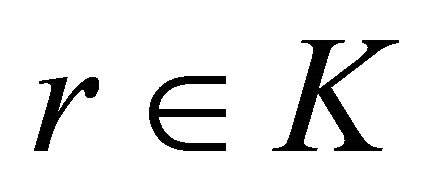 and
and
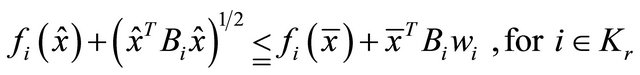
Using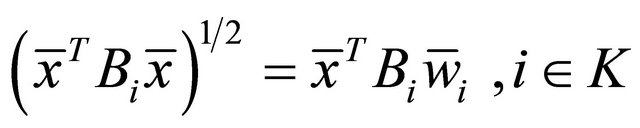 , we have
, we have
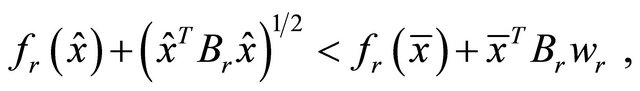
for some 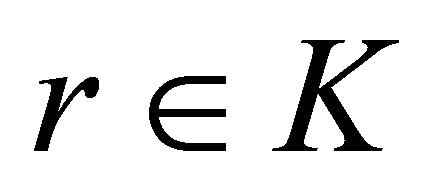

This contradicts Theorem 4.1. Hence is an efficient solution of (VEP).
is an efficient solution of (VEP).
5. A Special Case
If 
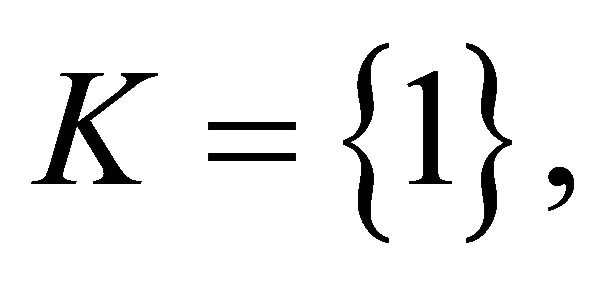 and
and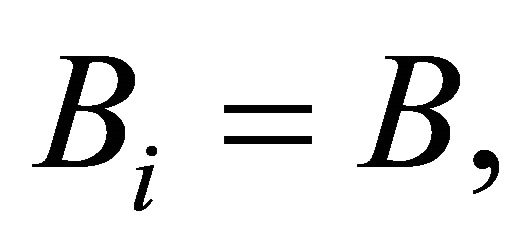 our problems reduce to the following problems recently studied by Husain and Srivastav [8]:
our problems reduce to the following problems recently studied by Husain and Srivastav [8]:
(EP): Minimize 
subject to
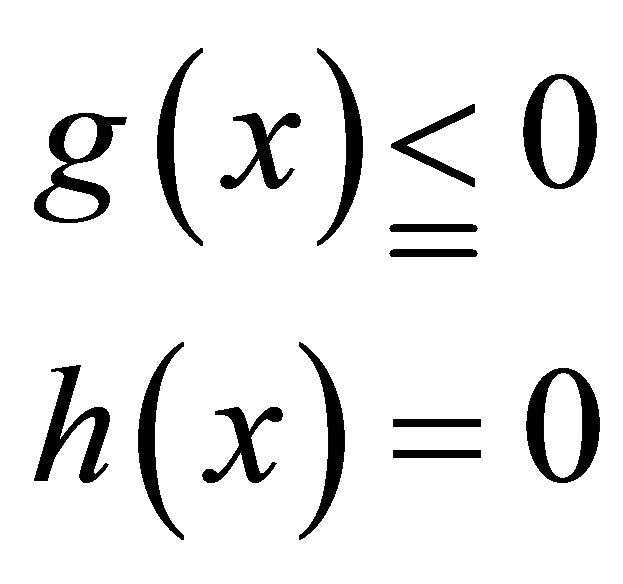
(M-WED): Maximize 
subject to
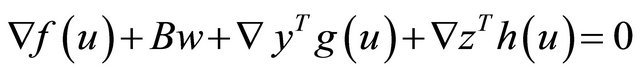

6. Conclusion
In this research optimality conditions are derived for a nondifferentiable multiobjective programming problem containing a certain square root of a quadratic form in each component of the objective function in the presence of equality and inequality constraints embodying many realistic problems. A Mond-Weir type dual to this problem is formulated and usual duality theorems are proved under appropriate generalized invexity conditions. A special case is also obtained from our duality results. Our results can be revisited in the multiobjective setting of a nondifferentiable control problem.
7. Acknowledgements
The authors acknowledge anonymous referees for their valuable comments which have improved the presentation of this research paper.