Reliability Measure of a Relay Parallel System under Dependence Conditions ()
1. Introduction
As in Barlow and Proschan [1], a complex coherent reliability system is completely characterized by its structure function 
assuming values in the set 
and where 
is a stochastic process assuming values in
. The stochastic process
, represents the state of the i-th component. 
if the component i is working at time t and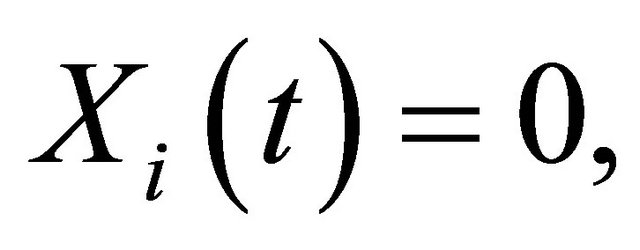 
i if the component i is in a failed state at time t. Also, the system state 
has such an interpretation, is increasing in each coordinate and each component is relevant, that is, there is a time t and a configuration of 
in which the functioning of the component i is fundamental for the functioning of the system.
A relay system is subject to two kinds of failure: failure to close and failure to open. Similarly, circuits construct from these relays are subject to the same kinds of failure. If the i-th relay responds correctly to a command to close, 
(that is, closes), and 
otherwise, i = 1; 2 and 
if the circuit responds correctly to a command to close (that is, closes) if, and only if, at least one of its components responds correctly to a command to close, and 0 otherwise, then,
is a parallel system. Next, let 
if the i-th relay responds correctly to a command to open (that is open), and 
otherwise, i = 1; 2. Let 
if the circuit responds correctly to a command to open (that is, open), and 0 otherwise. Then
a series system, the dual of
, is the system representing the correct system response to a command to open.
Generally, given a structure function
, its dual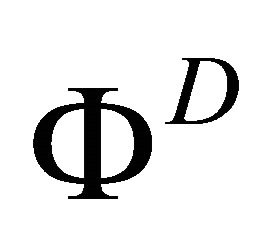 
is defined by
where
.
The concept of dual structure is useful in analyzing system of components subject to two kinds of failures, such as relays system and safety monitoring systems. It is interesting and useful to note that both failure to close and failure to open can be analyzed using the same structure function
. In this paper, under dependence conditions, we analyze the dual structure probability measure of a parallel system, through a transform of the failures counting processes compensators in the original probability space. In Section 2 we analyse the problem for a parallel system of two components. In Section 3 we generalize the results and in Section 4 we discuss some reliability preservation properties.
Without loss of generality, firstly, we consider a parallel system of two components. We observe two component lifetimes T and S, which are positive random variables defined in a complete probability space
through the family of sub
—algebras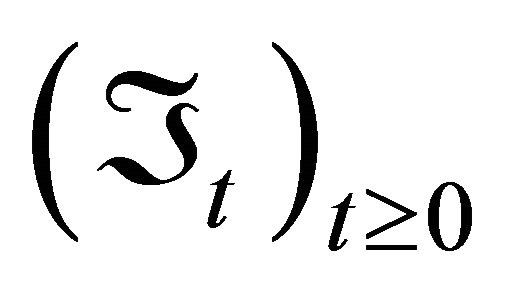 
of
, where
,
satisfies Dellacherie’s conditions.
In order to simplify the notation, in this paper we assume that relations such as 
between random variables and measurable sets, always hold with probability one. In what follows we assume that S and T are totally inaccessible 
-stopping time and that
, that is, the lifetimes can be dependent but simultaneous failures are ruled out.
The parallel operation of S and T is defined by the maximum between S and T and denoted by
If we denote the survival functions of S and T as
and 
respectively, it follows from Arjas and Yashin [2], that, under some conditions, the 
-compensator processes of 
and 
are given by
and
.
We assume such conditions and as S and T are totally inaccessible-stopping time the compensator processes are continuous.
Now we calculate
and therefore, in the set 
the 
-compensator of 
is
We intend to define compensator transformation of 
and 
to 
and 
in the way that the above expression is the sum 
which characterizes uniquely the lifetime of a series system and, therefore, the dual of such a parallel system. As this operation is symmetric on S and T, the idea is to combine compensator transformations in
and
.
Firstly, we consider the compensator transform
To prove the main Theorem of this section we are going to use the following Lemma:
Lemma 2.1
Under the above hypothesis the following process
is a nonnegative local 
-martingale and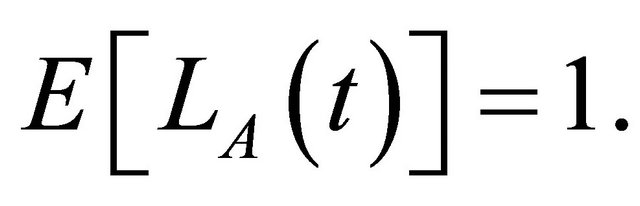 
Proof We consider the localization sequence, the 
-stopping time defined By
It is sufficient to prove that the process
is a bounded 
-martingale.
For any 
-stopping time 
we can write
The procedure is easy: On the set 
we have
Otherwise, on the set
, 
As the integrand
is an 
-predictable process and 
is an 
-martingale, 
is an 
-martingale with
Secondly, we consider the compensator transform
and with the same argument to prove Lemma 2.1 we can prove Lemma 2.2:
Lemma 2.2 Under the above hypothesis the following process
is a nonnegative
-martingale with
Observe that the same expression for the 
-compensator of 
is obtained through the transformation:
Then, we propose the compensator transforms:
and
to prove the main Theorem:
Theorem 2.3 Under the above hypothesis the following process
is a nonnegative local 
-martingale and
.
Proof. Using Lemma 2.1, Lemma 2.2 and the Stieltjes differentiation rule we have
As by assumption, 
and 
are continuous and 
we have
and therefore
in an local 
-martingale with 
and the theorem is proved.
Now, we are looking for a probability measure Q, such that, under Q, 
becomes the 
- compensator of 
with respect to this modified probability measure.
Under certain conditions, it is possible to find Q. Indeed, assume that the process 
is uniformly integrable. Then it follows from well known results on point process martingales (Girsanov Theorem,Bremaud [3]) that the desired measure Q is given by the Radon Nikodyn derivative
Remark:
In the case where T and S are identically distributed, we have 
and the compensator transform is given by
which is used in Bueno and Carmo [4], to de_ne active redundancy operation when the component and the spare are dependent but identically distributed.
Parallel operations are very important in reliability theory: the performance of a parallel system are always better than the performance of any coherent system with the same components; it is used in replacement models, to optimize system reliability through active redundancy. However, if the component are stochastically dependent the reliability of a coherent system is a difficult and tedious calculation involving multivariate distributions. The calculation becomes more tractable under the assumption of a series system, in which case the reliability is the survival function of a multivariate positive random vector. It is also can be easily done through the compensator processes. We can show this argument easily:
Corollary 2.4
Under the hypothesis of Theorem 2.3, and under Q such that
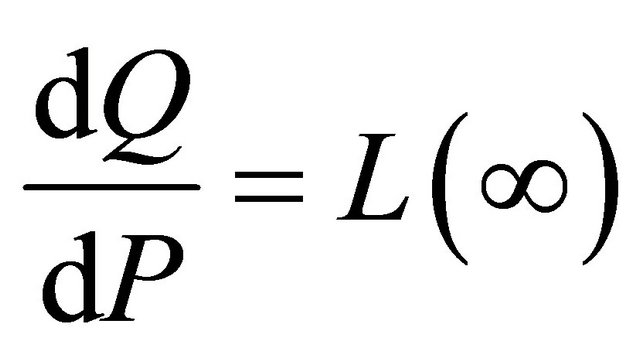we have
Proof As the compensators are deterministic before any failure, we can write:
As an application we calculate the Barlow and Proschan [1] reliability importance of a component for the system. In the independent and absolutely continuous case, it is the probability that the component causes the system failure. For dependent components, this quantity is
where 
This expression is an extension of the Barlow and Proschan reliability importance, by Bueno and Menezes [5] where the importance of the component S for the system is 
Now, we ask how we can use Corollary 2.4 to calculate the Barlow and Proscha relibility importance of component S for the system reliability. In a series representation we have:
In the above we use that
and
We expected such a relation since that the reliability of the dual system is 
and the measure Q is relative to the random vector 
To clarify this argument, suppose that we can define the reverse times, 
and 
such that the events 
and 
are equivalent to 
and 
respectively, then
2. A General Parallel System
The structural relationship between the lifetime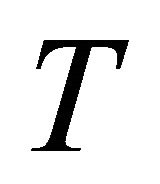
, of a parallel system and its components lifetime 
is given by
We intend to define a compensator transform to characterize the parallel system as a series system. As in Section 2, the idea is to combine compensator transformations on 
the compensator process of the lifetime counting failure process 
of component 
For 
define the compensator transform
where
and
Under the above hypothesis and notation we have
The main results, which follows from an adaptation of Girsanov Theorem, is
Theorem 3.1
Under the above hypothesis the following process
is a nonnegative 
-martingale with 
Remarks:
1) We have
2) If the components are dependent but identically distributed, we have
and
Therefore
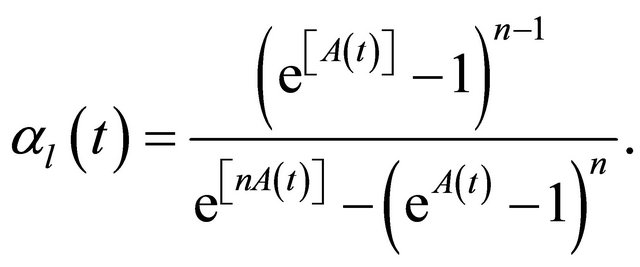
Remark:
As in Barlow and Proschan [1], we assume the series parallel decomposition of a coherent system:
where 
are minimal cut sets, that is, a minimal set of components whose joint failure causes the system to fail.
We can also define, for each 
the minimal parallel cut structure
and we can write
Therefore, using the compensator series transformation for each 
we get the series transformation for the system.
3. Preservations Results
In many reliability situations, we encounter structures of coherent systems where components share a load, so that a failure of one component results in increased load on each of the remaining components. Furthermore, the components in a coherent system could be subjected to the same set of stress. In such cases, the random variables of interest are not independent but rather associated.
Therefore, it is very interesting to verify whether the association properties of the lifetimes 
under P are preserved under Q.
We introduce the association definition. For this we give the concept of an upper set in 
A Borel set 
is called an upper set if for any 
implies that
. In the univariate case, 
is equal to either 
or
.
Definition 4.1
The random variables 
(or the corresponding random vector
) are associated, if for all upper sets 
and 
of 
In particular, this definition, formulated by Esary, Proschan and Walkup [6], Esary and Proschan [7], is useful to produce upper and lower bounds for system reliability. The measure Q preserves this property from the measure P.
Theorem 4.2
If T is associated under
, then also under
.
Proof
We consider the upper sets in
, 
and
, and the uniformly integrable 
-martingale,
and
It follows that there exists a unique 
-predictable process, such that the covariance process 
is increasing, right continuous, with 
such that
is an 
-martingale.
Since a martingale has a constant expectation, we have
and
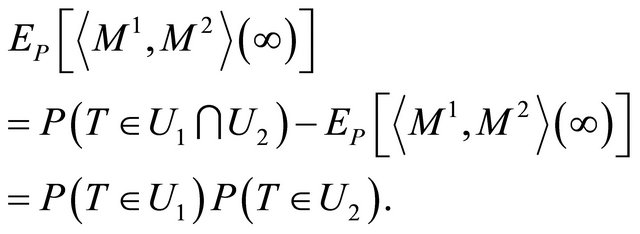
It follows that 
is associated if, and only if,
Now,
for 
a.s.
Classes of non-parametric distributions , such as increasing ( decreasing) failure rate (IFR (DFR)) distributions, new better (worse) than used (NBU (NWU)) distributions and others, have been extensively investigated in Reliability Theory. They can be used to achieve the benefit of a maintenance operation or to derive bounds on system reliability.
Several extensions of these concepts appeared in the literature, e.g. Harris [8], Barlow and Proschan [3], Marshall [9] and others. However, they all have in common that they don’t order the lifetime vectors in the sense of stochastic order as the univariate concept does. Arjas [10], considered to observe the components, continuously in time, based on a family of sub s-algebras
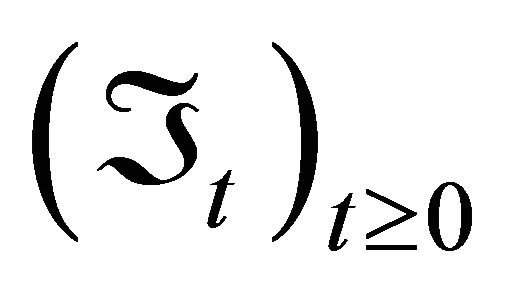. Arjas, introduced the notion of increasing failure rate distribution (new better than used distribution) relative to 
IFR
, (NBU
) generalizing the conventional definition of IFR (NBU) and extending these classes into a multivariate form, denoted by MIFR
, (MNBU
).
In order to introduce the concepts of Arjas [10], we define the residual lifetime of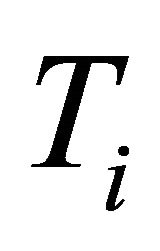 
at time 
as
Let 
Definition 4.3
(Arjas, [10]) We say that 
is multivariate increasing failure rate relative to 
, denoted by MIFR
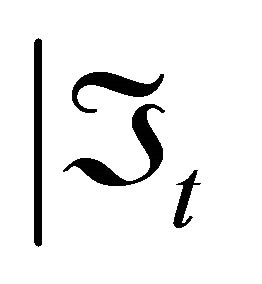, if for all 
and all open upper sets
,
Remark: Arjas [1] proved that the class of upper sets in the above definition can be restrict to the class
, of finite unions of open upper sets with corner point
, where 
are positive rational numbers. An open upper set with corner point
is defined by 
We want to prove that the MIFR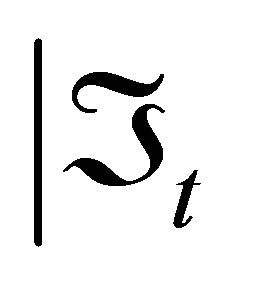
class under 
is preserved under
.
Theorem 4.4
If 
is multivariate IFR relative to
, under
, then also under
.
Proof First, we show that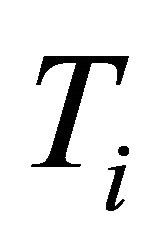 
is IFR
, under
. By hypothesis, we have
for all 
Now
However 
is a measurable random variable and can be written as a suitable approximating step function
, where 
are constants and 
are measurable.
As
, using the dominated convergence theorem we have
which is decreasing by hypothesis.
Herefore 
is IFR
under
. In order to prove that the vector 
is increasing failure rate relative to 
we use the relation
and the equivalent definition of MIFR
in terms of the open upper sets with corner point as in the above remark.
As 
is MIFR
,
.
The proof follows as above.
4. Conclusions
Relay system are very concerned in reliability theory, however, such a modeling is complicated under stochastically dependence conditions. The purpose of this paper is to provide a way to work with this situation using a point process martingale approach.
Some preservation important results in association and non parametric distributions classes useful in reliability theory are proved and an application in component importance is analised.
5. Acknowledgments
This work was partially supported by FAPESP, Proc. No. 2010/52227-0.