1. Introduction
The purpose of this article is to study the motion of an effectively massless “particle” (an asteroid) orbiting a massive “primary” (the sun), and being perturbed by yet another small (relative to the primary) “satellite” (Jupiter) whose motion is assumed to be perfectly circular and in the same plane as the massless-particle’s orbit. This is known as the planar, circular, restricted three-body problem which has been studied extensively in the past by various numerical, semi-analytical and (exceptionally, and with many restrictions) analytical techniques. In this article, we build a fully general, analytical (even though iterative) solution which, furthermore, does not rely on the averaging principle (which would eliminate all chaotic solutions—the very focus of our study).
Our main objective is to trace the source of chaos, which arises when the two orbital periods are in (or close to) a resonance (i.e. their ratio is a simple fraction, such as 3:1). It is known [1] that, under these circumstances, chaos occurs quite readily when the perturbing orbit has a non-zero eccentricity or inclination (mathematically, one can show that terms proportional to either of these two parameters are responsible for its creation); it is a lot more difficult to incite chaos (and find its exact source) in a planar, circular situation. From this point of view, the seemingly simplest case of the restricted three-body problem is also the most challenging! Furthermore, only some resonances lead to chaos in this case; we have selected the 7:4 resonance (the massless particle completing seven orbits, while the perturber finishes four) as their typical representative. It is hoped that this example will be a catalyst for a future, more systematic study of the phenomenon.
The technique we employ is based on KustaanheimoStiefel (K-S for short) formulation of the perturbed Kepler problem, which has several advantages over other techniques: it is fully analytic; it does not rely on any averaging; it can be made arbitrarily accurate (even though, in case of a chaotic motion, no solution can accurately follow the actual orbit indefinitely); it can also be made very simple (when we sacrifice high accuracy, yet maintain a good quantitative description of the motion: this is the approach taken by this article).
Vast literature exists on the subject of chaos in the context of the restricted three-body problem in resonance (a good, even though slightly dated, review of various techniques and results can be found in [2]). Most of it relies on numerical or, at best, semi-analytic exploration of the resulting motion (being of little relevance to our goal). The remaining articles usually concentrate on the elliptic version of the problem (the easy-to-explain chaos mentioned earlier), and are “tailored” to deal with only one specific resonance at a time. They also rely heavily on the averaging principle [3], thus eliminating the chaosinducing terms we are seeking to identify!
In the following three sections we
• present formulas for building a solution to a perturbed Kepler problem when the direction of perturbing force (yet unspecified) is always in the plane of the massless particle’s orbit;
• computing the perturbing force due to another orbiting body of relatively small mass that has a circular orbit and is in 7:4 resonance with the perturbed particle, and expanding this force in terms of orbital elements of the latter;
• finding and solving a set of differential equations for the orbital elements, and demonstrating the onset of chaos in some solutions.
2. Preliminaries
We start by reviewing the analytical, K-S based solution to a planar perturbed Kepler problem, which (unlike its three-dimensional analog), requites only complex (not quaternion) algebra. The following is a summary of the necessary formulas, presented in its general form (i.e. able to deal with any small perturbing force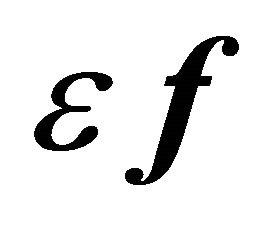 ).
).
To solve the corresponding set of two equations, namely
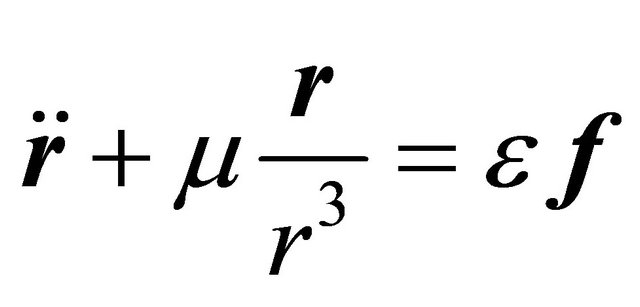 (1)
(1)
(assuming that both  and
and 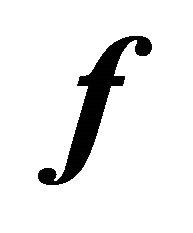 are two-dimensional vectors in their complex representation), we introduce a new dependent complex variable
are two-dimensional vectors in their complex representation), we introduce a new dependent complex variable  and a new real independent variable
and a new real independent variable  (called modified time) by
(called modified time) by
 (2)
(2)
and
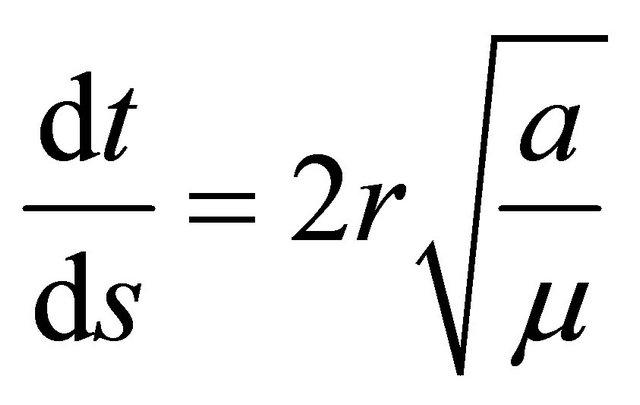 (3)
(3)
where
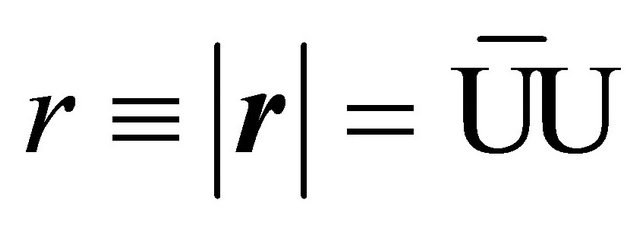
and  is the semi-major axis of the corresponding solution (the bar denotes complex conjugation). This is the celebrated K-S transformation (reduced to two dimensions).
is the semi-major axis of the corresponding solution (the bar denotes complex conjugation). This is the celebrated K-S transformation (reduced to two dimensions).
A prospective (trial) solution can be parametrized in the following way
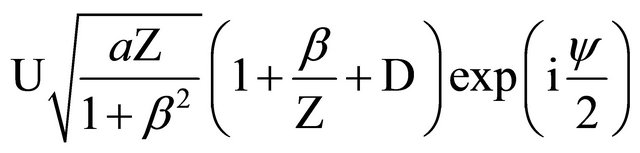
where 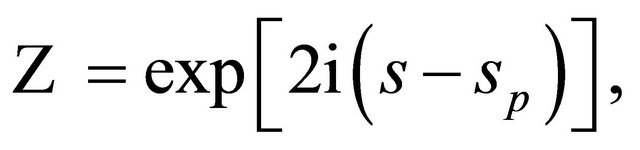
 is the value of modified time
is the value of modified time 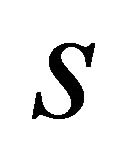 at aphelion (which itself is located at angle
at aphelion (which itself is located at angle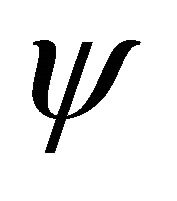 ), and
), and  yields the regular eccentricity
yields the regular eccentricity  via
via
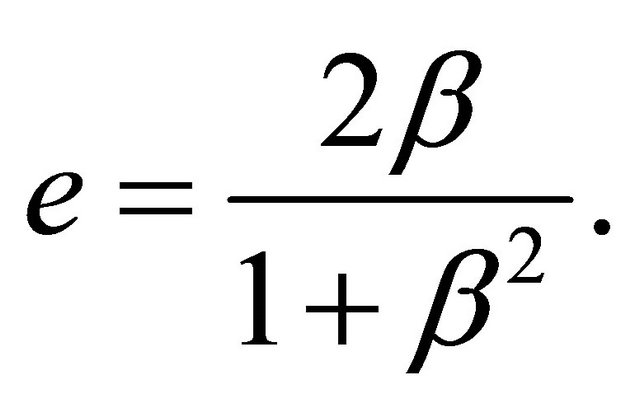 Note that when
Note that when 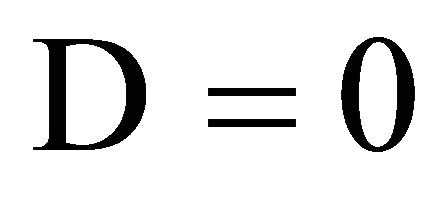 and the orbital elements
and the orbital elements 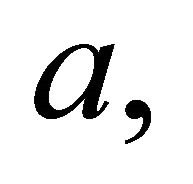
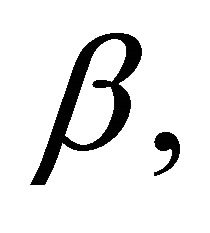
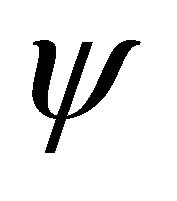 and
and  are constant, this solution represents the usual ellipse of the unperturbed Kepler problem
are constant, this solution represents the usual ellipse of the unperturbed Kepler problem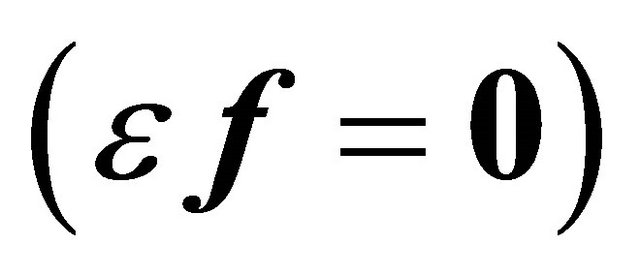 . In the perturbed case the orbital elements become (slow-varying) functions of modified time
. In the perturbed case the orbital elements become (slow-varying) functions of modified time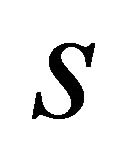 , and
, and 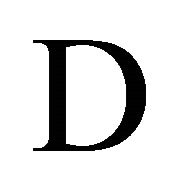 is an
is an 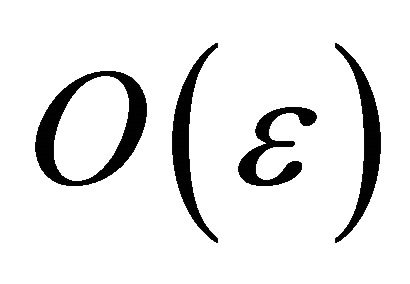 function of
function of  (taking care of the orbit’s small deviation from a perfect ellipse). At this point, we are yet to find expressions for the time derivatives of the orbital elements, and for the exact form of
(taking care of the orbit’s small deviation from a perfect ellipse). At this point, we are yet to find expressions for the time derivatives of the orbital elements, and for the exact form of  (thus constructing the actual solution).
(thus constructing the actual solution).
Using the proposed transformation (2) and (3), one can show that (1) is equivalent to
 (4)
(4)
where prime implies differentiation with respect to 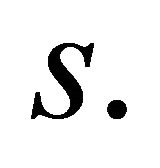
To solve the last equation, we start with the unperturbed solution
 (5)
(5)
(assuming constant orbital elements), evaluate the left hand side of (4) in the particle’s Kepler frame (i.e. a non-inertial frame in which the new 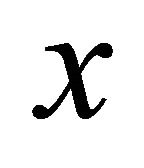 axis points towards the aphelion; this is achieved by multiplying the equation by
axis points towards the aphelion; this is achieved by multiplying the equation by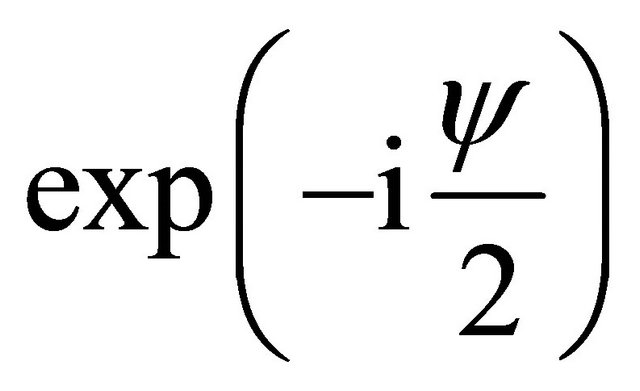 ) and call the resulting expression
) and call the resulting expression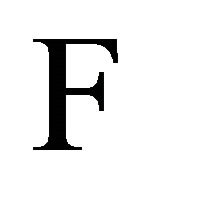 . When
. When  is an explicit function of
is an explicit function of , we must also make the following replacement:
, we must also make the following replacement:
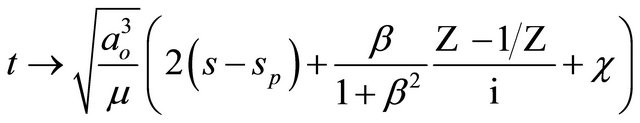 (6)
(6)
where 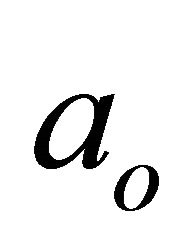 is a “typical” value of
is a “typical” value of  (in our case set to the resonant value of 1—see the next section), and
(in our case set to the resonant value of 1—see the next section), and  is a function of
is a function of 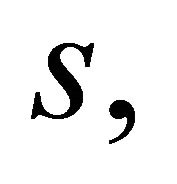 having the following s-derivative:
having the following s-derivative:
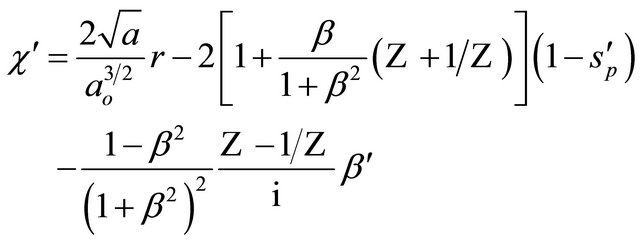 (7)
(7)
Once  (the left hand side of Equation (40)) has been computed, it needs to be converted to
(the left hand side of Equation (40)) has been computed, it needs to be converted to
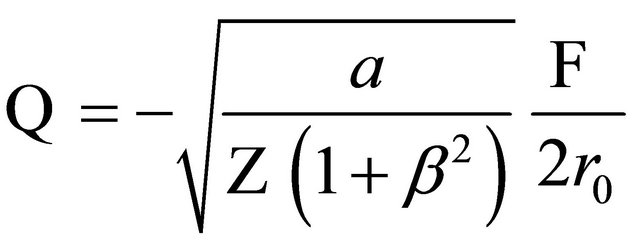 (8)
(8)
(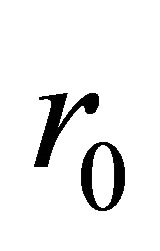 being the unperturbed
being the unperturbed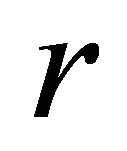 ), based on which we can find
), based on which we can find 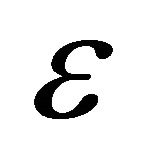 -accurate values of
-accurate values of  and of the orbital elements’ s-derivatives, by means of the following procedure.
and of the orbital elements’ s-derivatives, by means of the following procedure.
First,  needs to be expanded in powers of
needs to be expanded in powers of  (we are assuming a periodic perturbing force, which makes this expansion discrete), thus:
(we are assuming a periodic perturbing force, which makes this expansion discrete), thus:
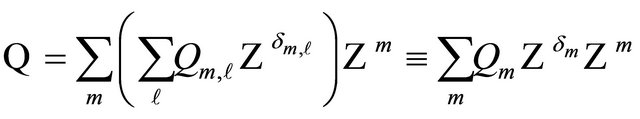
where 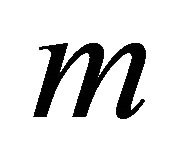 is an integer, and
is an integer, and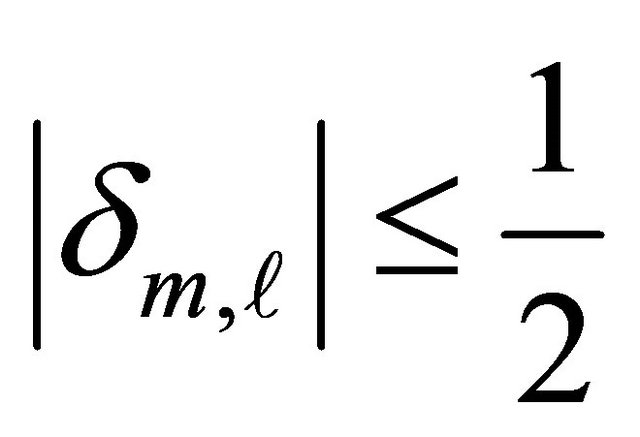 . The last identity serves to establish the following convention: from now on, in all expressions involving
. The last identity serves to establish the following convention: from now on, in all expressions involving 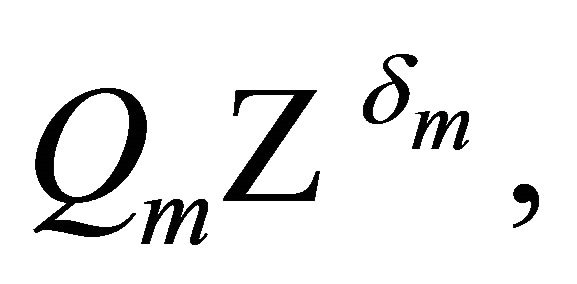 an extra summation (over the original
an extra summation (over the original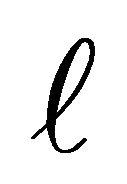 ) is implied.
) is implied.
Then, we find  and the orbital elements’ s-derivatives, using
and the orbital elements’ s-derivatives, using
 (9a)
(9a)
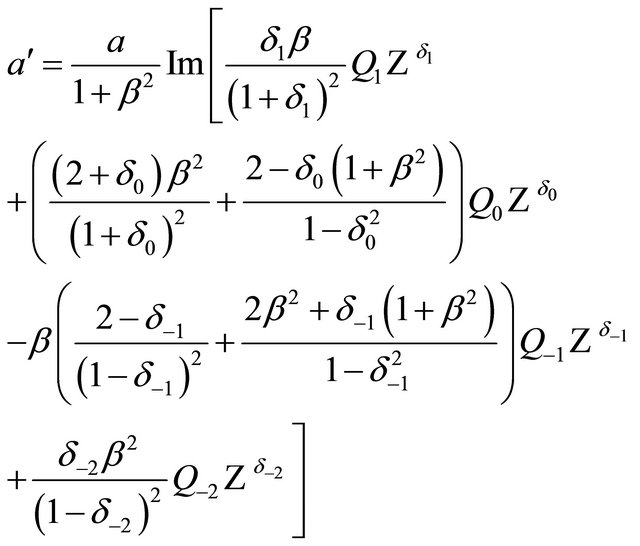 (9b)
(9b)
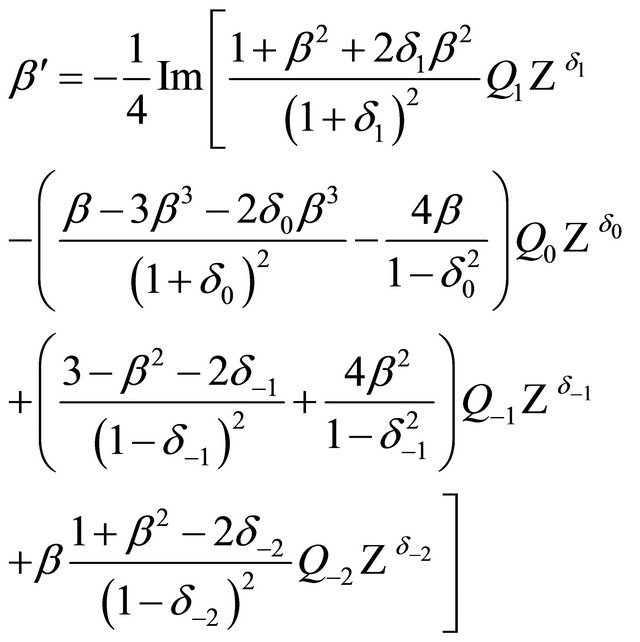 (9c)
(9c)

(9d)
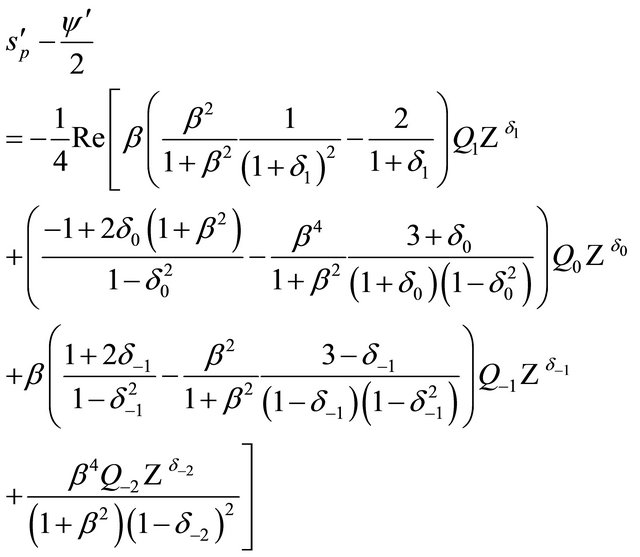
(9e)
(these can be computed with surprising ease by a few lines of Mathematica code).
To build an 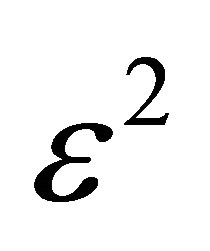 -accurate,
-accurate, 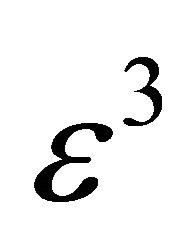 -accurate, etc. solution, we simply repeat the whole procedure in an iterative manner (the exact criteria for convergence of this procedure have not been worked out yet, but there is is enough computational evidence to feel more than safe with our
-accurate, etc. solution, we simply repeat the whole procedure in an iterative manner (the exact criteria for convergence of this procedure have not been worked out yet, but there is is enough computational evidence to feel more than safe with our ). The ensuing fast convergence enables us to construct an analytic solution to any level of accuracy (and be able to readily verify its correctness). To complete the solution, we divide
). The ensuing fast convergence enables us to construct an analytic solution to any level of accuracy (and be able to readily verify its correctness). To complete the solution, we divide 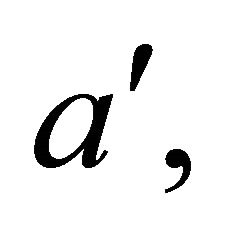
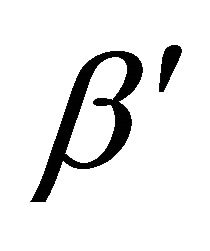 and
and 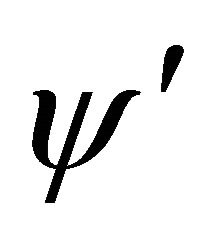 by
by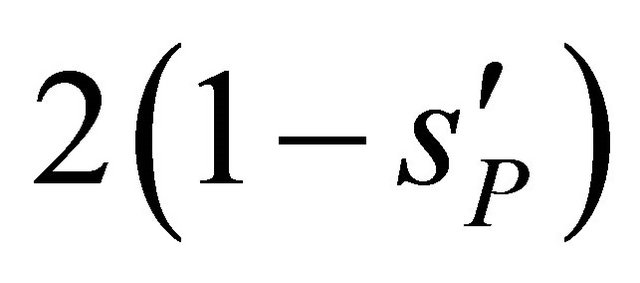 —thus replacing the physically meaningless independent variable
—thus replacing the physically meaningless independent variable  by the so called eccentric anomaly
by the so called eccentric anomaly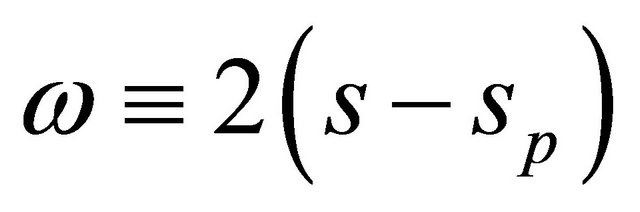 —and integrate the resulting differential equations. For full details, the reader should consult [4].
—and integrate the resulting differential equations. For full details, the reader should consult [4].
Quite often (as in this article), instead of high accuracy, we are interested in a solution which captures all qualitative features of the particle’s motion, using the smallest number of terms (to gain a valuable conceptual understanding of the problem). Luckily, in almost all cases (critical inclination of the main satellite problem being one of the few exception), this can be achieved with only a handful of terms of the 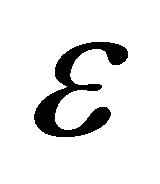 -accurate solution.
-accurate solution.
3. Perturbing Force for 7:4 Resonance
We now apply the formalism of the previous section to a special case of the restricted three-body problem (solving for the motion of the “massless” particle).
We assume that, by a choice of units, the primary’s (sun’s) gravitational mass 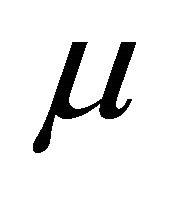 is equal to 1, the perturbing body’s (Jupiter’s) gravitational mass is
is equal to 1, the perturbing body’s (Jupiter’s) gravitational mass is 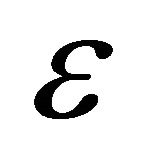 and its (circular) orbit is
and its (circular) orbit is
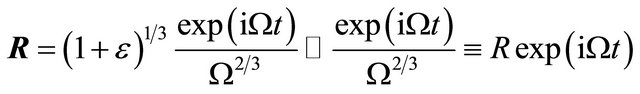 (10)
(10)
where 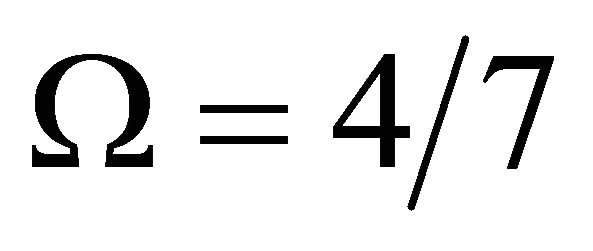 (to give a concrete example, we will concentrate on this specific resonance; one can investigate other resonances using the same approach—no special tailoring required). We investigate the motion of a particle (asteroid) of a negligible mass, whose semimajor axis
(to give a concrete example, we will concentrate on this specific resonance; one can investigate other resonances using the same approach—no special tailoring required). We investigate the motion of a particle (asteroid) of a negligible mass, whose semimajor axis  has values very close to 1 (we can thus take
has values very close to 1 (we can thus take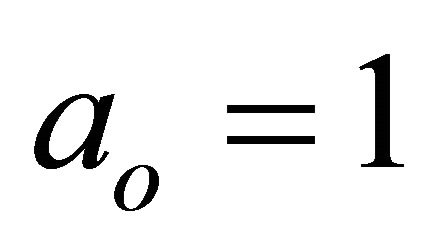 ), i.e. whose motion is in or near the corresponding resonance. In addition to this, we assume that both orbits are in the same plane (the so called planar, circular, restricted problem of three bodies; see [5]).
), i.e. whose motion is in or near the corresponding resonance. In addition to this, we assume that both orbits are in the same plane (the so called planar, circular, restricted problem of three bodies; see [5]).
The perturbing force (on the massless particle) is
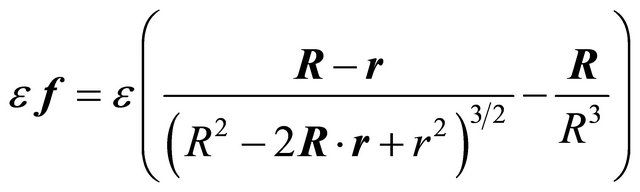
Utilizing (6), we can express  in the Kepler frame of the massless particle as
in the Kepler frame of the massless particle as
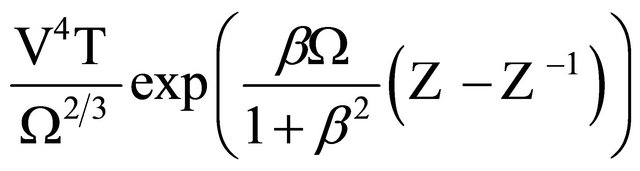
where
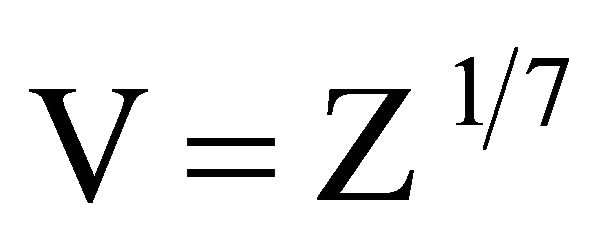
(based on the denominator of ), and
), and

where  is the so called resonance variable. It is a multiple of the angle from the small body’s aphelion to its conjunction with the larger orbiting body.
is the so called resonance variable. It is a multiple of the angle from the small body’s aphelion to its conjunction with the larger orbiting body.
The perturbing force (excluding the  factor) must then be expanded, first in
factor) must then be expanded, first in  (an inevitable step of this procedure), getting
(an inevitable step of this procedure), getting
 (11)
(11)
(in the actual computation we use terms up to an including  but they are too long to be quoted in full), and then in both
but they are too long to be quoted in full), and then in both  and
and  (as generalized Fourier expansion), utilizing
(as generalized Fourier expansion), utilizing
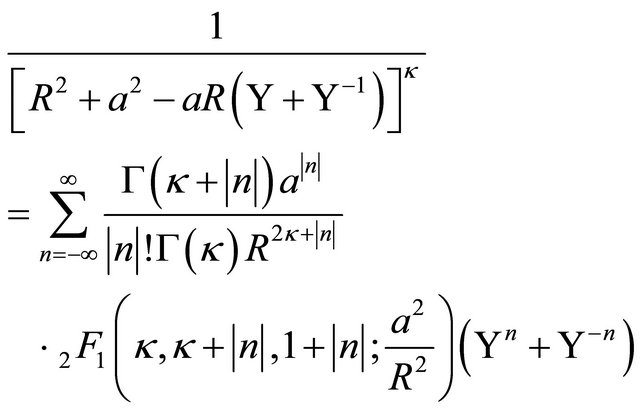
(where  is complex, of unit magnitude), truncated to a handful of predominant terms (sufficient to obtain
is complex, of unit magnitude), truncated to a handful of predominant terms (sufficient to obtain 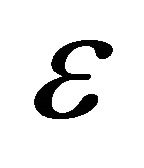 - accurate expressions for the rate of change of the orbital elements—see below).
- accurate expressions for the rate of change of the orbital elements—see below).
Finally, each 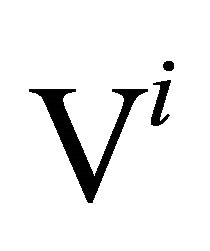 of this expansion is replaced by
of this expansion is replaced by
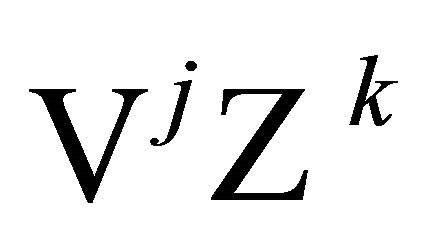
where 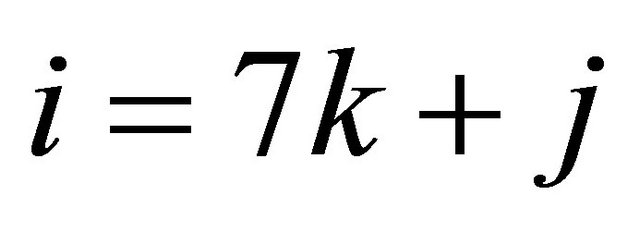 and
and 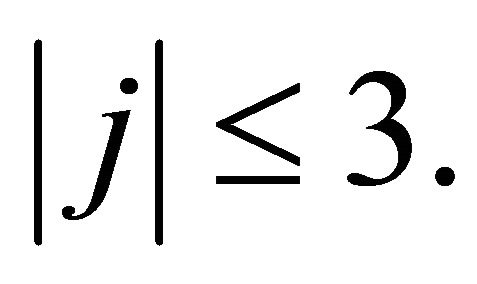 Applying the last two steps to (15) yields
Applying the last two steps to (15) yields

where we are displaying only the coefficients (in terms of the 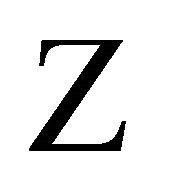 expansion) needed to compute time derivatives of the orbital elements (our only concern). We have also expanded the result in powers of
expansion) needed to compute time derivatives of the orbital elements (our only concern). We have also expanded the result in powers of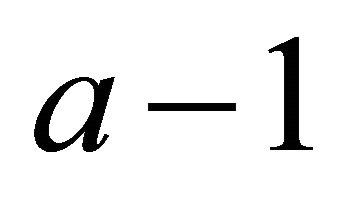 , quoting the leading term only (equivalent to setting
, quoting the leading term only (equivalent to setting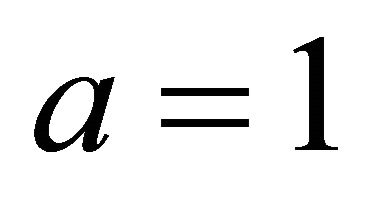 ). The leading (trailing) ellipsis indicates terms proportional to
). The leading (trailing) ellipsis indicates terms proportional to 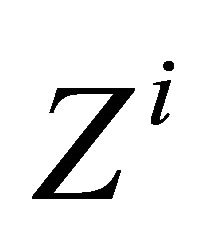 with
with 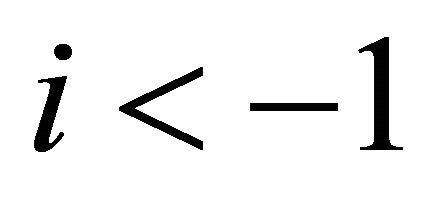
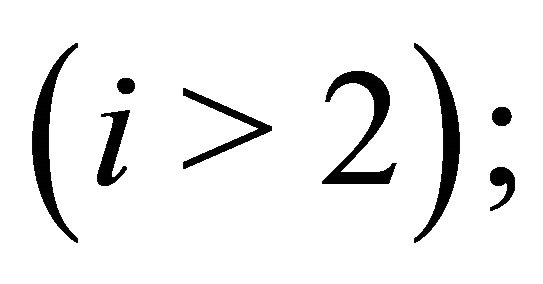 none of these contribute to the solution of the next section.
none of these contribute to the solution of the next section.
4. Resulting Solution
It is now fairly routine, by utilizing formulas of Section 2, to build the corresponding solution (at this point, we bring back additional terms of the  -expansion). For the purpose of this paper, we perform only one step of the iterative procedure, resulting in an
-expansion). For the purpose of this paper, we perform only one step of the iterative procedure, resulting in an 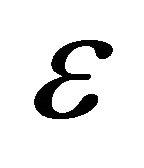 -accurate solution (whose typical accuracy within the next
-accurate solution (whose typical accuracy within the next 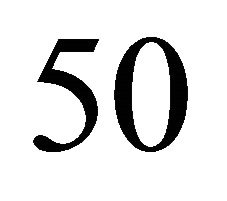 orbits is in the
orbits is in the 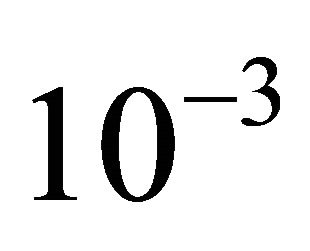 to
to 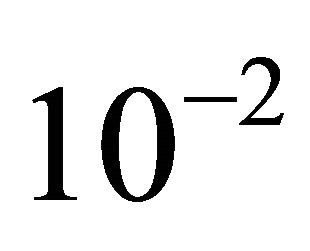 range—anyone interested in constructing a more accurate analytic solution using this method should consult [6]). Furthermore, due to high sensitivity to initial conditions, any solution will sooner or later diverge from the exact answer, and become practically useless for a long-range forecast. Luckily this is not our aim here—we want to find a solution which would capture all qualitative features of the corresponding motion, with the least number of terms—so let us proceed doing just that.
range—anyone interested in constructing a more accurate analytic solution using this method should consult [6]). Furthermore, due to high sensitivity to initial conditions, any solution will sooner or later diverge from the exact answer, and become practically useless for a long-range forecast. Luckily this is not our aim here—we want to find a solution which would capture all qualitative features of the corresponding motion, with the least number of terms—so let us proceed doing just that.
As the crudest approximation, we can apply the averaging “principle” (a euphemism for yet another, often crude, approximation) and discard all terms proportional to any non-zero power of  Furthermore, for each orbital-element derivative, we will keep only the leading term of the corresponding
Furthermore, for each orbital-element derivative, we will keep only the leading term of the corresponding  -expansion. This yields:
-expansion. This yields:
 (12)
(12)
Even though this set of equations has a surprising variety of solutions, these are always very regular (no trace of chaos, which we know some solutions should possess). Furthermore, the agreement with the “exact” (highly accurate numerical) solution is quite poor—the averaging principle is thus totally inadequate in this case. This is due to to the resonance being of the third order (the same kind of approximation would be sufficiently accurate for first-order resonances, such as 2:1, 3:2, etc.).
To correct the situation, we proceed to add the leading (in terms of the  expansion)
expansion)  -dependent term to each right-hand side of (16), getting
-dependent term to each right-hand side of (16), getting
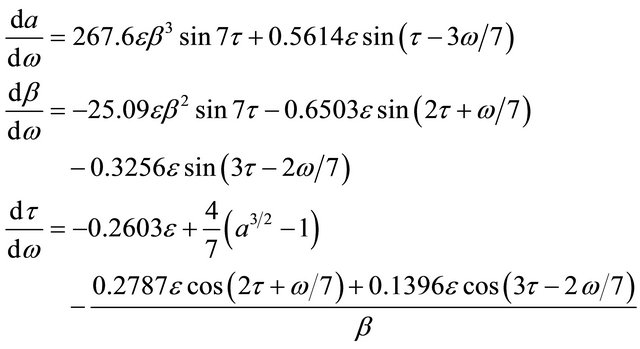
(13)
This time, the resulting solution is always (for relatively small  values) sufficiently close to the exact solution to be considered its adequate representation, with all the qualitative details (see Figure 1, where the solid, dotted and dashed lines represent the exact, the fully
values) sufficiently close to the exact solution to be considered its adequate representation, with all the qualitative details (see Figure 1, where the solid, dotted and dashed lines represent the exact, the fully  -accurate and the current, truncated solution, respectively; note that the solid and dotted lines practically overlap).
-accurate and the current, truncated solution, respectively; note that the solid and dotted lines practically overlap).
It is worth mentioning that we use our definition of orbital elements (adjusted for the orbit’s distortion) for all three solutions (the osculating orbital elements have a much more irregular behaviour than what we see in Figure 1). The exact solution has been obtained by highly accurate numerical integration of (1), converting the results to the corresponding variation in . The
. The 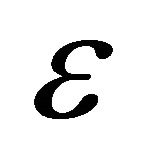 - accurate solution corresponds to a numerical solution of an untruncated (i.e. using all terms of the
- accurate solution corresponds to a numerical solution of an untruncated (i.e. using all terms of the  expansion) version of (13), and is nearly indistinguishabe from the exact solution. The “current” solution refers to the result of numerical integration of (13); this is the only solution which we continue to investigate further.
expansion) version of (13), and is nearly indistinguishabe from the exact solution. The “current” solution refers to the result of numerical integration of (13); this is the only solution which we continue to investigate further.
It is important to note that, unlike (12), the new set of Equations (13) already captures one of the most important feature of the exact solution, namely the occasional onset of chaos. This can be conveniently explored by the following analog of the Poincaré surfaces of section:
Using the numerical solution of (13), we collect the  and
and  values as found at the end of each anomalistic cycle (i.e. at
values as found at the end of each anomalistic cycle (i.e. at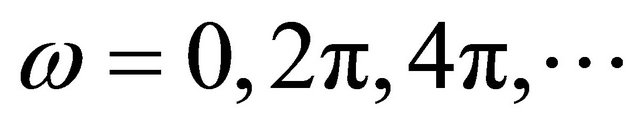 ), plotting these in a twodimensional graph. As a result, we discover an amazing variety of both open and closed, connected and disconnected curves on one hand (see Figure 2, for an example), or (using a slightly different set of initial conditions) a scattered cloud of disconnected point on the other (see Figure 3), indicating the presence of chaotic motion. Incidentally, when we apply the same technique to different solutions of (12), we always end up with a simple, (near) straight-line segment.
), plotting these in a twodimensional graph. As a result, we discover an amazing variety of both open and closed, connected and disconnected curves on one hand (see Figure 2, for an example), or (using a slightly different set of initial conditions) a scattered cloud of disconnected point on the other (see Figure 3), indicating the presence of chaotic motion. Incidentally, when we apply the same technique to different solutions of (12), we always end up with a simple, (near) straight-line segment.

Figure 1. Comparing exact and approximate solutions.
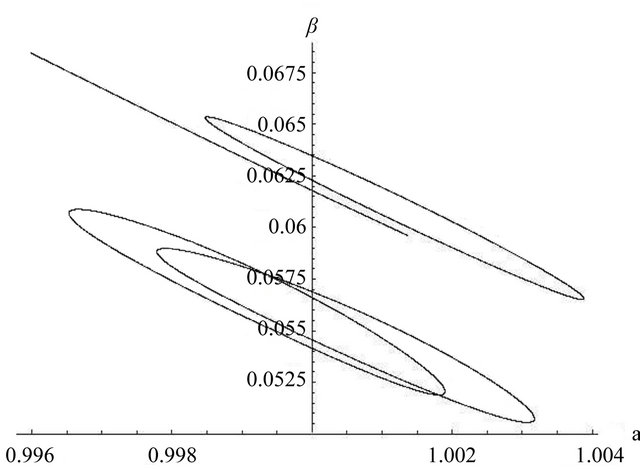
Figure 2. Poincaré section for regular solution.
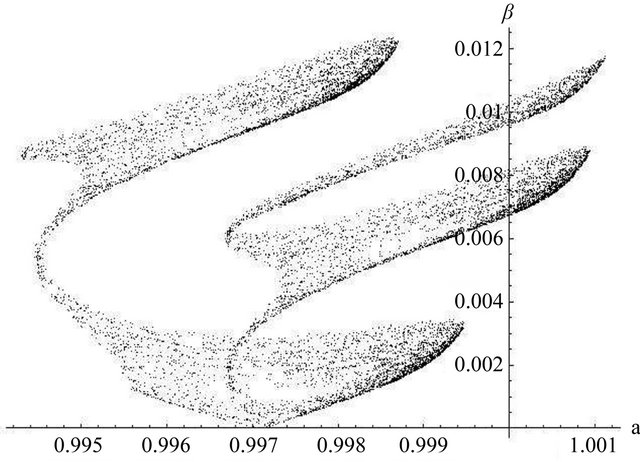
Figure 3. Poincaré section for chaotic solution.
5. Conclusion
We have thus illustrated that all qualitative features of the motion of a small body, in the 7:4 resonance with a bigger one, are encapsulated in three simple differential Equations (13). A similar set of equations can be easily constructed for any other resonance (a routine exercise— a systematic study of these is yet to be carried out). If desired, one can also add the effect of the large-body’s eccentricity and the two orbits’ inclination (a threedimensional version of the K-S technique will be required to deal with the latter). We believe that this technique opens a new level of understanding of resonances related to the three-body restricted problem, and of the resulting weak chaos.