MHD Stagnation Point Flow and Heat Transfer over a Permeable Surface ()
1. Introduction
In recent years, the requirements of modern technology have stimulated interest in fluid flow studies which involve interaction of several phenomena. One such study is stagnation point flow over a permeable surface which plays an important role in many engineering problems, petroleum industries, ground water flows, extrusion of a polymer sheet from a dye and boundary layer control. More importantly, the quality of the products, in the above mentioned processes, depends on the kinematics of stretching and the simultaneous heat and mass transfer rates during the fabrication process. Crane [1] studied the flow over a linearly stretching sheet in an ambient fluid and gave a similarity solution in closed analytical form for the study of two-dimensional problem. Heat transfer in the flow over a permeable surface has been investigated by several authors such as Gupta and Gupta [2], Carragher and Crane [3], Chiam [4], Magyari and Keller [5], Mahapatra and Gupta [6], Elbashbeshy and Bazid [7], Liao and Pop [8], Jat and Chaudhary [9,10] and Bhattacharya and Layek [11].
The object of the present paper is to study the stagnation point flow and heat transfer for an electrically conducting fluid over a permeable surface in the presence of a magnetic field. The fluid is acted upon by an external uniform magnetic field and a uniform injection or suction directed normal to the plane of the wall. The wall and stream temperatures are assumed to be constants. Numerical results are obtained for the momentum and energy equations using Shooting method.
2. Formulation of the Problem
Consider the steady two-dimensional stagnation point flow 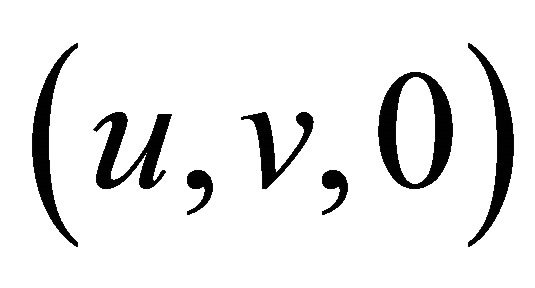 of a viscous incompressible electrically conducting fluid near a stagnation point over a permeable surface placed in the plane
of a viscous incompressible electrically conducting fluid near a stagnation point over a permeable surface placed in the plane 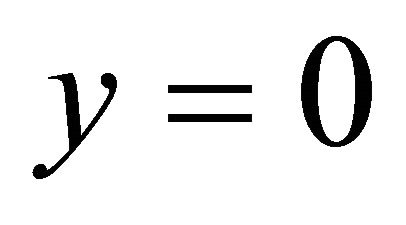 of a Cartesian coordinates system with the x-axis along the surface, in a uniform injection or suction velocity
of a Cartesian coordinates system with the x-axis along the surface, in a uniform injection or suction velocity  at the boundary of the surface and in the presence of an externally applied normal magnetic field of constant strength
at the boundary of the surface and in the presence of an externally applied normal magnetic field of constant strength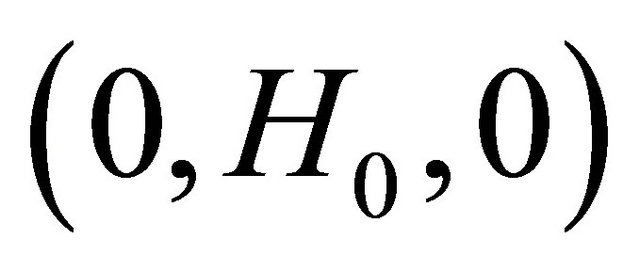 . The stretching surface has a uniform temperature
. The stretching surface has a uniform temperature  while the velocity of the flow external to the boundary layer is
while the velocity of the flow external to the boundary layer is  and temperature
and temperature . The system of boundary layer equations (which model Figure 1) are given by:
. The system of boundary layer equations (which model Figure 1) are given by:
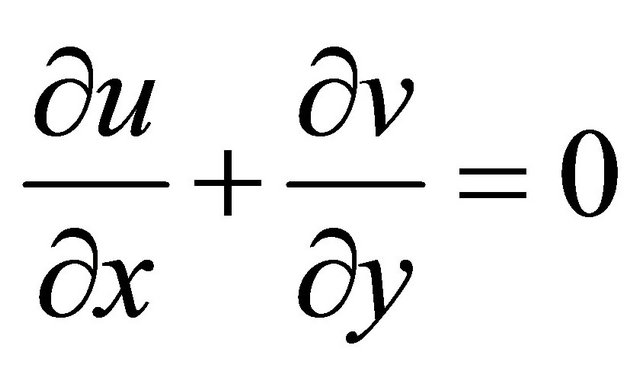 (1)
(1)
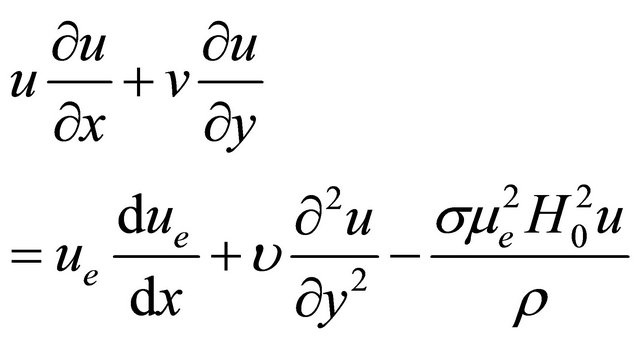 (2)
(2)
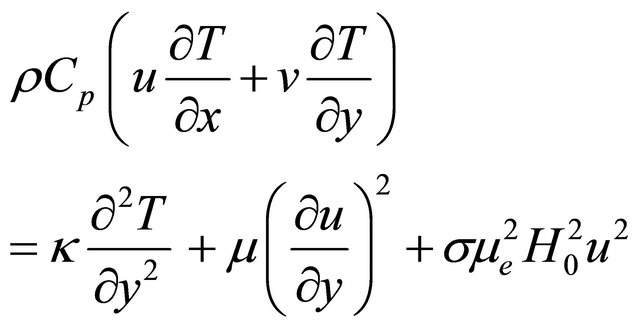 (3)
(3)
where 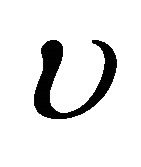 is the coefficient of kinematic viscosity,
is the coefficient of kinematic viscosity,  the electrical conductivity,
the electrical conductivity, 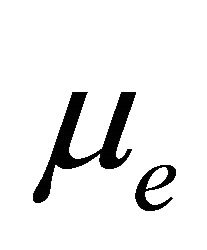 the magnetic permeability,
the magnetic permeability, 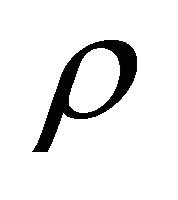 the density,
the density, 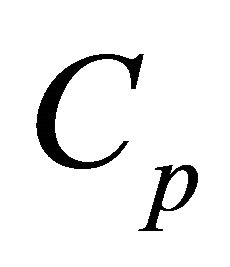 the specific heat at constant
the specific heat at constant

Figure 1. A sketch of the physical problem.
pressure,  the thermal conductivity and
the thermal conductivity and 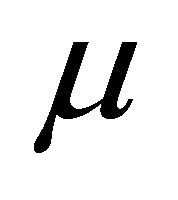 the coefficient of viscosity. The other symbols have their usual meanings.
the coefficient of viscosity. The other symbols have their usual meanings.
The boundary conditions are:
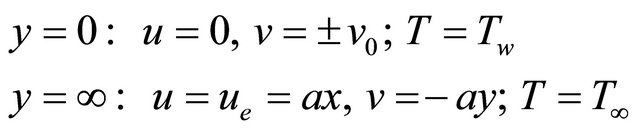 (4)
(4)
where  is a constant proportional to the free stream velocity far away from the stretching surface.
is a constant proportional to the free stream velocity far away from the stretching surface.
3. Analysis
The continuity Equation (1) is identically satisfied by stream function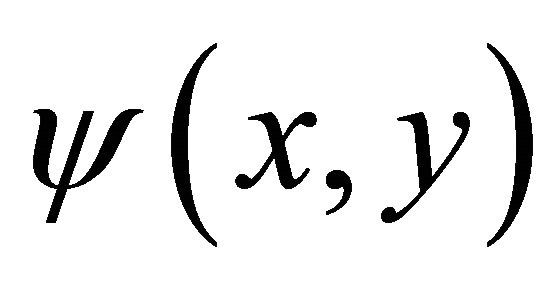 , defined as
, defined as
 (5)
(5)
For the solution of the momentum and the energy Equations (2) and (3), the following dimensionless variables are defined:
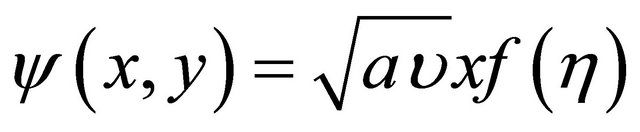 (6)
(6)
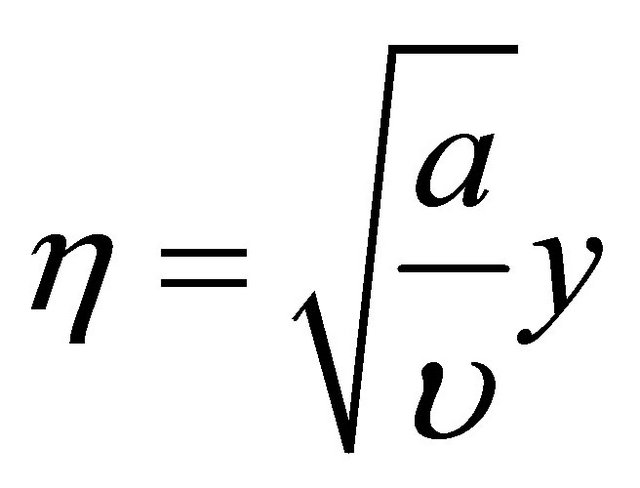 (7)
(7)
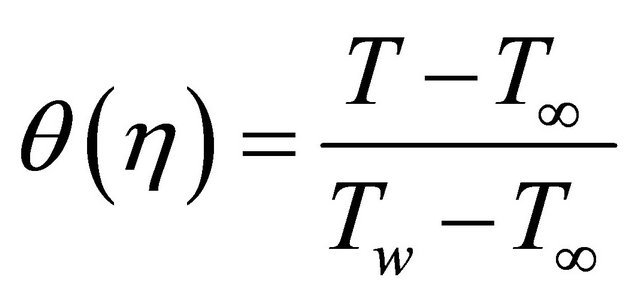 (8)
(8)
Equations (5) to (8), transform Equations (2) and (3) into
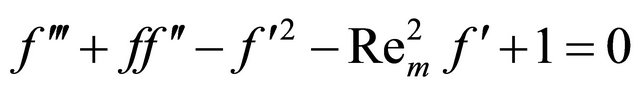 (9)
(9)
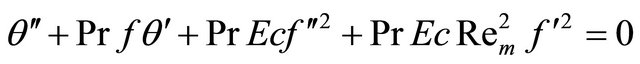 (10)
(10)
where a prime 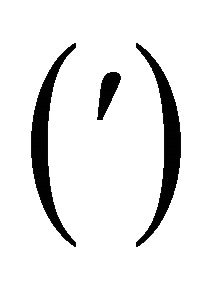 denotes differentiation with respect to
denotes differentiation with respect to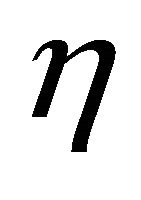 ,
, 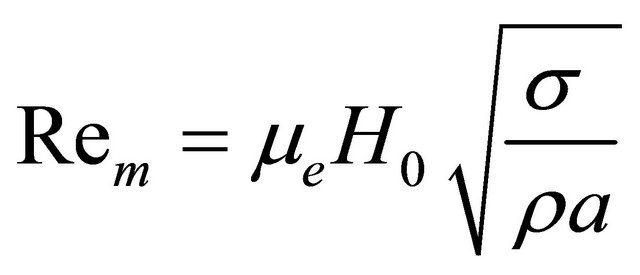 the Magnetic parameter,
the Magnetic parameter,
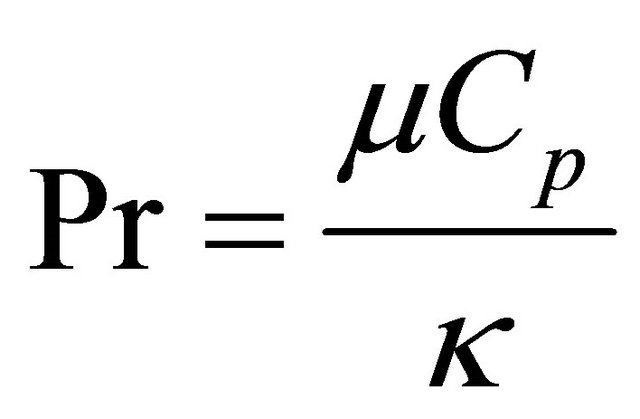 the Prandtl number and
the Prandtl number and 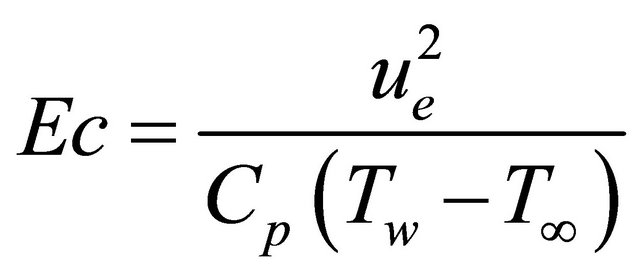
the Eckert number.
The corresponding boundary conditions are:
 (11)
(11)
where 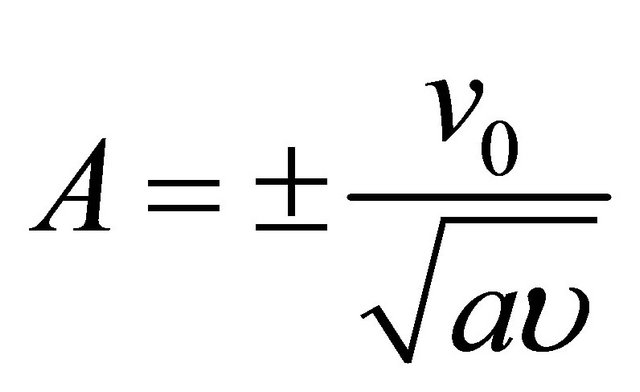 is the suction parameter.
is the suction parameter.
For numerical solution of the Equations (9) and (10), we apply the following power series in a small magnetic parameter  as:
as:
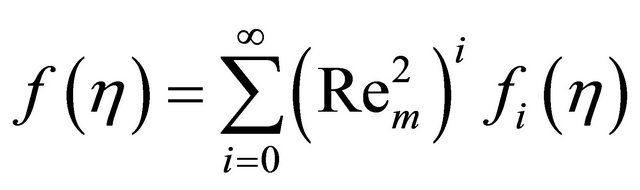 (12)
(12)
 (13)
(13)
Substituting Equations (12) and (13) and its derivatives in Equations (9) and (10) and then equating the coefficients of like powers of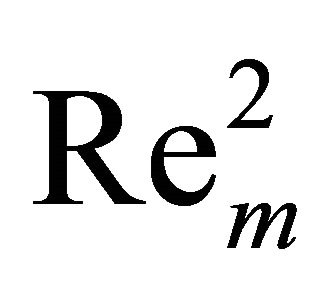 , we get the following set of equations:
, we get the following set of equations:
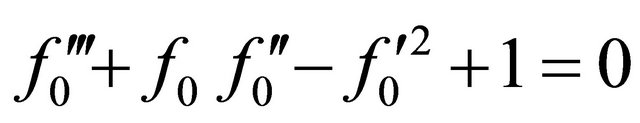 (14)
(14)
 (15)
(15)
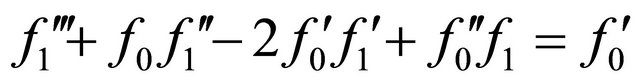 (16)
(16)
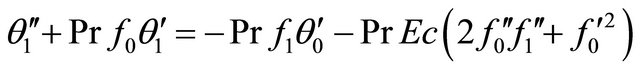 (17)
(17)
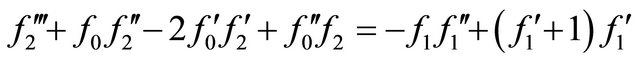 (18)
(18)
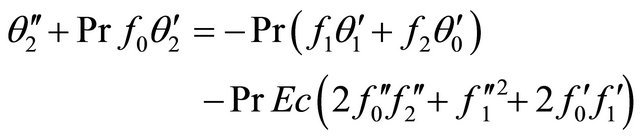 (19)
(19)
with the boundary conditions:
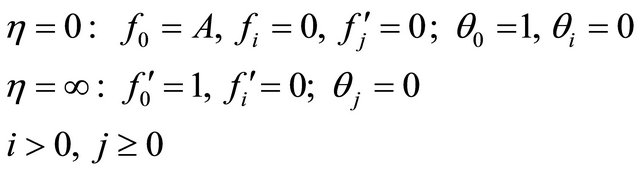 (20)
(20)
The Equation (14) is that obtained by Jat and Chaudhary [9] for the non-magnetic case and the remaining equations are ordinary linear differential equations and have been solved numerically by Shooting method. The velocity and temperature distributions for various values of parameters are shown in Figures 2-4 respectively.
4. Results and Discussion
The Figure 2 shows the variation of velocity distribution against 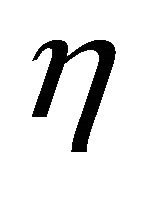 for various values of the suction parameter A and the magnetic parameter
for various values of the suction parameter A and the magnetic parameter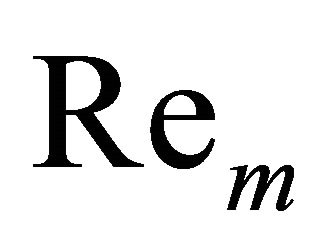 . It may be observed that the velocity increases as the suction parameter A
. It may be observed that the velocity increases as the suction parameter A
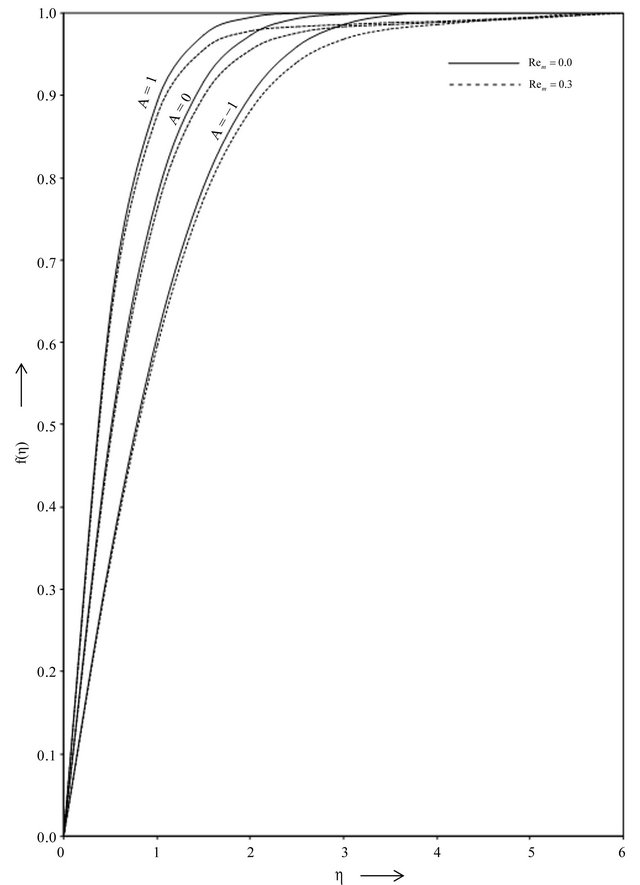
Figure 2. Velocity distribution against η for various values of A and Rem.
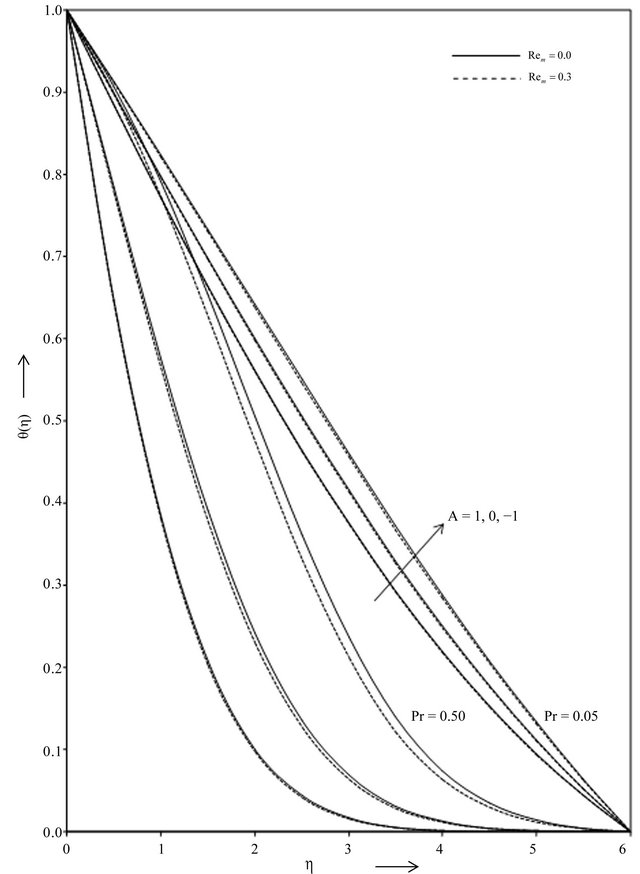
Figure 3. Temperature distribution against η for various values of A, Rem and Pr with Ec = 0.00.
increases, whereas it decreases as the magnetic parameter 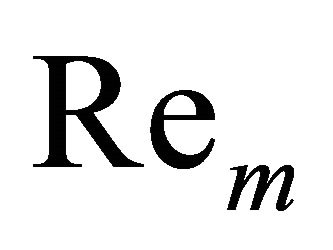 increases for a fixed
increases for a fixed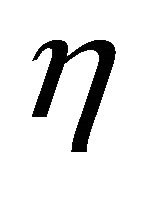 .
.
The Figures 3 and 4 show the variation of the temperature distribution against  for various values of the parameters such as the suction parameter A, the magnetic parameter
for various values of the parameters such as the suction parameter A, the magnetic parameter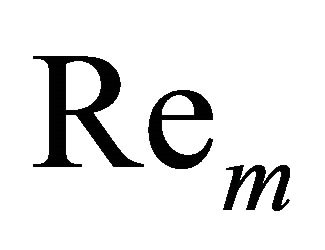 , the Prandtl number
, the Prandtl number 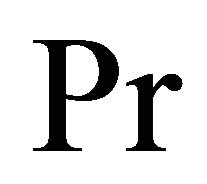 and the Eckert number
and the Eckert number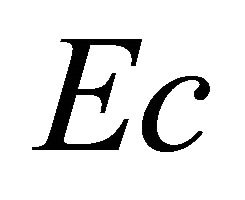 . From these figures it may be observed that the temperature distribution decreases with the increasing value of the suction parameter A and same phenomena occur for the Prandtl number Pr. It is further observed that in Figure 3 the temperature distribution decreases with the increasing value of the magnetic parameter
. From these figures it may be observed that the temperature distribution decreases with the increasing value of the suction parameter A and same phenomena occur for the Prandtl number Pr. It is further observed that in Figure 3 the temperature distribution decreases with the increasing value of the magnetic parameter
 . In Figure 4, for fixed suction parameter A temperature distribution decreases with the increasing value of the Eckert number
. In Figure 4, for fixed suction parameter A temperature distribution decreases with the increasing value of the Eckert number 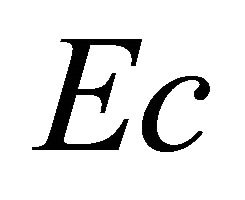 and reverse phenomena occurs for the magnetic parameter
and reverse phenomena occurs for the magnetic parameter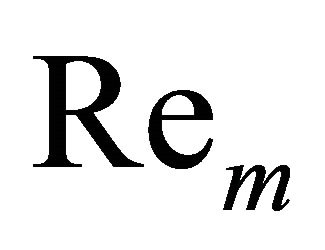 .
.
5. Conclusions
The steady two-dimensional stagnation point flow and heat transfer of a viscous incompressible electrically conducting fluid over a permeable surface has been analyzed. The similarity equations are obtained and solved numerically by a Shooting method. The effects of the
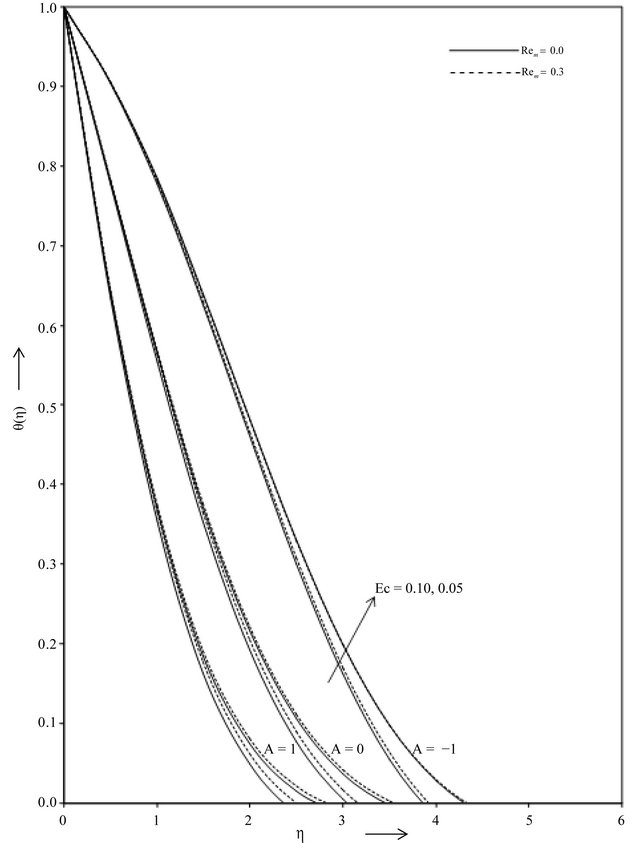
Figure 4. Temperature distribution against against η for various values of A, Rem and Ec with Pr = 0.50.
suction parameter, the magnetic parameter, the Prandtl number and the Eckert number are studied in detail. The velocity boundary layer thickness increases with the increasing value of the suction parameter while the reverse phenomenon is observed for thermal boundary layer thickness. Further concluded when the Eckert number equal to zero the velocity as well as thermal boundary layer thickness decreases with the increasing value of the magnetic parameter and the Prandtl number, whereas for the Eckert number not equal to zero, thermal boundary layer thickness increases with the increasing value of the magnetic parameter and decreases with the increasing value of the Eckert number.