1. Introduction
1.1. Background
The complex nature of data arising in the context of survival studies is such that it is common to make use of a multivariate regression model. Cox’s semi-parametric proportional hazards model [3] has enjoyed wide use in view of its broad applicability. The model makes the key assumption that the regression coefficients do not change with time and much study has gone into investigating and correcting for potential departures from these assumptions [4-10]. Sometimes we can anticipate in advance that the proportional hazards model may be too restrictive. The example which gave rise to our own interest in this question concerned 2174 breast cancer patients, followed over a period of 15 years at the Institut Curie in Paris, France. For these data, as well as a number of other studies in breast cancer, the presence of non-proportional hazards effects has been observed by several authors. Often this is ignored but this can seriously impact inferences.
The model used to make inferences will then often differ from that which can be assumed to have generated the observations. In situations of non proportional hazards, unless dealing with very large data sets relative to the number of studied covariates, it will often not be feasible to study the whole, possibly of infinite dimension,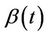 . Xu and O’Quigley [11] argue that an estimate of average effect can be used in a preliminary analysis of a data set with time varying regression effects. For a given sample, a single average effect can be estimated more accurately (and more easily) than the whole
. Xu and O’Quigley [11] argue that an estimate of average effect can be used in a preliminary analysis of a data set with time varying regression effects. For a given sample, a single average effect can be estimated more accurately (and more easily) than the whole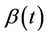 . Xu and O’Quigley [11] derive an estimate
. Xu and O’Quigley [11] derive an estimate 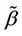 of an average regression effect
of an average regression effect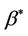 . They provide an interpretation of
. They provide an interpretation of 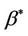 as a population average effect. It is approximated by
as a population average effect. It is approximated by 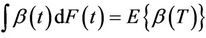 under certain conditions, where F is the marginal distribution function of the failure time random variable T. The purpose here is to test the null hypothesis;
under certain conditions, where F is the marginal distribution function of the failure time random variable T. The purpose here is to test the null hypothesis; 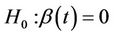 for all t against the alternatives
for all t against the alternatives 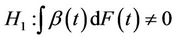 or
or 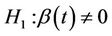 for some t. The development is based on Brownian motion, Donsker’s theorem and theorems from O’Quigley [1] and Xu and O’Quigley [2]. We show that the usual partial likelyhood score test arises as a special case. Large sample theory is straightforward.
for some t. The development is based on Brownian motion, Donsker’s theorem and theorems from O’Quigley [1] and Xu and O’Quigley [2]. We show that the usual partial likelyhood score test arises as a special case. Large sample theory is straightforward.
1.2. Notation
The probability structure, although quite simple, is not the immediate one which would come to mind. The random variables of interest are the failure time, 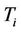 , the censoring time,
, the censoring time, 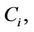 and the possibly time dependent covariate,
and the possibly time dependent covariate, 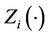 ,
, 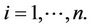 We view these as a random sample from the distribution of T, C and
We view these as a random sample from the distribution of T, C and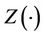 . It will not be particularly restrictive and is helpful to our development to assume that T and C have support on some finite interval. The time-dependent covariate
. It will not be particularly restrictive and is helpful to our development to assume that T and C have support on some finite interval. The time-dependent covariate 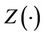 is assumed to be a predictable stochastic process and, for ease of exposition, taken to be of dimension one whenever possible. Let
is assumed to be a predictable stochastic process and, for ease of exposition, taken to be of dimension one whenever possible. Let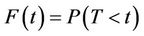 ,
, 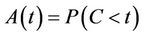
and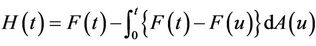 . For each subject i we observe
. For each subject i we observe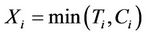 , and
, and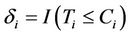 . The “at risk” indicator
. The “at risk” indicator  is defined as,
is defined as, 
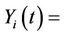 The counting process
The counting process 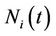 is defined as,
is defined as, 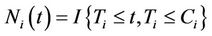 and we also define
and we also define
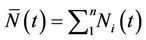 . The inverse function,
. The inverse function, 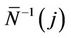 corresponds to the value
corresponds to the value 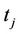 where
where
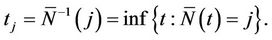 It is of notational convenience to define
It is of notational convenience to define
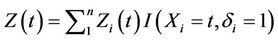 , in words a continuous function equal to zero apart from at the observed failures in which it assumes the covariate value of the subject that fails. The number of observed failures k is given by
, in words a continuous function equal to zero apart from at the observed failures in which it assumes the covariate value of the subject that fails. The number of observed failures k is given by 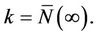 If there are ties in the data our suggestion is to split them randomly although there are a number of other suggested ways of dealing with ties. All of the techniques described here require only superficial modification in order to accommodate any of these other approaches for dealing with ties.
If there are ties in the data our suggestion is to split them randomly although there are a number of other suggested ways of dealing with ties. All of the techniques described here require only superficial modification in order to accommodate any of these other approaches for dealing with ties.
1.3. Models
Insight is helped when we group the models together under as general a heading a possible. The most general model is then the non proportional hazards model written,
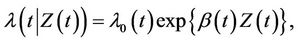 (1.1)
(1.1)
where 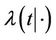 is the conditional hazard function,
is the conditional hazard function, 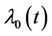 the baseline hazard and
the baseline hazard and 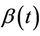 the time-varying regression effect. Whenever
the time-varying regression effect. Whenever 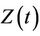 has dimension greater than one we view
has dimension greater than one we view 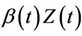 as an inner product,
as an inner product, 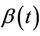 having the same dimension as
having the same dimension as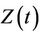 . In order to avoid problems of identifiability we assume that
. In order to avoid problems of identifiability we assume that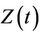 , if indeed time-dependent, has a clear interpretation such as the value of a prognostic factor measured over time, so that
, if indeed time-dependent, has a clear interpretation such as the value of a prognostic factor measured over time, so that 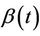 is precisely the regression effect of
is precisely the regression effect of 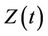 on the log hazard ratio at time t. The above model becomes a proportional hazards model under the restriction that
on the log hazard ratio at time t. The above model becomes a proportional hazards model under the restriction that 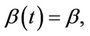 a constant i.e.
a constant i.e.
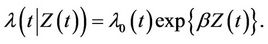 (1.2)
(1.2)
O’Quigley and Stare [12] introduced the name “partially proportional hazards models” to describe models in which at least one component of the function 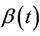 is constrained to be constant. Such models can be shown to include the stratified proportional hazards model [13] whereby;
is constrained to be constant. Such models can be shown to include the stratified proportional hazards model [13] whereby;
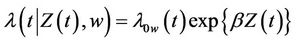 (1.3)
(1.3)
as well as random effects models [12].
2. Model Based Probabilities
The probability structure of the model, needed in our development, is described in O’Quigley [1]. We recall the main results in this section. Most often time is viewed as a set of indices to certain stochastic processes, so that, for example, we consider 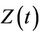 to be a random variable having different distributions for different t. Also, the failure time variable T can be viewed as a non-negative random variable with distribution
to be a random variable having different distributions for different t. Also, the failure time variable T can be viewed as a non-negative random variable with distribution 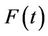 and, whenever the set of indices t to the stochastic process coincide with the support for T, then, not only can we talk about the random variables
and, whenever the set of indices t to the stochastic process coincide with the support for T, then, not only can we talk about the random variables 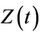 for which the distribution corresponds to
for which the distribution corresponds to 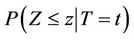 but also marginal quantities such as the random variable
but also marginal quantities such as the random variable 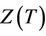 having distribution
having distribution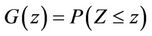 . An important result concerning the conditional distribution of
. An important result concerning the conditional distribution of 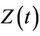 given
given 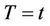 follows. First we need the following:
follows. First we need the following:
Definition 1. The discrete probabilities 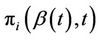 are given by;
are given by;
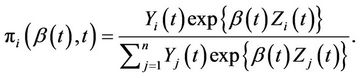 (2.1)
(2.1)
Under (1.2), i.e. the constraint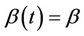 , the product of the
, the product of the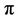 ’s over the observed failure times gives the partial likelihood [3]. When
’s over the observed failure times gives the partial likelihood [3]. When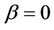 ,
, 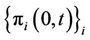 is the empirical distribution that assigns equal weight to each sample subject in the risk set. Based upon the
is the empirical distribution that assigns equal weight to each sample subject in the risk set. Based upon the 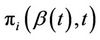 we have:
we have:
Definition 2. Moments of Z with respect to 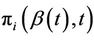 are given by;
are given by;
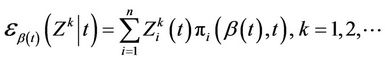 (2.2)
(2.2)
Definition 3. In order to distinguish conditionally independent censoring from independent censoring we define 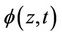 where;
where;
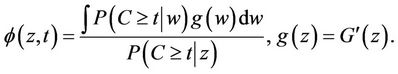
Note that when censoring does not depend upon z then 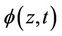 will depend upon neither z or t and is, in fact, equal to one. Otherwise, under a conditionally independent censoring assumption, we can consistently estimate
will depend upon neither z or t and is, in fact, equal to one. Otherwise, under a conditionally independent censoring assumption, we can consistently estimate 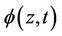 and we call this
and we call this 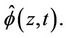 The following theorem underlies our development.
The following theorem underlies our development.
Theorem 1. Under model (1) and assuming 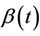 known, the conditional distribution function of
known, the conditional distribution function of 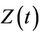 given
given 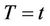 is consistently estimated by
is consistently estimated by
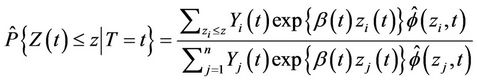 (2.3)
(2.3)
Proof. (see [1])
Straightforward applications of Slutsky’s theorem enable us to claim the result continues to hold whenever 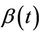 is replaced by any consistent estimator
is replaced by any consistent estimator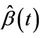 , in particular the partial likelihood estimator when we assume the more restricted model (1.2). □
, in particular the partial likelihood estimator when we assume the more restricted model (1.2). □
The theorem has many important consequences includeing;
Corollary 1. Under model (1) and an independent censorship, assuming  known, the conditional distribution function of
known, the conditional distribution function of 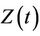 given
given 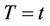 is consistently estimated by
is consistently estimated by
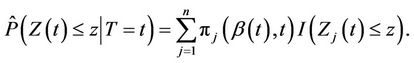 (2.4)
(2.4)
Corollary 2. For a conditionally independent censoring mechanism we have
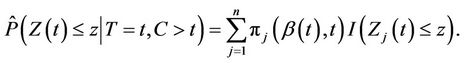 (2.5)
(2.5)
Again simple applications of Slutsky’s theorem shows that the result still holds for 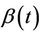 replaced by any consistent estimate. When the hypothesis of proportionality of risks is correct then the result holds for the estimate
replaced by any consistent estimate. When the hypothesis of proportionality of risks is correct then the result holds for the estimate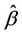 . Having first defined
. Having first defined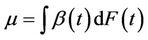 , it is also of interest to consider the approximation;
, it is also of interest to consider the approximation;
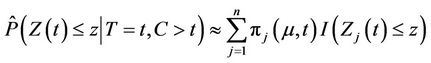 (2.6)
(2.6)
and, for the case of an independent censoring mechanism,
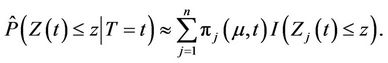 (2.7)
(2.7)
For small samples it will be unrealistic to hope to obtain reliable estimates of 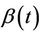 for all of t so that, often, we take an estimate of some summary measure, in particular
for all of t so that, often, we take an estimate of some summary measure, in particular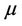 . It is in fact possible to estimate
. It is in fact possible to estimate 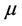 without estimating
without estimating 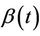 [11] although the usual partial likelyhood estimate does not accomplish this. In fact the partial likelihood estimate turns out to be equivalent to obtaining the solution of an estimating equation based upon
[11] although the usual partial likelyhood estimate does not accomplish this. In fact the partial likelihood estimate turns out to be equivalent to obtaining the solution of an estimating equation based upon 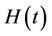 and using
and using 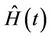 as an estimate whereas, to consistently estimate
as an estimate whereas, to consistently estimate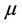 , it is necessary to work with some consistent estimate of
, it is necessary to work with some consistent estimate of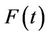 , in particular the Kaplan-Meier estimate. We firstly need some definition of what is being estimated when the data are generated by model (1.1) and we are working with model (1.2). This is contained in the following definition for
, in particular the Kaplan-Meier estimate. We firstly need some definition of what is being estimated when the data are generated by model (1.1) and we are working with model (1.2). This is contained in the following definition for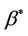 .
.
Definition 4. Let 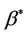 be the constant value satisfying
be the constant value satisfying
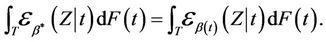 (2.8)
(2.8)
The definition enables us to make sense out of using estimates based on (1.2) when the data are in fact generated by (1.1). Since we can view T as being random, whenever 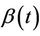 is not constant, we can think of having sampled from
is not constant, we can think of having sampled from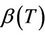 . The right hand side of the above equation is then a double expectation and
. The right hand side of the above equation is then a double expectation and 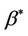 the best fitting value under the constraint that
the best fitting value under the constraint that 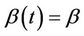 We can show the existence and uniqueness of solutions to Equation (8) [11] More importantly,
We can show the existence and uniqueness of solutions to Equation (8) [11] More importantly, 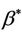 can be shown to have the following three properties; 1) under model (1.2)
can be shown to have the following three properties; 1) under model (1.2)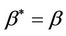 ; 2) under a subclass of the Harrington-Fleming models,
; 2) under a subclass of the Harrington-Fleming models, 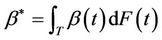 and 3) for general situations
and 3) for general situations 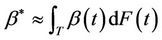 Estimates of
Estimates of 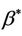 are discussed in [2,11] and, in the light of the foregoing, we can take these as estimates of
are discussed in [2,11] and, in the light of the foregoing, we can take these as estimates of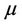 . We also have the further two corollaries to Therorem 1:
. We also have the further two corollaries to Therorem 1:
Corollary 3. For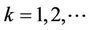 ,
, 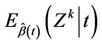 provides consistent estimates of
provides consistent estimates of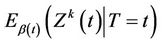 , under model (1). In particular
, under model (1). In particular 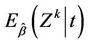 provides consistent estimates of
provides consistent estimates of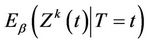 , under model (1.2).
, under model (1.2).
Furthermore, once again under the model, if we let 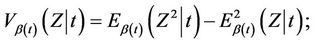 thenCorollary 4. Under model (1.2),
thenCorollary 4. Under model (1.2), 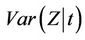 is consistently estimated by
is consistently estimated by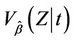 .
.
Theorem 1 and its corollaries provide the ingredients necessary to a construction from which several tests can be derived.
3. Important Empirical Processes
Consider the partial scores introduced by Wei [14];
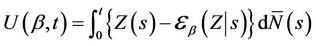 (3.1)
(3.1)
Wei was interested in goodness of fit for the two group problem and based a test on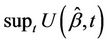 , large values indicating departures away from proportional hazards in the direction of non proportional hazards. Considerable exploration of this idea, and substantial generalization via the use of martingale based residuals, has been carried out by Lin, Wei and Ying [15]. These investigations showed that we could work with a much broader class of statistics that those based on the score so that a wide choice of functions, potentially describing different kinds of departures from the model, are available. Apart from the two group case, limiting distributions are complicated and usually approximated via simulation. Although the driving idea is that of goodness of fit, the same techniques can be applied to testing for the presence of regression effects against a null hypothesis that
, large values indicating departures away from proportional hazards in the direction of non proportional hazards. Considerable exploration of this idea, and substantial generalization via the use of martingale based residuals, has been carried out by Lin, Wei and Ying [15]. These investigations showed that we could work with a much broader class of statistics that those based on the score so that a wide choice of functions, potentially describing different kinds of departures from the model, are available. Apart from the two group case, limiting distributions are complicated and usually approximated via simulation. Although the driving idea is that of goodness of fit, the same techniques can be applied to testing for the presence of regression effects against a null hypothesis that  Furthermore, working directly with the increments of the process rather than the process itself, we can derive related processes for which the limiting distributions are available analytically. From the previous section the increments of the process
Furthermore, working directly with the increments of the process rather than the process itself, we can derive related processes for which the limiting distributions are available analytically. From the previous section the increments of the process 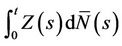 at
at  have mean
have mean 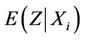 and variance
and variance . We can view these increments as being independent [16,17]. Thus only the existence of the variance is necessary in order to carry out appropriate standardization and to be able to appeal to the functional central limit theorem. We can then treat our observed process as though arising from a Brownian motion process. Simple calculations allow us to also work with the Brownian bridge, integrated Brownian motion and reflected Brownian motion, processes which will be useful under particular alternative to the model specified under the null hypothesis. Consider the process
. We can view these increments as being independent [16,17]. Thus only the existence of the variance is necessary in order to carry out appropriate standardization and to be able to appeal to the functional central limit theorem. We can then treat our observed process as though arising from a Brownian motion process. Simple calculations allow us to also work with the Brownian bridge, integrated Brownian motion and reflected Brownian motion, processes which will be useful under particular alternative to the model specified under the null hypothesis. Consider the process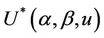 ,
, 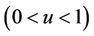 , in which
, in which
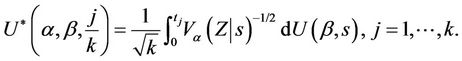 (3.2)
(3.2)
where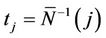 . This process is only defined on k equispaced points of the interval (0, 1] but we extend our definition to the whole interval via linear interpolation so that, for u in the interval
. This process is only defined on k equispaced points of the interval (0, 1] but we extend our definition to the whole interval via linear interpolation so that, for u in the interval 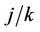 to
to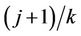 , we write;
, we write;
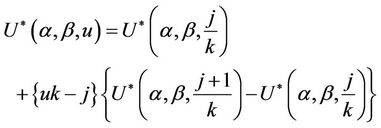
As n goes to infinity, under the usual Breslow and Crowley conditions, then we have that, for each j (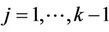 ),
), converges in distribution to a Gaussian process with mean zero and variance equal to
converges in distribution to a Gaussian process with mean zero and variance equal to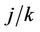 . This follows directly from Donsker’s theorem. Replacing
. This follows directly from Donsker’s theorem. Replacing 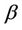 by a consistent estimate leaves asymptotic properties unaltered.
by a consistent estimate leaves asymptotic properties unaltered.
3.1. Some Remarks on the Notation 
Various aspects of the statistic 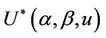 will be used to construct different tests. We choose the * symbol to indicate some kind of standardization as opposed to the non standardized U. The variance and the number of failure points are used to carry out the standardization. Added flexibility in test construction can be achieved by using the two parameters,
will be used to construct different tests. We choose the * symbol to indicate some kind of standardization as opposed to the non standardized U. The variance and the number of failure points are used to carry out the standardization. Added flexibility in test construction can be achieved by using the two parameters, 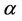 and
and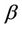 , rather than a single parameter
, rather than a single parameter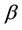 . In practice these are replaced by quantities which are either fixed or estimated under some hypothesis. For goodness of fit procedures which we consider later we will only use a single parameter, typically
. In practice these are replaced by quantities which are either fixed or estimated under some hypothesis. For goodness of fit procedures which we consider later we will only use a single parameter, typically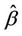 . Goodness of fit tests are most usefully viewed as tests of hypotheses of the form
. Goodness of fit tests are most usefully viewed as tests of hypotheses of the form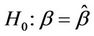 . A test then of a hypothesis
. A test then of a hypothesis 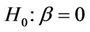 may not seem very different. This is true in principle. However, for a test of
may not seem very different. This is true in principle. However, for a test of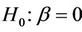 , we need keep in mind not only behaviour under the null but also under the alternative. Because of this it is often advantageous, under a null hypothesis of
, we need keep in mind not only behaviour under the null but also under the alternative. Because of this it is often advantageous, under a null hypothesis of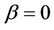 , to work with
, to work with 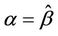 and
and 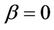 in the expression
in the expression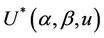 . Under the null,
. Under the null,  remains consistent for the value 0 and, in the light of Slutsky’s theorem, the large sample distribution of the test statistics will not be affected. Under the alternative however things look different. The increments of the process
remains consistent for the value 0 and, in the light of Slutsky’s theorem, the large sample distribution of the test statistics will not be affected. Under the alternative however things look different. The increments of the process 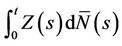 at
at  no longer have mean
no longer have mean 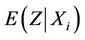 and adding them up will indicate departures from the null. But the denominator is also affected and, in order to keep the variance estimate not only correct but also as small as we can, it is preferable to use the value
and adding them up will indicate departures from the null. But the denominator is also affected and, in order to keep the variance estimate not only correct but also as small as we can, it is preferable to use the value 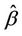 rather than zero.
rather than zero.
3.2. Some Properties of 
A very wide range of possible tests can be based upon the statistic 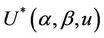 and we consider a number of these below. Well known tests such as the partial likelyhood score test obtain as a special cases. First we need to make some observations on the properties of
and we consider a number of these below. Well known tests such as the partial likelyhood score test obtain as a special cases. First we need to make some observations on the properties of 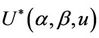 under different values of
under different values of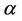 ,
, 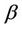 and u.
and u.
Lemma 1. The process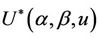 , for all finite
, for all finite 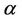 and
and 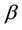 is continuous on [0, 1]. Also
is continuous on [0, 1]. Also 
Lemma 2. Under model 1.2 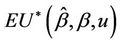 converges in probability to zero.
converges in probability to zero.
Lemma 3. Suppose that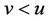 , then
, then
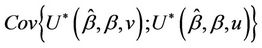 converges in probability to v.
converges in probability to v.
Proofs of the above lemmas are all immediate. Since the increments of the process are asymptotically independent we can treat 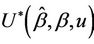 (as well as
(as well as 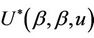
under some hypothesized ) as though it were Brownian motion. From Corollary 3 we have that
) as though it were Brownian motion. From Corollary 3 we have that 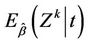 provides consistent estimates of
provides consistent estimates of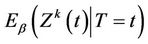 , under model (1.2) and that
, under model (1.2) and that 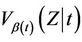 is consistent for
is consistent for .
.
Therefore, at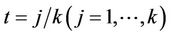 , the variance of
, the variance of
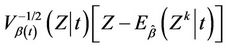 goes to the value one, as a simple application of Slutsky’s theorem. A further application of Slutsky’s theorem, together with theorems of Cox and Andersen and Gill [16,17] provide that the increments
goes to the value one, as a simple application of Slutsky’s theorem. A further application of Slutsky’s theorem, together with theorems of Cox and Andersen and Gill [16,17] provide that the increments  are asymptotically uncorrelated. Let
are asymptotically uncorrelated. Let
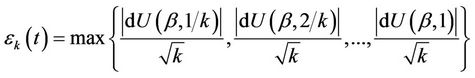
Then
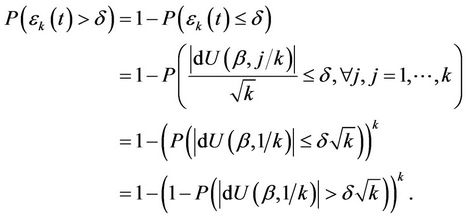
Applying the Chebyshev inequality,

from which

as k becomes large. Apart from the necessity for the existence of the third moment of Z we also require that, as k increases, the fluctuations of the process 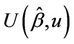 between successive failures become sufficiently small in probability, the so called tightness of the process [18]. We can assume this holds in real applications. We then conclude from Donsker’s theorem that
between successive failures become sufficiently small in probability, the so called tightness of the process [18]. We can assume this holds in real applications. We then conclude from Donsker’s theorem that 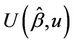 converges in distribution to Brownian motion. Replacing
converges in distribution to Brownian motion. Replacing 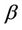 by a consistent estimate leaves asymptotic properties unaltered. Suppose that the assumption of zero effect, i.e.,
by a consistent estimate leaves asymptotic properties unaltered. Suppose that the assumption of zero effect, i.e., 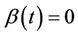 is incorrect, and, in particular, that
is incorrect, and, in particular, that 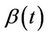 is a smoothly changing monotonic function of time. Without losing generality we will assume this monotonicity to be an increasing one. Now, at each time point t, instead of subtracting off
is a smoothly changing monotonic function of time. Without losing generality we will assume this monotonicity to be an increasing one. Now, at each time point t, instead of subtracting off 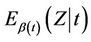 from the observed value of Z at that point, we subtract instead
from the observed value of Z at that point, we subtract instead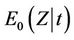 . The variance is also impacted but the variance is always positive (thereby impacting the average size but not the average sign of the increments). So, we will observe a positive trend in the standardized residuals, the early ones tending to be too large and the later ones tending to be too large also but negatively. A good model for this, at least as a first approximation, would be Brownian motion with drift [1]. For our purposes we note that, moving away from the model of zero regression effects, we anticipate observing some trend rather than zero mean Brownian motion. For decreasing
. The variance is also impacted but the variance is always positive (thereby impacting the average size but not the average sign of the increments). So, we will observe a positive trend in the standardized residuals, the early ones tending to be too large and the later ones tending to be too large also but negatively. A good model for this, at least as a first approximation, would be Brownian motion with drift [1]. For our purposes we note that, moving away from the model of zero regression effects, we anticipate observing some trend rather than zero mean Brownian motion. For decreasing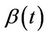 , the same argument holds leading to an approximation of Brownian motion with drift but with the sign changed. These assertions follow when
, the same argument holds leading to an approximation of Brownian motion with drift but with the sign changed. These assertions follow when 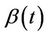 is monotone. Now suppose that
is monotone. Now suppose that 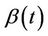 is not monotone. There are two cases of interest. The first is where
is not monotone. There are two cases of interest. The first is where  is broadly monotone, by which we mean the following. Divide the time interval into non overlapping time segments and take the average value of
is broadly monotone, by which we mean the following. Divide the time interval into non overlapping time segments and take the average value of 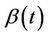 for each segment. We then suppose that the average value of
for each segment. We then suppose that the average value of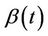 , over the different time segments, is monotone. We could make this intuitive idea more precise if needed. For this case we would expect, again, the procedure to work well. The second case of interest is where
, over the different time segments, is monotone. We could make this intuitive idea more precise if needed. For this case we would expect, again, the procedure to work well. The second case of interest is where 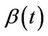 changes over the time period in question in a way that has no obvious pattern or trend. We would not expect to be able to detect such behavior and the power of the test procedures would be low. We would most likely conclude that there is no effect, a conclusion that, even though not correct, would be reasonable, at least as an approximation.
changes over the time period in question in a way that has no obvious pattern or trend. We would not expect to be able to detect such behavior and the power of the test procedures would be low. We would most likely conclude that there is no effect, a conclusion that, even though not correct, would be reasonable, at least as an approximation.
4. Nonand Partially Proportional Hazards Models
The Brownian motion approximations of the above section extend immediately to the case of non proportional hazards and partially proportional hazards models. The generalization of Equation (1) is natural and would lead to an unstandardized score;
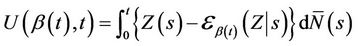 (4.1)
(4.1)
and, as before, under the null hypothesis that 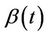 is correctly specified the function
is correctly specified the function 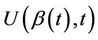 will be a sum of zero mean random variables. The range of possible alternative hypotheses is large and, mostly, we will not wish to consider anything too complex. Often the alternative hypothesis will specify an ordering, or a non zero value, for just one of the components of a vector values
will be a sum of zero mean random variables. The range of possible alternative hypotheses is large and, mostly, we will not wish to consider anything too complex. Often the alternative hypothesis will specify an ordering, or a non zero value, for just one of the components of a vector values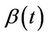 . In the exact same way as in the previous section, all of the calculations lean upon the main theorem and its corollaries. The increments of the process
. In the exact same way as in the previous section, all of the calculations lean upon the main theorem and its corollaries. The increments of the process
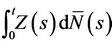 at t = Xi have mean
at t = Xi have mean 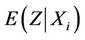 and variance
and variance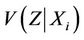 . A little bit of extra care is needed, in practice, in order to maintain the view of the independence of these increments. When
. A little bit of extra care is needed, in practice, in order to maintain the view of the independence of these increments. When 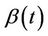 is known there is no problem but if, as usually happens, we wish to use estimates, then, for asymptotic theory to still hold, we require the sample size (number of failures) to become infinite relative to the dimension of
is known there is no problem but if, as usually happens, we wish to use estimates, then, for asymptotic theory to still hold, we require the sample size (number of failures) to become infinite relative to the dimension of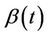 . Thus, if we wish to estimate the whole function
. Thus, if we wish to estimate the whole function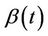 , then some restrictions will be needed because, full generality implies an infinite dimensional parameter
, then some restrictions will be needed because, full generality implies an infinite dimensional parameter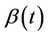 . For the stratified model and, generally, partially proportional hazards models, the problem does not arise because we do not estimate
. For the stratified model and, generally, partially proportional hazards models, the problem does not arise because we do not estimate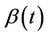 .
.
The sequentially standardized process will now be written , in which
, in which
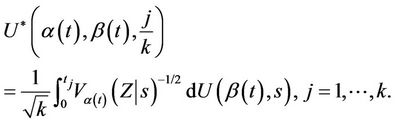
where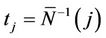 . This process can be made to cover the whole interval (0, 1] continuously by interpolating in exactly the same way as in the previous section. For this process we reach the same conclusion, i.e., that as n goes to infinity, under the usual Breslow and Crowley conditions [17], then we have that, for each j (
. This process can be made to cover the whole interval (0, 1] continuously by interpolating in exactly the same way as in the previous section. For this process we reach the same conclusion, i.e., that as n goes to infinity, under the usual Breslow and Crowley conditions [17], then we have that, for each j (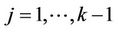 ),
),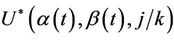 converges in distribution to a Gaussian process with mean zero and variance equal to
converges in distribution to a Gaussian process with mean zero and variance equal to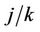 . The only potential difficulty is making use of Slutsky’s theorem whereby, if we replace
. The only potential difficulty is making use of Slutsky’s theorem whereby, if we replace 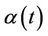 and
and 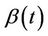 by consistent estimates the result still holds. The issue is that of having consistent estimates, which for an infinite dimensional unrestricted parameter we can not achieve. The solution is simply to either restrict these functions or to work with the stratified models in which we do not need to estimate them. Subsection 3.1 applies equally well here if we replace
by consistent estimates the result still holds. The issue is that of having consistent estimates, which for an infinite dimensional unrestricted parameter we can not achieve. The solution is simply to either restrict these functions or to work with the stratified models in which we do not need to estimate them. Subsection 3.1 applies equally well here if we replace 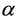 and
and 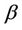 by
by 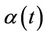 and
and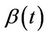 . The lemmas of the above section describing the properties of
. The lemmas of the above section describing the properties of 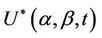 apply equally we if we are working with
apply equally we if we are working with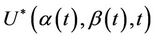 , specifically, the process
, specifically, the process 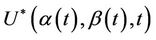 , for all finite
, for all finite 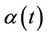 and
and 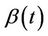 is continuous on [0, 1] and
is continuous on [0, 1] and 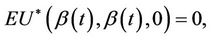 under model 1.2
under model 1.2 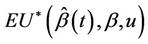 converges in probability to zero and for
converges in probability to zero and for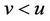 ,
, 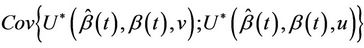 converges in probability to v. Since the increments of the process are asymptotically independent we will treat
converges in probability to v. Since the increments of the process are asymptotically independent we will treat  (as well as
(as well as 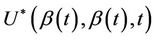 under some hypothesized
under some hypothesized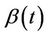 ) as though it were Brownian motion.
) as though it were Brownian motion.
5. Test Statistics
Several tests of point hypotheses can be constructed based on the theory of the previous section. These tests can also be used to construct test based confidence intervals of parameter estimates, obtained as solutions to an estimating equation. Among these tests are the following.
5.1. Distance Travelled at Time t
At time t, under the null hypothesis that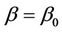 , often a hypothesis of absence of effect in which case
, often a hypothesis of absence of effect in which case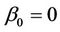 , we have that
, we have that 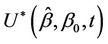 can be approximated by a normal distribution with mean zero and variance t. A p-value corresponding to the null hypothesis is then obtained from
can be approximated by a normal distribution with mean zero and variance t. A p-value corresponding to the null hypothesis is then obtained from
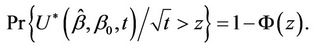
This p-value is for a one-sided test in the direction of the alternative 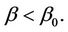 For a one-sided alternative in the opposite direction we would use;
For a one-sided alternative in the opposite direction we would use;
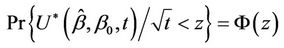
and, for a two sided alternative, we would, as usual, consider the absolute value of the test statistic and multiply 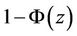 by two. Under the alternative, say
by two. Under the alternative, say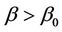 , if we take the first two terms of a Taylor series expansion of
, if we take the first two terms of a Taylor series expansion of 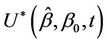 about
about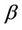 , we can deduce that a good approximation for this would be Brownian motion with drift. At time t this is then a good test for absence of effect (Brownian motion) against a proportional hazards alternative (Brownian motion with drift), good in the sense that type I error is controlled for and, under these alternatives, the test has good power properties. Power will be maximized by using the whole time interval, i.e., taking
, we can deduce that a good approximation for this would be Brownian motion with drift. At time t this is then a good test for absence of effect (Brownian motion) against a proportional hazards alternative (Brownian motion with drift), good in the sense that type I error is controlled for and, under these alternatives, the test has good power properties. Power will be maximized by using the whole time interval, i.e., taking 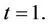 Nonetheless there may be situations in which we may opt to take a value of t less than one. If we know for instance that, under both the null and the alternative we can exclude the possibility of effects being persistent beyond some time
Nonetheless there may be situations in which we may opt to take a value of t less than one. If we know for instance that, under both the null and the alternative we can exclude the possibility of effects being persistent beyond some time 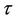 say, i.e., the hazard ratios beyond that point should be one or very close to that, then we will achieve greater power by taking t to be less than one, specifically some value around
say, i.e., the hazard ratios beyond that point should be one or very close to that, then we will achieve greater power by taking t to be less than one, specifically some value around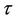 . A confidence interval for
. A confidence interval for 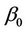 can be obtained using normal approximations or by constructing the interval
can be obtained using normal approximations or by constructing the interval 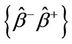 such that for any point b contained in the interval a test of the null hypothesis,
such that for any point b contained in the interval a test of the null hypothesis, 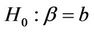 , is not rejected.
, is not rejected.
5.2. Greatest Distance from Origin at Time t
In cases where we wish to consider values of t less than one, we may have knowledge of some  of interest. Otherwise we might want to consider several possible values of
of interest. Otherwise we might want to consider several possible values of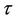 . Control on Type I error will be lost unless specific account is made of the multiplicity of tests. One simple way to address this issue is to consider the maximum value achieved by the process during the interval
. Control on Type I error will be lost unless specific account is made of the multiplicity of tests. One simple way to address this issue is to consider the maximum value achieved by the process during the interval 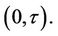 Again we can appeal to known results for some well known functions of Brownian motion. In particular we have;
Again we can appeal to known results for some well known functions of Brownian motion. In particular we have;
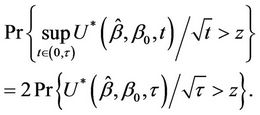
Under the null and proportional hazards alternatives this test, as opposed to the usual score test, would lose power comparable to carrying out a two sided rather than a one-sided test. Under non-proportional hazards alternatives this test could be of use, an extreme example being crossing hazards where the usual score test may have power close to zero. As the absolute value of the hazard ratio increases so would the maximum distance from the origin.
5.3. Brownian Bridge Test
Since we are viewing the process 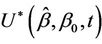 as though it were a realization of a Brownian motion, we can consider some other well known functions of Brownian motion. Consider then the bridged process
as though it were a realization of a Brownian motion, we can consider some other well known functions of Brownian motion. Consider then the bridged process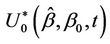 ;
;
Definition 5. The bridged process is defined by the transformation
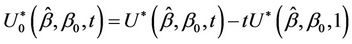
Lemma 4. The process 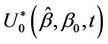 converges in distribution to the Brownian bridge, in particular, for large samples,
converges in distribution to the Brownian bridge, in particular, for large samples, 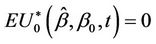 and
and
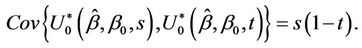
The Brownian bridge, also referred to as tied down Brownian motion for the obvious reason that at 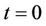 and
and 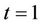 the process takes the value 0, will not be particularly useful for carrying out a test at
the process takes the value 0, will not be particularly useful for carrying out a test at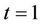 . It is more useful to consider, as a test statistic, the greatest distance of the bridged process from the time axis. We can then appeal to;
. It is more useful to consider, as a test statistic, the greatest distance of the bridged process from the time axis. We can then appeal to;
Lemma 5.
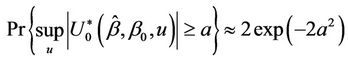 (5.1)
(5.1)
which follows as a large sample result since;
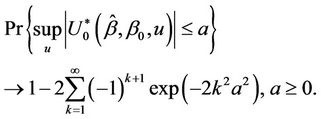
This is an alternating sign series and therefore, if we stop the series at k = 2 the error is bounded by 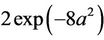 which for most values of a that we will be interested in will be small enough to ignore. For alternatives to the null hypothesis (
which for most values of a that we will be interested in will be small enough to ignore. For alternatives to the null hypothesis (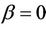 ) belonging to the proportional hazards class, the Brownian bridge test will be less powerful than the distance from origin test. It is more useful under alternatives of a non-proportional hazards nature, in particular an alternative in which
) belonging to the proportional hazards class, the Brownian bridge test will be less powerful than the distance from origin test. It is more useful under alternatives of a non-proportional hazards nature, in particular an alternative in which 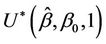 is close to zero, a situation we might anticipate when the hazard functions cross over. Its main use, in our view, is in testing goodness of fit, i.e., a hypothesis test of the form
is close to zero, a situation we might anticipate when the hazard functions cross over. Its main use, in our view, is in testing goodness of fit, i.e., a hypothesis test of the form 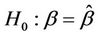 [1].
[1].
5.4. Reflected Brownian Motion
An interesting property of Brownian motion is the following. Let  be Brownian motion, choose some positive value r and define the process
be Brownian motion, choose some positive value r and define the process 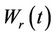 in the following way: If
in the following way: If 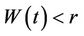 then
then 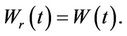 If
If 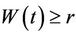 then
then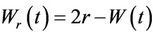 . It is easily shown that the reflected process
. It is easily shown that the reflected process 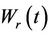 is also Brownian motion. Choosing r to be negative and defining
is also Brownian motion. Choosing r to be negative and defining 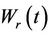 accordingly we have the same result. The process
accordingly we have the same result. The process 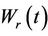 coincides exactly with
coincides exactly with 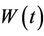 until such a time as a barrier is reached. We can imagine this barrier as a mirror and beyond the barrier the process
until such a time as a barrier is reached. We can imagine this barrier as a mirror and beyond the barrier the process 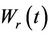 is a simple reflection of
is a simple reflection of . So, consider the process
. So, consider the process 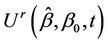 defined to be
defined to be 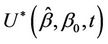 if
if 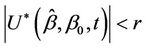 and to be equal to
and to be equal to 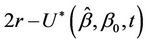 if
if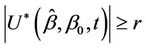 .
.
Lemma 6. The process 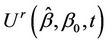 converges in distribution to Brownian motion, in particular, for large samples,
converges in distribution to Brownian motion, in particular, for large samples, 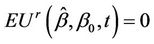 and
and 
Under proportional hazards there is no obvious role to be played by Ur. However, imagine a non-proportional hazards alternative where the effect reverses at some point, the so-called crossing hazards problem. The statistic 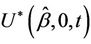 would increase up to some point and then decrease back to a value close to zero. If we knew this point, or had some reasons for guessing it in advance, thenwe could work with
would increase up to some point and then decrease back to a value close to zero. If we knew this point, or had some reasons for guessing it in advance, thenwe could work with 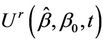 instead of
instead of 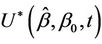 . A judicious choice of the point of reflection would result in a test statistic that continues to increase under such an alternative so that a distance from the origin test might have reasonable power. In practice we may not have any ideas on a potential point of reflection. We could then consider trying a whole class of points of reflection and choosing that point which results in the greatest test statistic. A bound for a supremum type test can be derived by applying the results of Davies [19,20]. Under the alternative hypothesis we could imagine increments of the same sign being added together until the value r is reached, at which point the sign of the increments changes. Under the alternative hypothesis the absolute value of the increments is strictly greater than zero. Under the null, r is not defined and, following the usual standardization, this set up fits in with that of Davies [19, 20]. We can define
. A judicious choice of the point of reflection would result in a test statistic that continues to increase under such an alternative so that a distance from the origin test might have reasonable power. In practice we may not have any ideas on a potential point of reflection. We could then consider trying a whole class of points of reflection and choosing that point which results in the greatest test statistic. A bound for a supremum type test can be derived by applying the results of Davies [19,20]. Under the alternative hypothesis we could imagine increments of the same sign being added together until the value r is reached, at which point the sign of the increments changes. Under the alternative hypothesis the absolute value of the increments is strictly greater than zero. Under the null, r is not defined and, following the usual standardization, this set up fits in with that of Davies [19, 20]. We can define 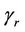 to be the time point satisfying
to be the time point satisfying 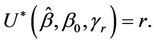 A two-sided test can then be based on the statistic
A two-sided test can then be based on the statistic 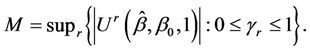 Inference can then be based upon;
Inference can then be based upon;
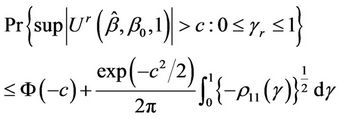 (5.2)
(5.2)
where Ф denotes the cumulative normal distribution function, 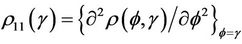 and where
and where 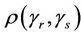 is the autocorrelation function between
is the autocorrelation function between 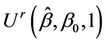 and
and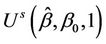 . In general the autocorrelation function
. In general the autocorrelation function 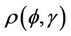 , needed to evaluate the test statistic is unknown. However, it can be consistently estimated using bootstrap resampling methods. For
, needed to evaluate the test statistic is unknown. However, it can be consistently estimated using bootstrap resampling methods. For 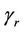 and
and 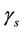 taken as fixed, we can take bootstrap samples from which several pairs of
taken as fixed, we can take bootstrap samples from which several pairs of 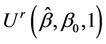 and
and 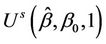 can be obtained. Using these pairs, an empirical, i.e. product moment, correlation coefficient can be calculated. Under the usual conditions [21,22], the empirical estimate provides a consistent estimate of the true value. This sampling strategy is investigated in related work by O’Quigley and Natarajan [23].
can be obtained. Using these pairs, an empirical, i.e. product moment, correlation coefficient can be calculated. Under the usual conditions [21,22], the empirical estimate provides a consistent estimate of the true value. This sampling strategy is investigated in related work by O’Quigley and Natarajan [23].
Davies also suggests an approximation in which the autocorrelation is not needed. This may be written down as
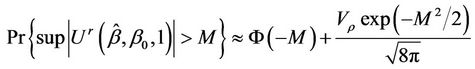 (5.3)
(5.3)
where 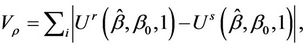 the
the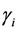 , ranging over (L, U), are the turning points of
, ranging over (L, U), are the turning points of 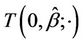 and M is the observed maximum of
and M is the observed maximum of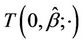 .
.
Turning points only occur at the k distinct failure times and, to keep the notation consistent with that of the next section, it suffices to take  as being located half way between adjacent failures,
as being located half way between adjacent failures, 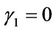 and
and 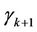 any value greater than the largest failure time. We would though require different inferential procedures for this.
any value greater than the largest failure time. We would though require different inferential procedures for this.
5.5. Partial Likelihood Score Test
Suppose that we wish to test 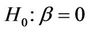 and instead of
and instead of 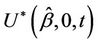 we choose to work with
we choose to work with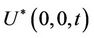 . In the light of Slutsky’s theorem it is readily seen that the large sample null distributions of the two test statistics are the same. Next, instead of standardizing by
. In the light of Slutsky’s theorem it is readily seen that the large sample null distributions of the two test statistics are the same. Next, instead of standardizing by 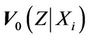 at each
at each 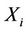 we take a simple average of such quantities, over the observed failures. To see this, note that
we take a simple average of such quantities, over the observed failures. To see this, note that 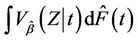 is consistent for
is consistent for 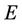
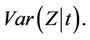 Rather than integrate with respect to
Rather than integrate with respect to 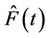 it is more common, in the counting process context, to integrate with respect to
it is more common, in the counting process context, to integrate with respect to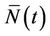 , the two coinciding in the absence of censoring. It is also more common to fix
, the two coinciding in the absence of censoring. It is also more common to fix 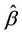 in
in 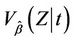 at its null value zero. This gives us:
at its null value zero. This gives us:
Definition 6. The empirical average conditional variance, 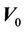 is defined as
is defined as
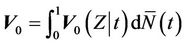 .
.
If, in Equation (3.2), we replace 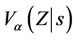 by
by 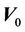 then the distance from origin test at time
then the distance from origin test at time 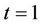 coincides exactly with the partial likelihood score test. Indeed this observation could be used to construct a characterization of the partial likelihood score test. In epidemiological applications it is often assumed that the conditional variance,
coincides exactly with the partial likelihood score test. Indeed this observation could be used to construct a characterization of the partial likelihood score test. In epidemiological applications it is often assumed that the conditional variance, 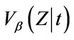 is constant through time. Otherwise time independence is often a good approximation to the true situation and gives further motivation to the partial likelihood test.
is constant through time. Otherwise time independence is often a good approximation to the true situation and gives further motivation to the partial likelihood test.
6. Multivariate Model
In practice it is the multivariate setting that we are most interested in; testing for the existence of effects in the presence of related covariates, or possibly testing the combined effects of several covariates. In this work we give very little specific attention to the multivariate setting, not because we do not feel it to be important but because the univariate extensions are almost always rather obvious and the main concepts come through more clearly in the relatively notationally uncluttered univariate case. Nonetheless, some thought is on occasion required. The basic theorem giving a consistent estimate of the distribution of the covariate at each time point t applies equally well when the covariate 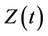 is multidimensional. Everything follows through in the same way and there is no need for additional theorems. In the multivariate case the product
is multidimensional. Everything follows through in the same way and there is no need for additional theorems. In the multivariate case the product 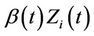 becomes a vector or inner product, a simple linear sum of the components of
becomes a vector or inner product, a simple linear sum of the components of 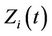 and the corresponding components of
and the corresponding components of 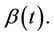 Suppose, for simplicity, that
Suppose, for simplicity, that 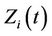 is two dimensional so that
is two dimensional so that 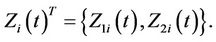 Then the
Then the 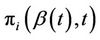 give our estimate for the joint distribution of
give our estimate for the joint distribution of 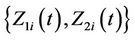 at time t. As for any multi-dimensional distribution if we wish to consider only the marginal distribution of, say,
at time t. As for any multi-dimensional distribution if we wish to consider only the marginal distribution of, say, 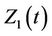 then we simply sum the
then we simply sum the 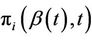 over the variable
over the variable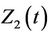 . In practice we work with the
. In practice we work with the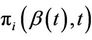 , defined to be of the highest dimension that we are interested in, for the problem in hand, and simply sum over the subsets of vector Z needed. To be completely concrete let us return to the partial scores,
, defined to be of the highest dimension that we are interested in, for the problem in hand, and simply sum over the subsets of vector Z needed. To be completely concrete let us return to the partial scores,
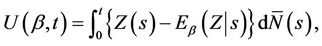 (6.1)
(6.1)
defined previously for the univariate case. Both 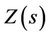 and
and 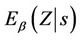 are vectors of the same dimension. So also is then
are vectors of the same dimension. So also is then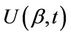 . The vector
. The vector 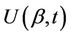 is made up of the component marginal processes any of which we may be interested in. For each marginal covariate, let’s say
is made up of the component marginal processes any of which we may be interested in. For each marginal covariate, let’s say 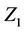 for instance, we also calculate
for instance, we also calculate 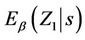 and we can do this either by first working out the marginal distribution of
and we can do this either by first working out the marginal distribution of 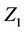 or just by summing over the joint probabilities. The result is the same and it is no doubt easier to work out all expectations with the respect to the joint distribution. Let us then write;
or just by summing over the joint probabilities. The result is the same and it is no doubt easier to work out all expectations with the respect to the joint distribution. Let us then write;
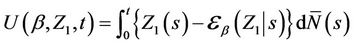 (6.2)
(6.2)
where the subscript “1” denotes the first component of the vector. The interesting thing is that  does not require any such additional notation, depending only on the joint
does not require any such additional notation, depending only on the joint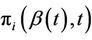 . As for the univariate case we can work with any function of the random vector Z, the expectation of the function being readily estimated by an application of an immediate generalization of Corollary 3. Note that the process we are constructing is not the same one that we would obtain were we to simply work with only
. As for the univariate case we can work with any function of the random vector Z, the expectation of the function being readily estimated by an application of an immediate generalization of Corollary 3. Note that the process we are constructing is not the same one that we would obtain were we to simply work with only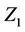 . This is because the
. This is because the 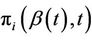 involve a univariate Z in the former case and a multivariate Z in the latter. The increments of the process
involve a univariate Z in the former case and a multivariate Z in the latter. The increments of the process 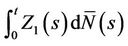 at
at 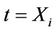 have mean
have mean 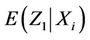 and variance
and variance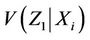 . As before, these increments can be taken to be independent [16,17] so that only the existence of the variance is necessary to be able to appeal to the functional central limit theorem. This observed process will also be treated as though arising from a Brownian motion process. The same calculations as above allow us to also work with the Brownian bridge, integrated Brownian motion and reflected Brownian motion. Our development is entirely analogous to that for the univariate case and we consider now the process
. As before, these increments can be taken to be independent [16,17] so that only the existence of the variance is necessary to be able to appeal to the functional central limit theorem. This observed process will also be treated as though arising from a Brownian motion process. The same calculations as above allow us to also work with the Brownian bridge, integrated Brownian motion and reflected Brownian motion. Our development is entirely analogous to that for the univariate case and we consider now the process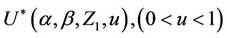 , in which
, in which
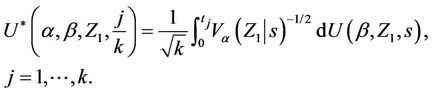
where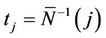 . This process is only defined on k equispaced points of the interval (0, 1] and, again, we extend our definition to the whole interval so that, for
. This process is only defined on k equispaced points of the interval (0, 1] and, again, we extend our definition to the whole interval so that, for 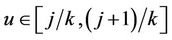 we can write
we can write 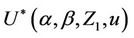 as;
as;
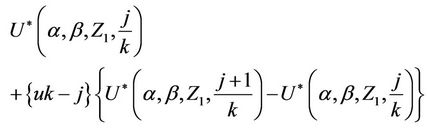
As n goes to infinity, under the usual Breslow and Crowley conditions [17], then we have that, for each j (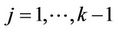 ),
),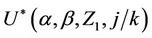 converges in distribution to a Gaussian process with mean zero and variance equal to
converges in distribution to a Gaussian process with mean zero and variance equal to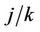 . This follows in the same way as for the univariate case, directly from Donsker’s theorem. Replacing
. This follows in the same way as for the univariate case, directly from Donsker’s theorem. Replacing 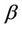 by a consistent estimate leaves asymptotic properties unaltered.
by a consistent estimate leaves asymptotic properties unaltered.
6.1. Some Further Remarks on the Notation
The notation 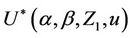 is a little heavy but becomes even heavier if we wish to treat the situation in great generality. The first component of Z is
is a little heavy but becomes even heavier if we wish to treat the situation in great generality. The first component of Z is 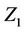 but of course this could be any component. Indeed
but of course this could be any component. Indeed 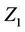 can itself be a vector, some collection of components of Z and, once we see the basic idea, it is clear what to do even though the notation starts to become slightly cumbersome. As for the notation,
can itself be a vector, some collection of components of Z and, once we see the basic idea, it is clear what to do even though the notation starts to become slightly cumbersome. As for the notation,  , in which there is only one Z and no need to specify it, the * symbol continues to indicate standardization by the variance and number of failure points. For the multivariate situation, the two parameters,
, in which there is only one Z and no need to specify it, the * symbol continues to indicate standardization by the variance and number of failure points. For the multivariate situation, the two parameters, 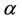 and
and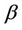 , are themselves, both vectors. The parameter
, are themselves, both vectors. The parameter 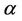 which indexes the variance will be, in practice, the estimated full vector
which indexes the variance will be, in practice, the estimated full vector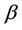 , i.e.,
, i.e., 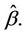 Note that, as for the process
Note that, as for the process 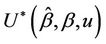 we use, for the first argument to this function, the unrestricted estimate. Exactly the same applies here. In the numerator however, under some hypothesis for
we use, for the first argument to this function, the unrestricted estimate. Exactly the same applies here. In the numerator however, under some hypothesis for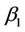 , say
, say 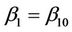 then, for the increments
then, for the increments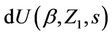 , we would have
, we would have  fixed at
fixed at 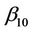 and the other components of the vector
and the other components of the vector 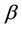 replaced by their restricted estimates, i.e., zeros of the estimating equations in which
replaced by their restricted estimates, i.e., zeros of the estimating equations in which 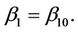
6.2. Some Properties of 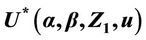
The same range of possible tests as before can be based upon the statistic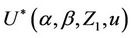 . To support this it is worth noting:
. To support this it is worth noting:
Lemma 7. The process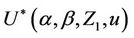 , for all finite
, for all finite 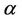 and
and 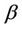 is continuous on [0, 1]. Also
is continuous on [0, 1]. Also 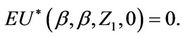
Lemma 8. Under model 2 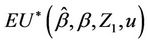 converges in probability to zero.
converges in probability to zero.
Lemma 9. Suppose that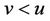 , then
, then

converges in probability to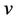 .
.
Since the increments of the process are asymptotically independent we can treat 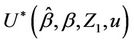 (as well as
(as well as  under some hypothesized
under some hypothesized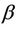 ) as though it were Brownian motion.
) as though it were Brownian motion.
6.3. Tests in the Multivariate Setting
When we carry out a test of 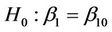 it is important to keep in mind the alternative hypothesis which is, usually,
it is important to keep in mind the alternative hypothesis which is, usually, 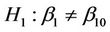 together with
together with 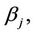
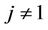 unspecified. Such a test can be carried out using
unspecified. Such a test can be carried out using 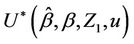 where, for the second argument
where, for the second argument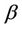 , the component
, the component  is replaced by
is replaced by 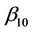 and the other components by estimates with the constraint that
and the other components by estimates with the constraint that 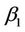 is fixed at
is fixed at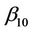 . Assuming our model is correct, or a good enough approximation, then we are testing for the effects of
. Assuming our model is correct, or a good enough approximation, then we are testing for the effects of 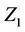 having “accounted for” the effects of the other covariates. The somewhat imprecise notion “having accounted for” is made precise in the context of a model. It is not of course the same test as that based on a model with only
having “accounted for” the effects of the other covariates. The somewhat imprecise notion “having accounted for” is made precise in the context of a model. It is not of course the same test as that based on a model with only 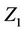 included as a covariate.
included as a covariate.
Another situation of interest in the multivariate setting is one where we wish to test simultaneously for more than one effect. This situation can come under one of two headings. The first, analogous to an analysis of variance, is where we wish to see if there exists any effect without being particularly concerned about which component or components of the vector Z may be causing the effect. As for an analysis of variance if we reject the global null we would probably wish to investigate further to determine which of the components appears to be the cause. The second is where we use, for the sake of argument, two covariates to represent a single entity, for instance 3 levels of treatment. Testing for whether or not treatment has an impact would require us to simultaneously consider the two covariates defining the groups. We would then consider, for a two variable model, 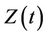 is a vector with components
is a vector with components 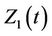 and
and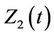 , step functions with discontinuities at the points
, step functions with discontinuities at the points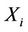 ,
, 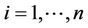 , where they take the values
, where they take the values 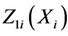 and
and 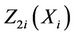 respectively. For this two dimensional case we consider the increments in the process
respectively. For this two dimensional case we consider the increments in the process

at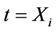 , having mean
, having mean

and variance
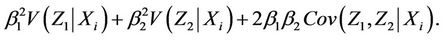
The remaining steps now follow through just as in the one dimensional case, 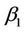 and
and 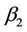 being replaced by
being replaced by 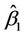 and
and 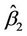 respectively, and the conditional expectations, variances and covariances being replaced using analogous results to Corollaries 3 and 4.
respectively, and the conditional expectations, variances and covariances being replaced using analogous results to Corollaries 3 and 4.
7. An Example
The classical example studied in Cox’s famous 1972 paper [3] concerning the two sample problem in a clinical trial in leukemia has been re-examined by several authors and we reconsider those data in the light of the work here. Our development sidesteps the issue of ties, a problem of sufficient importance for the Freireich data that it warranted lengthy discussion in Cox’s paper. Here we simply used a random split, although all of the suggested approaches for dealing with ties (see for example Kalbfleisch and Prentice [13] are accommodated without any additional difficulty. The distance from the origin at the maximum follow up time was equal to 3.92 (p < 0.001), a result which is to be anticipated since the proportional hazards assumption is known to be a good one for these data, and effects are strong. The partial likelyhood test produced the figure 3.94, confirming, at least here, the agreement we would expect given that the estimated conditional variance of the covariate given time is fairly constant with time itself. If the process is reflected at the time point t = 12, roughly the marginal median, then we obtain the value 0.58 which is what we might well expect. On the other hand if we use the reflected process, maximized across all potential times, then we obtain, again, a p-value less than 0.001 suggesting that little has been sacrificed by this more general approach even when the proportional hazards assumption appears well founded.