Optimal Estimation of High-Dimensional Covariance Matrices with Missing and Noisy Data

Meiyin Wang, Wanzhou Ye

Department of Mathematics, College of Science, Shanghai University, Shanghai, China.

DOI: 10.4236/apm.2024.144013                

Abstract

The estimation of covariance matrices is very important in many fields, such as statistics. In real applications, data are frequently influenced by high dimensions and noise. However, most relevant studies are based on complete data. This paper studies the optimal estimation of high-dimensional covariance matrices based on missing and noisy sample under the norm. First, the model with sub-Gaussian additive noise is presented. The generalized sample covariance is then modified to define a hard thresholding estimator , and the minimax upper bound is derived. After that, the minimax lower bound is derived, and it is concluded that the estimator presented in this article is rate-optimal. Finally, numerical simulation analysis is performed. The result shows that for missing samples with sub-Gaussian noise, if the true covariance matrix is sparse, the hard thresholding estimator outperforms the traditional estimate method.

Keywords

High-Dimensional Covariance Matrix, Missing Data, Sub-Gaussian Noise, Optimal Estimation

1. Introduction

The covariance matrix is a key component in various fields, particularly statistics. However, when dealing with many statistical situations, the covariance matrix is usually unknown. As a result, estimating the covariance matrix is extremely significant, and it is frequently utilized in signal processing, genomics, financial mathematics, and other domains. When the dimension p is fixed and the sample size n is sufficiently large, the sample covariance matrix is commonly used to estimate the true covariance matrix. However, with advancements in information technology and various other technologies, there is a growing challenge in estimating large covariance matrices. Issues such as dimensionality and noise can significantly impact the effectiveness of using the sample covariance matrix to estimate the true covariance matrix. Moreover, in the era of big data, missing data is a common occurrence, making research on the estimation of high-dimensional covariance matrices based on missing and noisy data essential.

Bickel and Levina [1] proposed thresholding as a commonly used method for estimating high-dimensional covariance matrices and and proved its consistency under the operator norm. However, there was no discussion on its optimality. Cai and Zhou studied the optimal estimation of sparse covariance matrices under the operator norm and Bregman divergence loss. They also proved that the thresholding estimator can achieve the optimal convergence rate under the spectral norm, see [2] . Cai and Zhou [3] provided the optimal estimation of the sparse covariance matrices under the $l_1$ norm loss. The thresholding described above is also referred to as hard thresholding, and its counterpart is soft thresholding [4] [5] . On this basis, Rothman, Levina, and Zhu [6] proposed generalized thresholding and proved its consistency. Cai and Liu [7] proposed adaptive thresholding. The adaptive estimation of high-dimensional sparse precision matrices was studied by Cai, Liu, and Zhou [8] . For bandable covariance matrices, [3] , [9] , and [10] conducted in-depth research.

In the case of missing data, Cai and Zhang [11] assumed that the missingness was independent of the data values and studied the optimal estimation of two classes of covariance matrices. Qi [12] explored the optimal estimation of sparse covariance matrices under the $l_1$ norm and the Fribenius norm, respectively. In addition, the lower bound for estimating bandable covariance matrices under the spectral norm was studied based on noisy and missing data, but its optimality is not considered. Shi [13] studied the optimal estimation of bandable covariance matrices based on missing and noisy sample data.

It is not difficult to find that the research on estimating high-dimensional covariance matrices is primarily based on complete data. However, the correlational research on missing data and noisy models remains critical. The articles listed above served as a tremendous source of inspiration for this paper’s study topic and methods. This paper will provide corresponding research for the aforementioned issues. Sparse covariance matrices are widely employed in a variety of applications, including genomics. As a result, it is necessary to investigate the estimate of this kind of covariance matrix. The research in this paper can help people better estimate the high-dimensional covariance matrix when the sample is noisy and missing. Thus, it is convenient for many fields to better use high-dimensional data to obtain more useful information, and this paper provides them with a reliable theoretical basis.

The remaining sections of this paper are as follows: Section 2 will provide the associated concepts and knowledge of covariance matrix estimation, which serves as the theoretical foundation for the research. In Section 3, we will study the optimal estimation of sparse covariance matrices with missing and noisy data. In Section 4, numerical simulation experiment will be performed to investigate the estimating effect of the estimator presented in Section 3. The fifth section summarizes the research content and discusses existing problems.

2. Theoretical Basis

This paper will primarily study the optimal estimation of covariance matrices under the $l_1$ norm. For a matrix $A=\left(a_{ij}\right)\in {ℝ}^{m\times n}$ , $\sigma \left(A\right)=\sqrt{\lambda \left(A^{H}A\right)}$ represents the singular values of $A$ , while $\lambda \left(A^{H}A\right)$ represents the eigenvalues of $A^{H}A$ . The operator norm of $A$ is defined as

${\Vert A\Vert }_a=\underset{{\Vert x\Vert }_a=1,x\in {ℝ}^n}{\max }{\Vert Ax\Vert }_a=\underset{x\ne 0,x\in {ℝ}^n}{\max }\frac{{\Vert Ax\Vert }_a}{{\Vert x\Vert }_a}$

There are three common operator norms:

(1) $l_1$ norm: ${\Vert A\Vert }_{l_1}={\Vert A\Vert }_1=\underset{1\le j\le n}{\max }{\displaystyle \underset{i=1}{\overset{m}{\sum }}\left|a_{ij}\right|}$ ;

(2) spectral norm: ${\Vert A\Vert }_{sp}={\Vert A\Vert }_2={\sigma }_1\left(A\right)={\max }_i{\sigma }_i\left(A\right)$ ;

(3) $l_{\infty }$ norm: ${\Vert A\Vert }_{\infty }=\underset{1\le i\le m}{\max }{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|a_{ij}\right|}$ .

Next, we will introduce the sub-Gaussian random vector. If there is a parameter $k>0$ such that $\mathbb{E}\left(e^{sX}\right)\le e^{k^2{s}^2/2},s\in ℝ$ , the random variable $X$ is considered a sub-Gaussian random variable with parameter $k$ , that is, $X\sim Sub\left(k\right)$ . It is easy to know that sub-Gaussian random variables include Gaussian random variables whose mean is 0 and all bounded random variables with a mean of 0. Assuming the random variable $X$ is sub-Gaussian, its sub-Gaussian norm is denoted by

${\Vert X\Vert }_{{\psi }_2}=\underset{p\ge 1}{\sup }{p}^{-1/2}{\left(\mathbb{E}{\left|X\right|}^p\right)}^{1/p}\text{.}$

A p-dimensional random vector $X={\left(X_1,X_2,\cdots X_p\right)}^T$ is called the sub-Gaussian random vector if any linear combination of $X_1,X_2,\cdots X_p$ is sub-Gaussian. That is, when $\tau >0$ , for any $t>0$ , $v\in {ℝ}^p$ , and ${\Vert v\Vert }_2=1$ , there is

$P\left\{\left|v^T\left({\rm X}-\mathbb{E}{\rm X}\right)\right|>t\right\}\le e^{-t^2/2\tau }.$

Assume that a p-dimensional random vector ${\rm X}\in {ℝ}^p$ has the mean $\mu$ and the covariance matrix $\Sigma$ . Covariance matrix estimation is the process of computing a covariance matrix $\hat{\Sigma }$ based on $n$ independent copies ${{\rm X}}_1,{{\rm X}}_2,\cdots {{\rm X}}_n\in {ℝ}^p$ of ${\rm X}$ and then using $\hat{\Sigma }$ to estimate $\Sigma$ , i.e., making $\hat{\Sigma }$ approximate $\Sigma$ in a certain sense. In this paper, minimax risk is used as a standard to measure the estimation effect. Suppose ${{\rm X}}_1$ has a certain class of covariance matrices, and $\mathcal{A}$ is a specific collection of ${{\rm X}}_1$ ’s distributions. Then, under the specified matrix norm $\Vert \cdot \Vert$ , [3] defines the minimax risk of estimating $\Sigma$ over $\mathcal{A}$ as

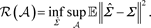
When the vector’s dimension $p$ is smaller than the sample size $n$ , the sample covariance matrix is typically utilized to estimate the true covariance matrix. The sample mean is

$\overline{{\rm X}}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{{\rm X}}_i},$

and the sample covariance matrix is

$\hat{\Sigma }={\left({\hat{\sigma }}_{ij}\right)}_{p\times p}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left({{\rm X}}_i-\overline{{\rm X}}\right)}{\left({{\rm X}}_i-\overline{{\rm X}}\right)}^T.$ (1)

However, as noted in Section 1, when the dimension $p$ is substantially larger than the sample size $n$ , utilizing the sample covariance matrix for estimating the true covariance matrix becomes inadequate. Based on the work of Cai et al., this paper will study the optimal estimation of high-dimensional covariance matrices based on missing and noisy data.

The missing completely at random (MCR) model is introduced below.MCR indicates that the missingness was random and independent of the data values. Suppose $\left\{{{\rm X}}_1,{{\rm X}}_2,\cdots {{\rm X}}_n\right\}$ is complete random sample from ${\rm X}$ . Introducing vector $S_k={\left\{0,1\right\}}^p,k=1,2,\cdots n$ as the observation index for ${{\rm X}}_k$ , then

$S_{jk}=\{\begin{array}{ll}1,\hfill & X_{jk}\text{isobserved},\hfill \\ 0,\hfill & X_{jk}\text{ismissing}.\hfill \end{array}$

$S_{jk}$ and $X_{jk}$ represent the $j$ th coordinate of vectors ${{\rm X}}_k$ and $S_k$ , respectively.

We denote ${{\rm X}}^{*}=\left\{{{\rm X}}_1^{*},{{\rm X}}_2^{*},\cdots ,{{\rm X}}_n^{*}\right\}$ as the sample with missing data, where ${{\rm X}}_i^{*}={\left(X_{1i}{S}_{1i},X_{2i}{S}_{2i},\cdots ,X_{pi}{S}_{pi}\right)}^T$ is the $i$ th observation sample. Additionally, define

$n_{ij}^{*}:={\displaystyle \underset{k=1}{\overset{n}{\sum }}{S}_{ik}{S}_{jk}},\text{1}\le i,j\le p.$

When $S_{ik}{S}_{jk}=1$ , the $i$ th and $j$ th components of vector ${{\rm X}}_k^{*}$ are observed simultaneously, whereas $S_{ik}{S}_{jk}=0$ indicates that they were not observed simultaneously. Thus, $n_{ij}^{*}$ denotes the number of times the $i$ th and $j$ th components of ${{\rm X}}^{*}$ are simultaneously observed. For convenience, let’s define

$n_i^{*}=n_{ii}^{*}$ , $n_{\min }^{*}=\underset{i,j}{\min }{n}_{ij}^{*}$ . It is simple to know that $n_{\min }^{*}\le n_{ij}^{*}\le \min \left\{n_i^{*},n_j^{*}\right\}$ . When the sample data are complete, $n_{ij}^{*}\equiv n$ .

For sample ${{\rm X}}^{*}$ with missing data, we substitute the generalized sample mean and generalized sample covariance matrix for the traditional sample mean and covariance matrix. The generalized sample mean is defined as the following:

${\overline{{\rm X}}}^{*}:={\left({\overline{{\rm X}}}_i^{*}\right)}_{1\le i\le p},{\overline{{\rm X}}}_i^{*}=\frac{1}{n_i^{*}}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{{\rm X}}_{ik}^{*}}=\frac{1}{n_i^{*}}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{{\rm X}}_{ik}}{S}_{ik},$

the generalized sample covariance matrix is defined as

${\hat{\Sigma }}^{*}:={\left({\hat{\sigma }}_{ij}^{*}\right)}_{1\le i,j\le p},{\hat{\sigma }}_{ij}^{*}=\frac{1}{n_{ij}^{*}}{\displaystyle \underset{k=1}{\overset{n}{\sum }}\left({{\rm X}}_{ik}-{\overline{{\rm X}}}_i^{*}\right)}\left({{\rm X}}_{jk}-{\overline{{\rm X}}}_j^{*}\right)S_{ik}{S}_{jk}.$ (2)

3. Covariance Matrix estimation

This paper assumes that the covariance matrix is sparse, which means that the majority of its components are 0 or insignificant, and the distribution of non-zero elements is irregular. First, we introduce the parameter space ${\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ of the sparse covariance matrices:

${\mathcal{G}}_q(\rho ,c_{n,p})=\left\{\Sigma ={\left({\sigma }_{ij}\right)}_{1\le i,j\le p}:\underset{1\le j\le p}{\max }\left\{{\left|{\sigma }_{[k]j}\right|}^q\right\}\le \frac{c_{n,p}}{k},\forall k，\max {\sigma }_{ii}\le \rho \right\}$ ,

where $0\le q<1$ , and ${\sigma }_{[k]j}$ represents the element with the $k$ th largest absolute value in the $j$ th column of matrix $\Sigma$ . When $q=0$ , each column of the matrices in ${\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ has at most $c_{n,p}$ non-zero components, usually assuming $c_{n,p}\ge 1$ .

3.1. Noisy Model

Assuming the complete random vector ${\rm X}\in {ℝ}^p$ has the covariance matrix ${\Sigma }_X={\left({\hat{\sigma }}_{ij}\right)}_{p\times p}$ . Using a $p$ -dimensional random vector $F$ to represent noisy data, the noisy model can be expressed as

$F=X+\epsilon ,$ (3)

where $\epsilon \in {ℝ}^p$ represents noise. In this section, we hope to build a $p\times p$ matrix ${\hat{\Sigma }}_F$ based on $n$ independent random noisy samples $F_1,F_2,\cdots F_n\in {ℝ}^p$ of $F$ . We next use ${\hat{\Sigma }}_F$ to estimate the covariance matrix ${\Sigma }_X$ of the random vector $X$ .

The noisy sample with missing data are represented by $F^{*}=\left\{F_1^{*},F_2^{*},\cdots ,F_n^{*}\right\}$ , where $F_i^{*}={\left(F_{1i}{S}_{1i},F_{2i}{S}_{2i},\cdots ,F_{pi}{S}_{pi}\right)}^T$ is the $i$ th observation sample. The definition of the generalized sample mean is as follows:

${\bar{F}}^{*}:={\left({\bar{F}}_i^{*}\right)}_{1\le i\le p},{\bar{F}}_i^{*}=\frac{1}{n_i^{*}}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{F}_{ik}^{*}}=\frac{1}{n_i^{*}}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{F}_{ik}}{S}_{ik},$

the generalized sample covariance matrix is defined as

${\hat{\Sigma }}_F^{\ast }:={\left({\hat{\sigma }}_{ij}^{*}\left(F\right)\right)}_{1\le i,j\le p},{\hat{\sigma }}_{ij}^{*}\left(F\right)=\frac{1}{n_{ij}^{*}}{\displaystyle \underset{k=1}{\overset{n}{\sum }}\left(F_{ik}-{\bar{F}}_i^{*}\right)\left(F_{jk}-{\bar{F}}_j^{*}\right)}{S}_{ik}{S}_{jk}.$ (4)

Two new assumptions in [12] are presented below.

Assumption 1. The observation index $S:=\left\{S_1,S_2,\cdots S_n\right\}$ can be random or deterministic, but it is independent of the noisy observation sample $F:=\left\{F_1,F_2,\cdots F_n\right\}$ .

Assumption 2. The random vectors $F_1,F_2,\cdots F_n$ are i.i.d., where $F_k=X_k+{\epsilon }_k$ , and

$X_k=\Gamma Z_k+\mu ,{\epsilon }_k={\Gamma }^{\epsilon }{Z}_k\text{,}k=1,2,\cdots n.$

$\mu$ represents a fixed $p$ -dimensional mean vector. $\Gamma \text{,}{\Gamma }^{\epsilon }\in {ℝ}^{p\times q}\left(p\le q\right)$ are fixed matrices with $\Gamma {\Gamma }^T=\Sigma$ and ${\Gamma }^{\epsilon }{\Gamma }^{\epsilon }{}^T={\Sigma }^{\epsilon }$ . Each component of the random vector $Z_k={\left(Z_{1k},Z_{2k},\cdots ,Z_{qk}\right)}^T$ i.i.d. sub-Gaussian with a variance of 1 and a mean of 0. For any $s>0$ , there exists a parameter $\tau >0$ such that $\mathbb{E}\left(e^{s{Z}_{ik}}\right)\le e^{\tau s^2/2}$ , that is, $Z_{ik}\sim Sub\left(\tau \right)$ .

3.2. Upper Bound for Estimating Sparse Covariance Matrix

The hard thresholding estimator based on complete data was proposed by [1] . When most of the elements in each row or column of the true covariance matrix are close to zero or negligible, set the elements of the sample covariance matrix below a certain threshold to 0, and leave the remaining elements unaltered to estimate the true covariance matrix, so as to reduce the error. In [2] ,

$P\left\{\left|{\hat{\sigma }}_{ij}-{\sigma }_{ij}\right|\le t\right\}\ge 1-C{p}^{-8}$

for $t=\gamma \sqrt{\log p/n}$ , where $C$ is a constant. The threshold is set to $\gamma \sqrt{\log p/n}$ .

In this paper, it is extended to the case of missing and noisy data. According to Lemma 4.6 in [12] , if Assumption 1 and Assumption 2 are both hold, then there are two absolute constants $C$ and $c$ greater than 0, such that

$P\left\{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|\le x\right\}\ge 1-C\exp \left\{-c{n}_{\min }^{\ast }\min \left(\frac{x^2}{{\tau }^4{\sigma }_{ii}{\sigma }_{jj}},\frac{x}{{\tau }^2\sqrt{{\sigma }_{ii}{\sigma }_{jj}}}\right)\right\}$ (5)

for any $x>0$ . Since ${\sigma }_{ii}{\sigma }_{jj}\le {\rho }^2$ , the above can be simplified to: there are constants $C>0$ and $\gamma >0$ , such that

$P\left\{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|\le x\right\}\ge 1-C\exp \left(-\frac{8}{{\gamma }^2}{n}_{\min }^{*}{x}^2\right).$ (6)

Where $x\le \rho$ , and the constants $C$ and $\gamma$ only depend on $\rho$ . Note that Inequality can be written as $P\left\{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|\le x\right\}\ge 1-C{p}^{-8}$ when $x=\gamma \sqrt{\log p/n_{\min }^{*}}$ .

The hard thresholding estimator ${\hat{\Sigma }}_F^{th}$ of the covariance matrices ${\Sigma }_X\in {\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ is defined by transforming the generalized sample covariance ${\hat{\sigma }}_{ij}^{*}\left(F\right)$ in Equation (4),

${\hat{\Sigma }}_F^{th}={\left({\hat{\sigma }}_{ij}^{th}\left(F\right)\right)}_{p\times p}={\left({\hat{\sigma }}_{ij}^{*}\left(F\right)\cdot I\left(\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)\right|\ge \lambda \right)\right)}_{p\times p},\lambda =\gamma \sqrt{\frac{\log p}{n_{\min }^{*}}},$ (7)

where $\gamma$ is a constant and $\gamma >0$ .

The following is Lemma 1, which plays an important role in studying the minimax upper bound. Lemma 1 generalizes Lemma 8 in [8] from complete to noisy and missing sample.

Lemma 1. Define event $A_{ij}:=\left\{\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|>4\min \left(\left|{\sigma }_{ij}\right|,\lambda =\gamma \sqrt{\log p/n_{\min }^{*}}\right)\right\}$ , then there is constant $c>0$ , which only depends on $\rho$ , such that

$P\left\{A_{ij}\right\}\le 2c{p}^{-\frac{9}{2}}.$

Proof : Firstly, define event $B_1:=\left\{\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)\right|\ge \lambda \right\}$ . It is easy to know that

$\begin{array}{l}{B}_1\subset \left\{\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|\ge \left|{\hat{\sigma }}_{ij}^{th}\left(F\right)\right|-\left|{\sigma }_{ij}\right|\ge \lambda -\left|{\sigma }_{ij}\right|\right\},\\ B_1^c\subset \left\{\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|\ge \left|{\sigma }_{ij}\right|-\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)\right|>\left|{\sigma }_{ij}\right|-\lambda \right\}.\end{array}$ (8)

According to the definition of ${\hat{\sigma }}_{ij}^{th}\left(F\right)$ in Equation (7),

$\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|=\left|{\hat{\sigma }}_{ij}^{\ast }\left(F\right)-{\sigma }_{ij}\right|I\left(B_1\right)+\left|{\sigma }_{ij}\right|I\left(B_1^c\right).$ (9)

Next, we will prove this lemma in different cases. It can be obtained by simple calculation:

$P\left\{\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|\le 4\min \left(\left|{\sigma }_{ij}\right|,\lambda \right)\right\}\{\begin{array}{ll}\ge 1-C{p}^{-9/2},\hfill & \left|{\sigma }_{ij}\right|<\lambda /4,\hfill \\ \ge 1-C{p}^{-8},\hfill & \lambda /4\le \left|{\sigma }_{ij}\right|\le 2\lambda ,\hfill \\ \ge 1-2C{p}^{-8}\hfill & \left|{\sigma }_{ij}\right|>2\lambda .\hfill \end{array}$

Therefore, there exists a constant $c>0$ , such that

$P\left\{\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|>4\min \left(\left|{\sigma }_{ij}\right|,\lambda \right)\right\}\le 2c{p}^{-9/2}$ .

Next, we can obtain the upper bound for estimating the sparse covariance matrices by utilizing the risk properties of thresholding estimator.

Theorem 1. If Assumption 1 and Assumption 2 hold, $\log p=o\left(\sqrt{n_{\min }^{*}}\right)$ and $p\ge \sqrt{n_{\min }^{*}}$ , then there is a constant $C>0$ such that the hard thresholding estimator ${\hat{\Sigma }}_F^{th}$ defined by Equation (7) satisfies

$\underset{{\Sigma }_X\in {\mathcal{G}}_q(\rho ,c_{n,p})}{\sup }\mathbb{E}{\Vert {\hat{\Sigma }}_F^{th}-{\Sigma }_X\Vert }_1^2\le C{c}_{n,p}^2{\left(\frac{\log p}{n_{\min }^{*}}\right)}^{1-q}.$ (10)

Proof: Easy to know, ${\Vert {\hat{\Sigma }}_F^{th}-{\Sigma }_X\Vert }_1^2={\left[\underset{j}{\max }{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|}\right]}^2$ . If event $A_{ij}$ occurs,

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|}>{\displaystyle \underset{i=1}{\overset{p}{\sum }}4\min \left(\left|{\sigma }_{ij}\right|,\lambda \right)}.$

Simple calculations show that

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\min \left(\left|{\sigma }_{ij}\right|,\lambda \right)=\left(\underset{i\le k^{\prime }}{\sum }+\underset{i>k^{\prime }}{\sum }\right)}\min \left(\left|{\sigma }_{ij}\right|,\lambda \right)\le \left(\underset{i\le k^{\prime }}{\sum }+\underset{i>k^{\prime }}{\sum }\right)\min \left(\left|{\sigma }_{[i]j}\right|,\gamma \sqrt{\frac{\log p}{n_{\min }^{*}}}\right).$

According to the definition of ${\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ , we know that $\underset{1\le j\le p}{\max }\left\{{\left|{\sigma }_{[i]j}\right|}^q\right\}\le c_{n,p}/i$ , so $\left|{\sigma }_{[i]j}\right|\le {\left(c_{n,p}/i\right)}^{1/q}$ . Select the constant $k^{\prime }$ to satisfy $k^{\prime }=\lfloor c_{n,p}{\left(n_{\min }^{*}/\log p\right)}^{q/2}\rfloor$ , so

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\min \left(\left|{\sigma }_{ij}\right|,\lambda \right)}\le {\displaystyle \underset{i\le k^{\prime }}{\sum }\min \left({\left(\frac{c_{n,p}}{i}\right)}^{\frac{1}{q}},\gamma \sqrt{\frac{\log p}{n_{\min }^{*}}}\right)}+{\displaystyle \underset{i>k^{\prime }}{\sum }\min \left({\left(\frac{c_{n,p}}{i}\right)}^{\frac{1}{q}},\gamma \sqrt{\frac{\log p}{n_{\min }^{*}}}\right)}\\ \le k^{\prime }\gamma \sqrt{\frac{\log p}{n_{\min }^{*}}}+{\displaystyle \underset{i>k^{\prime }}{\sum }{\left(\frac{c_{n,p}}{i}\right)}^{\frac{1}{q}}}\le C_1{c}_{n,p}{\left(\frac{\log p}{n_{\min }^{*}}\right)}^{\frac{1-q}{2}}.\end{array}$

Let the matrix $D={\left(d_{ij}\right)}_{p\times p}$ satisfy $d_{ij}=\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right|I\left(A_{ij}\right)$ , we have

$\mathbb{E}{\Vert {\hat{\Sigma }}_F^{th}-{\Sigma }_X\Vert }_1^2\le 2\mathbb{E}{\Vert {\hat{\Sigma }}_F^{th}-{\Sigma }_X-D\Vert }_1^2+2\mathbb{E}{\Vert D\Vert }_1^2.$

Then, it is straightforward to acquire

$\begin{array}{l}2\mathbb{E}{\Vert {\hat{\Sigma }}_F^{th}-{\Sigma }_X-D\Vert }_1^2=2\mathbb{E}{\left[\underset{j}{\max }{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|{\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}-\left({\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right)I\left(A_{ij}\right)\right|}\right]}^2\\ \le 2\mathbb{E}{\left[\underset{j}{\max }{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|\left({\hat{\sigma }}_{ij}^{th}\left(F\right)-{\sigma }_{ij}\right)I\left(A_{ij}^c\right)\right|}\right]}^2\le C_2{c}_{n,p}^2{\left(\frac{\log p}{n_{\min }^{*}}\right)}^{1-q}.\end{array}$

Therefore, we only need to prove that $2\mathbb{E}{\Vert D\Vert }_1^2$ is negligible.

Firstly,

$\begin{array}{l}\mathbb{E}{\Vert D\Vert }_1^2=\mathbb{E}{\left[\underset{j}{\max }{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|d_{ij}\right|}\right]}^2\le p^2\mathbb{E}{\left(\underset{i,j}{\max }{d}_{ij}\right)}^2\\ =p^2\mathbb{E}\left[\left(\underset{i,j}{\max }{d}_{ij}^2\right)I\left(A_{ij}\cap \left\{\left|{\hat{\sigma }}_{ij}^{*}(F)\right|\ge \lambda \right\}\right)\right]+p^2\mathbb{E}\left[\left(\underset{i,j}{\max }{d}_{ij}^2\right)I\left(A_{ij}\cap \left\{\left|{\hat{\sigma }}_{ij}^{*}(F)\right|<\lambda \right\}\right)\right]\\ \le p^2\mathbb{E}\left[{\left(\underset{i,j}{\max }\left|{\hat{\sigma }}_{ij}^{*}(F)-{\sigma }_{ij}\right|\right)}^{2}I\left(A_{ij}\right)\right]+p^2\mathbb{E}\left[{\left(\underset{i,j}{\max }\left|{\sigma }_{ij}\right|\right)}^{2}I\left(A_{ij}\right)\right]\\ =E_1+E_2.\end{array}$

According to the Cauchy-Schwartz inequality, we know that ${\left|{\sigma }_{ij}\right|}^2\le {\sigma }_{ii}{\sigma }_{jj}$ , and because $P\left\{A_{ij}\right\}\le 2c{p}^{-9/2}$ , $p\ge \sqrt{n_{\min }^{*}}$ , so

$E_2\le p^2\mathbb{E}\left(\underset{i,j}{\max }{\sigma }_{ii}{\sigma }_{jj}\right)P\left(A_{ij}\right)\le p^2{\rho }^{2}2c{p}^{-\frac{9}{2}}\le C_3{p}^{-\frac{5}{2}}\le \frac{C_4}{n_{\min }^{*}}.$

In addition, $E_1\le p^2\underset{i,j}{\max }\mathbb{E}{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|}^{2}P\left(A_{ij}\right)$ . From Inequality (5),

$\begin{array}{l}\mathbb{E}{\left|{\hat{\sigma }}_{ij}^{*}(F)-{\sigma }_{ij}\right|}^2={\displaystyle \int {\left|{\hat{\sigma }}_{ij}^{*}(F)-{\sigma }_{ij}\right|}^{2}dP}\le {\displaystyle {\int }_0^{\infty }xP\left\{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|\ge x\right\}dx}\\ \le {\displaystyle {\int }_0^{\rho }xP\left\{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|\ge x\right\}dx}+{\displaystyle {\int }_{\rho }^{\infty }xP\left\{\left|{\hat{\sigma }}_{ij}^{*}\left(F\right)-{\sigma }_{ij}\right|\ge x\right\}dx}\\ \le {\rho }^2+{\displaystyle {\int }_{\rho }^{\infty }x\exp \left(-C_5{n}_{\min }^{\ast }\frac{x}{\rho }\right)dx}\le {\rho }^2+\frac{{\rho }^2}{C_5{n}_{\min }^{\ast }}\exp \left(-C_5{n}_{\min }^{\ast }\right).\end{array}$

From Lemma 1, we have $P\left\{A_{ij}\right\}\le 2c{p}^{-9/2}$ and $p\ge \sqrt{n_{\min }^{*}}$ , so

$\begin{array}{l}{E}_1\le p^2\underset{i,j}{\max }\mathbb{E}{\left|{\hat{\sigma }}_{ij}^{*}(F)-{\sigma }_{ij}\right|}^{2}P\left(A_{ij}\right)\le p^2\left({\rho }^2+\frac{{\rho }^2}{C_5{n}_{\min }^{\ast }}\exp \left(-C_5{n}_{\min }^{\ast }\right)\right)2c{p}^{-9/2}\\ \le p^2{\rho }^{2}2c{p}^{-9/2}+p^2\frac{{\rho }^2}{C_5{n}_{\min }^{\ast }}\exp \left(-C_5{n}_{\min }^{\ast }\right)2c{p}^{-9/2}\\ \le \frac{C_4}{n_{\min }^{*}}+\frac{C_6}{n_{\min }^{*}}\le \frac{C_7}{n_{\min }^{*}}\end{array}$

To sum up,

$\mathbb{E}{\Vert D\Vert }_1^2\le E_1+E_2\le \frac{C_8}{n_{\min }^{*}}=O\left(\frac{1}{n_{\min }^{*}}\right)$ .

3.3. Lower Bound for Estimating Sparse Covariance Matrix

Before studying the lower bound, introduce some useful lemmas and symbols.

Lemma 2. Assume $P$ and $V$ are two probability measures, with $p$ and $v$ representing their probability density functions. The total variation distance between $P$ and $V$ is $V\left(P,V\right)=1-{\displaystyle \int \min }\left(dP,dP\right)$ . Define the total variation affinity as $\Vert P\wedge V\Vert :={\displaystyle \int \min }\left(dP,dP\right)={\displaystyle \int p\left(x\right)}\wedge v\left(x\right)dx$ . The Kullback divergence between $P$ and $V$ is expressed as $KL\left(P\Vert V\right)={\displaystyle \int p\left(x\right)}\log \left[p\left(x\right)/v\left(x\right)\right]dx$ . Thus, $\Vert P\wedge V\Vert$ and $KL\left(P\Vert V\right)$ satisfy the following inequality:

$1-\Vert P\wedge V\Vert \le \sqrt{\frac{KL\left(P\Vert V\right)}{2}}.$ (11)

Lemma 2 in [14] and Le Cam’s lemma and its corollary in [2] [12] introduced below are important tools for proving minimax lower bound.

Lemma 3 (Le Cam). Suppose $\Theta =\left\{{\theta }_0,{\theta }_1,\cdots ,{\theta }_m\right\}$ is a finite set of parameters. Let $L$ be a loss function and $l_{\min }:=\underset{1\le i\le m}{\min }\underset{t}{\inf }\left[L\left(t,{\theta }_0\right)+L\left(t,{\theta }_i\right)\right]$ , then

$\underset{\theta \in \Theta }{\sup }\mathbb{E}\left[L\left(\tilde{\theta },\theta \right)\right]\ge \frac{1}{2}{l}_{\min }\Vert P_{{\theta }_0}\wedge \bar{P}\Vert .$

$\tilde{\theta }$ is any estimator of $\theta$ based on the observed values of the probability measure $P_{\theta }\left(\theta \in \Theta \right)$ , and $\bar{P}=\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{P}_{{\theta }_i}}$ .

Lemma 4. Suppose $\tilde{\Sigma }$ be any estimator of ${\Sigma }_i$ based on the collection of probability measures $\left\{P_{{\Sigma }_0},P_{{\Sigma }_1},\cdots ,P_{{\Sigma }_m}\right\}$ . We get

$\underset{1\le i\le m}{\sup }\mathbb{E}{\Vert \tilde{\Sigma }-{\Sigma }_i\Vert }_1\ge \frac{1}{2}\Vert P_{{\Sigma }_0}\wedge \bar{P}\Vert \cdot \underset{1\le i\le m}{\inf }{\Vert {\Sigma }_i-{\Sigma }_0\Vert }_1,$

where $\bar{P}=\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{P}_{{\Sigma }_i}}$ .

Before studying the minimax risk lower bound, it is advisable to construct a matrix with all off-diagonal elements equal to 0 except the first row or column. Let $\mathcal{H}$ be the collection of $p\times p$ symmetric matrices in which exactly $k$ non-diagonal elements in the first row or column equal to 1 and all other elements are 0. Let $k=\lfloor c_{n,p}{\left(n_0/\log p\right)}^{q/2}\rfloor$ . Define

${\mathcal{G}}_0=\left\{\Sigma ={\left({\sigma }_{ij}\right)}_{1\le i,j\le p}:\Sigma =I_p或\Sigma =I_p+aH,H\in \mathcal{H}\right\},$ (12)

where $I_p$ represents the identity matrix of size $p\times p$ , $a=\sqrt{\delta \log p/n_0}$ , and $\delta$ is a constant. Assuming $\rho >1$ , $0<\delta <\min \left\{1,1/\left(4M\right)\right\}$ , it is easy to know that ${\mathcal{G}}_0\subset {\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ .

Obtaining the lower bound requires two steps. Firstly, the subset of the parameter space constructed above is selected to simplify the proof. Secondly, calculate the total variation affinity between two probability measures.

Theorem 2. Let $1\le n_0\le n_{\min }^{*}$ , $p\ge n_0^{\nu }\left(\nu >1\right)$ , and $\log p\le n_0$ . Assume $c_{n,p}\le M{\left(n_0/\log p\right)}^{\left(1-q\right)/2}$ with $0\le q<1,M>0$ . For any $1\le n_0\le n_{\min }^{*}$ , there exists a constant $c>0$ such that the minimax risk lower bound for estimating the covariance matrix ${\Sigma }_X$ satisfies

$\underset{{\tilde{\Sigma }}_F}{\inf }\underset{{\Sigma }_X\in {\mathcal{G}}_q(\rho ,c_{n,p})}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_X\Vert }_1^2\ge c{c}_{n,p}^2{\left(\frac{\log p}{n_0}\right)}^{1-q}.$ (13)

where ${\tilde{\Sigma }}_F$ is any estimator of ${\Sigma }_X$ based on noisy sample.

Proof: Assume ${\mathcal{G}}_0=\left\{{\Sigma }_0,{\Sigma }_1,\cdots ,{\Sigma }_{m^{\ast }}\right\}$ has $m^{\ast }+1$ elements, where ${\Sigma }_0$ represents the identity matrix and ${\Sigma }_i,i=1,\cdots ,m^{\ast }$ represent the non-identity matrix, then $m^{\ast }=Card\left({\mathcal{G}}_0\right)-1=C_{p-1}^k$ .

Assume that $X_l,l=1,\cdots ,n\stackrel{i.i.d.}{~}N\left(0,{\Sigma }_i\right),i=1,\cdots ,m^{\ast }$ , and the probability measure and probability density function are $P_{{\Sigma }_i}$ and $f_i$ , respectively, that is, ${\Sigma }_X\in {\mathcal{G}}_0$ . Let $F_l\stackrel{i.i.d.}{~}N\left(0,{\Sigma }_i\left(F\right)\right)$ with ${\Sigma }_i\left(F\right)={\Sigma }_i+s^2{I}_p$ and $P_{{\Sigma }_i}\left(F\right)$ is the probability measure. Since ${\mathcal{G}}_0\subset {\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ , it is easy to know that

$\underset{{\tilde{\Sigma }}_F}{\inf }\underset{{\Sigma }_X\in {\mathcal{G}}_q(\rho ,c_{n,p})}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_X\Vert }_1^2\ge \underset{{\tilde{\Sigma }}_F}{\inf }\underset{{\Sigma }_X\in {\mathcal{G}}_0}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_X\Vert }_1^2.$

Therefore, to prove Inequality (13), just prove the following Inequality:

$\underset{{\tilde{\Sigma }}_F}{\inf }\underset{{\Sigma }_X\in {\mathcal{G}}_0}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_X\Vert }_1^2\ge c{c}_{n,p}^2{\left(\frac{\log p}{n_0}\right)}^{1-q}.$ (14)

Lemma 3.3 shows that

$\underset{{\Sigma }_X\in {\mathcal{G}}_0}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-\Sigma \Vert }_1\ge \underset{1\le i\le m^{\ast }}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_i\Vert }_1\ge \frac{1}{2}\Vert P_{{\Sigma }_0}\left(F\right)\wedge \bar{P}\left(F\right)\Vert \cdot \underset{1\le i\le m^{\ast }}{\inf }{\Vert {\Sigma }_i\left(F\right)-{\Sigma }_0\left(F\right)\Vert }_1.$

Since $a=\sqrt{\delta \log p/n_0}$ and $k=\lfloor c_{n,p}{\left(n_0/\log p\right)}^{q/2}\rfloor$ , there exists a constant $c_1>0$ such that

$\begin{array}{l}\underset{1\le i\le m^{\ast }}{\inf }{\Vert {\Sigma }_i\left(F\right)-{\Sigma }_0\left(F\right)\Vert }_1=\underset{1\le i\le m^{\ast }}{\inf }{\Vert \left({\Sigma }_i+s^2{I}_p\right)-\left({\Sigma }_0+s^2{I}_p\right)\Vert }_1=\underset{1\le i\le m^{\ast }}{\inf }{\Vert aH\Vert }_1\\ =ka\ge c_{n,p}{\left(\frac{n_0}{\log p}\right)}^{q/2}\cdot \sqrt{\delta \frac{\log p}{n_0}}\ge c_1{c}_{n,p}{\left(\frac{\log p}{n_0}\right)}^{\frac{1-q}{2}}\end{array}$ (15)

Obviously, to prove Inequality (14), we only need to prove that there is a constant $c_2>0$ such that $\Vert P_{{\Sigma }_0}\left(F\right)\wedge \bar{P}\left(F\right)\Vert \ge c_2$ .

From $F_l\stackrel{i.i.d.}{~}N\left(0,{\Sigma }_i\left(F\right)\right)$ , we have

$KL\left(P_{{\Sigma }_0}\left(F\right)\Vert P_{{\Sigma }_i}\left(F\right)\right)=\frac{1}{2}\left[tr\left({\Sigma }_i^{-1}\left(F\right){\Sigma }_0\left(F\right)\right)-log\det \left({\Sigma }_i^{-1}\left(F\right){\Sigma }_0\left(F\right)\right)-p\right].$

Let $B=-aH$ , it is easy to know that ${\Sigma }_0\left(F\right)={\Sigma }_i\left(F\right)+B$ . Suppose the eigenvalues of $B{\Sigma }_i^{-1}\left(F\right)$ are ${\xi }_1,\cdots ,{\xi }_p$ , then there are

$tr\left({\Sigma }_i^{-1}\left(F\right){\Sigma }_0\left(F\right)\right)=tr\left[{\Sigma }_i^{-1}\left(F\right)\left({\Sigma }_i\left(F\right)+B\right)\right]=tr\left[I_p+B{\Sigma }_i^{-1}\left(F\right)\right]=p+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\xi }_i}.$ (16)

In addition, we can know that

$\log \det \left({\Sigma }_i^{-1}\left(F\right){\Sigma }_0\left(F\right)\right)={\displaystyle \underset{i=1}{\overset{p}{\sum }}\log \left(1+{\xi }_i\right)}=tr\left({\Sigma }_i^{-1}\left(F\right){\Sigma }_0\left(F\right)\right)-p-{\displaystyle \underset{i=1}{\overset{p}{\sum }}\frac{1}{2\left(1+\theta \right)}{\xi }_i^2},$ (17)

where $\theta$ is a number between 0 and ${\xi }_i$ . Putting Equation (16) and Equation (17) into $KL\left(P_{{\Sigma }_0}\left(F\right)\Vert P_{{\Sigma }_i}\left(F\right)\right)$ , we can get

$KL\left(P_{{\Sigma }_0}\left(F\right)\Vert P_{{\Sigma }_i}\left(F\right)\right)=\frac{1}{2}\left[p+{\displaystyle \underset{i=1}{\overset{p}{\sum }}\frac{1}{2\left(1+\theta \right)}{\xi }_i^2}-p\right]=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\frac{1}{2\left(1+\theta \right)}{\xi }_i^2}\le \frac{1}{4}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\xi }_i^2}.$

According to Theorem 1.3 in [12] ,

${\displaystyle \underset{i=1}{\overset{p}{\sum }}{\xi }_i^2}=tr\left({\left(B{\Sigma }_i^{-1}\left(F\right)\right)}^{H}B{\Sigma }_i^{-1}\left(F\right)\right)={\Vert B{\Sigma }_i^{-1}\left(F\right)\Vert }_F^2\le {\Vert {\Sigma }_i^{-1}\left(F\right)\Vert }_{sp}^2{\Vert B\Vert }_F^2\le 2k{a}^2.$

It is easy to see that $\bar{P}\left(F\right)=1/m^{\ast }{\displaystyle \underset{i=1}{\overset{m^{\ast }}{\sum }}{P}_{{\Sigma }_i}\left(F\right)}$ , hence

$KL\left(P_{{\Sigma }_0}\left(F\right)\Vert \bar{P}\left(F\right)\right)\le \frac{1}{m^{\ast }}{\displaystyle \underset{i=1}{\overset{m^{\ast }}{\sum }}KL\left(P_{{\Sigma }_0}\left(F\right)\Vert P_{{\Sigma }_i}\left(F\right)\right)}\le \frac{1}{8}.$

Lemma 2 implies

$\Vert P_{{\Sigma }_0}\left(F\right)\wedge \bar{P}\left(F\right)\Vert \ge 1-\sqrt{\frac{KL\left(P_{{\Sigma }_0}\left(F\right)\Vert \bar{P}\left(F\right)\right)}{2}}=\frac{3}{4}.$

That is, there exists a constant $c_2>0$ such that $\Vert P_{{\Sigma }_0}\left(F\right)\wedge \bar{P}\left(F\right)\Vert \ge c_2$ .

It is worth noting that Theorem 2 requires $c_{n,p}\le M{\left(n_0/\log p\right)}^{\left(1-q\right)/2}\left(M>0\right)$ , which is a necessary condition. If $c_{n,p}>M{\left(n_0/\log p\right)}^{\left(1-q\right)/2}$ , then

$\underset{{\tilde{\Sigma }}_F}{\inf }\underset{{\Sigma }_X\in {\mathcal{G}}_q\left(\rho ,c_{n,p}\right)}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_X\Vert }_1^2\ge \underset{{\tilde{\Sigma }}_F}{\inf }\underset{{\Sigma }_X\in {\mathcal{G}}_q\left(\rho ,M{\left(n_0/\log p\right)}^{\left(1-q\right)/2}\right)}{\sup }\mathbb{E}{\Vert {\tilde{\Sigma }}_F-{\Sigma }_X\Vert }_1^2\gtrsim M^2.$

${\Sigma }_X$ does not have a consistent estimator in this case.

Theorem 1 and Theorem 2 show that the estimator ${\hat{\Sigma }}_F^{th}$ we construct is rate-optimal over ${\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ under the $l_1$ norm.

4. Numerical Analysis

The optimal estimation of sparse covariance matrices based on missing and noisy data is derived in Section 3. This section compares the performance of the hard threshold estimator ${\hat{\Sigma }}_F^{th}$ , as defined in Section 3, against the traditional estimator using numerical simulation.

Some symbols are presented before the numerical simulation begins. Assume the $p$ -dimensional Gaussian random vector ${\rm X}$ has a mean of $\mu$ and a covariance matrix of ${\Sigma }_X$ . $n$ is the number of samples, and $p$ is their dimension.

Here are the specific steps of numerical simulation.

1) Construct the sparse covariance matrix.

Assume $\mu$ is a zero vector and ${\Sigma }_X$ is a sparse matrix ( ${\Sigma }_X\in {\mathcal{G}}_q\left(\rho ,c_{n,p}\right)$ ). Consult the construction of the sparse matrix in [11] , let

${\Sigma }_X=I_p+\left(B+B^T\right)/\left({\Vert B+B^T\Vert }_1+0.01\right),$

where $B={\left(b_{ij}\right)}_{p\times p}$ , and $P\left(b_{ij}=-1\right)=0.1$ , $P\left(b_{ij}=0\right)=0.8$ , $P\left(b_{ij}=1\right)=0.1$ .

2) Generate random samples according to the true covariance matrix.

After ${\Sigma }_X$ is constructed, $n$ $p$ -dimensional random samples are first generated from the multivariate normal distribution with mean $\mu$ and covariance matrix ${\Sigma }_X$ . The resulting $n$ samples are then subjected to noise with a sub-Gaussian distribution, followed by random missing processing. This method produces sample data with missing and sub-Gaussian noise.

3) Compare the estimation effect of different estimators.

Based on the sample data with missing and sub-Gaussian noise, calculate the generalized sample covariance matrix ${\hat{\Sigma }}_F^{\ast }$ and the hard thresholding estimator ${\hat{\Sigma }}_F^{th}$ according to Equation and Equation . Then compute the error between ${\hat{\Sigma }}_F^{\ast }$ and the real matrix ${\Sigma }_X$ , as well as the error between ${\hat{\Sigma }}_F^{th}$ and the real matrix ${\Sigma }_X$ , under the given norm.

After determining the values of $n$ and $p$ , repeat the above three steps 1), 2), and 3) 50 times, and take the mean value of the fifty error results as the standard for evaluating the estimation effect of different estimators in this case. The performance is better when the outcome is smaller. Table 1 shows the experimental results.

The values of $n$ and $p$ are shown in the first two columns of Table 1. Table 1 shows the average after 50 runs of the processes 1), 2), and 3) with $n$ and $p$ fixed. When the true covariance matrix ${\Sigma }_X$ is sparse, the hard thresholding estimator ${\hat{\Sigma }}_F^{th}$ has a substantially better performance than the generalized sample covariance matrix ${\hat{\Sigma }}_F^{\ast }$ under any norm, especially when $p$ is larger than $n$ , that is, the dimension is high.

Therefore, when the dimension is very small in comparison to the sample size, the sample covariance matrix can be used to estimate the population covariance matrix. When estimating a high-dimensional sparse covariance matrix with sub-Gaussian additive noise and missing data, it is best to choose the hard thresholding estimator ${\hat{\Sigma }}_F^{th}$ given in Equation (7). This section provides some suggestions for application statisticians on how to select estimation methods.

Table 1. Results of estimating sparse covariance matrix.

5. Summary and Outlook

In statistics and other fields, covariance matrix estimation is crucial. The estimation of high-dimensional covariance matrices has always been a hot topic with the rapid growth of numerous technologies.

Based on the missing and noisy sample data, this paper constructs a hard thresholding estimator ${\hat{\Sigma }}_F^{th}$ , and studies its optimality. Section 3 shows that the hard thresholding estimator given in this paper is rate-optimal. The numerical simulation shown in Section 4 demonstrates that the hard thresholding estimator works well in situations where the true covariance matrix is sparse. When the true covariance matrix is not sparse, the estimation effect of the hard thresholding estimator has not been discussed.

This paper’s research has limitations and areas that require more investigation:

1) This paper focuses solely on the optimal estimation of sparse covariance matrices based on noisy and missing data. More research is needed on the optimal estimation of other common high-dimensional covariance matrices.

2) If the sub-Gaussian distribution used in this article is replaced with the sub-exponential distribution with a larger range, the relevant issues merit additional investigation.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Bickel, P.J. and Levina, E. (2008) Covariance Regularization by Thresholding. The Annals of Statistics, 36, 2577-2604. https://doi.org/10.1214/08-AOS600
[2]	Cai, T.T. and Zhou, H.H. (2012) Optimal Rates of Convergence for Sparse Covariance Matrix Estimation. The Annals of Statistics, 40, 2389-2420. https://doi.org/10.1214/12-AOS998
[3]	Cai, T.T. and Zhou, H.H. (2012) Minimax Estimation of Large Covariance Matrices under L1-Norm. Statistica Sinica, 22, 1319-1349. https://doi.org/10.5705/ss.2010.253
[4]	Fan, J. and Li, R. (2001) Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. Journal of the American Statistical Association, 96, 1348-1360. http://www.jstor.org/stable/3085904 https://doi.org/10.1198/016214501753382273
[5]	Zou, H. (2006) The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association, 101, 1418-1429. https://doi.org/10.1198/016214506000000735
[6]	Rothman, A.J., Levina, E. and Zhu, J. (2009) Generalized Thresholding of Large Covariance Matrices. Journal of the American Statistical Association, 104, 177-186. https://doi.org/10.1198/jasa.2009.0101
[7]	Cai, T.T. and Liu, W. (2011) Adaptive Thresholding for Sparse Covariance Matrix Estimation. Journal of the American Statistical Association, 106, 672-684. http://www.jstor.org/stable/41416401 https://doi.org/10.1198/jasa.2011.tm10560
[8]	Cai, T.T., Liu, W. and Zhou, H.H. (2016) Estimating Sparse Precision Matrix: Optimal Rates of Convergence and Adaptive Estimation. The Annals of Statistics, 44, 455-488. https://doi.org/10.1214/13-AOS1171
[9]	Bickel, P.J. and Levina, E. (2008) Regularized Estimation of Large Covariance Matrices. The Annals of Statistics, 36, 199-227. https://doi.org/10.1214/009053607000000758
[10]	Cai, T.T., Zhang, C.H. and Zhou, H.H. (2010) Optimal Rates of Convergence for Covariance Matrix Estimation. The Annals of Statistics, 38, 2118-2144. https://doi.org/10.1214/09-AOS752
[11]	Cai, T.T. and Zhang, A. (2016) Minimax Rate-Optimal Estimation of High-Dimensional Covariance Matrices with Incomplete Data. Journal of Multivariate Analysis, 150, 55-74. https://doi.org/10.1016/j.jmva.2016.05.002
[12]	Qi, X. (2022) Low Rank Matrix Perturbation Analysis and Estimation for Two Classes of Sparse Covariance Matrices. Ph.D. Thesis, Beijing University, Beijing.
[13]	Shi, W. (2022) Optimal Estimation of Bandable Covariance Matrices Based on Noised Consored Data. MSc. Thesis, Beijing University, Beijing.
[14]	Tsybakov, A.B. (2009) Introduction to Nonparametric Estimation. Springer-Verlag, New York. https://doi.org/10.1007/b13794