Wave Turbulence of Exponential Oscillons and Pulsons

Victor A. Miroshnikov

Department of Mathematics and Data Analytics, University of Mount Saint Vincent, New York, USA.

DOI: 10.4236/ajcm.2024.141004                

Abstract

This paper represents a novel approach to wave turbulence, which may be called exact wave turbulence, since it is based on an exact solution for nonlinear (both resonant and nonresonant) interactions of turbulent waves, which are governed by the nonstationary Navier-Stokes equations in three dimensions. Exact wave turbulence is aimed to complement the well-known theories of wave turbulence: statistical wave turbulence and resonance wave turbulence. Presented results are focused on derivation and justification of the exact solution, which may be later used to explore the Eulerian, Lagrangian, and statistical properties of wave turbulence. The computed exact solution for wave turbulence generalizes the exact solutions for deterministic chaos of exponential oscillons and pulsons and for stochastic chaos of random exponential oscillons and pulsons, which have been developed with the help of the method of decomposition in invariant structures. For the aim of completeness, experimental and theoretical, deterministic, random, and time-complementary, scalar and vector, kinematic structures are briefly discussed. We also define and study experimental and theoretical, deterministic-deterministic, deterministic-random, random-deterministic, and random-random, scalar dynamic structures together with experimental and theoretical, deterministic-deterministic, deterministic-random, random-deterministic, and random-random, vector dynamic structures of the mth and nth families. The Helmholtz decomposition is used to expand the Dirichlet problems for the turbulent Navier-Stokes equations into the Archimedean, the turbulent Stokes, and the turbulent Navier problems. The kinematic structures are used to find solutions to the deterministic, random, and turbulent Stokes problems, which include the Dirichlet boundary conditions and conditions at infinities. The dynamic structures are employed to compute necessary and sufficient conditions of existence of the exact solution for wave turbulence of exponential oscillons and pulsons with the help of experimental and theoretical programming in Maple. The cumulative pressure field of the turbulent Navier-Stokes problem is derived in the scalar, kinematic, and dynamic structures, as well. Concluding remarks deal with the most interesting properties of the invariant structures and the exact solution and briefly review open problems.

Keywords

The Navier-Stokes Equations, Exact Solution, the Helmholtz Decomposition, Deterministic Chaos, Stochastic Chaos, Decomposition into Invariant Structures, Experimental and Theoretical Programming, Experimental and Theoretical, Deterministic-Random, Scalar and Vector, Dynamic Structures, Experimental and Theoretical, Random-Deterministic, Scalar and Vector, Dynamic Structures, Conservative Interaction of Turbulent Waves

1. Introduction

The decomposition of a velocity field of a turbulent flow into a mean value and a turbulent fluctuation was originally proposed by Osborne Reynolds in 1895. This decomposition is considered to be the beginning of the systematic mathematical analysis of the turbulent flow, while the mean values of the turbulent flow are taken as deterministic variables and the turbulent fluctuations are regarded as random variables. The Navier-Stokes equations are then reduced to an open chain of nonlinear equations, which requires a phenomenological hypothesis for closure of the perturbed Navier-Stokes equations. Numerous closure methods have been proposed, while truncation of higher-order terms is the simplest one. Other opportunities are connected with empirical relations between terms of higher and lower orders. However, none of these methods resulted in a satisfactory description of turbulence for all Reynolds numbers [1] .

The statistical theory of isotropic and homogeneous turbulence of vortex flows at high Reynolds numbers was initialized in three dimensions by Kolmogorov [2] [3] [4] [5] [6] , developed by Obukhov [7] [8] , and constructed in two dimensions by Batchelor [9] . The famous energy spectrum function of the Kolmogorov theory earned considerable experimental evidence [8] . In spite of this success, this theory is at present under revision since the existence of the Kolmogorov flow is still an open problem [10] [11] . Modern developments of the statistical theory of vortex turbulent flows [12] are also limited by the closure problem for higher-order moments of the statistical Navier-Stokes equations [13] .

There are two well-known theories of wave turbulence: statistical wave turbulence and resonance wave turbulence. The statistical theory of wave turbulence [14] , which continues the Kolmogorov theory, inherits the success and the open problems of the statistical theory of vortex turbulence. Solutions of this theory describe a turbulent wave system by kinetic equations and result in the Kolmogorov-Zakharov (KZ) energy spectra. The KZ energy spectra does not depend on an initial distribution of the kinetic energy of the turbulent wave system. Resonance wave turbulence [15] is focused on exact and quasi-resonances of turbulent waves, which are characterized by resonance clustering. This theory develops both integrable and chaotic dynamics, which are represented via the nonlinear resonance diagrams. So, nonresonant interactions of turbulent waves are outside of the realm of resonance wave turbulence.

A novel theoretical approach to wave turbulence, which may be called exact wave turbulence, is developed in the current paper. Exact wave turbulence deals with an exact solution for nonlinear (both resonant and nonresonant) interactions of turbulent waves, which are governed by the nonstationary Navier-Stokes equations in three dimensions. Represented results are focused on the derivation and justification of the exact solution, which may be later used to explore the Eulerian, Lagrangian, and Kolmogorovian (statistical) properties of wave turbulence. Thus, the effect of an initial distribution of the kinetic energy of the turbulent wave system may be treated, as well.

The exact solution for wave turbulence continues the exact solutions for deterministic chaos of exponential oscillons and pulsons [16] and for stochastic chaos of random exponential oscillons and pulsons [17] , which have been developed with the help of the method of decomposition in invariant structures [18] . Theoretical and experimental quantizations of the kinetic energy of deterministic chaos have been studied for the Fourier set of wave parameters in [19] and for the Bernoulli set of wave parameters in [20] , where it was shown that the Bernoulli set gives an opportunity to model turbulization of deterministic chaos. Theoretical quantization of the kinetic energy of stochastic chaos has been treated in [17] .

Studies [16] [17] [18] [19] [20] in stochastic chaos and deterministic chaos were initiated by papers [21] and [22] , respectively, which are devoted to the conservative interaction of two- and three-dimensional internal waves governed by the Navier-Stokes equations. The family of kinematic Euler-Fourier functions of the later paper produces an ultimate sophistication of the exact solution, which was computed using experimental and theoretical programming in Maple. This circumstance stipulated the development of the invariant structures in [16] [17] [18] to derive robust exact solutions of the Navier-Stokes equations.

The contents of this paper are as follows. For the aim of completeness, theoretical Deterministic Scalar Kinematic (tDSK) structures and experimental Deterministic Scalar Kinematic (eDSK) structures of [16] , theoretical Random Scalar Kinematic (tRSK) structures, experimental Random Scalar Kinematic (eRSK) structures, time-complementary tRSK (tRSKt) structures, and time-complementary eRSK (eRSKt) structures of [17] are briefly reviewed in Section 2. In Section 3, we continue the deterministic scalar kinematic structures by experimental Deterministic Vector Kinematic (eDVK) structures and theoretical Deterministic Vector Kinematic (tDVK) structures of [16] . The random scalar kinematic structures are complemented by experimental Random Vector Kinematic (eRVK) structures, theoretical Random Vector Kinematic (tRVK) structures, time-complementary eRVK (eRVKt) structures, and time-complementary tRVK (tRVKt) structures of [17] , as well. Alternative derivation of main results and multidimensional composition of the scalar and vector structures are also provided in Sections 2-3. The deterministic, random, and time-complementary, scalar and vector, kinematic structures are used to find scalar and vector variables of the turbulent Stokes problem of Section 6.

Section 4 deals with experimental Deterministic-Deterministic Scalar Dynamic (eDDSD) structures and theoretical Deterministic-Deterministic Scalar Dynamic (tDDSD) structures, experimental Deterministic-Random Scalar Dynamic (eDRSD) structures and theoretical Deterministic-Random Scalar Dynamic (tDRSD) structures, experimental Random-Deterministic Scalar Dynamic (eRDSD) structures and theoretical Random-Deterministic Scalar Dynamic (tRDSD) structures, experimental Random-Random Scalar Dynamic (eRRSD) structures and theoretical Random-Random Scalar Dynamic (tRRSD) structures, which are required to describe scalar variables of the turbulent Navier problem of Section 7. To express vector variables of this problem, experimental Deterministic-Deterministic Vector Dynamic (eDDVD) structures and theoretical Deterministic-Deterministic Vector Dynamic (tDDVD) structures of the mth and nth families, experimental Deterministic-Random Vector Dynamic (eDRVD) structures and theoretical Deterministic-Random Vector Dynamic (tDRVD) structures of the mth and nth families, experimental Random-Deterministic Vector Dynamic (eRDVD) structures and theoretical Random-Deterministic Vector Dynamic (tRDVD) structures of the mth and nth families, experimental Random-Random Vector Dynamic (eRRVD) structures and theoretical Random-Random Vector Dynamic (tRRVD) structures of the mth and nth families are defined and studied in Section 5.

Formulation of the turbulent Navier-Stokes problem and the Helmholtz decomposition of the turbulent Navier-Stokes problem into the Archimedean, the turbulent Stokes, and the turbulent Navier problems are treated in Section 6, where kinematic solutions of the deterministic Stokes problem, the random Stokes problem, and the turbulent Stokes problem, which are subjected to the Dirichlet boundary conditions and conditions at infinities, are derived. To find a dynamic pressure field of the turbulent Navier problem, expansion, potentialization, and reduction of the turbulent Navier field are computed in Section 7. The proof of a necessary condition of existence of the exact solution for wave turbulence is represented in Sections 7.1-7.3. The dynamic pressure field of the turbulent Navier problem and the cumulative pressure field of the turbulent Navier-Stokes problem are also treated in Section 7.4. Section 7 is concluded with the justification of the turbulent Navier problem in terms of the tDDVD, tDRVD, tRDVD, tRRVD, tDDSD, tDRSD, tRDSD, and tRRSD structures. Thus, Section 7.5 includes the proof of a sufficient condition of existence of the exact solution for wave turbulence. The most interesting properties of the invariant kinematic and dynamic structures are discussed in Section 8 together with important properties of the exact solution. A short list of open problems is also outlined there.

2. Scalar Kinematic Structures

2.1. Definitions of the tDSK and eDSK Structures

In agreement with (13) of [16] , the tDSK structures of the [i, m] family for turbulent systems s_d,i,m, s_d,x,i,m, s_d,y,i,m, s_d,x,y,i,m are defined in a modified notation as follows:

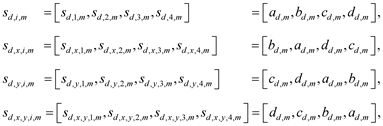(1)

where a_d,m, b_d,m, c_d,m, d_d,m are the eDSK structures of the mth family, i = 1, 2, ¼, I = 1, 2, 3, 4 is an index of deterministic wave groups, and m = 1, 2, ¼, M is an index of deterministic internal waves, M is a total number of internal waves in a deterministic wave group.

The tDSK structures are [1, 4, M, 1] arrays, which are displayed by 1 ´ 4 rows (1) of the eRSK structures. The tDSK structures may be also shown as M ´ 4 matrices, e.g.

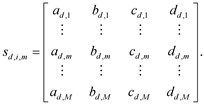(2)

Analogous to (1) of [16] , the eDSK structures of the mth family for turbulent systems are specified in terms of the following relations:

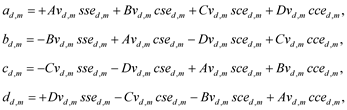(3)

where Av_d,m, Bv_d,m, Cv_d,m, Dv_d,m are functional amplitudes of a deterministic harmonic variable v_d(x, y, z, t). If Av_d,m = 1, Bv_d,m = Cv_d,m = Dv_d,m = 0, then the eDSK structures are reduced to the eDSK functions, i.e.

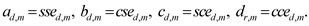(4)

In agreement with (1) and (2), the eDSK structures are [M, 1] arrays, which are displayed via M ´ 1 columns:

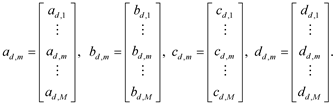(5)

The three-variables (3-v) eDSK functions [sse_d,m, cse_d,m, sce_d,m, cce_d,m](X_d,m, Y_d,m, z) are products

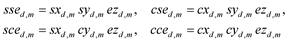(6)

of the following one-variable (1-v) eDSK functions [sx_d,m, cx_d,m](X_d,m), [sy_d,m, cy_d,m](Y_d,m), and ez_d,m = ez_d,m(z):

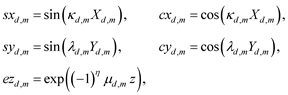(7)

where X_d,m = X_d,m(x, t) and Y_d,m = Y_d,m(y, t) are two-variables (2-v) deterministic propagation variables defined by

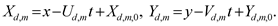(8)

In Equations (1)-(8), (x, y, z) is the Cartesian coordinate of a motionless frame of reference, t is time, (X_d,m, Y_d,m, z) is the Cartesian coordinate of a frame of reference moving with the mth deterministic internal wave, [U_d,m, V_d,m, 0] is a celerity of propagation of the mth deterministic internal wave, and [X_d,m,0, Y_d,m,0] is a reference value of [X_d,m, Y_d,m] at t = 0, x = 0, y = 0. A sign parameter η = 0 for z < 0 and η = 1 for z > 0, κ_d,m, λ_d,m, μ_d,m are wave numbers of the mth deterministic internal wave in the x-, y-, z-directions such that

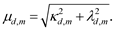(9)

2.2. Definitions of the tRSK and eRSK Structures

The tRSK, eRSK, tRSK_t, eRSK_t, eRVK, tRVK, eRVK_t, tRVK_t, eRRSD, tRRSD, eRRVD, and tRRVD structures for stochastic systems have been meticulously considered in Sections 2-5 of [17] . To demonstrate a deterministic-random invariance, we will briefly review their definitions and algebraic properties in the current paper.

Similar to (1), we also construct the tRSK structures of the [i, m] family for stochastic and turbulent systems s_r,i,m, s_r,x,i,m, s_r,y,i,m, s_r,x,y,i,m in the following form:

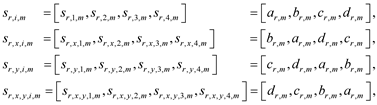(10)

where a_r,m, b_r,m, c_r,m, d_r,m are the eRSK structures of the mth family, i = 1, 2, ¼, I = 1, 2, 3, 4 is an index of random wave groups, and m = 1, 2, ¼, M is an index of random internal waves, M is a total number of internal waves in a random wave group.

The tRSK structures are [1, 4, M, 1] arrays, as well, which are represented by 1 ´ 4 rows (10) of the eRSK structures and by M ´ 4 matrices. For example,

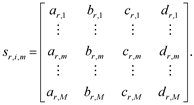(11)

Parallel to (3), the eRSK structures of the mth family may be written as

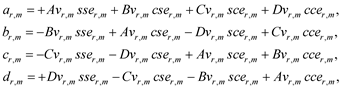(12)

where functional amplitudes of a random harmonic variable v_r(x, y, z, t)

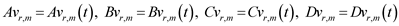(13)

are smooth random functions of time from C^∞. If Av_r,m = 1, Bv_r,m = Cv_r,m = Dv_r,m = 0, the eRSK structures are transformed into the eRSK functions, viz.

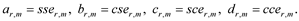(14)

In agreement with (11), the eRSK structures are [M, 1] arrays, which are exposed as M ´ 1 columns. Explicitly,

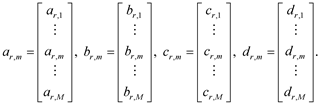(15)

The 3-v eRSK functions [sse_r,m, cse_r,m, sce_r,m, cce_r,m](X_r,m, Y_r,m, z) are specified by products

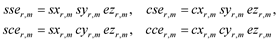(16)

of the following 1-v eRSK functions [sx_r,m, cx_r,m](X_r,m), [sy_r,m, cy_r,m](Y_r,m), and ez_r,m = ez_r,m(z):

(17)

where X_r,m = X_r,m(x, t) and Y_r,m = Y_r,m(y, t) are 2-v random propagation variables, which are given by the following relationships:

(18)

In Equations (10)-(18), (X_r,m, Y_r,m, z) is the Cartesian coordinate of a frame of reference moving with the mth random internal wave, [U_r,m, V_r,m, 0] is a celerity of propagation of the mth random internal wave, and [X_r,m,0, Y_r,m,0] is a reference value of [X_r,m, Y_r,m] at t = 0, x = 0, y = 0, and κ_r,m, λ_r,m, μ_r,m are wave numbers of the mth random internal wave in the x-, y-, z-directions, while

(19)

The wave numbers are random constants since otherwise the temporal derivative of the velocity potential does not commutate with the gradient. Propagation parameters

(20)

together with (13) are smooth random functions of time from C^∞.

2.2. Definitions of the tRSK_t and eRSK_t Structures

The tRSK_t structures of the [i, m] family for stochastic and turbulent systems are specified by

(21)

where a_r,t,m, b_r,t,m, c_r,t,m, d_r,t,m are the eRSK_t structures of the mth family.

Similar to (11), the tRSK_t structures are [1, 4, M, 1] arrays, which are displayed as 1 ´ 4 rows (21) of the eRSK_t structures and M ´ 4 matrices, e.g.,

(22)

Likewise (3) and (12), the eRSK_t structures are defined as follows:

(23)

where functional amplitudes

(24)

are the first derivatives of (13). Along with (13) and (20), functional amplitudes (24) are smooth random functions of time from C^∞.

In the view of (21), the eRSK_t structures are [M, 1] arrays, which are visualized by M ´ 1 columns,

(25)

2.4. Differentiation Tables

Computing first spatial derivatives of the eDSK functions (6)-(8) gives the following differentiation table:

(26)

Differentiation table (26) demonstrates the completeness of the eDSK functions with respect to differentiation in (x, y, z) of any order. The first derivatives of eDSK functions in (x, y) are covariant as they are proportional to cofunctions in the x- and y-directions, correspondingly. The first derivatives with respect to z are invariant since they are proportional to themselves.

We then compute the first spatial derivatives of the eRSK functions (16)-(20) in x, y, and z in the form of a differentiation table:

(27)

that shows the completeness of the eRSK functions with respect to differentiation in (x, y, z) of any order. In agreement with differentiation table (27), the first derivatives of eRSK functions in x and y are covariant and the first derivatives with respect to z are invariant.

It is a straightforward matter to show the completeness of the eDSK structures (3) with respect to differentiation in (x, y, z) of any order for the reason that a table of the first spatial derivatives becomes

(28)

In accordance with differentiation table (28), the first derivatives of the eDSK structures in x and y are covariant as they are proportional to eDSK costructures in the x- and y-directions, correspondingly. The first derivatives of the eDSK structures with respect to z are invariant.

We also find the first spatial derivatives of the eRSK structures (12)-(13) as follows:

(29)

Differentiation table (29) manifests the completeness of the eRSK structures with respect to differentiation in (x, y, z) of any order, as well. The first derivatives of the eRSK structures in (x, y) are covariant because they are proportional to costructures in the x- and y-directions, correspondingly. The first derivatives of the eRSK structures with respect to z are invariant as they are proportional to themselves.

Analogously, the completeness of the eRSK_t structures (23)-(24) with respect to spatial differentiation of any order follows from the following table of the first spatial derivatives:

(30)

In agreement with (30), the first derivatives of the eRSK_t in x and y are covariant as they are proportional to eRSK_t costructures in the x- and y-directions, respectively. The first derivatives of the eRSK_t structures with respect to z are invariant.

Comparison of differentiation tables (26) and (27) for the eDSK and eRSK functions and differentiation tables (28), (29), and (30) for the eDSK, eRSK, and eRSK_t structures exhibits the deterministic-random invariance with respect to the spatial differentiation in (x, y, z) of any order since differentiation table (26) becomes identical to differentiation table (27) after substituting

(31)

In similar fashion, differentiation table (28) is converted into differential table (29) and differential table (30) by substitutions

(32)

and

(33)

respectively. For brevity, further differentiation results in spatial differentiation will be shown only for the eDSK and tDSK structures. However, the eDSK, tDSK, eRSK, and tRSK structures will be treated separately in the case of temporal differentiation.

A differentiation table of the tDSK structures (1) in x, y, and z becomes

(34)

where sign parameters

(35)

Due to the deterministic-random invariance of spatial differentiation, differentiation tables for the tRSK and tRSK_t structures follow from (34) with the help of the following substitutions:

(36)

and

(37)

correspondingly. The differentiation tables for the tRSK and tRSK_t structures obtained by substitutions (36)-(37) coincide with differentiation tables (20) and (22) that are computed by differentiation in [17] .

Similar to the eDSK structures (28), the eRSK structures (29), and the eRSK_t structures (30), the first derivatives of the tDSK, tRSK, and tRSK_t structures in x and y are covariant because they are proportional to tDSK, tRSK, and tRSK_t costructures in the x- and y-directions. The first derivatives of the tDSK, tRSK, and tRSK_t structures with respect to z are invariant as they are proportional to themselves.

A sequence of the first spatial derivatives of each tDSK, tRSK, and tRSK_t structure in the x-, y-, and z-directions for i = 1, 2, ¼, I is equivalent to the differentiation tables of eDSK (28), eRSK (29), and eRSK_t (30) structures, correspondingly. Analogous to [16] and [17] , we see quadrality of the theory: there are four equivalent theoretical ways of explaining the experimental results. For brevity, further theoretical results of Section 2 will be demonstrated mainly via the tDSK structure s_d,i,m, the tRSK structure s_r,i,m, and the eRSK_t structure s_r,t,i,m that are sufficient for the generalization of experimental results.

Similarity of the differentiation tables for the eDSK and eRSK functions and the eDSK, eRSK, eRSK_t, tDSK, tRSK, and tRSK_t structures is displayed in terms of a differentiation diagram in Figure 1. The differentiation diagram demonstrates the transformation of the eDSK functions, the eRSK functions, the eDSK structures, the eRSK structures, the eRSK_t structures, the tDSK structures, the tRSK structures, the tRSK_t structures, the eDVK structures, the eRVK structures, the tDVK structures, and the tRVK structures (see Section 3 for vector kinematic structures) produced by spatial differentiation. Spatial differentiation is displayed with the help of blue arrows for derivatives in x, green arrows for derivatives in y, and red arrows for derivatives in z. The length of arrows showing derivatives in x, y, and z are proportional to differentiation scales κ_d,m, κ_r,m, λ_d,m, λ_r,m, (−1)^ημ_d,m, and (−1)^ημ_r,m, which are visualized with colors corresponding to those of arrows.

Differentiation in x, y, and (x, y) moves elements of a given list of functions and structures

(38)

from one corner of the differentiation rectangle to another one, whereas differentiation in z does not alter the locations of elements of the given list. For the given list of functions and structures, there are three lists of cofunctions and

Figure 1. A differentiation diagram of the first spatial derivatives of the eDSK and eRSK functions and the eDSK, eRSK, eRSK_t, tDSK, tRSK, tRSK_t, eDVK, eRVK, tDVK, and tRVK structures.

costructures. First, a list of cofunctions and costructures in the x-direction

(39)

which are located on the same horizontal leg as the elements of the given list at distances κ_d,m and κ_r,m. Second, a list of cofunctions and costructures in the y-direction

(40)

which are placed on the same vertical leg as the elements of the given list at distances λ_d,m and λ_r,m. Third, a list of cofunctions and costructures in the (x, y)-direction

(41)

which are set in opposite corners with respect to the elements of the given list.

Using table (28) of the first spatial derivatives of the tDSK structures, we compute the second spatial derivatives of the tDSK structure s_d,i,m in x, y, and z

(42)

A corresponding table for the tRSK structures, which follows from (42) by substitution (36), coincides with differentiation table (23) of [17] .

The differentiation diagram in Figure 1 evidently justifies the invariance of the repeated second spatial derivatives. The second-order differentiation shifts the tDSK and tRSK structures from a corner to an adjacent corner of the differentiation rectangle, transforming them into the tDSK and tRSK costructures, and then returns the tDSK and RSK costructures back both in the x- and y-directions, reestablishing the original tRSK and tRSK structures. Alike physical oscillation, this effect of differentiation is termed the scalar structural oscillation of the tDSK [16] and tRSK [17] structures.

In agreement with the differentiation diagram, the second derivatives of the tDSK and tRSK structures in (x, y) are converted into the tDSK and tRSK costructures covariant in (x, y), which are found at an opposite vertex of the differentiation rectangle to that of the original tDSK and tRSK structures. The second derivatives of the tDSK and tRSK structures in (x, z) and (y, z) are transformed into the tDSK and tRSK costructures in the x- and y-directions, respectively, since differentiation in z is invariant.

We sum up the repeated second derivatives of (42) to show that the tDSK structure s_d,i,m and the eDSK structures are harmonic since

(43)

due to (9). Harmonicity of the tRSK structure s_r,i,m and the eRSK structures follows from (43) and (36). The same result was established by (24) of [17] .

A first temporal derivative of the tDSK structure s_d,i,m takes the following form:

(44)

which validates completeness of the eDSK structures with respect to temporal differentiation of any order.

The first derivative of s_d,i,m in t is a superposition of the tDSK costructures in the x- and y-directions, which are located in the adjacent corner points of the differentiation rectangle. Amplitudes of the tDSK costructures depend on products of the celerities of propagation and the wave numbers in the (x, y) plane.

Using definitions (18), (20) and the spatial derivatives the tRSK structure s_r,i,m, we compute a first temporal derivative

(45)

where

(46)

are time-dependent amplitudes.

Consequently, the first temporal derivative of the tRSK structure s_r,i,m and the eRSK structures is produced by a superposition of the tRSK and eRSK costructures in x, y, and t, whereas the time-dependent amplitudes depend on temporal derivatives of U_r,m, V_r,m, X_r,m,0, and Y_r,m,0. The tRSK, tRSK_t, eRSK, and eRSK_t structures are closed with respect to temporal differentiation of the first order.

If

(47)

then the temporal derivative (45)-(46) of the tRSK structure s_r,i,m is converted into the temporal derivative (44) of the tDSK structure s_d,i,m.

3. Vector Kinematic Structures

3.1. Definitions of the eDVK and tDVK Structures

We follow (20) of [16] and define the eDVK structures of the mth family for turbulent systems a_d,m, b_d,m, c_d,m, d_d,m as gradients of the eDSK structures (3) in the following column form:

(48)

The eDVK structures are [3, 1, M, 1] arrays, which are visualized by 3 × 1 columns (48) of the eDSK structures multiplied by coefficients, where elements of columns (48) are [M, 1] arrays that are displayed in terms of M × 1 columns (5).

Consequently, the tDVK structures of the [i, m] family are introduced as follows:

(49)

Equations (49) establish a row definition of the tDVK structures.

With the help of the definition of gradient and the first spatial derivatives of the tDSK structures (34), we obtain definitions of the tDVK structures in the column form. For the tDVK structure s_d,i,m, we have

(50)

Expansions (1) of the tDSK structures s_d,x,i,m, s_d,y,i,m, s_d,i,m for i = 1, 2, 3, 4 give the following matrix definition of the tDVK structure s_d,i,m:

(51)

Since substitution of the eDVK structures in the column form (48) into the row definition of the tDVK structure s_d,i,m (49) results in the same matrix (51), the first of four-dimensional (4-d) row definitions (49) is equivalent to the three-dimensional (3-d) column definition (50). Therefore, s_d,i,m is a [3, 4, M, 1] array, which is visualized by 3 × 4 matrix (51) of the eDSK structures multiplied by coefficients. Elements of matrix (51) are [M, 1] arrays that are represented via M × 1 columns (5).

3.2. Definitions of the eRVK and tRVK Structures

In parallel to (48), we define the eRVK structures of the mth family for stochastic and turbulent systems a_r,m, b_r,m, c_r,m, d_r,m as gradients of the eRSK structures (12) in the following column form:

(52)

Thus, the eRVK structures represent the [3, 1, M, 1] arrays, which are set via 3 × 1 columns (52) of the eRSK structures multiplied by coefficients, where elements of columns (52) are [M, 1] arrays that are visualized in terms of M × 1 columns (15).

Therefore, the tRVK structures of the [i, m] family are expressed via the eRVK structures in the following row form:

(53)

We then compute the gradient of the tRSK structures to find a representation of the tRVK structures in the column form. For s_r,i,m, we obtain

(54)

Substituting (10), we compute that

(55)

which is a matrix definition of the tRVK structure s_r,i,m.

Because substitution of the column definition (52) of eRVK structures into the tRVK structure s_r,i,m in the row form (53) returns matrix (55), the first of 4-d row definitions (53) is equivalent to the 3-d column definition (54). Consequently, s_r,i,m represents the [3, 4, M, 1] array, which is displayed by 3 × 4 matrix (55) of the eRSK structures multiplied by coefficients, where elements of matrix (55) are [M, 1] arrays that are specified by M × 1 columns (15).

3.3. Definitions of the eRVK_t and tRVK_t Structures

Succeeding (52), the eRVK_t structures of the mth family for stochastic and turbulent systems a_r,t,m, b_r,t,m, c_r,t,m, d_r,t,m are expressed as gradients of the eRSK_t structures (23) in the following column form:

(56)

The eRVK_t structures are visualized by the [3, 1, M, 1] arrays, as well, which are represented via 3 × 1 columns (56) of the eRSK_t structures multiplied by coefficients. Elements of columns (56) are [M, 1] arrays that are shown by M × 1 columns (25).

Hence, we set the tRVK_t structures of the [i, m] family in the row form by

(57)

The column form of the tRVK_t structures is generated by the first spatial derivatives. For s_r,t,i,m, we get

(58)

Using (21), the matrix form of s_r,t,i,m may be written as

(59)

Thus, s_r,t,i,m is also the [3, 4, M, 1] array, which is displayed in terms of 3 × 4 matrix (59) of the eRVK_t structures multiplied by coefficients, while elements of matrix (59) are [M, 1] arrays, which are visualized by M × 1 columns (25).

Definitions of the tDVK structures (49), the tRVK structures (53), and tRVK_t structures (57), which are analogous to definitions of the tDSK structures (1), the tRSK structures (10), and tRSK_t structures (21), once more result in quadrality of theoretical formulas. Quadrality of the tDVK, tRVK, and tRVK_t structures is validated by tables of the divergence, the curl, the first spatial derivatives, the second spatial derivatives, the Laplacian, and the first temporal derivative, as well. For conciseness, further theoretical results of Section 3 will be represented mostly via the tDVK structure s_d,i,m, the tRVK structure s_r,i,m, and the tRVK_t structure s_r,t,i,m that are enough for the description of experimental results.

Similarity of definitions (49), (53), and (57) also yields the deterministic-random invariance of the tDVK, tRVK, and tRVK_t structures with respect to the spatial differentiation in (x, y, z) of any order. Hence differentiation tables of the tDVK structures become identical to differential tables of the tRVK and tRVK_t structures after substituting

(60)

and

(61)

respectively.

3.4. Differentiation Tables

Computing the divergence of the tDVK structure s_d,i,m with the help of (43) yields

(62)

So, s_d,i,m and eDVK structures are divergence-free due to (9). Solenoidality of the tRSK structure s_r,i,m and the eRSK structures follows from (62) and (60). The same result was obtained in (36) of [17] .

In agreement with the definition of the curl of the tDVK structures (49) and the first spatial derivatives (34) of the tDSK structures, we demonstrate that the tDVK structure s_d,i,m together with the eDVK structures are irrotational. Explicitly, we get

(63)

A corresponding formula for the tRSK structure s_r,i,m, which follows from (63) with the help of (60), coincides with formula (37) of [17] .

A straightforward but tedious computation of the differentiation table of the tDVK structures, using both the column definition (50) and the row definition (49), gives

(64)

A corresponding table for the tRVK structures, which results from (64) and (60), coincides with differentiation table (38) of [17] .

Differentiation table (34) of the tDSK structures is similar to differentiation table (64) of the tDVK structures because the differentiation tables of the scalar and vector structures become identical after substituting

(65)

This property of the tDSK, tDVK, tRSK, tRVK, eDSK, eDVK, eRSK, and eRVK structures is termed the scalar-vector invariance [16] [17] [18] of the theoretical and experimental invariant structures. The scalar-vector invariance is visualized by the differentiation diagram in Figure 1. The scalar-vector invariance is valid for the second spatial derivatives, the Laplacian, and the first temporal derivative, as well.

Namely, a differentiation table of the second spatial derivatives of the tDVK structure s_d,i,m, which have been obtained with the help of both the column definition (50) and the row definition (49),

(66)

looks like differentiation table (42). In agreement with the differentiation diagram in Figure 1, the repeated second spatial derivatives of the tDVK structure s_d,i,m and the eDVK structures are invariant and the mixed second spatial derivatives are covariant, what agrees with the second spatial derivatives of the tDSK structure s_d,i,m and the eDSK structures. Due to (66) and (60), a relevant table for the tRVK structure s_r,i,m is the same as differentiation table (40) of [17] .

To prove harmonicity of the tDVK structure s_d,i,m and the eDVK structures, we sum up the repeated second spatial derivatives of (66). Instead, the column definition of the tDVK structure s_d,i,m (50) and harmonicity of the tDSK structures yield a column Laplacian of s_d,i,m as follows:

(67)

The correspondent result of the combined application of (67) and (60) agrees with (41) of [17] .

We then find the first temporal derivative of s_d,i,m in the indexed form as follows:

(68)

The first temporal derivative of the tDVK structure s_d,i,m and the eDVK structures is a superposition of costructures in x and y. Equation (68) validates the completeness of the eDVK structures regarding temporal differentiation of any order.

Finally, computation of the first temporal derivative of s_r,i,m in the indexed form gives

(69)

where the time-dependent amplitudes X_r,t,m and Y_r,t,m are specified by (46). Similar to (45), the first temporal derivative of the tRVK structure s_r,i,m is produced by a superposition of the tRVK structures in x, y, and t.

The tRVK structure s_r,i,m and the eRVK structures are closed with respect to spatial differentiation in (x, y, z) of any order. Equation (69) stipulates the completeness of the tRVK structure s_r,i,m, the tRVK_t structure s_r,t,i,m, and the eRVK and eRVK_t structures with respect to temporal differentiation of the first order.

4. Scalar Dynamic Structures

4.1. Definitions of the eDDSD and tDDSD Structures

The eDDSD structures for turbulent systems are defined as all kinds of products of the eDSK structures (3) of the mth family a_d,m, b_d,m, c_d,m, d_d,m and the nth family a_d,n, b_d,n, c_d,n, d_d,n with indices of deterministic internal waves m = 1, 2, ¼, M and n = 1, 2, ¼, M:

(70)

The eDDSD structures are closed as they contain all possible products of the eDSK structures of the mth and nth families.

The eDDSD structures (70) are represented by [M, M] arrays, which are displayed via M × M matrices. For example,

(71)

Thus, the tDDSD structures are established via all kinds of products of the tDSK structures (1) of the [i, m] family s_d,i,m, s_d,x,i,m, s_d,y,i,m, s_d,x,y,i,m and the [j, n] family s_d,j,n, s_d,x,j,n, s_d,y,j,n, s_d,x,y,j,n as

(72)

where indices of deterministic wave groups i = 1, 2, ..., I and j = 1, 2, ..., I and indices of deterministic internal waves m = 1, 2, ..., M and n = 1, 2, ..., M. The tDDSD structures also are closed since they comprise all possible products of the tDSK structures of the [i, m] and [j, n] families.

In terms of the eDDSD structures,

(73)

Therefore, the tDDSD structure s_d,i,ms_d,j,n represents a [4, 4, M, M] array, which is displayed as 4 × 4 matrix (73) of the eDDSD structures. Elements of matrix (73) are the [M, M] arrays that are visualized like M × M matrices (71). Other tDDSD structures are also 4 × 4 matrices of the eDDSD structures arranged in different orders.

4.2. Definitions of the eDRSD and tDRSD Structures

We specify the eDRSD structures for turbulent systems as all kinds of products of the eDSK structures (3) of the mth family a_d,m, b_d,m, c_d,m, d_d,m and the eRSK structures (12) of the nth family a_r,n,b_r,n,c_r,n,d_r,n with indices of deterministic internal waves m = 1, 2, ¼, M and indices of random internal waves n = 1, 2, ¼, M:

(74)

Again, the eDRSD structures (74) are displayed as the [M, M] arrays, which are shown by the M × M matrices. Explicitly,

(75)

In turn, the tDRSD structures are defined through all kinds of products of the tDSK structures (1) of the [i, m] family s_d,i,m, s_d,x,i,m, s_d,y,i,m, s_d,x,y,i,m and the tRSK structures (10) of the [j, n] family s_r,j,n, s_r,x,j,n, s_r,y,j,n, s_r,x,y,j,n by

(76)

where i = 1, 2, ..., I are indices of deterministic wave groups, j = 1, 2, ..., I are indices of random wave groups, m = 1, 2, ..., M are indices of deterministic internal waves, and n = 1, 2, ..., M are indices of random internal waves.

In the eDRSD structures,

(77)

Consequently, the tDRSD structure s_d,i,ms_r,j,n is manifested by the [4, 4, M, M] array, which is 4 × 4 matrix (77) of the eDRSD structures. Elements of matrix (77) present the [M, M] arrays that are shown alike M × M matrix (75). Further tDRSD structures are the 4 × 4 matrices of the eDRSD structures, as well, which are organized in diverse orders.

4.3. Definitions of the eRDSD and tRDSD Structures

The eRDSD structures for turbulent systems are set up as all kinds of products of the eRSK structures (12) of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the eDSK structures (3) of the nth family a_d,n, b_d,n, c_d,n, d_d,n with indices of random internal waves m = 1, 2, ¼, M and indices of deterministic internal waves n = 1, 2, ¼, M:

(78)

The eDRSD and eRDSD structures are closed as they embrace all possible products of the eDSK and eRSK structures of the mth and nth families.

Likewise (71) and (75), the eRDSD structures (78) are manifested by the [M, M] arrays, which are specified via the M × M matrices. Namely,

(79)

In line with (76), the tRDSD structures are specified via all kinds of products of the tRSK structures of the [i, m]family s_r,i,m, s_r,x,i,m, s_r,y,i,m, s_r,x,y,i,m and the tDSK structures of the [j, n] family s_d,j,n, s_d,x,j,n, s_d,y,j,n, s_d,x,y,j,n as follows:

(80)

where i = 1, 2, ..., I are indices of random wave groups, j = 1, 2, ..., I are indices of deterministic wave groups, m = 1, 2, ..., M are indices of random internal waves, and n = 1, 2, ..., M are indices of deterministic internal waves. The tDRSD and tRDSD structures are closed as they embrace all possible products of the tDSK and tRSK structures of the [i, m] and [j, n] families.

Via the eRDSD structures,

(81)

Similarly, the tRDSD structure s_r,i,ms_d,j,n is expressed via the [4, 4, M, M] array, which is exposed as 4 × 4 matrix (81) of the eRDSD structures. Elements of matrix (81) are the [M, M] arrays that are displayed through M × M matrices (79). Another tRDSD structures are composed of the 4 × 4 matrices of the eRDSD structures, which are positioned in diverse orders.

4.4. Definitions of the eRRSD and tRRSD Structures

In agreement with (43) of [17] , we represent the eRRSD structures for stochastic and turbulent systems as all kinds of products of the eRSK structures (12) of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the nth family a_r,n, b_r,n, c_r,n, d_r,n with indices of random internal waves m = 1, 2, ..., M and n = 1, 2, ..., M:

(82)

The eRRSD structures are closed too for the reason that they comprise all possible products of the eRSK structures of the mth and nth families.

The eRRSD structures (82) are also displayed as the [M, M] arrays, which are visualized by the M × M matrices. For example,

(83)

Hence, the tRRSD structures are defined through all kinds of products of the tRSK structures (10) of the [i, m] family s_r,i,m, s_r,x,i,m, s_r,y,i,m, s_r,x,y,i,m and the [j, n] family s_r,j,n, s_r,x,j,n, s_r,y,j,n, s_r,x,y,j,n in the following form:

(84)

where i = 1, 2, ..., I and j = 1, 2, ..., I are indices of random wave groups and m = 1, 2, ..., M and n = 1, 2, ..., M are indices of random internal waves. The tRRSD structures are closed since they include all possible products of the tRSK structures of the [i, m] and [j, n] families.

Through the eRRSD structures,

(85)

The tRRSD structure s_r,i,ms_r,j,n is displayed by the [4, 4, M, M] array, which is represented via 4 × 4 matrix (85) of the eRRSD structures. Elements of matrix (85) are the [M, M] arrays that are exposed as M × M matrices (83). Other tRRSD structures are also the 4 × 4 matrices of the eRRSD structures listed in various orders.

4.5. Differentiation Tables

Taking the first spatial derivatives of s_d,i,ms_d,j,n, substituting the first spatial derivatives of the tDSK structures (34), and using (34) with substitution [i = j, m = n] gives

(86)

Proceeding the same way for the tDRSD structures yields

(87)

The differentiation table of the first spatial derivatives of the tRDSD structures becomes

(88)

Finally, we compute the differentiation table of the first spatial derivatives of the tRRSD structures in the following form:

(89)

which coincides with (47) of [17] .

Expansion of (86)-(89) in all group and wave indices demonstrates the completeness of the eDDSD, eDRSD, eRDSD, and eRRSD structures with respect to spatial differentiation of any order. The computed first derivatives of the tDDSD, tDRSD, tRDSD, tRRSD structures and the eDDSD, eDRSD, eRDSD, eRRSD structures with respect to z are invariant and with respect to x and y are covariant.

Theoretical Equations (86)-(89) for the tDDSD, tDRSD, tRDSD, and tRRSD structures have been verified by differentiation tables of the eDDSD, eDRSD, eRDSD, and eRRSD structures using experimental and theoretical programming in Maple, while each theoretical formula corresponds to a table of 16 experimental formulas. In view of a large size, Maple codes will be published elsewhere.

The gradient of the tDDSD, tDRSD, tRDSD, and tRRSD structures will be computed via the tDDVD, tDRVD, tRDVD, and tRRVD structures of the mth and nth families in Section 5.5.

5. Vector Dynamic Structures

5.1. Definitions of the eDDVD and tDDVD Structures

Analogous to (40) of [16] , we define the eDDVD structures of the mth family for turbulent systems as all kinds of products of the eDVK structures (48) of the mth family a_d,m, b_d,m, c_d,m, d_d,m and the eDSK structures (3) of the nth family a_d,n, b_d,n, c_d,n, d_d,n with indices of deterministic internal waves m = 1, 2, ¼, M and n = 1, 2, ¼, M:

(90)

Because the eDVK structures are gradients (48) of the eDSK structures, the eDDVD structures a_d,ma_d,n, a_d,mb_d,n, a_d,mc_d,n, a_d,md_d,n, etc. are visualized by the following columns:

(91)

Therefore, the eDDVD structures of the mth family are represented by [3, 1, M, M] arrays, which are manifested via 3 × 1 columns (91) of the eDDSD structures multiplied by coefficients, where elements of columns (91) are the [M, M] arrays that are exhibited as the M × M matrices analogous to matrix (71).

Consequently, we set the eDDVD structures of the nth family for turbulent systems as all kinds of products of the eDSK structures (3) of the mth family a_d,m, b_d,m, c_d,m, d_d,m and the eDVK structures (48) of the nth family a_d,n, b_d,n, c_d,n, d_d,n with indices of deterministic internal waves m = 1, 2, ¼, M and n = 1, 2, ¼, M:

(92)

The eDDVD structures of the mth and nth families are closed since they include all possible products of the eDVK and eDSK structures of the mth and nth families.

Since the eDVK structures are presented via gradients of the correspondent eDSK structures, the eDDVD structures of the nth family a_d,ma_d,n, a_d,mb_d,n, a_d,mc_d,n, a_d,md_d,n, etc. are shown by the following columns:

(93)

Thus, the eDDVD structures of the nth family are the [3, 1, M, M] arrays, which are exposed by 3 × 1 columns (93) of the eDDSD structures multiplied by coefficients, where elements of columns (93) are expressed via the [M, M] arrays that are displayed by the M × M matrices alike (71).

The tDDVD structures of the mth family are introduced as all kinds of products of the tDVK structures (49) of the [i, m] family and the tDSK structures (1) of the [j, n] family. Namely,

(94)

where i = 1, 2, ..., I and j = 1, 2, ..., I are indices of deterministic wave groups, m = 1, 2, ..., M and n = 1, 2, ..., M are indices of deterministic internal waves.

In terms of the eDDVD structures of the mth family (90),

(95)

The tDDVD structure of the mth family s_d,i,ms_d,j,n is a [4, 4, 3, 1, M, M] array that is visualized by 4 × 4 matrix (95) of the eDDVD structures of the mth family. So, elements of matrix (95) are the [3, 1, M, M] arrays that are displayed by the 3 × 1 columns of the M × M matrices of the eDDSD structures multiplied by coefficients. Another tDDVD structures of the mth family are the 4 × 4 matrices of the eDDVD structures of the mth family arranged in different orders.

The tDDVD structures of the nth family are set as all kinds of products of the tDSK structures (1) of the [i, m] family and the tDVK structures (49) of the [j, n] family. Explicitly,

(96)

where i = 1, 2, ..., I and j = 1, 2, ..., I are indices of deterministic wave groups, m = 1, 2, ..., M and n = 1, 2, ..., M are indices of deterministic internal waves.

The tDDVD structures of the mth and nth families are closed as they comprise all possible products of the tDVK and tDSK structures of the [i, m] and [j, n] families.

Through the eDDVD structures of the nth family (92),

(97)

The tDDVD structure of the nth family s_d,i,ms_d,j,n is also the [4, 4, 3, 1, M, M] array, which is displayed via 4 × 4 matrix (97) of the eDDVD structures of the nth family. Elements of matrix (97) are specified by the [3, 1, M, M] arrays that are shown through the 3 × 1 columns of the M × M matrices of the eDDSD structures multiplied by coefficients. Other tDDVD structures of the nth family are also visualized as the 4 × 4 matrices of the eDDVD structures of the nth family listed in various orders.

5.2. Definitions of the eDRVD and tDRVD structures

Alike (90), the eDRVD structures of the mth family for turbulent systems are specified as all kinds of products of the eDVK structures (48) of the mth family a_d,m, b_d,m, c_d,m, d_d,m with an index of deterministic internal waves m = 1, 2, ¼, M and the eRSK structures (12) of the nth family a_r,n, b_r,n, c_r,n, d_r,n with an index of random internal waves n = 1, 2, ¼, M:

(98)

Because the eDVK structures are presented via gradients (48) of the eDSK structures, the eDRVD structures a_d,ma_r,n, a_d,mb_r,n, a_d,mc_r,n, a_d,md_r,n, etc. are displayed as follows:

(99)

So, the eDRVD structures of the mth family are expressed through the [3, 1, M, M] arrays, which are exposed via 3 × 1 columns (99) of the eDRSD structures multiplied by coefficients, while elements of columns (99) are the [M, M] arrays that are manifested by the M × M matrices similar to matrix (75).

In the same way, the eDRVD structures of the nth family for turbulent systems are described by all kinds of products of the eDSK structures (3) of the mth family a_d,m, b_d,m, c_d,m, d_d,m with an index of deterministic internal waves m = 1, 2, ¼, M and the eRVK structures (52) of the nth family a_r,n, b_r,n, c_r,n, d_r,n with an index of random internal waves n = 1, 2, ¼, M:

(100)

Because the eRVK structures are defined as gradients of the eRSK structures, the eDRVD structures of the nth family a_d,ma_r,n, a_d,mb_r,n, a_d,mc_r,n, a_d,md_r,n, etc. are visualized by

(101)

Consequently, the eDRVD structures of the nth family are the [3, 1, M, M] arrays, as well, which are manifested in terms of 3 × 1 columns (101) of the eDRSD structures multiplied by coefficients, whereas elements of columns (101) are the [M, M] arrays that are exposed by the M × M matrices analogous to (75).

We specify the tDRVD structures of the mth family as all kinds of products of the tDVK structures (49) of the [i, m] family and the tRSK structures (10) of the [j, n] family:

(102)

where i = 1, 2, ..., I is an index of deterministic wave groups, j = 1, 2, ..., I is an index of random wave groups, m = 1, 2, ..., M is an index of deterministic internal waves, and n = 1, 2, ..., M is an index of random internal waves.

Via the eDRVD structures of the mth family (98),

(103)

So, the tDRVD structure of the mth family s_d,i,ms_r,j,n represents the [4, 4, 3, 1, M, M] array, which is displayed as 4 × 4 matrix (103) of the eDRVD structures of the mth family. Elements of matrix (103) are also the [3, 1, M, M] arrays that are shown by the 3 × 1 columns of the M × M matrices of the eDRSD structures multiplied by coefficients. Further tDRVD structures of the mth family are the 4 × 4 matrices of the eDRVD structures of the mth family, as well, organized in diverse orders.

The tDRVD of the nth family are computed as all kinds of products of the tDSK structures (1) of the [i, m] family and the tRVK structures (53) of the [j, n] family. Namely,

(104)

where i = 1, 2, ..., I is an index of deterministic wave groups, j = 1, 2, ..., I is an index of random wave groups, m = 1, 2, ..., M is an index of deterministic internal waves, and n = 1, 2, ..., M is an index of random internal waves.

In terms of the eDRVD structures of the nth family (100),

(105)

Thus, the tDRVD structure of the nth family s_d,i,ms_r,j,n presents the [4, 4, 3, 1, M, M] array, which is set by 4 × 4 matrix (105) of the eDRVD structures of the nth family. Elements of matrix (105) are also the [3, 1, M, M] arrays that are manifested via the 3 × 1 columns of the M × M matrices of the eDRSD structures multiplied by coefficients. Various tDRVD structures of the nth family are the 4 × 4 matrices of the eDRVD structures of the nth family positioned in diverse orders.

5.3. Definitions of the eRDVD and tRDVD Structures

Following (98), we introduce the eRDVD structures of the mth family for turbulent systems as all kinds of products of the eRVK structures (52) of the mth family a_r,m, b_r,m, c_r,m, d_r,m with an index of random internal waves m = 1, 2, ¼, M and the eDSK structures (3) of the nth family a_d,n, b_d,n, c_d,n, d_d,n with an index of deterministic internal waves n = 1, 2, ¼, M:

(106)

For the reason that the eRVK structures are gradients of the eRSK structures, the eRDVD structures a_r,ma_d,n, a_r,mb_d,n, a_r,mc_d,n, a_r,md_d,n, etc. become

(107)

The eRDVD structures of the mth family are described by the [3, 1, M, M] arrays, which are manifested via 3 × 1 columns (107) of the eRDSD structures multiplied by coefficients, where elements of columns (107) are the [M, M] arrays that are shown by the M × M matrices similar to matrix (79).

Analogously, we specify the eRDVD structures of the nth family for turbulent systems as all kinds of products of the eRSK structures (12) of the mth family a_r,m, b_r,m, c_r,m, d_r,m with an index of random internal waves m = 1, 2, ¼, M and the eDVK structures (48) of the nth family a_d,n, b_d,n, c_d,n, d_d,n with an index of deterministic internal waves n = 1, 2, ¼, M:

(108)

The experimental eDRVD and eRDVD structures of the mth and nth families are closed since they include all possible products of the eDVK, eRVK, eDSK, and eRSK structures of the mth and nth families.

Because the eDVK structures are represented by gradients of the eDSK structures, the eRDVD structures of the nth family a_r,ma_d,n, a_r,mb_d,n, a_r,mc_d,n, a_r,md_d,n, etc. are expressed as follows:

(109)

Thus, the eRDVD structures of the nth family are exhibited via the [3, 1, M, M] arrays, which are shown by 3 × 1 columns (109) of the eRDSD structures multiplied by coefficients, while elements of columns (109) are the [M, M] arrays that are displayed by the M × M matrices alike matrix (79).

The tRDVD structures of the mth family are constructed as all kinds of products of the tRVK structures (53) of the [i, m] family and the tDSK structures (1) of the [j, n] family

(110)

where i = 1, 2, ..., I is an index of random wave groups, j = 1, 2, ..., I is an index of deterministic wave groups, m = 1, 2, ..., M is an index of random internal waves, and n = 1, 2, ..., M is an index of deterministic internal waves.

In the eRDVD structures of the mth family (106),

(111)

The tRDVD structure of the mth family s_r,i,ms_d,j,n is set as the [4, 4, 3, 1, M, M] array, which is visualized by 4 × 4 matrix (111) of the eRDVD structures of the mth family. Once more, elements of matrix (111) present the [3, 1, M, M] arrays that are displayed by the 3 × 1 columns of the M × M matrices of the eRDSD structures multiplied by coefficients. Other tRDVD structures of the mth family are represented by the 4 × 4 matrices of the eRDVD structures of the mth family positioned in different orders.

The tRDVD structures of the nth family are composed as all kinds of products of the tRSK structures (10) of the [i, m] family and the tDVK structures (49) of the [j, n] family:

(112)

where i = 1, 2, ..., I is an index of random wave groups, j = 1, 2, ..., I is an index of deterministic wave groups, m = 1, 2, ..., M is an index of random internal waves, and n = 1, 2, ..., M is an index of deterministic internal waves.

The tDRVD structures and tRDVD structures of the mth and nth families are also closed because they include all possible products of the tDVK, tRVK, tDSK, and tRSK structures of the [i, m] and [j, n] families.

Via the eRDVD structures of the nth family (108),

(113)

The tRDVD structure of the nth family s_r,i,ms_d,j,n represents the [4, 4, 3, 1, M, M] array, which is specified via 4 × 4 matrix (113) of the eRDVD structures of the nth family. Elements of matrix (113) are given by the [3, 1, M, M] arrays that are shown in terms of the 3 × 1 columns of the M × M matrices of the eRDSD structures multiplied by coefficients. Further tRDVD structures of the nth family are displayed by the 4 × 4 matrices of the eRDVD structures of the nth family arranged in various orders.

5.4. Definitions of the eRRVD and tRRVD Structures

Following (52) of [17] , the eRRVD structures of the mth family for stochastic and turbulent systems are established as all kinds of products of the eRVK structures (52) of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the eRSK structures (12) of the nth family a_r,n, b_r,n, c_r,n, d_r,n with indices of random internal waves m = 1, 2, ..., M and n = 1, 2, ..., M:

(114)

For the eRVK structures are represented by gradients (52) of the eRSK structures, the eRRVD structures a_r,ma_r,n, a_r,mb_r,n, a_r,mc_r,n, a_r,md_r,n, etc. are manifested by the following columns:

(115)

Consequently, the eDRVD structures of the mth family are the [3, 1, M, M] arrays, which are displayed in terms of 3 × 1 columns (115) of the eRRSD structures multiplied by coefficients, where elements of columns (115) are the [M, M] arrays that are exhibited as the M × M matrices similar to matrix (83).

So, the eRRVD structures of the nth family for stochastic and turbulent systems are defined as all kinds of products of the eRSK structures (12) of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the eRVK structures (52) of the nth family a_r,n, b_r,n, c_r,n, d_r,n with indices of random internal waves m = 1, 2, ..., M and n = 1, 2, ..., M:

(116)

The experimental eRRVD structures of the mth and nth families are closed since they comprise all possible products of the eRVK and eRSK structures of the mth and nth families.

Since the eRVK structures are gradients of the correspondent eRSK structures, the eRRVD structures a_r,ma_r,n, a_r,mb_r,n, a_r,mc_r,n, a_r,md_r,n, etc. are visualized by the following columns:

(117)

Thus, the eRRVD structures of the nth family are represented by the [3, 1, M, M] arrays, as well, which are displayed in terms of 3 × 1 columns (117) of the eRRSD structures multiplied by coefficients, where elements of columns (117) are the [M, M] arrays that are shown by the M × M matrices like (83).

The tRRVD structures of the mth family are specified as all kinds of products of the tRVK structures (53) of the [i, m] family and the tRSK structures (10) of the [j, n] family. Explicitly,

(118)

where i = 1, 2, ..., I and j = 1, 2, ..., I are indices of random wave groups and m = 1, 2, ..., M and n = 1, 2, ..., M are indices of random internal waves.

Via the eRRVD structures of the mth family (114),

(119)

The tRRVD structure of the mth family s_r,i,ms_r,j,n is given by the [4, 4, 3, 1, M, M] array that is visualized as 4 × 4 matrix (119) of the eRRVD structures of the mth family. Elements of matrix (119) are specified in terms of the [3, 1, M, M] arrays that are displayed via the 3 × 1 columns of the M × M matrices of the eRRSD structures multiplied by coefficients. Other tRRVD structures of the mth family are the 4 × 4 matrices of the eRRVD structures of the mth family listed in various orders.

We then define the tRRVD of the nth family as all kinds of products of the tRSK structures (10) of the [i, m] family and the tRVK structures (53) of the [j, n] family. Namely,

(120)

where i = 1, 2, ..., I and j = 1, 2, ..., I are indices of random wave groups and m = 1, 2, ..., M and n = 1, 2, ..., M are indices of random internal waves.

The tRRVD structures of the mth and nth families are closed since they include all possible products of the tRVK and tRSK structures of the [i, m] and [j, n] families.

Through the eRRVD structures of the nth family (116),

(121)

The tRRVD structure of the nth family s_r,i,ms_r,j,n is also the [4, 4, 3, 1, M, M] array, which is displayed as 4 × 4 matrix (121) of the eRRVD structures of the nth family. Elements of matrix (121) are the [3, 1, M, M] arrays that are visualized by the 3 × 1 columns of the M × M matrices of the eRRSD structures multiplied by coefficients. Other tRRVD structures of the nth family are the 4 × 4 matrices of the eRRVD structures of the nth family arranged in diverse orders.

5.5. The Helmholtz Decomposition of the Directional Derivatives

Substitution of the first spatial derivatives of the tDSK (34) and tDVK (64) structures in the vector definitions of the directional derivative (42) of [16] and simplification yield an anticommutator and a commutator of the tDVK structures s_d,i,m and s_d,j,n, correspondingly, in the tDDVD structures of the mth (94) and nth (96) families in the following form:

(122)

(123)

In the similar way, we compute the anticommutator and the commutator of the tDVK structure s_d,i,m and the tRVK structure s_r,j,n, respectively, through the tDRVD structures of the mth (102) and nth (104) families as follows:

(124)

(125)

Analogously, the anticommutator and the commutator of the tRVK structure s_r,i,m and the tDVK structure s_d,j,n, correspondingly, in terms of the tRDVD structures of the mth (110) and nth (112) families become

(126)

(127)

Eventually, we obtain the anticommutator and the commutator of the tRVK structures s_r,i,m and s_r,j,n, respectively, via the tRRVD structures of the mth (118) and nth (120) families as

(128)

(129)

Expansion of the tDDVD structures of (122)-(123) into the tDDSD structures (72) and comparison with the gradient of the dot product and the curl of the cross product of the tDVK structures s_d,i,m and s_d,j,n, which have been also computed in the tDDSD structures using (49) and (55) of [16] , yield

(130)

We then represent the tDRVD structures of (124)-(125) in the tDRSD structures (76) and compare with the gradient of the dot product and the curl of the cross product of the tDVK structure s_d,i,m and the tRVK structure s_r,j,n, which have been also expressed in the tRDSD structures, to find that

(131)

Similarly, transformation of the tRDVD structures of (126)-(127) into the tRDSD structures (80) and comparison with the gradient of the dot product and the curl of the cross product of the tRVK structure s_r,i,m and the tDVK structure s_d,j,n, which have been obtained in the tRDSD structures too, give

(132)

Finally, we convert the tRRVD structures of (128)-(129) in the tRRSD structures (84) and compare with the gradient of the dot product and the curl of the cross product of the tRVK structures s_r,i,m and s_r,j,n, which have been displayed in the tRRSD structures, as well, to compute

(133)

In agreement with the Fundamental Theorem of Vector Analysis [23] , solving of (130) with respect to the directional derivatives returns the Helmholtz decomposition of the derivative of the tDVK structure s_d,j,n in the direction of the tDVK structure s_d,i,m and the derivative of the tDVK structure s_d,i,m in the direction of the tDVK structure s_d,j,n in the following form:

(134)

We also solve (131) with respect to the directional derivatives to find the Helmholtz decomposition of the derivative of the tRVK structure s_r,j,n in the direction of the tDVK structure s_d,i,m and the derivative of the tDVK structure s_d,i,m in the direction of the tRVK structure s_r,j,n as follows:

(135)

Solution of (132) with respect to the directional derivatives yields the Helmholtz decomposition of the derivative of the tDVK structure s_d,j,n in the direction of the tRVK structure s_r,i,m and the derivative of the tRVK structure s_r,i,m in the direction of the tDVK structure s_d,j,n as

(136)

Eventually, we resolve (133) with respect to the directional derivatives to compute the Helmholtz decomposition of the derivative of the tRVK structure s_r,j,n in the direction of the tRVK structure s_r,i,m and the derivative of the tRVK structure s_r,i,m in the direction of the tRVK structure s_r,j,n:

(137)

In Equation (134), the scalar Helmholtz potential and the vector Helmholtz potential are

(138)

The scalar and vector Helmholtz potentials of (135) may be written as follows:

(139)

Computation of the scalar and vector Helmholtz potentials of (136) gives

(140)

Finally, we find the scalar and vector Helmholtz potentials of (137) in the following form:

(141)

So, the scalar Helmholtz potentials of (138)-(141) are symmetrical and the vector Helmholtz potentials of (138)-(141) are asymmetrical.

Finally, we compute the gradient of the tDDSD structure s_d,i,ms_d,j,n, the tDRSD structure s_d,i,ms_r,j,n, the tRDSD structure s_r,i,ms_d,j,n, and the tRRSD structure s_r,i,ms_r,j,n in terms of the tDDVD structure, the tDRVD structure, the tRDVD structure, and the tRRVD structure of the mth and nth families, respectively, to obtain

(142)

Theoretical Equations (122)-(142) in terms the tDDVD, tDRVD, tRDVD, tRRVD structures of the mth and nth families have been verified by differentiation tables in the eDDVD, eDRVD, eRDVD, eRRVD structures of the mth and nth families with the help of experimental and theoretical programming in Maple, while each theoretical formula corresponds to a table of 16 experimental formulas.

6. The Turbulent Stokes Field

6.1. The Helmholtz Decomposition of the Turbulent Navier-Stokes Equations

Turbulent internal waves of a Newtonian fluid with a constant density ρ_c and a constant dynamic viscosity μ_c in a field of gravity g = [g_x, g_y, g_z] are governed by the momentum conservation law [24]

(143)

and the mass conservation law

(144)

where

(145)

is a velocity field of a turbulent flow,

(146)

is a cumulative pressure of the turbulent flow.

The quasi-scalar Dirichlet problems for the Navier-Stokes equations (143)-(144) may be set on the upper and lower boundaries of the upper domain

(147)

for the z-component u_t,z by

(148)

and on the upper and lower boundaries of the lower domain

(149)

via

(150)

where

(151)

is a turbulent boundary function, which will be considered in Section 6.3.

The configuration of the upper and lower domains of turbulent internal waves is shown in Figure 2. In agreement with boundary conditions (148) and (150), the turbulent internal waves are produced by turbulent surface waves propagating in a generation domain.

Figure 2. The configuration of the upper domain (147) and the lower domain (149) of the Dirichlet problems (148) and (150) for the turbulent Navier-Stokes equations (143)-(146).

From the standpoint of the Fundamental Theorem of Vector Analysis [23] , the quasi-scalar Dirichlet problems (148) and (150) for the turbulent Navier-Stokes equations (143)-(144) in vector and scalar variables (145)-(146) may be treated as problems of the Helmholtz decomposition of the Archimedean field

(152)

the turbulent Stokes field

(153)

and the turbulent Navier field

(154)

The Archimedean field, the turbulent Stokes field, and the turbulent Navier field are decomposed using the scalar Helmholtz potentials p_A, p_S,t, and p_N,t, correspondingly, in the following form:

(155)

where p_A denotes the hydrostatic pressure of the Archimedean problem, p_S,t signifies the kinematic pressure of the turbulent Stokes problem, and p_N,t stands for the dynamic pressure of the turbulent Navier problem.

Summations of (152)-(154) and (155) yield the Helmholtz decomposition of the turbulent Navier-Stokes equation (143)

(156)

where

(157)

is a cumulative pressure of the turbulent flow, i.e. p_c,t is a scalar Helmholtz potential of the sum of the Archimedean field, the turbulent Stokes field, and the turbulent Navier field.

The problem of finding the scalar Helmholtz potential p_A of the Archimedean field F_A has a general solution [24]

(158)

where p₀(t) is a reference pressure, which is a smooth random function of time from C^∞.

Following the Reynolds approach [1] , we set the velocity field u_t of a turbulent flow as a superposition of a velocity field u_d of a deterministic flow and a velocity field u_r of a random flow. Namely,

(159)

where

(160)

(161)

In agreement with (159), the turbulent Stokes field

(162)

where

(163)

is the deterministic Stokes field and

(164)

is the random Stokes field.

In the view of (162), the kinematic pressure of the turbulent Stokes flow

(165)

where p_S,d is a kinematic pressure of the deterministic Stokes problem and p_S,r is a kinematic pressure of the random Stokes problem. The deterministic and random kinematic pressures are defined as the scalar Helmholtz potentials of the deterministic and random Stokes field, respectively, by

(166)

Combining (157) and (165) yields that the cumulative pressure of the turbulent flow

(167)

Following (159), we decompose the turbulent boundary function (151) by

(168)

A problem of calculating the deterministic velocity field u_d and the scalar Helmholtz potential p_S,d of the deterministic Stokes field F_S,d takes the following form:

(169)

(170)

(171)

Similarly, a problem of finding the random velocity field u_r and the scalar Helmholtz potential p_S,r of the random Stokes field F_S,r may be written as follows:

(172)

(173)

(174)

Problem (169)-(171) will be called afterwards the deterministic Stokes problem and problem (172)-(174) will be termed the random Stokes problem. Contrary to the classical Stokes equations that are treated for small Reynolds numbers, the deterministic Stokes problem and the random Stokes problem are set for all Reynolds numbers.

A problem of computing the scalar Helmholtz potential p_N,t of the turbulent Navier field F_N,t for u_t given by (159), u_d of the deterministic Stokes problem (169)-(171), and u_r of the random Stokes problem (172)-(174)

(175)

will be later referred to as the turbulent Navier problem. Since we are looking for an exact solution to Equations (143)-(151), the turbulent Navier problem is set for all Reynolds numbers, as well.

6.2. The Turbulent Stokes Problem

A general wave solution of the deterministic Stokes Equations (169)-(170) is

(176)

(177)

where j_u,d is the scalar Helmholtz potential of the deterministic velocity field that should be harmonic, i.e.

(178)

and the temporal derivative of j_u,d must commutate with the gradient.

The deterministic velocity field u_d is formed by velocity fields u_d,i of I deterministic wave groups with M internal waves per group. Thus,

(179)

Because of quadrality of the tDVK structures, we use the simplest tDVK structure s_d,i,m to expand the velocity fields of I wave groups as follows:

(180)

for i = 1, 2, ..., I.

Combining (179)-(180) and changing the order of summation yields

(181)

Using definition (49) of the tDVK structures via the tDSK structures, we get

(182)

In agreement with the Helmholtz decomposition of the velocity field (176), the scalar Helmholtz potential represented via the tDSK structure s_d,i,m takes the following form:

(183)

Indeed, the Laplace Equation (178) is satisfied identically since s_d,i,m is harmonic (43).

We then substitute the velocity potential (183) in (177) and use the temporal derivative (44) of s_d,i,m to find the kinematic pressure of the deterministic Stokes problem that is expanded in the tDSK structures s_d,x,i,m and s_d,y,i,m as follows:

(184)

To verify the general solution (181) and (184) of the deterministic Stokes Equations (169)-(170) in the tDVK and tDSK structures, we use the temporal derivative (68) of the tDVK structure s_d,i,m to find

(185)

Since s_d,i,m is harmonic (67),

(186)

Computing the gradient of p_S,d with the help of gradient (49) of the tDSK structures s_d,x,i,m and s_d,y,i,m gives

(187)

Substitution of (185)-(187) in the momentum conservation law (169) of the deterministic Stokes problem shows that it is satisfied identically. Because the tDVK structure s_d,i,m is divergence-free (62), the mass conservation law (170) of the deterministic Stokes problem is fulfilled identically, as well.

A general wave solution of the random Stokes Equations (172)-(173) may be written as follows:

(188)

(189)

where j_u,r is the scalar Helmholtz potential of the random velocity field that must be harmonic, viz.

(190)

and the temporal derivative of j_u,r have to commutate with the gradient.

The random velocity field u_r is generated by velocity fields u_r,i of I random wave groups with M internal waves per group. Consequently,

(191)

Due to quadrality of the tRVK structures and consistency with the deterministic Stokes problem, we employ the tRVK structure s_r,i,m to decompose the random velocity fields of I wave groups in the following form:

(192)

for i = 1, 2, ..., I.

We then combine (191)-(192) and change the order of summation to get

(193)

Usage of definition (53) of the tRVK structures via the tRSK structures gives

(194)

In accordance with the Helmholtz decomposition of the velocity field (188), the scalar Helmholtz potential written via the tRSK structure s_r,i,m becomes

(195)

Certainly, the Laplace equation (190) is fulfilled because s_r,i,m is harmonic.

Substituting the velocity potential (195) in (189) and using the temporal derivative (45) of s_r,i,m, we compute the kinematic pressure of the random Stokes problem decomposed in the tRSK structures s_r,x,i,m, s_r,y,i,m and the tRSK_t structure s_r,t,i,m in the following form:

(196)

We then justify the general solution (193) and (196) of the random Stokes Equations (172)-(173) in the tRVK, tRSK, and tRSK_t structures by taking the temporary derivative (69) of the tRVK structure s_r,i,m as follows:

(197)

As s_r,i,m is harmonic,

(198)

Using the gradient of the tRSK structures s_r,x,i,m, s_r,y,i,m (53) and the tRSK_t structure s_r,t,i,m (57), we compute the gradient of p_S,r as follows:

(199)

Substitution of Equations (197)-(199) in the momentum conservation law (172) of the random Stokes problem gives that it is fulfilled. The tRVK structure s_r,i,m is divergence-free. Thus, the mass conservation law (173) of the random Stokes problem is also satisfied.

Combining (159), (181), (193), (183), (195), (165), (184), and (196), we compute the turbulent velocity field

(200)

the scalar Helmholtz potential of the turbulent velocity field

(201)

and the turbulent kinematic pressure

(202)

in terms of the tDVK, tRVK, tDSK, tRSK, and tRSK_t structures, where the time-dependent amplitudes are provided by (46).

6.3. The Turbulent Boundary Function

To find an admissible form of the deterministic boundary function of (168), we compute a general solution for a z-component u_d,z of the deterministic velocity field. In agreement with (176), (183), (34), and (9),

(203)

Similar to the 3-v tDSK structure s_d,i,m = [a_d,m, b_d,m, c_d,m, d_d,m](X_d,m, Y_d,m, z) (1), define a 2-v tDSK boundary structure

(204)

where [a_b,d,m, b_b,d,m, c_b,d,m, d_b,d,m](X_b,d,m, Y_b,d,m) are 2-v eDSK boundary structures, which are defined in the following form:

(205)

where m = 1, 2, ..., M is an index of boundary deterministic waves, M is a total number of boundary waves in a deterministic wave group, Av_b,d,m, Bv_b,d,m, Cv_b,d,m, Dv_b,d,m are boundary amplitudes of v_d(x, y, z, t).

Here, 2-v eDSK boundary functions [ss_b,d,m, cs_b,d,m, sc_b,d,m, cc_b,d,m](X_b,d,m, Y_b,d,m) are products

(206)

of the following 1-v eDSK boundary functions [sx_b,d,m, cx_b,d,m](X_b,d,m) and [sy_b,d,m, cy_b,d,m](Y_b,d,m):

(207)

where X_b,d,m = X_b,d,m(x, t) and Y_b,d,m = Y_b,d,m(y, t) are 2-v boundary deterministic propagation variables defined by

(208)

In Equations (204)-(208), [X_b,d,m, Y_b,d,m] is the Cartesian coordinate of a frame of reference moving with the mth boundary deterministic wave, [U_b,d,m, V_b,d,m] is the celerity of propagation of the mth boundary deterministic wave, [X_b,d,m,0, Y_b,d,m,0] is a reference value of [X_b,d,m, Y_b,d,m] at t = 0, x = 0, y = 0.

In terms of the tDSK boundary structure s_b,d,i,m (204), the deterministic boundary function

(209)

If and only if

(210)

then the 2-v deterministic propagation variables, the 1-v eDSK functions, the 3-v eDSK functions, the 3-v eDSK structures, and the 3-v tDSK structure s_d,i,m are related with the correspondent boundary variables as follows:

(211)

and the Dirichlet boundary condition of (171)

(212)

is fulfilled identically both for U and L. The conditions at infinities of (171) are also fulfilled since ez_d,m(z) becomes the decay model both in U and L due to the sign parameter η.

To compute an admissible form of the random boundary function of (168), we find a general solution for the z-component u_r,z of the random velocity field. In the view of (188), (195), and (19),

(213)

Continuing the 3-v tRSK structure s_r,i,m = [a_r,m, b_r,m, c_r,m, d_r,m](X_r,m, Y_r,m, z) (10), we define a 2-v tRSK boundary structure

(214)

where [a_b,r,m, b_b,r,m, c_b,r,m, d_b,r,m](X_b,r,m, Y_b,r,m) are 2-v eRSK boundary structures, which are specified as

(215)

In (215), m = 1, 2, ..., M is an index of boundary random waves, M is a number of boundary waves in a random wave group,

(216)

are boundary amplitudes of v_r(x, y, z, t).

Here, 2-v eRSK boundary functions [ss_b,r,m, cs_b,r,m, sc_b,r,m, cc_b,r,m](X_b,r,m, Y_b,r,m) are specified by products

(217)

of the following 1-v eRSK boundary functions [sx_b,r,m, cx_b,r,m](X_b,r,m) and [sy_b,r,m, cy_b,r,m](Y_b,r,m):

(218)

where X_b,r,m = X_b,r,m(x, t) and Y_b,r,m = Y_b,r,m(y, t) are 2-v boundary random propagation variables set by

(219)

In Equations (214)-(219), [X_b,r,m, Y_b,r,m] is the Cartesian coordinate of a frame of reference moving with the mth boundary random wave, [U_b,r,m, V_b,r,m] is a celerity of propagation of the mth boundary random wave, [X_b,r,m,0, Y_b,r,m,0] is a reference value of [X_b,r,m, Y_b,r,m] at t = 0, x = 0, y = 0, and parameters

(220)

together with (216) are smooth random functions of time from C^∞. The wave numbers κ_b,r,m and λ_b,r,m are random constants.

In the tRSK boundary structure s_b,r,i,m (214), the random boundary function

(221)

If and only if

(222)

then the 2-v random propagation variables, the 1-v eRSK functions, the 3-v eRSK functions, the 3-v eRSK structures, and the 3-v tRSK structure s_r,i,m are connected with the relevant boundary variables as

(223)

and the Dirichlet boundary condition of (174)

(224)

is satisfied exactly for U and L. The conditions at infinities of (174) is satisfied, as well, because ez_r,m(z) expresses the decay model both in U and L.

Combining (168), (209), and (221) yields the turbulent boundary function

(225)

7. The Turbulent Navier Field

7.1. Expansion of the Turbulent Navier Field

For the turbulent Navier field F_N,t (154)-(155), the turbulent Navier problem of computing the scalar Helmholtz potential p_N,t of F_N,t is reduced to solving the turbulent Navier equation (175).

Complementing kinematic expansions (179)-(180) of u_d for dynamic problems, we have two expansions in the velocity fields of I deterministic wave groups

(226)

with M internal waves per deterministic wave group. The velocity fields u_d,i and u_d,j are expanded in the tDVK structures as follows:

(227)

Combining (226) and (227) yields four equivalent presentations of the deterministic velocity field

(228)

viz. quadrality of u_d.

Analogously, continuation of (191)-(192) for dynamic problems yields two decompositions of u_r via the velocity fields of I random wave groups

(229)

with M internal waves per random wave group. The velocity fields u_r,i and u_r,j are decomposed in the tRVK structures in the following form:

(230)

We then combine (229) and (230) to show quadrality of the random velocity field as

(231)

Substitution of the flow decomposition (159) in the turbulent Navier field (154) and expansion of the dot product of u_t and ∇ gives

(232)

(233)

where F_N,d,d is the Navier field of self-interaction of the deterministic flow, F_N,d,r is the Navier field of interaction between the deterministic and random flows, F_N,r,d is the Navier field of interaction between the random and deterministic flows, and F_N,r,r is the Navier field of self-interaction of the random flow.

Substitution of the group decompositions (227), (230) in the Navier fields (233), expansion of the dot products, and reduction of the product of two one-dimensional (1-d) sums to a two-dimensional (2-d) sum by

(234)

yields

(235)

Since a sum of terms transposed in (i, j) is equivalent to the sum of original terms, i.e.

(236)

a sum of the interaction Navier fields F_N,d,r and F_N,r,d may be recast to a symmetrical form

(237)

With the help of (117) of [17]

(238)

we convert the rectangular summation of (235) into the diagonal and triangular summations with the aim of computing a decomposition of F_N,t into five Navier fields

(239)

First, the diagonal (j = i) Navier field F_N,g,d,i,d,i of I selfsame deterministic wave groups

(240)

where F_N,d,i,d,i is the Navier field of diagonal interaction of the selfsame ith deterministic wave group, which is described by the half of the anticommutator of [u_d,i, u_d,i] for i = 1, 2, ..., I.

Second, the non-diagonal (j > i) Navier field F_N,g,d,i,d,j of non-diagonal interaction between I(I − 1)/2 distinct deterministic wave groups

(241)

where F_N,d,i,d,j is the Navier field of non-diagonal interaction between the distinct ith and jth deterministic wave groups, which is given by the anticommutator of [u_d,i, u_d,j] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I.

Third, the Navier field F_N,g,d,i,r,j of interaction between I² (all diagonal and non-diagonal) deterministic and random wave groups

(242)

where F_N,d,i,r,j is the Navier field of interaction between the ith deterministic and jth random wave groups, which is provided by the anticommutator of [u_d,i, u_r,j] for i = 1, 2, ..., I, j = 1, 2, ..., I.

Fourth, the non-diagonal Navier field F_N,g,r,i,r,j of non-diagonal interaction between I(I − 1)/2 distinct random wave groups

(243)

where F_N,r,i,r,j is the Navier field of non-diagonal interaction between the distinct ith and jth random wave groups, which is specified by the anticommutator of [u_r,i, u_r,j] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I.

Fifth, the diagonal Navier field F_N,g,r,i,r,i of I selfsame random wave groups

(244)

where F_N,r,i,r,i is the Navier field of diagonal interaction of the selfsame ith random wave group, which is expressed by the half of the anticommutator of [u_r,i, u_r,i] for i = 1, 2, ..., I.

There are following relationships between constituents of the rectangular, diagonal, and triangular expansions of the Navier field F_N,t:

(245)

Consequently, the five-terms expansion (239) of the turbulent Navier field may be reduced to a three-terms expansion

(246)

Rectangular summation matrices

(247)

of the Navier fields (235) are shown in Figure 3 in the decomposed form via diagonal elements and elements of the lower and upper triangular matrices.

Figure 3. The summation matrices M_N,d,d, M_N,d,r, M_N,r,d, and M_N,r,r (247) are shown by (a), (b), (c), and (d), correspondingly.

Interchange of group indices [i = j, j = i] describes transposition of elements of all four matrices with respect to local group diagonals j = i for matrix elements (u_d,i×∇)u_d,j and (u_d,j×∇)u_d,i, (u_d,i×∇)u_r,j and (u_d,j×∇)u_r,i, (u_r,i×∇)u_d,j and (u_r,j×∇)u_d,i, (u_r,i×∇)u_r,j and (u_r,j×∇)u_r,i. Interchange of pairs of group indices [d = r, i = j, r = d, j = i] corresponds to transposition of elements of matrices M_N,d,r and M_N,r,d with respect to a global group diagonal j = i, which coincides with the local group diagonals of matrices M_N,d,d and M_N,r,r. For instance consider matrix elements (u_d,i×∇)u_r,j and (u_r,j×∇)u_d,i,(u_d,j×∇)u_r,i and (u_r,i×∇)u_d,j.

The global group diagonal coincides with a local diagonal of a summation matrix

(248)

of the Navier field (232). So, M_N,t is a summation matrix of with elements M_N,d,d, M_N,d,r, M_N,r,d, and M_N,r,r, which are matrices themselves shown in Figure 3, because

(249)

In Figure 3(a), the general term (u_d,i×∇)u_d,i of F_N,d,i,d,i (240) sums up diagonal elements of M_N,d,d. Since the first index of the directional derivative is a counter of rows and the second index is a counter of columns, the first general term (u_d,i×∇)u_d,j of F_N,d,i,d,j (241) sums up by rows elements of the upper triangular matrix of M_N,d,d and the second general term (u_d,j×∇)u_d,i sums up by columns elements of the lower triangular matrix of M_N,d,d.

In Figure 3(b) and Figure 3(c), the first general term (u_d,i×∇)u_r,j of F_N,d,i,r,j (242) sums up by rows all elements of matrix M_N,d,r, and the second general term (u_r,j×∇)u_d,i sums up by columns all elements of matrix M_N,r,d.

In Figure 3(d), the general term (u_r,i×∇)u_r,i of F_N,r,i,r,i (244) sums up diagonal elements of M_N,r,r, the first general term (u_r,i×∇)u_r,j of F_N,r,i,r,j (243) sums up by rows elements of the upper triangular matrix of M_N,r,r, and the second general term (u_r,j×∇)u_r,i sums up by columns elements of the lower triangular matrix of M_N,r,r.

We then substitute the decomposition of the velocity fields (227) and (230) in (240)-(244), expand the dot products, and combine the product of 1-d sums into a 2-d sum to get the following rectangular expansions:

(250)

To use Equation (238) in the case of rectangular summation in internal waves (250), we substitute in (238) i = m, j = n, I = M to compute

(251)

Using (250)-(251) yields that the Navier field F_N,d,i,d,i (240) is expanded in two sums:

(252)

First, the internal (n = m) sum of the Navier field F_{N,d,i,m,d,i,m} of propagation of the mth wave from the selfsame the ith deterministic wave group

(253)

which is represented via the half-anticommutator of the tDVK structures [s_d,i,m, s_d,i,m] for i = 1, 2, ..., I and m = 1, 2, ..., M.

Second, the external (n > m) sum of the Navier field F_{N,d,i,m,d,i,n} of diagonal interaction between the distinct mth and nth waves from the selfsame ith deterministic wave group

(254)

which is described by the anticommutator of the tDVK structures [s_d,i,m, s_d,i,n] for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

Similarly, the Navier field F_N,d,i,d,j (241) may be decomposed in two sums

(255)

First, the internal sum of the Navier field F_{N,d,i,m,d,j,m} of non-diagonal interaction between the mth waves from the distinct ith and jth deterministic wave groups

(256)

which is expressed in terms of the anticommutator of the tDVK structures [s_d,i,m, s_d,j,m] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

Second, the external sum of the Navier fields F_{N,d,i,m,d,j,n} of non-diagonal interaction between the distinct mth and nth waves from the distinct ith and jth deterministic wave groups

(257)

which is presented by two anticommutators of the tDVK structures [s_d,i,m, s_d,j,n] and [s_d,i,n, s_d,j,m] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

We then use (250)-(251) to find that the Navier field F_N,d,i,r,j (242) is also superposed in two sums

(258)

First, the internal sum of the Navier fields F_{N,d,i,m,r,j,m} of non-diagonal interaction between the mth waves from all ith deterministic and jth random wave groups

(259)

which is implemented by the anticommutator of the tDVK and tRVK structures [s_d,i,m, s_r,j,m] for i = 1, 2, ..., I, j = 1, 2, ..., I, and m = 1, 2, ..., M.

Second, the external sum of the Navier fields F_{N,d,i,m,r,j,n} of non-diagonal interaction between the distinct mth and nth waves from all ith deterministic and jth random wave groups

(260)

which is displayed by two anticommutators of the tDVK and tRVK structures [s_d,i,m, s_r,j,n] and [s_d,i,n, s_r,j,m] for i = 1, 2, ..., I, j = 1, 2, ..., I, m = 1, 2, ..., M, and n = 1, 2, ..., M.

Analogously, the Navier field F_N,r,i,r,j (243) is again expanded in two sums

(261)

First, the internal sum of the Navier field F_{N,r,i,m,r,j,m} of non-diagonal interaction between the mth waves from the distinct ith and jth random wave groups

(262)

which is described via the anticommutator of the tRVK structures [s_r,i,m, s_r,j,m] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

Second, the external sum of Navier field F_{N,r,i,m,r,j,n} of non-diagonal interaction between the distinct mth and nth waves from the distinct ith and jth random wave groups

(263)

which is demonstrated by two anticommutators of the tRVK structures [s_r,i,m, s_r,j,n] and [s_r,i,n, s_r,j,m] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

Finally, usage of (250)-(251) shows that the Navier field F_N,r,i,r,i (244) is decomposed in two sums, as well,

(264)

First, the internal sum of the Navier field F_{N,r,i,m,r,i,m} of propagation of the mth wave from the selfsame ith random wave group

(265)

which is presented via the half-anticommutator of the tRVK structures [s_r,i,m, s_r,i,m] for i = 1, 2, ..., I and m = 1, 2, ..., M.

Second, the external sum of the Navier field F_{N,r,i,m,r,i,n} of diagonal interaction between the distinct mth and nth waves from the selfsame ith random wave group

(266)

which is displayed by the anticommutator of the tRVK structures [s_r,i,m, s_r,i,n] for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

Rectangular summation matrices

(267)

of the Navier fields (250) are shown in Figure 4 in the decomposed form in terms of diagonal elements and elements of the lower and upper triangular matrices.

Summation matrix M_N,d,i,d,i of element (u_d,i×∇)u_d,i of summation matrix M_N,d,d, which is shown in Figure 3(a), is represented in Figure 4(a). The general term (s_d,i,m×∇)s_d,i,m of F_{N,d,i,m,d,i,m} (253) sums up diagonal elements of M_N,d,i,d,i, the first general term (s_d,i,m×∇)s_d,i,n of F_{N,d,i,m,d,i,n} (254) sums up by rows elements of the upper triangular matrix of M_N,d,i,d,i, and the second general term (s_d,i,n×∇)s_d,i,m sums up by columns elements of the lower triangular matrix of M_N,d,i,d,i.

In Figure 4(b), summation matrix M_N,d,i,d,j of the sum of elements (u_d,i×∇)u_d,j + (u_d,j×∇)u_d,i of summation matrix M_N,d,d, which are displayed in Figure 3(a), is visualized. The general term (s_d,i,m×∇)s_d,j,m + (s_d,j,m×∇)s_d,i,m of F_{N,d,i,m,d,j,m} (256) sums up diagonal elements of M_N,d,i,d,j. The first general term (s_d,i,m×∇)s_d,j,n + (s_d,j,m×∇)s_d,i,n of F_{N,d,i,m,d,j,n} (257) sums up by rows elements of the upper triangular matrix of M_N,d,i,d,j. The second general term (s_d,i,n×∇)s_d,j,m + (s_d,j,n×∇)s_d,i,m sums up by columns elements of the lower triangular matrix of M_N,d,i,d,j.

Summation matrix M_N,d,i,r,j of the sum of elements (u_d,i×∇)u_r,j + (u_r,j×∇)u_d,i of summation matrices M_N,d,r and M_N,r,d, which are shown in Figure 3(b) and Figure 3(c), respectively, is presented in Figure 4(c). The general term (s_d,i,m×∇)s_r,j,m + (s_r,j,m×∇)s_d,i,m of F_{N,d,i,m,r,j,m} (259) sums up diagonal elements of M_N,d,i,r,j. The first general term (s_d,i,m×∇)s_r,j,n + (s_r,j,m×∇)s_d,i,n of F_{N,d,i,m,r,j,n} (260) sums up by rows elements of the upper triangular matrix of M_N,d,i,r,j. The second general term (s_d,i,n×∇)s_r,j,m + (s_r,j,n×∇)s_d,i,m sums up by columns elements of the lower triangular matrix of M_N,d,i,r,j.

(a)(b)(c)(d)(e)

Figure 4. The summation matrices M_N,d,i,d,i, M_N,d,i,d,j, M_N,d,i,r,j, M_N,r,i,r,j, and M_N,r,i,r,i (267) are displayed by (a), (b), (c), (d), and (e), respectively.

In Figure 4(d), summation matrix M_N,r,i,r,j of the sum of elements(u_r,i×∇)u_r,j + (u_r,j×∇)u_r,i of summation matrix M_N,r,r, which is displayed in Figure 3(d), is represented. The general term (s_r,i,m×∇)s_r,j,m + (s_r,j,m×∇)s_r,i,m of F_{N,r,i,m,r,j,m} (262) returns a sum of diagonal elements of M_N,r,i,r,j. The first general term (s_r,i,m×∇)s_r,j,n + (s_r,j,m×∇)s_r,i,n of F_{N,r,i,m,r,j,n} (263) sums up by rows elements of the upper triangular matrix of M_N,r,i,r,j. The second general term (s_r,i,n×∇)s_r,j,m + (s_r,j,n×∇)s_r,i,m sums up by columns elements of the lower triangular matrix of M_N,r,i,r,j.

Summation matrix M_N,r,i,r,i of element (u_r,i×∇)u_r,i of summation matrix M_N,r,r, which is shown in Figure 3(d), is presented in Figure 4(e). The general term (s_r,i,m×∇)s_r,i,m of F_{N,r,i,m,r,i,m} (265) computes a sum of diagonal elements of M_N,r,i,r,i, the first general term (s_r,i,m×∇)s_r,i,n of F_{N,r,i,m,r,i,n} (266) sums up by rows elements of the upper triangular matrix of M_N,r,i,r,i, and the second general term (s_r,i,n×∇)s_r,i,m finds by columns a sum of elements of the lower triangular matrix of M_N,r,i,r,i.

7.2. Potentialization of the Turbulent Navier Field

The Navier fields F_{N,d,i,m,d,i,m} (253) and F_{N,d,i,m,d,i,n} (254) may be transformed into a potential form with the help of the Helmholtz decomposition (134) and (138) of the derivative of s_d,i,m in the direction of s_d,i,m, the derivative of s_d,i,n in the direction of s_d,i,m, and the derivative of s_d,i,m in the direction of s_d,i,n. Explicitly,

(268)

We then compute the anticommutator

(269)

which shows cancelling out the vector Helmholtz potentials and potentialization of the anticommutator of [s_d,i,m, s_d,i,n].

Substituting anticommutators of (268)-(269) in (252)-(254) and factoring the gradients yield

(270)

Analogously, we compute the Helmholtz decomposition of the derivative of s_d,j,m in the direction of s_d,i,m, the derivative of s_d,i,m in the direction of s_d,j,m, the derivative of s_d,j,n in the direction of s_d,i,m, the derivative of s_d,i,m in the direction of s_d,j,n, the derivative of s_d,j,m in the direction of s_d,i,n, and the derivative of s_d,i,n in the direction of s_d,j,m in the following form:

(271)

Therefore, three anticommutators become

(272)

So, cancelling out the vector Helmholtz potentials once more produces potentialization of the anticommutators of [s_d,i,m, s_d,j,m], [s_d,i,m, s_d,j,n], and [s_d,i,n, s_d,j,m].

Substituting anticommutators (272) in (255)-(257) and taking out the gradient operator give

(273)

To potentialize the Navier fields F_{N,d,i,m,r,j,m} (259) and F_{N,d,i,m,r,j,n} (260), we use the Helmholtz decomposition (135)-(136) and (139)-(140) of the derivative of s_r,j,m in the direction of s_d,i,m, the derivative of s_d,i,m in the direction of s_r,j,m, the derivative of s_r,j,n in the direction of s_d,i,m, the derivative of s_d,i,m in the direction of s_r,j,n, the derivative of s_r,j,m in the direction of s_d,i,n, and the derivative of s_d,i,n in the direction of s_r,j,m. Specifically,

(274)

Computation of three anticommutators

(275)

again results in cancelling out the vector Helmholtz potentials and potentialization of the anticommutators of [s_d,i,m, s_r,j,m], [s_d,i,m, s_r,j,n], and [s_d,i,n, s_r,j,m].

Substitution of anticommutators (275) in (258)-(260) returns a potentialized form of

(276)

Analogously, the Helmholtz decomposition (137) and (141) of the derivative of s_r,j,m in the direction of s_r,i,m, the derivative of s_r,i,m in the direction of s_r,j,m, the derivative of s_r,j,n in the direction of s_r,i,m, the derivative of s_r,i,m in the direction of s_r,j,n, the derivative of s_r,j,m in the direction of s_r,i,n, and the derivative of s_r,i,n in the direction of s_r,j,m are following:

(277)

Using directional derivatives (277), we obtain three anticommutators

(278)

The vector Helmholtz potentials are cancelled out and the anticommutators of [s_r,i,m, s_r,j,m], [s_r,i,m, s_r,j,n], and [s_r,i,n, s_r,j,m] are potentialized, as well.

Substitution of anticommutators (278) in (261)-(263) returns a potentialized form of the Navier field

(279)

Eventually, the Navier fields F_{N,r,i,m,r,i,m} (265) and F_{N,r,i,m,r,i,n} (266) may be converted into the potential form with the help of the Helmholtz decomposition of the derivative of s_r,i,m in the direction of s_r,i,m, the derivative of s_r,i,n in the direction of s_r,i,m, and the derivative of s_r,i,m in the direction of s_r,i,n. Namely,

(280)

Calculation of the anticommutator

(281)

again produces cancelling out the vector Helmholtz potentials and potentialization of the anticommutator of [s_r,i,m, s_r,i,n].

Substituting anticommutators of (280)-(281) in (264)-(266) and pulling out the gradient operator give

(282)

Finally, we combine the potentialized Navier fields (270), (273), (276), (279), (282) in agreement with (240)-(245) to obtain a potentialized form of the Navier field of the deterministic flow

(283)

the Navier field of the deterministic-random flow

(284)

and the Navier field of the random flow

(285)

The vector Helmholtz potentials cancel out due to the third Newton law since the vector Helmholtz potentials express internal forces of interaction between the turbulent internal waves. In accordance with the third Newton law, the internal forces possess the same magnitudes and opposite directions, i.e. compensate each other. The scalar Helmholtz potentials describe external forces with a non-trivial resultant, which moves the turbulent internal waves in agreement with the second Newton law.

7.3. Reduction of the Turbulent Navier Field

The orders of diagonal summations in i and m, triangular summations in (i, j) and (m, n), and the rectangular summation in (i, j) may be interchanged as follows:

(286)

(287)

(288)

(289)

(290)

(291)

(292)

(293)

Using (286)-(290), the Navier field (283) of the deterministic flow may be converted to

(294)

With the help of (291)-(293), the commutative symmetry of the dot product, and the invariance of the transposed summation

(295)

the Navier field (284) of the deterministic-random flow is transformed into

(296)

Similarly to (294), the Navier field of the random flow becomes

(297)

Analogous to (238), we compute the following inverse reductions of the diagonal and triangular summations to the rectangular summation in (i, j)

(298)

(299)

Usage of (298)-(299) enables to eliminate the diagonal and triangular summations in (i, j) and transform the Navier field (294) of the deterministic flows and the Navier field (297) of the random flow to

(300)

(301)

Summation of (300), (296), and (301) in the view of (246), the invariance of the transposed summation (295), and factoring return the Navier field of the turbulent flow

(302)

Similar to (251), we then find the following inverse reductions of the diagonal and triangular summations to the rectangular summation in (m, n)

(303)

(304)

To derive (304), the general term A_m·A_n of sums of (303) is replaced with the summation matrix of A_i,m·A_j,n in (i, j). Equation (304) is reduced to (303) for I = 1. All theoretical relationships between the diagonal, triangular, and rectangular summations (234), (236), (238), (251), (286)-(293), (295), (298)-(299), (303)-(304), (329)-(330), (332), (334), and (336) have been also justified using experimental programming in Maple.

In the view of (304), the diagonal and triangular summations in (m, n) are replaced with the rectangular summation of (302) to conclude with a last potentialized form of the Navier field of the turbulent flow

(305)

Using the definition of the kinetic energy and velocity expansions (159), (226), (228), (229), (231), we change the orders of summation to get the following alternative presentations of the kinetic energy of turbulent flow

(306)

Comparison of (305) with (306) and (155) yields a relationship between the turbulent Navier field and the kinetic energy

(307)

and the scalar Helmholtz potential of the turbulent Navier field

(308)

7.4. The Dynamic and Cumulative Pressure Fields of the Turbulent Navier-Stokes Problem

The kinetic energy of the turbulent flow (306) may be decomposed in four constituents

(309)

where

(310)

is the kinetic energy of self-interaction of the deterministic flow,

(311)

is the kinetic energy of interaction between the deterministic and random flows,

(312)

is the kinetic energy of interaction between the random and deterministic flows, and

(313)

is the kinetic energy of self-interaction of the random flow.

Using the alternative definition (308) of the kinetic energy via the dynamic pressure and the dot product of the tDVK (50) and tRVK (54) structures, we obtain the dynamic pressure of self-interaction of the deterministic flow

(314)

in the tDDSD structures (72), the dynamic pressure of interaction between the deterministic and random flows

(315)

in the tDRSD structures (76), the dynamic pressure of interaction between the random and deterministic flows

(316)

in the tRDSD structures (80), and the dynamic pressure of self-interaction of the random flow

(317)

in the tRRSD structures (84).

In agreement with (308)-(309),

(318)

Combining the scalar Helmholtz potentials of the superposition of the Archimedean field (158), the turbulent Stokes field (202), and the turbulent Navier field (314)-(318) returns the cumulative pressure of the turbulent flow

(319)

in terms of the tDSK, tRSK, tRSK_t, tDDSD, tDRSD, tRDSD, and tRRSD structures.

7.5. Justification of the Turbulent Navier Problem

To verify the turbulent solution (159), (228), (231), (314)-(318) by (175), we use an expanded vector form of the directional derivatives (233)

(320)

In agreement with (228) and (231), the x-, y-, z-components of u_d are

(321)

the x-, y-, z-components of u_r are

(322)

and the deterministic and random velocity fields are, respectively,

(323)

Substitution of (321)-(323) in (320) and combining sums gives

(324)

We then substitute the spatial derivatives (34) and (64) of the tDSK, tRSK, tDVK, and tRVK structures and collect like terms to represent the derivative of u_d in the direction of u_d in terms of the tDDVD structures of the nth family (96)

(325)

the derivative of u_r in the direction of u_d via the tDRVD structures of the nth family (104)

(326)

the derivative of u_d in the direction of u_r through the tRDVD structures of the nth family (112)

(327)

and the derivative of u_r in the direction of u_r in the tRRVD structures of the nth family (120)

(328)

Application of the 4-d summation of transposed elements with indices [j = i, i = j, n = m, m = n]

(329)

yields an identity

(330)

Therefore, directional derivative (325) may be represented via the tDDVD structures of the mth (94) and nth (96) families in the following symmetric form:

(331)

Similarly, using (329), we have

(332)

So, (326) may be rewritten in a symmetrical form in terms of the tRDVD structures of the mth family (110) and the tDRVD structures of the nth family (104) as follows:

(333)

With the help of (329), we obtain an identity

(334)

which enables to recast (327) through the tDRVD structures of the mth family (102) and the tRDVD structures of the nth family (112) as

(335)

Eventually, we use (329) to get

(336)

The last identity gives an opportunity to transform (328) symmetrically in the tRRVD structures of the mth (118) and nth (120) families

(337)

Using the product rule of vector differentiation [23] ,

(338)

we then split the gradient ∇p_N,d,d of the deterministic dynamic pressure (314) into two parts. In the first part named ∇_mp_N,d,d, terms including ∇[s_d,x,i,m, s_d,y,i,m, s_d,i,m] = [s_d,x,i,m, s_d,y,i,m, s_d,i,m] are collected. In the second part specified as ∇_np_N,d,d, terms with ∇[s_d,x,j,n, s_d,y,j,n, s_d,j,n] = [s_d,x,j,n, s_d,y,j,n, s_d,j,n] are included. Explicitly,

(339)

where, in agreement with (142),

(340)

is computed in terms of the tDDVD structures of the mth family (94) and

(341)

via the tDDVD structures of the nth family (96).

With the help of (338), the gradient ∇p_N,d,r of the deterministic-random dynamic pressure (315) is decomposed into two parts. The first part, which is termed ∇_mp_N,d,r, includes ∇[s_d,x,i,m, s_d,y,i,m, s_d,i,m] = [s_d,x,i,m, s_d,y,i,m, s_d,i,m]. The second part, which is named as ∇_np_N,d,r, contains terms with ∇[s_r,x,j,n, s_r,y,j,n, s_r,j,n] = [s_r,x,j,n, s_r,y,j,n, s_r,j,n]. Namely,

(342)

where

(343)

is expressed in the tDRVD structures of the mth family (102) and

(344)

through the tDRVD structures of the nth family (104).

Similarly, we split the gradient ∇p_N,r,d of the random-deterministic dynamic pressure (316) into two parts. In the first part named ∇_mp_N,r,d, terms containing ∇[s_r,x,i,m, s_r,y,i,m, s_r,i,m] = [s_r,x,i,m, s_r,y,i,m, s_r,i,m] are presented. In the second part termed ∇_np_N,r,d, terms with ∇[s_d,x,j,n, s_d,y,j,n, s_d,j,n] = [s_d,x,j,n, s_d,y,j,n, s_d,j,n] are collected. Specifically,

(345)

where

(346)

is represented with the help of the tRDVD structures of the mth family (110) and

(347)

using the tRDVD structures of the nth family (112).

In agreement with (338), the gradient ∇p_N,r,r of the random dynamic pressure (317) is expanded into two parts. The first part that is named ∇_mp_N,r,r contains ∇[s_r,x,i,m, s_r,y,i,m, s_r,i,m] = [s_r,x,i,m, s_r,y,i,m, s_r,i,m]. The second part that is termed ∇_np_N,r,r includes terms with ∇[s_r,x,j,n, s_r,y,j,n, s_r,j,n] = [s_r,x,j,n, s_r,y,j,n, s_r,j,n]. Therefore,

(348)

where

(349)

is computed via the tRRVD structures of the mth family (118) and

(350)

with the help of the tRRVD structures of the nth family (120).

Combining (233), (331), (339)-(341) yields

(351)

and the following deterministic Navier equation for the Navier field F_N,d,d of the deterministic flow and its scalar Helmholtz potential p_N,d,d (314)

(352)

is satisfied identically.

In accordance with (233), (333), (346), (344),

(353)

and the Navier field F_N,d,r of interaction between the deterministic and random flows is not a potential field as

(354)

In the view of (233), (335), (343), (347),

(355)

and the Navier field F_N,r,d of interaction between the random and deterministic flows is not a potential field, as well, since

(356)

However, in agreement with (245), (353), (355), (342), (345),

(357)

where

(358)

and the following deterministic-random equation for the Navier field F_N,g,d,i,r,j of the deterministic-random flow and its scalar Helmholtz potential p_N,g,d,i,r,j (358), (315), (316)

(359)

is fulfilled exactly.

We combine (233), (337), (348)-(350) to show that

(360)

and the following random Navier equation for the Navier field F_N,r,r of the random flow and its scalar Helmholtz potential p_N,r,r (317)

(361)

is accomplished precisely.

Finally, we use (232), (233), (351), (357), (360), and (318) to derive that

(362)

and the turbulent Navier equation (175) for the Navier field F_N,t of the turbulent flow and its scalar Helmholtz potential p_N,t is strictly justified.

8. Conclusion

The most interesting properties of the scalar and vector kinematic structures that are treated in Sections 2-3 are the deterministic-random invariance with respect to the spatial differentiation, the scalar and vector structural oscillations, the scalar-vector duality, the equiprobability of the experimental and theoretical, scalar and vector, kinematic structures [16] , and quadrality of the theoretical, scalar and vector, kinematic structures.

The differentiation diagram in Figure 1 represents a mathematical 2-d dice, where all vertices have exactly the same probability despite the various scales of differentiation in the x- and y-directions.

The success of the scalar and vector dynamic structures that are defined and studied in Sections 4-5 is stipulated by similarity of their algebraic structure to that of the Navier-Stokes equations since the momentum conservation law (143) is expressed in terms of a superposition of kinematic terms and dynamic terms with an algebraic nonlinearity.

A further attractive feature of the scalar and vector, kinematic and dynamic structures is absence of formal restrictions on functional amplitudes, wave parameters, Reynolds numbers, Cartesian coordinates, and times. The algebraic structure of the vector dynamic structures is actually displayed by five-dimensional arrays, where two dimensions are produced by interaction of M deterministic and M random waves, one dimension refers to a vector in the 3-d Cartesian coordinates, and two dimensions are generated by interaction of I deterministic and I random wave groups.

The large number of the experimental scalar and dynamic structures, 16 and 32, respectively, is required for the completeness of expansions of the directional derivatives of the velocity field and the gradient of the dynamic pressure since otherwise the vortical forces produced by the vector potential (138)-(141) of the Helmholtz decomposition will not compensate each other and potentialization of the Navier fields (283)-(285) will become impossible.

Consequently, experimental and theoretical programming in Maple, which facilitates computation and verification of numerous arrays of the scalar and vector dynamic structures, is essential for the proof of the necessary (Sections 7.1-7.3) and sufficient (Section 7.5) conditions of existence of the exact solution to the turbulent Navier problem (175).

Since the exact solution to the turbulent Navier-Stokes equations (143)-(144) is not effected by viscous dissipation it may serve as the 3-d model of conservative propagation and interaction of turbulent internal waves in ocean and atmosphere via the exponential oscillons and pulsons. Thus, exact wave turbulence demonstrates accumulation and conservation of green kinetic energy via oceanic internal waves.

Initially, a smooth random function of time as a part of the exact solution of fluid dynamics appeared in the form of a reference pressure p₀(t) in the Cauchy integral of motion. The exact solution for wave turbulence of exponential oscillons and pulsons includes numerous smooth random function of time (13), (20), (24), (216), and (220) for m = 1, 2, ¼, M from C^∞, which are required to specify random exponential oscillons and pulsons and interaction between deterministic and random exponential oscillons and pulsons. So, construction of smooth random functions of time with oscillatory and pulsatory topology is an open problem, which will give an opportunity to visualize and analyze random and turbulent internal waves.

It is also interesting to develop theoretical and experimental quantizations of exact wave turbulence, which generalize the theoretical and experimental quantizations of the deterministic chaos for the Fourier [19] and Bernoulli [20] sets of wave parameters and the theoretical quantization of the stochastic chaos [17] . Indeed, it looks appealing to study the Eulerian, Lagrangian, and Kolmogorovian properties of exact wave turbulence and compare them with results obtained in the frames of statistical wave turbulence and resonant wave turbulence.

Acknowledgements

The support of CAAM and the University of Mount Saint Vincent is gratefully acknowledged. The author thanks a reviewer for helpful comments, which have perfected the paper.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Davidson, P.A. (2004) Turbulence—An Introduction for Scientists and Engineers. Oxford University Press, Oxford.
[2]	Kolmogorov, A.N. (1941) The Local Structure of Turbulence in Incompressible Viscous Flow for Very Large Reynolds Numbers. Doklady Akademii Nauk SSSR, 30, 299-303.
[3]	Kolmogorov, A.N. (1941) On Degeneration (Decay) of Isotropic Turbulence in an Incompressible Viscous Liquid. Doklady Akademii Nauk SSSR, 31, 538-541.
[4]	Kolmogorov, A.N. (1941) Dissipation of Energy in the Locally Isotropic Turbulence. Doklady Akademii Nauk SSSR, 32, 19-21.
[5]	Kolmogorov, A.N. (1962) A Refinement of Previous Hypotheses Concerning the Local Structure of Turbulence in a Viscous Incompressible Fluid at High Reynolds Number. Journal of Fluid Mechanics, 13, 82-85. https://doi.org/10.1017/S0022112062000518
[6]	Frisch, U. (1995) Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781139170666
[7]	Obukhov, A.M. (1941) On the Energy Distribution in the Spectrum of a Turbulent Flow. Doklady Akademii Nauk SSSR, 32, 22-24.
[8]	Obukhov, A.M. (1983) The Kolmogorov Flow and Laboratory Simulation of It. Russian Mathematical Surveys, 35, 113-126. https://doi.org/10.1070/RM1983v038n04ABEH004207
[9]	Batchelor, G.K. (1953) The Theory of Homogeneous Turbulence. Cambridge University Press, Cambridge.
[10]	Chandler, G. and Kerswell, R. (2013) Invariant Recurrent Solutions Embedded in a Turbulent Two-Dimensional Kolmogorov Flow. Journal of Fluid Mechanics, 722, 554-595. https://doi.org/10.1017/jfm.2013.122
[11]	Revina, S.V. (2017) Stability of the Kolmogorov Flow and Its Modifications. Computational Mathematics and Mathematical Physics, 57, 995-1012. https://doi.org/10.1134/S0965542517020130
[12]	Monin, A.S. and Yaglom, A.M. (2007) Statistical Fluid Mechanics, Volume 1: Mechanics of Turbulence. Dover Publications, New York.
[13]	Teodorovich, E.V. (2013) Possible Way of Closing of the Chain of Equations for Statistical Moments in Turbulence Theory. Journal of Applied Mathematics and Mechanics, 77, 17-24.
[14]	Zakharov, V.E., L’vov, V.S. and Falkovich, G. (1992) Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-50052-7
[15]	Kartashova, E. (2010) Nonlinear Resonance Analysis. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511779046
[16]	Miroshnikov, V.A. (2020) Deterministic Chaos of Exponential Oscillons and Pulsons. American Journal of Computational Mathematics, 10, 43-72. https://doi.org/10.4236/ajcm.2020.101004
[17]	Miroshnikov, V.A. (2023) Stochastic Chaos of Exponential Oscillons and Pulsons. American Journal of Computational Mathematics, 13, 533-577. https://doi.org/10.4236/ajcm.2023.134030
[18]	Miroshnikov, V.A. (2017) Harmonic Wave Systems: Partial Differential Equations of the Helmholtz Decomposition. Scientific Research Publishing, Wuhan. http://www.scirp.org/book/DetailedInforOfABook.aspx?bookID=2494
[19]	Miroshnikov, V.A. (2023) Quantization of the Kinetic Energy of Deterministic Chaos. American Journal of Computational Mathematics, 13, 1-81. https://doi.org/10.4236/ajcm.2023.131001
[20]	Miroshnikov, V.A. (2023) Quantization and Turbulization of Deterministic Chaos of the Exponential Oscillons and Pulsons. BP International, India. https://stm.bookpi.org/QTDCEOP/issue/view/1045 https://doi.org/10.9734/bpi/mono/978-81-19217-39-7
[21]	Miroshnikov, V.A. (2014) Conservative Interaction of N Stochastic Waves in Two Dimensions. American Journal of Computational Mathematics, 4, 289-303. https://doi.org/10.4236/ajcm.2014.44025
[22]	Miroshnikov, V.A. (2014) Conservative Interaction of N Internal Waves in Three Dimensions. American Journal of Computational Mathematics, 4, 329-356. https://doi.org/10.4236/ajcm.2014.44029
[23]	Korn, G.A. and Korn, T.M. (2000) Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. Dover Publications, New York.
[24]	Pozrikidis, C. (2011) Introduction to Theoretical and Computational Fluid Dynamics. 2nd Edition, Oxford University Press, Oxford.