Using Extreme Value Theory Approaches to Estimate High Quantiles for Stroke Data ()
1. Introduction
Recurrent stroke is considered one of the leading causes of death and disability worldwide, accounting for approximately 5 million deaths annually, which constitutes 9% of the total. Additionally, another 5 million people suffer from long-term disability.
According to the literature, numerous risk factors for recurrent stroke exist, including age, sex, smoking status, high blood pressure measurement, and lipid metabolism. Several researchers have identified these risk factors, as noted by [1] . Their findings reveal a significant increase in systolic blood pressure among patients with late recurrent stroke. Besides, [2] identified hypertension as the leading cause of recurrent stroke.
Furthermore, [3] discovered a significantly higher stroke recurrence rate in men, older individuals, and those with a prior history of ischemic stroke compared to women, younger individuals, and those with no history of stroke. Moreover, in their results, [4] recommend considering hypertension, diabetes mellitus, atrial fibrillation, and coronary heart disease as factors associated with a high risk of stroke recurrence.
In the context of this paper, the time of stroke occurrence is treated as survival data. Survival or (time-to-event) data analysis problems have arisen in a number of scientific fields. For instance, an event time of interest can be the survival time of a stroke patient in a medical study, the time to high school dropout studied by sociologists, the survival time of a new business addressed in economic research, or a lifetime of a part under stress evaluated in an engineering reliability study.
A common characteristic of survival data is often the presence of incomplete time-to-event information due to censoring or truncation. Here, we consider that the censoring appeared when a time to-event is known to have occurred only within certain intervals. Besides, truncation is defined as a condition which excludes certain subjects from the study population for more details see [5] . However, survival data analysis needs an appropriate statistical approach which takes into account a different form of censoring. Many authors have addressed this issue, we can cite a few among them [6] [7] [8] [9] for more details.
Nowadays, due to the progress in technology, it is possible for some covariate information to be recorded simultaneously with the quantity of interest in some sort of continuum. This continuum may have a link with time, and space or originate from multiple sources. For those kinds of problems, we deal with the statistical unit as a curve, a space or any more complex mathematic object having the concept of some continuum feature. Then such data are called function data by enumerating few of authors who work with the functional data such as [10] [11] .
This paper proposes to focus on three statistical aspects in order to derive a methodology for estimating conditional extreme quantiles where the variable of interest has a heavy-tailed distribution under right random censoring in the presence of functional random covariate.
Let us consider
independent identically distributed copies of random variable of time to the event of interest Y. It has become a challenge in several fields to estimate extreme quantiles of the distribution of Y which has the form
, with
is small such that
closed to zero as the sample size is large enough. Further, that quantile falls beyond the range of the observed data
. According to the literature, extreme value theory has been proven to be a powerful tool for studying the behavior of extreme event distributions and is widely used in the estimation of the extreme value index (tail) of the distribution of Y. The extreme value index measures the tail heaviness of the distribution of Y and thus has a key role in the analysis of extreme event distribution. One of the known famous results in extreme value theory is the Fisher-Tippett-Gnedenko Theorem [12] [13] .
As aforementioned, the estimation of the extreme-value index or tail-index is a cornerstone when we deal with various problems in extreme value analysis such as the estimation of the conditional extreme quantile of a random variable in the presence of covariate. Nevertheless, in this paper, we consider the situation where some covariate information X is available to the investigator, and the distribution of Y depends on X. Our focus centers on the problem of estimating a conditional extreme quantile of a heavy-tailed distribution when there is access to functional covariate information
is available, where
is an infinite dimensional space associated with a semi-metric
.
Recently, many authors have been interested in the estimation of the extreme value index and extreme quantile we can enumerate a few of them such as [14] [15] [16] [17] have considered the cases of the estimation of extreme value index and extreme quantile from censored data when the covariate information is not available. In [14] the authors proposed to estimate the extreme value index by using the modification of Hill’s estimator version. In [18] [19] [20] authors proposed the Bayesian extreme value index and extreme quantile for the case of uncensored data. [21] [22] [23] investigated the estimation of extreme value index and extreme quantile where there is no covariate information and censored data are taken into consideration. [7] investigate the estimation of the conditional extreme value-index and conditional extreme quantile under randomly right censored with the presence of covariate for finite dimension.
Motivated by studies that utilize conditional extreme quantiles to assess the probability of survival for AIDS patients across various age groups within heavy-tailed distributions in the presence of finite-dimensional covariates, this study aims to estimate the conditionally extreme quantile of recurrent stroke occurrence time distribution under right random censoring. The ambulatory blood pressure curve will be considered as a functionally random covariate. However, the aim of this study is to estimate the conditionally extreme quantile of the time of occurrence of recurrent stroke distribution under right random censoring, with the ambulatory blood pressure curve as a functionally random covariate.
The remainder of this paper is organized as follows. Section 2 is devoted to the data description and the theoretical framework. A real data application illustrates the use of our estimators in Section 3, while Section 4 presents the discussion of our results. Finally, the conclusion and some perspectives are presented in Section 5.
2. Materials and Methods
2.1. Data Description
The data used in paper obtained by considering
stroke patients, consists of triplet
, where
is the 24-hr ambulatory blood pressure curve of ith patient, while
is indicator function equal to one when a patient i is uncensored, otherwise equal to zero. The censoring rate is 40%. Finally,
is an interesting clinical outcome about ith stroke patients. The primary endpoint is the time to the composite stroke recurrent event, including death, disability, or vascular events (see [24] for more details). Each patient’s systolic blood pressure (SBP) is measured every 15 min starting from 19:00 for 24 hr. The covariate
is thus defined by
with
the SBP for each patient for all
.
The data is available online at https://amstat.tandfonline.com/doi/suppl/10.1080/01621459.2019.1602047/suppl_file/uasa_a_1602047_sm0766.zip. Figure 1 below illustrates some realizations of random curves of the given functional random variable
. The covariate
is in fact a discretized curve but the fineness of the grid spanning the discretization allows us to consider each subject as a continuous curve as stated in [25] . Hence, the covariate can be considered as belonging to an infinite dimensional space
. Figure 2 shows an estimated density of the time to recurrent stroke.
![]()
Figure 1. Measurement of blood pressure at
.
![]()
Figure 2. Density function of the time to stroke.
2.2. Extreme Value Theory
Let
be the survival time,
be the censoring time and then let
be a functional random variable covariate. Let
be the independent copies of the random pairs
, where Y is positive real random variable and
, where
is an infinite dimensional space associated to a semi-metric
. Therefore, we really observe independent triplets
, where
and
for
where
is the indicator function of the event A.
Let
and
be the conditional cumulative distribution functions of random variables Y and C given
respectively.
Let
and
be the conditional survival function of random variable Y and C given
respectively.
In this paper, we focus on heavy tails. More specifically, we assume that the conditional survival functions satisfy the following assumption.
(A1).
(1)
and
(2)
where
are positive unknown functions of the covariate x,
are positive functions and
,
are continuous and ultimately decreasing to zero. From (1) and (2), we can state that the conditional distribution functions of Y and C given
are in Fréchet maximal domain of attraction. Thus,
and
are taken as the conditional extreme tail index functions. Therefore, for all
,
and
are regularly varying functions at infinity with index
and
respectively. Thus,
(3)
where for x fixed,
and
are slowly varying functions at infinity, that is, for all
,
By conditional independence between Y and C, the conditional survival function
of Z given
is also a regularly varying function at infinity
with index
as expressed as follows:
(4)
with
where
is the ultimate proportion of uncensored observations among
; (see [15] [26] for more details) and
,
.
2.3. Estimation of Conditional Extreme Tail Index
Let
,
, be independent realizations of the random vector
where
and
for
and
.
If
were uncensored it means that
for all i. In this situation, [27] proposed a Hill’s version of the conditional extreme value index when the covariate response is in
. Following the same idea, we propose a functional Hill-type estimator depending on a semi-metric
:
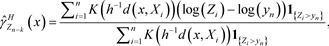 (5)
(5)
where
is a real-valued kernel function on
,
is a positive non-random bandwidth sequence such that
as
and
is a local non-random threshold sequence for estimation with
as
. Here, as stated in [27] , a local threshold means a threshold depending on the point x in the covariate space where the estimation takes place, though the threshold is constant in a neighbourhood of x.
The estimator (5) is not consistent for
if it is directly applied to the censored sample
. Indeed, under appropriate regularity assumptions, estimator (5) will converge to the extreme-value index
of the conditional distribution of Z given
. To accommodate censoring, we suggest, like in [7] , to divide (5) by the proportion
of uncensored observations among the
that are larger than
, in a neighborhood of x:
(6)
where
, 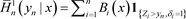 and
are the well-known Nadaraya-Watson weights defined by
and
are the well-known Nadaraya-Watson weights defined by
(7)
The survival functions
and
can be rewritten as follow:
and
respectively, where
and
.
Therefore we propose to estimate
by
(8)
This estimator depends on the bandwidth h, the threshold
and the semi-metric
. The choice of the semi-metric is a crucial point in nonparametric functional data analysis (see [11] ). Once the semi-metric has been chosen, packages are available in the literature (see https://cran.r-project.org/web/packages/fda.usc/index.html) to evaluate proximities between functional data. The semi-metric distance based on the derivative will be used to determine the distance between two curves
and
. We consider the semi-metric:
(9)
where q is the degree of derivative and where
denotes the qth derivative of X. In the following, second, third and fourth derivatives are considered. The impact of the degree of derivatives on the performance of our estimator we will be discussed when semi-metric based on derivatives are considered for smooth curves as covariates.
2.4. Estimation of Conditional Extreme Quantile
We now investigate the estimation of large conditional quantile
of order
of
for a variable Y given
defined by
with
as
. To define our estimator, we have in the first step to define
the functional estimator of a large conditional quantile
within the sample.
Let us consider the Kernel conditional Kaplan-Meier estimator of the conditional survival function
, for all
and
defined as follows :
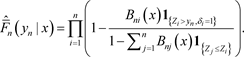 (10)
(10)
This function may be rewritten as
 (11)
(11)
and zero otherwise where
denoted the order statistics of
.
By taking into account the estimator in Equation (11), we propose to estimate conditional quantile
within the sample of observation (i.e. for fixed
) as a generalized inverse of
as
(12)
where
as
, we propose to estimate the conditional extreme quantile
by Weissman-type estimator
(13)
The term
is an extrapolation factor allowing to estimate arbitrary large quantiles and
is the estimator of the censored functional conditional extreme value index
.
3. Results
In recurrent stroke patients, clinical outcomes were assessed using ambulatory blood pressure measurements from 297 patients to estimate conditional extreme values. This estimation considers that the time of occurrence of the recurrent stroke is randomly right-censored. We examined the distribution of time to recurrent strokes is whether they follow a heavy-tailed distribution. In statistics, a quantile-quantile Q-Q plot is a powerful tool to check whether the sample comes from a specific distribution. In EVT, the QQ plot is plotted against the standard exponential distribution to measure the heaviness of the tail of the distribution.
Besides, another tool to examine whether the sample comes from a specific distribution in extreme value theory is the sample mean excess function (MEF). The MEF is a sum of the excess over a threshold
divided by the number of data points that exceed the threshold
. A positive gradient above a certain threshold
of the empirical MEF, is a sign that the data has a heavy tailed distribution with a positive extreme value index
as illustrated in Figure 3.
We therefore carry out our analysis of the conditional tail index quantile using the methodology described in [8] . The results, presented in Table 1, give an overview of the estimates of conditional extreme value index for different degrees of derivative for semi-metric distance. In addition, the confidence interval is provided using resampling techniques which reveal that the confidence interval becomes narrow as the degree of derivative increases. To get these empirical confidence intervals, we suggest a bootstrap methodology described as follows:
1) Draw
samples of the indexes of our dataset from
with replacement.
![]()
Table 1. Table of estimation result of
and
for the stroke data, [∙] Bootstrap 95%-empirical confidence interval for
and
, (∙) empirical width of the confidence interval for
.
ACI presents the asymptotic confidence interval. LCI presents length of confidence interval.
2) Generate
samples of
for corresponding indexes sampled in the first step.
3) Carry out on each of these N samples the estimation of the conditional extreme value index by
using the procedure described in [9] (with the same
).
4) Also for each of these N samples, we work out the estimation of the conditional extreme quantile
which corresponding to each
for the same
).
5) Take the interval bounded by the 2.5% and 97.5% quantile of the conditional extreme value index estimates as a confidence interval. Therefore, the average of low and upper bounds formed the 95%-level asymptotic empirical confidence interval presented in Table 1.
4. Discussion
In this paper, we address the estimation of the tail index and extreme quantiles of a heavy-tailed distribution when some functional covariate information is available and the data are randomly right-censored.
To the best of our knowledge, this is the first study about ischemic stroke and transient ischemic attack patients, with the main objective of studying a functional relationship between ambulatory blood pressure trajectories and clinical outcomes in stroke patients using a concept of conditional extreme value analysis.
To achieve our goal, we are interested in evaluating the conditional extreme quantile of Y the time to recurrent stroke in days given the ambulatory blood pressure trajectory as a functional covariate. In this paper, we assess the quantile
of order
of the conditional distribution of time to recurrent stroke Y given x, for x has the value
,
and
with
denoted the empirical standard deviation of
. For example, the estimated conditional extreme quantiles of the time to recurrent stroke were 203.5339, 186.3794 and 175.718 days at 95% of confidence interval [203.2135, 203.8543], [186.0163, 186.7425] and [175.4108, 176.0252] for lower, middle and higher the ambulatory blood pressure trajectories respectively at fourth derivative as described above.
Furthermore, the average bootstrap of low and upper bounds formed the 95%-level asymptotic empirical confidence interval for estimate
and
presented in Table 1 where the confidence interval becomes narrow as the degree of derivative increases.
As illustrated in Table 1 the stroke patients with higher blood pressure measurements had a higher risk of occurrence of recurrent stroke at early time. This result is not a surprise because the hypertension was an independent predictor of recurrent stroke according to the literature for more details [28] .
5. Conclusions
We have explored the estimation of the functional Weissman kernel type estimator in the presence of a functional random covariate, valued in an infinite-dimensional space, alongside a right-censored scalar response variable. Our primary application revolves around discerning the potential impact of ambulatory blood pressure trajectories on the time of stroke recurrence.
Our findings suggest that higher blood pressure measurements significantly elevate the risk of stroke recurrence within a short time period, consistently observed across multiple quantiles of the time-to-recurrence distribution, as revealed by the estimated extreme quantiles.
The application of extreme value theory in the medical field, particularly those involving functional covariates, is still in its infancy. Nevertheless, various intriguing topics within this domain warrant further investigation in future research.