The Origin of Cosmic Structures Part 6: CMB Anisotropy

J. C. Botke

Ronin Institute, Montclair, New Jersey, USA.

DOI: 10.4236/jhepgc.2024.101020                

Abstract

In a recent series of papers, we introduced a new model of nucleosynthesis in which the matter content of the universe came into existence at a time of about 4 × 10^-5 s. At that time, a small percentage of the vacuum energy was converted into neutron/antineutron pairs with a very small excess of neutrons. This process was regulated by an imprint that was established in the vacuum during an initial Plank-era inflation. Immediately after their inception, annihilation and charge exchange reactions proceeded at a very high rate and ran to completion after an interval of about 10^-11 s. By then, all the antibaryons had disappeared thereby establishing the matter/antimatter asymmetry of the universe. What remained were very high densities of mesons and leptons, somewhat lower densities of protons and neutrons, and finally, the very high density of photons that eventually became the CMB. The density of matter so created varied from one location to another in such a manner as to account for all cosmic structures and because the energy density of the photons varied in proportion to that of the matter, the CMB-to-be came into existence with an anisotropic spectrum already in place. For structures, the size of galaxy clusters, the initial anisotropy magnitudes were on the order of 25%. In this paper, we will follow the subsequent evolution of the photons and show that this model predicts with accuracy the temperature of the warmest anisotropies in the observed CMB spectrum.

Keywords

CMB, Anisotropy, Dispersion, Nucleosynthesis, Early Universe, Time-Varying Curvature

1. Introduction

Unlike the case with the standard model of cosmology, according to our new model of cosmology [1] [2] [3] , there was no existence other than the vacuum until a time of about 4 × 10⁻⁵ s. At that point, a small percentage of the vacuum energy was converted into neutron-antineutron pairs with a very small excess of neutrons. This process, which was regulated by an imprint established in the vacuum at the time of the initial Planck era inflation, created higher densities of matter in the regions that became cosmic structures and lower densities in the regions that became voids. Immediately after their creation, charge exchange reactions began to create proton/antiproton pairs, and simultaneously matter/antimatter pairs underwent annihilations leaving behind mesons, leptons, protons, and neutrons together with the radiation that became the cosmic microwave background (CMB).

We will begin with a quick orientation. In Figure 1, we show the CMB power spectrum from the Planck survey, [4] . In [2] , we showed that the first peak has the dimension of superclusters, and in [3] we showed that creation of the superclusters resulted in the creation of a radiation field with the same spatial dimensions.

In Figure 2, we show a small portion of the CMB as seen by the Planck satellite, [5] . We have subdivided the 10˚ square with a 1˚ grid.

Figure 1. CMB power spectrum from the Planck survey.

Figure 2. A portion of the CMB as seen by the Planck satellite.

The orange regions that take up much of the area are the superclusters that make up the cosmic web. We see that 1˚ is characteristic of both the sizes of the superclusters and the repetition spacing. Even though the superclusters are not the brightest objects in the CMB, their regular pattern results in a large correlation function. The result is the 1˚ peak in the power spectrum.

Next, consider the brightest source in Figure 2. Its size of about 1/5^th of a degree which we will see later matches the angular size that galaxy clusters had at the time of recombination. Referring back to Figure 1, we see that there is a peak in the power spectrum at that angular size, even though the brightest sources are galaxy clusters, they are not numerous and are randomly distributed within the superclusters. The result is that the peak has a smaller magnitude than the supercluster peak.

Our interest in this paper is the evolution of the CMB and, in particular, the temperature of the brightest sources. The properties of the CMB that need to be explained are first the origin and present-day temperature of the CMB which we have already done [3] . The second problem is to account for the black-body (BB) spectrum of the radiation. In a study that we have not yet completed, we show that the CMB acquired a black body spectrum very soon after the annihilation phase as a consequence of various deep inelastic scattering reactions involving baryons, leptons, and particularly pi mesons.

The remaining problem is to account for the present-day anisotropy spectrum. Because the initial energy density of the radiation was directly proportional to the energy density of the matter created during the annihilation phase, the radiation in regions that became structures had higher temperatures than did the radiation in regions that became voids. Thus, the radiation that became the CMB came into existence with an initial anisotropy spectrum already in place. We showed in [3] [6] , for example, that the region that became the Virgo galaxy cluster had an initial radiation temperature about 25% greater than that of the background. The issue then is not to account for anisotropy but to explain how an initial anisotropy $\Delta T/T\approx 1.25$ became the observed anisotropy ratio $\Delta T/T\approx {10}^{-4}$ . There are only two possibilities; either the initial excess radiation energy was dissipated locally before nucleosynthesis proper began via, for example, particle pair production, or the energy density of the radiation dissipated via photon dispersion over a long period beginning around the time of recombination. As a result of the expansion of the universe, the energy density of the radiation dropped below the minimal energy for any sort of pair production shortly after a time of 1 second which means that any local mechanism must have run to completion within a period of, as we will see, less than 30 seconds. Our incomplete study of this epoch, however, shows no indication of any such local reduction process.

In this paper, we will follow the dispersion of the radiation associated with a model galaxy cluster, and in particular, we will make an accurate prediction of the temperature of the brightest CMB anisotropies.

2. Preliminaries

We will study the diffusion of the CMB anisotropy radiation as a function of time beginning at the time when the temperature of the CMB dropped below the deuteron breakup energy, $t_{2.2}\approx 0.1\text{s}$ . To model this process, we need to set up a framework that embodies the main features of the evolution of the galaxy clusters. We will assume spherical symmetry and use Virgo cluster dimensions to quantify our model. We imagine dividing a cluster into a series of concentric spheres. The first step is to determine the evolution of the boundaries of these spheres which we did earlier in [6] . There, we solved the problem of the evolution of an initial distribution of a proton (and electron) gas that later became cosmic structures. The only accelerations acting on the gas were gravitation and that of the expansion of the universe. We showed that the evolution was completely dominated by the expansion and it wasn’t until very close to the time of galaxy formation that gravitation began to have any influence. In the case of the Virgo cluster, we found that the initial density excess relative to the background matter density was about 2.5 and its initial size was about 7.3 times larger than its final size in present-day terms.

We start with an initial body of matter to which we assign an initial density distribution. Based on the results of [6] and [7] , a reasonable distribution has a moderate negative slope and is not too peaked at the origin. An example is shown in Figure 3.

Figure 3. Example matter density distribution at the initiation of nucleosynthesis.

We now solve for the evolution of the spheres using the procedure described in [6] . The result for a count of 30 spheres is shown in Figure 4. The vertical distance from the horizontal axis to any curve is the distance from the center of the structure. The radii are equally spaced although they don’t appear to be so because of the logarithmic scale¹.

We also define a corresponding set of radiation spheres. Since the photon energy is $E\propto T^4$ , we can obtain its initial temperature distribution from the matter distribution. We divide the initial photon distribution into the same set of concentric spheres used for the matter profiles with the results shown in Figure 5.

Figure 4. Matter profiles. The single diagonal line represents the causality limit.

Figure 5. Photon profiles.

The photon spheres don’t respond to the gravitational attraction of the cluster mass so the spheres continue to expand rather than level off as do the matter spheres.

Each sphere extended from the center of the structure out to its boundary. The next step is to define a set of shells as the difference between successive spheres. The matter shells are fully defined because, with the matter particles at rest, the content of each matter shell does not change. The photon shells, on the other hand, are just a set of bins into which the photons are grouped during the calculation. The dimensions of the photon shells vary with the expansion of the universe similar to those of the material shells but the photon content of each shell changes as the calculation proceeds which, of course, is the whole point of our exercise.

We initialize the model with a set of randomly positioned “photons” whose initial temperatures are fixed as described above. We then start things going by assigning to each “photon” a step in a random direction based on considerations to be discussed below. From that start, we then follow the evolution of all the “photons” allowing for random walk scattering off the free electrons before the time of recombination and straight-line motion afterward.

3. How Many Electrons?

Given an initial large structure such as a galaxy cluster together with its population of higher-than-average-temperature photons, our goal is to determine how rapidly the photons disperse from the higher temperature regions inside the structure to the lower temperature regions outside the structure. At the time $t_{2.2}\approx 0.1\text{s}$ , the CMB radiation dropped below the temperature of deuteron break-up (2.2 MeV). Because the protons are much more massive than the electrons, the photon-proton scattering cross section is very small so it is only electron-photon scattering that had any impact on the evolution of the photons. That being the case, we clearly need to establish how many electrons (and positrons) were then in existence.

The naïve answer would be that the positrons would have all been annihilated and that the number of electrons must equal the number of protons since the universe was charge neutral. This, however, overlooks the fact that during the initial annihilation phase of nucleosynthesis, along with a very high density of photons, there came into existence an almost equal number of ${\text{e}}^{-}{\text{e}}^{+}$ pairs with an equilibrium between the two maintained by the $\gamma +\gamma \leftrightarrow {\text{e}}^{-}{\text{e}}^{+}$ reaction pair and this situation existed up until the time that the temperature of the photons dropped below the $\gamma +\gamma \to {\text{e}}^{-}{\text{e}}^{+}$ cutoff energy of 1.02 MeV.

To determine when this cutoff was reached, we integrate the black-body (BB) spectrum from 1 MeV to infinity and compare that with the integral over the entire energy range. The BB spectrum is given by

$n\left(kT\right)=\frac{8\pi }{{\left(ch\right)}^3}\frac{E^2\text{d}E}{{\text{e}}^{E/kT}-1}$ (3-1)

so the fraction of the photons with energies ≥ 1 MeV is given by

$f\left(kT\right)=\frac{1}{2\zeta \left(3\right)}{\displaystyle {\int }_{1/kT}^{\infty }\text{d}x\frac{x^2}{{\text{e}}^x-1}}$ . (3-2)

After integrating numerically, we determine that the ratio drops very rapidly with temperature. Setting the cutoff to an arbitrary value of 10⁻⁷, we find that it occurs at a temperature of $T\approx 6\times {10}^8\text{K}$ . Using the scaling from [2] with $H_0=73$ , we find that this corresponds to a time of $t\approx 30\text{s}$ , so from that time onward, there were no photons left with energies greater than the pair production cutoff.

According to the model in our as-yet unfinished paper describing the epoch, the density of photons and ${\text{e}}^{-}{\text{e}}^{+}$ pairs at $t=t_{2.2}$ was on the order of 10³⁸ m⁻³. The next step is to determine how long those ${\text{e}}^{-}{\text{e}}^{+}$ pairs lasted. We can get a reasonable estimate of the time span through the use of a simplified reaction rate formula. The change in the number of electrons or positions is given by

$\frac{\text{d}n}{\text{d}t}=n^{2}c{\sigma }_T$ (3-3)

where n is the number of either assuming that their densities were the same. The Thompson cross section is ${\sigma }_T\approx {10}^{-29}{\text{m}}^2$ , and c is the speed of light. The rate is high, on the order of 10⁵⁵ s⁻¹∙m⁻³. The solution of this differential equation is

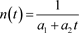. (3-4)

At the time of about 30 s, the density of protons was about $n_p=8\times {10}^{24}{\text{m}}^{-3}$ and we ask, how much time elapsed after the ${\text{e}}^{-}{\text{e}}^{+}$ cutoff before the density of the pairs dropped to the level of the proton density? Putting in numbers we find that the elapsed time was about 10⁻⁵ s so from $t\approx 30\text{s}$ onwards, the only electrons remaining were those associated with the population of protons.

We next consider the mean free path (MFP) of a photon subject to scattering by an electron. This is given by $l_{mfp}={\left(N\sigma \right)}^{-1}$ where N is the number density of the electrons and $\sigma$ is the scattering cross section. At each scattering the incident photon is scattered into a new direction. Because of the huge number of particles involved, it is a reasonable approximation to assume that there is no preferred direction so we assume that the photons on average were scattered uniformly in all directions.

Given that assumption, the path of any photon becomes a random walk (RW) in 3-dimensions. The RW distance [8] traveled by a photon from some starting point is given by $l_{rw}=l_{mfp}\sqrt{n_{steps}}$ where $n_{steps}$ is the number of scatterings during the period of interest. Setting $t_{step}=l_{mfp}/c$ to be the time duration of a single step, the number of steps in an interval $\Delta t$ is $n_{steps}=\Delta t/t_{step}=c\Delta t/l_{mfp}$ . The average distance a photon will travel during an interval $\Delta t$ is then

$l_{rw}=\sqrt{l_{mfp}c\Delta t}$ . (3-5)

This result depends on the Compton scattering cross section which is given by

(3-6)

where $x\equiv E_{\gamma }/\left(m_e{c}^2\right)$ . For small energies, this reduces to $\sigma \left(E_{\gamma }\right)\approx {\sigma }_T\left(1-2x\right)$ . Because we know the densities of each matter shell, we can precompute the MFP of the photons in each shell. (This is simplified by the fact that the photon shells are identical to the matter shells up until near the time of galaxy formation but the scattering ends at the time of recombination which came much earlier.)

To get an idea of the importance of the scattering, we show the calculated results in Figure 6 assuming a time step equal to the elapsed time.

The red curves are the MFP in each case. We see that even close to $t_{rec}$ , the MFP is only a small fraction of the shell radius for the inner shell and an even smaller percentage for the middle and outer shells. The blue curves are the random walk distances determined using (3-5) with the time taken to the total elapsed time since $t=t_{2.2}$ . What we find is that the scattering prevents a significant amount of shell-to-shell dispersion of the photons so they tend to stay in their original shells. At $t=t_{rec}$ , however, the scattering abruptly stops². From then on, the photons travel unimpeded.

Another important consideration that follows from the causality line is that, from the time that the photons were no longer impeded by the scattering, they could also travel the full distance across the structure.

4. Simulation Model Details

We have defined the shells and now we need to populate these with test particles. First, because the actual photons are distributed with a BB spectrum, instead of trying to introduce a large number of test photons representative of such a spectrum,

Figure 6. Illustration of photon mean free path and random walk for the inner-most, middle, and outermost shells.

we define “cmb” particles, each of which represents a volume of real photons distributed according to the BB spectrum. Each cmb is characterized by its temperature so its energy density is proportional to $T^4$ . At any point in time, each shell contains some number of cmbs so the total energy of any shell is the sum of the energies of its cmbs. The energy of the i^th cmb is

$E_i=\text{Const}\text{.}{T}_i{}^4$ (4-1)

so the total energy of the shell is

$E_{shell}=\text{Const}\text{.}\left({\displaystyle \underset{1}{\overset{N}{\sum }}{n}_i{T}_i{}^4}\right)$ (4-2)

Since the shell temperature is a function of the average of the cmb energies, it is not strongly dependent on either the number of cmbs in the shell or the temperature of any single cmb.

We now need to initialize the shell populations. We first specify a nominal number of cmbs to be contained in the outer shell. We then determine the corresponding density by dividing that number by the volume of that shell. The nominal density is based on an assumed temperature equal to the background CMB temperature. Each shell, however, has a temperature determined by the assumed matter density of the corresponding matter shell (which initially had the same dimensions as the photon shell).

The photon density of a BB spectrum is proportional to $T^3$ so we now assign a count of cmbs to each shell (including the outer shell) determined by multiplying the volume of the shell by the nominal density adjusted by the ratio of ${\left(T_{shell}/T_{CMB}\right)}^3$ . With 30 shells and a nominal count of 4000 for the outer shell, we end up with a total of 81,700 cmbs. The positions of the cmbs are specified in terms of spherical coordinates and their initial positions are fixed by assigning to each a random radius within its parent shell and a random angular position. Each cmb’s initial temperature is set to be that of its parent shell.

Finally, we calculate the photon/cmb count ratio by multiplying the photon density, given by

$n\left(t\right)=\frac{2\zeta \left(3\right)}{{\pi }^2{\left(c\hslash \right)}^3}{\left(kT\right)}^3$ (4-3)

where T is the background CMB temperature, by the volume, and then dividing by the assumed nominal number of cmbs. For a nominal count of 4000, the ratio is 6 × 10⁷⁵. Both are characterized by just their temperatures so this ratio is constant under the expansion of the universe.

We have now dealt with the photons filling the structure. We also need to include the background photons lying outside the structure because, not only will interior photons escape the structure, exterior CMB photons will enter the structure and later, in most cases reemerge as escaped particles.

Before $t=t_{rec}$ the interior cmbs are largely immobilized by the high scattering rate (very small MFP.) and by the same token, external cmbs would have been largely locked out of the structure. Nevertheless, some outer shell cmbs do exit the structure so to compensate, we tried moving an equal number of external cmbs into the outer shell at random positions; a process we called reflection. We ran simulations both with and without reflection and found that it makes no difference to the results.

For times $t>t_{rec}$ , the situation is quite different because the photons then traveled unimpeded so both photon escape and capture become significant. We define a single exterior shell with its inner boundary set to the outer boundary of the structure and its thickness set to $c\Delta t_{calc}$ where $t_{calc}$ is the calculation time step. That thickness is the largest distance a cmb could travel in a single time step. We populate the exterior shell with cmbs positioned randomly using a density based on the CMB temperature. The actual number varies with time because both the volume and density change but 290,000 is a representative value. Each cmb is assigned a random direction and then advanced by the length of the calculation step. Finally, those that entered the structure were deemed to have been captured and are assigned to the corresponding photon shell.

At each time step, some number of cmbs escape carrying an average temperature greater than the CMB temperature to become the anisotropy radiation, and some external cmbs at the CMB temperature are captured. The result is that the structure is cooled both by warm photons leaving and cool photons entering. Each step of the calculation cycles through the following steps:

1) Update the temperatures and radial coordinates of the cmbs by the ratio of the scaling.

2) Search the list of cmbs for escapees and remove them from the list of interior cmbs.

3) Populate the external shell with randomly located BB cmbs. Assign to each a random direction, advance them according to the duration of the time step, and search for captures. Add the latter to the list of interior cmbs.

4) Thermalize each shell by averaging the contained cmbs temperatures. Before recombination, the evolution is dominated by the scattering which would thermalize the photons so the temperature of all the cmbs in each shell is set to the average temperature. After recombination, leave the cmbs temperatures unchanged.

5) Before recombination, scatter each cmb in a random direction and advance by an amount given by the RW distance. After recombination, advance each cmb in its original direction (no scattering) by a distance $c\Delta t$ .

6) Calculate the observed temperature at the present-day location of the telescope. The method is discussed below.

5. Evolution of the Structure

We now just turn the crank. We use a logarithmic time variable defined by $\tau =\ln \left(\chi \right)$ with $\chi =t/t_{2.2}$ . The time step interval is defined in terms of a constant $\Delta \tau$ . From Figure 6, we see that the MFP is very small for times $t\ll t_{rec}$ so we chose to start the calculation at $\chi =1.0\times {10}^9$ which is well within the range where the MFPs are very small.

In Figure 7, we show the resulting temperature profiles for a sequence of times. The profiles in blue occur before $t_{rec}$ and those in red, after.

The reference temperature is taken to be the temperature of the outer shell at the starting time of the simulation ( $\chi =1.0\times {10}^9$ ). The reference length, $R_0$ , is the present-day radius of the Virgo cluster (2.2 Mpc).

In Figure 8, we show the same curves plotted against a linear horizontal scale which makes it a little easier to appreciate the spatial dependence of the profiles.

Figure 7. Dispersion temperature profiles for a series of time values.

Figure 8. Dispersion temperature profiles of Figure 7 plotted using a linear scale.

Looking at the blue profiles, we see that, aside from the overall expansion of the universe and corresponding decrease in temperature, they show very little change and, in fact, from the tabulated numerical results (not shown), the degree of anisotropy changes by no more than 3% during the interval between the starting time and $t=t_{rec}$ . This lack of diffusion is fully in agreement with our expectations based on the random walk results shown in Figure 6.

After $t_{rec}$ , things are different. With the motion of the photons unimpeded, the warm photons move out and the cold external photons move in. The result is that the anisotropy steadily disappears (the curves flatten out) and by a time of $t\approx 1.3\times {10}^{15}\text{s}$ ( $\chi \approx 1.3\times {10}^{16}$ ), the temperature anisotropy of the radiation has ceased to exist.

It is important to realize that this is a model-independent result. It only depends on the fact that the scattering of photons ceased at the time of recombination.

6. The Emitted Radiation

As mentioned earlier, the dissipation of the structure’s temperature distribution was the result of both internal photons escaping and external photons being captured. We will now focus on the escaped photons since they became the observed anisotropy.

After a bit of experimentation, we found that the temperatures of the escaped cmbs at any time lie between the current CMB temperature and 1.5 times that value. Using that range, at each time step we define a set of temperature bins covering that range and then sort the escaped cmbs into those bins. We also include a single bin with the current CMB temperature and another with a slightly larger temperature.

Two examples containing 42 bins are shown in Figure 9 and Figure 10. In addition to the numbers in each bin, we show in each case the counts of cmbs that either escaped or were captured. The hins shown in red contain the warm photons that originated within the structure. The blue bin contains the count of photons with exactly the current CMB temperature.

Notice that both the numbers of escaped and captured cmbs increase with time and that for late times, the captured particles completely dominate the population so we have a huge number of cmbs at the CMB temperature and a much smaller count of higher temperature cmbs.

For each such distribution, we calculate the average temperature using the formulas given earlier (4-1) - (4-3) and then the temperature ratio. The latter is defined by $T_{ratio}\equiv T_{avg}/T_{CMB}$ and from this, we get the temperature fraction defined by $f_T\equiv T_{ratio}-1$ . The result is shown in Figure 11 where the fraction is plotted as a function of time. Note that this curve is not the path of anything but instead, each point is a separate event; namely, the temperature of the radiation emitted by the structure at that particular point in time. We also show the maximum anisotropy temperatures determined by both the WMAP and Planck

Figure 9. Example escaped radiation distributions at $t=1\times {10}^{13}\text{s}$ .

Figure 10. Example escaped radiation distributions at $t=1\times {10}^{15}\text{s}$ .

Figure 11. Anisotropy fraction at the outer boundary of the structure. The green and red horizontal lines are the actual maximum anisotropy temperature determined by the WMAP and Planck collaborations respectively.

collaborations. Anisotropy energies are always positive so that, even though the range of anisotropy temperatures is quoted in the WMAP case from −200 μK to 200 μK, the actual range is 0 to 400 μK, [9] . Similarly, it is 0 to 600 μK instead of −300 μK to 300 μK in the Planck case, [10] . The cool regions are not areas in which energy has been removed by, for example, gravitational redshifts but instead are areas in which relatively little energy was added during proto-structure formation during nucleosynthesis. We will explain later why the Planck collaboration finds a larger range of temperatures and it is not because the Plank satellite sees the sources in greater detail.

7. The Observed Anisotropy

The final step is to follow the evolution of the emitted photons as they travel from the structure to the telescope. If we imagine a photon moving away from the structure, its distance $l\left(t\right)$ from the structure will change both because of the expansion of the universe and the fact that the photon is moving at the speed of light. Thus, for a small increment in time, we have

$l\left(t+\Delta t\right)=l\left(t\right)\frac{a\left(t+\Delta t\right)}{a\left(t\right)}+c\Delta t$ . (7-1)

After substituting $a\left(t+\Delta t\right)=a\left(t\right)+\stackrel{\dot{}}{a}\left(t\right)\Delta t$ , this becomes a differential equation

(7-2)

From the formula for the scaling, [2] , we have

$\frac{\stackrel{\dot{}}{a}\left(t\right)}{a\left(t\right)}=\frac{{\gamma }_{*}}{t}+\frac{c_1}{t_0}$ (7-3)

where ${\gamma }_{*}=1/2$ and with $H_0=73$ , $c_1=0.53$ . It simplifies matters if we restate this equation in terms of a dimensionless time, $\eta \equiv t/t_0$ and distance, $r\equiv l/a_0$ . In terms of these, the present-day observer’s time coordinate is $\eta =1$ . After substituting the numerical values just given, we obtain

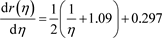(7-4)

Mathematica gives us the solution which contains a single integration constant. To fix the constant, we require that at the time of emission, ${\eta }_e$ , the photon is located at the outer boundary of the structure. Solving for the constant and substituting gives

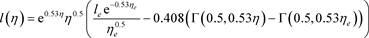(7-5)

where $\Gamma \left(x,y\right)$ is the incomplete upper gamma function. It is obvious that $l\left({\eta }_e\right)=l_e$ .

We are actually only interested in the present-day distance of the photon which we find by setting $\eta =1$ .

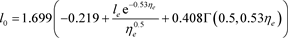(7-6)

What we are after is the volume of space occupied by the photons that escaped during any single time step. A cmb is deemed to have escaped when its position is outside the expanding boundary of the structure. During any time step, the maximum distance a cmb could have traveled outside the boundary is $c\Delta t$ but almost no photons reach that distance because first, most are coming from the interior of the structure and second, they are not necessarily traveling in the radial direction. To estimate the actual distance, we calculated the mean distance for several simulation time steps and found that $\langle \left(r-r_b\right)/c\Delta t\rangle \approx 0.23$ is a reasonable average. We now assume that a thickness of twice the mean, $0.46c\Delta t$ , will enclose most of the photons. We next advance the escaped volume to the present day using (7-6). The volume expands and the temperatures of the cmbs decrease. When the escaped particles eventually arrive, they are contained within that expanded volume but they are not there alone because the volume is also filled with BB radiation at a temperature of 2.73 K.

The density of the latter is given by (4-4) and since we know the volume, we can determine the number of CMB photons that are occupying the same space as the escaped photons. We will eventually calculate the average temperature of the mix but before we do, we need to take into account the fact that the temperature of the escaped photons is only diluted by those CMB photons that enter the telescope since the photons themselves do not interact.

In Figure 12, we illustrate the general idea. The escape photons share the escape volume with the background photons. A small fraction of all the escaped photons determined by the aperture of the telescope is detected. Simultaneously, the telescope also receives that percentage of the background photons that arrive within the limits of its angular resolution.

The surface area of a spherical cone is given by

$A=2\pi r^2\left(1-\cos \left(\theta \right)\right)\approx \pi {\left(r\theta \right)}^2$ (7-7)

Figure 12. Escape volume with telescope.

and dividing this by the total surface gives us the fraction of the background photons that will enter the telescope, $f={\theta }^2/4$ so the total for the entire volume is given by the product of the density (4-4), the escaped volume, and the fraction. We can now compute the average observed temperature for the combined population of photons using (4-1) - (4-3).

The angular resolutions for the three principal CMB surveys are shown in Table 1, [11] [12] [13] . We take these values to be the full width so our angle $\theta$ would be half these values.

In Figure 13, we show the results. The model predictions agree with the maximum observed anisotropy temperatures in both the WMAP and Planck cases.

We can now understand the greater temperature range in the Planck case relative to the WMAP case. It is not because the Planck satellite is seeing sources in greater detail, it is because narrowing the angular resolution reduces the dilution of the source photons by the background CMB photons thereby increasing the observed anisotropy temperature.

In Figure 14, we show a comparison between the results of the three surveys, [5] .

Figure 13. Model predictions of the CMB anisotropy magnitude for the three principal CMB surveys.

Figure 14. Comparison of the resolutions of the three principal surveys. Each square is 10˚ on a side.

Table 1. CMB anisotropy survey telescope angular resolutions.

By comparing the colors of the warmest object (upper left), we see that the images are in close agreement with the predictions. The Planck results show a slightly higher maximum temperature than the WMAP result and both show much higher temperatures than does the COBE result.

8. Discussion

Now that we have presented the main result of this study, we will finish with a few comments and observations.

First, we mentioned earlier that the structures that emitted the radiation that became the anisotropies were several times larger than their final size in present-day terms. For example, the proton-Virgo cluster was 7.3 times larger than the Virgo final size. But the radiation that became the anisotropy was emitted by the proto-structure so the observed anisotropies would appear to be that same multiple larger. In [2] , we derived the formula that gives the angular size of a structure in terms of its present-day size,

${\theta }_{obs}=95.5\frac{D\left(t_0\right)}{a_0}\mathrm{deg}$ (8-1)

where $D\left(t_0\right)$ is the present-day size of the structure. The present-day diameter of the Virgo cluster is 4.4 Mpc so ${\theta }_{Virgo}={0.03}^{\circ }=1.8^{\prime }$ which is considerably smaller than the angular resolution of the telescopes. The anisotropy, on the other hand, is the product of the proto-structure which, in this case, was 7.3 times larger so the angular size of the anisotropy would be ${\theta }_{anisotropy}=13^{\prime }$ which matches the resolutions of the WMAP and Planck telescopes. This means that those telescopes are just able to see the actual size of anisotropy. This value also matches our estimate of the size of the anisotropy using the 1˚ grid in Figure 2. With anything smaller such as a galaxy, one would be viewing a diffraction peak with a dimension fixed by the aperture of the telescope.

We are now in a position to understand the anisotropy power spectrum. In Figure 15, we have added a curve to indicate the secondary peaks of the supercluster spectrum.

The large peak is the primary supercluster peak that reflects the dominance of the 1˚ structure of Figure 2. The second peak, at an angle of about 0.4˚ - 0.5˚, is a consequence of features that are apparent in Figure 2 on that angular scale. These do not correspond to some class of identifiable structure but are just variations in the density of the filaments making up the superclusters. The remaining secondary peaks reflect similar variations on still smaller angular scales.

Figure 15. Interpretation of the anisotropy power spectrum.

Given the regular spacing of the secondary peaks, the third peak which we have identified as being the result of galaxy clusters is likely sitting on top of another secondary peak. The fact that this peak stands out from the others indicates a separate existence.

After galaxy clusters, the next step down is to galaxies. Applying (8-1) to the Milky Way using its present-day diameter gives us an angular size of 2 × 10⁻⁴ deg. At the time of recombination, however, the Milky Way was 55 times larger than its present-day size so its anisotropy angular size is 0.01˚ which is just off the edge of the chart.

The argument just given shows that the peak structure of the spectrum can be understood in terms of the physical sizes of the structures as seen in Figure 2. The magnitude of those features, however, cannot be used to estimate the corresponding temperatures because the power spectrum represents an averaging over features with various temperatures.

We remind the reader that gravitation had nothing to do with the CMB or its anisotropies. Neither did baryonic acoustic oscillations which we proved in [14] are nonsense. The initial densities and temperatures were regulated at the time of nucleosynthesis by the Planck-era vacuum imprint. The subsequent evolution was entirely a consequence of the expansion of the universe until a time long after the time of recombination so it is well not to try to make too much out of the details of the power spectrum.

The next point is that the structures that were responsible for the anisotropies had redshifts on the order of 1500. Eventually, these proto-clusters became actual clusters with the same redshift and since the largest redshifts being observed at present are on the order of 10 - 15, the structures responsible for the anisotropies are far too distant to be seen.

For many decades, researchers have been searching for one or more non-primordial processes that could account for the anisotropy either wholly or in part but with not much success. There is general agreement that Compton scattering of the CMB photons off hot electrons (the Sunyaev-Zel’dovich effect) would have to be a major player but results for large-scale anisotropies are tentative because the straightforward photon scattering off thermal electrons does not seem to yield anisotropies that are bright enough. Kinematic processes dependent on collective motions of large regions of electrons might solve that problem but that process as a universal solution seem unlikely since it would require that all structures had large peculiar velocities at the time of galaxy formation which we have shown in [6] is not possible.

We showed in [7] that both galaxy and galaxy cluster stability required that all galaxies acquired a supermassive black hole immediately after starting a free-fall collapse at the time of galaxy formation. This leads to the possibility of contributions to the anisotropy spectrum but any such contributions could be easily distinguished from the primordial anisotropies for the reasons just discussed and by the fact that the radiation would be much hotter than the 20 K temperature the CMB had at the time of galaxy formation.

Another point to consider is the impact of the ionized intergalactic medium (IGM). Because the density of the IGM is low, the MFP of the radiation is very large so scattering would be minimal. More to the point is that, while energy transfer to the IGM electrons might result in a slight shift in the overall average temperature of the radiation, it would not result in any relative change in the magnitude of the anisotropies.

Putting these ideas together, we find that anisotropies of primordial origin can be distinguished from ones of a recent origin because first, their positions will not correlate with the positions of observed structures and second, their angular sizes will be many times larger than the sizes expected based on the present-day sizes of the equivalent structures.

Finally, we note that any particular anisotropy has a limited lifetime. From Figure 13, we see that the lifetime of the brightest anisotropies would be on the order of (2 - 3) × 10⁵ yr. This means that such anisotropies can only be observed over a very narrow range of redshifts and consequently we will only ever be able to detect the anisotropies within a very thin shell of the universe.

9. Conclusion

We showed in [3] that our new model of nucleosynthesis can readily account for the existence of a CMB with an initial anisotropy spectrum. In this paper, we have extended that investigation to show that by following the evolution of the radiation emitted during the subsequent dispersion of photons from the original structures, we can accurately predict the temperature of the brightest anisotropies. To our knowledge, this is the first actual calculation of the anisotropy temperature.

NOTES

¹The very observant might notice that our indicated time of galaxy formation doesn’t agree with the calculated curves. Galaxies are now commonly being observed with redshifts in the z = 6 - 7 range with a few outliers in the z ≈ 14 range which indicates that our model prediction of the time of galaxy formation is not quite correct. Because the redshift curve becomes very steep in this time range, only a small adjustment to our predicted time of galaxy formation is needed. We note also that our time of recombination is about a factor of 10 earlier in time compared to the standard model value. This is a consequence of the difference in the model expansion rates. In terms of redshift, however, the models agree.

²We recognize that recombination progressed over a period of time but because that time scale was short compared with that of the events we are studying, we simplified the model by assuming that recombination occurred at a single moment of time.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Botke, J.C. (2023) Cosmology with Time-Varying Curvature: A Summary, Book Chapter. https://www.intechopen.com/online-first/1167416
[2]	Botke, J.C. (2020) A Different Cosmology: Thoughts from Outside the Box. Journal of High Energy Physics, Gravitation and Cosmology, 6, 473-566. https://doi.org/10.4236/jhepgc.2020.63037
[3]	Botke, J.C. (2022) The Origin of Cosmic Structures Part 4: Nucleosynthesis. Journal of High Energy Physics, Gravitation and Cosmology, 8, 768-799. https://doi.org/10.4236/jhepgc.2022.83053
[4]	Aghanim, N., et al. (2020) Planck 2018 Results, V. CMB Power Spectra and Likelihoods. Astronomy and Astrophysics, 641, A5. https://doi.org/10.1051/0004-6361/202039265 https://www.aanda.org/articles/aa/pdf/2020/09/aa36386-19.pdf
[5]	NASA, Cosmic Microwave Background (CMB). https://lambda.gsfc.nasa.gov/education/graphic_history/microwaves.html
[6]	Botke, J.C. (2021) The Origin of Cosmic Structure, Part 1: Stars to Superclusters, Journal of High Energy Physics, Gravitation and Cosmology, 7, 1373-1409. https://doi.org/10.4236/jhepgc.2021.74085
[7]	Botke, J.C. (2022) The Origin of Cosmic Structure, Part 3: Supermassive Black Holes and Galaxy Cluster Evolution. Journal of High Energy Physics, Gravitation and Cosmology, 8, 345-371. https://doi.org/10.4236/jhepgc.2022.82028
[8]	(2023) Random Walk. Wikipedia. https://en.wikipedia.org/wiki/Random_walk
[9]	Hinshaw, G., et al. (2009) Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations; Data Processing, Sky Maps, & Basic Results. The Astrophysical Journal Supplement, 180, 225-245. https://ui.adsabs.harvard.edu/abs/2009ApJS..180..225H/abstract
[10]	Aghanim, N., et al. (2020) Planck 2018 Results. I. Overview and the Cosmological Legacy of Planck. Astronomy and Astrophysics, 641, E1. https://www.aanda.org/articles/aa/full_html/2020/09/aa33880-18/aa33880-18.html https://doi.org/10.1051/0004-6361/202039265
[11]	(2023) Cosmic Background Explorer. Wikipedia. https://en.wikipedia.org/wiki/Cosmic_Background_Explorer
[12]	(2023) Wilkinson Microwave Anisotropy Probe. Wikipedia. https://en.wikipedia.org/wiki/Wilkinson_Microwave_Anisotropy_Probe
[13]	Dooling, D. (2019) Planck-European Space Agency Satellite. https://www.britannica.com/topic/Planck
[14]	Botke, J.C. (2023) The Origin of Cosmic Structure, Part 5: Resolution of the Hubble Tension Problem. Journal of High Energy Physics, Gravitation and Cosmology, 9, 60-82. https://doi.org/10.4236/jhepgc.2023.91007