Damage Identification under Incomplete Mode Shape Data Using Optimization Technique Based on Generalized Flexibility Matrix

Qianhui Gao, Zhu Li, Yongping Yu, Shaopeng Zheng^*

College of Construction Engineering, Jilin University, Changchun, China.

DOI: 10.4236/jamp.2023.1112246                

Abstract

A generalized flexibility–based objective function utilized for structure damage identification is constructed for solving the constrained nonlinear least squares optimized problem. To begin with, the generalized flexibility matrix (GFM) proposed to solve the damage identification problem is recalled and a modal expansion method is introduced. Next, the objective function for iterative optimization process based on the GFM is formulated, and the Trust-Region algorithm is utilized to obtain the solution of the optimization problem for multiple damage cases. And then for computing the objective function gradient, the sensitivity analysis regarding design variables is derived. In addition, due to the spatial incompleteness, the influence of stiffness reduction and incomplete modal measurement data is discussed by means of two numerical examples with several damage cases. Finally, based on the computational results, it is evident that the presented approach provides good validity and reliability for the large and complicated engineering structures.

Keywords

Generalized Flexibility Matrix, Damage Identification, Constrained Nonlinear Least Squares, Trust-Region Algorithm, Sensitivity Analysis, Incomplete Modal Data

1. Introduction

Due to influences of working environment, material aging and overloading, structural deterioration will occur in various types of structures such as civil engineering, mechanical engineering, marine engineering and so on. Once the structure is unstable and failure, casualties and financial losses will follow. Therefore, damage identification for engineering structures during the early stage is very necessary [1] . In actual projects, damage identification methods are classified into two types of methods as destructive and non-destructive methods [2] .

As one of the non-destructive methods, vibration-based methods have been widely applied. This kind of method generally uses variations in the dynamic properties of damaged and undamaged structures, especially in the utilization of natural frequency, mode shapes, and modal flexibility [3] . For example, Maity et al. evaluated the differences in natural frequencies with Genetic Algorithm (GA) method to estimate structural damage extents [4] . For dealing with damage regions of complex shapes, a level set model was proposed to depict the damage regions by Zhang et al. [5] . Based on frequency response data, Guo et al. developed an objective function with constitutive relation error, and transformed the damage detection into a nonlinear optimization problem [6] . According to relative natural frequency change curves, Sha et al. [7] presented a new probabilistic damage metric via the use of Bayesian data fusion. By using discrepancies in natural frequencies as frequency shift coefficient (FSC), Dubey et al. [8] utilized the minimization of FSC to access a roughly quantitative damage extent. However, the natural frequency is easy to be effected by working temperature, ambient humidity and other external environment factors [9] .

Compared with the natural frequency, the vibration mode could provide more abundant information about structures with less sensitive to environmental changes. An improved form of the curvature mode shape was applied in beam structures for detecting multiple damage cases by Cao et al. [10] . Based on the eigen-sensitivity analysis, Yan et al. [11] developed a closed-form solution for modal flexibility sensitivity to determine the damage position as well as its severity. For multiple damage cases of truss structures, Seyedpoor [12] developed a damage identification approach by utilizing flexibility-based damage indicator and differential evolution method. In consideration of high sensitivity for strain modes, Cui et al. utilized eigensystem realization algorithm based on strain response to develop a novel damage identification method [13] . Dahak et al. monitored variations of natural frequency and curvature mode shapes of measured structures to detect structural damage condition [14] . Pooya et al. [15] used the discrepancies between the modal curvature obtained from the impaired structure and the computed modal curvature as an indicator to detect damage locations. In addition, modal strain energy (MSE) has been employed for analyzing the damage condition of complex bridges [16] and a jacket offshore platform [17] .

The definition of GFM [18] was firstly introduced by Li et al. in 2010. In comparison with the initial flexibility matrix method [19] , the effect of high-order modes in GFM is decreased reasonably and only few low-order natural modes and frequencies are required. Therefore, the GFM has received widespread attention. Masoumi et al. presented an objective function on the basis of GFM for solving a constrained optimization problem in damage detection procedure via Imperialist Competitive Algorithm (ICA) [20] . Considering the non-negativity of the damage index, an improved GFM approach without and with noises was proposed by Liu et al. [21] . Later, the improved GFM is applied to deal with incomplete mode shape data of structural damage problem [22] . A damage identification process for a jacket-type offshore platform structure was presented by using GFM and optimal genetic algorithm by Aghaeidoost et al. [23] .

The number of degrees of freedom (DOFs) of the measured modal shapes matching that of the finite element model (FEM) is essential in the damage identification process. However, in practice, only a portion of DOFs can be measured because of the restricted number of sensors, especially for large engineering structures. This problem can be solved by modal condensation or modal expansion. Mirza et al. [24] developed a simplified FEM of the physical test substructure and used a model updating technique to correct the initial finite element model to generate more information of DOFs. Based on improved eigenvalue equations and eigenvalue shifting technique, Qu et al. [25] proposed dynamic cohesive matrix constraint equations and a new iteration format to improve computational accuracy and efficiency.

The article is organized as follows. Primarily, in Section 2, the damage identification problem is constructed. Meanwhile, FEM and the modal expansion method for incomplete modal data are reviewed. In Section 3, an optimized mathematical framework for structure damage identification is established, and an objective function is developed through calculating differences of GFM of the structures before and after damaged. Furthermore, the derivation for sensitivity analysis for solving the optimized problem by Trust-Region algorithm is then given. Numerical examples and conclusions are presented in the last two sections.

2. The Generalized Flexibility Matrix

2.1. Formulation

In this article, only the reduction of structural stiffness for each element is assumed to be the main cause of the structural damage and the mass matrix before and after damage keep unchanged, as well as the number of degree of freedoms (DOFs). Based on this assumption, the stiffness matrix of the damaged structure is described as

${{\rm K}}_d\left(\alpha \right)=K_u-{\displaystyle \underset{j=1}{\overset{N_e}{\sum }}{\alpha }_j}{K}_{uj}^e$ , (1)

where $K_d$ and $K_u$ represent overall stiffness matrix of the damaged prediction model with dimension n × n and the one of the undamaged structure, respectively. $K_{uj}^e$ describes the stiffness matrix of the jth element in an undamaged structure with expended dimension n × n. ${\alpha }_j\left(0\le {\alpha }_j\le 1.0\right)$ denotes the dimensionless damage index of corresponding jth element stiffness matrix, and ${\alpha }_j=0$ indicates that the corresponding element has not been harmed. ${\alpha }_j$ can be interpreted as any geometric or physical parameter of the prediction model, such as moment of inertia, stiffness, boundary condition and so on. $N_e$ is the count of finite elements. Therefore, the damage identification problem becomes the problem of finding a set of values ${\alpha }_j\left(j=1,2,\cdots ,N_e\right)$ .

2.2. The Generalized Flexibility Matrix

The GFM is reviewed in this section. First, consider the free vibration of structural eigenproblem with the expression

$K\Phi =M\Phi \Lambda$ , (2)

where $K$ and $M$ are structural stiffness and mass matrix with dimension n×n. $\Lambda =diag\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\right)$ and $\Phi =\left[{\phi }_1,{\phi }_2,\cdots ,{\phi }_n\right]$ are matrices of eigenvalues and corresponding eigenvectors, and satisfy the mass-normalized condition, such that

${\Phi }^{\text{T}}K\Phi =\Lambda$ , (3)

and

${\Phi }^{\text{T}}M\Phi =I$ , (4)

where $I$ is the identity matrix with dimension n×n. As the flexibility matrix $F$ is the inverse matrix of $K$ in Equation (3), $F$ can be expressed by

$F=K^{-1}=\Phi {\Lambda }^{-1}{\Phi }^{\text{T}}={\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{{\phi }_j{\phi }_j^{\text{T}}}{{\omega }_j^2}}$ . (5)

Note that the flexible matrix described above contains complete mode shapes of a structure. However, its application in actual operation has indicated that only a few low-order modes could be obtained accurately during the modal identification procedure.

With the combination of the mass-normalized condition and Equation (5), the GFM $F^g$ is defined as [18]

$F^g=F{\left(MF\right)}^L=\Phi {\Lambda }^{-1}{\Phi }^{\text{T}}{\left(M\Phi {\Lambda }^{-1}{\Phi }^{\text{T}}\right)}^{-L}=\Phi {\Lambda }^{-1-L}{\Phi }^{\text{T}}$ . (6)

Compared with flexibility matrix in Equation (5), it demonstrates that the GFM has a greater impact by several lower-order modes. In particular, when $L=0$ , Equation (6) becomes $F$ in Equation (5). For $L=1$ , the GFM $F^g$ is expressed as

$F^g=\Phi {\Lambda }^{-2}{\Phi }^{\text{T}}$ . (7)

In this paper, only $L=1$ is considered.

3. The Proposed Method

3.1. Objective Function

On the basis of GFM, an optimization model is employed as a damage detection problem for searching a series of damage extents $0\le {\alpha }_j\le 1.0\left(j=1,2,\cdots ,N_e\right)$ , i.e.

$f\left(\alpha \right)=F_{exp}^g-F_d^g\left(\alpha \right)$ , (8)

where $F_{exp}^g$ is the n × n experimental measured GFM, i.e. $F_{exp}^g={\Phi }_{exp}{\Lambda }_{exp}^{-2}{\Phi }_{exp}^{\text{T}}$ , ${\Phi }_{exp}$ and ${\Lambda }_{exp}$ are eigenvector matrices and eigenvalue matrices of the actual damaged structure, respectively. $F_d^g\left(\alpha \right)$ is the analytical GFM which corresponds to global stiffness matrix $K_d$ of the damaged prediction model, expressed by

$F_d^g\left(\alpha \right)={\Phi }_d\left(\alpha \right){\Lambda }_d^{-2}\left(\alpha \right){\Phi }_d{\left(\alpha \right)}^{\text{T}}$ , (9)

where ${\Lambda }_d\left(\alpha \right)$ and ${\Phi }_d\left(\alpha \right)$ are matrices of eigenvalues and the corresponding eigenvectors for the damage prediction model. The issue is to find a set of values $0\le {\alpha }_j\le 1.0\left(j=1,2,\cdots ,N_e\right)$ through minimizing the discrepancy between data from experimental measurement and data from the analytical damaged model. When 2-norm is applied to analyze the discrepancy quantitatively, the objective function becomes

${\Pi }_o\left(\alpha \right)={\Vert vec\left(f\left(\alpha \right)\right)\Vert }_2^2$ , (10)

and

$vec\left(f\left(\alpha \right)\right)=\left[\begin{array}{c}{f}_1\\ f_2\\ ⋮\\ f_n\end{array}\right]$ , (11)

where $vec\left(f\left(\alpha \right)\right)$ is a vector with dimension $n^2\times 1$ by stacking columns of $f\left(\alpha \right)$ , and $f_i\left(i=1,2,\cdots ,n\right)$ is the ith column.

In order to avoid erroneous estimates that would be induced by very small values of 2-norm, Equation (10) is modified with dividing by the initial estimate, so that the final minimization problem is formulated as

$\begin{array}{l}\underset{\alpha }{\min }\Pi =\frac{{\Vert vec\left(f\left(\alpha \right)\right)\Vert }_2^2}{{\Vert vec\left(f\left({\alpha }_0\right)\right)\Vert }_2^2}\\ \text{s}\text{.t}.0\le {\alpha }_j\le 1\left(j=1,2,\cdots ,N_e\right)\end{array}$ (12)

3.2. Optimization Algorithm

The optimization model above is actually a nonlinear least squares problem (NLS) with constraint conditions and can be solved by Trust-Region (TR) algorithm. For this propose, the TR algorithm is firstly reviewed [26] [27] . The general formulation of the question is expressed by

$\begin{array}{l}\underset{x}{\min }{\Vert G\left(x\right)\Vert }_2^2={\Vert y-A\left(x\right)\Vert }_2^2\\ \text{s}\text{.t}.l_i\le x_i\le u_i,i=1,2,\cdots ,m\end{array}$ (13)

where $A\in R^m,x\in R^m$ and $y\in R^m$ . The TR algorithm provides the principle idea of transforming Equation (13) into the kth step iterative TR sub-problem

$\begin{array}{l}\underset{x}{\min }{\Psi }_k\left(s_k\right)={\Vert G\left(x_k\right)+J\left(x_k\right)s_k\Vert }_2^2\\ \text{s}\text{.t}.\{\begin{array}{l}{\Vert s_k\Vert }_2\le {\Delta }_k\\ l_i\le x_i\le u_i,i=1,2,\cdots ,m\end{array}\end{array}$ (14)

where $x_k$ represents the current point, $s_k$ denotes the solution of Equation (14), ${\Delta }_k$ represents trust-region area at kth step. $J\left(x_k\right)$ is the Jacobian matrix of $A\left(x\right)$ . Then the actual reduction is defined as

$Are{s}_k=G\left(x_k\right)-G\left(x_k+s_k\right)$ , (15)

the predicted reduction is described as

$Pre{s}_k=\Psi \left(x_k\right)-\Psi \left(x_k+s_k\right)$ , (16)

and the ratio of actual reduction to predicted one is defined as

$r_k=\frac{Are{s}_k}{Pre{s}_k}$ . (17)

For solving the NLS with constraint condition, the framework of Trust-Region (TR) algorithm is given in Table 1 as follows.

Significantly, the TR algorithm requires the Jacobian matrix of the objective function with related design variable ${\alpha }_j\left(j=1,2,\cdots ,N_e\right)$ , i.e.

$J\left(\alpha \right)=\left[J\left({\alpha }_1\right),J\left({\alpha }_2\right),\cdots ,J\left({\alpha }_{N_e}\right)\right]$ , (18)

and

$\begin{array}{l}J\left({\alpha }_i\right)=vec\left(\frac{\partial f}{\partial {\alpha }_i}\right)\\ =vec\left[-\frac{\partial \Phi }{\partial {\alpha }_i}{\Lambda }^{-2}{\Phi }^{\text{T}}+2\Phi {\Lambda }^{-3}\frac{\partial \Lambda }{\partial {\alpha }_{{}_i}}{\Phi }^{\text{T}}-\Phi {\Lambda }^{-2}\frac{\partial {\Phi }^{\text{T}}}{\partial {\alpha }_i}\right],i=1,2,\cdots ,N_e\end{array}$ (19)

where $J\left(\alpha \right)$ is the Jacobian matrix with size $n^2\times N_e$ . Then, the sensitivities of eigenvalues and eigenvectors to the model updating parameter ${\alpha }_j\left(j=1,2,\cdots ,N_e\right)$ will be deduced below by nelson method [28] .

3.3. Sensitivity Analysis

In this paper, it is supposed that the ith eigenvalue ${\lambda }_i$ is simple so that the corresponding eigenvector ${\phi }_i$ is unique. Directly differentiation Equation (2) with respect to ${\alpha }_j$ yields

$\left(K-{\lambda }_{i}M\right)\frac{\partial {\phi }_i}{\partial {\alpha }_j}+\left(\frac{\partial K}{\partial {\alpha }_j}-{\lambda }_i\frac{\partial M}{\partial {\alpha }_j}-\frac{\partial {\lambda }_i}{\partial {\alpha }_j}M\right){\phi }_i=0,j=1,2,\cdots ,N_e$ . (20)

Premultiplying Equation (20) by ${\phi }_i^{\text{T}}$ and combining with Equation (2), the sensitivity of the ith eigenvalue ${\lambda }_i$ can be achieved, i.e.

$\frac{\partial {\lambda }_i}{\partial {\alpha }_j}={\phi }_i^{\text{T}}\left(\frac{\partial K}{\partial {\alpha }_j}-{\lambda }_i\frac{\partial M}{\partial {\alpha }_j}\right){\phi }_i\text{,}j=1,2,\cdots ,N_e$ . (21)

For obtaining the sensitivity of the ith eigenvector ${\phi }_i$ , the expression in Equation (20) becomes

$\left(K-{\lambda }_{i}M\right)\frac{\partial {\phi }_i}{\partial {\alpha }_j}=-\left(\frac{\partial K}{\partial {\alpha }_j}-{\lambda }_i\frac{\partial M}{\partial {\alpha }_j}-\frac{\partial {\lambda }_i}{\partial {\alpha }_j}M\right){\phi }_i$ . (22)

Table 1. Trust-Region (TR) algorithm.

Note that coefficient matrix $K-{\lambda }_{i}M$ in Equation (22) has a rank of $n-1$ , and ordinary methods cannot be directly used to solve the equation. Based on Nelson method, the maximum absolute value in ${\phi }_i$ needs to be firstly determined, and its location is recorded as k. After that, a new coefficient matrix $A_i$ is formed by taking the kth row and column of $K-{\lambda }_{i}M$ to be zero while the kth diagonal elements of the matrix to 1. Setting the kth row of the coefficient

matrix on the right side of Equation (22) be zero to form $B_i$ . The particular solution $x_i$ of Equation (22) can be obtained by solving $A_i{x}_i=B_i$ , and the eigenvector derivative $\frac{\partial {\phi }_i}{\partial {\alpha }_j}$ can be defined as

$\frac{\partial {\phi }_i}{\partial {\alpha }_j}=x_i+c_{ij}{\phi }_i$ . (23)

Considering the derivative of Equation (4) with related ${\alpha }_j$ and Equation (23), one obtains

$c_{ij}=-{\phi }_i^{\text{T}}M{x}_i$ . (24)

As a result, the sensitivities of eigenvalues and eigenvectors can be given

$\{\begin{array}{l}\frac{\partial {\lambda }_i}{\partial {\alpha }_j}={\phi }_i^{\text{T}}\left(\frac{\partial K}{\partial {\alpha }_j}-{\lambda }_i\frac{\partial M}{\partial {\alpha }_j}\right){\phi }_i\hfill \\ \frac{\partial {\phi }_i}{\partial {\alpha }_j}=x_i{c}_{ij}-{\phi }_i^{\text{T}}M{x}_i{\phi }_i\hfill \end{array}\text{,}i=1,2,\cdots ,NR;j=1,2,\cdots ,N_e$ . (25)

3.4. Modal Expansion Method

Since the number of DOFs obtained from the experiment is less than that of finite element model, the modal expansion method is adopted in this paper. The assumption is that the total DOFs of FEM of the structure are in two parts, measured and unmeasured DOFs, which are denoted by subscripts m and s, respectively. Thus, Equation (2) can be represented by a partition matrix in the following form

$\left[\begin{array}{cc}{K}_{mm}& K_{ms}\\ K_{sm}& K_{ss}\end{array}\right]\left\{\begin{array}{c}{\phi }_{mj}\\ {\phi }_{sj}\end{array}\right\}={\lambda }_j\left[\begin{array}{cc}{M}_{mm}& M_{ms}\\ M_{sm}& M_{ss}\end{array}\right]\left\{\begin{array}{c}{\phi }_{mj}\\ {\phi }_{sj}\end{array}\right\}$ . (26)

From Equation (26), it can be seen that

$K_{sm}{\phi }_{mj}+K_{ss}{\phi }_{sj}={\lambda }_j\left(M_{sm}{\phi }_{mj}+M_{ss}{\phi }_{sj}\right)$ . (27)

According to Equation (27), the unmeasured model data ${\phi }_{sj}$ can be calculated as

${\phi }_{sj}=-{\left(K_{ss}-{\lambda }_j{M}_{ss}\right)}^{-1}\left(K_{sm}-{\lambda }_j{M}_{sm}\right){\phi }_{mj}$ . (28)

Setting the coefficient matrix of Equation (28) to the transformation matrix $T$ , we have

$T=-{\left(K_{ss}-{\lambda }_j{M}_{ss}\right)}^{-1}\left(K_{sm}-{\lambda }_j{M}_{sm}\right)$ , (29)

where $T$ is estimated from the undamaged structure. Therefore, total DOFs can be expressed by the unit matrix $I$ , the transformation matrix $T$ and the measured data ${\phi }_{mj}$ , i.e.

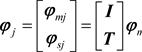. (30)

4. Numerical Examples

Two simulation models are introduced in this part. Each of the two examples takes account of two damage scenarios. All the simulated damage scenarios only result in reducing stiffness of specified elements. If the calculated extent of damage is less than 5%, the related element is considered to be undamaged [18] . All NLS with constraint conditions problems included in the examples are implemented by the trnlspbc command in Intel^® oneAPI Math Kernel Library.

Example 1: A grid structure model is introduced in Figure 1. The modulus of elasticity of the material is $E=207\text{Gpa}$ , the mass density is $\rho =7800\text{kg}/{\text{m}}^{\text{3}}$ , and the Poisson’s ratio is $\nu =0.3$ . The width and height of the structure are 40 m and 4 m. The corresponding finite element model has 160 elements and 50 nodes. Each node of the model has 6 DOFs and the bottom four nodes are constrained so that the number of total DOFs is 276. Two damage cases with complete modal data presented in Table 2 are preset for this example.

Figure 1. A grid structure.

Table 2. Damage scenarios in example 1.

In this example, damage condition can be ascertained simply by the use of the first frequency and the related vibration shape, and the corresponding measured model data is considered to be complete. The damage positions for the cases given in Table 2 are illustrated in Figure 2 as well as the corresponding computational results using the presented approach are illustrated in Figure 3. For damage scenario I, the predefined damage positions are mapped exactly on element 146 with damage extents 0.1411, and element 150 with stiffness reduction 0.2105. In other words, the relative errors to the preset values are 0.89% and 1.05%, respectively. In scenario II, the damage extents and locations calculated are 0.1393, 0.2158and 0.2394 for elements No. 104, No. 105 and No. 113, respectively. It can also be obtained that in comparison with the preset values, the relative errors of the calculated results are 1.07%, 1.58% and 1.06%, respectively. All these results indicate that this approach has the capability of precise identification of the damaged elements.

Example 2: A steel truss bridge is presented in Figure 4. The bridge is 12 meters wide, 10.5 meters high and 90 meters long. The material properties are listed below: modulus of elasticity $E=210\text{Gpa}$ , mass density $\rho =7800\text{kg}/{\text{m}}^{\text{3}}$ , Poisson’s ratio $\nu =0.31$ . The structural finite element model has 94 elements and 40 nodes, and the rotations in all three directions of every node are ignored. The boundary conditions are defined as all displacement constraints at two points on the left side and two horizontal displacement constraints at two points on the right side at the bottom. Thus, with the exception of the constrained nodes, each node has 3 DOFs, and the total measured DOFs is 112.

By using the modal expansion technique, the improved algorithm can be applied to solve incomplete mode problems. Herein, just the first two low-order frequencies as well as the corresponding mode shapes have been utilized in example 2. Figure 5 illustrates two preset damage locations, which are shown in Table 3, along with the extent of damage. The scenario I shown in Figure 5(a) depicts the damage locations occurring on element 10 and 37 with damage extents of incomplete mode shown in Figure 6(a) are 0.1445 and 0. 1714, and the corresponding results calculated from complete modal data are 0.1217 and 0.1757. Therefore, it can be seen that the results from the incomplete modes are not as accurate as the results from the complete modes, but the errors to the preset values are only 4.45% and 2.14%, respectively. The results for scenario II shown in Figure 6(b) expresses that the estimation of incomplete mode is fairly accurate, i.e., the damage locations occurring on element 6, 7 and 32 with 0.0868, 0.1125 and 0.1812 damage extents. From the calculations, the errors to the preset values are 1.32%, 1.25%and 3.12%, respectively. In comparison with complete modal data, damage condition is generally determined despite incorrect classification of few elements in different positions. These results show that this approach can produce good approximations to the preset values even with incomplete modal data.

(a)(b)

Figure 2. Damage presets of the grid structure for the two scenarios in Table 2. (a) Scenario I. (b) Scenario II.

(a)(b)

Figure 3. Simulation results of the grid bridge structure for the two scenarios in Table 2. (a) Scenario I. (b) Scenario II.

Figure 4. A steel truss bridge.

(a)(b)

Figure 5. Damage presets of the steel truss bridge structure for all scenarios in Table 3. (a) Scenario I. (b) Scenario II.

Table 3. Damage scenarios in example 2.

(a)(b)

Figure 6. Simulation results of the steel truss bridge structure for all scenarios in Table 3. (a) Scenario I. (b) Scenario II.

5. Conclusion

This article presents a new way to detect structural damage via solving constrained nonlinear least squares optimized problem. It is proposed on the basis of generalized flexibility matrix to construct an objective function and Nelson’s method is utilized to calculate the objective function gradient for each design variable. Also, the modal expansion method is employed for solving incomplete mode problems. Then, the proposed method has been verified on two complex engineering structures with different damage scenarios for both complete and incomplete modal data. It is concluded from computational results that the proposed approach provides accurate location and extent of damage with only several low-order eigenpairs. As a result, the method could be applied to other large engineering structures for damage detection or health monitoring.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Li, J., Li, Z. and Zhong, H. (2012) Structural Damage Detection Using Generalized Flexibility Matrix and Changes in Natural Frequencies. AIAA Journal, 50, 1072-1078. https://doi.org/10.2514/1.J051107
[2]	Seyedpoor, S.M., Ahmadi, A. and Pahnabi, N. (2019) Structural Damage Detection Using Time Domain Responses and an Optimization Method. Inverse Problems in Science & Engineering, 27, 669-688. https://doi.org/10.1080/17415977.2018.1505884
[3]	Feng, D. and Feng, M. (2018) Computer Version for SHM of Civil Infrastructure: From Dynamic Response Measurement to Damage Detection—A Review. Engineering Structures, 156, 105-117. https://doi.org/10.1016/j.engstruct.2017.11.018
[4]	Maity, D. and Tripathy, R.R. (2005) Damage Assessment of Structures from Changes in Natural Frequencies Using Genetic Algorithm. Structural Engineering & Mechanics, 19, 21-42. https://doi.org/10.12989/sem.2005.19.1.021
[5]	Zhang, W., Du, Z., Sun, G. and Guo, X. (2017) A Level Set Approach for Dam-Age Identification of Continuum Structures Based on Dynamic Responses. Journal of Sound and Vibration, 386, 100-115. https://doi.org/10.1016/j.jsv.2016.06.014
[6]	Guo, J., Wang, L. and Takewaki, I. (2019) Frequency Response-Based Damage Identification in Frames by Minimum Constitutive Relation Error and Sparse Regularization. Journal of Sound and Vibration, 443, 270-292. https://doi.org/10.1016/j.jsv.2018.11.020
[7]	Sha, G., Radziehski, M., Cao, M. and Ostachowicz, W. (2019) A Novel Method for Single and Multiple Damage Detection in Beams Using Relative Natural Frequency Changes. Mechanical Systems and Signal Processing, 132, 335-352. https://doi.org/10.1016/j.ymssp.2019.06.027
[8]	Dubey, A., Denid, V. and Serra, R. (2022) Sensitivity and Efficiency of the Frequency Shift Coefficient Based on the Damage Identification Algorithm: Modeling Uncertainty on Natural Frequencies. Vibration, 5, 59-79. https://doi.org/10.3390/vibration5010003
[9]	Kim, J., Park, J. and Lee, B. (2007) Vibration-Based Damage Monitoring in Model Plate-Girder Bridges under Uncertain Temperature Conditions. Engineering Structures, 29, 1354-1365. https://doi.org/10.1016/j.engstruct.2006.07.024
[10]	Cao, M., Radzienski, M., Xu, W. and Ostachowica, W. (2014) Identification of Multiple Damage in Beams Based on Robust Curvature Mode Shapes. Mechanical Systems and Signal Processing, 46, 468-480. https://doi.org/10.1016/j.ymssp.2014.01.004
[11]	Yan, W. and Ren, W. (2014) Closed-Form Modal Flexibility Sensitivity and Its Application to Structural Damage Detection without Modal Truncation Error. Journal of Vibration and Control, 20, 1816-1830. https://doi.org/10.1177/1077546313476724
[12]	Seyedpoor, S.M. and Montazer, M. (2016) A Damage Identification Method for Truss Structures Using a Flexibility-Based Damage Probability Index and Differential Evolution Algorithm. Inverse Problems in Science and Engineering, 24, 1303-1322. https://doi.org/10.1080/17415977.2015.1101761
[13]	Cui, H., Xu, X., Peng, W., Zhou, Z. and Hong, M. (2018) A Damage Detection Method Based on Strain Modes for Structures under Ambient Excitation. Measurement, 125, 438-446. https://doi.org/10.1016/j.measurement.2018.05.004
[14]	Dahak, M., Touat, N. and Kharoubi, M. (2019) Damage Detection in Beam through Change in Measured Frequency and Undamaged Curvature Mode Shape. Inverse Problems in Science & Engineering, 27, 89-114. https://doi.org/10.1080/17415977.2018.1442834
[15]	Pooya, S.M.H. and Massumi, A. (2021) A Novel and Efficient Method for Damage Detection in Beam-Like Structures Solely Based on Damaged Structure Data and Using Mode Shape Curvature Estimation. Applied Mathematical Modelling, 91, 670-694. https://doi.org/10.1016/j.apm.2020.09.012
[16]	Najafabadi, A.A., Daneshjoo, F. and Ahmadi, H.R. (2020) Multiple Damage Detection in Complex Bridges Based on Strain Energy Extracted from Single Point Measurement. Frontiers of Structural and Civil Engineering, 14, 722-730. https://doi.org/10.1007/s11709-020-0624-5
[17]	Liu, G., Zhai, Y., Leng, D., Tian, X. and Mu, W. (2017) Research on Structural Damage Detection of Offshore Platforms Based on Grouping Modal Strain Energy. Ocean Engineering, 8, 43-49. https://doi.org/10.1016/j.oceaneng.2017.05.021
[18]	Li, J., Wu, B., Zeng, Q.C. and Lim, C.W. (2010) A Generalized Flexibility Matrix Based Approach for Structural Damage Detection. Journal of Sound and Vibration, 329, 4583-4587. https://doi.org/10.1016/j.jsv.2010.05.024
[19]	Yang, Q.W. and Liu, J.K. (2009) Damage Identification by the Eigenparameter Decomposition of Structural Flexibility Change. International Journal for Numerical Methods in Engineering, 78, 444-459. https://doi.org/10.1002/nme.2494
[20]	Masoumi, M., Jamshidi, E. and Bamdad, M. (2015) Application of Generalized Flexibility Matrix in Damage Identification Using Imperialist Competitive. KSCE Journal of Civil Engineering, 19, 994-1001. https://doi.org/10.1007/s12205-015-0224-4
[21]	Liu, H. and Li, Z. (2020) An Improved Generalized Flexibility Matrix Approach for Structural Damage Detection. Inverse Problems in Science and Engineering, 28, 877-893. https://doi.org/10.1080/17415977.2019.1683174
[22]	Liu, H., Wu, B. and Li, Z. (2021) The Generalized Flexibility Matrix Method for Structural Damage Detection with Incomplete Mode Shape Data. Inverse Problems in Science and Engineering, 29, 2019-2039. https://doi.org/10.1080/17415977.2021.1900840
[23]	Aghaeidoost, V., Afshar, S., Tajaddod, N.Z., Asgarian, B. and Shokrgozar, H.R. (2023) Damage Detection in Jacket-Type Offshore Platforms via Generalized Flexibility Matrix and Optimal Genetic Algorithm (GFM-OGA). Ocean Engineering, 281, Article ID: 114841. https://doi.org/10.1016/j.oceaneng.2023.114841
[24]	Mirza, W.W.I., Rani, M.N.A., Yunus, M.A., Sani, M.S.M. and Zin, M.S.M. (2019) The Prediction of the Dynamic Behaviour of a Structure Using Model Updating and Frequency Based Substructuring. IOP Conference Series: Materials Science and Engineering, 506, Article ID: 012011. https://doi.org/10.1088/1757-899X/506/1/012011
[25]	Qu, Z.Q. and Fu, Z.F. (2012) New Structural Dynamic Condensation Method for Finite Element Models. AIAA Journal, 36, 1320-1324. https://doi.org/10.2514/2.517
[26]	Zhang, J. and Wang, Y. (2003) A New Trust Region Method for Nonlinear Equations. Mathematical Methods of Operations Research, 58, 283-298. https://doi.org/10.1007/s001860300302
[27]	Yuan, Y. (2015) Recent Advances in Trust Region Algorithms. Mathematical Programming, 151, 249-281. https://doi.org/10.1007/s10107-015-0893-2
[28]	Nelson, R.B. (1976) Simplified Calculation of Eigenvector Derivatives. AIAA Journal, 14, 1201-1205. https://doi.org/10.2514/3.7211