The Theoretical Significance and Reality of Imaginary Number

Wenbing Wu, Xiaojian Yuan

School of Big Data, Fuzhou University of Foreign Studies and Trade, Fuzhou, China.

DOI: 10.4236/ns.2023.1511021                

Abstract

It is a fact that imaginary numbers do not have practical significance. But the role of imaginary numbers is very broad and enormous, due to the existence of Euler’s formula. Due to Euler’s formula, imaginary numbers have been applied in many theoretical theories. One of the biggest functions of imaginary numbers is to represent changes in phase, which is indispensable in signal analysis theory. The imaginary numbers in quantum mechanics pose a greater mystery: do the imaginary numbers really exist? This question still needs further scientific development to be answered.

Keywords

Imaginary Number, Euler’s Formula, Phase, Quantum Mechanics

1. INTRODUCTION

To trace the trajectory of the appearance of imaginary numbers, it is necessary to relate the process of their relative real number appearance. We know that real numbers correspond to imaginary numbers, including rational and irrational numbers, which means that they are real numbers.

The term “imaginary number” was coined by the famous mathematician and philosopher Descartes in the 17th century, because the concept at that time believed that it was a real number that did not exist. Later, it was discovered that imaginary numbers can correspond to the vertical axis on the plane, and are equally true to real numbers corresponding to the horizontal axis on the plane.

People have found that even using all rational and irrational numbers cannot solve the problem of solving algebraic equations. Like x² = 1 the simplest quadratic equation of 1 = 0 has no solution in the real number range. The 12th-century Indian mathematician Vashgaro believed that this equation had no solution. He believes that the square of a positive number is a positive number, and the square of a negative number is also a positive number. Therefore, the square root of a positive number is twofold; a positive number and a negative number, negative numbers have no square root, so negative numbers are not square numbers. This is equivalent to denying the existence of the negative square root of the equation.

It was not until the early 19th century that Gauss systematically used the symbol j and advocated using even numbers (a, b) to represent a + b_j, known as complex numbers, that imaginary numbers gradually became popular.

When imaginary numbers entered the field of numbers, people were unaware of their practical use, and in real life, there seemed to be no quantity expressed in the plural. Therefore, for a long time, people had various doubts and misunderstandings about them. The original meaning of Descartes’ term “imaginary number” refers to its being false; Leibniz believed that “imaginary numbers are wonderful and strange hiding places for gods, almost amphibians that exist and do not exist.” Although Euler used imaginary numbers in many places, he also said that all mathematical formulas such as $\sqrt{-1}$ and $\sqrt{-2}$ are impossible, imaginary numbers because they represent the square root of negative numbers. For these types of numbers, we can only assert that they are neither nothing nor more than nothing, nor less than nothing. They are pure illusions.

After Euler, Norwegian surveyor Wessel proposed to represent complex numbers (a + b_j) as points on a plane. Later, Gauss proposed the concept of complex planes, which finally gave complex numbers a foothold and opened up the way for their application. Nowadays, complex numbers are generally used to represent vectors (directed quantities), which are widely used in water conservancy, cartography, and aviation. Virtual numbers are increasingly showing their rich content [1-4].

What is Euler’s formula? Why is the Euler formula called the most perfect formula in the world? Let’s take a look together now.

$e^{i_{\theta }}=\cos \theta +i\sin \theta$

The complex plane is shown in Figure 1.

So the complex relationship between the current and voltage of the capacitor indicates a phase difference of 90 degrees between the two:

$i_C=\sqrt{2}{I}_C\cos \left(\omega t+{\psi }_i\right)$

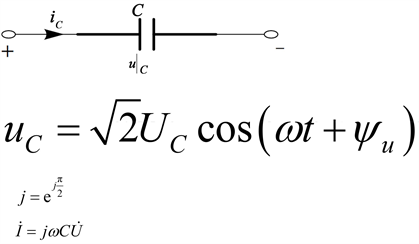
From the above inference, it can be inferred that the imaginary number j in front of the capacitance volt ampere relationship actually only represents that the current of the capacitive component will lead the voltage by 90 degrees in phase, as shown in Figure 2.

That is to say, complex numbers provide a method for representing the phase relationship between two physical quantities.

However, we know that the phase difference between the current and voltage of a capacitor is essentially caused by the differential relationship between the two. This phase difference problem does not necessarily need to be obtained through complex numbers. In Figure 1, the time-domain form of voltage is a cosine function, while the current is a sine, which is sufficient to indicate the phase difference between the two [5-7].

It seems that the emergence of complex numbers provides an analytical method for representing the phase relationship between two different physical quantities, which is sometimes simpler and more convenient compared to the field of real numbers.

However, this method is not essential as it can be substituted in the field of real numbers.

Figure 1. The complex plane.

Figure 2. The phrases of current and voltage.

But in quantum mechanics, there is a so-called Schrödinger equation that describes how the wave function changes over time. There is an imaginary unit i in this equation, which seems to be caused by the phase difference between the physical quantities on both sides of the equation:

$i\hslash \frac{\partial }{\partial t}\psi \left(x,t\right)=\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}\right]+V\left(x,t\right)\psi \left(x,t\right)$

Physicists have never fully determined what this is all about. When Schrödinger deduced the Schrödinger equation, he wanted to remove i. In 1926, he wrote a letter to Hendric Lorenz, “What makes me uneasy is the use of the plural.”, ψ It must be a basic real function

Schrödinger’s idea is certainly reasonable from a mathematical perspective, as any property of a complex number can be achieved by combining real numbers with new rules, opening up mathematical possibilities for the practical foundation of quantum mechanics.

However, simulating complex quantum mechanics with real numbers is a clumsy and abstract task, and Schrödinger realized that his all real number equation was too cumbersome for daily use. In less than a year, he represented the wave function in complex numbers.

However, the true formula of quantum mechanics has always believed that the complex version is only a choice. For example, a study in 2008 showed that the results of the famous quantum physics experiment, the Bell test, could be perfectly predicted without i.

However, with the development of quantum mechanics theory, complex numbers gradually exhibit a certain intuitive irreducibility. In theory, the Schrödinger equation, which is the cornerstone of quantum mechanics, and the Heisenberg commutation relationship themselves rely on complex numbers to be written. In the experiment, people directly measured the real and imaginary parts of the wave function. This indicates that the complex number may not be a subjectively introduced computational symbol, but rather a physical reality that can be experimentally detected.

An experiment conducted by the University of Science and Technology of China showed that real numbers cannot fully describe standard quantum mechanics, establishing the objective reality of complex numbers. We are curious about why complex numbers are necessary and play an important role in quantum mechanics, “said quantum physicist Lu Chaoyang from the University of Science and Technology of China.”

Despite doubts, many physicists unanimously believe that the new discovery of “complex numbers are necessary for quantum theory” is convincing.

If the conclusion that complex numbers are necessary for quantum theory is ultimately proven to be correct, it can only indicate that a certain equation based on which the creator originally created all things did indeed use imaginary numbers, and it also indicates that the creator’s ideas are still elusive, and this world can ultimately be understood by us humans.

2. CONCLUSIONS

In short, the emergence of imaginary numbers:

Firstly, it provides a convenient method for people to solve certain practical problems;

The second is to further deepen people’s exploration of science.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Sullivan, D. (1982) Disjoint Spheres, Approximation by Imaginary Quadratic Numbers, and the Logarithm Law for Geodesics. Acta Mathematica, 149, 215-237. https://doi.org/10.1007/BF02392354
[2]	Antonov, A.A. (2014) Correction of the Special Theory of Relativity: Physical Reality and Nature of Imaginary and Complex Numbers. American Journal of Scientific and Industrial Research, 5, 40-52.
[3]	Zazkis, D. and Zazkis, R. (2014) Script Writing in the Mathematics Classroom: Imaginary Conversations on the Structure of Numbers. Research in Mathematics Education, 16, 54-70. https://doi.org/10.1080/14794802.2013.876157
[4]	Byeon, D. and Lee, S. (2008) Divisibility of Class Numbers of Imaginary Quadratic Fields Whose Discriminant Has Only Two Prime Factors. Proceedings of the Japan Academy Series A Mathematical Sciences, 84, 8-10. https://doi.org/10.3792/pjaa.84.8
[5]	Villeda, J.G. (2021) A Computable Formula for the Class Number of the Imaginary Quadratic Field . Electronic Research Archive, 29, 3853-3865. https://doi.org/10.3934/era.2021065
[6]	Barth, H.G. (2020) The Quantum Astrologer’s Handbook: A History of the Renaissance Mathematics That Birthed Imaginary Numbers, Probability, and the New Physics of the Universe. Isis: An International Review Devoted to the History of Science and Its Cultural Influences, 111, 874-875.
[7]	Kohnen, W. and Ono, K. (1999) Indivisibility of Class Numbers of Imaginary Quadratic Fields and Orders of Tate-Shafarevich Groups of Elliptic Curves with Complex Multiplication. Inventiones Mathematicae, 135, 387-398. https://doi.org/10.1007/s002220050290