An Unbounded Fully Homomorphic Encryption Scheme Based on Ideal Lattices and Chinese Remainder Theorem

Zhiyong Zheng¹, Fengxia Liu^2*, Kun Tian^1*

¹Engineering Research Center of Ministry of Education for Financial Computing and Digital Engineering, Henan Academy of Sciences, Renmin University of China, Beijing, China.
²Beijing Advanced Innovation Center for Future Blockchain and Privacy Computing, Institute of Artificial Intelligence, Beijing, China.

DOI: 10.4236/jis.2023.144021                

Abstract

We propose an unbounded fully homomorphic encryption scheme, i.e. a scheme that allows one to compute on encrypted data for any desired functions without needing to decrypt the data or knowing the decryption keys. This is a rational solution to an old problem proposed by Rivest, Adleman, and Dertouzos [1] in 1978, and to some new problems that appeared in Peikert [2] as open questions 10 and open questions 11 a few years ago. Our scheme is completely different from the breakthrough work [3] of Gentry in 2009. Gentry’s bootstrapping technique constructs a fully homomorphic encryption (FHE) scheme from a somewhat homomorphic one that is powerful enough to evaluate its own decryption function. To date, it remains the only known way of obtaining unbounded FHE. Our construction of an unbounded FHE scheme is straightforward and can handle unbounded homomorphic computation on any refreshed ciphertexts without bootstrapping transformation technique.

Keywords

Fully Homomorphic Encryption, Ideal Lattices, Chinese Remainder Theorem, General Compact Knapsacks Problem

1. Introduction

In 1978, Rivest, Adleman, and Dertouzos [1] proposed a concept which has come to be known as fully homomorphic encryption (FHE), at the time they called it a privacy homomorphism. In brief, we write a cryptosystem by $\mathcal{P}\stackrel{f}{\to }\mathcal{C}\stackrel{f^{-1}}{\to }\mathcal{P}$ , where $\mathcal{P}$ is the plaintexts space, and $\mathcal{C}$ is the ciphertexts space, f is the encryption function depends on public keys, and $f^{-1}$ is the decryption function depends on secret keys. Suppose that $\mathcal{P}$ and $\mathcal{C}$ are two commutative rings, and $f^{-1}\left(c_1+c_2\right)=f^{-1}\left(c_1\right)+f^{-1}\left(c_2\right)\mathrm{,}{f}^{-1}\left(c_1{c}_2\right)=f^{-1}\left(c_1\right)f^{-1}\left(c_2\right)\mathrm{,}\forall c_1\mathrm{,}{c}_2\in \mathcal{C}\mathrm{,}$ then f is called a fully homomorphic encryption, or FHE. Under a FHE f, for any polynomials $p\left(x\right)\in \mathcal{C}\left[x\right]$ , it is easy to see that $f^{-1}\left(p\left(c\right)\right)=p^{\mathrm{<mo>\; *\; </mo>}}\left(f^{-1}\left(c\right)\right)\mathrm{,}\forall c\in \mathcal{C}\mathrm{,}$ where $p^{\mathrm{<mo>\; *\; </mo>}}\left(x\right)\in \mathcal{P}\left[x\right]$ is the corresponding polynomial over $\mathcal{P}$ . Since all elementary functions can be approximated by polynomials, we can do any desired computation on ciphertexts without the decryption of data.

1.1. Unbounded FHE Schemes

Fully homomorphic encryption was known to have abundant applications in cryptography, but for more than three decades no plausibly secure scheme was known. This changed in 2009 when Gentry [3] [4] proposed a candidate FHE scheme based on ideal lattices. The candidate FHE scheme means a somewhat homomorphic scheme that supports only a bounded amount of homomorphic computation on fresh ciphertexts, then, one applies the bootstrapping transformation to convert the scheme into one that can handle unbounded homomorphic computation. Gentry’s breakthrough seminal work generated tremendous excitement and was quickly followed by many works [5] - [16] . Despite significant advances, bootstrapping is computationally quite expensive, because it involves homomorphically evaluating the entire decryption function. In addition, bootstrapping for unbounded FHE requires one to make a “circular security” assumption, i.e., it is secure to reveal an encryption of the secret key under itself. So far, such assumptions are poorly understood, and we have little theoretical evidence to support them, in particular, no worst-case hardness. Because of this, Peikert [2] put out two open problems relating to unbounded FHE as follows.

· Open Question 10: Is there an unbounded FHE scheme that does not rely on bootstrapping? Is there a version of bootstrapping that uses a lighter-weight computation than full decryption?

· Open Question 11: Is there an unbounded FHE scheme that can be proved secure solely under a worst-case complexity assumption?

1.2. The FHE Schemes from LWE Distribution

To date, all known full homomorphic encryption schemes follow the same basic template from Gentry’s initial work [3] . In a sequence of work, Brakerski and Vaikuntanathan [7] [8] gave a “second generation” of FHE constructions based on LWE distribution [17] [18] . In 2013, Gentry, Sahai, and Waters [19] proposed another interesting LWE-based FHE scheme that has some unique and advantageous properties. For example, the GSW Scheme can be used to bootstrap with only a small polynomial-factor growth in the error rate. We describe these schemes in detail here.

· BV FHE Scheme Let $1<t<q$ be two positive integers such that $\left(t,q\right)=1$ . In the BV system, a secret key s is an LWE secret and encrypts a plaintext $u\in {\mathbb{Z}}_t$ using an LWE sample for modulus q. We use the most significant bit encoding to obtain a ciphertext c by

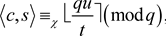
where $\chi$ is a discrete Gauss distribution over ${\mathbb{Z}}_q$ , and 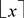is the rounding of a real number x to the nearest integer. We use secret key s to decrypt the ciphertext c by

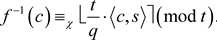
Obviously, one has $f^{-1}\left(c\right)=u$ (see [20] ). To explain this scheme is a somewhat FHE scheme, we may use the least significant bit encoding of the message (The equivalence of two encodings is referred to in Appendix A of [21] ). In fact, the ciphertext c satisfies

$\langle s\mathrm{,}c\rangle {\equiv }_{\chi }m\left(\mathrm{mod}q\right)\mathrm{,}\text{and}m\in \left\{nt+u|n\in \mathbb{Z}\right\}\cap \left[-\frac{q}{2}\mathrm{,}\frac{q}{2}\right)\mathrm{.}$

To decrypt c, one just compute $\langle s\mathrm{,}c\rangle \in {\mathbb{Z}}_q$ , lifts the result to its unique representative m in $\mathbb{Z}\cap \left[-\frac{q}{2}\mathrm{,}\frac{q}{2}\right)$ , and the outputs $u\equiv m\left(\mathrm{mod}t\right)$ . It is easily seen that the homomorphic computation on ciphertext c induces some noises, which, if too large, will destroy the plaintext. Therefore, the bootstrapping technique that re-encrypts a ciphertext and reduces the noise level remains the only known way of building the unbounded FHE schemes.

· GSW FHE Scheme The GSW FHE scheme is presented most simply in terms of the gadget-based trapdoor described in [22] [23] [24] [25] [26] . The heart of the GSW scheme is the following additive and multiplicative homomorphisms for tags and trapdoors. Let $\bar{A}\in {\mathbb{Z}}_q^{n\times \bar{m}}$ be LWE samples with a secret key $\bar{s}\in {\mathbb{Z}}_q^{n-1}$ , and for $i=\mathrm{1,2}$ , let $A_i=x_{i}G-\bar{A}{R}_i\mathrm{,}$

where $x_i\in {\mathbb{Z}}_q$ , G is the block-diagonal gadget matrix of dimension $n\times nl$ , $R_i\in {\mathbb{Z}}_q^{\bar{m}\times n}$ are random Gauss matrices over ${\mathbb{Z}}_q$ , and $\bar{m}=n+nl$ (see p.50 of [2] ). Since $\left(\begin{array}{l}{R}_i\hfill \\ I_n\hfill \end{array}\right)$ is a trapdoor with a tag $x_i{I}_n$ for matrix $\left[\bar{A}\mathrm{,}{A}_i\right]$ , it is easy to verify that $A_1+A_2=\left(x_1+x_2\right)G-\bar{A}\left(R_1+R_2\right)$ and $A_1{G}^{-1}\left(A_2\right)=x_1{x}_{2}G-\bar{A}\underset{R}{\underset{︸}{\left(R_1{G}^{-1}\left(A_2\right)+x_1{R}_2\right)}}\mathrm{.}$

In other words, $\left(\begin{array}{c}{R}_1+R_2\\ I_n\end{array}\right)$ is a trapdoor with a tag $\left(x_1+x_2\right)I_n$ for matrix $\left[\bar{A}\mathrm{,}{A}_1+A_2\right]$ , and $\left(\begin{array}{l}R\hfill \\ I_n\hfill \end{array}\right)$ is a trapdoor with a tag $x_1{x}_2{I}_n$ for matrix $\left[\bar{A}\mathrm{,}{A}_1{G}^{-1}\left(A_2\right)\right]$ . Even with all of the above techniques, homomorphic operations always increase the error rate of a ciphertext, by as much as a polynomial factor per operation. Therefore, the schemes described here can only homomorghically evaluate circuits of an a-priori bounded depth.

1.3. The FHE Schemes from Ring-LWE

Several constructions based on Ring-LWE are today among the most promising FHE candidates. There are three most popular FHE schemes from Ring-LWE: (1) TFHE [27] [28] particularly suitable for combinatorial operations on individual slots and tolerating large noise and thus, large multiplicative depth; (2) B/FV [5] [29] [30] allowing to perform large vectorial arithmetic operations as long as the multiplicative depth of the evaluated circuit remains small; (3) HEAAN [31] [32] —a mixed encryption scheme shown to be very efficient for floating-point computations. We introduce these schemes slightly in detail as follows.

· TFHE Scheme TFHE consists of three major encryption/decryption schemes, each represented by a different plaintext space. First, the scheme TLWE encrypts messages over the entire torus $\mathbb{T}$ and produces ciphertexts in ${\mathbb{T}}^{N+1}$ . The other two schemes are:

­ TRGSW encrypts elements of the ring ${\mathcal{R}}_{\mathbb{Z}}$ (integer polynomials) with bounded $l^{\infty }$ -norms (of the corresponding vectors in ${\mathbb{Z}}^N$ under the natural identification $\mathcal{R}\simeq {\mathbb{Z}}^N$ ).

­ TRLWE encrypts elements $\mu$ of the ${\mathcal{R}}_{\mathbb{Z}}$ -module ${\mathbb{T}}_{\mathcal{R}}$ that can also be viewed as elements of ${\mathbb{T}}^N$ via the natural bijection ${\mathbb{T}}_{\mathcal{R}}\simeq {\mathbb{T}}^N$ .

There is an external product ${⊡}_{\alpha }$ depending on a noise parameter $\alpha$ (see Corollary 3.14 [28] ) which yields a FHE module structure on the schemes TRGSW and TRLWE.

In TFHE, TLWE ciphertexts of a message $\mu \in \mathbb{T}$ have the form $\left(a\mathrm{,}b=\langle s\mathrm{,}a\rangle +\mu +e\right)\in {\mathbb{T}}^{N+1}$ where $s\in {\left\{\mathrm{0,1}\right\}}^N$ is the secret key, $a\in {\mathbb{T}}^N$ is uniformly random and $e\in \mathbb{T}$ is sampled according to a noise distribution centered at zero. Similarly, for TRLWE, ciphertexts of $\mu \in {\mathbb{T}}_{\mathcal{R}}$ are of the form $\left(a\mathrm{,}b=s\cdot a+\mu +e\right)\in {\mathbb{T}}_{\mathcal{R}}^2$ where $s\in \mathcal{B}$ , $a\in {\mathbb{T}}_{\mathcal{R}}$ is uniformly random and $e\in {\mathbb{T}}_{\mathcal{R}}$ .

The decryption in TLWE (resp. TRLWE) uses a secret $\kappa$ -Lipschitz function (here, $\kappa >0$ is small and we mean “with respect to the $l^{\infty }$ -norm on the torus”) ${\phi }_s\mathrm{<mo>\; :\; </mo>}{\mathbb{T}}^N\times \mathbb{T}\to \mathbb{T}$ (resp. ${\phi }_s\mathrm{<mo>\; :\; </mo>}{\mathbb{T}}_{\mathcal{R}}\times {\mathbb{T}}_{\mathcal{R}}\to {\mathbb{T}}_{\mathcal{R}}$ ) called phase parametrized by a small (often binary) secret key $s\in {\left\{\mathrm{0,1}\right\}}^N$ (resp. $s\in \mathcal{B}$ ) and defined by $\left(a\mathrm{,}b\right)\in {\mathbb{T}}^N\times \mathbb{T}\to b-\langle s\mathrm{,}a\rangle$ (resp. $\left(a\mathrm{,}b\right)\to b-s\cdot a$ ). The fact that the phrase is a $\kappa$ -Lipschitz function for small $\kappa \le N+1$ makes the decryption tolerant to errors and allows working with approximated numbers.

Ciphertexts are either fresh (i.e., generated by directly encrypting a plaintext) or they are produced by a sequence of homomorphic operations. In both cases, one views the ciphertext as a random variable depending on the random coins used to generate a and e as well as all random coins used in all these homomorphic operations.

Since ${\phi }_s\left(a,b\right)=b-s\cdot a=\mu +e$ , the decryption $\mu$ and the noise parameter $\alpha$ are the mean and the standard deviation of the phase function ${\phi }_s\left(a,b\right)$ , respectively (here, the mean and standard deviation are computed over the random coins in the encryption algorithm).

· B/FV Scheme In this scheme, the message space is the finite ring ${\mathcal{R}}_p={\mathbb{Z}}_p\left[x\right]/\langle x^N+1\rangle$ for some integer p (typically a power of 2 or a prime number). A message $\mu \in {\mathcal{R}}_p$ is encrypted on a quotient ring ${\mathcal{R}}_q$ (for a larger modulus q) as a ciphertext $\left(a\mathrm{,}b\right)\in {\mathcal{R}}_q^2$ where $a\in {\mathcal{R}}_q$ is chosen uniformly at random and b is sampled from ${\mathcal{D}}_{{\mathcal{R}}_q\mathrm{,}\sigma \mathrm{,}s\cdot a+\frac{p}{q}\mu }$ . Here, ${\mathcal{D}}_{{\mathcal{R}}_q\mathrm{,}\sigma \mathrm{,}\mu }$ is the discrete Gaussian distribution over ${\mathcal{R}}_q$ centered at $\mu$ with standard deviation $\sigma$ (discrete means that the values are integers only). In addition, $s\in \mathcal{B}$ is the secret key.

Homomorphic addition of two ciphertexts $\left(a_1\mathrm{,}{b}_1\right)$ and $\left(a_2\mathrm{,}{b}_2\right)$ is achieved by component-wise addition. The idea behind the homomorphic multiplication of two ciphertexts $\left(a_1\mathrm{,}{b}_1\right)$ and $\left(a_2\mathrm{,}{b}_2\right)$ is a technique referred to as relinearization: one first lifts $\left(a_i\mathrm{,}{b}_i\right)\in {\mathcal{R}}_q^2$ to $\left({\tilde{a}}_i\mathrm{,}{\tilde{b}}_i\right)\in {\mathcal{R}}^2$ where each coefficient is lifted to $\left[-q/2\mathrm{,}q/2\right)$ and then views of ${\mu }_i$ as being expressed as a linear polynomial on s (i.e., ${\mu }_i~\frac{p}{q}\left(b_i+s\cdot a_i\right)$ ). One then computes the quadratic polynomial corresponding to the product, namely $\frac{p}{q}\left(b_1+s\cdot a_1\right)\cdot \frac{p}{q}\left(b_2+s\cdot a_2\right)$ , and uses the relinearization described in [30] to write this product as $\frac{p}{q}\left(b+s\cdot a\right)$ and determine the coefficients $\left(a\mathrm{,}b\right)\in {\mathcal{R}}_q$ .

The noise amplitude grows by a small factor $O\left(N\right)$ on average after each multiplication, so it is a common practice to perform a modulus-rescaling step, that divides and rounds each coefficient as well as the modulus q by the same scalar in order to bring the noise amplitude back to $O\left(1\right)$ so that the subsequent operations continue on smaller ciphertexts.

· HEAAN Scheme In this scheme, the message space is the subset of ${\mathcal{R}}_q$ containing all elements of norm $\le B$ for some bound B, where the norm of an element $x\in {\mathcal{R}}_q$ is defined as ${\Vert \tilde{x}\Vert }_{\infty }$ . Here $\tilde{x}\in {\mathcal{R}}_{ℝ}$ is the minimal lift of x, i.e., coefficients lifted to $\left[-q/2\mathrm{,}q/2\right)$ . The message is decrypted up to a constant number of the least significant bits which are considered as noise.

A HEAAN ciphertext is also a Ring-LWE pair $\left(a\mathrm{,}b\right)\in {\mathcal{R}}_q^2$ where $a\in {\mathcal{R}}_q$ is uniformly random and b is equal to $s\cdot a+\mu$ up to a Gaussian error of small standard deviation. This time, plaintexts and ciphertexts share the same space, so no rescaling factor p/q is used. Multiplication of two messages uses the same formula as in B/FV including relinearization: if both input messages are bounded by B with $O\left(1\right)$ noise, the product is a message bounded by B² with noise $O\left(B\right)$ , so it is a common practice at this point to perform a modulusrescaling step that divides everything by B to bring the noise back to $O\left(1\right)$ (see [32] ). Unlike B/FV, this division in the modulus switching scales not only the ciphertext but also the plaintext by B. This can be fixed by adding a (public) tag to the ciphertext to track the number of divisions by B performed.

Recently, Boura, Gama, Georgieva, and Jetchev [33] proposed a practical hybrid solution for combining and switching between the above three Ring-LWE-based FHE schemes. They achieved it by first mapping the different plaintext spaces to a common algebra structure and then by applying efficient switching algorithms. This approach has many practical applications, for example, it becomes an integral tool for the recent standardization initiatives of homomorphic schemes and common APIs.

1.4. Other Related Works

At Eurocrypt 2010, van Dijk, Gentry, Halevi, and Vaikuntanathan [34] described a fully homomorphic encryption scheme over the integers (see also [9] [10] [11] ). As in Gentry’s scheme, the authors first describe a somewhat homomorphic scheme supporting a limited number of additions and multiplications over encrypted bits. Then they apply Gentry’s squash decryption technique to get a bootstrappable scheme and then Gentry’s ciphertext refresh procedure to get a full homomorphic scheme. The main appeal of the scheme (compared to the original Gentry’s scheme) is its conceptual simplicity, namely, all operations are done over those integers instead of ideal lattices. However, the public key was too large for any practical system. In [10] and [11] , the authors reduced the public key site

from $\tilde{\mathcal{O}}\left({\lambda }^{10}\right)$ to $\tilde{\mathcal{O}}\left({\lambda }^7\right)$ by encrypting with a quadratic form in the public key elements, instead of a linear form.

It is the latest scheme, without using noise reduction techniques (see [35] ). In 2015, Yagisawa proposed a non-associative octonion ring over a finite field fully homomorphic encryption scheme [36] . This scheme’s cryptographic robustness is based on the complexity of multivariate algebraic equations with high degree. In his next paper, he developed some improvements to the scheme [37] . Liu presented a symmetric fully homomorphic encryption scheme based on non-commutative rings [38] . Liu’s scheme provides an arbitrary number of additions and multiplications, and the correct decryption in contempt of the amount of noise reduction mechanisms and based on the approximating-GCD complexity. Noise-free symmetric fully homomorphic encryption scheme was proposed by Li and Wang [39] that used matrices over non-commutative rings. Needless to say, those noise-free schemes are not the solutions to problems of the FHE scheme, because of using non-associative and non-commutative rings for the plaintexts and ciphertexts.

1.5. Our Contribution

Our contribution to the unbounded FHE scheme is straightforward, which is completely different from Gentry’s initial construction. More precisely, our FHE scheme can handle unbounded homomorphic computation on any refreshed ciphertexts without bootstrapping transformation. This is a rational solution to open problems on fully homomorphic encryption.

Our solution comes in three steps. First, we provide a general noise-free construction based on ideal lattices and the Chinese Remainder Theorem, which includes three efficient algorithms for generating secret key, public key and decryption. The plaintext space is the direct sum of rings ${\mathbb{Z}}_{t_i}$ , where $t_i$ is the one-dimensional modulus of each ideal lattice $I_i$ ( $1\le i\le m$ ). The ciphertext space ${\mathbb{Z}}^n$ is a commutative ring with the addition and convolutional product $\otimes$ of vectors, needless to say, the algebraic structures for homomorphic computation are simplest. The main ideal is to set up a multiplicative operation for ${\mathbb{Z}}^n$ , such that ${\mathbb{Z}}^n$ becomes a commutative ring, therefore, one views $I\subset {\mathbb{Z}}^n$ both as an ideal and as a lattice in ${\mathbb{Z}}^n$ , in particular, ${\mathbb{Z}}^n/I$ becomes a quotient ring. Working with the ring $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ , we can efficiently utilize the Chinese Remainder Theorem for generating of public key. Next, we provide a probabilistic algorithm for public keys, so that the encryption algorithms are secure against indistinguishable under chosen-plaintext attacks, namely, our scheme is IND-CPA secure. Finally, we discuss the IND-CCA security of our scheme based on the general compact knapsacks problem for arbitrary rings, we show that the security is solely under the worst-case complexity assumption. This is also a solution to open question 11 of Peikert [2] . In the last section of this paper, we provide a practical system based on some basic results from cyclotomic fields [40] . The novelty of this practical system is to establish a connection between a cryptosystem and the ancient hard problem in mathematics: how to find a solution to an algebraic equation with a high degree. By the famous Galois theory, there is no general method to find a solution when the degree of an algebraic equation is bigger than 5.

The generalization of compact knapsack problem for arbitrary ring may be described as follows: given m ring elements $a_1\mathrm{,}{a}_2\mathrm{,}\cdots ,a_m\in R$ and a target value $b\in R$ , find coefficients $x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_m\in X\subset R$ such that ${\displaystyle {\sum }_{i=1}^m}{a}_i{x}_i=b$ . The computational complexity of this problem depends on the choice of ring R and the size of X. This problem is known to be solvable in quasi polynomial time when R is the ring of integers and X is the set of small integers $\left\{\mathrm{0,1,}\cdots {\mathrm{,2}}^{m-1}\right\}$ (see [41] and [42] ). Micciancio [42] studied the knapsack problem when R is an appropriately chosen ring of modulo polynomials and X is the subset of polynomials with small coefficients, he has shown that the complexity is as hard to solve on the average as the worst-case instance of approximating the covering radius of any cyclic lattice within a polynomial factor.

We generalize this result to any ideal lattices, such that our FHE scheme is as hard to solve on the average as the worst case of approximating the covering radius of any ideal lattices.

2. The General Construction without Disturbance

Let $\mathbb{Z}\left[x\right]$ be the ring of integer coefficients polynomials with variable x, $\varphi \left(x\right)\in \mathbb{Z}\left[x\right]$ , and $\varphi \left(x\right)=x^n-{\varphi }_{n-1}{x}^{n-1}-\cdots -{\varphi }_{1}x-{\varphi }_0$ with ${\varphi }_0\ne 0$ be a given polynomial, $\langle \varphi \left(x\right)\rangle$ be the principal ideal generated by $\varphi \left(x\right)$ in $\mathbb{Z}\left[x\right]$ , $R=\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ be the quotient ring. Let ${ℝ}^n$ be the n dimensional Euclidean space, and ${\mathbb{Z}}^n\subset {ℝ}^n$ be all of integer vectors in ${ℝ}^n$ . We use column notation for vectors in ${ℝ}^n$ .

There is a one to one correspondence between the quotient ring $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ and all the integer vectors ${\mathbb{Z}}^n$ :

$a\left(x\right)\text{=}{a}_0+a_{1}x+\cdots +a_{n-1}{x}^{n-1}\in \mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle \stackrel{\tau }{\to }a=\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_{n-1}\end{array}\right)\in {\mathbb{Z}}^n\mathrm{,}$ (2.1)

we write $\tau \left(a\left(x\right)\right)=a$ , or ${\tau }^{-1}\left(a\right)=a\left(x\right)$ . Since $\tau \left(a\left(x\right)+b\left(x\right)\right)=\tau \left(a\left(x\right)\right)+\tau \left(b\left(x\right)\right)$ , $\tau$ is an isomorphism of additive groups in fact. To regard $\tau$ as an isomorphism of rings, we need to define a multiplicative operator in ${\mathbb{Z}}^n$ . To do this, let the rotation matrix $H=H_{\varphi }$ be given by

$H\mathrm{<mo>\; =\; </mo>}\left(\begin{array}{cccc}0& \cdots & 0& {\varphi }_0\\ & & & {\varphi }_1\\ & I_{n-1}& & ⋮\\ & & & {\varphi }_{n-1}\end{array}\right)$

where $I_{n-1}$ is the unit matrix of $n-1$ dimension.

DEFINITION 2.1 For any $\alpha \in {ℝ}^n$ , the ideal matrix generated by $\alpha$ is defined by

$H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)=\left[\alpha \mathrm{,}H\alpha \mathrm{,}\cdots \mathrm{,}{H}^{n-1}\alpha \right]\in {ℝ}^{n\times n}\mathrm{.}$

Some basic properties about ideal matrix may be described as the following lemma, its proof is referred to Lemma 2.5 of [43] , or Lemma 5.2.4 of [44] .

Lemma 2.1 Let $\alpha =\left(\begin{array}{c}{\alpha }_0\\ {\alpha }_1\\ ⋮\\ {\alpha }_{n-1}\end{array}\right)$ and $\beta =\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_{n-1}\end{array}\right)$ be any two vectors in ${ℝ}^n$ , then one has

(i) $H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)={\alpha }_0{I}_n+{\alpha }_{1}H+\cdots +{\alpha }_{n-1}{H}^{n-1}$ ;

(ii) $H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)H^{\mathrm{<mo>\; *\; </mo>}}\left(\beta \right)=H^{\mathrm{<mo>\; *\; </mo>}}\left(\beta \right)H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)$ ;

(iii) $H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)H^{\mathrm{<mo>\; *\; </mo>}}\left(\beta \right)=H^{\mathrm{<mo>\; *\; </mo>}}\left(H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)\beta \right)$ ;

(iv) $\det \left(H^{*}\left(\alpha \right)\right)={\displaystyle \underset{i=1}{\overset{n}{\prod }}}\alpha \left({\omega }_i\right)$ ;

where $\det \left(H^{*}\left(\alpha \right)\right)$ is the determinant of $H^{*}\left(\alpha \right)$ , $\alpha \left(x\right)={\tau }^{-1}\left(\alpha \right)$ , and ${\omega }_1\mathrm{,}{\omega }_2\mathrm{,}\cdots \mathrm{,}{\omega }_n$ are n roots of $\varphi \left(x\right)$ .

By (iv) of Lemma 2.1, $H^{*}\left(\alpha \right)$ is an invertible matrix if and only if $\alpha \left(x\right)$ and $\varphi \left(x\right)$ have no common roots in complex numbers field. Now, we may define a multiplicative operator in ${\mathbb{Z}}^n$ in terms of the ideal matrix.

DEFINITION 2.2 Let $\alpha \mathrm{,}\beta \in {\mathbb{Z}}^n$ be two integer vectors, we define the convolutional product $\alpha \otimes \beta$ by $\alpha \otimes \beta =H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)\beta \mathrm{.}$

Obviously, under the convolutional product $\alpha \otimes \beta$ , ${\mathbb{Z}}^n$ becomes a commutative ring with the unit element $e=\left(\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right)\in {\mathbb{Z}}^n$ , since $\alpha \otimes \beta =\beta \otimes \alpha$ and $\alpha \otimes e=e\otimes \alpha =\alpha ,\forall \alpha \in {\mathbb{Z}}^n.$

Sometimes, we write this ring by $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)={\mathbb{Z}}^n$ .

Lemma 2.2 The correspondence $\tau$ given by (2.1) is a ring isomorphism between ${\mathbb{Z}}^n/\langle \varphi \left(x\right)\rangle$ and ${\mathbb{Z}}^n$ , namely, we have

$\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle \cong \left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)\mathrm{.}$

Proof. By Lemma 2.4 of [43] or Lemma 5.2.5 of [44] , it is easy to see that

$\begin{array}{l}\tau \left(\alpha \left(x\right)+\beta \left(x\right)\right)=\alpha +\beta =\tau \left(\alpha \left(x\right)\right)+\tau \left(\beta \left(x\right)\right)\mathrm{,}\\ \tau \left(\alpha \left(x\right)\beta \left(x\right)\right)=\alpha \otimes \beta =\tau \left(\alpha \left(x\right)\right)\otimes \tau \left(\beta \left(x\right)\right)\mathrm{.}\end{array}$

The conclusion follows immediately.

According to the definition of ideal lattices [2] [42] [45] [46] [47] [48] , an ideal lattice $I\subset {\mathbb{Z}}^n$ , just is an ideal of $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ , we view $I\subset {\mathbb{Z}}^n$ both as an ideal of ${\mathbb{Z}}^n$ and as a lattice in ${\mathbb{Z}}^n$ , in particular, ${\mathbb{Z}}^n/I$ is a quotient ring.

A lattice $I\subset {ℝ}^n$ is a discrete additive group of ${ℝ}^n$ [46] [49] [50] , we write $I=\mathcal{L}\left(B\right)$ as usual, where $B=\left[{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}\cdots \mathrm{,}{\beta }_n\right]\in {ℝ}^{n\times n}$ is the generated matrix or a basis of I. All lattices we discuss here are the full rank lattice, it means that $\det \left(B\right)\ne 0$ . If $I\subset {\mathbb{Z}}^n$ , then I is called an integer lattice. The Hermite Normal Form base B [40] [51] for an integer lattice is an upper triangular matrix $B={\left(b_{ij}\right)}_{n\times n}\in {\mathbb{Z}}^{n\times n}$ satisfying $b_{ii}\ge 1$ ( $1\le i\le n$ ) and

$b_{ij}=\mathrm{0,}\text{if}0\le j<i\le n\mathrm{,}\text{and}0\le b_{ij}<b_{ii}\mathrm{,}\text{if}0\le i<j\le n\mathrm{.}$

It is known that there is a unique HNF basis for an integer lattice and its Gram-Schmidt orthogonal basis is a diagonal matrix, more precisely, if $B=\left[{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}\cdots \mathrm{,}{\beta }_n\right]$ is the HNF basis of an integer lattice, $B^{\mathrm{<mo>\; *\; </mo>}}=\left[{\beta }_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\beta }_2^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}\cdots \mathrm{,}{\beta }_n^{\mathrm{<mo>\; *\; </mo>}}\right]$ is the corresponding orthogonal basis obtained by Gram-Schmidt orthogonal method, then $B^{\mathrm{<mo>\; *\; </mo>}}=\text{diag}\left\{b_{11}\mathrm{,}{b}_{22}\mathrm{,}\cdots \mathrm{,}{b}_{nn}\right\}$ is a diagonal matrix (see Lemma 7.26 of [40] ).

DEFINITION 2.3 $b_{11}$ is called the one dimensional modulus of an ideal lattice $I=\mathcal{L}\left({\beta }_1\mathrm{,}{\beta }_2\mathrm{,}\cdots \mathrm{,}{\beta }_n\right)$ , and denoted by $t\left(I\right)=b_{11}$ .

Let $I\subset \left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ be an ideal lattice, to obtain a set of representative elements for the quotient ring ${\mathbb{Z}}^n/I$ , we use the notation of orthogonal parallelepiped due to Micciancio [51] . The following lemma is referred to as Lemma 7.45 and (7.131) of [40] , or §4.1 of [51] , and a proof will be appeared in Lemma 2.6 below.

Lemma 2.3 Suppose that $I=\mathcal{L}\left(B\right)$ is a full rank ideal of ${\mathbb{Z}}^n$ , B is the HNF basis of I, and $B^{\mathrm{<mo>\; *\; </mo>}}=\text{diag}\left\{b_{11}\mathrm{,}{b}_{22}\mathrm{,}\cdots \mathrm{,}{b}_{nn}\right\}$ is the corresponding orthogonal basis, then a set of representative elements of the quotient ring ${\mathbb{Z}}^n/I$ is $\mathcal{F}\left(I\right)=\left\{x=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)\in {\mathbb{Z}}^n\mathrm{<mo>\; |\; </mo>}0\le x_i<b_{ii}\mathrm{,}1\le i\le n\right\}\mathrm{,}$ and $\mathcal{F}\left(I\right)$ is called the orthogonal parallelepiped of I.

Next, we turn to discuss the ideal lattices and the ring $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ . Let $\alpha \in {\mathbb{Z}}^n$ be a given vector, the principal ideal lattice $\langle \alpha \rangle$ is a principal ideal generated by $\alpha$ in ${\mathbb{Z}}^n$ . It is easily verified that

$\langle \alpha \rangle =\left\{\alpha \otimes x\mathrm{<mo>\; |\; </mo>}x\in {\mathbb{Z}}^n\right\}=\mathcal{L}\left(H^{\mathrm{<mo>\; *\; </mo>}}\left(\alpha \right)\right)\mathrm{.}$

Thus, the generated matrix of a principle ideal lattice $\langle \alpha \rangle$ just is the ideal matrix generated by $\alpha$ .

The operations among the ideal lattices in $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ are defined as usual, in particular, the addition and multiplication for two ideals, I and J are defined by $I+J=\left\{\alpha +\beta \mathrm{<mo>\; |\; </mo>}\alpha \in I\mathrm{,}\beta \in J\right\}\mathrm{,}$ $IJ=\left\{{\displaystyle \underset{i<\infty }{\sum }}{\alpha }_i\otimes {\beta }_i|{\alpha }_i\in I,{\beta }_i\in J\right\},$ and $I\cap J=\left\{\gamma \mathrm{<mo>\; |\; </mo>}\gamma \in I\mathrm{,}\text{and}\gamma \in J\right\}\mathrm{.}$

Since $I+J$ , $IJ$ and $I\cap J$ are also the ideals of ${\mathbb{Z}}^n$ , therefore, all of them are ideal lattices.

DEFINITION 2.4 Let $I\subset {\mathbb{Z}}^n$ , $J\subset {\mathbb{Z}}^n$ be two ideal lattices. If $I+J={\mathbb{Z}}^n$ , we call I and J to be relatively prime, and denoted by $\left(I\mathrm{,}J\right)=1$ .

It is easy to see that two ideal lattices I and J are relatively prime, if and only if there are $\alpha \in I$ and $\beta \in J$ such that $\alpha +\beta =e$ , where e is the unit element of $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ .

To construct a FHE scheme, we utilize the Chinese Remainder Theorem in the ring $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ , which is a well-known theorem in Number Theory.

THEOREM 1 (Chinese Remainder Theorem) Let $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ be pairwise relatively prime ideal lattices in ${\mathbb{Z}}^n$ , and ${\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_m\in {\mathbb{Z}}^n$ be m target vectors in ${\mathbb{Z}}^n$ , then there exists a common solution of the following congruences: $x\equiv {\alpha }_i\left(\mathrm{mod}{I}_i\right)\mathrm{,}1\le i\le m\mathrm{,}$ and the solution of $x\in {\mathbb{Z}}^n$ is a unique modulo-ideal lattice $I_1\cap I_2\cdots \cap I_m$ .

For arbitrary pairwise relatively prime lattices $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ , it is known that

$I_1\cap I_2\cdots \cap I_m=I_1{I}_2\cdots I_m\mathrm{.}$

By the above Chinese Remainder Theorem, one has the following consequence immediately.

Corollary 2.1 Suppose that $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ are pairwise relatively prime ideal lattices in ${\mathbb{Z}}^n$ , then we have the following ring isomorphism

${\mathbb{Z}}^n/I_1{I}_2\cdots I_m\cong {\mathbb{Z}}^n/I_1\oplus {\mathbb{Z}}^n/I_2\oplus \cdots \oplus {\mathbb{Z}}^n/I_m\mathrm{.}$ (2.2)

The right-hand side of (2.2) is the direct sum of m quotient ring ${\mathbb{Z}}^n/I_i$ ( $1\le i\le m$ ), and the addition and multiplication of $\underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}^n/I_i$ are given by $\left(a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_m\right)+\left(b_1\mathrm{,}{b}_2\mathrm{,}\cdots \mathrm{,}{b}_m\right)=\left(a_1+b_1\mathrm{,}{a}_2+b_2\mathrm{,}\cdots \mathrm{,}{a}_m+b_m\right)$ and $\left(a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_m\right)\otimes \left(b_1\mathrm{,}{b}_2\mathrm{,}\cdots \mathrm{,}{b}_m\right)=\left(a_1\otimes b_1\mathrm{,}{a}_2\otimes b_2\mathrm{,}\cdots \mathrm{,}{a}_m\otimes b_m\right)\mathrm{.}$

Proof. Since $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ are pairwise prime, by Theorem 1, there are m vectors $A_i$ ( $1\le i\le m$ ) in ${\mathbb{Z}}^n$ such that $A_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{A}_i\equiv 0\left(\mathrm{mod}{I}_j\right)\mathrm{,}\text{if}j\ne i\mathrm{.}$

For any $\alpha =\left({\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_m\right)\in {\mathbb{Z}}^n/I_1\oplus {\mathbb{Z}}^n/I_2\oplus \cdots \oplus {\mathbb{Z}}^n/I_m$ , by Theorem 1 again, there is a unique solution $x\in {\mathbb{Z}}^n/I_1{I}_2\cdots I_m$ such that

$\{\begin{array}{l}x\equiv {\alpha }_1\left(\mathrm{mod}{I}_1\right)\\ ⋮\\ x\equiv {\alpha }_m\left(\mathrm{mod}{I}_m\right)\end{array}$

We define $f\left(\alpha \right)=x$ , which is the ring isomorphism from ${\mathbb{Z}}^n/I_1\oplus {\mathbb{Z}}^n/I_2\oplus \cdots \oplus {\mathbb{Z}}^n/I_m$ to ${\mathbb{Z}}^n/I_1{I}_2\cdots I_m$ as we desired. Using $A_1\mathrm{,}{A}_2\mathrm{,}\cdots \mathrm{,}{A}_m$ , one may clearly write down f by $f\left(\alpha \right)=f\left(\left({\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_m\right)\right)={\alpha }_1\otimes A_1+\cdots +{\alpha }_m\otimes A_m\mathrm{.}$

Let $\beta =\left({\beta }_1\mathrm{,}{\beta }_2\mathrm{,}\cdots \mathrm{,}{\beta }_m\right)$ be another element of $\underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}^n/I_i$ , it is easy to see that

$\begin{array}{c}f\left(\alpha +\beta \right)=f\left(\left({\alpha }_1+{\beta }_1\mathrm{,}{\alpha }_2+{\beta }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_m+{\beta }_m\right)\right)\\ ={\alpha }_1\otimes A_1+\cdots +{\alpha }_m\otimes A_m+{\beta }_1\otimes A_1+\cdots +{\beta }_m\otimes A_m\\ =f\left(\alpha \right)+f\left(\beta \right)\mathrm{.}\end{array}$

To verify $f\left(\alpha \otimes \beta \right)=f\left(\alpha \right)\otimes f\left(\beta \right)$ , since $f\left(\alpha \right)\equiv {\alpha }_i\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}f\left(\beta \right)\equiv {\beta }_i\left(\mathrm{mod}{I}_i\right)\mathrm{,}1\le i\le m\mathrm{.}$

It follows that $f\left(\alpha \right)\otimes f\left(\beta \right)\equiv {\alpha }_i\otimes {\beta }_i\left(\mathrm{mod}{I}_i\right)\mathrm{,}1\le i\le m\mathrm{.}$

By the definition of f, we have $f\left(\alpha \otimes \beta \right)=f\left(\left({\alpha }_1\otimes {\beta }_1\mathrm{,}{\alpha }_2\otimes {\beta }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_m\otimes {\beta }_m\right)\right)=f\left(\alpha \right)\otimes f\left(\beta \right)\mathrm{.}$

This proves that f is a ring isomorphism.

We extend the inverse isomorphism $f^{-1}$ to the whole space ${\mathbb{Z}}^n$ by $f^{\mathrm{<mo>\; *\; </mo>}}=f\circ \pi$ : $f^{*}:{\mathbb{Z}}^n\stackrel{\pi }{\to }{\mathbb{Z}}^n/I_1{I}_2\cdots I_m\stackrel{f^{-1}}{\to }\underset{i=1}{\overset{m}{{\displaystyle \underset{}{{\displaystyle \oplus }}}}}{\mathbb{Z}}^n/I_i,$ where $\pi$ is the natural homomorphism from ${\mathbb{Z}}^n$ to its quotient ring ${\mathbb{Z}}^n/I_1{I}_2\cdots I_m$ . It is easy to see that $f^{\mathrm{<mo>\; *\; </mo>}}$ is a homomorphism from ${\mathbb{Z}}^n$ to $\underset{i=1}{\overset{m}{{\displaystyle \underset{}{{\displaystyle \oplus }}}}}{\mathbb{Z}}^n/I_i$ , and

$f^{*}\left(f\left(u\right)\right)=f^{-1}\left(f\left(u\right)\right)=u,\forall u\in \underset{i=1}{\overset{m}{{\displaystyle \underset{}{{\displaystyle \oplus }}}}}{\mathbb{Z}}^n/I_i,$ (2.3)

$f^{\mathrm{<mo>\; *\; </mo>}}$ will play the role of decryption in our scheme, and always write down $f^{\mathrm{<mo>\; *\; </mo>}}$ by $f^{-1}$ in the following discussion.

Since $\mathbb{Z}$ is a ring, we wish to embed this ring into $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ . To do this, we define an embedding mapping from $\mathbb{Z}$ to ${\mathbb{Z}}^n$ by

$\forall a\in \mathbb{Z}\mathrm{,}a\to \bar{a}=\left(\begin{array}{c}a\\ 0\\ ⋮\\ 0\end{array}\right)\in {\mathbb{Z}}^n\mathrm{.}$ (2.4)

Lemma 2.4 Under the embedding mapping $a\to \bar{a}$ , $\mathbb{Z}$ becomes a subring of $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ , namely, for any $a\in \mathbb{Z}$ , $b\in \mathbb{Z}$ , one has $\overline{a+b}=\bar{a}+\bar{b}$ and $\overline{ab}=\bar{a}\otimes \bar{b}$ .

Proof. By (2.4), we have

$\overline{a+b}=\left(\begin{array}{c}a+b\\ 0\\ ⋮\\ 0\end{array}\right)=\left(\begin{array}{c}a\\ 0\\ ⋮\\ 0\end{array}\right)+\left(\begin{array}{c}b\\ 0\\ ⋮\\ 0\end{array}\right)=\bar{a}+\bar{b}$

and

$\bar{a}\otimes \bar{b}=\left(\begin{array}{c}ab\\ 0\\ ⋮\\ 0\end{array}\right)=\overline{a\cdot b},$

the lemma follows at once.

Lemma 2.5 Let $I\subset {\mathbb{Z}}^n$ be an ideal lattice, and $t=t\left(I\right)$ be its one dimensional modulus given by DEFINATION 2.3. Then, for any $a\mathrm{,}b\in \mathbb{Z}$ , we have $a\equiv b\left(\mathrm{mod}t\right)\iff \bar{a}\equiv \bar{b}\left(\mathrm{mod}I\right).$

Proof. By assumption, I is a full rank lattice and its HNF basis may be written by

$B=\left(\begin{array}{cccc}{b}_{11}& \ast & \ast & \ast \\ & b_{22}& \ast & \ast \\ & 0& \ddots & \ast \\ & & & b_{nn}\end{array}\right)\mathrm{.}$

If $\bar{a}\equiv \bar{b}\left(\mathrm{mod}I\right)$ , then there is a vector $x=\left(\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right)\in {\mathbb{Z}}^n$ such that

$\bar{a}-\bar{b}=Bx=\left(\begin{array}{c}a-b\\ 0\\ ⋮\\ 0\end{array}\right).$

Since $b_{nn}{x}_n=0$ , and $b_{nn}\ge 1$ , we have $x_n=0$ , similarly, since $b_{n-1,n-1}{x}_{n-1}+b_{n-1,n}{x}_n=0$ , it follows that $x_{n-1}=0$ . Therefore, we have $x_n=x_{n-1}=\cdots =x_2=0$ , and $a-b=x_1{b}_{11}=x_{1}t\Rightarrow a\equiv b\left(\mathrm{mod}t\right)$ . Conversely, if $a\equiv b\left(\mathrm{mod}t\right)$ , then $a-b=qt$ , and

$\bar{a}-\bar{b}=B\left(\begin{array}{c}q\\ 0\\ ⋮\\ 0\end{array}\right)\in I\Rightarrow \bar{a}\equiv \bar{b}\left(\mathrm{mod}I\right).$

The assertion is true.

For arbitrary given pairwise relatively prime ideal lattices $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ , one uses the Chinese Remainder Theorem to generate the public key $A_1\mathrm{,}{A}_2\mathrm{,}\cdots \mathrm{,}{A}_m$ , where $A_i\in {\mathbb{Z}}^n\left(1\le i\le m\right)$ such that

$A_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{A}_i\equiv 0\left(\mathrm{mod}{I}_j\right)\mathrm{,}\text{if}j\ne i\mathrm{,}$ (2.5)

where $e=\left(\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right)\in {\mathbb{Z}}^n$ is the unit element of $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ .

Now, we describe a scheme for unbounded fully homomorphic encryption as follows.

To verify the homomorphic addition and multiplication for the above scheme, by Lemma 2.4, $\mathbb{Z}$ is a subring of $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ . By Lemma 2.5, we can embed the direct sum $\underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}_{t_i}$ into $\underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}^n/I_i$ , so that $\underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}_{t_i}$ also is a subring of $\underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}^n/I_i$ . Therefore, the property of fully homomorphism directly follows by $f^{\mathrm{<mo>\; *\; </mo>}}$ (or $f^{-1}$ ) a ring homomorphism: $\underset{i=1}{\overset{m}{{\displaystyle \underset{}{{\displaystyle \oplus }}}}}{\mathbb{Z}}_{t_i}$ ↪ $\underset{i=1}{\overset{m}{{\displaystyle \underset{}{{\displaystyle \oplus }}}}}{\mathbb{Z}}^n/I_i\stackrel{f}{\to }{\mathbb{Z}}^n/I_1{I}_2\cdots I_m\stackrel{f^{*}}{\leftarrow }{\mathbb{Z}}^n.$

More precisely, let $c_1=f\left(u\right)$ , and $c_2=f\left(v\right)$ be arbitrary two ciphertexts, where $u=\left(u_1,u_2,\cdots ,u_m\right)\in \underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}_{t_i}$ , and $v=\left(v_1,v_2,\cdots ,v_m\right)\in \underset{i=1}{\overset{m}{{\displaystyle {{\displaystyle \oplus }}_{}}}}{\mathbb{Z}}_{t_i}$ , we note that for all i, $1\le i\le m$ , $c_1+c_2\equiv \overline{u_i}+\overline{v_i}\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{c}_1\otimes c_2\equiv \overline{u_i}\otimes \overline{v_i}\left(\mathrm{mod}{I}_i\right)\mathrm{.}$

By Lemma 2.4, it follows that

$c_1+c_2\equiv \overline{u_i+v_i}\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{c}_1\otimes c_2\equiv \overline{u_i{v}_i}\left(\mathrm{mod}{I}_i\right)\mathrm{.}$

Therefore, by Lemma 2.5, we have

$\begin{array}{c}{f}^{-1}\left(c_1+c_2\right)=\left(u_1+v_1\mathrm{,}{u}_2+v_2\mathrm{,}\cdots \mathrm{,}{u}_m+v_m\right)\\ =\left(u_1\mathrm{,}{u}_2\mathrm{,}\cdots \mathrm{,}{u}_m\right)+\left(v_1\mathrm{,}{v}_2\mathrm{,}\cdots \mathrm{,}{v}_m\right)\\ =f^{-1}\left(c_1\right)+f^{-1}\left(c_2\right)\mathrm{,}\end{array}$

and

$\begin{array}{c}{f}^{-1}\left(c_1\otimes c_2\right)=\left(u_1{v}_1\mathrm{,}{u}_2{v}_2\mathrm{,}\cdots \mathrm{,}{u}_m{v}_m\right)\\ =\left(u_1\mathrm{,}{u}_2\mathrm{,}\cdots \mathrm{,}{u}_m\right)\left(v_1\mathrm{,}{v}_2\mathrm{,}\cdots \mathrm{,}{v}_m\right)\\ =f^{-1}\left(c_1\right)\cdot f^{-1}\left(c_2\right)\mathrm{.}\end{array}$

This is an unbounded fully homomorphic encryption as we desired.

How to decrypt the ciphertext $c\in {\mathbb{Z}}^n$ using the secret key $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ in our algorithm for the general unbounded FHE scheme? Here we give a lemma to show that there is only one vector $\overline{u_i}\in {\mathbb{Z}}^n$ in the orthogonal parallelepiped $\mathcal{F}\left(I_i\right)$ of $I_i$ such that $c\equiv \overline{u_i}\left(\mathrm{mod}{I}_i\right)$ , and give an algorithm to calculate $\overline{u_i}$ in detail.

Lemma 2.6 Given an ideal lattice I, for any vector $c\in {\mathbb{Z}}^n$ , there is only one vector $w\in \mathcal{F}\left(I\right)$ such that $c\equiv w\left(\mathrm{mod}I\right)$ .

Proof. Assume $B=\left[{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}\cdots \mathrm{,}{\beta }_n\right]$ is the HNF basis of I, and $B^{\mathrm{<mo>\; *\; </mo>}}=\left[{\beta }_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\beta }_2^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}\cdots \mathrm{,}{\beta }_n^{\mathrm{<mo>\; *\; </mo>}}\right]$ is the corresponding orthogonal basis of B. Write c as the linear combination of $\left[{\beta }_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\beta }_2^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}\cdots \mathrm{,}{\beta }_n^{\mathrm{<mo>\; *\; </mo>}}\right]$ , i.e.

$c={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{c}_i{\beta }_i^{*},c_i=\frac{\langle c,{\beta }_i^{*}\rangle }{\langle {\beta }_i^{*},{\beta }_i^{*}\rangle }.$

Let $w={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{c}_i{\beta }_i^{*}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{k}_i{\beta }_i$ , $k_1\mathrm{,}{k}_2\mathrm{,}\cdots \mathrm{,}{k}_n\in \mathbb{Z}$ , then $c-w={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{k}_i{\beta }_i\in I$ . Next, we prove that there is only one group of integers $k_1\mathrm{,}{k}_2\mathrm{,}\cdots \mathrm{,}{k}_n$ such that $w\in \mathcal{F}\left(I\right)$ , i.e. $w_i=\frac{\langle w\mathrm{,}{\beta }_i^{\mathrm{<mo>\; *\; </mo>}}\rangle }{\langle {\beta }_i^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\beta }_i^{\mathrm{<mo>\; *\; </mo>}}\rangle }\in \left[\mathrm{0,1}\right)\mathrm{,}\forall 1\le i\le n\mathrm{.}$

Firstly, we determine the value of $k_n$ . Since $w_n=\frac{\langle w,{\beta }_n^{*}\rangle }{\langle {\beta }_n^{*},{\beta }_n^{*}\rangle }=c_n-k_n\frac{\langle {\beta }_n,{\beta }_n^{*}\rangle }{\langle {\beta }_n^{*},{\beta }_n^{*}\rangle }=c_n-k_n,$ therefore, when $k_n=\left[c_n\right]$ , here $\left[x\right]$ means the largest integer no more than real number x, we have $w_n\in \left[\mathrm{0,1}\right)$ . Secondly, we determine $k_{n-1}$ . Note that $w_{n-1}=\frac{\langle w,{\beta }_{n-1}^{*}\rangle }{\langle {\beta }_{n-1}^{*},{\beta }_{n-1}^{*}\rangle }=c_{n-1}-k_{n-1}-k_n\frac{\langle {\beta }_n,{\beta }_{n-1}^{*}\rangle }{\langle {\beta }_{n-1}^{*},{\beta }_{n-1}^{*}\rangle },$ so there is only one integer $k_{n-1}=\left[c_{n-1}-\left[c_n\right]\frac{\langle {\beta }_n,{\beta }_{n-1}^{*}\rangle }{\langle {\beta }_{n-1}^{*},{\beta }_{n-1}^{*}\rangle }\right]$ such that $w_{n-1}\in \left[\mathrm{0,1}\right)$ . Similarly, we could determine any $k_i$ , $\forall 1\le i\le n-1$ , $w_i=\frac{\langle w,{\beta }_i^{*}\rangle }{\langle {\beta }_i^{*},{\beta }_i^{*}\rangle }=c_i-k_i-\frac{\langle {\displaystyle \underset{j=i+1}{\overset{n}{\sum }}}{k}_j{\beta }_j,{\beta }_i^{*}\rangle }{\langle {\beta }_i^{*},{\beta }_i^{*}\rangle },$ hence, there is only one integer $k_i=\left[c_i-\frac{\langle {\displaystyle \underset{j=i+1}{\overset{n}{\sum }}}{k}_j{\beta }_j,{\beta }_i^{*}\rangle }{\langle {\beta }_i^{*},{\beta }_i^{*}\rangle }\right]$ such that $w_i\in \left[\mathrm{0,1}\right)$ , $\forall 1\le i\le n-1$ . Above all, there is only one vector $w={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{c}_i{\beta }_i^{*}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{k}_i{\beta }_i\in \mathcal{F}\left(I\right)$ such that $c\equiv w\left(\mathrm{mod}I\right)$ .

Based on Lemma 2.6, we give an algorithm for the decryption of our general FHE scheme.

To create an efficient algorithm for generating the secret key of the above unbounded FHE scheme, we assume that $\varphi \left(x\right)$ is an irreducible polynomial, so that the principal ideal $\langle \varphi \left(x\right)\rangle$ is a prime ideal in $\mathbb{Z}\left[x\right]$ , and the quotient ring $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ is a domain, equivalently, $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ becomes a domain. Under this assumption, we see that arbitrary many pairwise relatively prime ideals in ${\mathbb{Z}}^n$ almost come in automatically, we describe the process as follows.

To construct an efficient algorithm for finding public key, we first show that

Lemma 2.7 Suppose that $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ are pairwise relatively ideals in ${\mathbb{Z}}^n$ , and each $I_i$ is a principal ideal generated by ${\alpha }_i$ , namely, $I_i=\langle {\alpha }_i\rangle$ . Let

$d_i=\underset{j=1,j\ne i}{\overset{m}{{\displaystyle \otimes }}}{\alpha }_j,1\le i\le m.$

Then for every $d_i$ , there is a vector ${\mathcal{D}}_i\in {\mathbb{Z}}^n$ such that

$d_i\otimes {\mathcal{D}}_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}1\le i\le m\mathrm{.}$

Proof. Since $I_1\mathrm{,}{I}_2\mathrm{,}\cdots \mathrm{,}{I}_m$ are pairwise relatively prime by assumption, we have

$\left(I_i\mathrm{,}{I}_1{I}_2\cdots I_{i-1}{I}_{i+1}\cdots I_m\right)=\mathrm{1,}1\le i\le m\mathrm{.}$

In other words, we have $\left(I_i\mathrm{,}\langle d_i\rangle \right)=1$ , or

$\langle {\alpha }_i\rangle +\langle d_i\rangle ={\mathbb{Z}}^n\mathrm{.}$

Therefore, there is a vector ${\mathcal{D}}_i\in {\mathbb{Z}}^n$ such that $d_i\otimes {\mathcal{D}}_i\equiv e\left(\mathrm{mod}{I}_i\right)$ , and we have Lemma 2.7 immediately.

How to find the vector ${\mathcal{D}}_i$ defined by Lemma 2.7? We introduce a polynomial algorithm to obtain ${\mathcal{D}}_i$ ( $1\le i\le m$ ), and generate the public key $\left\{A_1\mathrm{,}{A}_2\mathrm{,}\cdots \mathrm{,}{A}_m\right\}$ by taking $A_i=d_i\otimes {\mathcal{D}}_i$ ( $1\le i\le m$ ).

3. A Probabilistic Algorithm for Encryption

In our general construction for unbounded FHE, the encryption formula (2.6) is deterministic, so it is not IND-CPA secure, i.e. it is not secure against indistinguishable under chosen-plaintexts attack. To improve the encryption algorithm, we require to add some noises to the generating algorithm for public keys.

Let $\chi =\left({\chi }_1\mathrm{,}{\chi }_2\mathrm{,}\cdots \mathrm{,}{\chi }_m\right)$ be an arbitrary multiple discrete probability distributions over ${\mathbb{Z}}_{t_1}\times {\mathbb{Z}}_{t_2}\times \cdots \times {\mathbb{Z}}_{t_m}$ , where ${\chi }_i$ be any discrete distribution over ${\mathbb{Z}}_{t_i}\left(1\le i\le m\right)$ . Let $a_i\leftarrow {\chi }_i$ and $a_i\in {\mathbb{Z}}_{t_i}\left(1\le i\le m\right)$ , so that $a=\left(a_1,a_2,\cdots ,a_m\right)\in {\mathbb{Z}}_{t_1}\times {\mathbb{Z}}_{t_2}\times \cdots \times {\mathbb{Z}}_{t_m}$ are the samples drawn from the distribution $\chi$ . By Theorem 1, we have m vectors $E_i\left(1\le i\le m\right)$ in ${\mathbb{Z}}^n$ such that

$E_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{E}_i\equiv \overline{a_j}\left(\mathrm{mod}{I}_j\right)\mathrm{,}\text{if}j\ne i\mathrm{,}$ (3.1)

where e is the unit element of ${\mathbb{Z}}^n$ and $\overline{a_j}$ is the embedding of $a_j$ given by (2.4). According to the probabilistic distribution $\chi$ , we generate the public keys $A_{\chi }=\left\{{A^{\prime }}_1\mathrm{,}{A^{\prime }}_2\mathrm{,}\cdots \mathrm{,}{A^{\prime }}_m\right\}$ with noises by

${A^{\prime }}_i=A_i\otimes E_i\mathrm{,}1\le i\le m\mathrm{,}$ (3.2)

where $A_i$ given by (2.5), and $E_i$ given by (3.1). Therefore, the encryption algorithm (2.6) in our general construction (see algorithm 1) becomes the following formula for any $u=\left(u_1,u_2,\cdots ,u_m\right)\in {\mathbb{Z}}_{t_1}\oplus \cdots \oplus {\mathbb{Z}}_{t_m}$ ,

$f_{\chi }\left(u\right)=\overline{u_1}\otimes {A^{\prime }}_1+\overline{u_2}\otimes {A^{\prime }}_2+\cdots +\overline{u_m}\otimes {A^{\prime }}_m\mathrm{.}$ (3.3)

Lemma 3.1 For arbitrary samples $a=\left(a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_m\right)$ drawn from the distribution $\chi$ , we have ( $1\le i\le m$ )

${A^{\prime }}_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{A^{\prime }}_i\equiv 0\left(\mathrm{mod}{I}_j\right)\mathrm{,}\text{if}j\ne i\mathrm{.}$

Proof. By (2.5), for every $i\left(1\le i\le m\right)$ we have $A_i\equiv e\left(\mathrm{mod}{I}_i\right)$ , and $A_i\equiv 0\left(\mathrm{mod}{I}_j\right)$ when $j\ne i$ , it follows that

${A^{\prime }}_i\equiv A_i\otimes E_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{A^{\prime }}_i\equiv 0\left(\mathrm{mod}{I}_j\right)\mathrm{,}\text{if}j\ne i\mathrm{.}$

The dramatic effect of the above lemma is that the probabilistic encryption function $f_{\chi }$ shares the same decryption formula (see Algorithm 2) with the deterministic encryption algorithm f given by (2.6). In other words, there are no noises occurred in the decryption procedure, although the encryption algorithms with disturbance. It explains why we may obtain an unbounded FHE scheme without Gentry’s bootstrapping transformation technique.

Next, we discuss how to randomly find the public keys $A_{\chi }=\left\{{A^{\prime }}_1\mathrm{,}{A^{\prime }}_2\mathrm{,}\cdots \mathrm{,}{A^{\prime }}_m\right\}$ according to the probabilistic distribution $\chi$ , the following lemma tells us how to obtain the error term $E_i$ .

Lemma 3.2 Let $a=\left(a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_m\right)\leftarrow \chi$ , and $A=\left\{A_1\mathrm{,}{A}_2\mathrm{,}\cdots \mathrm{,}{A}_m\right\}$ be given by Algorithm 4, then we have

$\begin{array}{l}{E}_i=\overline{a_1}\otimes A_1+\cdots +\overline{a_{i-1}}\otimes A_{i-1}+A_i+\overline{a_{i+1}}\otimes A_{i+1}+\cdots +\overline{a_m}\otimes A_m\mathrm{,}\\ 1\le i\le m\mathrm{,}\end{array}$ (3.4)

where $\overline{a_j}$ is the embedding of $a_j$ .

Proof. Since $A_i\equiv e\left(\mathrm{mod}{I}_i\right)$ , and $A_i\equiv 0\left(\mathrm{mod}{I}_j\right)$ for $j\ne i$ , it follows that

$E_i\equiv e\left(\mathrm{mod}{I}_i\right)\mathrm{,}\text{and}{E}_i\equiv \overline{a_j}\left(\mathrm{mod}{I}_j\right)\mathrm{,}\text{if}j\ne i\mathrm{.}$

We have the lemma immediately.

Now, we give the final algorithm for the unbounded FHE scheme as follows.

Because of the decryption procedure without noises, and the homomorphic computation on ciphertexts, we claim that the above Algorithm 5 is the unbounded FHE scheme as we desired.

Remark Since the probabilistic distribution $\chi$ is arbitrary, an alternative method to add noises to public key $A=\left\{A_1\mathrm{,}{A}_2\mathrm{,}\cdots \mathrm{,}{A}_m\right\}$ may be described as follows: Randomly find m vectors ${\gamma }_1\mathrm{,}{\gamma }_2\mathrm{,}\cdots \mathrm{,}{\gamma }_m$ in ${\mathbb{Z}}^n$ , and put

${\Gamma }_i={\gamma }_1\otimes A_1+\cdots +{\gamma }_{i-1}\otimes A_{i-1}+A_i+{\gamma }_{i+1}\otimes A_{i+1}+\cdots +{\gamma }_m\otimes A_m\mathrm{,}1\le i\le m\mathrm{,}$ (3.6)

and then let ${A^{″}}_i=A_i\otimes {\Gamma }_i$ . Thus, we obtain the public key $A_{p_k}=\left\{{A^{″}}_1,{A^{″}}_2,\cdots ,{A^{″}}_m\right\}$ with noises, which guarantees the encryption formula (2.6) is not deterministic.

To discuss the security of this scheme, we observe that all risks come from the encryption algorithm (3.5). This algorithm contains some noises for public keys and guarantees the scheme could resist CPA attack. We describe the other risk as a generalized compact knapsack problem over the ring $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ as follows:

${\displaystyle \underset{i=1}{\overset{m}{\sum }}}{a}_i\otimes x_i=u,\left|x_i\right|\le \beta ,$ (3.7)

where $a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_m$ are given m vectors in ${\mathbb{Z}}^n$ , $u\in {\mathbb{Z}}^n$ is a target vector, and $\beta =\underset{1\le i\le m}{\max }{t}_i$ . Next section, we will show that the security of our scheme is solely under a worst-case complexity assumption, this is also a solution to open question 11 of [2] .

4. The Generalized Compact Knapsack Problem over ${\mathbb{Z}}^n$

In this section, we discuss the security of our scheme based on the general compact knapsack problem over the ring $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ . In [42] , Micciancio has proved that if we can solve the knapsack problem over ${\mathbb{Z}}_q^n$ for some sufficiently large positive integer number q, then there is a probabilistic polynomial algorithm solving the covering radius problem for any n dimensional full rank cyclic lattice. First we generalize Micciancio’s result to arbitrary ideal lattices based on our precious work [48] , and then solving the knapsack problem from ${\mathbb{Z}}_q^n$ to $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ . We give an entire proof for the reason of completeness, although the method we present here is quite similar to Micciancio’s original proof.

DEFINITION 4.1 Let L be a full rank lattice, $\gamma \left(n\right)$ is a parameter of n, $\gamma \left(n\right)\ge 1$ , ${\text{CDP}}_{\gamma }$ problem is to find an r such that $\rho \left(L\right)\le r\le \gamma \left(n\right)\rho \left(L\right)\mathrm{,}$ where $\rho \left(L\right)=\underset{x\in {ℝ}^n}{\max }\text{dist}\left(x\mathrm{,}L\right)$ and $\text{dist}\left(x\mathrm{,}L\right)=\underset{\alpha \in L}{\min }\left|x-\alpha \right|$ .

DEFINITION 4.2 Let L be a full rank lattice, $S=\left\{s_1\mathrm{,}{s}_2\mathrm{,}\cdots \mathrm{,}{s}_n\right\}\subset L$ be n linearly independent lattice vectors. $S^{\mathrm{<mo>\; *\; </mo>}}=\left\{s_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{s}_2^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}\cdots \mathrm{,}{s}_n^{\mathrm{<mo>\; *\; </mo>}}\right\}$ is the orthogonal basis corresponding to S by the Gram-Schmidt method. We define

$\sigma \left(S\right)={\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\left|s_i^{*}\right|}^2\right)}^{\frac{1}{2}}.$

Here we give our main result to show that the generalized knapsack problem over ${\mathbb{Z}}^n$ is at least as hard as the covering radius problem for any n dimensional full rank ideal lattice.

THEOREM 2 Let $m=O\left(\log n\right)$ , $k=\tilde{O}\left(\log n\right)$ ,

${\left|\varphi \right|}^2={\varphi }_0^2+{\varphi }_1^2+\cdots +{\varphi }_{{}_{n-1}}^2$ , $M=\sqrt{2+2{\left|\varphi \right|}^2}$ , $W=\frac{M^n-1}{M-1}$ , $\gamma \ge 16mk{n}^{3}W$ , if we can solve the knapsack problem (3.7), then there is a positive probabilistic polynomial algorithm solving the covering radius problem ${\text{CDP}}_{\gamma }$ for any n dimensional full rank ideal lattice L.

Remark In the original work of Micciancio [42] , the parameter $\gamma$ is bigger than $16mk{n}^3$ , we require $\gamma \ge 16mk{n}^{3}W$ , where W is given by $\frac{M^n-1}{M-1}$ . The maindifference is to estimate the length of convolutional product $\alpha \otimes \beta$ for any two vectors $\alpha$ and $\beta$ . It is clearly that $\left|\alpha \otimes \beta \right|\le \sqrt{n}\left|\alpha \right|\left|\beta \right|$ in the case of circulant lattice, but it is non-trivial in the case of ideal lattices.

Lemma 4.1 For any $\alpha \mathrm{,}\beta \in {\mathbb{Z}}^n$ , we have

$\left|\alpha \otimes \beta \right|\le W\left|\alpha \right|\cdot \left|\beta \right|\mathrm{,}$

where W is defined in Theorem 2.

Proof. We first prove $\left|H\alpha \right|\le M\left|\alpha \right|$ . Let $\alpha ={\left({\alpha }_0\mathrm{,}{\alpha }_1\mathrm{,}\cdots \mathrm{,}{\alpha }_{n-1}\right)}^{\text{T}}$ , then

$\begin{array}{c}{\left|H\alpha \right|}^2={\varphi }_0^2{\alpha }_{\text{n}-\text{1}}^2+{\left({\alpha }_0+{\varphi }_1{\alpha }_{\text{n}-\text{1}}\right)}^2+\cdots +{\left({\alpha }_{n-2}+{\varphi }_{n-1}{\alpha }_{n-1}\right)}^2\\ \le {\varphi }_0^2{\alpha }_{\text{n}-\text{1}}^2+2\left({\alpha }_0^2+{\varphi }_1^2{\alpha }_{\text{n}-\text{1}}^2\right)+\cdots +2\left({\alpha }_{n-2}^2+{\varphi }_{n-1}^2{\alpha }_{n-1}^2\right)\\ \le 2\left({\alpha }_0^2+\cdots +{\alpha }_{n-2}^2\right)+2{\left|\varphi \right|}^2\left({\alpha }_0^2+{\alpha }_1^2+\cdots +{\alpha }_{n-1}^2\right)\\ \le \left(2+2{\left|\varphi \right|}^2\right){\left|\alpha \right|}^2.\end{array}$

So $\left|H\alpha \right|\le M\left|\alpha \right|$ . Similarly,

$\left|H^2\alpha \right|\le M\left|H\alpha \right|\le M^2\left|\alpha \right|\mathrm{.}$

In the same way, we can get $\left|H^k\alpha \right|\le M^k\left|\alpha \right|$ , $\forall 1\le k\le n-1$ . Let $\beta ={\left({\beta }_0\mathrm{,}{\beta }_1\mathrm{,}\cdots \mathrm{,}{\beta }_{n-1}\right)}^{\text{T}}$ , it follows that

$\begin{array}{c}\left|\alpha \otimes \beta \right|=\left|H^{*}\left(\alpha \right)\beta \right|=\left|{\beta }_0\alpha +{\beta }_{1}H\alpha +\cdots +{\beta }_{n-1}{H}^{n-1}\alpha \right|\\ \le {\displaystyle \underset{i=0}{\overset{n-1}{\sum }}}\left|{\beta }_i{H}^i\alpha \right|\le {\displaystyle \underset{i=0}{\overset{n-1}{\sum }}}{M}^i\left|\alpha \right|\left|\beta \right|=\frac{M^n-1}{M-1}\left|\alpha \right|\cdot \left|\beta \right|.\end{array}$

We complete this proof.

Let $L=\mathcal{L}\left(B\right)\subset {ℝ}^n$ be a full rank ideal lattice, $q\ge 4mk{n}^2{W}^2$ , $\left\{e_0\mathrm{,}{e}_1\mathrm{,}\cdots \mathrm{,}{e}_{n-1}\right\}\subset {\mathbb{Z}}_q^n$ is a standard orthogonal basis, $S=\left\{s_1\mathrm{,}{s}_2\mathrm{,}\cdots \mathrm{,}{s}_n\right\}\subset L$ is a set of n linearly independent vectors. We define the parameter

$\mu =\left(\frac{4nq}{\gamma }+\frac{W}{2}\right)\sigma \left(S\right)\mathrm{.}$ (4.1)

According to Lemma 1.6 in Chapter 3 in [44] , there is a lattice vector $c\in L$ such that $\left|c-\mu e_0\right|\le \frac{1}{2}\sigma \left(S\right)$ , let $B^{\prime }=q{\left(H^{\mathrm{<mo>\; *\; </mo>}}\left(c\right)\right)}^{-1}B$ . It follows that the lattice $\mathcal{L}\left(B^{\prime }\right)$ generated by $B^{\prime }$ satisfies $q{\mathbb{Z}}^n\subset \mathcal{L}\left(B^{\prime }\right)$ according to Lemma 2.1 in Chapter 3 in [44] . Therefore, $q{\mathbb{Z}}^n$ is an additive subgroup in $\mathcal{L}\left(B^{\prime }\right)$ . Randomly choose mk elements ${x^{\prime }}_{ij}\left(1\le i\le m\mathrm{,1}\le j\le k\right)$ in the quotient group $G=\mathcal{L}\left(B^{\prime }\right)/q{\mathbb{Z}}^n$ , the integral vectors $w_{ij}^{\mathrm{<mo>\; \text{'}\; </mo>}}$ of ${x^{\prime }}_{ij}$ is defined by

Let

$a_{ij}\equiv {w^{\prime }}_{ij}\left(\mathrm{mod}q\right),a_i\equiv {\displaystyle \underset{j=1}{\overset{k}{\sum }}}{w^{\prime }}_{ij}\left(\mathrm{mod}q\right),$

Assume $A=\left(a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_m\right)\in {\mathbb{Z}}_q^{n\times m}$ . Since the knapsack problem (3.7) is solvable on ${\mathbb{Z}}^n$ , it could also be solved on ${\mathbb{Z}}_q^n$ . Let $y=\left(y_1\mathrm{,}{y}_2\mathrm{,}\cdots \mathrm{,}{y}_m\right)\in {\mathbb{Z}}_q^{n\times m}$ and $\hat{y}=\left({\hat{y}}_1\mathrm{,}{\hat{y}}_2\mathrm{,}\cdots \mathrm{,}{\hat{y}}_m\right)\in {\mathbb{Z}}_q^{n\times m}$ be two different integer matrices such that ${\displaystyle \underset{i=1}{\overset{m}{\sum }}}{a}_i\otimes \left(y_i-{\hat{y}}_i\right)=0$ , $\left|y_i\right|\le \sqrt{n}$ , $\left|{\hat{y}}_i\right|\le \sqrt{n}$ , $\forall 1\le i\le m$ . We define $x_{ij}=\frac{1}{q}{H}^{*}\left(c\right){x^{\prime }}_{ij},w_{ij}=\frac{1}{q}{H}^{*}\left(c\right){w^{\prime }}_{ij},1\le i\le m,1\le j\le k,$ and

$s^{\prime }={\displaystyle \underset{i=1}{\overset{m}{\sum }}}{\displaystyle \underset{j=1}{\overset{k}{\sum }}}\left(x_{ij}-w_{ij}\right)\otimes \left(y_i-{\hat{y}}_i\right).$ (4.2)

Then $x_{ij}$ is a lattice vector in the given ideal lattice $L=\mathcal{L}\left(B\right)$ ( $1\le i\le m$ , $1\le j\le k$ ), and $s^{\prime }$ is also a lattice vector in $L=\mathcal{L}\left(B\right)$ based on Lemma 2.2 in Chapter 3 in [44] .

The next lemma gives an estimation of the length of $s^{\prime }$ , which has some differences from the proof of Micciancio’s.

Lemma 4.2 Let $S=\left\{s_1\mathrm{,}{s}_2\mathrm{,}\cdots \mathrm{,}{s}_n\right\}\subset L$ be a set of n linearly independent vectors in the full rank ideal lattice L. Denote $\left|S\right|=\underset{1\le i\le n}{\max }\left|s_i\right|$ , $s^{\prime }$ is the lattice vector defined in (4.2), then $\left|s^{\prime }\right|\le \frac{1}{2}\left|S\right|\mathrm{.}$

Proof. This proof is similar to that of Lemma 2.3 in Chapter 3 in [44] except some computations about the parameters. We prove $\left|s^{\prime }\right|\le \frac{1}{2\sqrt{n}}\sigma \left(S\right)$ first. Basedon the definition of $s^{\prime }$ in (4.2),

$\left|s^{\prime }\right|\le {\displaystyle \underset{i=1}{\overset{m}{\sum }}}{\displaystyle \underset{j=1}{\overset{k}{\sum }}}\left|\left(x_{ij}-w_{ij}\right)\otimes \left(y_i-{\hat{y}}_i\right)\right|.$ (4.3)

$x_{ij}-w_{ij}=\frac{1}{q}{H}^{*}\left(c\right)\left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)=\frac{1}{q}c\otimes \left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right).$

Let $\alpha =c-\mu e_0$ , where $\mu$ is defined in (4.1). Then $\left|\alpha \right|\le \frac{1}{2}\sigma \left(S\right)$ , and

$\begin{array}{c}{x}_{ij}-w_{ij}=\frac{1}{q}\left(\alpha +\mu e_0\right)\otimes \left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)=\frac{1}{q}{H}^{*}\left(\alpha +\mu e_0\right)\left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)\\ =\frac{1}{q}\mu H^{*}\left(e_0\right)\left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)+\frac{1}{q}{H}^{*}\left(\alpha \right)\left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)\\ =\frac{\mu }{q}\left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)+\frac{1}{q}{H}^{*}\left(\alpha \right)\left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right).\end{array}$

Since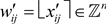, we have

$\left|{x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right|\le \frac{1}{2}\sqrt{n}\mathrm{,}$

combine with Lemma 4.1, we get

$\begin{array}{c}\left|x_{ij}-w_{ij}\right|\le \frac{\mu }{q}\left|{x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right|+\frac{1}{q}\left|\alpha \otimes \left({x^{\prime }}_{ij}-{w^{\prime }}_{ij}\right)\right|\le \frac{\mu }{q}\cdot \frac{1}{2}\sqrt{n}+\frac{1}{q}\cdot W\cdot \frac{1}{2}\sigma \left(S\right)\cdot \frac{\sqrt{n}}{2}\\ =\frac{\sqrt{n}}{2q}\left(\frac{4nq}{\gamma }+\frac{W}{2}\right)\sigma \left(S\right)+\frac{\sqrt{n}W}{4q}\sigma \left(S\right)=\sigma \left(S\right)\left(\frac{2n^{\frac{3}{2}}}{\gamma }+\frac{\sqrt{n}W}{2q}\right)\\ \le \sigma \left(S\right)\left(\frac{1}{8}\cdot \frac{1}{mk{n}^{\frac{3}{2}}W}+\frac{1}{8}\cdot \frac{1}{mk{n}^{\frac{3}{2}}W}\right)=\sigma \left(S\right)\frac{1}{4mk{n}^{\frac{3}{2}}W}\mathrm{.}\end{array}$

Based on (4.3), we know

$\begin{array}{c}\left|s^{\prime }\right|\le mkW\underset{i\mathrm{,}j}{\max }\left|x_{ij}-w_{ij}\right|\cdot \underset{i}{\max }\left|y_i-{\hat{y}}_i\right|\\ \le mkW\cdot \frac{\sigma \left(S\right)}{4mk{n}^{\frac{3}{2}}W}\cdot 2\sqrt{n}=\frac{\sigma \left(S\right)}{2\sqrt{n}}\mathrm{.}\end{array}$

Since

$\sigma \left(S\right)\le {\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\left|s_i\right|}^2\right)}^{\frac{1}{2}}\le \sqrt{n}\left|S\right|$

We can get

$\left|s^{\prime }\right|\le \frac{\sigma \left(S\right)}{2\sqrt{n}}\le \frac{\sqrt{n}\left|S\right|}{2\sqrt{n}}=\frac{1}{2}\left|S\right|.$

So we complete the proof of Lemma 4.2.

Based on the above lemmas, Theorem 2 follows directly from Micciancio’s method [42] . From Theorem 2, we can see that the general compact knapsack problem over ${\mathbb{Z}}^n$ is at least as hard as the covering radius problem ${\text{CDP}}_{\gamma }$ of any ideal lattice. Therefore, the security of our unbounded FHE scheme is solely under the worst-case complexity assumption, as a result, it is a reasonable solution to Open Question 11 of [2] .

5. A Practical System

As an example, we introduce a practical system for FHE using some basic results about the cyclotomic field [50] . Suppose that p is an odd prime number and $Q\left({\xi }_p\right)$ is the cyclotomic field, where ${\xi }_p={\text{e}}^{\frac{2\pi i}{p}}$ is a primitive p-th root of the unit.

Let

$\mathbb{Z}\left[{\xi }_p\right]=\left\{{\displaystyle \underset{i=0}{\overset{p-1}{\sum }}}{a}_i{\xi }_p^i|a_i\in \mathbb{Z}\right\}.$

It is known that $\mathbb{Z}\left[{\xi }_p\right]$ is the ring of algebraic integers of field $Q\left({\xi }_p\right)$ . Therefore $\mathbb{Z}\left[{\xi }_p\right]$ is a Dedekind domain (so we have unique factorization into prime ideals, etc. see Proposition 1.2 of [50] ).

To construct a commutative ring for ${\mathbb{Z}}^n$ , we select $\varphi \left(x\right)=x^{p-1}+x^{p-2}+\cdots +x+1\in \mathbb{Z}\left[x\right]$ . Obviously, $\varphi \left(x\right)$ is the minimal polynomial of ${\xi }_p$ . Let $n=p-1$ , then we obtain a ring $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ in terms of $\varphi \left(x\right)$ and the rotation matrix $H_{\varphi }$ , it is easy to see that (see (3.2) of [43] )

$\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)\cong \mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle \cong \mathbb{Z}\left[{\xi }_p\right]\mathrm{.}$

Thus, ${\mathbb{Z}}^n$ becomes a Dedekind domain.

For any integer $q\in \mathbb{Z}$ , we define an integer vector ${\alpha }_q\in {\mathbb{Z}}^n$ by

${\alpha }_q=\left(\begin{array}{c}q\\ 0\\ ⋮\\ 0\\ 1\end{array}\right)\in {\mathbb{Z}}^n\mathrm{.}$

The principal ideal $\langle {\alpha }_q\rangle$ generated by ${\alpha }_q$ is denoted by

$I_q=\langle {\alpha }_q\rangle =\mathcal{L}\left(H^{*}\left({\alpha }_q\right)\right).$

Lemma 5.1 If $q_1$ and $q_2$ are two different prime numbers, then $I_{q_1}$ and $I_{q_2}$ are relatively prime ideal lattices in ${\mathbb{Z}}^n$ .

Proof. Suppose that q is a prime number. Since $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)\cong \mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ , we see the polynomial ${\tau }^{-1}\left({\alpha }_q\right)={\alpha }_q\left(x\right)=x^{n-1}+q\in \mathbb{Z}\left[x\right]$ , which is the type polynomial of Eisenstein, thus it is an irreducible polynomial over $\mathbb{Z}\left[x\right]$ . Regarding ${\alpha }_q\left(x\right)$ as the polynomial of $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ , clearly, it is also an irreducible polynomial in $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ . By assumption, $q_1$ and $q_2$ are different prime numbers, we show that the principal ideals $\langle {\alpha }_{q_1}\left(x\right)\rangle$ , and $\langle {\alpha }_{q_2}\left(x\right)\rangle$ are relatively prime ideals in $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ . Since $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ is a Dedekind domain, if $\langle {\alpha }_{q_1}\left(x\right)\rangle$ and $\langle {\alpha }_{q_2}\left(x\right)\rangle$ are not relatively prime, then, there exists a prime ideal P in $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ such that

$\langle {\alpha }_{q_1}\left(x\right)\rangle \subset P\mathrm{,}\text{and}\langle {\alpha }_{q_2}\left(x\right)\rangle \subset P\mathrm{.}$

It follows for any positive integer $k\ge 1$ that

$\langle {\alpha }_{q_1}^k\left(x\right)\rangle \subset P^k\mathrm{,}\text{and}\langle {\alpha }_{q_2}^k\left(x\right)\rangle \subset P^k\mathrm{.}$

It is known that three exists a positive integer $k\ge 1$ , such that $P^k=\langle d\left(x\right)\rangle$ is a principal ideal, we thus have

$\langle {\alpha }_{q_1}^k\left(x\right)\rangle \subset \langle d\left(x\right)\rangle \mathrm{,}\text{and}\langle {\alpha }_{q_2}^k\left(x\right)\rangle \subset \langle d\left(x\right)\rangle \mathrm{.}$

In other words, we have $d\left(x\right)|{\alpha }_{q_1}^k\left(x\right)$ , and $d\left(x\right)|{\alpha }_{q_2}^k\left(x\right)$ . However, this is impossible, since ${\alpha }_{q_1}\left(x\right)$ and ${\alpha }_{q_2}\left(x\right)$ are two irreducible polynomials in $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ , and ${\alpha }_{q_1}\left(x\right)\ne {\alpha }_{q_2}\left(x\right)$ .

This proves that $\langle {\alpha }_{q_1}\left(x\right)\rangle$ and $\langle {\alpha }_{q_2}\left(x\right)\rangle$ are relatively prime ideals in $\mathbb{Z}\left[x\right]/\langle \varphi \left(x\right)\rangle$ . Equivalently, $I_{q_1}$ and $I_{q_2}$ are two relatively prime ideal lattices in ${\mathbb{Z}}^n$ .

Lemma 5.2 The one dimensional modulus of the principal ideal $I_q$ is

$t_q=t\left(I_q\right)=q^n-q^{n-1}+\cdots -q+1.$

Proof. It is not hard to compute that $\text{det}\left(H^{\mathrm{<mo>\; *\; </mo>}}\left({\alpha }_q\right)\right)=q^n-q^{n-1}+\cdots -q+1$ . Since the polynomial $x^n-x^{n-1}+\cdots -x+1$ is an irreducible polynomial over $\mathbb{Z}$ , we have the assertion of lemma immediately.

According to Lemma 5.1 and Lemma 5.2, we obtain a generating algorithm for the secret key as follows:

To get an attainable algorithm for public key, we define m vectors $d_i\left(1\le i\le m\right)$ by

$d_i={\alpha }_{q_1}\otimes {\alpha }_{q_2}\otimes \cdots \otimes {\alpha }_{q_{i-1}}\otimes {\alpha }_{q_{i+1}}\otimes \cdots \otimes {\alpha }_{q_m}={\otimes }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^m{\alpha }_{q_j},1\le i\le m.$

Lemma 5.3 For every vector $d_i\left(1\le i\le m\right)$ , there is a vector ${\mathcal{D}}_i\in {\mathbb{Z}}^n$ such that

$d_i\otimes {\mathcal{D}}_i\equiv e\left(\text{mod}{I}_{q_i}\right)\mathrm{,}$

where $e=\left(\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right)$ is the unit element of rimg $\left({\mathbb{Z}}^n\mathrm{,}+\mathrm{,}\otimes \right)$ .

Proof. By lemma 5.1, $I_{q_1}\mathrm{,}{I}_{q_2}\mathrm{,}\cdots \mathrm{,}{I}_{q_m}$ are pairwise relatively prime ideals, hence we have $\left(I_{q_i},I_{q_1}{I}_{q_2}\cdots I_{q_{i-1}}{I}_{q_{i+1}}\cdots I_{q_m}\right)=1$ . In other words, we have $\left(\langle {\alpha }_{q_i}\rangle ,\langle d_i\rangle \right)=1$ , or $\langle {\alpha }_{q_i}\rangle +\langle d_i\rangle ={\mathbb{Z}}^n.$

Therefore, there is a vector ${\mathcal{D}}_i\in {\mathbb{Z}}^n$ such that ${\mathcal{D}}_i\otimes d_i\equiv e\left(\mathrm{mod}{I}_{q_i}\right)$ . We have Lemma 5.3.

We propose a polynomial algorithm to find the vector ${\mathcal{D}}_i$ appeared in Lemma 5.3, and then put $A_i=d_i\otimes {\mathcal{D}}_i$ getting the public key $A_1\mathrm{,}{A}_2\mathrm{,}\cdots \mathrm{,}{A}_m$ . The polynomial algorithm for finding vector ${\mathcal{D}}_i$ like follows.

Now, we describe an attainable algorithm for our FHE Scheme based on cyclotomic field as follows.

The property of FHE follows immediately from the general construction. We mainly discuss the security of this practical system for FHE. Obviously, an additional risk comes from the messages of one-dimensional modulus $t_i\left(1\le i\le m\right)$ . It is equivalent to find a solution to the algebraic equation with a high degree of

$x^n-x^{n-1}+\cdots -x+1=t$

For a given target value $t\in \mathbb{Z}$ . This is an ancient hard problem in mathematics, there is no general method to find the solution according to the famous Galois theory. Therefore, we conclude that there are no special risks coming from the one-dimensional modulus $t_i$ of $I_{q_i}$ .

6. Conclusions

In this work, we construct the first unbounded fully homomorphic encryption scheme without the bootstrapping transformation technique. In the encryption algorithm (3.5), we see that $H^{\mathrm{<mo>\; *\; </mo>}}\left(\bar{a}\right)=a{I}_n$ for any $a\in \mathbb{Z}$ . Therefore, the problem of security may transfer to the standard Ring-SIS problem: suppose that

$A_{\chi }=\left[{A^{\prime }}_1\mathrm{,}{A^{\prime }}_2\mathrm{,}\cdots \mathrm{,}{A^{\prime }}_m\right]\in {\mathbb{Z}}^{n\times m}$ , where ${A^{\prime }}_i$ is given by (3.2), $u\in {\mathbb{Z}}^n$ is a target vector, find $x=\left(\begin{array}{c}{x}_1\\ ⋮\\ x_m\end{array}\right)\in {\mathbb{Z}}^m$ such that $Ax=u$ , and $0<\left|x\right|\le \beta$ . Let q be a sufficiently large positive integer, if one can show that every column ${A^{\prime }}_i$ of $A_{\chi }$ is uniformly random vectors in ${\mathbb{Z}}_q^n$ , then this problem can be changed to an inhomogeneous version of the SIS problem, which is to find a short integer solution to $Ax\equiv u\left(\mathrm{mod}q\right)$ . It is not hard to show that the homogeneous and inhomogeneous problems are essentially equivalent to typical parameters.

According to Ajtai’s seminal work [23] [41] , the hardness of the SIS problem is relative to the worst-case lattice problem. More precisely, for any $m=\text{poly}\left(n\right)$ , any $\beta >0$ , and any sufficiently large $q\ge \beta \cdot \text{poly}\left(n\right)$ , solving ${\text{SIS}}_{n\mathrm{,}q\mathrm{,}\beta \mathrm{,}m}$ with non-negligible probability is at least as hard as solving the decisional approximate shortest vector problem ${\text{GapSVP}}_{\gamma }$ for some $\gamma =\beta \cdot \text{poly}\left(n\right)$ (also see [52] and Theorem 4.1.2 of [2] ). Perhaps, we may find another proof that the security of our FHE scheme is solely under a worst-case complexity assumption.

On the other hand, the fully homomorphic signature is the dual question of the fully homomorphic encryption, we will develop a scheme for a fully homomorphic signature in another article.

Acknowledgements

This work was prepared during our visit to Henan Academy of Sciences, the authors appreciate Professor Tianze Wang and Professor Jingluo Huang for their invitation and hosting. This work was supported by the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (No. 2020030254).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Rivest, R.L., Adleman, L. and Dertouzos, M.L. (1978) On Data Banks and Privacy Homomorphisms. Foundations of Secure Computation, 4, 169-180.
[2]	Peikert, C. (2016) A Decade of Lattice Cryptography. Now Foundations and Trends, Boston, 1-90. https://doi.org/10.1561/9781680831139
[3]	Gentry, C. (2009) A Fully Homomorphic Encryption Scheme. Ph.D. Thesis, Stanford University, Stanford.
[4]	Gentry, C. (2009) Fully Homomorphic Encryption Using Ideal Lattices. Proceedings of the 41st Annual ACM Symposium on Theory of Computing, Bethesda, 31 May-2 June 2009, 169-178. https://doi.org/10.1145/1536414.1536440
[5]	Brakerski, Z. (2012) Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. Advances in Cryptology-CRYPTO 2012, Santa Barbara, 19-23 August 2012, 868-886. https://doi.org/10.1007/978-3-642-32009-5_50
[6]	Brakerski, Z., Gentry, C. and Vaikuntanathan, V. (2014) (Leveled) Fully Homomorphic Encryption without Bootstrapping. Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, 8-10 January 2012, 309-325. https://doi.org/10.1145/2090236.2090262
[7]	Brakerski, Z. and Vaikuntanathan, V. (2011) Fully Homomorphic Encryption from Ring-LWE and Security for Key Dependent Messages. Advances in Cryptology-CRYPTO 2011, Santa Barbara, 14-18 August 2011, 505-524. https://doi.org/10.1007/978-3-642-22792-9_29
[8]	Brakerski, Z. and Vaikuntanathan, V. (2014) Efficient Fully Homomorphic Encryption from (Standard) LWE. SIAM Journal on Computing, 43, 831-871. https://doi.org/10.1137/120868669
[9]	Cheon, J.H., Coron, J.-S., Kim, J., Lee, M.S., Lepoint, T., Tibouchi, M. and Yun, A. (2013) Batch Fully Homomorphic Encryption over the Integers. Advances in Cryptology-EUROCRYPT 2013, Athens, 26-30 May 2013, 315-335. https://doi.org/10.1007/978-3-642-38348-9_20
[10]	Coron, J.-S., Mandal, A., Naccache, D. and Tibouchi, M. (2011) Fully Homomorphic Encryption over the Integers with Shorter Public Keys. Advances in Cryptology-CRYPTO 2011, Santa Barbara, 14-18 August 2011, 487-504. https://doi.org/10.1007/978-3-642-22792-9_28
[11]	Coron, J.-S., Naccache, D. and Tibouchi, M. (2012) Public Key Compression and Modulus Switching for Fully Homomorphic Encryption over the Integers. Advances in Cryptology-EUROCRYPT 2012, Cambridge, 15-19 April 2012, 446-464. https://doi.org/10.1007/978-3-642-29011-4_27
[12]	Gentry, C. (2010) Computing Arbitrary Functions of Encrypted Data. Communications of the ACM, 53, 97-105. https://doi.org/10.1145/1666420.1666444
[13]	Gentry, C. (2010) Toward Basing Fully Homomorphic Encryption on Worst-Case Hardness. Advances in Cryptology-CRYPTO 2010, Santa Barbara, 15-19 August 2010, 116-137. https://doi.org/10.1007/978-3-642-14623-7_7
[14]	Gentry, C., Halevi, S., Peikert, C. and Smart, N.P. (2012) Field Switching in BGV-Style Homomorphic Encryption. Journal of Computer Security, 21, 663-684. https://doi.org/10.3233/JCS-130480
[15]	Gentry, C., Halevi, S. and Smart, N.P. (2012) Fully Homomorphic Encryption with Polylog Overhead. Advances in Cryptology-EUROCRYPT 2012, Cambridge, 15-19 April 2012. 465-482. https://doi.org/10.1007/978-3-642-29011-4_28
[16]	Smart, N.P. and Vercauteren, F. (2014) Fully Homomorphic SIMD Operations. Designs, Codes and Cryptography, 71, 57-81. https://doi.org/10.1007/s10623-012-9720-4
[17]	Regev, O. (2009) On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. JOURNAL OF THE ACM, 56, Article No. 34. https://doi.org/10.1145/1568318.1568324
[18]	Regev, O. (2010) The Learning with Errors Problem. IEEE Conference on Computational Complexity, Cambridge, 9-11 June 2010, 191-204. https://doi.org/10.1109/CCC.2010.26
[19]	Gentry, C., Sahai, A. and Waters, B. (2013) Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based. Advances in Cryptology-CRYPTO 2013, Santa Barbara, 18-22 August 2013, 75-92. https://doi.org/10.1007/978-3-642-40041-4_5
[20]	Zheng, Z. and Tian, K. (2022) On the LWE Cryptosystem with More General Disturbance. Journal of Information Security, 13, 127-139. https://doi.org/10.4236/jis.2022.133008
[21]	Alperin-Sheriff, J. and Peikert, C. (2013) Practical Bootstrapping in Quasilinear Time. Advances in Cryptology-CRYPTO 2013, Santa Barbara, 18-22 August 2013, 1-20. https://doi.org/10.1007/978-3-642-40041-4_1
[22]	Agrawal, S., Boneh, D. and Boyen, X. (2010) Efficient Lattice (H)IBE in the Standard Model. EUROCRYPT, Monaco, 30 May-3 June 2010, 553-572. https://doi.org/10.1007/978-3-642-13190-5_28
[23]	Ajtai, M. (1999) Generating Hard Instances of the Short Basis Problem. In: Wiedermann, J., Boas, P.E. and Nielsen, M., Eds., Automata, Languages and Programming, Springer, Berlin, 1-9. https://doi.org/10.1007/3-540-48523-6_1
[24]	Alwen, J. and Peikert, C. (2009) Generating Shorter Bases for Hard Random Lattices. Theory of Computing Systems, 48, 535-553. https://doi.org/10.1007/s00224-010-9278-3
[25]	Micciancio, D. and Peikert, C. (2012) Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller. Advances in Cryptology-EUROCRYPT 2012, Cambridge, 15-19 April 2012, 700-718. https://doi.org/10.1007/978-3-642-29011-4_41
[26]	Peikert, C. and Waters, B. (2011) Lossy Trapdoor Functions and Their Applications. SIAM Journal on Computing, 40, 1803-1844. https://doi.org/10.1137/080733954
[27]	Chillotti, I., Gama, N., Georgieva, M. and Izabachene, M. (2016) Faster Fully Homomorphic Encryption: Bootstrapping in Less than 0.1 Seconds. Advances in Cryptology-ASIACRYPT 2016, Hanoi, 4-8 December 2016, 3-33. https://doi.org/10.1007/978-3-662-53887-6_1
[28]	Chillotti, I., Gama, N., Georgieva, M. and Izabachene, M. (2018) TFHE: Fast Fully Homomorphic Encryption over the Torus. Journal of Cryptology, 33, 34-91. https://doi.org/10.1007/s00145-019-09319-x
[29]	Chen, H., Laine, K. and Player, R. (2017) Simple Encrypted Arithmetic Library-SEAL v2.1. FC 2017 International Workshops, WAHC, BITCOIN, VOTING, WTSC, and TA, Sliema, 7 April 2017, 3-18. https://doi.org/10.1007/978-3-319-70278-0_1
[30]	Fan, J. and Vercauteren, F. (2012) Somewhat Practical Fully Homomorphic Encryption. IACR Cryptology ePrint Archive.
[31]	Cheon, J.H., Han, K., Kim, A., Kim, M. and Song, Y. (2018) Bootstrapping for Approximate Homomorphic Encryption. Advances in Cryptology-EUROCRYPT 2018, Tel Aviv, 29 April-3 May 2018, 360-384. https://doi.org/10.1007/978-3-319-78381-9_14
[32]	Cheon, J.H., Kim, A., Kim, M. and Song, Y.S. (2017) Homomorphic Encryption for Arithmetic of Approximate Numbers. Advances in Cryptology-ASIACRYPT 2017, Hong Kong, 3-7 December 2017, 409-437. https://doi.org/10.1007/978-3-319-70694-8_15
[33]	Boura, C., Gama, N., Georgieva, M. and Jetchev, D. (2020) CHIMERA: Combining Ring-LWE-Based Fully Homomorphic Encryption Schemes. Journal of Mathematical Cryptology, 14, 316-338. https://doi.org/10.1515/jmc-2019-0026
[34]	van Dijk, M., Gentry, C., Halevi, S. and Vaikuntanathan, V. (2010) Fully Homomorphic Encryption over the Integers. Advances in Cryptology-EUROCRYPT 2010, French Riviera, 30 May-3 June 2010, 24-43. https://doi.org/10.1007/978-3-642-13190-5_2
[35]	Kogos, K.G., Filippova, K.S. and Epishkina, A.V. (2017) Fully Homomorphic Encryption Schemes: The State of the Art. 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, St. Petersburg, 1-3 February 2017, 463-466. https://doi.org/10.1109/EIConRus.2017.7910591
[36]	Yagisawa, M. (2015) Fully Homomorphic Encryption without Bootstrapping. Cryptology ePrint Archive.
[37]	Yagisawa, M. (2015) Fully Homomorphic Encryption on Octonion Ring. Cryptology ePrint Archive.
[38]	Liu, D. (2015) Practical Fully Homomorphic Encryption without Noise Reduction. Cryptology ePrint Archive.
[39]	Li, J. and Wang, L. (2015) Noise-Free Symmetric Fully Homomorphic Encryption Based on Non-Commutative Rings. Cryptology ePrint Archive.
[40]	Zheng, Z. (2022) Modern Cryptography Volume 1—A Classical Introduction to Informational and Mathematical Principle. Springer, Berlin. https://doi.org/10.1007/978-981-19-0920-7
[41]	Ajtai, M. (1996) Generating Hard Instances of Lattice Problems. Quaderni di Matematica, 13, 99-108. https://doi.org/10.1145/237814.237838
[42]	Micciancio, D. (2002) Generalized Compact Knapsacks, Cyclic Lattices, and Efficient One-Way Functions from Worst-Case Complexity Assumptions. The 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, 16-19 November 2002, 356-365.
[43]	Zheng, Z., Liu, F. and Chen, M. (2022) On the High Dimensional RSA Algorithm—A Public Key Cryptosystem Based on Lattice and Algebraic Number Theory. International Journal of Latest Research in Engineering and Technology, 8, 1-16.
[44]	Zheng, , Z., Tian, K. and Liu, F. (2022) Modern Cryptography Volume 2—A Classical Introduction to Informational and Mathematical Principle. Springer, Berlin. https://doi.org/10.1007/978-981-19-7644-5
[45]	Lyubashevsky, V., Peikert, C. and Regev, O. (2010) On Ideal Lattices and Learning with Errors over Rings. Advances in Cryptology-EUROCRYPT 2010, French Riviera, 30 May-3 June 2010, 1-23. https://doi.org/10.1007/978-3-642-13190-5_1
[46]	Micciancio, D. and Regev, O. (2009) Lattice-Based Cryptography. In: Bernstein, D.J., Buchmann, J. and Dahmen, E., Eds., Post-Quantum Cryptography, Springer, Berlin, 147-191. https://doi.org/10.1007/978-3-540-88702-7_5
[47]	Zheng, Z., Liu, F., Huang, W., Xu, J. and Tian, K. (2022) A Generalization of NTRUEncrypt—Cryptosystem Based on Ideal Lattice. Journal of Information Security, 13, 165-180. https://doi.org/10.4236/jis.2022.133010
[48]	Zheng, Z., Liu, F., Lu, Y. and Tian, K. (2022) Cyclic Lattices, Ideal Lattices and Bounds for the Smoothing Parameter. Journal of Information Security, 13, 272-293. https://doi.org/10.4236/jis.2022.134015
[49]	Micciancio, D. and Regev, O. (2007) Worst-Case to Average-Case Reductions Based on Gaussian Measures. SIAM Journal on Computing, 37, 267-302. https://doi.org/10.1137/S0097539705447360
[50]	Washington, L.C. (1980) Graduate Texts in Mathematics—Introduction to Cyclotomic Fields. Springer-Verlag, New York.
[51]	Micciancio, D. (2001) Improving Lattice Based Cryptosystems Using the Hermite Normal Form. In: Silverman, J.H., Ed., Cryptography and Lattices, Springer, Berlin, 126-145. https://doi.org/10.1007/3-540-44670-2_11
[52]	Micciancio, D. and Peikert, C. (2013) Hardness of SIS and LWE with Small Parameters. Advances in Cryptology-CRYPTO 2013, Santa Barbara, 18-22 August 2013, 21-39. https://doi.org/10.1007/978-3-642-40041-4_2