1. Introduction: Prerequisites
In a previous paper, the author introduced the concepts of free ordered product and ordered semigroup amalgam showing that an ordered semigroup amalgam is embeddable in an ordered semigroup if and only if it is naturally embedded in its free ordered product. Howie [1] gave sufficient conditions under which a (semigroup) amalgam can be embedded in a semigroup. To do this Howie generalized the concept of unitariness to that of almost unitariness and his basic result is based on almost unitariness of a subset of semigroup. In this paper we study “similar concepts” in case of ordered semigroups applying the (usual for ordered semigroups) following “technique”: if
is an ordered semigroup, then, instead of an identity element, we consider an element e of S such that
and also for a nonempty subset A of S we usually consider the subsets of S,
and
. In this paper, taking into account Howie’s definitions (see [1] [2] (§VIII.3) and ( [3] §9.4)) we introduce the concepts of unitary, almost unitary and strongly almost unitary subset of an ordered semigroup S in terms of left and right translations of an ordered semigroup S (as well as the translational hull of S). For the definitions and results presented in this paragraph, we refer to [4] [5] . An ordered semigroup
is a semigroup
with an order relation “
” which is compatible with the operation “
” (i.e. for
,
implies
and
). Now let
be an ordered semigroup and
.
•
is called a left translation of S if
i)
for all
.
ii) For
,
implies
(i.e.
is an isotone mapping).
•
is called a right translation of S if
i)
for all
.
ii) For
,
implies
(i.e.
is an isotone mapping).
It is readily to prove that the set
(resp.
) of all left (resp. right) translations of S is a semigroup under the usual composition of mappings. On the set:
•
we define a binary relation
for all
•
we define a binary relation
for all
Then it is straightforward to verify that
,
are ordered semigroups. If
, then
• The mapping
,
is called inner left translation induced by α.
• The mapping
,
is called inner right translation induced by α.
It is a matter of routine to prove that
(resp.
) is a left (resp. right) translation of S and
.
A left translation
and a right translation
are linked if for every
,
and then the pair
is called a bitranslation of S. Clearly
is a bitranslation of S for every
. It is easy to verify that the “product” of two bitranslations of S, say
,
, defined by
is again a bitranslation of S. Therefore the set
of all bitranslations of S under the operation “
” defined above is a semigroup. Also the binary relation “
” on
defined by the rule that
can be easily shown that it is an order relation on
compatible with the operation “
” and hence
is an ordered semigroup called translational hull of S. The concept of translational hull of an ordered semigroup was introduced by the author in his Doctoral Dissertation.
If U is a nonempty subset of S, then we denote
•
•
Let now T be a subsemigroup of
. Then
is an ordered semigroup where “
” and “
” are the restrictions of the operation “
” and order relation “
” of S on T respectively, that is,
(
) and
It is clear that if T is a subsemigroup of S, then
and
are subsemigroups of S. In the following, when we have a subsemigroup T of S, we shall always consider T as an ordered semigroup with the previous structure
and hence, if A is a nonempty subset of T, then
•
•
Obviously
and
2. Unitary Subsets of an Ordered Semigroup
Definition 2.1: Let
be an ordered semigroup and U be a nonempty subset of S.
i) U is called left unitary in S if
Ι)
ΙΙ) for
and
such that
, we have
for some
ii) U is called right unitary in S if
Ι)
ΙΙ) for
and
such that
, we have
for some
iii) U is called unitary in S if it is both left and right unitary. □
Proposition 2.2: Let
be an ordered semigroup, U be a left (resp. right) unitary subset of S and T be a subsemigroup of S containing U. Then U is a left (resp. right) unitary subset of T.
Proof: As we mentioned above, since T is a subsemigroup of S, we consider T as an ordered semigroup endowed with the operation and order relation defined by
,
and
and hence, since
, by definition we have
and
To prove that
, suppose
. Since
, we have
and hence
. Since U is a left unitary subset of S (Definition 2.1 i) I)) then
and hence
. Next we shall show that the condition i)ΙΙ) of Definition 2.1 is true. Let
and
such that
. Clearly
and
. Since U is a left unitary subset of S (Definition 2.1 i) II)) there exists
such that
, i.e.
. Therefore the conditions I), II) of Definition 2.1 i) hold and so U is a left unitary subset of T. □
Remark 2.3: By Proposition 2.2 it follows directly that if
is an ordered semigroup, U is a unitary subset of S and T is a subsemigroup of S containing U, then U is a unitary subset of T. □
Proposition 2.4: Let
be an ordered semigroup, U be a nonempty subset of S and T be a subsemigroup of S containing U. The following are equivalent:
i) U is a left (resp. right) unitary subset of T.
ii) α)
β) If
and
with
(resp.
), then there exists
such that
.
Proof: As we mentioned above, since T is a subsemigroup of S, we consider T as an ordered semigroup
where
,
and
i)
ii) It is clear that U is a nonempty subset of T.
α) From Definition 2.1 we have
and hence
β) Let
and
such that
. From the definitions of “
” and “
” we immediately have (since
)
and consequently (since U is a left unitary subset of T) there exists
such that
. Thus (since
)
.
ii)
i) From α) we obtain directly
, that is
. Now let
and
such that
. From the definitions of “
” and “
” we have (since
)
and so, by β), there exists
such that
which clearly means that
. Then, from Definition 2.1 i), it follows immediately that U is a left unitary subset of T. □
By Definition 2.1 and Proposition 2.4 we directly have the following
Proposition 2.5: Let
be an ordered semigroup, U be a nonempty subset of S and T be a subsemigroup of S containing U. The following are equivalent:
i) U is unitary in T.
ii) α)
β) If
and
with
, then there exists
such that
.
γ) If
and
with
, then there exists
such that
. □
3. Almost Unitary Subsets of an Ordered Semigroup
Proposition 3.1: Let
be an ordered semigroup,
be a left translation of S and
be a right translation of S such that
. Then
is a subsemigroup of S.
Proof: Suppose
. Then
(
is a left translation of S)
(
)
(
is a right translation of S)
that is,
. Hence
and so, since clearly
is a nonempty subset of S,
is a subsemigroup of S. □
Definition 3.2: Let
be an ordered semigroup and U be a nonempty subset of S. The subset U is said to be almost unitary in S if there exist mappings
(called associated mappings) with the following properties:
i)
is a bitranslation of S (i.e.
ii)
(i.e.
commutes with
)
iii)
and
for all
iv)
and
for all
v) U is unitary in
. □
Remark 3.3: By Proposition 3.1 we deduce directly that if
is a left translation of S and
is a right translation of S such that
, then
is a subsemigroup of S and hence the v) of Definition 3.2 is meaningful. □
Theorem 3.4: Let
be an ordered semigroup,
such that
and U be a subset of S such that for all
,
and
. Then
i)
is a subsemigroup of S
ii) U is almost unitary in S if and only if U is unitary in
.
Proof:
i) Since
is clearly a subsemigroup of S then
is also a subsemigroup of S.
ii) For each
we have
whence it follows immediately that
.
(
) Let U be almost unitary in S. Then there exist mappings
with the properties i) - v) of Definition 3.2. By condition iv) of Definition 3.2, it follows that
and
. Hence for every
we have
(
is a left translation of S)
(
is a right translation of S)
that is,
. Thus
and so
. By Proposition 3.1 (since
, see Definition 3.2 ii)) we have
is a subsemigroup of S and hence
is a subsemigroup of S. Therefore, since
is a subsemigroup of S containing
and
is a subsemigroup of S then we immediately have
is a subsemigroup of
and so, since
and (by Definition 3.2 v)) U is unitary in
, it follows from Remark 4.3 that U is unitary in
.
(
) Let U be unitary in
. We take for
and
the inner left and inner right translation
,
respectively, that is
,
and
,
We shall show that U is almost unitary in S with
,
as associated mappings. The conditions i), ii), iv) of Definition 3.2 clearly hold. For the iii) of Definition 3.2, take
. Then
that is,
. Similarly
. Regarding v) of Definition 3.2, we observe that
whence it follows immediately that
. Consequently, since U is unitary in
, we deduce that U is unitary in
(i.e. the condition v) of Definition 3.2 is true). Therefore, according to Definition 3.2, U is almost unitary in S. □
Remark 3.5: From the proof of Theorem 3.4, we immediately observe that Theorem 3.4 also holds without the condition iii) of Definition 3.2 and the property that
,
are linked. □
For
and T a nonempty subset of S we denote
.
Theorem 3.6: Let
be an ordered semigroup, U be a nonempty subset of S and
. Also let
be an ordered semigroup with the following properties:
i)
,
ii)
,
iii)
iv)
v)
and
for every
vi)
is unitary in
.
Then U is almost unitary in S.
Proof: Set
•
,
•
,
Because of ii), it is evident that
,
are well defined. Also for
we have
o
o
So
is a left translation of S. Similarly
is a right translation of S. Moreover for
we have
and hence
,
are linked on S. Thus
is a bitranslation of S (i.e. the condition i) of Definition 3.2 holds). Since for any
then the condition ii) of Definition 3.2 is true. Moreover by v) for
we directly have
(1)
and so for each
Thus
Similarly we show that
. Therefore the condition iii) of Definition 3.2 holds. Also, by v), for every
we have
and in a similar way we show that
. Consequently the condition iv) of Definition 3.2 holds.
I) Since for any
,
then clearly
.
ΙI)
is a subsemigroup of S (see Remark 3.3).
III)
:
Let
. Then by v) we have
Thus
and since
then
. Obviously
and hence, by iii), it follows that
. Therefore
and so
.
IV)
:
Let
. Since
then
for some
and so, by iii),
which obviously means that
. Also since
then there exists
such that
and so, by iii),
. Hence
. Consequently
But
is unitary in
and so, by Definition 2.1,
Therefore
and thus there exists
such that
. Since
it follows that
or
. If
then
. Contradiction (see iv)). Therefore
and since
, we have (see iii))
and so
. Consequently
V) Let
and
such that
. We shall prove that
,
. Indeed:
Since
we have
and
for some
. Hence (see iii))
. Therefore
. Also since
, then (see i), iii))
. But (see vi) and Definition 2.1 iii))
is a left unitary subset of
. Consequently (see Proposition 2.4 i)
ii)β)) there exists
such that
. Since
it follows that
or
. If
then
. Contradiction (see iv)). Therefore
and since
, we have (see iii))
. From II) - V) and Proposition 2.4 ii)
i) it follows directly that U is a left unitary subset of
. Similarly we show that U is a right unitary subset of
.
Therefore (see Definition 2.1 iii)) U is a unitary subset of
and so
the condition v) of Definition 3.2 holds. This (see Definition 3.2) completes the proof. □
4. Strongly Almost Unitary Subsets of an Ordered Semigroup
Remark 4.1: From the proof of the Theorem 3.6 we immediately have that if
(instead of
), then for every
,
and
(where
,
are the mappings defined in the proof of the previous Theorem). □
Now due to Remark 4.1 it follows immediately the next
Theorem 4.2: Let
be an ordered semigroup, U be a nonempty subset of S and
. Also let
be an ordered semigroup with the following properties:
i)
,
ii)
,
iii)
iv)
v)
vi)
and
for every
vii)
is unitary in
.
Then there exist mappings
such that
α)
,
β) U is almost unitary in S with associated mappings
,
. □
Remark 4.3: Observe that, due to Theorem 3.4 ii), we can equivalently replace the conditions vi), vii) of Theorems 3.6, 4.2 with the condition “
is almost unitary in
”. So, if the ordered semigroup
satisfies the conditions i) - v) of Theorem 3.6 (resp. the conditions i) - vi) of Theorem 4.2) and also
is almost unitary in
, then the conclusion of Theorem 3.6 (resp. of Theorem 4.2) remains true. This helps us better understand the connection between “almost unitary in S” and “almost unitary in
”. □
Definition 4.4: Let
be an ordered semigroup and U be a nonempty subset of S. The subset U is said to be strongly almost unitary in S if there exist mappings
(called associated mappings) with the following properties:
i)
is a bitranslation of S (i.e.
ii)
(i.e.
commutes with
)
iii)
and
for all
iv)
and
for all
v) U is unitary in
. □
Remark 4.5: Evidently if U is strongly almost unitary in S, then U is almost unitary in S (see Definitions 4.4, 3.2). □
From Theorem 4.2, Remark 4.3 and Definitions 3.2, 4.4 we immediately have the following
Theorem 4.6: Let
be an ordered semigroup, U be a nonempty subset of S and
. Also let
be an ordered semigroup with the following properties:
i)
,
ii)
,
iii)
iv)
v)
and
for every
vi)
is unitary in
(equivalently:
is almost unitary in
).
Then U is strongly almost unitary in S. □
The reverse of the previous Theorem also holds:
Theorem 4.7: Let
be an ordered semigroup, U be a nonempty subset of S such that U is strongly almost unitary in S and
. Then we can define an operation “
” and an order relation “
” on
with the following properties:
i)
,
ii)
,
iii)
iv)
v)
is an ordered semigroup
vi)
and
for every
vii)
is unitary in
.
Proof: Since U is strongly almost unitary in S then there exist mappings
satisfying the properties of Definition 4.4. On
we define
and
Then
is a semigroup (§9.4). Also clearly “
” is an order relation on S.
We shall prove that “
” is compatible with the operation “
”:
Let
such that
. We shall show that
and
. Since
and
we distinguish the cases
or
.
A)
Then obviously
. For
we have the cases
or
.
A1)
Since
then
and
. Hence
A2)
Since
then
and
. Hence
Β)
Since
we have the cases
or
.
B1)
Obviously
and
. Thus
B2)
Since
then
and
. Thus
From A), B) we immediately have
. Similarly we show that
. Therefore
is an ordered semigroup. It is evident that the required conditions i) - v) are true. For the condition vi), take
. We shall prove that
and
. By definition of “
” we have
. Since U is strongly almost unitary in S, it follows by Definition 4.4 iv) that
and hence
. From iv) we immediately have
. Similarly we show that
and thus the condition vi) holds. Now it remains to be shown that the condition vii) is also true.
I) Obviously
is a subsemigroup of
and so
is also a subsemigroup of
.
II) Since clearly
for all
then
. We shall show that
:
Let
. Then
,
. Since
and, from the definition of “
”,
, then it follows immediately that
. Now take
. Then
,
. Since
and, from the definition of “
”,
, then we have
.
III)
:
First we shall show that
. Let
. Then
that is,
. Thus
and since clearly
then it is readily verified that
.
IV)
:
Let
. Then, since
, there exists
such that
. Since
, we have two cases:
IV1)
Then
and so, by definition of “
”, we have
. It is evident now that
.
IV2)
Since
and
, then, by definition of “
”, it follows that
and
. Thus
. Also, since
, there exists
such that
. But
and so, by definition of “
”, we have
and
. Since
then, by definition of “
”, we clearly have
and so, by II),
. Consequently
and hence
. By Definition 4.4 v), U is unitary in
and so, by Proposition 2.5 i)
ii)α), we have
. Thus
whence
for some
. Since, by definition of “
”,
then it clear that
.
V) Let
and
such that
. We shall prove that
,
:
Since
then
and
for some
. If
then obviously
. Suppose
, i.e.
. Since
, then, by definition of “
”, we have
and
. By definition of “
”, since
, it follows that
. Also, since
then
or
. If
, then
and so, by definition of “
”, we immediately have
which, by definition of “
”, means that
. This is impossible and so
. Since
we have the following two cases:
V1)
Then
. Also
Then, from IV), we immediately have
and hence
for some
. But
and so
.
V2)
Since
then
and thus
. Also since
and
then, by i) and definition of “
”, we have
. Therefore we have
and
such that
. But, by Definition 4.4 v), U is unitary in
and so (see Proposition 2.5 i)
ii)β)) there exists
such that
which means (see the definition of “
”) that
.
From I), III) - V) and Proposition 2.4 ii)
i) it follows directly that
is a left unitary subset of
. Similarly we show that
is a right unitary subset of
. Therefore (see Definition 2.1 iii))
is a unitary subset of
and so the condition vii) of the Theorem holds. This completes the proof.
□
Writing down Theorems 4.7, 4.6 together, we immediately obtain the following fundamental Theorem which actually summarizes the main results of the paper.
Theorem 4.8: Let
be an ordered semigroup, U be a nonempty subset of S and
. The following are equivalent:
I) U is strongly almost unitary in S.
II) We can define an operation “
” and an order relation “
” on
with the following properties:
i)
,
ii)
,
iii) 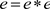
iv)
v)
is an ordered semigroup
vi)
and
for every
vii)
is unitary in
(equivalently:
is almost unitary in
).
□
The results presented in the paper generalize the analogous ones of semigroups without order (cf. [2] §VIII.3 and [3] §9.4) because we can consider that every semigroup without order is an ordered semigroup with order relation being the equality relation. In general, researchers in ordered semigroups should arrive at results that hold in the case of semigroups without order by considering them as ordered semigroups in the previous sense and will therefore have more general results. Note that in Section 1 we mention a technique that can be applied by any researcher studying the topic of the paper.