1. Introduction
It is frequently impossible to analyze problems using traditional research methods because so many fields, including economics, engineering, environmental science, sociology, and medicine, include ambiguous data. Therefore, to resolve the problem of dealing with uncertainty, new mathematical techniques are required. These techniques must function as efficient tools for addressing various forms of uncertainty and imprecision in embedded systems. The idea of soft sets, which Molodtsov [1] initially articulated in 1999, has received a lot of momentum due to its adaptability, level of detail, and breadth of problem-solving. Soft set operations and applications have been examined by Chen et al. [2] and Maji et al. [3] [4] . Maji et al. [5] also presented the idea of fuzzy soft sets and looked into their characteristics. This idea was also used to address various decision-making issues by Roy and Maji [6] . As a generalization of soft sets, Alkhazaleh et al. [7] presented the idea of soft multisets. Additionally, they provided definitions for probability fuzzy soft sets and fuzzy parameterized interval-valued fuzzy soft sets in [8] [9] , as well as examples of how they might be used in decision-making and medical diagnostics. The idea of generalized fuzzy soft sets and related operations, as well as their use for decisions and diagnostics in medicine, was introduced by Majumdar and Samanta in 2010 [10] .
Although effective, the previous models looked at typically only one expert. Several operations, including joint and crossover, must be carried out if you want to accept the viewpoints of multiple experts. For the user, this is problematic. The ideas of soft expert sets and fuzzy soft expert sets were established by Alkhazaleh and Salleh [11] [12] in order to overcome this issue. The user can view all expert opinions in one model without any alteration. The user can access expert viewpoints despite any tampering. By eliminating their inconsistencies, Serdar and Hilal [13] make several adjustments to the soft expert sets that are crucial for the notion of soft sets. Generalized fuzzy soft expert sets (GFSESs), which are utilized to assess a decision problem, are a novel idea that Hazaymeh et al. [14] acquire as well. In the context of soft expert sets, Lancy and Arockiarani [15] identify various matrix types and suggest a decision paradigm based on the soft expert sets.
The definition of generalized soft expert is introduced in this study. We describe its basic operations, including complement, union, intersection, AND, and OR, and look at how they work. We give an illustration of a decision-problem where this concept is used. The definition of a generalized soft expert matrix and a method for solving a decision problem are also provided. The important sections of this essay are summarized below. Section 3 introduces the idea of generalized soft expert sets. Section 4 provides the basic steps and some properties of generalized soft expert sets. In Section 5, an approach of the generalized soft expert set is demonstrated. Section 6 describes a generalized soft expert matrix and how to utilize it to resolve decision-making issues.
2. Preliminaries
In this section, we review several fundamental ideas that are relevance to this study.
Definition 2.1 Let V be a universe set and H a set of parameters. Let
denote the power set of V and
. A pair
is called a soft set over V, where F is a mapping
.
In other words, a soft set over V is a parameterized family of subsets of the universe V. For
,
is one of the approximate components of
.
Definition 2.2 Let V be a universe set and H a set of parameters. Let
denote the power set of all fuzzy subsets of V,
. A pair
is called a fuzzy soft set over V, where F is defined by
.
Definition 2.3 Let
be the universal set of element and
the parameters set. The pair
will be called a soft universe. Let
and
a fuzzy subset of H; that is,
, where
is the collection of all fuzzy subsets of V.
is defined as
.
Then
is called a generalized fuzzy soft set (GFSS) over the soft set
. Here for each parameter
,
indicates not only the degree of belongingness of the elements of V in
but also the degree of possibility of such belongingness which is represented by
. So we can write as follows:
,
where
are the degree of belongingness,
is the degree of possibility of such belongingness.
Definition 2.4 Let V be a universe set, H a parameters set, X an experts set, O = {1 = agree, 0 = disagree} an opinions set. Let
and
. Then
is known as a soft expert set over V and F is given by
,
where
denotes a power set of V.
Example 2.1 Let
be a universe set,
a parameters set and
be an experts set,
. We define a function
as follows:
,
,
,
,
,
,
,
.
Then
consists of the following approximate sets:
Definition 2.5 Let V be a set of universe, H a set of parameters, X a set of experts, O an opinions set. Let
,
. Let
be a fuzzy set of U which is defined by
. Then
is known as an generalized fuzzy soft expert set over U and
is given by
,
where
is denoted as all fuzzy subsets of V.
Definition 2.6 Let
be a universe set,
a parameters set, X a set of experts. Let O = {1 = agree, 0 = disagree} be an opinions set,
,
, F is a mapping given by
.
Then the matrix representation of the soft expert set over
is defined as
or
,
where
.
represents the level of acceptance of
in the soft expert set
,
represents the level non-acceptance of
in the soft expert set
.
Definition 2.7 Let
and
be two soft expert matrices, then we define addition of A and B as
, where
,
.
Definition 2.8 Let
and
be two soft expert matrices, then we define subtraction of A and B as
, where
,
.
3. Generalized Soft Expert Set
In this part, we develop the generalized soft expert set idea and investigate some of its aspects.
Let V be a universe set, H a parameters set, X an experts set, and O = {1 = agree, 0 = disagree} a set of opinions. Let
and
,
be a fuzzy set of U; that is,
.
Definition 3.1 A pair
is called a generalized soft expert set (GSES in short) over V, where
is given by
, (1)
where
denotes the collection of all subsets of V. Here for each
,
indicates not only the degree of belongingness of the elements of V in
, but also the degree of possibility of such belongingness which is represented by
.
Example 3.1 Let
be a universe set,
a parameters set,
an experts set. Let
,
a fuzzy set of U, that is,
. Define a function
as follows:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Then
consists of the following approximate sets:
Definition 3.2 Let
,
are two GSESs over V,
is called the generalized soft expert subset of
, if
, for all
,
. If
, then
is known as the generalized soft expert superset of
.
Example 3.2 Consider example 3.1. Let
be defined as follows:
.
Apparently,
.
and
be two GSESs of V as follows:
and
Therefore
.
Proposition 3.1 Let
and
be two GSESs over V, then
. (2)
Definition 3.3 Two GSESs
and
over V are said to be equal, if
and
.
Proposition 3.2 If
,
and
are three GSESs over V, then
1)
,
2)
and
.
Definition 3.4 The subset
of
which is called an agree-GSES is defined as
, (3)
where
and
.
Definition 3.5 The subset
of
which is called a disagree-GSES is defined as
, (4)
where
and
.
Example 3.3 Consider example 3.1, the agree-GSES
over V is
The disagree-GSES
over V is
Definition 3.6 The complement of
which is denoted by
, is defined as
, where
is given by
(5)
for all
,
and
is a generalized complement.
Example 3.4 Consider example 3.1, then the complement of
is
Proposition 3.3 If
is a GSES over V, then
1)
,
2)
,
3)
.
4. Some Operations of the GSESs
In this part, we will present several GSES operations, deduce their features, and provide some examples.
Definition 4.1 The union of the GSESs
and
of V is defined as
, where
, for all
,
(6)
Example 4.1 Consider example 3.1, suppose
,
.
Let
and
are two GSESs over V such that
and
Then
, where
Proposition 4.1 Let
,
and
be three GSESs over V. Then
1)
,
2)
,
3)
.
Definition 4.2 The intersection of the GSESs
and
of V is denoted by
, where
for all
and
(7)
Example 4.2 Consider Example 4.1, we have
,
where
.
Proposition 4.2 If
,
and
are three GSESs over V, then
,
,
,
.
Definition 4.3 Let
and
be two GSESs over V, then
is defined as
, (8)
where for all
,
.
Definition 4.4 Let
and
be two GSESs over V, then
is defined as
, (9)
where for all
,
.
Example 4.3 Let
and
Then
Proposition 4.3 If
,
and
are three GSESs over V, then
1)
,
2)
,
3)
,
4)
.
5. An Application of GSES in Decision-Making
We provide an application of generalized soft expert set theory to a decision-making issue in this section.
Suppose one enterprise needs to find an employee. Let
be a collection of applicant compositions,
a set of parameters, where
indicate “good attitude”, “cheerful personality”, “good English” and “good communication skills”, respectively. To make a fair selection, three experts form a committee members set
. Let O = {1 = agree, 0 = disagree} be a set of experts opinions. T he following algorithm may be used to fill the position.
Algorithm 1:
1) Input the GSES
.
2) Find the agree-GSES and the disagree-GSES.
3) Compute
of the agree-GSES.
4) Compute
of the disagree-GSES.
5) Compute
.
6) Find m, for which
. If m has more than one value, then the company can choose any one of them.
After careful consideration, the committee obtains the GSES as follows:
We show the agree-GSES and the disagree-GSES in Table 1 and Table 2, where
and
.
Now according to the formula
, we can find the best choices for the company to fill the position. From Table 1 and Table 2, we get Table 3.
Because max
, the best option is
.
6. An Application of Expert Matric of GSES in Decision-Making
In this part, we create generalized expert matrices and then give complement, addition, and subtraction operations. Then, we show how the generalized expert matrices were used in a decision-making situation.
Definition 6.1 Let
be a set of universe,
a parameters set and X an experts set. Let O = {1 = agree, 0 = disagree} be a set of opinions,
and
. Let
a fuzzy set over H which is defined by
and
is given by
. (10)
Then the expert matrix of the GSES
is defined as
or
, (11)
where
,
indicates the acceptance level of
over
,
indicates the non-acceptance level of
over
,
indicates the possible degree of the acceptance level of
, and
indicates the possible degree of the level of the non-acceptance level of
.
Example 6.1 Think about example 3.1. Three expert matrices can be produced with three experts making the decision.
,
,
.
Definition 6.2 If
and
are two expert matrices of a GSES, then A is equal to B, if for
, there are
,
,
and
. (12)
Definition 6.3 If
is an expert matrix of the GSES, where
. Then the complement of the expert matrix is defined as
, where for
, there are
,
. (13)
Definition 6.4 If
and
are two expert matrices of the same form over the GSESs, then the addition of A and B is denoted by
, where
,
,
. (14)
Definition 6.5 If
and
are two expert matrices over the GSESs, then the subtraction of A and B is denoted by
, where
,
,
. (15)
Example 6.2 If A and B are two expert matrices over the GSESs as follows:
,
.
Then
,
.
Proposition 6.1 If A and B are two expert matrices of the same form over the GSESs, then
1)
,
2)
.
According to the expert matrices of a GSES, we describe a different approach to the issue raised in Section 5 as an example. The committee may employ the next algorithm.
Algorithm 2:
1) Input the GSES
.
2) Find the expert matrices over the GSES
.
3) Find the complement expert matrices.
4) Find the addition expert matrices.
5) Find the adaptation matrices.
6) Compute the
. The top scorer will be chosen as the selector.
Consider the problem of section 5, the GSES
as follows:
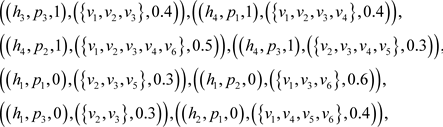
Then we can obtain the expert matrices over GSES
,
,
,
.
And the complement expert matrices are
,
,
,
We complete the remaining steps in the algorithm:
,
,
,
,
,
,
.
Finally, we compute the
as follows:
,
,
,
,
 ,
,
.
Due to
,
then the decision is
.
7. Conclusion
We presented the idea of a generalized soft expert set in this paper and looked at some of its characteristics. On the generalized soft expert set, the complement, union, intersection, AND and OR operations have been defined. This theory is put to use to resolve a decision-making issue. We also present complement, addition, and subtraction operations as well as a definition of the generalized soft expert matrices. Last but not least, we show how the generalized soft expert matrices were used in a decision-making scenario. Two methods are applied in the paper to deal with the same decision problem. Although the conclusions are the same, the use of generalized soft expert matrices is significantly more straightforward when comparing the two methods.