Optimization Approach to Constrained Break Even Points with Respect to Price

Enkhbat Rentsen^1*, Battuvshin Chuluundorj², Tungalag Natsagdorj³

¹Institute of Mathematics and Digital Technology, Mongolian Academy of Sciences, Ulaanbaatar, Mongolia.
²University of Humanities, Ulaanbaatar, Mongolia.
³School of Business, National University of Mongolia, Ulaanbaatar, Mongolia.

DOI: 10.4236/ib.2023.153014                

Abstract

Break even and profitability analysis is a classical and widely used topic in business analysis. Break-Even Point or point of equilibrium is the point of sales volume making neither a profit nor a loss. It is a valuable number to know. Traditional break-even analysis is used to determine how much sales volume your business needs to start making a profit. In this paper, we extend the classical break-even point concept by introducing a new notion of constrained break-even points with respect to prices. In this case, a traditional method of calculating break even point may fail. For this purpose, for finding constrained break-even points, we propose an optimization approach based on solving convex and nonconvex optimization problems. Convex minimization and convex maximization algorithms are used. We show that global minimum, local maximum, and stationary points of both problems are the constrained break-even points with respect to price. The proposed approaches illustrated on some fictitious business examples providing numerical results.

Keywords

Business Decision-Making, Break-Even Points, Set of Constrained Break-Even Points, Optimization, Convex Minimization, Convex Maximization

1. Introduction

Break even analysis, as a part of cost-volume-profit analysis of business industry, provides management with important information about the relationship between costs, product volume, and profits. Break even analysis is based on the assumption that all costs can be classified into fixed and variable costs. Fixed costs are constant over the range of the analysis while variable costs are proportional to volume. Break even analysis is used to determine the level of sales which is required to recover all costs incurred during the period. In other words, the break even point is the level at which cost and revenue are equal ( Heisinger & Hoyle, 2012 ).

If sales fall below the break even point, losses will be incurred. Management must determine the break even point to compute the margin of safety, which indicates how much sales may decrease from the targeted level before the company will incur losses. The objective of break even analysis is to determine the volume of sales to achieve a zero profit. There are many works devoted to break even analysis, but most of them deal with one type of product case ( Abdullahi et al., 2017 ; Ankiti et al., 2021 ). However, there is a very simple weighted average contribution margin method developed for multi product case ( Paff, 2021 ). It was shown that, break even analysis is one of the most important tools for management in decision making ( Adedeji & Ituma, 2020 ). In Oppusunggu (2020) , the break even analysis has been applied in all businesses and any industry, whether large or small. The research done in ( Gubio et al., 2022 ) recommended that block industries should use break even analysis for profit maximization purpose. To improve the efficiency of reusable products and obtain an environmental benefit, break even analysis has been used in Cottafava et al. (2021) . Break even analysis for milk production of selected EU countries was done in ( Jurkenaite & Mikelionyte, 2021 ; Syrucek et al., 2022 ). In Neidhardt et al. (2022) , Salam et al., (2021) , Cao et al., (2021) and Abdurofi et al. (2021) break even analysis in the battery production has been analyzed. Uncertainty in parameters, based on uncertainty in the prices, and a risk-return analysis have been examined from a view point of portfolio optimization in Kara et al. (2019) . A Joint Products CVP Analysis case was developed in Enyi (2019) .

Taking into account the existing literature on break even analysis, it seems that less attention has been paid to constrained break even points which arise naturally from the traditional break even analysis by imposing constraints on parameters of cost-volume-profit analysis. To fulfill this gap, we propose a new mathematical methodology based on optimization methods. On the other hand, we continue a recent research done in Rentsen & Natsagdorj (2023) on profitability analysis of business. In this paper, we define constrained break even points with respect to price. The proposed approach was illustrated on some examples.

The paper is organized as follows. Chapter 2 is devoted to the traditional break even points. A new concept of sets of constrained break even points has been defined in Chapter 3. Chapter 4 is devoted to optimization methods for finding constrained break even points. Convex minimization algorithm has been proposed in Chapter 4. Convex maximization approach has been considered in Chapter 5. The numerical implementation of the proposed approaches has been illustrated in Chapter 6.

2. Traditional Break Even Points

The total profit of a company for a multi-product case can be written as

$\pi ={\displaystyle \underset{j=1}{\overset{n}{\sum }}}{p}_j{x}_j-{\displaystyle \underset{j=1}{\overset{n}{\sum }}}{c}_j{x}_j-F$ (1)

where, $\pi$ -total profit, $p_j$ -price per unit of j-th product, $x_j$ -quantity of product sold, $c_j$ -variable cost per unit of j-th product, F-total fixed cost, $p_j>c_j$ . By definition of break even points

$\pi =0.$ (2)

Define a set of break even points with respect to price as follows:

$B_p=\left\{p\in R^n|{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left(p_j-{\bar{c}}_j\right){\bar{x}}_j=F,x_j\ge 0,j=1,\cdots ,n\right\}$ (3)

where, average products and variable costs ${\bar{x}}_j,{\bar{c}}_j,j=1,\cdots ,n$ , and F are fixed. Note that the following inequalities must be satisfied:

${\bar{c}}_j\le p_j^{\min }\le p_j\le p_j^{\max }\le \frac{F+{\bar{c}}_j{\bar{x}}_j}{{\bar{x}}_j},\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}j=1,\cdots ,n.$ (4)

In order to find break even points analytically, we construct points

$A_j\left(0,0,\cdots ,\frac{F+{\bar{c}}_j{\bar{x}}_j}{{\bar{x}}_j},\cdots ,0\right),j=1,\cdots ,n$

such that $A_j\in B_p$ .

Define the set of convex combinations of $A_j$ in the following.

$C=\left\{p\in R^n|\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}p={\displaystyle \underset{j=1}{\overset{n}{\sum }}}{\alpha }_j{A}_j,{\displaystyle \underset{j=1}{\overset{n}{\sum }}}{\alpha }_j=1,{\alpha }_j\ge 0,j=1,\cdots ,n\right\}.$ (5)

Lemma 2.1. $B_p=C$

Proof. We can easily check that $C\subset B_p$ . Indeed, take any point $p\in C$ such that $p={\displaystyle {\sum }_{j=1}^n}{\alpha }_j{A}_j$ , ${\displaystyle {\sum }_{j=1}^n}{\alpha }_j=1$ , ${\alpha }_j\ge 0$ then, we compute

${\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left(p_j-{\bar{c}}_j\right){\bar{x}}_j={\displaystyle \underset{j=1}{\overset{n}{\sum }}}{\alpha }_j\left(\frac{F+{\bar{c}}_j{\bar{x}}_j}{{\bar{x}}_j}-c_j\right){\bar{x}}_j=F$

which shows $C\subset B_p$ . Inverse conclusion $B_p\subset C$ is obvious.

Lemma 2.1 allows us to find break even points as many as possible as convex combinations of points $A_j,j=1,\cdots ,n$ . Similarly, we can introduce the sets of break even points with respect to CVP parameters. For instance, the set of break even points with respect to cost c is:

$B_c=\left\{c\in R^n|\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left({\bar{p}}_j-c_j\right){\bar{x}}_j=F,c_j\ge 0,j=1,\cdots ,n\right\}$

where, 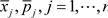and F are fixed.

3. Constrained Break Even Points

Assume that average volumes of products and variable costs ${\bar{x}}_j,{\bar{c}}_j,j=1,\cdots ,n$ , and F are given.

We introduce the set $D_p$ , called the set of constrained break even points with respect to price, defined as follows:

$D_p=\left\{p\in R^n|\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left(p_j-{\bar{c}}_j\right){\bar{x}}_j=F,p_j^{\min }\le p_j\le p_j^{\max },j=1,\cdots ,n\right\},$

where, $p_j^{\min }$ and $p_j^{\max }$ are low and upper bounds of prices for j-th product $j=\mathrm{1,}\cdots \mathrm{,}n$ , which satisfy conditions (4).

The main difference between traditional break even analysis and proposed optimization approach is the following. In traditional approach a single break even point can be found satisfying the equation $\pi =0$ for fixed cost and products. The break even point in the literature is

${\tilde{p}}_j={\alpha }_j\left(\frac{F+{\bar{c}}_j{\bar{x}}_j}{{\bar{x}}_j}\right).$ (6)

Also, the points extended by (6):

$p={\displaystyle \underset{j=1}{\overset{n}{\sum }}}{\alpha }_j\left(\frac{F+{\bar{c}}_j{\bar{x}}_j}{{\bar{x}}_j}\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}{\alpha }_j=1,j=1,\cdots ,n.$

are break even points in a traditional sense, but may not be constrained break even points for certain ${\alpha }_j$ . In optimization approach, we find a set of constrained break even points with respect to prices by solving convex minimization algorithm.

4. Convex Programming Approach

In order to find a feasible point in the set of constrained break even points, we need to solve the following convex programming problem.

$\underset{x\in D_p}{\min }f={\Vert x-u^0\Vert }^2$ (7)

where, $u^0\in R^n$ is an arbitrary initial point and

$D_p=\left\{p\in R^n|\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left(p_j-c_j\right)x_j=F,x_j^{\min }\le p_j\le p_j^{\max },\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}j=1,\cdots ,n\right\}.$

If we solve problem (7) for different initial points $u^j,j=1,\cdots ,m$ , then its corresponding solutions $x^j,j=1,\cdots ,m$ , are constrained break even points in $D_p$ . That is,

$\underset{x\in D_p}{\min }{\Vert x-u^j\Vert }^2={\Vert x^j-u^j\Vert }^2,\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}j=1,\cdots ,m.$

It is obvious that the points $z_{\alpha }$ constructed by

$z_{\alpha }={\displaystyle \underset{j=1}{\overset{m}{\sum }}}{\alpha }_j{x}^j$

for any ${\alpha }_j$ such that

${\displaystyle \underset{j=1}{\overset{m}{\sum }}}{\alpha }_j=1,{\alpha }_j\ge 0,j=1,\cdots ,m$

are also the constrained break even points.

Since the set of constrained break even points is compact consisting of linear constraints, for solving problem (7), we use Conditional Gradient Method ( Bertsekas, 1999 ).

Algorithm of Conditional Gradient Method is the following.

Algorithm of Conditional Gradient Method (CGA1)

Step 1: Choose an arbitrary point $x^0\in R^n$ . $x^k\in R^n,k=0$

Step 2: Solve a linear programming problem

$\underset{x\in D_p}{\min }\langle f^{\prime }\left(x^k\right)\mathrm{,}x\rangle$

Let ${\bar{x}}^k$ be a solution, that is

$\underset{x\in D_p}{\min }\langle f^{\prime }\left(x^k\right)\mathrm{,}x\rangle =\langle f^{\prime }\left(x^k\right)\mathrm{,}{\bar{x}}^k\rangle$

Step 3: Compute a value of ${\eta }_k$ as

${\eta }_k=\langle f^{\prime }\left(x^k\right)\mathrm{,}{\bar{x}}^k-x^k\rangle$

Step 4: If ${\eta }_k=0$ then stop, $x^k$ is a solution to problem; Otherwise, go to next step.

Step 5: Consruct a ray for $\alpha \in \left[\mathrm{0,1}\right]$ :

$x^k\left(\alpha \right)=x^k+\alpha \left({\bar{x}}^k-x^k\right)\mathrm{.}$

Choose ${\alpha }_k$ from the condition $f\left(x^k\left(\alpha \right)\right)<f\left(x^k\right)$ or

$\underset{\alpha \in \left[\mathrm{0,1}\right]}{\min }f\left(x^k\left(\alpha \right)\right)=f\left(x^k\left({\alpha }_k\right)\right)\mathrm{.}$

Step 6: Construct a next approximation point $x^{k+1}$

$x^{k+1}=x^k+{\alpha }_k\left({\bar{x}}^k-x^k\right)\mathrm{,}$

set $k:=k+1$ , and go to step 2.

Note that in order to find a stepsize ${\alpha }_k$ in Step 5 of the algorithm, first we need to solve unconstrained one dimensional quadratic minimization problem:

$\underset{\alpha \in R}{\min }f\left(x^k\left(\alpha \right)\right)=f\left(x^k\left(\bar{\alpha }\right)\right)\mathrm{.}$

Since $f\left(x^k\left(\alpha \right)\right)$ is strongly convex quadratic function, its global minimum computed easily as

$\bar{\alpha }=-\frac{{\eta }_k}{{\Vert {\bar{x}}^k-x^k\Vert }^2}\mathrm{.}$

Now, taking into account $\alpha \in \left[\mathrm{0,1}\right]$ , we conclude that

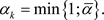
Theorem 4.1. ( Bertsekas, 1999 ) The sequence $\left\{x^k,k=0,1,\cdots \right\}$ generated by the algorithm-CGA1 is a minimizing sequence, that is ${\lim }_{k\to \infty }f\left(x^k\right)={\min }_{x\in D_p}f\left(x\right)$ .

Any limit point of $x^k$ is a solution to problem:

$\underset{k\to \infty }{\lim }{x}^k=x^{*}=\arg {\min }_{x\in D_p}f\left(x\right).$

5. Convex Maximization Approach

In order to find constrained break even points in $D_p$ , it is also possible to solve the following convex maximization problem.

$\underset{x\in D_p}{\max }\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}Q={\Vert x-u^0\Vert }^2$ (8)

where, $u^0\in R^n$ is an arbitrary initial point.

Unlike problem (7), this problem is nonconvex and has a finite number of local maximum points.

If we solve problem (8) for different initial points $u^j\mathrm{,}j=\mathrm{1,}\cdots \mathrm{,}m$ , then its corresponding local solutions or stationary points $x^j\mathrm{,}j=\mathrm{1,}\cdots \mathrm{,}m$ , are constrained break even points in $D_p$ . That is,

$\underset{x\in D_p}{\max }{\Vert x-u^j\Vert }^2={\Vert x^j-u^j\Vert }^2,\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}j=1,\cdots ,m.$

It is clear that the points $z_{\alpha }$ constructed by

$z_{\alpha }={\displaystyle \underset{j=1}{\overset{m}{\sum }}}{\alpha }_j{x}^j$

for any ${\alpha }_j$ such that

${\displaystyle \underset{j=1}{\overset{m}{\sum }}}{\alpha }_j=1,{\alpha }_j\ge 0,j=1,\cdots ,m$

are also the constrained break even points.

Since problem (8) is nonconvex, Algorithm of Conditional Gradient Method cannot always guarantee finding global solutions to the convex maximization problem, but may provide local solutions or stationary points for the problem. Then algorithm of conditional gradient method (CGA1) is modified for the problem as follows.

Algorithm of Conditional Gradient Method (CGA2)

Step 1: Choose an arbitrary point $x^0\in R^n$ . $x^k\in R^n,k=0$

Step 2: Solve a linear programming problem

$\underset{x\in D_p}{\max }\langle Q^{\prime }\left(x^k\right)\mathrm{,}x\rangle$

Let ${\bar{x}}^k$ be a solution, that is

$\underset{x\in D_p}{\max }\langle Q^{\prime }\left(x^k\right)\mathrm{,}x\rangle =\langle Q^{\prime }\left(x^k\right)\mathrm{,}{\bar{x}}^k\rangle$

Step 3: Compute a value of ${\eta }_k$ as

${\eta }_k=\langle Q^{\prime }\left(x^k\right)\mathrm{,}{\bar{x}}^k-x^k\rangle$

Step 4: If ${\eta }_k=0$ then stop, $x^k$ is a solution to problem; Otherwise, go to next step.

Step 5: Consruct a ray for $\alpha \in \left[\mathrm{0,1}\right]$ :

$x^k\left(\alpha \right)=x^k+\alpha \left({\bar{x}}^k-x^k\right)\mathrm{.}$

Choose ${\alpha }_k$ from the condition $f\left(x^k\left(\alpha \right)\right)>f\left(x^k\right)$ by the bisection method.

Step 6: Construct a next approximation point $x^{k+1}$

$x^{k+1}=x^k+{\alpha }_k\left({\bar{x}}^k-x^k\right)\mathrm{,}$

set $k:=k+1$ , and go to step 2.

Theorem 5.1. ( Boyd & Vandenberghe, 2002 ) The sequence $\left\{x^k,k=0,1,\cdots \right\}$ generated by the algorithm-CGA2 converges to a stationary point of problem (8), that is

$\underset{k\to \infty }{lim}\langle Q^{\prime }\left(x^k\right)\mathrm{,}{\bar{x}}^k-x^k\rangle =0.$

6. Numerical Implementation

In order to illustrate the proposed approaches numerically, we use company's parameters such as price, volume, variable cost and fixed cost.

Consider a company with the fixed cost of $F=14000.0$ and parameters given in Table 1. Also, average products ${\bar{x}}_1=21$ , ${\bar{x}}_2=12$ and, ${\bar{x}}_3=50$ are given. Using these parameters, in Table 2, we find constrained break even points with respect to price by convex minimization algorithm. Constrained break even points have been found by Algorithm-CGA1 for different 10 initial points of x⁰.

In Table 3, we provide constrained break even points found by convex maximization algorithm for 10 different initial points of x⁰. In this case Algorithm

Table 1. Parameters.

Table 2. Convex minimization.

Table 3. Convex maximization.

CGA2 has found only two constrained break even points since the problem as the convex maxmimization has a finite number of boundary solutions.

7. Conclusion

In this paper, a new notion of constrained break points with respect to price has been introduced. The constrained break even points arise when lower and upper constraints are imposed on the price. In this case, a traditional method for defining break even points may fail even for a single product. We propose a new methodology for finding constrained break even points for multi-product case using optimization methods. The proposed approaches were tested on some examples providing numerical results obtained on Matlab. Similarly, the proposed approach can be easily extended for the constrained break even points with respect to a variable cost. It can be examined in a next paper.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Abdullahi, S. R., Sulaimon, B. A., Mukhtar, I. S., & Musa, M. H. (2017). Cost-Volume-Profit Analysis as a Management Tool for Decision Making in Small Business Enterprise within Bayero University, Kano. IOSR Journal of Business and Management, 19, 40-45. https://doi.org/10.9790/487X-1902014045
[2]	Abdurofi, I., Ismail, M. M., Ismail, N. W., & Abdullah, A. M. (2021). Application of Cost-Benefit and Break Even Analysis for the Development of Stingless Bees Farming in Malaysia. International Journal of Business and Society, 22, 846-861. https://doi.org/10.33736/ijbs.3763.2021
[3]	Adedeji, E. A., & Ituma, N. K. (2020). Break Even Analysis as a Management Tool for Decision Making in Babcock University Water Corporation. European Journal of Business and Management, 12, 159-181.
[4]	Bertsekas, D. (1999). Nonlinear Programming. Athena Scientific.
[5]	Boyd, S., & Vandenberghe, L. (2002). Convex Optimization. Cambridge University Press.
[6]	Cao, Y., Mohammadian, M., Pirouzfar, V., Su, C.-H., & Khan, A. (2021). Break Even Point Analysis of Liquefied Natural Gas Process and Optimization of Its Refrigeration Cycles with Technical and Economic Considerations. Energy, 237, 1461-1477. https://doi.org/10.1016/j.energy.2021.121643
[7]	Cottafava, D., Costamagna, M., Baricco, M., Corazza, L., Miceli, D., & Riccardo, L. E. (2021). Assessment of the Environmental Break-Even Point for Deposit Return Systems through an LCA Analysis of Single-Use and Reusable Cups. Sustainable Production and Consumption, 27, 228-241. https://doi.org/10.1016/j.spc.2020.11.002
[8]	Enyi, E. P. (2019). Joint Products CVP Analysis—Time for Methodical Review. Journal of Social and Political Sciences, 2, 1288-1297. https://doi.org/10.31014/aior.1992.02.04.168
[9]	Gubio, Z. D., Mustapha, L. O., & Agbi, S. E. (2022). The Effect of Break-Even-Point Analysis in Decision Making in some selected Block Industries within Kaduna Metropolis. Journal of Research in Business and Management, 10, 22-32.
[10]	Heisinger, K., & Hoyle, J. (2012). Managerial Accounting. Saylor Foundation.
[11]	Jurkėnaitė, N., & Mikelionyte, D. (2021). Raw Milk Price Transmission in the Selected EU Countries. Scientific Papers Series Management, Economic Engineering in Agriculture and Rural Development, 21, 477-482.
[12]	Kara, G., Özmen, A., & Weber, G.-W. (2019). Stability Advances in Robust Portfolio Optimization under Parallelepiped Uncertainty. Central European Journal of Operations Research, 27, 241-261. https://doi.org/10.1007/s10100-017-0508-5
[13]	Neidhardt, M., Mas-Peiro, J., Schulz-Moenninghoff, M., Pou, J. O., Gonzalez-Olmos, R., Kwade, A., & Schmuelling, B. (2022). Forecasting the Global Battery Material Flow: Analyzing the Break-Even Points at Which Secondary Battery Raw Materials Can Substitute Primary Materials in the Battery Production. Applied Sciences, 12, Article No. 4790. https://doi.org/10.3390/app12094790
[14]	Oppusunggu, L. S. (2020). Importance of Break-EVEN Analysis for the Micro, Small and Medium Enterprises. International Journal of Research-GRANTHAALAYAH, 8, 212-218. https://doi.org/10.29121/granthaalayah.v8.i6.2020.502
[15]	Paff, L. (2021). Financial and Managerial Accounting. Pressbooks.
[16]	Rentsen, E., & Natsagdorj, T. (2023). A Sphere Packing Approach to Break Even and Profitability Analysis. Journal of Indusdrial and Management Optimization, 19, 3436-3443. https://doi.org/10.3934/jimo.2022237
[17]	Salam, M., Fudjaja, L., Darma, R., Diansari, P., Viantika, N. M., & Nafisa, M. (2021). Revenue Analysis of Mobile Rice Milling Business. IOP Conference Series: Earth and Environmental Science, 681, Article ID: 012095. https://doi.org/10.1088/1755-1315/681/1/012095
[18]	Sharma, A., Kohar, A., Jakhar, S. K., & Sonia (2021). Profit Maximizing Hub Location Problem in the Airline Industry under Coopetition. Computers & Industrial Engineering, 160, 107-563. https://doi.org/10.1016/j.cie.2021.107563
[19]	Syrůček, J., Bartoň, L., & Burdych, J. (2022). Break-Even Point Analysis for Milk Production—Selected EU Countries. Agricultural Economics, 68, 199-206. https://doi.org/10.17221/40/2022-AGRICECON