Modelling Dependence of Cryptocurrencies Using Copula Garch

Eric M. Kimani¹, Anthony Ngunyi², Joseph K. Mungatu³

¹Department of Mathematics, Pan African University, Nairobi, Kenya.
²Department of Mathematics, Statistics and Actuarial Sciences, Dedan Kimathi University of Science and Technology, Nyeri, Kenya.
³Department of Statistics and Actuarial Sciences, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya.

DOI: 10.4236/jmf.2023.133020                

Abstract

Cryptocurrencies are considered to be among the most disruptive innovations done in the financial sector within the last decade. It is a digital asset that is designed to serve as a medium of exchange using cryptography. Financial modeling of cryptocurrencies is needed in order to determine the presence of dependence between currencies. Copulas functions assist in modeling dependency structure by making it possible to separate marginal distributions of a given multivariate distribution. The purpose of the study was to model dependencies of cryptocurrencies using copula Garch. The study proposed the use of copula Garch model to model the dependence of cryptocurrency price data. Bivariate copula was extended to Bivariate Copula Garch in order to model prices and measure the cryptocurrency dependence. Prices of the four cryptocurrencies (Bitcoin, Binance, Litecoin and Dogecoin) were analyzed to establish whether there exists any dependency. The results showed standard Garch (1,1) under the highly flexible ARMA-GARCH model was appropriate to identify the true patterns of index returns. Fitting the copula standard Garch (1,1) model to the currencies, it was observed that the pair Litecoin and Bitcoin has the highest tail dependence among the selected cryptocurrencies, which implies that change in prices of Litecoin will influence the prices of Bitcoin and vice versa is true. Optimization of the cryptocurrencies showed that Dogecoin has the best optimization. The results of this study indicate that investing on Dogecoin significantly reduces risk irrespective of significant correlation among Litecoin, Bitcoin and Binance. Standard Garch (1,1) is the best in identifying dependence between the cryptocurrencies.

Keywords

Cryptocurrency, Copula Garch, GARCH-Model, Dependence

1. Introduction

Cryptocurrency is a virtual or digital currency secured through cryptography; hence it is safe from counterfeit [1] . Blockchain technology has been used in a decentralizing cryptocurrency network. It is not issued by the government, thus immune from interference and manipulation by the central banking system in a country according to [2] . This currency is mostly used as a medium of exchange in online trading where digital ledgers are applied. There is a need for strong cryptography in securing transaction record entries. The transactions do not exist physically, and the individuals involved may not know each other physically [3] . Bitcoin which was the first cryptocurrency, released in 2019 by open-source software, has consistently been used in many countries. It is still famous; however, various alternative coins have been created afterward, with some being bitcoin clones or forks. Litcoin, Namecoin, Peercoin, and Cardano are some of Bitcoin’s competing cryptocurrencies. To model and measure the dependencies in cryptocurrencies, the study proposed the use of copulas where copulas have been distinguished in different families namely, Elliptical copulas, Archimedean copulas, Empirical copulas and Periodic copulas. Each family has different types of copulas depending with the distribution of the functions [4] . Copulas is relevant in finance mainly in portfolio management, risk management, derivative pricing and optimization.

The autoregressive conditional heteroscedastic (ARCH) model [5] and generalized conditional heteroscedastic (GARCH) model that was stated by [6] have been used widely financial time series to model return variance processes. It has been observed that financial time series data exhibit heavy tails and extreme value theory (EVT) has been established as a useful tool in modelling tail behaviour of the distribution instead of the entire distribution. Extreme events study is key in financial risk management mainly to investors since it gives rare events that have catastrophic effects which may comprise of extreme default losses, market crashes and currency crisis. This GARCH-EVT combination has an advantage of being able to capture conditional heteroskedasticity in the given data through the GARCH framework, and at the same time apply EVT method to model the extreme tail behaviour. Linear correlation has been used as a measure of dependence for multivariate variable while calculating the dependence between different asset returns. Gaussian, log-normal and Student-t are multivariate distributions that have been widely used. However, they cannot be applied in the case of assymetrical data. Copulas provides a solution in addressing dependence structure problem, and it offers flexibility unlike correlation approach [7] , hence providing an opportunity for one to examine separately marginal distributions from random variables dependency structures.

This study’s primary objective is to fit the most appropriate GARCH model in modelling cryptocurrencies data, examine the dependence structure of Cryptocurrencies using Copula GARCH model and select a portfolio of cryptocurrencies with the best optimization. Therefore, this study’s main contribution was to model cryptocurrency and selection of the cryptocurrency with the best optimization using Copula standard Garch model.

The paper is organized as follows: Section 2 describes the methods of the study; Section 3 presents main results, simulation study results; Section 4 presents conclusion and suggestions for further research.

2. Methods

2.1. The ARMA-Model

ARMA models can be used in modeling trends and seasonality in time series data. They are mostly constructed on white noise basis whose variance is denoted as ${\sigma }_Z^2$ . These models belong to a class of stationary univariate time series models which is utilized in a time series to capture (linear) serial dependence. These combines the two classes of time series models, namely; moving average (MA) process and autoregressive process (AR) that results in a parsimonious polynomial model which combines both moving averages and autoregressive models.

Definition The ARMA(p, q) process Let ${\left(Z_t\right)}_{t\in \mathbb{Z}}~WN\left(\mathrm{0,}{\sigma }^2\right)$ for some, ${\sigma }^2>0$ be a white noise sequence on $\left(\Omega \mathrm{,}F\mathrm{,}P\right)$ . Let $p,q\in \mathbb{Z}$ and ${\varphi }_1\mathrm{,}\cdots \mathrm{,}{\varphi }_p$ and ${\theta }_1\mathrm{,}\cdots \mathrm{,}{\theta }_q\in ℝ$ . Then we have any stationary time series ${\left(X_t\right)}_{t\in \mathbb{Z}}$ on $\left(\Omega \mathrm{,}F\mathrm{,}P\right)$ satisfying $E\left[X_0\right]=0$ and

$X_t-{\varphi }_1{X}_{t-1}-\cdots -{\varphi }_p{X}_{t-p}=Z_t+{\theta }_1-Z_{t-1}+{\theta }_q-Z_{t-q}\forall t\in \mathbb{Z}$ (1)

${\left(X_t\right)}_{t\in \mathbb{Z}}$ being an ARMA(p, q) process whose mean $\mu$ ,having ${\left(X_t\mu \right)}_{t\in \mathbb{Z}}$ as an ARMA(p, q) process, $\mu \in ℝ$ . We can write Equation (1) in compact notation that is based on the backshift operator which is given as follows

$\Phi \left(B\right)X_t=\Theta \left(B\right)Z_t\forall t\in \mathbb{Z}$ (2)

where $\Phi \left(B\right)=1-{\varphi }_{1}B-\cdots -{\varphi }_p{B}^p$ is given as the “autoregressive polynomial of degree p” and we have $\Theta \left(B\right)=1+{\theta }_{1}B+\cdots +{\theta }_q{B}^q$ given as the “moving average polynomial of degree q”. One can either use only the moving average or the autoregressive part of a given ARMA equation.

Definition (AR(p)-process)

In Equation (1), let q = 0 thus $\Theta \left(z\right)=1$ . Hence the equation can be simplified to

$X_t-{\varphi }_1{X}_{t-1}-\cdots -{\varphi }_p{X}_{t-p}=Z_t\text{for}\text{all}t\in \mathbb{Z}$

$\theta \left(B\right)X_t=Z_t\text{for}\text{all}t\in \mathbb{Z}$

Given that p = 1, then we have the AR(1)-process

$X_t-{\varphi }_1{X}_{t-1}=z_t$

Theorem 3.1. Given that $\Phi \left(z\right)\ne 0$ $\forall z\in ℂ$ with $\left|z\right|\le 1$ , then we have the ARMA model as given in Equation (1) having unique stationary solution

$X_t={\displaystyle {\sum }_{j=-\infty }^{\infty }{\Psi }_j{Z}_{t-j}}\forall t\in \mathbb{Z}$ (3)

where we can determine the coefficients ${\left({\Psi }_j\right)}_{j\in \mathbb{Z}}$ by

$\Theta \left(z\right)\Phi {\left(z\right)}^{-1}={\displaystyle {\sum }_{j=-\infty }^{\infty }{\Psi }_j{Z}^j}=\Psi \left(z\right)\text{,}\text{with}{r}^{-1}\left|z\right|<r$ (4)

for any $r>1$

Definition(MA(q)-process) In Equation (1), let p = 0 and hence $\Phi \left(z\right)=1$ . The equation then simplifies to

$X_t=Z_t+{\theta }_1{Z}_{t-1}+\cdots +{\theta }_q{Z}_{t-q}\text{for}\text{all}t\in \mathbb{Z}$

$X_t=\Theta \left(B\right)Z_t\text{for}\text{all}t\in \mathbb{Z}$

For q = 1, then we get the MA(1)-process

$X_t=Z_t+{\theta }_1{Z}_{t-1}.$

2.2. The GARCH-Model

The Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model which was introduced by [6] is a generalized form of the ARCH models which was introduced by [5] . The Autoregressive (AR) process considers observations made in the past up to a given degree into the present and utilizes a feedback mechanism. GARCH model “conditional component” implies variance dependence on immediate past, while “heteroscedasticity” implies time varying volatility. A standard ARCH(p) process that has p lag terms and is designed to capture volatility clustering which can be expressed as

${\sigma }_t^2={\alpha }_0+{\displaystyle {\sum }_{i=1}^p{\alpha }_i{\epsilon }_{t-i}^2}$ (5)

where ${\alpha }_0>0$ and ${\alpha }_i\ge 0$ , for $i=1,2,\cdots ,p$ which ensures finite variance and we have ${\alpha }_1+\cdots +{\alpha }_p<1$ in stationarity. Large persistence in volatility leads the ARCH model to require a large number of lags p which can be used to fit the data.

Definition GARCH(p, q) The stochastic process ${\left({\epsilon }_t\right)}_{t\in \mathbb{Z}}$ on a probability space $\left(\Omega \mathrm{,}F\mathrm{,}P\right)$ where $\Omega$ is given by a GARCH(p, q) process if it gives a solution to ${\epsilon }_t={\sigma }_t{z}_t$ with ${\left(Z_t\right)}_{t\in \mathbb{Z}}$ being an iid sequence and the conditional variance of a GARCH(p, q) being

${\sigma }_t^2={\alpha }_0+{\displaystyle {\sum }_{i=1}^p{\alpha }_i{\epsilon }_{t-1}^2}+{\displaystyle {\sum }_{j=1}^p{\beta }_j{\sigma }_{t-j}^2}$ (6)

The GARCH model parameters must satisfy the following conditions in order for conditional variance to be finite and positive

${\alpha }_0>0$ , ${\alpha }_i\ge 0,i=1,\cdots ,p$ and ${\beta }_j\ge 0$ for $j=1,\cdots ,q$

Different versions and extensions have been made on GARCH model. Equation (6) gives a symmetric model which implies positive and negative shocks have the similar volatility effects. However, positive (negative) innovations to volatility have been suggested to correlate with negative (positive) innovations to returns by empirical literature.

We intend to consider two extensions of the standard GARCH model in order to account for leverage effects and symmetry [8] gave a proposal of a Boolean indicator being introduced in the GARCH Equation (6). We get the GJR-GARCH model conditional variance being given by

${\sigma }_t^2={\alpha }_0+{\displaystyle {\sum }_{i=1}^p{\alpha }_i{\epsilon }_{t-1}^2}+{\displaystyle {\sum }_{i=1}^p{\epsilon }_i\Psi \left({\epsilon }_{t-1}\right){\epsilon }_{t-1}^2}+{\displaystyle {\sum }_{j=1}^q{\beta }_j{\sigma }_{t-j}^2}$ (7)

where we have $\Psi \left({\epsilon }_t\right)=1$ given that 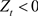and it is 0 if $Z_t\ge 0$ .

The term ${\epsilon }_i\Psi \left({\epsilon }_{t-1}\right)$ also captures the shock in addition to the symmetrical GARCH(p, q) model which is given in (6). GJR-GARCH model is normally used to nest the standard GARCH model by equating all the gi coefficients to zero, hence reducing the GJR-GARCH model to the standard GARCH model. ${\alpha }_0\mathrm{,}{\alpha }_i\mathrm{,}{\beta }_j$ and $\left({\alpha }_i+{\epsilon }_i\right)$ parameters are constrained to be non-negative in order to ensure positivity and stationarity of the GARCH specifications. Non-negativity constraints are too restrictive as argued by [9] , this advocated inclusion of asymmetric volatility response to innovations with the EGARCH model in Nelson’s exponential GARCH model, it is given as

$\log \left({\sigma }_t^2\right)={\alpha }_0+{\displaystyle {\sum }_{i=1}^p{\alpha }_i\left|Z_{t-1}\right|}+{\displaystyle {\sum }_{i=1}^p{\epsilon }_i{Z}_{t-1}}+{\displaystyle {\sum }_{j=1}^q{\beta }_j\log \left({\sigma }_{t-j}^2\right)}$ (8)

Parameters ${\epsilon }_i$ with negative ${\epsilon }_i$ is used to capture asymmetry, higher impact on valatility are experienced in negative shocks than positive shocks. Marginal distributions of standardized residuals $z_t$ should be specified in order to complete univariate model specification.

2.3. Copulas and Dependence Structure

2.3.1. Definition of Copulas and Its Properties

Definition Let C be a copula of a multivariate PDF which is defined on ${\left[\mathrm{0,1}\right]}^n$ , while its variables marginal probability distribution are uniformly distributed in [0, 1] [10]

Definition For a 2-dimensional copula we have a function $C:\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right]$ , which fulfils:

1) For every $a,b\in \left[0,1\right]$ :

$C\left(a,0\right)=C\left(0,b\right)=0$

2) For every $a,b\in \left[0,1\right]$ :

$C\left(a\mathrm{,1}\right)\text{and}C\left(\mathrm{1,}b\right)=b$

3) For every $a_1\mathrm{,}{a}_2\mathrm{,}{b}_1\mathrm{,}{b}_2\in \left[0,1\right]$ with $a_1$ and $\le a_2$ and $b_1\le b_2$ :

$C\left(u_2\mathrm{,}{v}_2\right)-C\left(u_2\mathrm{,}{v}_1\right)-C\left(u_1\mathrm{,}{v}_2\right)+C\left(u_1\mathrm{,}{v}_1\right)=C\left(\mathrm{0,}v\right)\ge 0$

Functions fulfilling the first property are referred to as grounded. Implying, that for both outcomes the joint probability is zero given that the marginal probability of either outcome is zero. The second property is known as the copula boundary condition while the third property is known as two-dimensional analogue for a function that is one-dimensional and non-decreasing. Such a function is called 2-increasing.

The theorem presented next establishes the continuity of copulas via a Lipschitz condition on $\left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]$ :

Theorem 1 Let C to be a copula. Then we have that for every $a_1\mathrm{,}{a}_2\mathrm{,}{b}_1\mathrm{,}{b}_2\in \left[0,1\right]$

$\left|C\left(a_2\mathrm{,}{b}_2\right)\right|-\left|\left(a_1\mathrm{<mo>\; ;\; </mo>}{b}_1\right)\right|\le \left|a_2\mathrm{,}{a}_1\right|+\left|b_2{b}_1\right|$ (9)

Theorem 2 Let C to be a copula. Then we have that for every $a\in \left[\mathrm{0,1}\right]$ . We have the partial derivative $\partial C/\partial$ a existing in almost all $v\in \left[\mathrm{0,1}\right]$ . Given that a and b, one exists for almost all $b\in \left[\mathrm{0,1}\right]$ . having a and b one has

$0\le \frac{\partial }{\partial v}C\left(a\mathrm{,}b\right)\le 1$ (10)

The partial derivative analogous statement is true for $\partial C/\partial u$ . In addition, we have the function $a{\stackrel{C}{\to }}_b\left(a\right)\equiv \partial C\left(a\mathrm{,}b\right)/\partial b$ and $b{\stackrel{C}{\to }}_{a}b\equiv \partial C_{a}b/\partial a$ on [0, 1] being defined and non-decreasing in almost everywhere .

Definition

Copula density. We let C to be a two times and two-dimensional partial differentiable copula, therefore we have the function $c:{\left[\mathrm{0,1}\right]}^2\to \left[\mathrm{0,1}\right]$ hence

$c\left(a_1\mathrm{,}{a}_2\right)=\frac{{\partial }^{2}C\left(a_1\mathrm{,}{a}_2\right)}{\partial a_1\partial a_2}\mathrm{,}{a}_1\mathrm{,}{a}_2\in \left[\mathrm{0,1}\right]$ (11)

is referred to as copula density for C

The fundamental theorem of copulas theory is key. It is stated by Sklar’s theorem [11] . Sklar’s theorem issues key properties for copulas

Lemma (Sklar’s theorem) [10]

Let $F\left(x_1\mathrm{,}{x}_2\right)$ to be a two dimensional joint probability distribution function for two random variables illustrated as X₁ and X₂ whose marginal distributions are F₁ and F₂. Then we have a 2-dimensional copula C, where by $\forall \left(x_1\mathrm{,}{x}_2\right)\in {ℝ}^2\mathrm{,}\left[F\left(x_1\mathrm{,}{x}_2\right)=C\left(F_1\left(x_1\right)\mathrm{,}{F}_2\left(x_2\right)\right)\right]$ holds. For the continuous F₁ and F₂ and we have C as unique and defined through

$C\left(x_1\mathrm{,}{x}_2\right)=F\left(F_1^{-1}\left(x_1\right)\mathrm{,}{F}_2^{-1}\left(x_2\right)\right)$

Conversely, having C as a copula and marginal distribution functions F₁ and F₂, then we have the function F being defined in equation (iv) as a bivariate joint distribution function whose margins are F₁ and F₂.

From the theorem 3 the bivariate distribution density function $f\left(\right)$ be written in copula form.

$f\left(x_1\mathrm{,}{x}_2\right)=c\left\{F_1\left(x_1\right)\mathrm{,}{F}_2\left(x_2\right)\right\}{f}_1\left(x_1\right)f_2\left(x_2\right)\mathrm{,}{x}_1\mathrm{,}{x}_2\in ℝ$ (12)

Copulas capture only dependency features that are invariant under increasing transformations [12] .

2.3.2. Bivariate Two-Parameter Copula Families

The families of bivariate two-parameter copula are key in capturing dependencies that are more than one such as upper and lower tail dependence or in finding dependence in one of the tails and concordance [13] .

Definition (Bivariate two-parameter copula families)

These copula families take the form

$C\left(a,b\right)=\Psi \left(-\log K\left({\mu }^{-{\Psi }^{-1}}\left(a\right),{\mu }^{-{\Psi }^{-1}}\left(v\right)\right)\right)$ (13)

where we have K being maximal infinite divisible which we can denote as (max-id). [We have K as max-id given that for all a > 0, $K^{\alpha }$ is a cdf] and we have $\Psi$ as a Laplace-transform (LT).

Given that $\delta$ and $\Psi$ are used to parametrize K by parameter $\theta$ (denoted by ${\psi }_{\theta }$ ) then we result to Two-parameter families. Having K increase in its concordance as $\delta$ increases, then definately there is an increase in concordance of C as $\delta$ increases while we have $\theta$ being fixed. It is harder to check concordance ordering, $\delta$ being fixed with $\theta$ varying. K taking the Archimedean copula form, then we have C taking the Archimedean copula form. That is, if $K\left(x\mathrm{,}y\mathrm{<mo>\; ;\; </mo>}\delta \right)={\varphi }_{\delta }\left({\varphi }_{\delta }^{-1}\left(x\right)\right)+{\varphi }_{\delta }\left({\varphi }_{\delta }^{-1}\left(y\right)\right)$ for ${\varphi }_{\delta }$ family, then

$\begin{array}{c}C\left(a,b;\theta ;\delta \right)={\Psi }_{\theta }\left(-\log {\varphi }_{\theta }\left[{\varphi }_{\theta }^{-1}\left({\mu }^{{\Psi }^{-1}}\left(a\right)\right)+{\varphi }_{\delta }^{-1}\left({\mu }^{{\Psi }^{-1}}\left(b\right)\right)\right]\right)\\ ={\eta }_{\theta ,\delta }\left({\eta }_{\theta ,\delta }^{-1}\left(a\right)+{\eta }_{\theta ,\delta }^{-1}\left(b\right)\right),\end{array}$ (14)

where ${\eta }_{\theta \mathrm{,}\delta }^{-1}\left(s\right)={\Psi }_{\theta }(-\log {\varphi }_{\delta }(\; s\; ))$

For $\delta$ being fixed and ${\theta }_2>{\theta }_1$ , with ${\eta }_i={\eta }_{\theta ,\delta },i=1,2$ the ordering of the concordance being $C\left(\cdot \mathrm{<mo>\; ;\; </mo>}{\theta }_1\mathrm{,}\delta \right)$ and $C\left(\cdot \mathrm{<mo>\; ;\; </mo>}{\theta }_2\mathrm{,}\delta \right)$ could then be established through showing that $\omega ={\eta }_2^{-1}\circ {\eta }_1$ is superadditive.

BB1-copula

The definition of BB1-copula is given by

$\begin{array}{c}C\left(a,b;\theta ;\delta \right)={\left\{1+{\left[{\left(a^{-\theta }-1\right)}^{\delta }+{\left(b^{-\theta }-1\right)}^{\delta }\right]}^{\frac{1}{\delta }}\right\}}^{-\frac{1}{\theta }}\\ =\eta \left({\eta }^{-1}\left(a\right)\right)+\eta \left({\eta }^{-1}\left(b\right)\right)\theta >0,\delta \ge 1\end{array}$ (15)

where

$\eta \left(s\right)={\eta }_{\theta ,\delta }\left(s\right)={\left(1+s^{\frac{1}{\theta }}\right)}^{-\frac{1}{\theta }}$

We have the copula density being

$\begin{array}{c}C\left(a,b;\theta ;\delta \right)={\left\{1+{\left[{\left(a^{-\theta }-1\right)}^{\delta }+{\left(b^{-\theta }-1\right)}^{\delta }\right]}^{\frac{1}{\delta }}\right\}}^{-\frac{1}{\theta }-2}\\ \times {\left[{\left(-\theta -1\right)}^{\delta }+{\left(b^{-\theta }-1\right)}^{\delta }\right]}^{\frac{2}{\delta }-2}\\ \times \left\{\theta \delta +1+\theta \left(\delta -1\right){\left[\left(a^{-\theta }-1\right)+{\left(b^{-\theta }-1\right)}^{\delta }\right]}^{-\frac{1}{\delta }}\right\}\\ \times {\left(a^{-\theta }-1\right)}^{\delta -1}{a}^{-\theta -1}{\left(b^{-\theta }-1\right)}^{\delta -1}{b}^{-\theta -1}\end{array}$ (16)

We consider BB1-copula as an example of a bivariate Archimedean copula whose generator function is $\varphi \left(s\mathrm{<mo>\; ;\; </mo>}\theta \mathrm{,}\delta \right)={\left(s^{-\theta }-1\right)}^{\delta }$ .

BB7-copula

The BB7-copula, is at times considered as Joe-Clayton copula, with a similar structure as the one of the BB1-copula, The Archimedean generator function is given by $\varphi \left(s\mathrm{<mo>\; ;\; </mo>}\theta \mathrm{,}\delta \right)={\left[1-{\left(1-s\right)}^{\theta }\right]}^{-\delta }-1$ whereby it is defined as

$C_{JC}\left(a\mathrm{,}b\mathrm{<mo>\; ;\; </mo>}\theta \mathrm{<mo>\; ;\; </mo>}\delta \right)\mathrm{<mo>\; =\; </mo>1}-{\left(1-{\left[1-{\left(1-a\right)}^{\theta }\right]}^{-\delta }+{\left[1-{\left(1-b\right)}^{\theta }\right]}^{-\theta }-1^{-\frac{1}{\theta }}\right)}^{\frac{1}{\theta }}$

$\eta \left({\eta }^{-1}\left(a\right)+{\eta }^{-1}\left(b\right)\right),\theta \ge 1,\delta >0$ (17)

where $\eta \left(s\right)={\eta }_{\theta ,\delta }\left(s\right)=1-{\left[1-{\left(1+s\right)}^{-\frac{1}{\delta }}\right]}^{\frac{1}{\theta }}$

Copula density is given by

$c\left(a\mathrm{,}b\mathrm{<mo>\; ;\; </mo>}\theta \mathrm{<mo>\; ;\; </mo>}\delta \right)=\left(-\frac{1}{\theta }\right)\left(\frac{1}{\delta }-1\right)\cdot h^{\frac{1}{\theta }-1}dabh$ (18)

In BB7-copula the lower and upper tail dependence can range on each other from zero to anywhere freely.

2.3.3. Bivariate Dependence Measures

Pearson Correlation Coefficient

Pearson’s correlation which is also referred to as correlation coefficient or product moment correlation is a measure used widely in measuring linear correlation given two random variables. Correlation and dependence can be used interchangeably.

Definition Let ${\left(X\mathrm{,}Y\right)}^{\text{T}}$ to be a vector of random variables which have nonzero finite variances. Linear correlation coefficient can be defined as

$\rho \left(X\mathrm{,}Y\right)=\frac{Cov\left(X\mathrm{,}Y\right)}{\sqrt{Var\left(X\right)}\sqrt{Var\left(Y\right)}}$ (19)

The correlation coefficient properties (ρ) are

1). $\left|\rho \left(X\mathrm{,}Y\right)\right|\le 1$

2) X and Y being independent, then we have $\rho \left(X,Y\right)=0$ .

3) $\left|\rho \left(X\mathrm{,}Y\right)\right|=1$ if $\exists a$ and $b\ne 0$ such that $P\left(X=a+bY\right)=1$

4) $\rho \left(\alpha X+\beta Y\mathrm{,}\Upsilon Y+\delta \right)=sgn\left(\alpha \Upsilon \right)\rho \left(X\mathrm{,}Y\right)$

5) X and Y being joint bivariate normal distribution that have standard normal margins then we have, correlation coefficient $\rho$ being uniquely defined by the existing joint distribution.

Definition The correlation coefficient can be estimated using

$\hat{\rho }=\frac{{\displaystyle {\sum }_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_1-\bar{Y}\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(X_i-\bar{X}\right)}^2{\left(Y_1-\bar{Y}\right)}^2}}}$

Linear correlation is popular due to its ease in calculations but cannot be applied as a canonical dependence measure. It is commonly used in elliptical distributions.

Kendall’s tau

Kendall’s tau for a given vector, given ${\left(X\mathrm{,}Y\right)}^{\text{T}}$ is given by finding the probability of concordance in the pair of random variables minus the probability of discordance in the pair of random variables chosen in a population version which can expressed in the following definition by [7] [14] [15] .

Therefore, Kendall’s tau can simply be defined as the probability of concordance minus the probability of discordance.

Definition (Kendall’s τ) Let $\left(X_1\mathrm{,}{Y}_1\right)$ and $\left(X_2\mathrm{,}{Y}_2\right)$ be two pairs of independent random variables whose joint distribution, denoted as F and marginal distributions denoted as $F_X$ and $F_Y$ . Therefore Kendall’s tau can be illustrated by

$\begin{array}{c}{\rho }_{\tau }\left(X,Y\right)=P\left(X_1-X_2\right)\left(Y_1-Y_2\right)>0-P\left(X_1-X_2\right)\left(Y_1-Y_2\right)<0\\ =P\left(X_1<X_2,Y_1>Y_2\right)-P\left(X_1>X_2,Y_1<Y_2\right)\end{array}$ (20)

In the equation, $P\left(X_1-X_2\right)\left(Y_1-Y_2\right)>0$ ), is referred to as P (concordance), while, $P\left(X_1-X_2\right)\left(Y_1-Y_2\right)<0$ is P (discordance). Therefore, ${\rho }_{\tau }\left(X\mathrm{,}Y\right)=P\left(\text{concordance}\right)-P\left(\text{discordance}\right)$ .

An alternative definition making use of the mathematical expectation operator, expresses Kendall’s tau as

${\rho }_{\tau }\left(X\mathrm{,}Y\right)=E\left(sign\left(\left(X_1-X_2\right)\left(Y_1-Y_2\right)\right)\right)$ (21)

The empirical version of this expression is

$r_{\tau }\left(X_i,X_j\right)={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}{\displaystyle \underset{1\le t<s\le n}{\sum }}sign\left(X_{t,i}-X_{s,i}\right)\left(X_{t,j}-X_{s,j}\right)$ (22)

where we have $X_{t\mathrm{,}i}$ and $X_{t\mathrm{,}j}$ referring to the t-th observations in the two random vectors that have n observations.

Kendall’s tau can also be represented in terms of copula; the illustration is given as follows

${\rho }_{\tau }=4{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{1}C\left(u,v\right)\text{d}C\left(u,v\right)}}-1$ (23)

Theorem Kendall’s tau for a bivariate Archimedean copula C whose generator function is given by $\phi$ in one-dimensional integral can be written as [16]

$\tau =1+4{\displaystyle {\int }_0^1}\frac{{\phi }^{-1}\left(t\right)}{{\left({\phi }^{-1}\right)}^{\prime }\left(t\right)}\text{d}t$ (24)

2.4. Tail Dependence

Tail dependence concept is mostly applied in non-normal multivariate families, especially in financial applications. In a bivariate distribution, tail dependence can be represented by the probability of first variable exceeding its q-quantile, when the other also exceeds its own q-quantile. Upper tail dependence coefficient is the limiting probability as q goes to infinity, where we have the copula as the upper tail dependent given that it is not zero. The lower tail dependence is said to be analogously defined. The implication is that given two continuous random variables X and Y, then the tail dependence is a copula property and whose amount of tail dependence will be invariant given strict increasing transformations of X an Y [17] .

Definition (Tail dependence) Let ${\left(X\mathrm{,}Y\right)}^{\text{T}}$ to be a vector for continuous random variables whose marginal distribution functions denoted as F and G. The upper tail dependence coefficient ${\lambda }_U$ of ${\left(X\mathrm{,}Y\right)}^{\text{T}}$ is therefore the limit of the conditional probability for Y being greater than the a-th percentile for G given that we have X being greater than the a-th percentile for F as a approaches 1, i.e.

${\lambda }_A=\underset{a\nearrow 1}{\lim }P\left(Y\ge G_Y^{-1}\left(a\right)|X\ge F_X^{-1}\left(a\right)\right)$ (25)

provided that limit ${\lambda }_A\exists \mathrm{<mo>\; |\; </mo>0,1\; <mo>\; |\; </mo>}$ exists. If ${\lambda }_A\exists \mathrm{<mo>\; |\; </mo>0,1\; <mo>\; |\; </mo>}$ , X, Y are asymptotically dependent in upper tail; if ${\lambda }_A=0$ , X and Y are asymptotically independent in upper tail. Similarly the lower tail dependence, ${\lambda }_B$ .

${\lambda }_B=\underset{a\searrow 1}{\lim }P\left(Y\le G_Y^{-1}\left(a\right)|X\le F_X^{-1}\left(a\right)\right)$ (26)

Definition (Upper tail dependence for copulas)

The coefficient for upper tail dependence of the given bivariate copula family denoted as C is such that

${\lambda }_A=\underset{a\searrow }{lim}\frac{1-2a+C\left(a,a\right)}{1-a}$ (27)

Then C has a lower tail dependence if we have ${\lambda }_B\exists \left[\mathrm{0,1}\right]$ , and is lower tail dependence if ${\lambda }_B=0$ .

Coefficients of upper and lower tail dependence in bivariate margins are needed to show the difference in two-dimensional Student and Gaussian copulas.

Given X and Y are continuous random variables with Student-t copula, C and the parameters $\rho$ and $\nu$ , hence the coefficients of the two tail dependence are equal and they are given by:

${\gamma }_B\left(X,Y\right)={\gamma }_A\left(X,Y\right)=2t_{\nu +1}(-\sqrt{v+1}\sqrt{\frac{1-\rho }{1+\rho }}$

where we have $t_{\nu +1}$ denoting the univariate Student-t distribution function that has $\nu +1$ degrees of freedom and the value of $\lambda$ is seen to depend on parameters with Student-t-copula has both the lower and upper tail dependence.

In contrast, the Gaussian copula does not have the tail dependence at all; there is neither lower nor upper tail dependence. Hence the Gaussian copula which has parameter $\rho \in \left(-\mathrm{1,1}\right)$ , thus the tail dependence is given by

$\lambda =\underset{x\to \infty }{\lim }2\left(1-\Phi \left(\frac{x\sqrt{1-\rho }}{1+\rho }\right)\right)=0$

Therefore there is no tail dependence in the Gaussian copula.

Tail dependence in the Archimedean copulas can be expressed in form of generator function.

Theorem Let a strict generator be $\phi$ such that ${\phi }^{-1}$ is seen to belong in the class of Laplace transformation for random variables that are strictly positive. If ${\phi }^{-1}\left(0\right)$ being finite then we have

$C\left(a_1\mathrm{,}{a}_2\right)={\phi }^{-1}\left(\phi \left(a_1\right)+\phi \left(a_2\right)\right)$

The upper tail dependence does not exist. If copula C has upper tail dependence, ${\phi }^{-1}\left(0\right)=-\infty$ and the upper tail dependence coefficient is given by

${\lambda }_A=2-2\underset{s\searrow 0}{lim}\left(\frac{{\phi }^{-1}\left(2s\right)}{{\phi }^{-1}\left(s\right)}\right)\cdot$ (28)

The proof is seen in [7] [18] .

Theorem Letting $\phi$ as denoted in Theorem The lower tail dependence coefficient for copula $C\left(a_1\mathrm{,}{a}_2\right)={\phi }^{-1}\left(\phi \left(a_1\right)+\phi \left(a_2\right)\right)$ is equal to

${\lambda }_B=2-2\underset{s\to \infty }{lim}\left(\frac{{\phi }^{-1}\left(2s\right)}{{\phi }^{-1}\left(s\right)}\right)\cdot$ (29)

2.5. Copula Parameter Estimation

Full Maximum Likelihood (FML)

The representation of canonical copula is

$f\left(x_1\mathrm{,}\cdots \mathrm{,}{x}_n\right)=c\left(F_1\left(x_1\right)\mathrm{,}\cdots \mathrm{,}{F}_n\left(x_n\right)\right){\displaystyle {\prod }_{j\mathrm{<mo>\; =\; </mo>1}}^d{f}_j\left(x_j\right)}$ (30)

Let the sample data matrix be ${\left\{x_u,\cdots ,x_{nt}\right\}}_{t=1}^T$ . Then the log-likelihood function is given by

$l\left(\theta \right)={\displaystyle \underset{t=1}{\overset{T}{\sum }}}Inc\left(F_1\left(x_{1t}\right),\cdots ,F_n\left(x_{nt}\right)\right)+{\displaystyle \underset{t=1}{\overset{T}{\sum }}}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\ln f_j\left(x_{jt}\right)$ (31)

where the set of marginal parameters and the copula are given as $\theta$ . Therefore, with a copula and marginal density probability function set the maximum likelihood estimator is obtain through maximization

${\hat{\theta }}_{MLE}={\max }_{\theta }l\left(\theta \right)$ (32)

Holding the usual regulatory conditions, then the maximum likelihood estimator being asymptotically efficient and consistent, with the covariance matrix being asymptotically normally distributed given Fisher’s information matrix inverse [19] . Exact MLE computation is intensive in a high dimension case since the margin and copula parameters are jointly estimated.

2.6. Goodness of Fit Test Based on Kendall’s Tau

Hence goodness-of-fit measures gives a summary of discrepancy in expected and observed values in a given model. Mostly it is applied in hypothesis testing however in this case we test if the underlying copula data fits in a chosen copula.

$H_0:C\in L=\left\{C_{\theta }:\theta \in \Theta \right\}\text{vs}{H}_1:C\in L=\left\{C_{\theta }:\theta \in \Theta \right\}$

where $\Theta$ is a parameter space and L as the set of copulas. We apply Cramer-von Mises statistic as the test statistic, defined as

$S_n^{Cn}={\displaystyle {\int }_{|0,1|}}{C}_n^2\left(u\right)\text{d}{C}_n\left(u\right)$ (33)

where we have $U_1\mathrm{,}\cdots \mathrm{,}{U}_n$ being observations made from an unknown distribution.

$C_n\left(u\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}}1\left(U_{i1}\le u_1,\cdots ,U_{id}\le u_d\right)$ (34)

Given the indicator function as the empirical distribution, $u=\left(u_1,\cdots ,u_d\right)\in {\left[0,1\right]}^d$ , $1(\cdot )$ and $C_n=\sqrt{n}\left(C_n-C_{{\theta }_n}\right)$ . A rejection of H₀ is made if the statistic leads to large values.

Computing p-values based on test statistic in the empirical process required generating N as the large number of size n independent sample from $C_{{\theta }_n}$ and further computing the statistics corresponding values. $S_n^{Cn}$ test statistics depending on copula under H₀ with the parameter $\theta$ being unknown.

3. Main Results

3.1. Descriptive Statistics

From Table 1 the results showed that none of the crypto was normally distributed since Jarque-Bera statistics are statistically significant, and the data series are negatively skewed except for Bitcoin in addition the data also exhibit excess kurtosis. The summary statistics suggest that the probability distribution for Cryptocurrencies are negatively skewed indicating that left tails are bigger than the right tails except for Bitcoin which is positively skewed

Figure 1 shows that there is a medium to high correlation between the currencies. Interestingly, the currencies are positively correlated with each other. These currencies (Litecoin, Dogecoin and Bitcoin) have a very strong correlation. First, Litecoin has a positive fairly strong correlation with Bitcoin namely Bitcoin (0.63). Second, Dogecoin has a positive very strong correlation with Binance coin, namely, Binance (0.82). Third, Bitcoin has a positive strong correlation with Binance (0.85). Therefore from the results there is no stable cryptocurrency.

3.2. Testing for ARCH Effects

The Box-Ljung test is used to test for the existence of ARCH effects using the squared residuals from the fitted mean equation. The tests null hypothesis is that there are no ARCH effects, while the alternative hypothesis is that there are ARCH effects. Since the p-value’s are less than 0.05, ARCH effects are present in the four Cryptocurrencies. Thus we reject the null hypothesis that there are no ARCH effects as indicated in Table 2. This provides evidence of presence of conditional heteroscedasticity in the mean of cryptocurrencies (Bitcoin, Binance, Litecoin and Dogecoin) returns hence GARCH model that accounts for volatility needs to be employed in modeling Binance, Litecoin, Dogecoin and Bitcoin.

3.3. Selection of the GARCH Models

We observe that the standard GARCH specification of order (1,1) under the highly flexible ARMA-GARCH model is appropriate to identify the true patterns

Table 1. Descriptive statistics.

Table 2. Box-Lyung test for ARCH effects.

Figure 1. Correlation matrix.

of the studied index returns, Table 3. And having a well specified marginal model is central to robust copula construction.

3.4. Copula Parameter Estimation

After obtaining standardized residuals from the different specifications of GARCH models, next step was to model the marginals distribution using copula. Since our interest is on dependence structure between Litecoin, Dogecoin and Binance coin prices and Bitcoin prices, we consider the following currency prices pairs; Binance - Bitcoin, Litecoin - Bitcoin and Dogecoin - Bitcoin and we estimate copula model parameters. The best fit copula parameter was determined using AIC, BIC and the log likelihood function.

Table 3. Selected sGARCH Models.

3.4.1. Copula Parameters Binance - Bitcoin Prices

Table 4 presents a summary of BB8 copula parameters. The BB8 provides the best fit since it has the lowest AIC and BIC. The bivariate BB8 copula has two parameters.

3.4.2. Copula Parameters Dogecoin - Bitcoin Prices

Table 5 presents a summary of BB8 copula parameters. The BB8 provides the best fit since it has the lowest AIC and BIC. The bivariate BB8 copula has two parameters.

3.4.3. Copula Parameters Litecoin - Bitcoin Prices

Table 6 presents a summary of BB1 copula parameters. The BB8 provides the best fit since it has the lowest AIC and BIC. The bivariate BB1 copula has two parameters.

3.5. Dependence

Tail Dependence

Tables 4-6 also report the estimated tail dependence coefficients of BB8 and BB1 copulas. The results indicate that for all the studied pairs of returns, the tail dependence parameters, ${\tau }_u$ and ${\tau }_l$ of the BB1 copulas are statistically significant, suggesting that the dependence at the lower and upper tails is symmetric. The results also show that the pair Litecoin and Bitcoin has the highest tail dependence among the the selected cryptocurrencies, this implies that change in prices of Litecoin will influence the prices of Bitcoin and vice versa is true. There was no tail dependence is detected for the pair Binance and Bitcoin, and Dogecoin and Bitcoin. The BB1 copula is the most suitable to describe the dependence structure in the cryptocurrencies.

3.6. Optimization of Cryptocurrency Portfolio

The optimization process produces 24 different portfolios and displays the optimal portfolio investment, which was constructed by maximizing the Sharpe ratio (Figure 2 and Figure 3). The optimal coin portfolio shows a Sharpe ratio of 0.101. These portfolios are optimal as they locate at the efficient frontier. This observation confirms the assumption of the Markowitz model that allocating assets to a portfolio reduces the overall risk compared to the individual risk of these related assets. The optimization process results into a mean of 0.70% and a volatility of 10.38% for the optimal coin portfolio. Further, the maximized return

Table 4. Copula parameter estimation Binance - Bitcoin.

Table 5. Copula parameter estimation Dogecoin - Bitcoin.

Table 6. Copula parameter estimation Litecoin - Bitcoin.

Figure 2. Coin efficient frontier.

portfolios comprise the full invested (i.e. 100%) of Dogecoin portfolio. However, the maximized return portfolio will not serve as a benchmark portfolio in this analysis. The diversification effect of constructing portfolios of cryptocurrencies, in this case coins significantly reduces risk irrespective of significant correlation among the cryptocurrencies chosen in this analysis.

3.7. Discussion

Exploratory data analysis was first carried out on cryptocurrencies to verify their properties of returns such as normality. It was found that the returns were heavily tailed and negatively skewed except for Bitcoin with presence of ARCH

Figure 3. Portfolio optimization plot.

effects which was examine by using by Ljung box test. sGARCH(1,1) was selected with different specifications where AIC was used to select the most viable GARCH(1,1) model for each cryptocurrency returns. The standardized residuals were used to estimate the marginal distribution for each series. The results showed that BB8 and BB1 copula provides the best fit for the combinations of Litecoin, Binance and Dogecoin and Bitcoin return. Copula GARCH was used to model dependence structure between Litecoin, Binance and Dogecoin returns and Bitcoin returns, where BB1 copula was found to be the most appropriate for examining the dependence between the cryptocurrencies. Optimization of the cryptocurrencies showed that Dogecoin have the best optimization and investing on this coin significantly reduces risk irrespective of significant correlation among Litecoin, Bitcoin and Binance.

4. Conclusions and Suggestions

Cryptocurrencies has attracted a lot of attention to digital market investor and currently there more than 50 cryptocurrencies are actively traded in the market. Economists, financial analysts and investors have focused largely on Bitcoin since it accounts for more than 60% market capitalization. Currently the market knowledge points to the fact that Bitcoin is the most preferred asset in optimization of a portfolio. The study focuses on modelling cryptocurrencies, investigating the currency dependencies and determining an optimal portfolio. Cryptocurrencies are high-risk assets; however, an optimal portfolio eliminates high-risk. The study showed that, standard GARCH of order (1,1) under highly flexible ARMA-GARCH model is the most appropriate model in modelling the cryptocurrency prices and can identify the true pattern of index returns. Cryptocurrency in the market is also highly dependent as Bitcoin, Binance coin, Dogecoin and Litecoin were correlated. Litecoin and Bitcoin have a higher tail dependence and this implied that a change in prices of Litecoin will affect the prices of Bitcoin and vice versa. On optimizing a portfolio composed of cryptocurrencies that is more than necessary for potential investment decisions, Dogecoin has the best optimization. The research contributes to the literature on modelling cryptocurrencies and estimating risk management.

The author of this paper invites scientific community to perform a similar study as this one by considering Bayesian copula Garch which allows model to be data driven and compare the findings.

Acknowledgements

Sincere thanks to my supervisors Dr. Anthony Ngunyi and Dr. Joseph K Mungatu for their professional guidance and performance, and special thanks to my wife and parents for their moral support and rare attitude of high quality.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Rose, C. (2015) The Evolution of Digital Currencies: Bitcoin, a Cryptocurrency Causing a Monetary Revolution. International Business & Economics Research Journal, 14, 617-622. https://doi.org/10.19030/iber.v14i4.9353
[2]	Bhosale, J. and Mavale, S. (2018) Volatility of Select Crypto-Currencies: A Comparison of Bitcoin, Ethereum and Litecoin. Annual Research Journal of SCMS Pune, 6.
[3]	Ali, R., Barrdear, J., Clews, R. and Southgate, J. (2014) Innovations in Payment Technologies and the Emergence of Digital Currencies. Bank of England Quarterly Bulletin.
[4]	Durante, F. and Sempi, C. (2016) Principles of Copula Theory. CRC Press, Boca Raton. https://doi.org/10.1201/b18674
[5]	Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica: Journal of the Econometric Society, 50, 987-1007. https://doi.org/10.2307/1912773
[6]	Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307-327. https://doi.org/10.1016/0304-4076(86)90063-1
[7]	Embrechts, P., Lindskog, F. and McNeil, A. (2001) Modelling Dependence with Copulas. Rapport Technique, Département de mathématiques, Institut Fédéral de Technologie de Zurich.
[8]	Glosten, L.R., Jagannathan, R. and Runkle, D.E. (1993) On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance, 48, 1779-1801. https://doi.org/10.1111/j.1540-6261.1993.tb05128.x
[9]	Nelson, D.B. and Cao, C.Q. (1992) Inequality Constraints in the Univariate Garch Model. Journal of Business & Economic Statistics, 10, 229-235. https://doi.org/10.1080/07350015.1992.10509902
[10]	Sklar, A. (1973) Random Variables, Joint Distribution Functions, and Copulas. Kybernetika, 9, 449-460.
[11]	Ruschendorf, L. (2009) On the Distributional Transform, Sklar’S Theorem, and the Empirical Copula Process. Journal of Statistical Planning and Inference, 139, 3921-3927. https://doi.org/10.1016/j.jspi.2009.05.030
[12]	Nelsen, R.B. (2002) Concordance and Copulas: A Survey. In: Cuadras, C.M., Fortiana, J. and Rodriguez-Lallena, J.A., Eds., Distributions with Given Marginals and Statistical Modelling, Springer, Dordrecht, 169-177. https://doi.org/10.1007/978-94-017-0061-0_18
[13]	Joe, H. (2014) Dependence Modeling with Copulas. CRC Press, New York. https://doi.org/10.1201/b17116
[14]	Lindskog, F., McNeil, A. and Schmock, U. (2003) Kendall’s Tau for Elliptical Distributions. In: Bol, G., Nakhaeizadeh, G., Rachev, S.T., Ridder, T. and Vollmer, K.H., Eds., Credit Risk, Physica-Verlag Heidelberg Publisher, Berlin, 149-156. https://doi.org/10.1007/978-3-642-59365-9_8
[15]	McNeil, A.J., Neslehova, J.G. and Smith, A.D. (2020) On Mixtures of Extremal Copulas and Attainability of Concordance Signatures. arXiv e-prints, Pages arXiv-2009.
[16]	Genest, C. and MacKay, J. (1986) The Joy of Copulas: Bivariate Distributions with Uniform Marginals. The American Statistician, 40, 280-283. https://doi.org/10.1080/00031305.1986.10475414
[17]	Schmidt, R. (2005) Tail dependence. In: Čížek, P., Weron, R. and Härdle, W., Eds., Statistical Tools for Finance and Insurance, Springer, Berlin, 65-91. https://doi.org/10.1007/3-540-27395-6_3
[18]	Embrechts, P., Hofert, M. and Wang, R. (2016) Bernoulli and Tail-Dependence Compatibility. The Annals of Applied Probability, 26, 1636-1658. https://doi.org/10.1214/15-AAP1128
[19]	Cherubini, U., Mulinacci, S., Gobbi, F. and Romagnoli, S. (2011) Dynamic Copula Methods in Finance. John Wiley & Sons, New York. https://doi.org/10.1002/9781118467404